Genomic BLUP Decoded: A Look into the Black Box of Genomic Prediction

Abstract

Genomic best linear unbiased prediction (BLUP) is a statistical method that uses relationships between individuals calculated from single-nucleotide polymorphisms (SNPs) to capture relationships at quantitative trait loci (QTL). We show that genomic BLUP exploits not only linkage disequilibrium (LD) and additive-genetic relationships, but also cosegregation to capture relationships at QTL. Simulations were used to study the contributions of those types of information to accuracy of genomic estimated breeding values (GEBVs), their persistence over generations without retraining, and their effect on the correlation of GEBVs within families. We show that accuracy of GEBVs based on additive-genetic relationships can decline with increasing training data size and speculate that modeling polygenic effects via pedigree relationships jointly with genomic breeding values using Bayesian methods may prevent that decline. Cosegregation information from half sibs contributes little to accuracy of GEBVs in current dairy cattle breeding schemes but from full sibs it contributes considerably to accuracy within family in corn breeding. Cosegregation information also declines with increasing training data size, and its persistence over generations is lower than that of LD, suggesting the need to model LD and cosegregation explicitly. The correlation between GEBVs within families depends largely on additive-genetic relationship information, which is determined by the effective number of SNPs and training data size. As genomic BLUP cannot capture short-range LD information well, we recommend Bayesian methods with t-distributed priors.

GENOMIC best linear unbiased prediction (BLUP) is a statistical method that has been used to predict height in humans (Yang et al. 2010) and breeding values for selection in animal and plant breeding (VanRaden 2008). It uses a so-called genomic relationship matrix that describes genetic relationships between individuals calculated from genotypes at single-nucleotide polymorphisms (SNPs). In genomic selection applications (Meuwissen et al. 2001), those individuals comprise both training individuals that are phenotyped for a quantitative trait and genotyped at SNPs and selection candidates that are genotyped only.

Genomic BLUP differs from the traditional pedigree BLUP (Henderson 1975) in the replacement of the pedigree relationship matrix with a genomic relationship matrix. Coefficients of the pedigree relationship matrix describe additive-genetic relationships (Malécot 1948) between individuals at quantitative trait loci (QTL) conditional on pedigree information, but it is not obvious to what extent the genomic relationship matrix explains genetic covariances between individuals at QTL. Despite this, several authors called the genomic relationship matrix the actual (Hill and Weir 2011) or realized relationship matrix (Goddard 2009; Hayes et al. 2009b; Lee et al. 2010) as it describes identity-by-descent at SNPs (Hayes et al. 2009b), assuming an ancient founder population. However, these terms are misleading because only genetic relationships at QTL matter in quantitative-genetic analyses.

To understand better how genomic relationships capture relationships at QTL, we propose to apply concepts of pedigree analyses that define founders in a recent past generation. Based on these concepts, we show that coefficients of the genomic relationship matrix do not explain genetic covariances between individuals at QTL unless either there is linkage disequilibrium (LD) between QTL and SNPs measured in founders or selection candidates are related by pedigree to the training individuals. The latter results in cosegregation of alleles at QTL and SNPs that are linked, also known as linkage information, and in additive-genetic relationships at QTL captured by SNPs. These three types of information affect differently the persistence of accuracy of genomic estimated breeding values (GEBVs) from BLUP over generations (Habier et al. 2007), realized selection intensities, and inbreeding. The contributions of these parameters to accuracy of GEBVs depending on training data size, extent of LD, and mating design have not been demonstrated; a better understanding will allow us to optimize statistical models, training data, and selection strategies.

LD observed in the training data were first believed to be the only source of information until Habier et al. (2007) and Gianola et al. (2009) demonstrated that SNP genotypes also capture pedigree relationships. Habier et al. (2007) partitioned the observed accuracy of GEBVs into a part due to LD in the training data and a remainder due to pedigree relationships. Accuracy due to LD is the component of accuracy that persists over generations without retraining and provides the accuracy for individuals that are unrelated to the training individuals. Compared to Bayesian methods with t-distributed priors (Meuwissen et al. 2001), accuracy due to LD tends to be lower with genomic BLUP (Habier et al. 2007, 2010a, 2011).

Goddard (2009) presented formulas for calculating the accuracy due to LD, but derivations assume that the markers completely capture the variability at the QTL. Nevertheless, that accuracy was calculated as a function of the effective number of chromosomal segments, which was estimated only from effective population size and genome length. Real data analyses have shown that accuracy due to LD varies for quantitative traits with similar heritability (Habier et al. 2010a, 2011), and thus different genetic architectures cannot be described by those and similar formulas (Daetwyler et al. 2008, 2010). Also, modeling pedigree relationships between training individuals and selection candidates is not straightforward if only LD parameters are used to explain accuracy.

Cosegregation is traditionally exploited in linkage analyses. The advantage of cosegregation information is the ability to explain both rare allelic variants and structural variations if they segregate within families. Several authors (Goddard 2009; Hayes et al. 2009b; Habier et al. 2010a; Goddard et al. 2011) assumed it is utilized in genomic BLUP, but that has never been formally proven in the presence of LD and pedigree relationships or quantified. A statistical method that explicitly models both LD and cosegregation was proposed for genomic selection (Calus et al. 2008), but it did not outperform a Bayesian method similar to BayesA (Meuwissen et al. 2001). The question remains, how much cosegregation is captured implicitly by genomic BLUP compared to methods that model LD and cosegregation explicitly (e.g., Meuwissen et al. 2002; Fernando 2003; Pérez-Enciso 2003; Legarra and Fernando 2009)?

This article has two objectives: (1) to present concepts that allow us to disentangle LD, cosegregation, and additive-genetic relationships and (2) to study the contributions of these parameters to accuracy of GEBVs depending on SNP density, training data size, and extent of LD. Dairy cattle and corn breeding scenarios were simulated to evaluate accuracy of GEBVs both within and across families obtained by different types of information, discrepancy between accuracy of GEBVs due to additive-genetic relationships and accuracy of traditional pedigree-based selection indexes, persistence of accuracy due to LD and due to cosegregation from one generation to the next without retraining, and the effect of each type of information on the correlation of GEBVs within families. Accuracies within families for the case of linkage equilibrium between QTL and SNPs were used to demonstrate unambiguously that genomic BLUP captures cosegregation, as there are no additive-genetic relationships within family. In addition, formulas for the covariance between true and estimated breeding values were derived for a simplified scenario to prove that all three sources of information are utilized by genomic BLUP.

Theory

Genetic model

Trait phenotypes of training individuals are simulated by the assumed true genetic model

$$y=1\mu +Wa+e$$ (1)

(Goddard 2009; Hayes et al. 2009b: Goddard et al. 2011), where y, a, and e are vectors containing trait phenotypes, additive QTL effects, and residual effects, respectively; μ is the overall mean; and W is a matrix of genotype scores at biallelic QTL. Each score is coded as the number of one of the two alleles at a locus adjusted by twice the frequency of the counted allele in founders. Both QTL and residual effects are treated as random with mean zero and with variance–covariance matrices $I{\sigma }_a^2$ and $I{\sigma }_e^2$, respectively. The aim of the following statistical analysis is to use y for estimating the true breeding value of an individual i given by $g_i=w_i^{\prime }a$, where $w_i^{\prime }$ contains QTL genotype scores.

Statistical model

Phenotypes generated by the genetic model are used in

$$y=1\mu +g+\epsilon ,$$ (2)

where g and ε are vectors containing breeding values and residual effects, respectively. Breeding values in g are random with mean zero and variance–covariance matrix $G{\sigma }_{\beta }^2$, where G = ZZ′, Z is a matrix of genotype scores at K SNPs (VanRaden 2008), ${\sigma }_{\beta }^2={\sigma }_A^2/2{\displaystyle {\sum }_{k=1}^K{p}_k\left(1-p_k\right)}$ (Habier et al. 2007), ${\sigma }_A^2={\sigma }_a^2{\displaystyle {\sum }_{q=1}^{N_{qtl}}2p_q\left(1-p_q\right)}$ is the additive-genetic variance (Gianola et al. 2009, Equation 18), ${\sigma }_a^2$ is the variance of additive QTL effects with mean zero, p_q is the allele frequency at QTL q in founders, and p_k is the allele frequency at SNP k in founders. The genotype score of a training individual at SNP k is the number of one of its alleles adjusted by 2p_k. Residual effects have mean zero and variance $I{\sigma }_{\epsilon }^2$.

Statistical methods

Following Henderson (1973), the breeding value of individual i can be estimated by BLUP as

$${\widehat{g}}_i=G_{i-}{\left(G+I\lambda \right)}^{-1}\left(y-1\widehat{\mu }\right),$$

where $G_{i-}=z_i^{\prime }{Z}^{\prime }$ is a vector of genomic relationships between individual i and the training individuals, $z_i^{\prime }$ is a vector of adjusted SNP genotype scores of individual i, and $\lambda ={\sigma }_{\epsilon }^2/{\sigma }_{\beta }^2$. The overall mean, μ, is estimated by generalized least squares.

The three types of quantitative-genetic information

In pedigree analyses that model LD and cosegregation explicitly (e.g., Pérez-Enciso 2003), genotype scores are realized values of random processes that start with the sampling of founder alleles and continue with the transmission of those alleles from generation to generation down the pedigree. Founder alleles from different loci, but on the same gamete, are not sampled independently if loci are in LD; and nonfounder alleles from different loci, but on the same gamete, are not transmitted independently if loci are linked. We define the following:

• Linkage disequilibrium: Statistical dependency between alleles at two or more loci on the same gamete. It is measured only in founders and therefore summarizes historic population events and describes genetic relationships between founders.

• Cosegregation: Deviation from independent segregation of alleles on the same gamete if loci are linked. In other words, it describes the inheritance of alleles at linked loci. Thus, it is unnecessary to measure LD either in nonfounder generations or within families, because such LD is sufficiently explained by LD in founders and cosegregation.

• Additive-genetic relationships: Statistical dependency between alleles from the same locus but from two different gametes. In genomic BLUP, any SNP can contribute additive-genetic relationship information between two individuals at QTL because, if there is a possibility that the SNP alleles on the two gametes can be traced back to a common founder allele, the same would be true at any QTL.

In pedigree analyses, these principles used to model dependence between allele states at different loci on a gamete are analogous to those used to model additive-genetic covariances between pedigree members, using a single additive-genetic variance defined in the founders together with the additive-genetic relationship matrix constructed for the pedigree. In many analyses, however, the pedigree is ignored and only a single value of LD is used to characterize the dependence between alleles at different loci. In modeling covariances, this is analogous to ignoring the pedigree and estimating a single additive-genetic variance for the entire pedigree, which is not done in practice. In other situations, LD is defined for each family. This is analogous to defining a family-specific additive-genetic variance, which also is not done.

Simulations

The aim was to study contributions of LD, cosegregation, and additive-genetic relationships to accuracy of GEBVs in dairy cattle and corn breeding scenarios. Factors analyzed were SNP density, training data size, extent of LD, and different relationships between training and validation individuals.

Designs for analyzing different types of information

Four designs were considered that differ in the types of genetic information utilized in genomic BLUP. As summarized in Table 1, these designs utilized (1) only founder LD (LD only), (2) only additive-genetic relationships (RS) (RS only), (3) additive-genetic relationships and cosegregation (CS) (RS + CS), and (4) all three sources of information (RS + CS + LD). In LD only, training and validation individuals were unrelated, whereas in all other cases each validation individual had the same number of relatives in training. In RS only, QTL were located on different chromosomes than SNPs to avoid linkage between these two types of loci, and chromosomes carrying the QTL were simulated independently from the chromosomes with SNPs to exclude LD between QTL and SNPs. In designs with cosegregation or LD, all loci were located on the same chromosomes to ensure linkage. In the RS + CS design, QTL and SNPs were in linkage equilibrium by resampling founder alleles at QTL, using founder allele frequencies. Importantly, SNPs were always in LD, because this has a large effect on capturing information from additive-genetic relationships and cosegregation. In RS + CS + LD, QTL and SNPs were in LD.

Table 1. Simulated designs that differ in the quantitative-genetic information available for genomic prediction.

	QTL and SNPs are
Design	Linked	In LDa	SNPs are in LDa	Relatedb
LD only	Yes	Yes	Yes	No
RS only	No	No	Yes	Yes
RS + CS	Yes	No	Yes	Yes
RS + CS + LD	Yes	Yes	Yes	Yes

^aLD measured in founders.

^bTraining and validation individuals are related.

Pedigree structure

Two types of pedigrees were simulated as summarized in Table 2: one represents a cross-validation scenario from dairy cattle breeding, and the other one is a top-cross design (Falconer and Mackay 1996, p. 276) from corn breeding similar to those in Albrecht et al. (2011). The dairy cattle pedigree consisted of 14, 143, or 285 families, each having 7 half sibs in training and 10 in validation. Hence, each validation individual had 7 half sibs in training. In the LD-only design, none of the validation individuals was related to the training individuals, while the half-sib structure in training was retained to capture the same LD information as in the other information designs. The total numbers of training individuals were 98, 1001, and 1995, according to the number of half-sib families in the pedigree.

Table 2. Dairy cattle and corn breeding scenarios simulated in combination with short- and long-range LD, the four information designs, various SNP densities, and 20 QTL per chromosome.

Pedigree type	No. chromosomes	h2	Family type	Family size in traininga	Scenario	No. families	Training size	No. replicates
Dairy cattle	29	0.5	Half sibs	7	1	14	98	750
					2	143	1001	300
					3	285	1995	75
Corn	10	0.33	Full sibs	30	4	15	450	1000
					5	60	1800	200

^aCorresponds to the number of relatives of a validation individual in training.

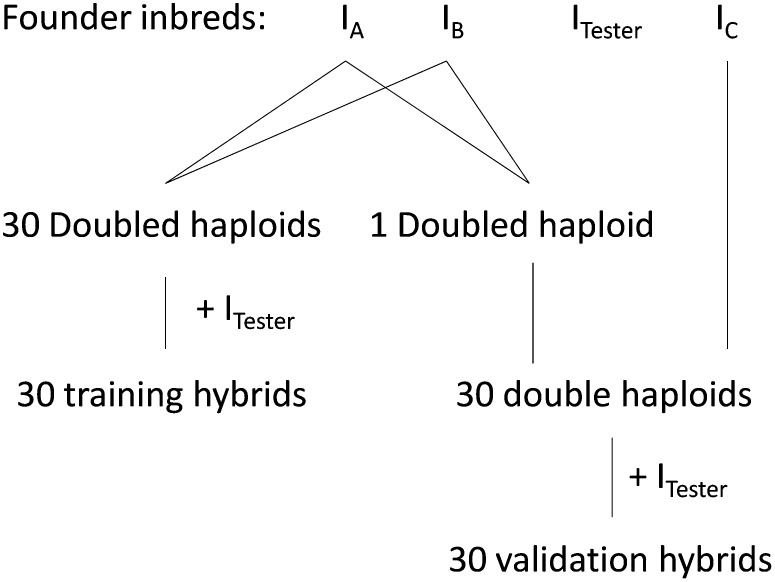
The corn breeding pedigree consisted of either 15 or 60 families, each having 60 doubled haploids (Bernardo 2010) that descended from two inbred parents. Each doubled haploid was crossed to a single inbred called tester (Bernardo 2010) that is used across all families to generate hybrids. Half of the hybrids were used for training and the other half for validation, so that each validation hybrid had 30 closely related hybrids in training. In the LD-only design, training and validation hybrids were unrelated. In total, the training set consisted of either 450 or 1800 hybrids depending on the number of families simulated (Table 2). Persistence of LD and cosegregation information without retraining was evaluated by simulating validation hybrids that were derived from the next generation of doubled-haploid families (Figure 1). These doubled haploids were the grand-progeny of the original inbred parents, where one parent was a founder, while the other parent was a full sib of those doubled haploids that had training hybrids. A family of the next generation had 30 doubled haploids, each having one validation hybrid, where the tester was the same in both generations.

Figure 1.

Top-cross design showing one of the families used in cross-validations with training hybrids descending from the first generation of doubled haploids and validation hybrids descending from the next generation of doubled haploids. Both training and validation hybrids come from the same inbred tester, I_Tester.

Genome structure

The number of chromosomes, their length, and the number of SNPs per chromosome differed for the two types of pedigrees. These data were provided by DuPont Pioneer for maize and by the US Department of Agriculture (USDA) for dairy cattle (G. Wiggans, personal communication) as presented in Supporting Information, File S2 and File S3, respectively. The ten Zea mays chromosomes with 55,843 SNPs were used in the corn breeding scenario, and the 29 bovine autosomes with 47,833 SNPs were used in the dairy cattle scenario. SNPs were evenly spaced and 200 QTL were randomly positioned on each chromosome in addition to the SNPs.

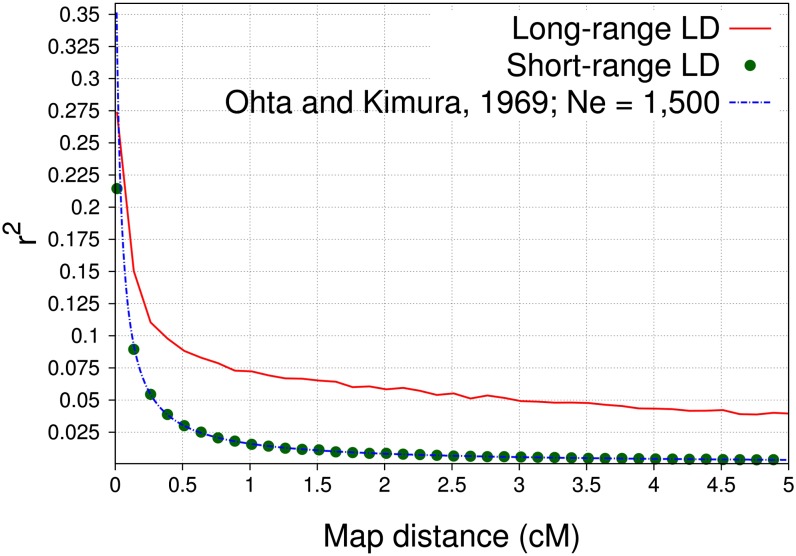
LD was simulated by starting with a base population of 1500 individuals in linkage and Hardy–Weinberg equilibria and allele frequencies of 0.5. As outlined in Table 3, this population was randomly mated, excluding selfing, for 1000 discrete generations to generate short-range LD due to genetic drift between biallelic loci. Afterward, the population was reduced to a size of 100 individuals and randomly mated for another 15 discrete generations to extend the range of LD. The same simulation scheme was used by Habier et al. (2010b), showing good agreement between simulated LD and LD observed in real dairy cattle populations (De Roos et al. 2008). Simulations using short-range LD were generated by omitting the last 15 generations with 100 individuals. For comparisons of accuracies from the pedigree-based selection index with accuracies of GEBVs due to additive-genetic relationships, founders of simulated pedigrees were not allowed to be closely related. Therefore, in the scenario with long-range LD (short-range LD) the 100 (1500) individuals from generation 1015 (1000) were randomly mated to create 10,000 offspring, which were then randomly mated for another 2 discrete generations, while retaining a constant population size (Table 3). Founders of pedigrees used to simulate training and validation individuals were drawn without replacement from the last generation of 10,000 individuals. The number of crossovers in meiosis was simulated by a binomial mapping function with mean of 1 crossover per morgan (Karlin 1984), crossover positions were uniform, and the mutation rate was 2.5 × 10⁻⁵ as in other simulations (Habier et al. 2007, 2009; Daetwyler et al. 2010; Calus and Veerkamp 2011; Bastiaansen et al. 2012). The average LD between adjacent SNPs in the scenarios long-range LD and short-range LD was 0.21 and 0.15, respectively, and LD between QTL and SNPs is depicted in Figure 2.

Table 3. Number of generations of random mating and population size used to generate short-range and long-range LD.

Short-range LD		Long-range LD
Generation	Size	Generation	Size
1	1,500	1	1,500
1,000	1,500	1,000	1,500
1,001	10,000	1,001	100
1,003 (founders)	10,000	1,015	100
		1,016	10,000
		1,018 (founders)	10,000

Figure 2.

Linkage disequilibrium between QTL and SNPs measured as r² against map distance in centimorgans for the two scenarios long-range and short-range LD and using formulas by Ohta and Kimura (1969) with an effective population size of 1500.

SNP density was varied by sampling a subset of SNPs for each analysis from the total number of available SNPs, where the number of SNPs per chromosome was proportional to chromosome length as shown in File S2 and File S3. In the corn breeding designs, 195, 996, 4995, 9995, 19,995, and 39,996 SNPs were used in the statistical analysis, while in the dairy cattle designs 564, 2885, 14,483, 28,984, 43,483, and 47,831 SNPs were used. From the 200 QTL that were initially positioned on each chromosome, only 20 were randomly selected in each replicate and effects were sampled from a standard normal distribution. These QTL effects were standardized such that the additive-genetic variance was 1 in founders of the dairy cattle pedigrees and 2 in inbred founders of the corn breeding pedigrees.

Phenotypes

Phenotypes of training individuals followed the genetic model of Equation 1, where the residual effects were sampled from a standard normal distribution. Consequently, heritability was 0.5 in cattle scenarios, whereas only one-third of the variance of hybrid phenotypes was due to additive-genetic effects as a result of the single tester.

Evaluation criteria:

Accuracy of GEBVs was defined as correlation between GEBVs and true breeding values of validation individuals and was estimated both within and across families. Across families means that one correlation was calculated using validation individuals from all families, whereas within families means that a correlation was calculated for each family. These accuracies were calculated for each replicate of the simulation and averaged across replicates. Accuracy of the pedigree-based selection index (pedigree index) was calculated for the dairy cattle scenario by

$${\rho }_{g_i,{\widehat{I}}_i}=0.5\sqrt{\frac{n}{n+(4-h^2)/h^2}}$$

(Mrode 2005, p. 9), where n is the number of half sibs of validation individual i in training, and h² is the heritability. Another criterion of interest regarding the avoidance of inbreeding and improving selection intensities in breeding schemes is the correlation between GEBVs of selection candidates from the same family, ${\rho }_{{\widehat{g}}_i{\widehat{g}}_{i^{\prime }}}$ (Hill 1976). It can be estimated by the intraclass correlation (Snedecor and Cochran 1967) with

$${\widehat{\rho }}_{{\widehat{g}}_i{\widehat{g}}_{i\prime }}=\frac{{\sigma }_{\text{b}}^2}{{\sigma }_{\text{b}}^2+{\sigma }_{\text{w}}^2},$$

where ${\sigma }_{\text{b}}^2$ and ${\sigma }_{\text{w}}^2$ are variances between and within families, respectively, estimated by a one-way ANOVA (Snedecor and Cochran 1967). This intraclass correlation is used here to determine the role of additive-genetic relationships in the presence of LD and cosegregation as detailed in Discussion.

Results

Dairy cattle pedigree

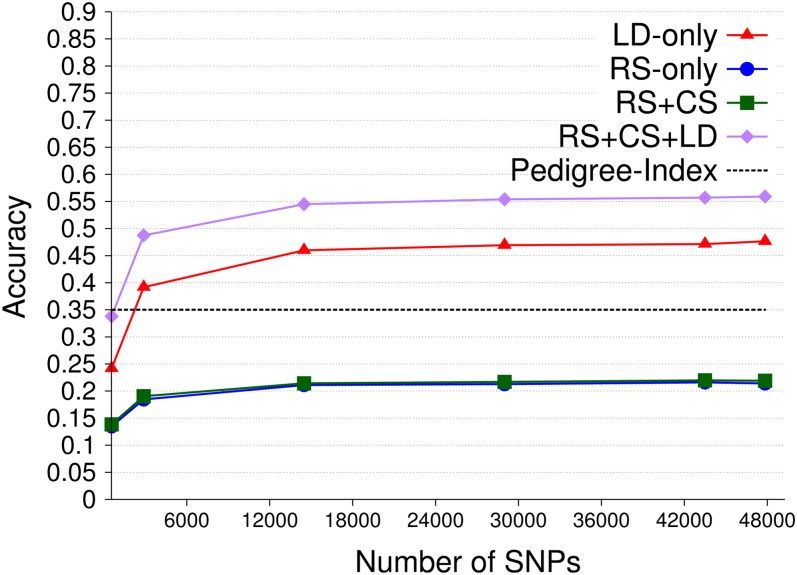
Accuracies of GEBVs across families obtained with long-range LD and 1001 training individuals are shown in Figure 3. Accuracies increased with SNP density and reached plateaus in all four information designs, where those of RS only and RS + CS plateaued at a lower SNP density than those of LD only and RS + CS + LD. Even at the highest SNP density, accuracy for RS only was 0.14 (±0.002), lower than that for the pedigree index. Cosegregation information contributed only little to accuracy, both across (RS + CS) and within half-sib families (results not shown). With LD, genomic BLUP outperformed pedigree index with an accuracy of 0.56 (±0.002) when each validation individual had seven half sibs in training (RS + CS + LD), while the accuracy for an unrelated validation individual was 0.09 (±0.002) lower (LD only). Figure 4A depicts accuracies of GEBVs with increasing training set size obtained with long-range LD and 47,831 SNPs. As expected, accuracy due to LD increased with training set size (LD only), but accuracy due to additive-genetic relationships declined (RS only), thereby increasing the discrepancy to accuracy of pedigree index. Similarly, cosegregation contributes less with increasing training set size, both across (Figure 4A, RS + CS) and within families (results not shown). As a result, the difference in accuracy for validation individuals that were either related or unrelated to the training data decreased from 0.21 (±0.005) to 0.05 (±0.003) (LD only vs. RS + CS + LD). Accuracies from LD only were lower for short-range LD than those for long-range LD, while those from RS only and RS + CS were higher (Figure 4B vs. 4A).

Figure 3.

Accuracy of GEBVs obtained by genomic BLUP, long-range LD, and 47,831 SNPs for the four information designs and accuracy of pedigree index using 1001 training individuals structured into 143 half-sib families and a heritability of 0.5. Each validation individual had 7 half sibs in training in all designs but LD only. The number of replicates was 300.

Figure 4.

(A and B) Accuracy of GEBVs and standard errors obtained by genomic BLUP and 47,831 SNPs for the four information designs according to training data size and extent of LD and accuracy of pedigree index using a heritability of 0.5. Training data were structured into half-sib families of size seven, and each validation individual had seven half sibs in training in all designs but LD only. The numbers of replicates for training data sizes 98, 1001, and 1995 were 750, 300, and 75, respectively.

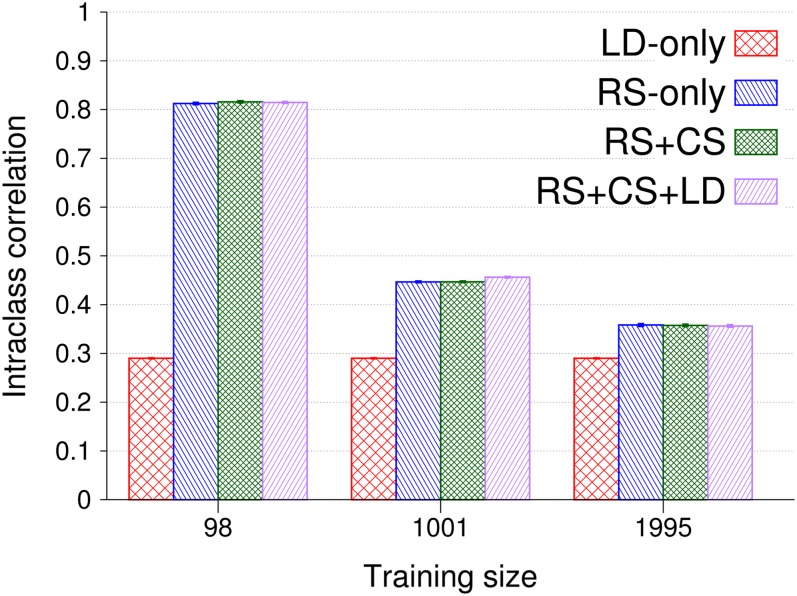
Intraclass correlations were 0.25 (±0.002) at low SNP density, increased with increasing SNP density (results not shown), and quickly plateaued at values shown in Figure 5 for different training set sizes and information designs using long-range LD. In general, a low intraclass correlation is favorable in mass selection for low inbreeding and high realized selection intensities. For LD only, intraclass correlations were 0.29 (±0.002) across all training set sizes, but when training and validation individuals were related, they decreased with increasing training set size irrespective of LD and cosegregation from 0.81 (±0.002) to 0.37 (±0.002). Thus, intraclass correlations were very similar at a given training set size for the information designs RS only, RS + CS, and RS + CS + LD. The explanation is that the variance of GEBVs both within and between families increased with LD and cosegregation information.

Figure 5.

Intraclass correlations and standard errors for GEBVs within half-sib families obtained by genomic BLUP, long-range LD, and 47,831 SNPs according to training data size and information design. Training data were structured into half-sib families of size seven, and each validation individual had seven half sibs in training in all designs but LD only. The numbers of replicates for training data sizes 98, 1001, and 1995 were 750, 300, and 75, respectively.

Corn breeding pedigree

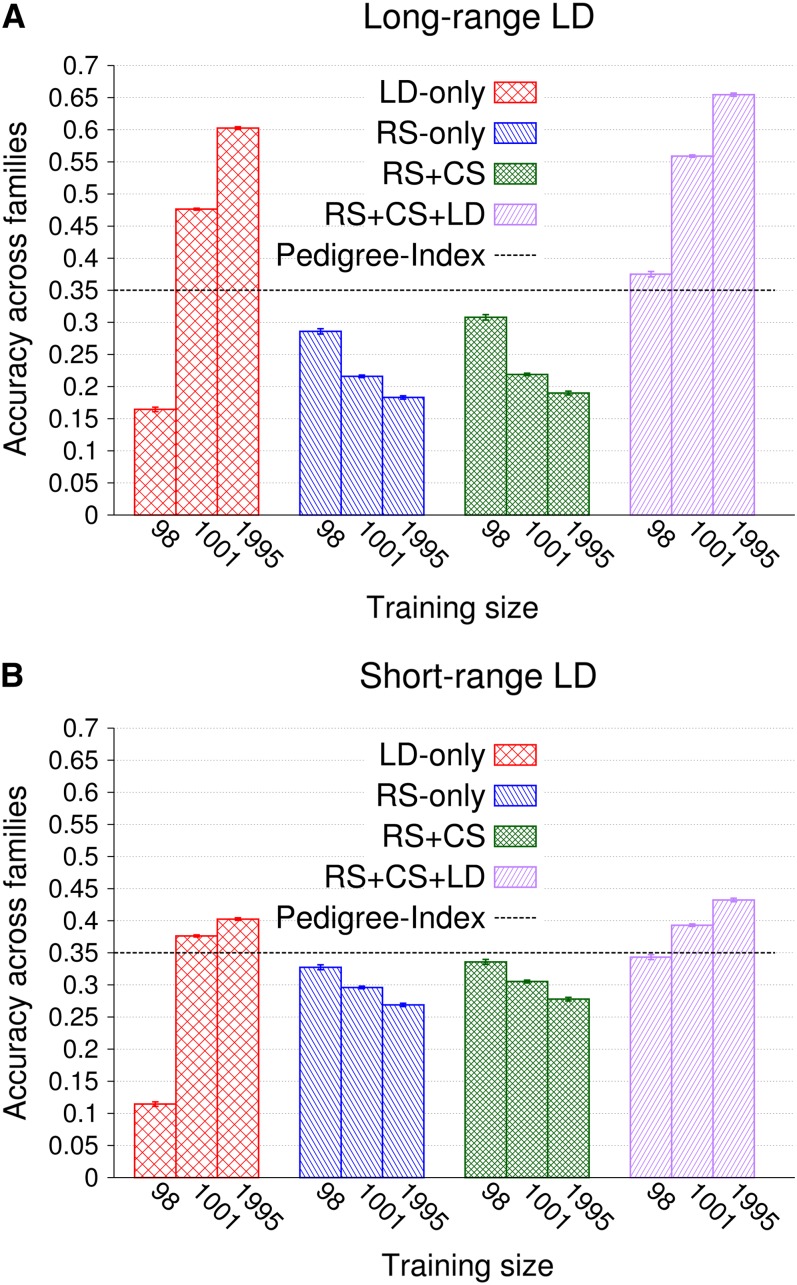
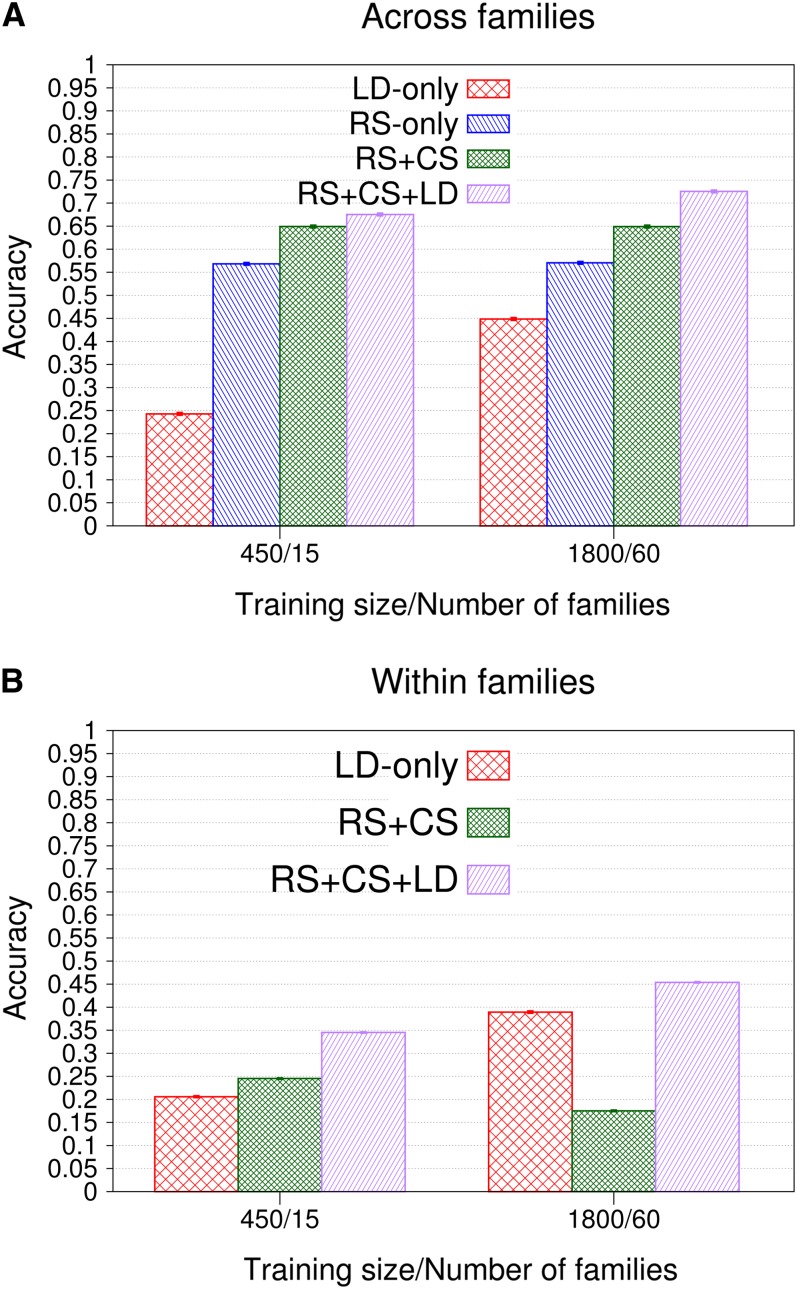
Accuracies of GEBVs within and across families increased with SNP density and plateaued at different levels, depending on information utilized. In designs with LD, plateaus were reached at higher SNP densities than in RS only and RS + CS, especially as training set size increased (results not shown). Figure 6A depicts accuracies of GEBVs across families obtained with long-range LD and 39,996 SNPs for 15 and 60 doubled-haploid families used in cross-validations. Accuracies were much higher for validation individuals that were related to the training data (LD only vs. other designs), because 30 related training hybrids per validation individual provided extensive additive-genetic relationships, resulting in an accuracy of 0.56 (±0.003) for RS only. Cosegregation information increased that accuracy considerably by 0.09 (±0.004), while LD added only little more (RS only vs. RS + CS and RS + CS vs. RS + CS + LD). As training set size increased from 450 to 1800 hybrids, accuracies of LD only and RS + CS + LD increased by 0.2 (±0.003) and 0.05 (±0.003), respectively, whereas those of RS only and RS + CS remained constant (Figure 6A). Accuracies within families are depicted in Figure 6B for all information designs but RS only, because additive-genetic relationships explain no variation of GEBVs within families. For 15 families, cosegregation provided more information than LD (RS + CS vs. LD only). The difference between the designs LD only and RS + CS + LD shows the contribution of cosegregation in the presence of LD, which was 0.15 (±0.003). As training set size increased, more LD information and less cosegregation information were exploited, so that accuracies of LD only and RS + CS + LD increased by 0.19 (±0.003) and 0.11 (±0.002), respectively, while the accuracy of RS + CS decreased by 0.07 (±0.002). Consequently, the contribution of cosegregation in the presence of LD decreased by 0.09 (±0.002) to 0.06 (±0.002) (LD only vs. RS + CS + LD).

Figure 6.

(A and B) Accuracy of GEBVs and standard errors within and across families obtained by genomic BLUP, long-range LD, and 39,991 SNPs for the four information designs using 450 and 1800 training hybrids structured into families of size 30. Each validation hybrid had 30 related hybrids in training in all designs but LD only. The numbers of replicates for training data sizes 450 and 1800 were 1000 and 200, respectively.

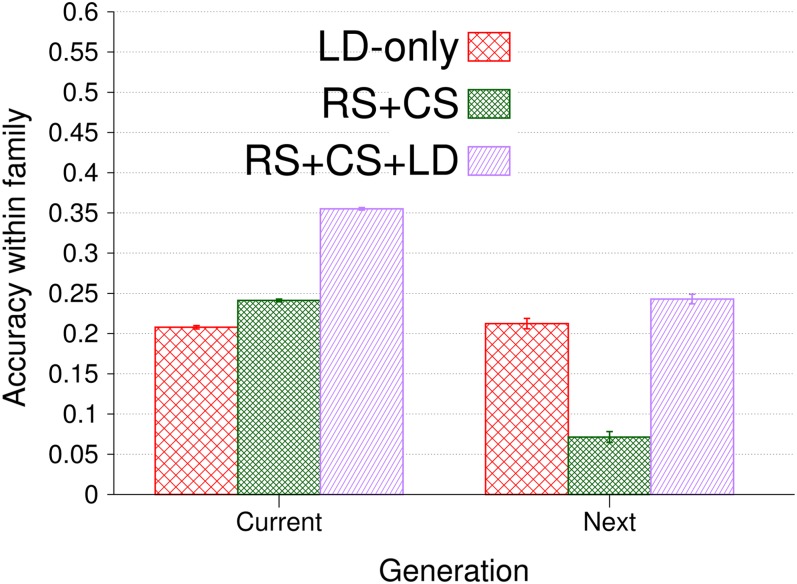
Figure 7 depicts accuracies within families for validation hybrids of both the same generation as the 450 training hybrids and the next generation. Accuracy of LD only remained constant from one generation to the next, whereas the accuracies of RS + CS and RS + CS + LD dropped by 0.17 (±0.007) and 0.11 (±0.006), respectively, due to the decline of cosegregation information.

Figure 7.

Accuracy of GEBVs and standard errors within families obtained by genomic BLUP, long-range LD, and 39,991 SNPs for validation hybrids of the same (current) and following (next) generation and for the designs LD only, RS + CS, and RS + CS + LD, using 450 training hybrids. Each validation hybrid had 30 related hybrids in training in all designs but LD only. The number of replicates was 1000.

Discussion

The objectives of this article were (1) to present concepts that allow us to disentangle LD in founders, cosegregation, and additive-genetic relationships and (2) to study their contributions to accuracy of GEBVs by simulation of four designs that differ in the types of information available (Table 1). In addition, formulas were derived in File S1 and File S4 for a simplified scenario proving that the three types of information contribute to accuracy of GEBVs. In the following, mechanisms that lead to the results are elaborated and then consequences for practical application of genomic BLUP are discussed.

Concepts and simulation designs

The concepts presented here can be applied to any statistical method. As for all pedigree analyses, contributions attributed to the three types of information depend on pedigree depth. Generally, cosegregation is expected to become more important as pedigree depth increases, but this requires further investigations. Here, the pedigree consisted of only one nonfounder generation in training, which allowed us to evaluate cosegregation information from half- and full-sib families. If the pedigree had more nonfounder generations in training, cosegregation would also comprise information from more distant relatives. Thus, a better understanding can be gained by varying pedigree depth.

The LD-only design is a realistic scenario, whereas RS only and RS + CS seem contrived. However, RS only always occurs in reality when a SNP on one chromosome explains variation at a QTL on another chromosome that is not explained by LD and cosegregation. Also, intraclass correlations have shown that the findings from RS only are relevant for realistic scenarios, which are detailed later. As for RS + CS, LD patterns vary across the genome; hence there may be QTL that are in low LD with SNPs.

Information from LD

In the LD-only design, extent and amount of LD determine both SNP density at which the plateau is reached (Figure 3) and accuracy of GEBVs at the plateau (Figure 4A vs. 4B). For short-range LD as in humans (Reich et al. 2001) that SNP density is expected to be higher and accuracy to be lower than for long-range LD found in animals and plants under selection (Andreescu et al. 2007). The reason is that with increasing SNP density the shrinkage of SNP effects in genomic BLUP becomes stronger. An extreme case was described by Fernando et al. (2007) in which loci were in linkage equilibrium, but QTL were included together with SNPs in genomic BLUP and BayesB (Meuwissen et al. 2001). While BayesB found the QTL and provided high accuracies, the accuracies of genomic BLUP decreased with increasing SNP density until approaching the accuracy of pedigree BLUP. This does not happen under realistic conditions, because with increasing SNP density more SNPs support the same QTL and compensate shrinkage, which results in a balance expressed by the accuracy at the plateau. Under long-range LD, QTL effects are captured by more SNPs than with short-range LD, so that shrinkage has a smaller impact. Even if QTL are included in the statistical model for genomic BLUP, accuracy of GEBVs obtained under short-range LD did not change for training data sizes used in this study. In humans, training data sizes are much larger, but also millions of SNPs that affect shrinkage are used. Therefore, as the amount of LD information is responsible for missing heritability in humans (Yang et al. 2010), we argue that Bayesian methods with t-distributed priors, which are expected to exploit LD better than genomic BLUP (Fernando et al. 2007; Habier et al. 2007, 2010a, 2011), are more suitable than genomic BLUP. This disagrees with results from Ober et al. (2012), but that study used only 124 training individuals.

Information from additive-genetic relationships and cosegregation

It can be shown that additive-genetic relationships are captured best when SNPs are in linkage equilibrium, segregate independently, and have a minor allele frequency of 0.5. These SNPs are referred here to as ideal SNPs. In Habier et al. (2007, 2010a), the accuracy of GEBVs due to additive-genetic relationships obtained by genomic BLUP approached the accuracy of pedigree BLUP when the number of simulated ideal SNPs exceeded the number of training individuals. In reality, however, SNPs are in LD, linked on a limited number of chromosomes, and the average minor allele frequency is <0.5. Thus, the actual number of SNPs in the model is not informative about the ability to explain additive-genetic relationships. Therefore, we define the effective number of SNPs (M_SNP) as the number of ideal SNPs that gives the same accuracy due to additive-genetic relationships as the actual number of SNPs in the model for a given cross-validation scenario. The effective number of SNPs was estimated here by additional simulations of the RS-only design, using only ideal SNPs. For accuracies of 0.22 and 0.3 obtained with long-range and short-range LD (Figure 4, A and B, RS only), respectively, using 1001 training individuals and 47,831 actual SNPs, M_SNP was ∼2000 for long-range LD and 6000 for short-range LD. Thus, M_SNP decreases with increasing range of LD and therefore depends on effective population size. Also, M_SNP is smaller than the number of SNPs on high-density SNP chips, which explains why the accuracy due to additive-genetic relationships did not improve beyond a certain SNP density (Figure 3). Cosegregation is also captured best when SNPs are in linkage equilibrium and have high minor allele frequencies, because each family can have most distinctive SNP haplotypes around QTL. With increasing range of LD, however, SNP haplotypes become similar across families, so that the ability to capture cosegregation decreases.

Information with increasing training data size

The increase in accuracy due to LD with training data size is well known, whereas the decrease in accuracy of GEBVs due to additive-genetic relationships in the dairy cattle design is new. This decrease is related to the effective number of SNPs and the level of additive-genetic relationships between individuals. In RS only, consider the genomic relationship matrix as an estimate of the pedigree relationship matrix (Habier et al. 2007; Gianola et al. 2009). Deviations between the coefficients of these two matrices cause the linear combinations of phenotypes for estimating GEBVs to become inaccurate. For example, phenotypes of training individuals that are unrelated to the validation individual contribute to the GEBV of a validation individual in genomic BLUP. As training data size increases, more erroneous contributions occur. The decay of accuracy with increasing training data size was lower with short-range LD than with long-range LD, because the effective number of SNPs was larger under short-range LD, resulting in smaller deviations between those two matrices. In the corn breeding scenarios, accuracies due to additive-genetic relationships did not decrease with increasing training data size (Figure 6) because the level of pedigree relationships was higher than in dairy cattle designs; with a higher level, the importance of inaccurately weighted phenotypes relative to the phenotypes of related training individuals becomes smaller.

In practice, decreasing information from additive-genetic relationships may result in a smaller increase of accuracy observed with real data or even a decay if LD information cannot compensate for that loss. This can be suspected from results of Habier et al. (2011), because the increase in accuracy due to LD from 4000–6500 training bulls was small. Also, combining training data from different breeds (Hayes et al. 2009a) may risk a reduction in accuracy due to additive-genetic relationships. In contrast, if training data sets from the same breed but different breeding regions are combined, accuracy due to additive-genetic relationships can increase if individuals are closely related as for example in dairy cattle (Lund et al. 2011). The decline in accuracy due to additive-genetic relationships with increasing training data size may be avoided by simultaneously fitting polygenic effects via traditional pedigree relationships together with genomic breeding values using Bayesian methods (Calus and Veerkamp 2007). This simultaneous inference of effects is necessary because the partitioning of the genetic variance into polygenic and genomic components depends on training data size.

Cosegregation information decreased with increasing training data size (Figure 6) for similar reasons to those described for additive-genetic relationships: genomic relationships estimate covariances between individuals at QTL, where deviations from true covariances result in prediction errors of GEBVs. Modeling LD and cosegregation explicitly may avoid this decline in accuracy due to cosegregation. Also, multiallelic markers such as copy number variants, which are available from sequence data, may enhance utilization of additive-genetic relationships and cosegregation.

Contributions to accuracy of GEBVs

The four information designs allowed us to evaluate the maximal contribution of LD, cosegregation, and additive-genetic relationships. The level of accuracy due to LD depends on genome structure (Figure 4) and hardly on the number of QTL (Daetwyler et al. 2010). However, this may not be misinterpreted such that genetic architecture does not affect the accuracy due to LD. Results of Habier et al. (2010a, 2011) showed that even traits with similar heritability, such as fat and protein yield, can have very different accuracies due to LD. One explanation is that QTL of different traits are in different LD with SNPs, because the genome consists of long- and short-range LD patterns (Qanbari et al. 2010). However, the difference in accuracy between those two traits was even larger with BayesA and BayesB (Habier et al. 2011), which have different shrinkage mechanisms than genomic BLUP. Thus, an explanation may be epistasis.

Accuracy due to additive-genetic relationships and cosegregation can be regarded as lower bounds if accuracy due to LD is small as for somatic cell score in dairy cattle (Habier et al. 2011). However, that accuracy depends largely on the number of close relatives in training such as parents and siblings; for more distant relatives, the effective number of SNPs may not be sufficient. This may be an emerging problem in dairy cattle, because information from parents and siblings will not be available anymore due to accelerated selection cycles by genomic selection. In dairy cattle, cosegregation from half sibs plays a minor role, because selection candidates have a limited number of half sibs in training (Habier et al. 2010a), a few selection candidates have only one or two full sibs, and parents do not provide cosegregation information. Additionally, the number of half-sib families is large, which is unfavorable for capturing cosegregation (Figure 4). In plants, a top-cross design provides extensive additive-genetic relationship information to the accuracy across families due to many training hybrids that are related to a validation hybrid. For the same reasons, cosegregation contributes notably to the accuracy within family. Therefore, if LD information does not increase further with training data size, large full- or half-sib families can be generated for training to exploit cosegregation information.

Correlation between GEBVs within family

Intraclass correlations were evaluated to estimate correlations between GEBVs within half-sib families, which give additional insight into the use of additive-genetic relationships in the presence of LD and cosegregation. There are at least two notions: the accuracy of GEBVs is either (1) due to LD plus a remainder due to additive-genetic relationships and cosegregation (LD only vs. RS + CS + LD) or (2) due to additive-genetic relationships plus a remainder due to LD and cosegregation (RS only vs. RS + CS + LD). If accuracy due to LD is high, the first notion, which was suggested by Habier et al. (2007), can underestimate the importance of additive-genetic relationships captured by SNPs for genomic prediction as demonstrated by the intraclass correlations. These were similar for all information designs in which validation individuals were related to the training data despite LD and cosegregation information and decreased with increasing training data size (Figure 5). Thus, the correlation of GEBVs within families depends mostly on additive-genetic relationships captured by SNPs, and therefore they are similarly important for realized selection intensities and expected inbreeding in genomic selection with and without cosegregation and LD information.

Persistence of LD and cosegregation information

Persistence of accuracy across generations without retraining is an important criterion in genomic selection. Results of the corn breeding scenarios showed that LD is more persistent than cosegregation from a single full-sib family (Figure 7). Thus, the decay of accuracy within families for individuals from the first few generations after training may be due to the decay of cosegregation information caused by recombinations of haplotypes surrounding QTL (Figure 7, RS + CS + LD). The surprisingly large decay of cosegregation information may indicate that cosegregation was explained by rather large chromosome segments. However, if the training data contain multigeneration families, persistence of cosegregation information might be different. As capturing additive-genetic relationships becomes more difficult with decreasing genetic relatedness between training and validation individuals when training data size is large, capturing cosegregation may be even more difficult. This also suggests modeling LD and cosegregation explicitly (e.g., Calus et al. 2008) if LD information is captured at least as well as with BayesA and BayesB.

Conclusions

We showed that genomic BLUP exploits LD, cosegregation, and additive-genetic relationships captured by SNPs in analyses that explicitly define LD and cosegregation information. We demonstrated that additive-genetic relationship information can decline with increasing training data size, depending on extent of LD and level of additive-genetic relationships. This suggests that polygenic effects should be modeled jointly with either SNP effects or genomic breeding values by a pedigree relationship matrix using Bayesian methods. The correlation of genomic estimated breeding values within families—an important parameter in breeding schemes—depends largely on additive-genetic relationship information, which is determined by the effective number of SNPs and training data size. Little cosegregation information comes from half sibs in current dairy cattle breeding designs, but cosegregation information from full sibs can contribute considerably to accuracy within families in corn breeding. However, its persistence is lower than that of LD information because cosegregation information declines quickly with increasing training data size and over generations without retraining. Thus, LD and cosegregation should be modeled explicitly. As genomic BLUP is not suitable to capture LD information in genome regions in which LD decays rapidly with map distance, we recommend Bayesian methods with t-distributed priors.