Estimating Variable Effective Population Sizes from Multiple Genomes: A Sequentially Markov Conditional Sampling Distribution Approach

Abstract

Throughout history, the population size of modern humans has varied considerably due to changes in environment, culture, and technology. More accurate estimates of population size changes, and when they occurred, should provide a clearer picture of human colonization history and help remove confounding effects from natural selection inference. Demography influences the pattern of genetic variation in a population, and thus genomic data of multiple individuals sampled from one or more present-day populations contain valuable information about the past demographic history. Recently, Li and Durbin developed a coalescent-based hidden Markov model, called the pairwise sequentially Markovian coalescent (PSMC), for a pair of chromosomes (or one diploid individual) to estimate past population sizes. This is an efficient, useful approach, but its accuracy in the very recent past is hampered by the fact that, because of the small sample size, only few coalescence events occur in that period. Multiple genomes from the same population contain more information about the recent past, but are also more computationally challenging to study jointly in a coalescent framework. Here, we present a new coalescent-based method that can efficiently infer population size changes from multiple genomes, providing access to a new store of information about the recent past. Our work generalizes the recently developed sequentially Markov conditional sampling distribution framework, which provides an accurate approximation of the probability of observing a newly sampled haplotype given a set of previously sampled haplotypes. Simulation results demonstrate that we can accurately reconstruct the true population histories, with a significant improvement over the PSMC in the recent past. We apply our method, called diCal, to the genomes of multiple human individuals of European and African ancestry to obtain a detailed population size change history during recent times.

WITH the rise of new sequencing technologies, it has become easier to obtain genetic data from multiple individuals at many loci. Such data have been providing a new wealth of information from which to estimate population genetic parameters such as mutation rates, recombination rates, effective population sizes, divergence times, and migration rates. More data should enable more accurate parameter estimation, but it is both theoretically and computationally challenging to model the evolution of many individuals.

Much can be learned about ancient population history from present-day DNA data, since the genome of each individual is an imperfect mosaic of the genomes of its ancestors. Accurately inferring the past demographic changes of humans has several important applications, including properly accounting for population structure in association studies and reducing confounding effects in inferences about natural selection. It may also help to resolve archaeological and historical questions. Humans are not the only organism for which demography raises important questions. For example, the demography of Drosophila has very interesting dynamics, as investigated by several recent studies (Haddrill et al. 2005; Thornton and Andolfatto 2006; Wang and Hey 2010).

In humans, ancient effective population size estimates vary widely, as do the time estimates of demographic events such as the out-of-Africa migration. Gronau et al. (2011) used a coalescent-based approach with six diploid genomes each from a different population and estimated that Eurasians and Africans diverged ∼38–64 thousand years ago (KYA) and that the effective population size of humans in the ancient past was ∼9000. Gravel et al. (2011) used low-coverage whole-genome data and high-coverage exome data to fit a one-bottleneck model followed by exponential growth in European and Asian populations. They estimated that the timing of the out-of-Africa migration was ∼51 KYA and that the effective population size in the ancient past was ∼7300, which then increased to ∼14,500 at ∼150 KYA.

In their analysis, Gronau et al. considered 37,574 loci each of length 1 kb and, for computational tractability, assumed that the loci are all independent and that there is no recombination within each locus. The method employed by Gravel et al. (2011) is based on fitting allele frequency spectra, assuming that all sites are independent. Incidentally, Myers et al. (2008) investigated the limits of inferring population size changes from the allele frequency spectrum alone and showed that two distinct population size histories may yield exactly the same expected allele frequency spectra. It remains an open question whether taking linkage information into account may remedy the problem of nonidentifiability.

The distribution of lengths of shared identity-by-descent (IBD) tracts between pairs of unrelated individuals is informative of recent demographic history. Recently, Palamara et al. (2012) utilized the empirical distribution of IBD sharing in pairs of 500 Ashkenazi Jewish individuals to infer two rapid population expansions separated by a severe founder event over the past 200 generations. This approach requires first inferring IBD tracts from data, but the accuracy of existing IBD detection methods has not been fully characterized when the population under consideration has undergone a complex demographic history.

The pairwise sequentially Markovian coalescent (PSMC), recently developed by Li and Durbin (2011) to estimate an arbitrary piecewise constant population size history, does take linkage information into account and efficiently models recombination between sites, using the sequentially Markov coalescent (McVean and Cardin 2005; Marjoram and Wall 2006) for a pair of sequences. The PSMC is based on a hidden Markov model (HMM) in which the hidden state at a given position corresponds to the coalescence time of the two lineages at that position and the observed state corresponds to the observed genotype (homozygous/heterozygous) at the position. As one moves along the sequence, the coalescence time may change as a result of recombination, and the spatial distribution of homozygous and heterozygous sites is informative of the distribution of coalescence times, which depends on the past population sizes. While this elegant approach produces reasonably accurate population size estimates overall, its accuracy in the very recent past is hampered by the fact that, because of the small sample size, few coalescence events occur in that period. As a consequence, the information in the pattern of genetic variation for a pair of sequences is insufficient to resolve very recent demographic history.

The major obstacle to generalizing the PSMC to multiple sequences is the explosion in the state space with the number of sequences; the number of distinct coalescent tree topologies grows superexponentially with the number of leaves, and we furthermore need to consider edge-weighted trees (i.e., include time information). In a related line of research, interesting progress has been made (Hobolth et al. 2007; Dutheil et al. 2009; Mailund et al. 2011) in performing “ancestral population genomic” inference under a coalescent HMM, but its applicability is limited to only a modest number of sequences, again due to the explosion in the state space.

In this article, we describe an alternative method that is efficient in the number of sequences, while retaining the key generality of the PSMC in incorporating an arbitrary piecewise constant population size history. More precisely, the computational complexity of our method depends quadratically on the number of sequences, and the computation involved can be easily parallelized. As more sequences are considered, we expect to see a larger number of coalescence events during the recent past and should be able to estimate recent population sizes at a higher resolution. With only two sequences, the distribution of coalescence events is shifted toward the ancient past, relative to the distribution of the time a new lineage joins a coalescent tree for multiple sequences. Thus, even if all sequences are considered pairwise, the resolution in the recent past may not be as clear as that achieved by jointly modeling multiple sequences.

The input to our method, which is also based on an HMM, is a collection of haplotype sequences. At present, our method assumes that mutation and recombination rates are given, and it employs the expectation-maximization (EM) algorithm to infer a piecewise constant history of population sizes, with an arbitrary number of change points.

Our work generalizes the recently developed sequentially Markov conditional sampling distribution (SMCSD) framework (Paul et al. 2011) to incorporate variable population size. This approach provides an accurate approximation of the probability of observing a newly sampled haplotype given a set of previously sampled haplotypes, and it allows one to approximate the joint probability of an arbitrary number of haplotypes. Through a simulation study, we demonstrate that we can accurately reconstruct the true population histories, with a significant improvement over the PSMC in the recent past. Moreover, we apply our method to the genomes of multiple human individuals of European and African ancestry to obtain a detailed population size change history during recent times. Our software, called demographic inference using composite approximate likelihood (diCal), is publicly available at https://sourceforge.net/projects/dical.

Notation and a Review of the SMCSD Framework

Our work stems from the SMCSD framework (Paul et al. 2011), which describes the conditional genealogical process of a newly sampled haplotype given a set of previously sampled haplotypes. In what follows, we briefly review the key concepts underlying the SMCSD model.

We consider haplotypes each of length L from the same genomic region. Suppose we have already observed n haplotypes, $\mathcal{O}$_n = {h₁, … , h_n} sampled at random from a well-mixed population; note that some of the observed haplotypes may be identical. In this article, we use the terms “sites” and “loci” interchangeably. Recombination may occur between any pair of consecutive loci, and we denote the set of potential recombination breakpoints by B = {(1, 2), … ,(L − 1, L)}. Given a haplotype h, we denote by h[ℓ] the allele at locus ℓ and by h[ℓ: ℓ′] (for ℓ ≤ ℓ′) the subsequence (h[ℓ], … , h[ℓ′]).

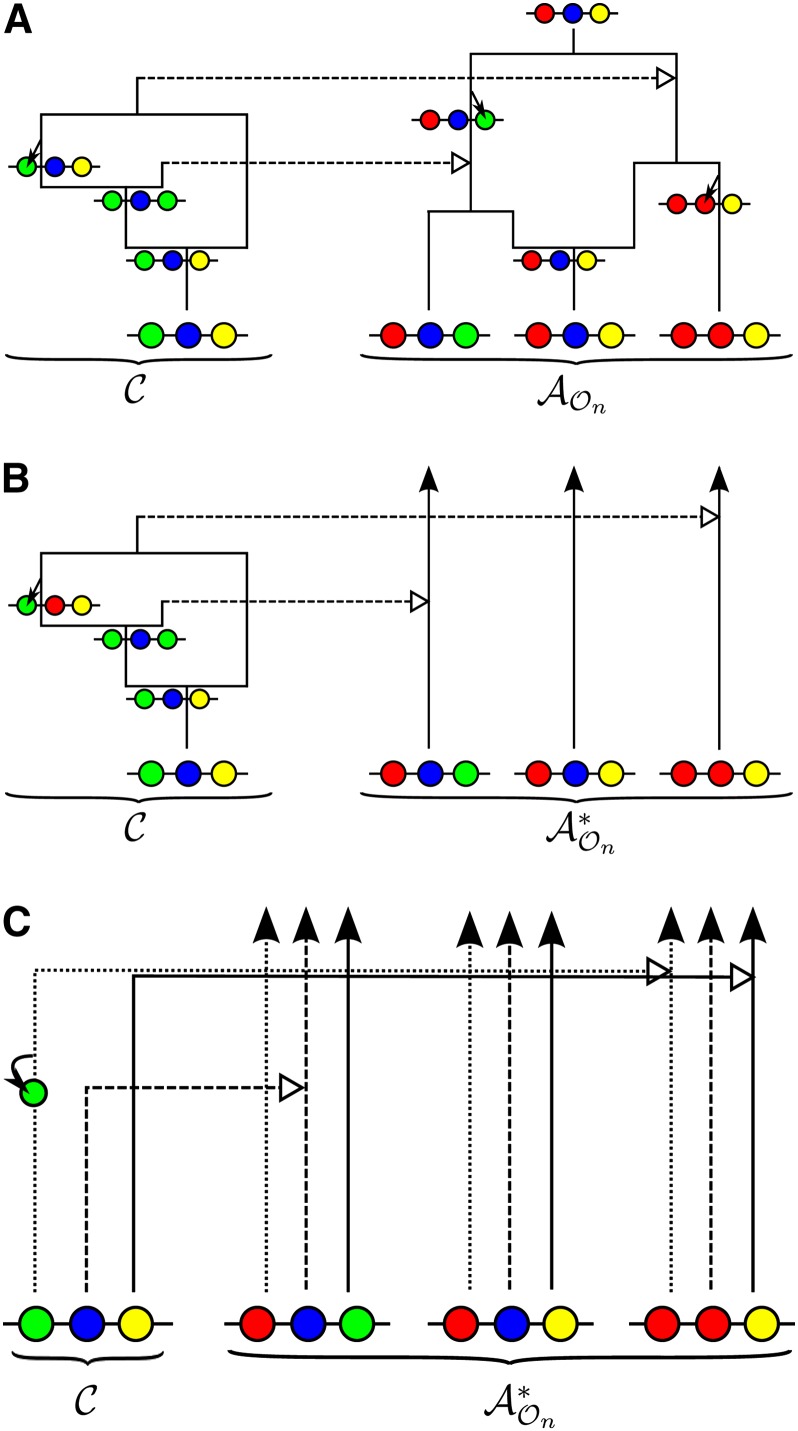
As described in Paul and Song (2010), given the genealogy ${\mathcal{A}}_{{\mathcal{O}}_n}$ for the already observed sample $\mathcal{O}$_n, it is possible to sample a conditional genealogy $\mathcal{C}$ for the additional haplotype according to the following description: An ancestral lineage in $\mathcal{C}$ undergoes mutation at locus ℓ at rate θ_ℓ/2 according to the stochastic mutation transition matrix P^(ℓ). Further, as in the ordinary coalescent with recombination, an ancestral lineage in $\mathcal{C}$ undergoes recombination at breakpoint b ∈ B at rate ρ_b/2, giving rise to two lineages. Each pair of lineages within $\mathcal{C}$ coalesces with rate 1, and lineages in $\mathcal{C}$ get absorbed into the known genealogy ${\mathcal{A}}_{{\mathcal{O}}_n}$ at rate 1 for each pair of lineages. See Figure 1A for an illustration.

Figure 1.

Illustration of a conditional genealogy $\mathcal{C}$ for a three-locus model. The three loci of a haplotype are each represented by a solid circle, with the color indicating the allelic type at that locus. Mutation events, along with the locus and resulting haplotype, are indicated by small arrows. Recombination events, and the resulting haplotype, are indicated by branching events. Absorption events are indicated by dotted horizontal lines. (A) The true genealogy ${\mathcal{A}}_{{\mathcal{O}}_n}$ for the already observed sample $\mathcal{O}$_n. (B) Approximation by the trunk genealogy ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$. Lineages in the trunk do not mutate, recombine, or coalesce. (C) Marginal conditional genealogy for each locus.

Unfortunately, we do not generally have access to the true genealogy ${\mathcal{A}}_{{\mathcal{O}}_n}$, and marginalizing over all possibilities is a challenging problem. However, Paul and Song (2010) showed that the diffusion-generator approximation described in De Iorio and Griffiths (2004a,b; Griffiths et al. 2008) implies the following approximation to ${\mathcal{A}}_{{\mathcal{O}}_n}$, which simplifies the problem considerably.

Approximation 1 (the trunk genealogy)

Approximate ${\mathcal{A}}_{{\mathcal{O}}_n}$ by the so-called trunk genealogy ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$ in which lineages do not mutate, recombine, or coalesce with one another, but instead form a nonrandom “trunk” extending infinitely into the past, as illustrated in Figure 1B. Although ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$ is not a proper genealogy, it is still possible to sample a well-defined conditional genealogy $\mathcal{C}$ for the additional haplotype given ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$ in much the same way as described above, except that rates need to be modified. Specifically, lineages within $\mathcal{C}$ evolve backward in time subject to the following events:

• Mutation: Each lineage undergoes mutation at locus ℓ with rate θ_ℓ according to P^(ℓ).

• Recombination: Each lineage undergoes recombination at breakpoint b ∈ B with rate ρ_b.

• Coalescence: Each pair of lineages coalesces with rate 2.

• Absorption: Each lineage is absorbed into a lineage of ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$ with rate 1.

The genealogical process described above completely characterizes a conditional sampling distribution (CSD), which Paul and Song (2010) denoted by ${\widehat{\pi }}_{\text{PS}}$. Observe that the rate of absorption is the same as before, but the rates for mutation, recombination, and coalescence are each a factor of 2 larger than those mentioned earlier. Intuitively, this rate adjustment accounts for using the (inexact) trunk genealogy ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$, which remains static. Note that the adjustment follows as a mathematical consequence of the diffusion-generator approximation (De Iorio and Griffiths 2004a,b; Griffiths et al. 2008), and it is supported by the fact that the CSD ${\widehat{\pi }}_{\text{PS}}$ has been shown to be exact for a one-locus model with parent-independent mutation (Paul and Song 2010).

It can be deduced from the diffusion-generator approximation that ${\widehat{\pi }}_{\text{PS}}\left(\alpha |{\mathcal{O}}_n\right)$, the conditional probability of sampling an additional haplotype α given a set of previously sampled haplotypes $\mathcal{O}$_n, satisfies a recursion. Unfortunately, this recursion is computationally intractable to solve for even modest-sized data sets. To address this issue, Paul et al. (2011) proposed further approximations, described below, to obtain a CSD that admits efficient implementation, while retaining the accuracy of ${\widehat{\pi }}_{\text{PS}}$.

Approximation 2 (sequentially Markov CSD)

A given conditional genealogy $\mathcal{C}$ contains a marginal conditional genealogy (MCG) for each locus, where each MCG comprises a series of mutation events and the eventual absorption into a lineage of the trunk ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$. See Figure 1C for an illustration. The key insight (Wiuf and Hein 1999) is that we can generate the conditional genealogy as a sequence of MCGs across the sequence, rather than backward in time. Although the sequential process is actually not Markov, it is well approximated (McVean and Cardin 2005; Marjoram and Wall 2006; Paul et al. 2011) by a Markov process, using a two-locus transition density. Applying this approximation to ${\widehat{\pi }}_{\text{PS}}$ yields the sequentially Markov CSD, ${\widehat{\pi }}_{\text{SMC}}$.

Conditional on the MCG $\mathcal{C}$_ℓ−1 at locus ℓ − 1, the MCG $\mathcal{C}$_ℓ at locus ℓ can be sampled by first placing recombination events onto $\mathcal{C}$_ℓ−1 according to a Poisson process with rate ρ_{(ℓ−1,ℓ)}. If no recombination occurs, $\mathcal{C}$_ℓ is identical to $\mathcal{C}$_ℓ−1. If recombination does occur, $\mathcal{C}$_ℓ is identical to $\mathcal{C}$_ℓ−1 up to the time T_r of the most recent recombination event. At this point, the lineage at locus ℓ, independently of the lineage at locus ℓ − 1, proceeds backward in time until being absorbed into a lineage of the trunk. This transition mechanism for the Markov process is illustrated in Figure 2. McVean and Cardin (2005) use this approximation as well, while the transition process in Marjoram and Wall (2006) does allow the lineage to coalesce back into itself.

Figure 2.

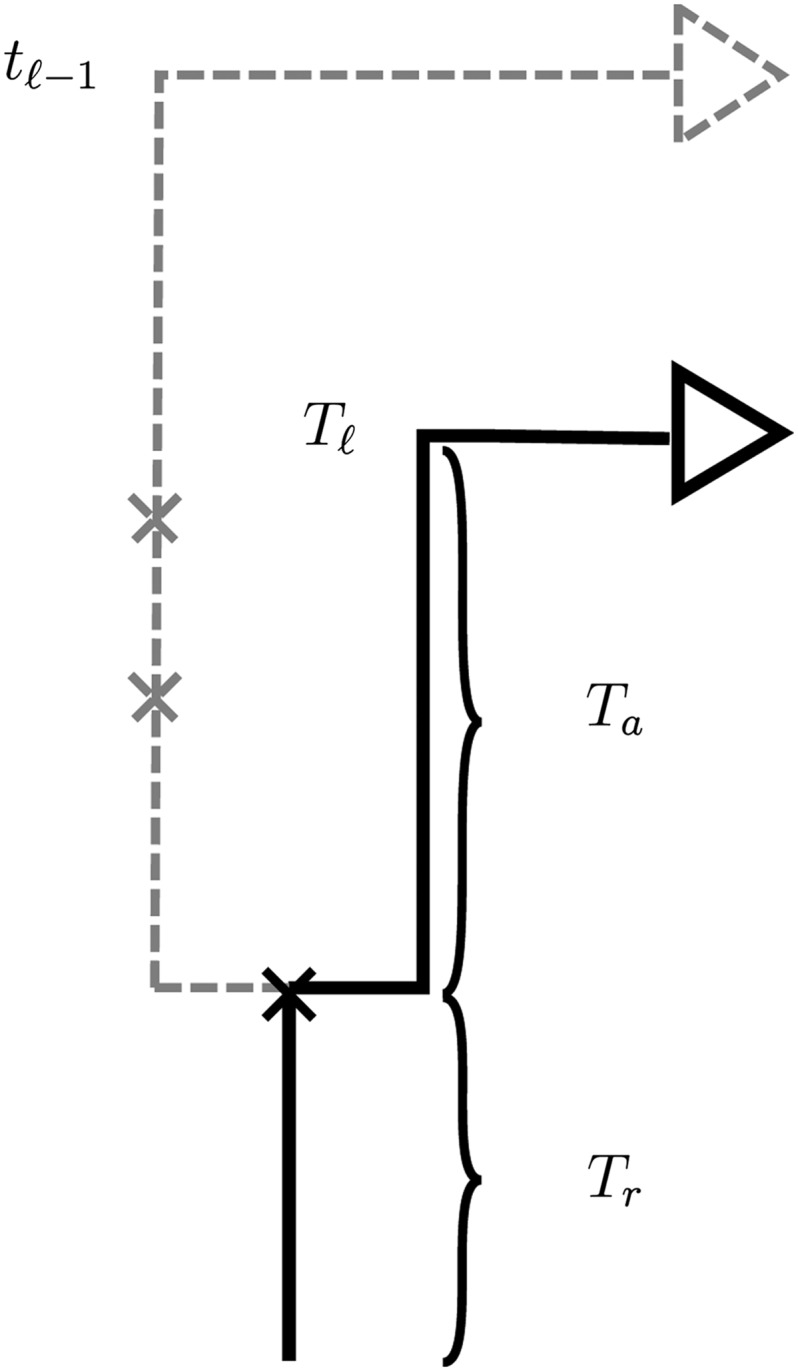
Illustration of the sequentially Markov approximation in which the absorption time T_ℓ at locus ℓ is sampled conditionally on the absorption time T_ℓ−1 = t_ℓ−1 at the previous locus. In the marginal conditional genealogy $\mathcal{C}$_ℓ−1 for locus ℓ − 1, recombination breakpoints are realized as a Poisson process with rate ρ_{(ℓ−1,ℓ)}. If no recombination occurs, $\mathcal{C}$_ℓ is identical to $\mathcal{C}$_ℓ−1. If recombination does occur, as in the example here, $\mathcal{C}$_ℓ is identical to $\mathcal{C}$_ℓ−1 up to the time T_r of the most recent recombination event. At this point, the lineage at locus ℓ, independently of the lineage at locus ℓ − 1, proceeds backward in time until being absorbed into a lineage of the trunk. The absorption time at locus ℓ is T_ℓ = T_r + T_a, where T_a is the remaining absorption time after the recombination event.

Given $\mathcal{C}$_ℓ, mutations are superimposed onto it according to a Poisson process with rate θ_ℓ. The MCG is absorbed into a trunk lineage corresponding to some haplotype h, which specifies an “ancestral” allele h[ℓ]. This allele is then propagated to the present according to the superimposed mutations and the transition matrix P^(ℓ), thereby generating an allele at locus ℓ of the additional haplotype α. We refer to the associated distribution of alleles as the emission distribution.

The generative process described above for the SMCSD ${\widehat{\pi }}_{\text{SMC}}$ can be formulated as an HMM, in which the hidden state at locus ℓ corresponds to the MCG $\mathcal{C}$_ℓ, excluding mutation events: We denote the hidden state at locus ℓ in the HMM by S_ℓ = (T_ℓ, H_ℓ), where T_ℓ ∈ [0, ∞) is the absorption time and H_ℓ ∈ $\mathcal{O}$_n is the absorption haplotype. The emission at locus ℓ corresponds to the allele α[ℓ]. See Paul et al. (2011) for explicit expressions for the initial, transition, and emission densities in the case of a constant population size.

Incorporating Variable Population Size

Here, we extend the SMCSD framework described in the previous section to incorporate variable population size. A history of relative effective population size is described by the function

$$\lambda \left(t\right)=\frac{N\left(t\right)}{N_{\text{ref}}},$$ (1)

where t ∈ [0, ∞), with t = 0 corresponding to the present time, N_ref is some reference effective population size, and N(t) is the effective population size at time t in the past. The population-scaled recombination and mutation rates are defined with respect to N_ref. Specifically, for b = (ℓ − 1, ℓ), we define ρ_b = 4N_refr_b, where r_b denotes the recombination rate per generation per individual between loci ℓ − 1 and ℓ, and θ_ℓ = 4N_refμ_ℓ, where μ_ℓ denotes the mutation rate per generation per individual at locus ℓ.

Initial density

In the case of a constant population size, the absorption time T_ℓ for locus ℓ follows an exponential distribution, but with a variable population size the absorption time is described by a nonhomogeneous Markov chain. See Griffiths and Tavaré (1994) for a more thorough discussion of the coalescent with variable population size. As in the constant population size case, however, the prior distribution of absorption haplotype H_ℓ is still uniform over the observed haplotypes $\mathcal{O}$_n in the trunk genealogy. In summary, the marginal density of the hidden state s_ℓ = (t, h) is given by

$${\zeta }^{\left(\lambda \right)}\left(t,h\right)=\frac{n_h}{\lambda \left(t\right)}\text{exp}\left(-n{\displaystyle {\int }_0^t\frac{1}{\lambda \left(\tau \right)}\text{d}\tau }\right),$$ (2)

where n_h denotes the number of haplotypes in $\mathcal{O}$_n that are identical to haplotype h.

Transition density

To obtain the transition density, we need to take into account recombination, which causes changes in the hidden state of our HMM. If no recombination occurs between loci ℓ − 1 and ℓ (prior to T_ℓ−1), then s_ℓ = s_ℓ−1. If a recombination event occurs between loci ℓ − 1 and ℓ, the absorption time for locus ℓ will be T_ℓ = T_r + T_a, where T_r is the time of recombination (which must be less than T_ℓ−1 and T_ℓ) and T_a is the remaining additional time to absorption, as illustrated in Figure 2. To compute the transition density, we need to convolve the hidden variables T_r and T_a. Letting b = (ℓ −1, ℓ) for ease of notation, the transition density from s_ℓ−1 = (t, h) to s_ℓ = (t′, h′) is given by

$$\begin{array}{l}{\phi }^{\left(\lambda \right)}\left(s_{\ell }|s_{\ell -1}\right)\\ =e^{-{\rho }_{\text{b}}t}\cdot {\delta }_{s_{\ell -1},s_{\ell }}+{\displaystyle {\int }_0^{\text{min}\left(t,t\prime \right)}{\rho }_{\text{b}}{e}^{-{\rho }_{\text{b}}{t}_{\text{r}}}\left[\frac{{\zeta }^{\left(\lambda \right)}\left(t\prime ,h\prime \right)}{{\displaystyle {\int }_{t_{\text{r}}}^{\mathrm{\infty }}{\zeta }^{\left(\lambda \right)}\left(\tau \right)\text{d}\tau }}\right]\text{d}{t}_{\text{r}}},\end{array}$$ (3)

where ζ^(λ)(t′, h′) is defined in (2) and ${\zeta }^{\left(\lambda \right)}\left(\tau \right):={\displaystyle {\sum }_{h\in {\mathcal{O}}_n}{\zeta }^{\left(\lambda \right)}\left(\tau ,h\right)}$. Note that ${\displaystyle {\int }_0^{\mathrm{\infty }}{\zeta }^{\left(\lambda \right)}\left(\tau \right)\text{d}\tau }=1$.

Emission probability

The probability of emitting allele a at locus ℓ (i.e., α[ℓ] = a) given hidden state s_ℓ = (t, h) is

$${\xi }^{\left(\lambda \right)}\left(a|s_{\ell }\right)=e^{-{\theta }_{\ell }t}{\displaystyle \sum _{m=0}^{\mathrm{\infty }}\frac{1}{m!}{\left({\theta }_{\ell }t\right)}^m{\left[{\left(P^{\left(\ell \right)}\right)}^m\right]}_{h\left[\ell \right],a}.}$$ (4)

This is the same emission probability as in Paul et al. (2011), but when we discretize the state space in the following section we have to take into account the effects of variable population size.

Sequentially Markov conditional sampling probability

Using the initial, transition, and emission densities described above, we can write down an integral recursion for the forward probability $f_{\text{SMC}}^{\left(\lambda \right)}\left(\alpha \left[1:\ell \right],s_{\ell }\right)$ of observing the first ℓ alleles α[1], … , α[ℓ] and the state at locus ℓ being s_ℓ. For 2 ≤ ℓ ≤ L,

$$\begin{array}{l}{f}_{\text{SMC}}^{\left(\lambda \right)}\left(\alpha \left[1:\ell \right],s_{\ell }\right)\\ ={\xi }^{\left(\lambda \right)}\left(\alpha \left[\ell \right]|s_{\ell }\right)\cdot {\displaystyle \int {\phi }^{\left(\lambda \right)}\left(s_{\ell }|s_{\ell -1}\right)f_{\text{SMC}}^{\left(\lambda \right)}\left(\alpha \left[1:\ell -1\right],s_{\ell -1}\right)\text{d}{s}_{\ell -1}},\end{array}$$ (5)

with base case

$$f_{\text{SMC}}^{\left(\lambda \right)}\left(\alpha \left[1\right],s_1\right)={\xi }^{\left(\lambda \right)}\left(\alpha \left[1\right]|s_1\right)\cdot {\zeta }^{\left(\lambda \right)}\left(s_1\right).$$

Finally, the conditional probability of sampling an additional haplotype α having previously observed $\mathcal{O}$_n = {h₁, … , h_n} is given by

$${\widehat{\pi }}_{\text{SMC}}^{\left(\lambda \right)}\left(\alpha |{\mathcal{O}}_n\right)={\displaystyle \int f_{\text{SMC}}^{\left(\lambda \right)}\left(\alpha \left[1:L\right],s_L\right)\text{d}{s}_L}.$$ (6)

As with the constant population size HMM, a backward algorithm can also be devised to compute ${\widehat{\pi }}_{\text{SMC}}^{\left(\lambda \right)}\left(\alpha |{\mathcal{O}}_n\right)$, although we do not present it here.

Discretizing the State Space

To efficiently evaluate the recursion (5) and the marginalization (6), we discretize the time component of the state space. We partition time (in units of 2N_ref generations) into d intervals, demarcated by

$$t_0=0<t_1<\cdots <t_d=\mathrm{\infty },$$

and assume that λ(t) defined in (1) has a constant value λ_i in each interval D_i := [t_i−1, t_i), for i = 1, … , d,

$$\lambda (t)={\displaystyle \sum _{i=1}^{d}1\left(t_{i-1}\le t<t_i\right){\lambda }_i,}$$ (7)

where 1(⋅) is the indicator function. Using this piecewise constant λ(t), we can write the HMM probabilities in a more workable form, as detailed below.

Initial probability

For t ∈ D_i, (7) implies that the initial density (2) can be written as

$${\zeta }^{\left(\lambda \right)}\left(t,h\right)=\frac{n_h}{{\lambda }_i}{e}^{-n\left(t-t_{i-1}\right)/{\lambda }_i}{\displaystyle \prod _{j=1}^{i-1}{e}^{-n\left(t_j-t_{j-1}\right)/{\lambda }_j}.}$$ (8)

To obtain the initial probability in the time-discretized model, we integrate over the time interval D_i to obtain

$${\widehat{\zeta }}^{\left(\lambda \right)}\left(D_i,h\right)={\displaystyle {\int }_{D_i}{\zeta }^{\left(\lambda \right)}\left(t,h\right)\text{d}t}=\frac{n_h}{n}{w}^{\left(i\right),}$$ (9)

where

$$w^{\left(i\right)}=\left[1-e^{-n\left(t_i-t_{i-1}\right)/{\lambda }_i}\right]{\displaystyle \prod _{m=1}^{i-1}{e}^{-n\left(t_m-t_{m-1}\right)/{\lambda }_m},}$$

which corresponds to the probability that a lineage in the conditional genealogy gets absorbed into the trunk genealogy within the interval D_i.

Transition probability

For the transition density from state s_ℓ−1 = (t, h) to state s_ℓ = (t′, h′), we let i denote the time interval index such that t ∈ D_i = [t_i−1, t_i) and let j denote the index such that t′ ∈ D_j = [t_j−1, t_j). After some simplification, the transition density (3) becomes

$$\begin{array}{l}{\phi }^{\left(\lambda \right)}\left(s_{\ell }|s_{\ell -1}\right)\\ =e^{-{\rho }_{b}t}\cdot {\delta }_{s_{\ell -1},s_{\ell }}+\frac{n_h}{{\lambda }_j}{e}^{-n\left(t\prime -t_{j-1}\right)/{\lambda }_j}\left[{\displaystyle \prod _{m=1}^{j-1}}{e}^{-n\left(t_m-t_{m-1}\right)/{\lambda }_m}\right]R\left(i,t;j,t\prime \right),\end{array}$$ (10)

where R(i, t; j, t′) is defined in the Appendix.

To compute the transition probability in the time-discretized model, we use Bayes’ rule and integrate the transition density function to obtain

$$\begin{array}{l}{\widehat{\phi }}^{\left(\lambda \right)}\left(D_j,h\prime |D_i,h\right)\\ =\frac{1}{{\widehat{\zeta }}^{\left(\lambda \right)}\left(D_i,h\right)}{\displaystyle {\int }_{D_j}{\displaystyle {\int }_{D_i}{\phi }^{\left(\lambda \right)}\left(t\prime ,h\prime |t,h\right){\zeta }^{\left(\lambda \right)}\left(t,h\right)\text{d}t}}\text{d}t\prime \\ =:y^{\left(i\right)}\cdot {\delta }_{i,j}{\delta }_{h,h\prime }+z^{\left(i,j\right)}\cdot \frac{n_{h\prime }}{n},\end{array}$$ (11)

where ${\widehat{\zeta }}^{\left(\lambda \right)}\left(D_i,h\right)$ is defined in (9), and explicit formulas for y⁽ⁱ⁾ and z^(i,j) are provided in the Appendix. The first term arises from the case of no recombination, while the second term accounts for the case when recombination does occur. Note that y⁽ⁱ⁾ and z^(i,j) depend only on the time interval and not on the absorbing haplotype.

Emission probability

Although thus far the emission density has not been affected by the population size being variable, discretizing time introduces dependence on the function λ(t). Let a denote the emitted allele of the newly sampled haplotype α at locus ℓ. Using Bayes’ rule again and then integrating over the absorption time interval gives

$$\begin{array}{l}{\widehat{\xi }}^{\left(\lambda \right)}\left(a|D_i,h\right)\\ =\frac{1}{{\widehat{\zeta }}^{\left(\lambda \right)}\left(D_i,h\right)}{\displaystyle {\int }_{D_i}{\xi }^{\left(\lambda \right)}\left(a|t,h\right){\zeta }^{\left(\lambda \right)}\left(t,h\right)} \text{d}t\\ ={\displaystyle \sum _{m=0}^{\mathrm{\infty }}{v}^{\left(i\right)} \left(m\right)}\cdot {\left[{\left(P^{\left(\ell \right)}\right)}^m\right]}_{h\left[\ell \right],a},\end{array}$$ (12)

where a formula for v⁽ⁱ⁾(m) is provided in the Appendix.

Discretizing time and grouping parameters

To discover periods of population expansion or contraction with the SMCSD, it is necessary to specify a time discretization that has high resolution during such time periods. This is challenging in cases where we have little a priori knowledge of the demographic history. Ideally the (unknown) coalescence events would be distributed uniformly across the time intervals of our discretization; if very few coalescence events occur in an interval, the corresponding population size will often be overestimated, leading to runaway behavior. In our implementation, we employ a heuristic method, detailed in the Appendix, for choosing the discretization time points t₁, … , t_d−1 based on the spacing of SNPs in the data, with the aim for coalescence events to be distributed evenly across the d time intervals. Alternatively, users have the option of specifying their own discretization time points to achieve a desired resolution.

As noted by Li and Durbin (2011), allowing separate population size parameters during time intervals that contain too few expected coalescence events can lead to inaccurate estimates. Following their lead, we mitigate this problem by constraining a few consecutive time intervals to have the same population size.

Modifying the Trunk Genealogy

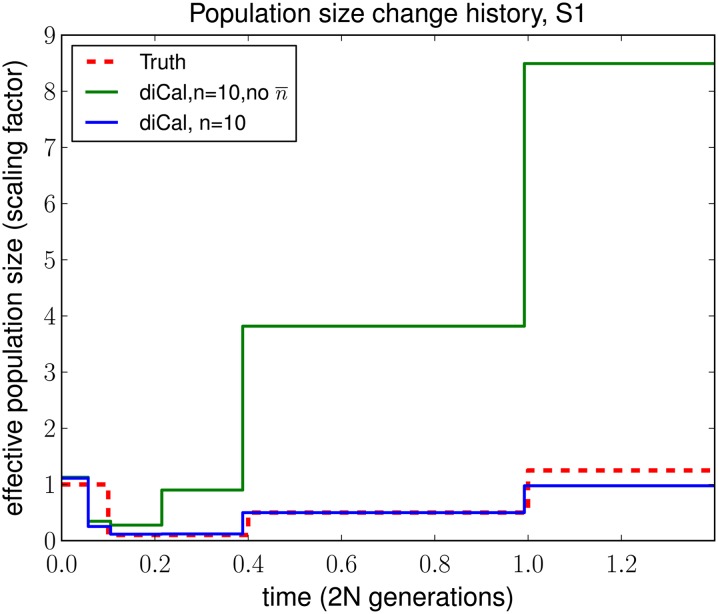
The trunk genealogy approximation in Paul and Song (2010) was derived by making an approximation in the diffusion process dual to the coalescent for a constant population size. It yields an accurate approximate CSD in the case of a population at equilibrium, and for parent-independent mutation models, the CSD becomes exact in the limit as the recombination rate approaches ∞. However, in the variable population size setting, we must modify the trunk genealogy approximation for the following reason: In the formulation described earlier, the trunk absorbs a lineage in the conditional genealogy $\mathcal{C}$ at the rate ndt/λ(t) at time t. Our HMM uses this inverse dependence and the inferred distribution of absorption times to estimate the population size scaling function λ(t). In reality, at time t the number of ancestral lineages is n(t) ≤ n and a lineage in $\mathcal{C}$ gets absorbed at rate n(t)dt/λ(t). Hence, assuming that the trunk genealogy contains n lineages in every time interval causes absorption events to occur too quickly, leaving the ancient population sizes overestimated. We later provide empirical results that support this intuition (see Figure 8).

Figure 8.

A comparison of the SMCSD-based leave-one-out likelihood approach in diCal, using the wedding-cake genealogy (blue line), with that using the unmodified trunk genealogy (green line). The results shown are for n = 10 haplotypes simulated under history S1 with two alleles. Without the wedding-cake genealogy, absorption of the left-out lineage into the trunk occurs too quickly, and the lack of absorption events in the midpast to the ancient past leads to substantial overestimation of the population sizes. Recent population sizes remain unaffected since during these times the absorption rates in the wedding-cake genealogy and in the trunk genealogy are roughly the same. In this example, we grouped adjacent parameters to fit roughly with population size change points for illustration purposes.

To remedy the problem described above, in our work we use the expected number of lineages in the trunk to modify the rate of absorption, while still forbidding mutation, recombination, and coalescence in the trunk genealogy. Let A_n(t) denote the number of lineages at time t ancestral to a sample of size n at time 0. Under the coalescent, the probability distribution of A_n(t) is known in closed form (Tavaré 1984), but using it directly to compute the expected number of lineages leads to numerically unstable results, due to alternating signs. However, one can obtain the following expression for the expectation (Tavaré 1984, equation 5.11), which is numerically stable:

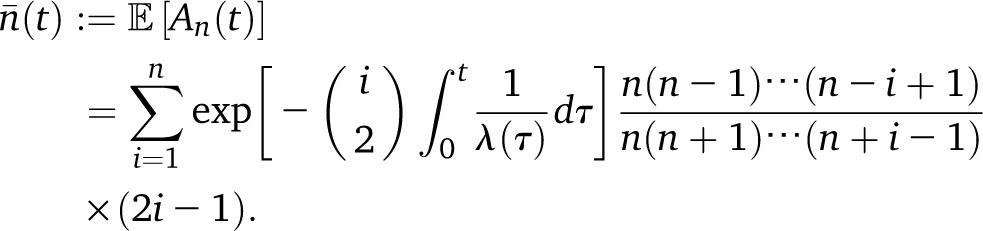(13)

For simplicity, we assume that throughout time interval D_i = [t_i−1, t_i), there are $\overline{n}\left(t_{i-1}\right)$ lineages, creating what we call a “wedding-cake genealogy,” as illustrated in Figure 3.

Figure 3.

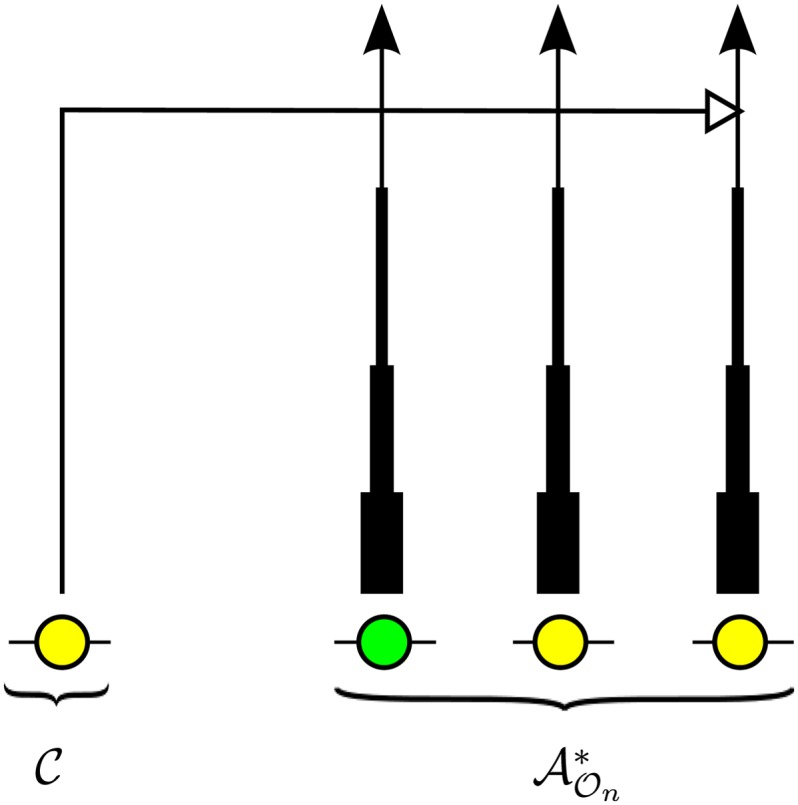
Illustration of the wedding-cake genealogy approximation, in which the varying thickness of a lineage in ${\mathcal{A}}_{{\mathcal{O}}_n}^{*}$ schematically represents the amount of contribution to the absorption rate. As shown, the wedding-cake genealogy never actually loses any of the n lineages, and absorption into any of the n lineages is allowed at all times; we are modifying the absorption rate only as a function of time.

To modify the HMM formulas, we simply replace each n in (9), (11), and (12) with the appropriate $\overline{n}(\cdot )$ from (13), except in the ratio n_h/n multiplying w⁽ⁱ⁾ in (9) and the ratio $n_{h\prime }/n$ multiplying z^(i,j) in (11) (these ratios are kept intact to preserve the relative contributions of different haplotypes). Note that the trunk genealogy never actually loses any of the n lineages, and absorption into any of the n lineages is allowed at all times; we are modifying the absorption rate only as a function of time. In the case of two sequences (one trunk lineage and one additionally sampled lineage), $\overline{n}\left(t\right)=1$ for all t, so the wedding-cake approximation does not change the model. Making the number of lineages more accurate by using this approximation improves our ability to estimate absorption times and therefore population sizes.

Population Size Inference with Expectation Maximization

To utilize all our data in an exchangeable way, we use a “leave-one-out” approach where we leave each haplotype out in turn and perform the SMCSD computation. More precisely, we define the leave-one-out composite likelihood (LCL) as

$$L_{\text{LCL}}\left(\lambda ;h_1,\dots ,h_n\right)={\displaystyle \prod _{i=1}^n{\widehat{\pi }}_{\text{SMC}}^{\left(\lambda \right)}\left(h_i|h_1,\dots ,h_{i-1},h_{i+1},\dots ,h_n\right).}$$ (14)

Because we compute the conditional sampling probability through dynamic programming and the probability depends on the effective population sizes in complex ways, we cannot find the maximum-likelihood estimates analytically. Although direct optimization could be used, it is computationally expensive. Thus we employ an EM algorithm to estimate the piecewise constant function λ(t). Our current implementation assumes that the population-scaled recombination rates ρ_b and mutation rates θ_ℓ, as well as the mutation transition matrices P^(ℓ), are given and fixed. For computational simplicity we currently assume that θ_ℓ and P^(ℓ) are the same for each site ℓ and ρ_b is the same for each pair of consecutive sites. The time discretization is fixed throughout the EM algorithm. The output of the algorithm is an estimated population size scaling factor λ_i for each interval D_i = [t_i−1, t_i). To convert these scaling factors into diploid effective population sizes, one would need to multiply by N_ref. Similarly, the discretization times can be converted to years by multiplying them by 2N_refg, where g is an average number of years per generation.

The standard Baum–Welch algorithm gives an EM procedure for learning the parameters of an HMM in which the transition probabilities and emission probabilities are treated as unknown independent parameters. However, our HMM is more constrained than a general one, with (dn)² + d|Σ|² (where Σ is the alphabet of alleles) unknown probabilities ${\widehat{\phi }}^{\left(\lambda \right)}\left(D_j,h\prime |D_i,h\right)$ and ${\widehat{\xi }}^{\left(\lambda \right)}\left(\alpha \left[\ell \right]|D_i,h\right)$ that are functions of the d parameters λ₁, … , λ_d. During the E-step, we compute the matrix [A_ij] of the expected number of D_i to D_j transitions. We also compute the matrix [E_i(b)] of the expected number of times allele b is emitted from time interval i. Then, during the M-step we maximize the likelihood function

$$\begin{array}{l}\left({\lambda }_1^{\left(k+1\right)},\dots ,{\lambda }_d^{\left(k+1\right)}\right)\\ =\underset{{\lambda }^{\left(k\right)}}{\text{argmax}}{\displaystyle \prod _{i,j}{\left[{\widehat{\phi }}^{\left({\lambda }^{\left(k\right)}\right)}\left(D_j|D_i\right)\right]}^{A_{ij}^{\left(k\right)}}}{\displaystyle \prod _{i,b}{\left[{\widehat{\xi }}^{\left({\lambda }^{\left(k\right)}\right)}\left(b|D_i\right)\right]}^{E_i^{\left(k\right)}\left(b\right)}},\end{array}$$ (15)

where ${\widehat{\phi }}^{\left(\lambda \right)}\left(D_j|D_i\right)$ and ${\widehat{\xi }}^{\left(\lambda \right)}\left(b|D_i\right)$ refer to the transition and emission probabilities where we have marginalized over the absorption haplotype.

We initialize the algorithm with λ_i = 1 for all i = 1, … , d. To compute [A_ij] and [E_i(b)], we use the forward and backward probabilities of our HMM. The exact details of making this step computationally efficient are provided in the Appendix. After the E-step, we use the Nelder–Mead optimization routine (Nelder and Mead 1965) to update the parameters in the M-step. Because of local maxima in the likelihood surface, we run this optimization routine several times (≈10) with different starting conditions and then retain the estimates with the largest likelihood. In the analysis discussed in this article, we ran the EM procedure for 20 iterations to obtain convergence. As pointed out by Li and Durbin (2011), running the EM procedure for many iterations often leads to overfitting.

Results

We compared the performance of our method, diCal, with that of PSMC (Li and Durbin 2011) on both simulated and real data. We compared diCal, using an n-haplotype leave-one-out scheme (Equation 14), with PSMC, using the same n haplotypes paired up sequentially (i.e., haplotype 1 paired with haplotype 2, haplotype 3 with haplotype 4, etc.).

Unless stated otherwise, we used 16 discretization intervals and inferred seven free population size parameters in both PSMC and diCal. In the notation introduced by Li and Durbin (2011), the pattern we used is “3 + 2 + 2 + 2 + 2 + 2 + 3,” which means that the first parameter spans the first three discretization intervals, the second parameter spans the next two intervals, and so on. We found that grouping a few consecutive intervals to share the same parameter significantly improved the accuracy of estimates. For example, due to an insufficient number of coalescence events, the first and last intervals are particularly susceptible to runaway behavior if they are assigned their own free parameters, but grouping them with their neighboring intervals prevented such pathological behavior. See Supporting Information, File S1 for further details of running PSMC and our method.

The accuracy of population size inference on simulated data

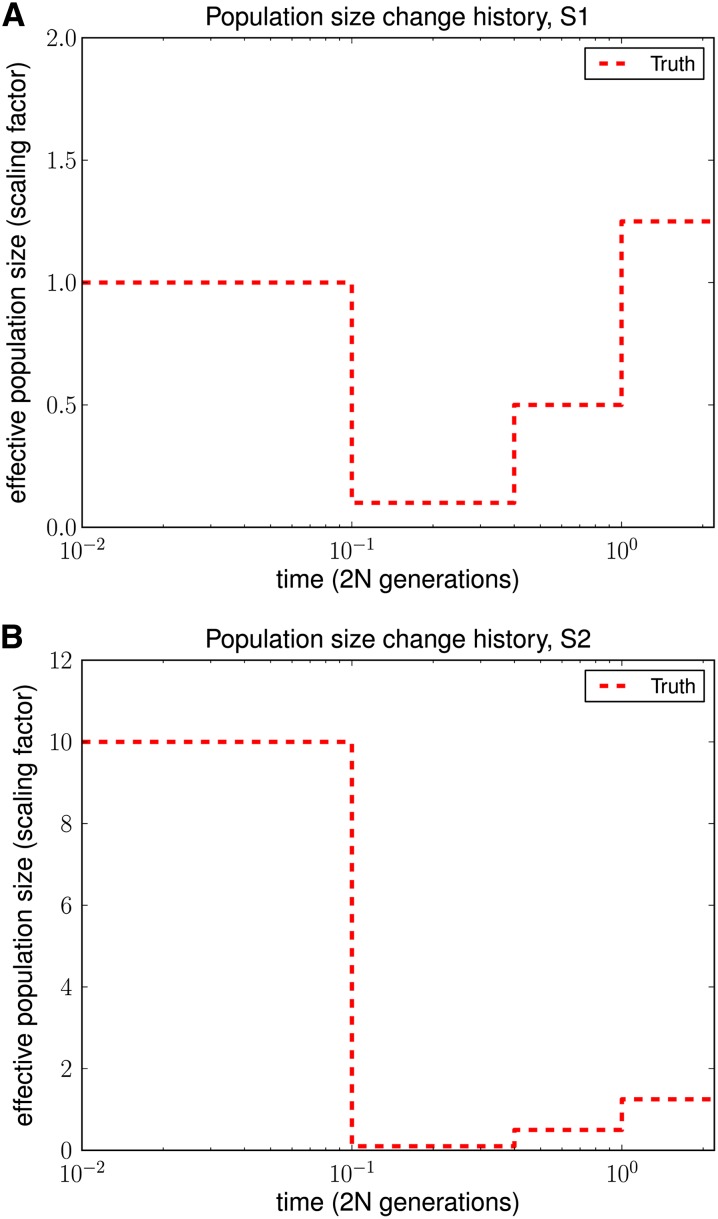
We used ms (Hudson 2002) to simulate full ancestral recombination graphs (ARGs) under two different population histories and then superimposed a quadra-allelic, finite-sites mutation process on the ARGs to generate sequence data over {A, C, G, T}. As illustrated in Figure 4, both histories contained bottlenecks in the moderately recent past. History S2 in Figure 4B in addition contained a recent rapid population expansion relative to the ancient population size. For each history, we simulated 10 independent ARGs for L = 10⁶ sites and 10 haplotypes, with the population-scaled recombination rate set to 0.01 per site in ms. To add mutations, we set the population-scaled mutation rate to 0.014 per site and used the quadra-allelic mutation matrix described in File S1.

Figure 4.

Population size histories considered in our simulation study, with time t = 0 corresponding to the present. (A) History S1 containing a bottleneck. (B) History S2 containing a bottleneck followed by a rapid expansion.

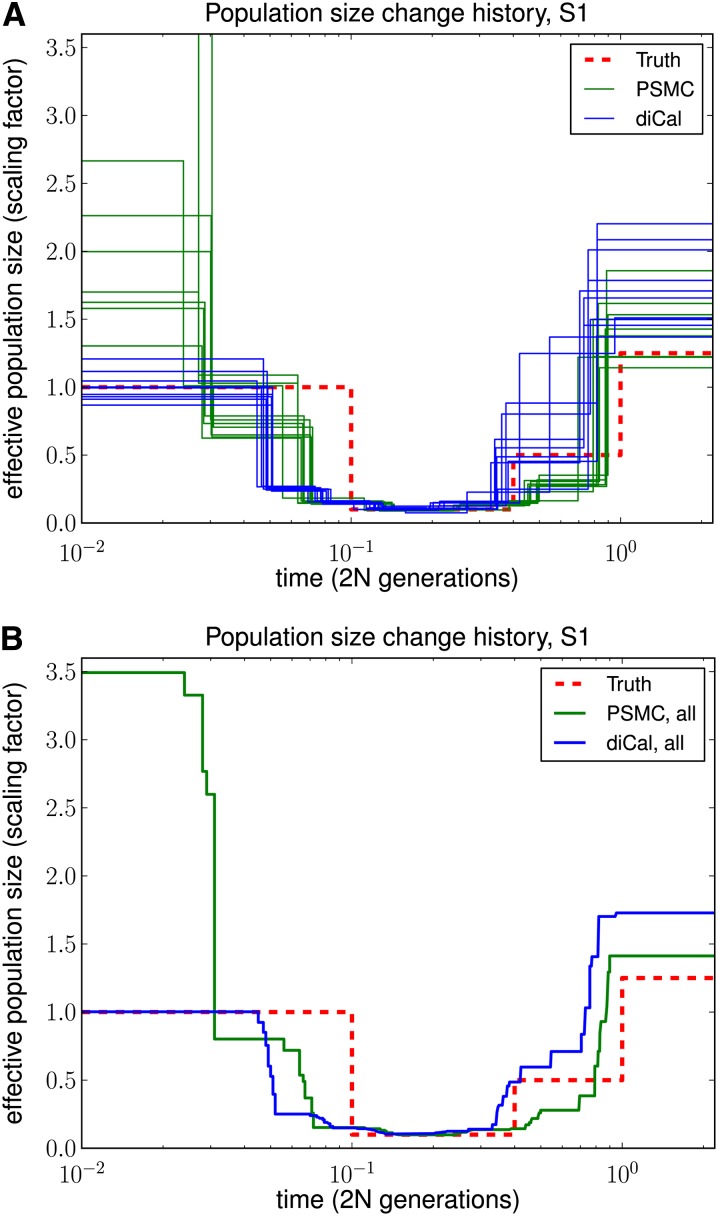
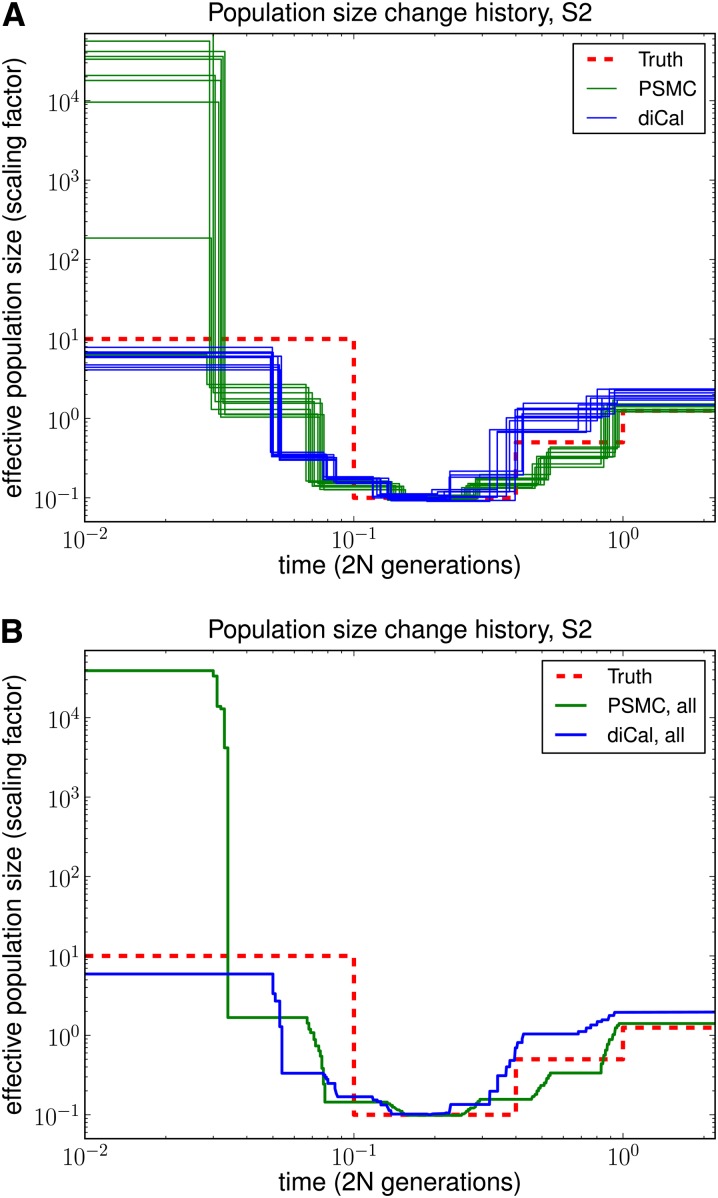
As shown in Figures 5 and 6, our method performed much better in the recent past than did PSMC. PSMC often had the type of runaway behavior shown in Figure 6, where it overestimated the most recent population size by over three orders of magnitude. We note that our method began to lose accuracy for more ancient times, most likely because ancient absorption events in a 1-Mb region are few and sparsely distributed in time in the leave-one-out SMCSD computation. Both methods tend to smooth out sudden changes in population size, which is why the inferred recovery time from a bottleneck is more recent than it should be. To quantify the improvement in accuracy of our method over PSMC, we used an error metric described in Li and Durbin (2011), which is a normalized integral of the absolute difference between the true ms history and the inferred history over time. The results, summarized in Table 1, show that our method had a substantially lower overall error than PSMC.

Figure 5.

Results of PSMC and diCal on data sets simulated under history S1 with sample size n = 10 and four alleles (A, C, G, and T). PSMC significantly overestimates the most recent population size, whereas we obtain good estimates up until the very ancient past. (A) Results for 10 different data sets. (B) Average over the 10 data sets.

Figure 6.

Results of PSMC and diCal on data sets simulated under history S2 with sample size n = 10 and four alleles (A, C, G, and T). The PSMC shows runaway behavior during the recent past, overestimating the most recent time by over three orders of magnitude on average. (A) Results for 10 different data sets. (B) Average over the 10 data sets.

Table 1. Goodness-of-fit for PSMC and diCal, averaged over 10 simulated data sets, each with a sample of n = 10 haplotypes.

Simulated history	PSMC error	diCal error
S1	0.40328	0.10283
S2	0.71498	0.29992

The underlying population size histories are shown in Figure 4. The error metric used is a normalized integral of the absolute difference between the true history and the inferred history over time. These results demonstrate that diCal is substantially more accurate than the PSMC method.

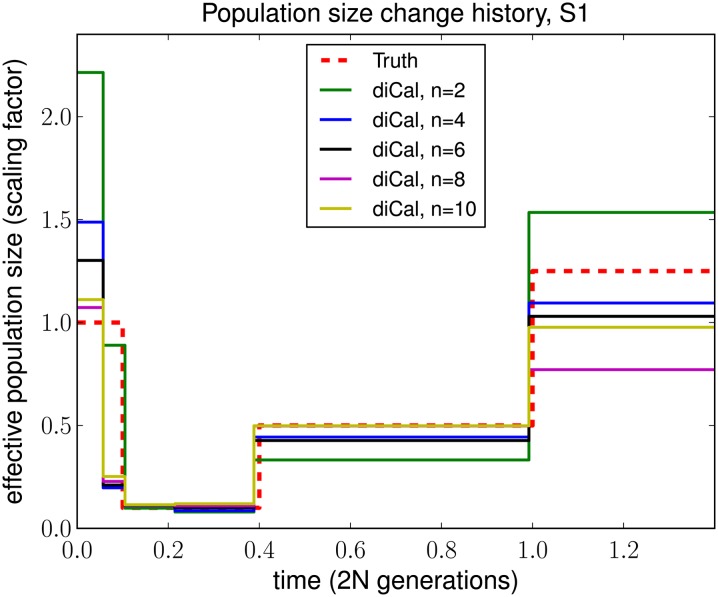
For inference using diCal, we examined the impact of considering more haplotypes on the accuracy of population size estimation. In this study, we focused on history S1 and grouped adjacent parameters to fit roughly with population size change points for illustration purposes. Figure 7 shows qualitatively that increasing the sample size n makes our estimate of the recent population size more accurate. Intermediate sizes changed little with increasing n, and ancient sizes were somewhat variable depending on the distribution of coalescence events. Note that for n = 2, our method is very similar to PSMC; we compute the transition probabilities slightly differently, but the wedding-cake approximation does not change the model in this case. We used the same error metric mentioned above to quantify the advantage of increasing the sample size. As shown in Table 2, the overall error decreased as the sample size increased, with improvement tapering to ∼8–10 haplotypes for this particular history.

Figure 7.

The effect of considering more haplotypes in diCal, using the SMCSD-based leave-one-out likelihood approach. Data were simulated under population size history S1 with two alleles. In this study, we grouped adjacent parameters to fit roughly with population size change points for illustration purposes. Shown is the increase in the accuracy of our method with an increasing sample size n. The recent sizes are the most dramatically affected, while intermediate sizes remain accurate even with few haplotypes.

Table 2. Goodness-of-fit for diCal on simulated bottlenecked history S1 for different sample sizes.

Sample size n	diCal error
2	0.2914
4	0.1901
6	0.1446
8	0.0802
10	0.0899

We used the same error metric as in Table 1. As the sample size n increases, the error decreases, with global improvement tapering at ∼8–10 haplotypes.

Impact of the wedding-cake genealogy approximation

We examined the advantage of using the wedding-cake genealogy approximation in the SMCSD computation, compared to assuming an unmodified trunk genealogy. Figure 8 illustrates that the unmodified trunk genealogy leads to overestimation of population sizes in the distant past, as discussed in Modifying the Trunk Genealogy. The wedding-cake genealogy approximation, which adjusts the absorption rate by accounting for the expected number of ancestral lineages of the already observed sample, leads to a significant improvement in the accuracy of population size inference in the ancient past.

Accuracy of estimated coalescence times

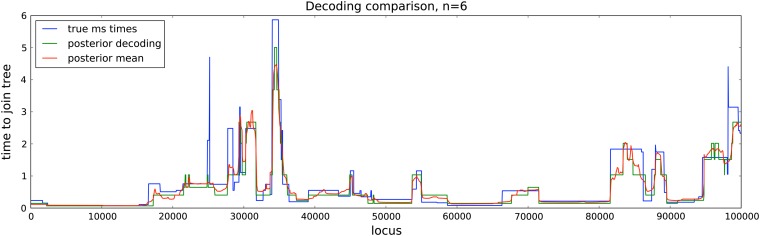
To assess the accuracy of estimated coalescence times, we produced the posterior decoding and the posterior mean of the times that a left-out haplotype got absorbed into a wedding-cake genealogy. The data were simulated under the full coalescent with recombination, using ms assuming a constant population size. The true coalescence time at each site was taken as the time the left-out lineage joined the rest of the coalescent tree at that site. As shown in Figure 9, we found that our estimated absorption times closely tracked the true coalescence times.

Figure 9.

Estimated absorption times in diCal using the leave-one-out SMCSD method vs. the true coalescence times for a 100-kb region. The data were simulated using ms for n = 6 haplotypes, assuming a constant population size. The true coalescence time at each site, obtained from ms, was taken as the time the ancestral lineage of a left-out haplotype joined the rest of the coalescent tree at that site. Shown is the true coalescence time for the nth haplotype and our corresponding inferred absorption times, obtained from the posterior decoding and the posterior mean. Our estimates generally track the true coalescence times closely.

Results on real data

We applied our method to data from 10 of the 179 human genomes that were sequenced at low coverage and phased as part of the 1000 Genomes pilot project. Five of the individuals were Yorubans from Ibadan, Nigeria (YRI) and five were Utah residents of central European descent (CEU) (1000 Genomes Project Consortium 2010). To minimize potential confounding effects from natural selection, we chose a 3-Mb region on chromosome 1 with no genes and then used the middle 2 Mb for analysis. We used the human reference (version 36) to create a full multiple-sequence alignment of 10 haplotypes (five diploid individuals) for each of the CEU and YRI populations. Although we filtered out unphased individuals and sites, the final sequences are based on low-coverage short read data, so phasing and imputation errors could affect the accuracy of our coalescence time inference. We assumed a per-generation mutation rate of μ = 1.25 × 10⁻⁸ per site, which is consistent with recent studies of de novo mutation in human trios (Awadalla et al. 2010; Roach et al. 2010; Kong et al. 2012), and a mutation transition matrix estimated from the human and the chimp reference genomes (shown in File S1). For simplicity, we assumed that the per-generation recombination rate r between consecutive bases is constant and equal to μ. The generation time was assumed to be 25 years. For a reference population size, we used N_ref = 10,000.

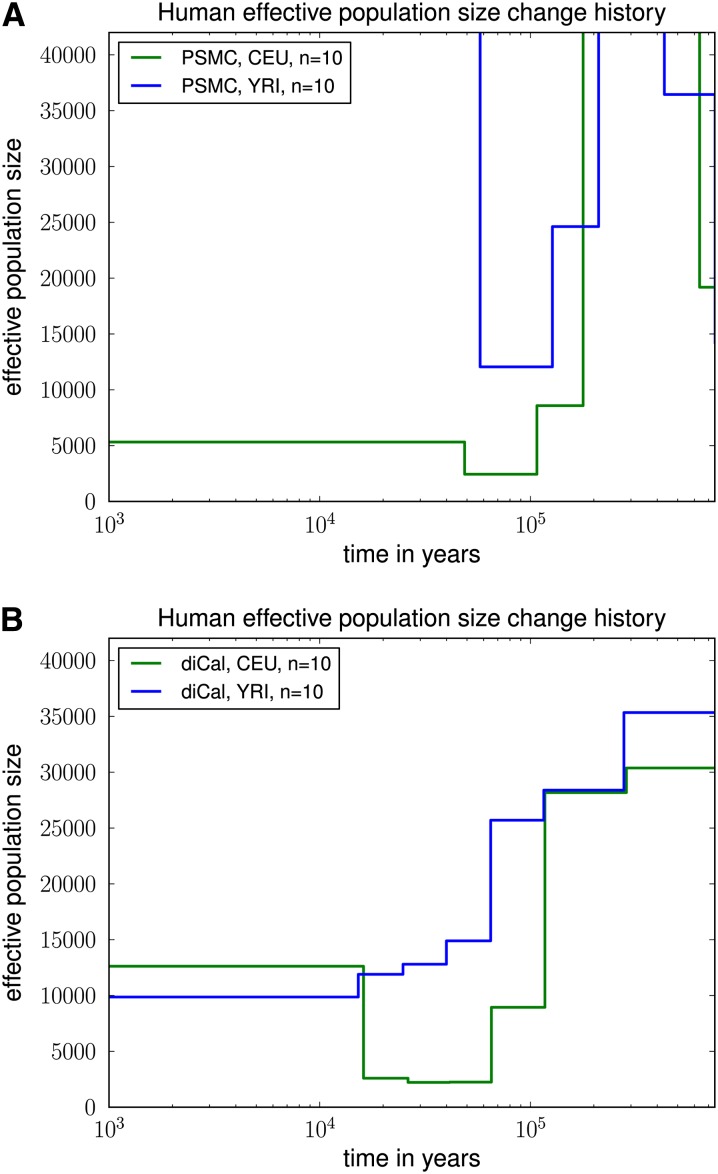
The results of PSMC and our method are shown in Figure 10. PSMC displayed runaway behavior and produced rather unrealistic results; see Figure 10A, for which we truncated the y-axis at 40,000 for ease of comparison with Figure 10B. The data set may be too small for PSMC to work accurately. We note that PSMC was able to produce more reasonable results on simulated data sets, probably because they were generated with much higher mutation and recombination rates, thus representing a larger genomic region for humans.

Figure 10.

Variable effective population size inferred from real human data for European (CEU) and African (YRI) populations. For each population, we analyzed a 2-Mb region on chromosome 1 from five diploid individuals (10 haplotypes), assuming a per-generation mutation rate of μ = 1.25 × 10⁻⁸ per site. (A) The results of PSMC, which had some runaway behavior and unrealistic results. The data set is probably too small for PSMC to work accurately. (B) The results of diCal. We inferred that the European population size underwent a severe bottleneck ∼117 KYA and recovered in the past 16,000 years to an effective size of ≈12,500. In contrast, our results suggest that the YRI population size did not experience such a significant drop during the early out-of-Africa bottleneck phase in Europeans.

As shown in Figure 10B, our method inferred that CEU and YRI had very similar histories in the distant past up until ∼117 KYA; discrepancies up to this point are most likely due to few observed ancient coalescence events with the leave-one-out approach. We inferred that the European population underwent a severe (out-of-Africa) bottleneck starting ∼117 KYA, with the effective population size dropping by a factor of ∼12 from ≈28,000 to ≈2250. Furthermore, at the level of resolution provided by our time discretization, our results suggest that the European population has recovered from the bottleneck to an average effective size of ≈12,500 for the past 16,000 years.

In contrast to previous findings (e.g., Li and Durbin 2011), our method did not infer a significant drop in the YRI population size during the early out-of-Africa bottleneck phase in Europeans. Instead, the African effective population size seems to have decreased more gradually over time (possibly due to changes in structure) to an average effective size of ≈10,000 for the past 16,000 years. We note that our results for real data are fairly robust to the choice of discretization, given that a sufficient number of coalescence events occur within each set of grouped intervals.

Run time

The run time of our method is O(Ld(d + n)n), where n is the number of sequences, L is the number of bases in each sequence, and d is the number of time discretization intervals; the run time for each CSD computation is O(Ld(d + n)), and each sequence is left out in turn (although this step is parallelizable). The run time for PSMC is O(Ld²P), where P is the number of pairs of sequences analyzed. In practice, PSMC can run much faster when consecutive sites are grouped into bins of size 100; a bin is considered heterozygous if it contains at least one SNP and homozygous otherwise. Creating a reasonable binning scheme for multiple sequences is less clear. We are currently exploring this avenue, which could significantly improve our runtime and potentially enable whole-genome analysis.

Discussion and Future Work

In this article, we have generalized the recently developed sequentially Markov conditional sampling distribution framework (Paul et al. 2011) to accommodate a variable population size. One important new idea central to the success and accuracy of our method is the wedding-cake genealogy approximation, which modifies the rate of absorption into the trunk by accounting for the varying number of lineages over time. Under simulated data, we have shown that our method produces substantially more accurate estimates of the recent effective population size than does PSMC (Li and Durbin 2011).

Applying our method to a 2-Mb intergenic region of chromosome 1 from five Europeans and five Africans, sequenced as part of the 1000 Genomes Project, and using a per-generation mutation rate of μ = 1.25 × 10⁻⁸ per site, we have inferred a severe (out-of-Africa) bottleneck in Europeans that began ∼117 KYA, with a drop in the effective population size by a factor of 12. In contrast, we have observed a much more mild population size decrease in the African population. We remark that our estimate of the timing of the bottleneck may not be very accurate, since we used only 16 discretization intervals and seven free population size parameters. Furthermore, all of our inferred times and population sizes would be smaller by a factor of 2 if we had used μ = 2.5 × 10⁻⁸. See Scally and Durbin (2012) for a more thorough discussion of how new mutation rate estimates are changing the way we view ancient population history. An earlier initial human dispersal out of Africa would fit with archaeological evidence of human artifacts dated at 74 KYA in India and 64 KYA in China (Scally and Durbin 2012).

During the recent past, our results demonstrate that the effective population size of Europeans has grown in the past 16,000 years, slightly surpassing the effective population size of Africans, which does not show a growth at this resolution. Recent studies (Gutenkunst et al. 2009; Gravel et al. 2011) suggest that the European population size recently grew much faster than the African population size, although the sample size we considered is not large enough to confirm this.

The main strength of our method is in the recent past. Large-scale sequencing studies (Coventry et al. 2010; Keinan and Clark 2012; Nelson et al. 2012) of a subset of genes suggest that humans underwent recent explosive population growth. Our method should be well equipped to infer such recent demographic histories, but we would need to consider a very large sample to accurately infer the rate of expansion and the time of onset. Because of issues of computational speed and memory footprint, our current implementation of the SMCSD computation can handle up to ∼20 haplotypes and a few megabases, but we are in the process of exploring ways to increase the scalability. One way in which we should be able to reduce our run time is by incorporating recently developed algorithms for blockwise HMM computation (Paul and Song 2012), which have been shown to result in a speedup of several orders of magnitude for large data sets.

All the results in this article make use of a leave-one-out approach (Equation 14) instead of the well-used product of approximate conditionals (PAC) method proposed by Li and Stephens (2003). Briefly, the PAC approach utilizes the approximate likelihood $\widehat{\pi }\left(h_{\sigma \left(1\right)}\right)\widehat{\pi }\left(h_{\sigma \left(2\right)}|h_{\sigma \left(1\right)}\right)\cdots \widehat{\pi }\left(h_{\sigma \left(n\right)}|h_{\sigma \left(1\right)},\dots ,h_{\sigma \left(n-1\right)}\right)$, where $\widehat{\pi }$ is an approximate conditional sampling distribution and σ is some permutation of {1, … , n}. A well-known drawback of this approach is that different permutations may produce vastly different likelihoods. Li and Stephens suggested averaging the PAC likelihood over several random permutations to alleviate this problem and this strategy seems to work reasonably well in practice. In our work, we have avoided the problem by adopting the leave-one-out approach, which yields accurate estimates of population sizes for the recent past, but not as good results for the ancient past. Employing the PAC approach may produce accurate estimates for all times, but a challenge that needs to be addressed in the SMCSD framework is that the wedding-cake genealogy, which is based on the prior expectation of the number of lineages, may not be accurate when there are few lineages, since coalescence times are more variable when they involve fewer lineages. We are working on improving the accuracy of the SMCSD computation by using the posterior absorption time distributions in a recursive fashion so that locus-specific absorption rates tailored to data can be used. This approach, together with the PAC model, should yield more accurate estimates of population sizes.

One factor that we have not investigated is the impact of variable recombination (and/or mutation) rates, although it is conceptually straightforward for our method to accommodate them. We have chosen not to incorporate recombination rate variation into our present implementation as it would make the method even more computationally expensive, since the transition probabilities would then be potentially different at each site. In addition, most fine-scale recombination maps (Crawford et al. 2004; McVean et al. 2004; Fearnhead and Smith 2005; Chan et al. 2012) are inferred under the assumption of a constant population size, which is exactly the assumption we are not making. We also note that Li and Durbin (2011) found that recombination hotspots did not affect their results significantly and that the important parameter is the average recombination rate.

A good choice of time discretization is critical to the performance of both diCal and PSMC. It is better to subdivide time more finely during periods with small population size than during periods with large population size when few coalescences occur. However, since the demography is what we are trying to infer, selecting an initial discretization is very difficult. Creating adaptive discretization schemes for coalescent HMMs is an important area of future research.

We have shown that posterior decodings of diCal enable accurate inference of coalescence times. Using this information, it should be possible to develop an efficient method of sampling marginal coalescent trees from the posterior distribution. We expect such local tree inference to have interesting applications, including genome-wide association studies and tests of selective neutrality.

The SMCSD framework has been recently extended (Steinrücken et al. 2013) to incorporate structured populations with migration. We are currently working on combining this extension with the work presented here to implement an integrated inference tool (to be incorporated into diCal) for general demographic models. Such a method could provide a detailed picture of the demographic history that created the diversity we see today in humans and other species.

Appendix

HMM Formulas

The expression R(i, t; j, t′) in (10) is defined as

$$R\left(i,t;j,t^{\prime }\right)=\{\begin{array}{cc}\left(R^{\left(i\right)}\left(t\right)+{\displaystyle {\sum }_{k=0}^{i-1}{R}^{\left(k\right)}}\right),& \text{if} i<j,\\ \left(R^{\left(j\right)}\left(t\prime \right)+{\displaystyle {\sum }_{k=0}^{j-1}{R}^{\left(k\right)}}\right),& \text{if} i>j,\\ \left(R^{\left(i\right)}\left(t\wedge t\prime \right)+{\displaystyle {\sum }_{k=0}^{i-1}{R}^{\left(k\right)}}\right),& \text{if} i=j,\end{array}$$

where ∧ denotes the minimum operator and, for u ∈ [t_k−1, t_k),

$$R^{\left(k\right)}\left(u\right):=\frac{{\rho }_{\text{b}}{\lambda }_k}{n-{\rho }_{\text{b}}{\lambda }_k}\left(e^{-{\rho }_{\text{b}}u+n\left(u-t_{k-1}\right)/{\lambda }_k}-e^{-{\rho }_{\text{b}}{t}_{k-1}}\right){\displaystyle \prod _{m=1}^{k-1}}{e}^{n\left(t_m-t_{m-1}\right)/{\lambda }_m},$$

$$R^{\left(k\right)}:=\frac{{\rho }_{\text{b}}{\lambda }_k}{n-{\rho }_{\text{b}}{\lambda }_k}\left(e^{-{\rho }_{\text{b}}{t}_k+n\left(t_k-t_{k-1}\right)/{\lambda }_k}-e^{-{\rho }_{\text{b}}{t}_{k-1}}\right){\displaystyle \prod _{m=1}^{k-1}}{e}^{n\left(t_m-t_{m-1}\right)/{\lambda }_m}.$$

After the state space has been discretized, we compute the transition probabilities using y⁽ⁱ⁾ (the probability that no recombination occurs) and z^(i,j) (the probability that recombination does occur),

$$\begin{array}{c}{y}^{\left(i\right)}=\frac{1}{{\widehat{\zeta }}^{\left(\lambda \right)}\left(D_i,h\right)}{\displaystyle {\int }_{t_{i-1}}^{t_i}{\zeta }^{\left(\lambda \right)}\left(t,h\right)e^{-{\rho }_{\text{b}}t}}dt\\ =\frac{1}{w^{\left(i\right)}}\frac{n}{n+{\rho }_{\text{b}}{\lambda }_i}{\displaystyle \prod _{k=1}^{i-1}{e}^{-n\left(t_k-t_{k-1}\right)/{\lambda }_k}\left(e^{-{\rho }_{\text{b}}{t}_{i-1}}-e^{-{\rho }_{\text{b}}{t}_i-n\left(t_i-t_{i-1}\right)/{\lambda }_i}\right)}\end{array}$$

and

$$\begin{array}{l}{z}^{\left(i,j\right)}=\frac{n}{w^{\left(i\right)}{n}_{h_{\ell -1}}}{\displaystyle {\int }_{t_{j-1}}^{t_j}{\displaystyle {\int }_{t_{i-1}}^{t_i}{\displaystyle {\int }_0^{t_{\ell -1}\wedge t_{\ell }}{\rho }_{\text{b}}{e}^{-{\rho }_{\text{b}}{t}_{\text{r}}}\frac{{\zeta }^{\left(\lambda \right)}\left(t_{\ell },h_{\ell }\right)}{{{\displaystyle \int }}_{t_{\text{r}}}^{\mathrm{\infty }}{\zeta }^{\left(\lambda \right)}\left(\tau \right)d\tau }{\zeta }^{\left(\lambda \right)}\left(t_{\ell -1},h_{\ell -1}\right)d{t}_{\text{r}}}}}d{t}_{\ell -1}d{t}_{\ell }\\ :=Z^{\left(i,j\right)}+w^{\left(j\right)}{\displaystyle \sum _{k=1}^{i\wedge j-1}{R}^{\left(k\right)}},\end{array}$$

where Z^(i,j) corresponds to the case when the recombination event occurs during the time interval $D_{i\wedge j}$ (i.e., the latest it could) and R^(k) corresponds to a recombination event in the time interval D_k. R^(k) is defined as before, and Z^(i,j) is

$$Z^{\left(i,j\right)}=\frac{n}{w^{\left(i\right)}{n}_{h_{\ell -1}}}{\displaystyle {\int }_{t_{j-1}}^{t_j}{\displaystyle {\int }_{t_{i-1}}^{t_i}{\displaystyle {\int }_{t_{\left(i\wedge j\right)-1}}^{t_{\ell -1}\wedge t_{\ell }}{\rho }_{\text{b}}{e}^{-{\rho }_{\text{b}}{t}_{\text{r}}}\frac{{\zeta }^{\left(\lambda \right)}\left(t_{\ell },h_{\ell }\right)}{{{\displaystyle \int }}_{t_{\text{r}}}^{\mathrm{\infty }}{\zeta }^{\left(\lambda \right)}\left(\tau \right)d\tau }}{\zeta }^{\left(\lambda \right)}}\left(t_{\ell -1},h_{\ell -1}\right)d{t}_{\text{r}}}d{t}_{\ell -1}d{t}_{\ell }.$$

To evaluate Z^(i,j), we must separate the computation into the cases i < j, i > j, and i = j,

$$Z^{\left(i,j\right)}=\{\begin{array}{cc}\frac{w^{\left(j\right)}}{w^{\left(i\right)}}{f}^{\left(i\right)},& \text{if} i<j\\ f^{\left(j\right)},& \text{if} i>j\\ \frac{1}{w^{\left(i\right)}}(\frac{{\rho }_{\text{b}}{\lambda }_i}{n+{\rho }_{\text{b}}{\lambda }_i}{e}^{-{\rho }_{\text{b}}{t}_{i-1}}-2e^{-n\left(t_i-t_{i-1}\right)/{\lambda }_i-{\rho }_{\text{b}}{t}_{i-1}}-\frac{{\rho }_{\text{b}}{\lambda }_i}{n-{\lambda }_i\rho }{e}^{-{\rho }_{\text{b}}{t}_{i-1}-2n\left(t_i-t_{i-1}\right)/{\lambda }_i}& \\ +\hspace{0.5em}\frac{2n^2}{\left(n-{\lambda }_i\rho \right)\left(n+{\lambda }_i\rho \right)}{e}^{-{\rho }_{\text{b}}{t}_i-n(t_i-t_{i-1})/{\lambda }_i)}){\displaystyle \prod _{m=1}^{i-1}{e}^{-n\left(t_m-t_{m-1}\right)/{\lambda }_m},}& \text{if} i=j,\end{array}$$

where we define

$$f^{\left(i\right)}:=e^{-{\rho }_{\text{b}}{t}_{i-1}}+\frac{{\lambda }_i{\rho }_{\text{b}}}{n-{\lambda }_i{\rho }_{\text{b}}}{e}^{-n\left(t_i-t_{i-1}\right)/{\lambda }_i-{\rho }_{\text{b}}{t}_{i-1}}-\frac{n}{n-{\lambda }_i{\rho }_{\text{b}}}{e}^{-{\rho }_{\text{b}}{t}_i}.$$

To compute the emission probabilities we define v⁽ⁱ⁾(k) below,

$$v^{\left(i\right)}\left(k\right):=\frac{n{\left({\theta }_{\ell }\right)}^k}{{\lambda }_i{w}^{\left(i\right)}k!}{e}^{n{t}_{i-1}/{\lambda }_i}{\displaystyle \prod _{j=1}^{i-1}{e}^{-n\left(t_j-t_{j-1}\right)/{\lambda }_j}}{\displaystyle \sum _{j=0}^k{c}_i^{-\left(j+1\right)}\frac{k!}{\left(k-j\right)!}\left[e^{-c_i{t}_{i-1}}{t}_{i-1}^{k-j}-e^{-c_i{t}_i}{t}_i^{k-j}\right]},$$

where

$$c_i:={\theta }_{\ell }+\frac{n}{{\lambda }_i}.$$

Computation of the Expected Transition Counts During the E-Step

Naively, if we compute the expected number of transitions from state s_ℓ−1 = (D_i, h_ℓ−1) to state s_ℓ = (D_j, h_ℓ) and then marginalize over the haplotypes, we obtain an O(n²) algorithm. To improve the run time, we can decompose the probability that a transition is used between locus ℓ − 1 and ℓ into a part that depends on the absorption haplotype and a part that depends on the absorption time interval, and thus we can reduce the run time to O(n). First we compute the posterior probability A^(ℓ)(s_ℓ−1, s_ℓ) that a particular transition is used between locus ℓ − 1 and ℓ, in terms of the discretized forward and backward probabilities F_ℓ(⋅) and B_ℓ(⋅). Let the newly sampled haplotype have allele a at locus ℓ, so α[ℓ] = a. Then

$$A^{\left(\ell \right)}\left(s_{\ell -1},s_{\ell }\right)=\frac{1}{\widehat{\pi }\left(\alpha \right)}\cdot F_{\ell -1}\left(s_{\ell -1}\right)\cdot {\widehat{\phi }}^{\left(\lambda \right)}\left(s_{\ell }|s_{\ell -1}\right)\cdot {\widehat{\xi }}^{\left(\lambda \right)}\left(a|s_{\ell }\right)\cdot B_{\ell }\left(s_{\ell }\right).$$

Now we marginalize over the haplotypes, plugging in the transition density formula

$$\begin{array}{c}{\displaystyle \sum _{h_{\ell -1}}{\displaystyle \sum _{h_{\ell }}{A}^{\left(\ell \right)}\left(s_{\ell -1},s_{\ell }\right)}}=\frac{1}{\widehat{\pi }\left(\alpha \right)}{\displaystyle \sum _{h_{\ell -1}}{\displaystyle \sum _{h_{\ell }}{F}_{\ell -1}\left(s_{\ell -1}\right)\cdot {\widehat{\phi }}^{\left(\lambda \right)}\left(s_{\ell }|s_{\ell -1}\right)\cdot {\widehat{\xi }}^{\left(\lambda \right)}\left(a|s_{\ell }\right)\cdot B_{\ell }\left(s_{\ell }\right)}}\\ A^{\left(\ell \right)}\left(D_i,D_j\right)=\frac{1}{\widehat{\pi }\left(\alpha \right)}{\displaystyle \sum _{h_{\ell -1}}{\displaystyle \sum _{h_{\ell }}{F}_{\ell -1}\left(s_{\ell -1}\right)\cdot {\widehat{\xi }}^{\left(\lambda \right)}\left(a|s_{\ell }\right)\cdot B_{\ell }\left(s_{\ell }\right)\left(y^{\left(i\right)}{\delta }_{s_{\ell -1},s_{\ell }}+z^{\left(i,j\right)}\frac{n_{h_{\ell }}}{n}\right)}}\\ =\frac{1}{\widehat{\pi }\left(\alpha \right)}[{\delta }_{i,j}{y}^{\left(i\right)}\left({\displaystyle \sum _h{F}_{\ell -1}\left(D_i,h\right){\widehat{\xi }}^{\left(\lambda \right)}\left(a|D_i,h\right)B_{\ell }\left(D_i,h\right)}\right)\\ +\hspace{0.5em}{z}^{\left(i,j\right)}\left({\displaystyle \sum _{h_{\ell -1}}{F}_{\ell -1}\left(s_{\ell -1}\right)}\right)\left({\displaystyle \sum _{h_{\ell }}\frac{n_{h_{\ell }}}{n}{\widehat{\xi }}^{\left(\lambda \right)}\left(a\hspace{0.17em}|s_{\ell }\right)B_{\ell }\left(s_{\ell }\right)}\right)],\end{array}$$

which is linear in n since we are only ever summing over one haplotype. To get the expected transition counts, we then sum over all the breakpoints, so $A_{ij}={\displaystyle {\sum }_{\ell =2}^L{A}^{\left(\ell \right)}\left(D_i,D_j\right)}$.

Discretizing Time

With an ideal time discretization, coalescence events would be uniformly distributed across intervals, but inferring the distribution of coalescence times is equivalent to the problem of population size estimation. Our heuristic discretization procedure seeks to avoid poor discretization by using the observed spacing of SNPs in the data. Let $\mathcal{T}$ be the empirical distribution of absorption times for all the contiguous segments inferred by a posterior decoding of our data set. Then, for a discretization with d intervals, our goal is to compute t₁, … , t_d−1 such that we see the same number (i.e., |$\mathcal{T}$|/d) of absorption times in each interval.

We first tackle the problem of breaking up our data into segments with the same pairwise coalescence time and then compute the expectation of this time. The locations of ancestral recombination breakpoints divide up a sequence pair into segments that each have a single coalescence time, but we do not know these breakpoints. However, it will often be the case that all the base pairs between two adjacent SNPs will coalesce at the same time or be split between just two different times on either side of a recombination breakpoint. Moreover, in many cases, the positional distribution of SNPs and that of recombination breakpoints will be correlated—in particular, both SNPs and recombination breakpoints will be spaced farthest apart in regions of recent coalescence time. With this rationale, we take the observed distances between SNPs as a proxy for the length distribution of nonrecombining segments. To be more specific, let ℒ be the list of all lengths between adjacent SNPs for all pairs of haplotypes, and let the d empirical quantiles of ℒ be bounded by L₁, … , L_d−1.

Now we need the expectated coalescence time of an l-base segment with no mutation or recombination. Conditional on m mutation events and r recombination events, the coalescence time for two lineages under a constant population size is distributed as Γ(1 + m + r, 1 + lθ + lρ) (see Tajima 1983 for a derivation with mutation only), so the expected coalescence time for m = r = 0 is

$$\frac{1}{1+l\left(\theta +\rho \right)}.$$

In our implementation, we drop the 1 in the denominator since this represents our prior under constant population sizes of two lineages coalescing at rate 1. We want to minimize the use of our prior, so we put more weight on the term related to the empirical length distribution. Putting this all together, we plug the quantiles of ℒ into this formula to obtain t_i:

$$t_i=\frac{1}{L_{d-i}\left(\rho +\theta \right)}.$$

If an approximate time range of interest is known (for example, in humans we might be interested in the last 1 million years), then the user can specify an end-time T_max. Then all times are scaled by T_max/t_d−1.