A Continuous Method for Gene Flow

Abstract

Most modern population genetics inference methods are based on the coalescence framework. Methods that allow estimating parameters of structured populations commonly insert migration events into the genealogies. For these methods the calculation of the coalescence probability density of a genealogy requires a product over all time periods between events. Data sets that contain populations with high rates of gene flow among them require an enormous number of calculations. A new method, transition probability-structured coalescence (TPSC), replaces the discrete migration events with probability statements. Because the speed of calculation is independent of the amount of gene flow, this method allows calculating the coalescence densities efficiently. The current implementation of TPSC uses an approximation simplifying the interaction among lineages. Simulations and coverage comparisons of TPSC vs. MIGRATE show that TPSC allows estimation of high migration rates more precisely, but because of the approximation the estimation of low migration rates is biased. The implementation of TPSC into programs that calculate quantities on phylogenetic tree structures is straightforward, so the TPSC approach will facilitate more general inferences in many computer programs.

THE estimation of population genetics parameters such as migration rates and effective population sizes is a common task for researchers in such fields as conservation biology, population biology, and biogeography. The theory of coalescence, introduced in 1982 by Kingman (1982a,b,c), is a formidable framework for describing population genetic processes.

It has changed the inference of population genetic parameters completely. We can calculate probabilities of complex interactions among individuals within and between populations, using the structured coalescent (Strobeck 1987; Notohara 1990; Wilkinson-Herbots 1998). Probabilistic inferences built on the structured coalescent (Kuhner et al. 1995; Kuhner 2006; Beerli 1998, 2006; Beerli and Felsenstein 1999; Hey 2010) are now used by many researchers. Routinely, complex population models are evaluated and, more recently, compared to each other (Beerli and Palczewski 2010). These approaches commonly integrate over many genealogies G that are augmented with migration or divergence events, using the Felsenstein equation

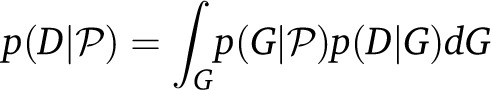(1)

(Hey 2007), where D is the data and 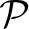is a set of model parameters, for example the effective population size N_e and immigration rates m. Beerli and Felsenstein (1999) expressed the coalescence probability density of a genealogy given the parameters

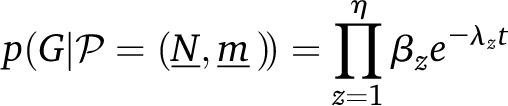(2)

with η number of events on the tree. The rate at which the zth event happens is

$${\lambda }_z={\displaystyle \sum _j^n\frac{k_j^z\left(k_j^z-1\right)}{4N_j}+{\displaystyle \sum _i^n{\displaystyle \sum _{j,j\ne i}^n{k}_j^z{m}_{ij}}},}$$ (3)

where $k_j^z$ is the number of lineages currently in population j corresponding to the time before event z, and m_ij is a migration rate defined as the percentage of individuals in population j that were previously in i. The variable β_z is the contribution of the current event to the sum that makes λ. In other words, β_z is the rate of the event considered. This rate of coalescence is $2/4N_j$ for a given pair of lineages and the rate of migration is m_ij for a given lineage.

This method allows for n² parameters, where n is the number of populations; the parameters can be partitioned into n population sizes and n(n − 1) migration rates, thus allowing for asymmetric migration rates.

Often, we will not be able to estimate the absolute quantities of N_e and m, but only the parameter Θ, which is 4 × N_e × μ, and M, which is m/μ. For both Θ and M the mutation rate μ is the scalar.

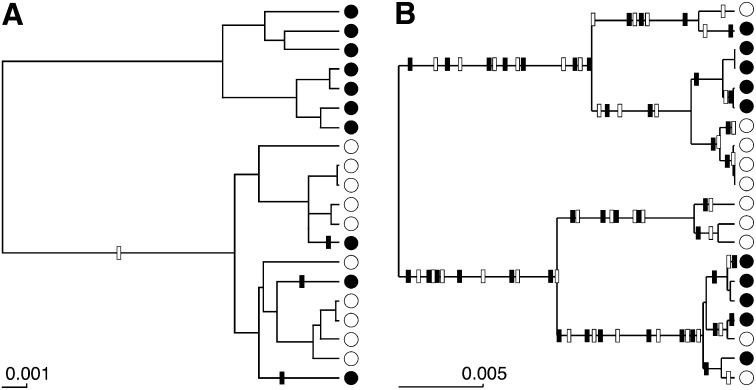
Equation 2 is a potentially large product over all events in the genealogy, including coalescences and migration events. The state space for such augmented genealogies is potentially huge because the number of events depends on the magnitude of the parameters. For example, a low migration parameter suggests that there are few migration events in the genealogy whereas a large migration rate suggests that there are many (Figure 1).

Figure 1.

Number of migration events in genealogies. (A) Genealogy generated with Nm = 0.400 into the population marked with open circles (○) and Nm = 0.267 into the population marked with solid circles (●). (B) Immigration rates are 10 times higher. Migration events on the genealogy are shaded according to the receiving population, looking forward in time.

The calculation of the likelihood p(D|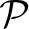) is analytically intractable and is commonly solved using Markov chain Monte Carlo (MCMC) methods (Metropolis et al. 1953; Hastings 1970). This can be very time consuming because the Markov chain needs to visit not only large numbers of probable topologies and parameter sets but also an even larger number of different configurations of migration events. Particularly, data sets that were generated by models with high migration rates among subsets of populations are difficult to analyze.

Here we propose a method that reduces the integration over all of these different migration events. Instead of relying on Monte Carlo methods to simulate many of these events, a one-dimensional numerical integration is proposed. This greatly simplifies the number of possible tree topologies that need to be explored. Although for any data stemming from multiple populations, there are an infinite number of possible genealogies augmented by migration events, the number of possible topologies when migration events are excluded is large but finite. Furthermore these genealogies are much simpler, since they include only coalescences. The analysis of such genealogies requires less time for situations with high migration rates where the standard methods augment the genealogies with many migration events (Figure 1).

Methods

Transition-probability structured coalescence framework

Our new framework, the transition-probability structured coalescence (TPSC), does not depend on explicit migration events, but integrates over all possible population assignments. We contrast TPSC with the event-based structured coalescence (ESC) presently incorporated into MIGRATE (Beerli 1998; Beerli and Felsenstein 1999). Although the TPSC allows for complex population structure, we describe the method using a simple two-population model with four parameters (Figure 2).

Figure 2.

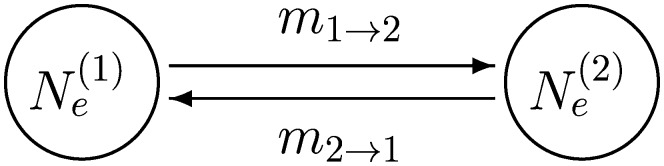
Two-population model.

Assume that there is a single stretch of nonrecombining genome L₀; at the present time it is in population 1. Looking backward in time, there is an exponential distribution for the waiting time until this lineage migrates from a different population.

The probability density of the waiting time until the sample changes population one or more times during the time interval from 0 to t is

$$m_{21}{e}^{-m_{21}t}$$ (4)

with the immigration rate m₂₁ from population 2 to 1; t is measured in generations and m is measured in terms of the proportion of offspring coming from a new population. A similar function can be applied to a sample from the other population.

To predict the probability of a particular lineage L_i being in a particular population Z_i we use a continuous-time Markov process. First construct a transition rate matrix Q of migration rates,

$$Q=\left[\begin{array}{cc}-m_{21}& m_{21}\\ m_{12}& -m_{12}\end{array}\right]$$ (5)

and a vector of initial probabilities

$$P_0=\left[\begin{array}{cc}P\left(L\in Z_1\hspace{0.17em}|t_0\right)& P\left(L\in Z_2\hspace{0.17em}|t_0\right)\end{array}\right].$$ (6)

Now we can compute the probabilities of being in each population at time t:

$$\left[\begin{array}{c}P\left(L\in Z_1\hspace{0.17em}|t\right)\\ P\left(L\in Z_2\hspace{0.17em}|t\right)\end{array}\right]=P_0{e}^{Qt}.$$ (7)

This framework can be extended to more than two populations: Q would still be a square matrix of migration rates, but Q would have size n, the number of populations:

$$Q=\left[\begin{array}{cccc}-{\displaystyle {\sum }_{i=1}^n{m}_{i1}}& m_{21}& \dots & m_{n1}\\ m_{12}& -{\displaystyle {\sum }_{i=1}^n{m}_{i2}}& \dots & m_{n2}\\ ⋮& ⋮& \ddots & ⋮\\ m_{1}n& m_{2}n& \dots & {\displaystyle {\sum }_{i=1}^n{m}_{in}}\end{array}\right].$$ (8)

With this framework it is possible to compute the probability density of one lineage going back in time. When looking at multiple lineages, one must also take into account coalescence events. The rate of standard coalescence for two lineages is the inverse of the population size or two times the population size for diploids. The probability density of the time t to coalescence of two independent lineages in the same population with no migration is

$$P\left(t\right)=\frac{1}{2N_{\text{e}}}{e}^{\left(-(t/2N_{\text{e}})\right)}.$$ (9)

Two lineages that are not in the same population do not coalesce. Their rate of coalescence is zero. Calculating the probability that two lineages are in the same population at a specific time would require a conditional probability. This would increase the size of the Q matrix, which would include both lineages and possible coalescences. Instead we make a simplification and estimate the joint probability by assuming independence.

Thus, we can combine the probability of being in a particular population with the rate of coalescence to estimate the rate of two independent lineages coalescing in population Z_p; from now on we mark Z_p only by its indicator p,

$${\lambda }_{1,2,p}\left(t\right)=\frac{P\left(L_1\in p,L_2\in p\right)}{2N_p}\approx \frac{P\left(L_1\in p\right)P\left(L_2\in p\right)}{2N_p},$$ (10)

where N_p is the effective population size of population p. The total rate of coalescence of the two lineages is the sum over all K populations:

$${\lambda }_{1,2}\left(t\right)={\displaystyle \sum _{k=1}^K{\lambda }_{1,2,k}\left(t\right)}={\displaystyle \sum _{k=1}^K\frac{P\left(L_1\in k\right)P\left(L_2\in k\right)}{2N_k}.}$$ (11)

Expanding to multiple lineages, the total rate of coalescence is

$$\lambda \left(t\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne i}^n\frac{{\lambda }_{i,j}\left(t\right)}{2}}}={\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne i}^n\frac{P\left(L_i\in k\right)P\left(L_j\in k\right)}{4N_k}}}.}$$ (12)

The 2 in the divisor offsets the double counting of the coalescence of λ_i,j and λ_j,i; n is the total number of all sampled lineages. For computational efficiency we transform to

$$\lambda \left(t\right)={\displaystyle \sum _{k=1}^K\left[\frac{1}{4N_k}{\displaystyle \sum _{i=1}^{n}P\left(L_i\in k\right)\left(K_k-P\left(L_i\in k\right)\right)}\right]}$$ (13)

with

$$K_k={\displaystyle \sum _{j=1}^{n}P\left(L_j\in k\right).}$$ (14)

Disregarding the time it takes to calculate individual P(L_i ∈ k), both Equations 13 and 14 can be calculated in O(nk) time.

The probability that a specific coalescent of two lineages has happened in a particular population can be calculated as the ratio of the rate that lineages coalesce in that population to the total coalescence rate,

$$P\left(\text{coalescence}\in p|L_i,L_j,t\right)=\frac{{\lambda }_{i,j,p}\left(t\right)}{{\lambda }_{i,j}\left(t\right).}$$ (15)

With this framework it is possible to calculate the probability of an entire genealogy given the population sizes and migration rates. The probability of each coalescent event is modeled by a nonhomogeneous Poisson process. Therefore the probability of two lineages L_x and L_y coalescing at time t is

$$P\left(L_x,L_y,t\right)={\lambda }_{x,y}\left(t\right)e^{\left(-{\displaystyle {\int }_{t_0}^t\lambda \left(t\right)dt}\right).}$$ (16)

Here x and y are the indexes of the lineages in question.

Multiplying all coalescence probabilities results in the probability of the genealogy G given the model parameters. For our two-population model we get

$$P\left(G|N_1,N_2,m_{21},m_{12}\right)={\displaystyle \prod _i^{n-1}\text{P}\left(L_{i,x},L_{i,y},t_i\right)}$$. (17)

Here L_i,x and L_i,y represent the ith coalescent even on the tree where lineages x and y coalesce.

Testing the TPSC

To evaluate the merit of our approach, we evaluated the TPSC for three different situations: We calculated exact probabilities for two individuals collected in two different populations. We calculated the maximum-likelihood estimates of model parameters and compared coverage and parameter estimates of a Bayesian implementation of TPSC with MIGRATE for various simulated data sets.

Likelihood calculations

The likelihood of the genetic data D given the parameters is calculated using the Felsenstein et al. (1999) equation

$$\begin{array}{l}p\left(D|N_1,N_2,m_{21},m_{12},M_{\mu }\right)\\ ={\displaystyle \sum _{G}p\left(G|N_1,N_2,m_{21},m_{12}\right)\hspace{0.17em}p\left(D|G,M_{\mu }\right).}\end{array}$$ (18)

For the mutation model M_μ we used the F84 model (Felsenstein and Churchill 1996). Without additional information the population size parameters and the mutation rate are confounded and we express the parameters of interest as a combination of μ and a scalar, so that for diploid organisms we report

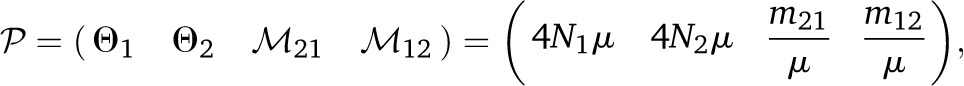(19)

where Θ_i is the mutation-scaled effective population size and M_ji is the mutation-scaled immigration rate.

Bayesian inference using TPSC

We construct a Bayesian estimator

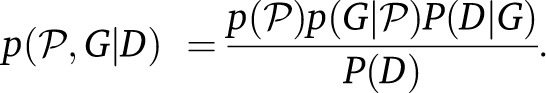(20)

The marginal posterior density for the parameters was estimated using the Metropolis–Hastings (MH) method. The implementation of such a method uses updates on the genealogy and the population genetic model parameters (Ronquist and Huelsenbeck 2003; Drummond and Rambaut 2007).

We implemented an MH algorithm, using a tree-update method similar to the one described by Nielsen (2000). The tree is updated by picking a random internal node representing a coalescence event and changing the time of the event up or down on the genealogy. In our algorithm, the probability of choosing any coalescence event is uniform, whereas in Nielsen’s algorithm the coalescence event selection is proportional to the length of a branch away from the root. The distance that each internal node is moved is a random value drawn from a normal distribution as in Nielsen’s algorithm, but unlike Nielsen’s algorithm the variance for this normal distribution is not arbitrary but is adapted to the information content of the data during the burn-in period (Appendix).

For parameter updates we use a method similar to the sliding-window proposal implemented in Mr. Bayes (Huelsenbeck et al. 2001; Ronquist and Huelsenbeck 2003). Unlike Mr. Bayes’ sliding-window proposal, which uses a uniform random number, we update the parameter by adding a normally distributed random variable. The variance of the normally distributed random variable is also adapted to information content of the data during the burn-in period. Our adaptive scheme is outlined in the Appendix.

Results

To analyze the effectiveness of our new method we have done three types of analysis. The first is an analytic treatment of two simple cases. We take a look at the probability density of time until a coalescent event. For a simple case, we can solve this analyticaly and compare the exact solution to the TPSC approximation. In the second study we simulate genealogies and use TPSC to infer the parameters used to generate these genealogies. Knowing all details of a genealogy is a rather unrealistic scenario. However, this second study tests the new model directly and without the complication of a mutation model needed to fit data to the genealogy. Finally, we did full simulation tests using DNA sequence data. We compared the ability of TPSC to the program MIGRATE, which uses a discrete coalescent method, to infer the simulated parameters.

Analysis for two lineages

Symmetric model:

First, we analyzed the structured coalescent of a two-population model with identical population sizes (N) and symmetrical migration rates (m). At the present time there are two lineages of interest, one in each population. This can be modeled by a continuous-time Markov model with the following exact transition probability matrix:

$$Q_e=\left[\begin{array}{ccc}0& 0& 0\\ \frac{1}{N}& -\frac{1}{N}-2m& 2m\\ 0& 2m& -2m\end{array}\right].$$ (21)

There are three states: State 3, represented by the third row, is the initial state of the lineages being in different populations. Looking backward in time, each lineage can migrate at the rate m. Either lineage migrating will result in both lineages existing in the same population. State 2, represented by the second row, is the state of both lineages existing in the same population. Either lineage can immigrate at the rate m, per lineage, or the two lineages can coalesce at the rate $\frac{1}{N}$. State 1, represented by the first row, is an absorbing state. Once the lineages are coalesced we are no longer interested in them. The probability density of time to coalescence is the derivative of the probability that the lineage is in state 1:

$$p\left(t_{\text{coal}=t}\right)=\frac{d}{dt}P\left(t_{\text{coal}}<t\right)=\frac{d}{dt}{\left(e^{Q_{e}t}\right)}_{\left(3,1\right).}$$ (22)

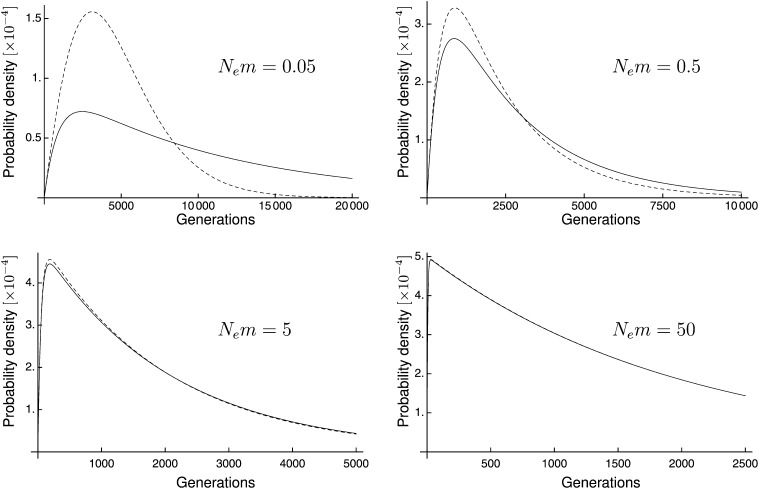
An analytic solution for this matrix exponential and derivative exists. However, the equation is very long and inconsequential. Instead of writing it out we have plotted it in Figure 4, but we have included it as a Mathematica worksheet with Supporting Information, File S1.

Figure 4.

Graphs showing the probability density of time to coalescence of two lineages in a two-population scenario with symmetric migration. The dashed line is the exact probability density whereas the solid line is the TPSC approximation. The effective population size for each panel is N_e = 1000.

This simple two-population model analyzed using TPSC leads to the transition probability matrix that takes into account only migration events:

$$Q_m=\left[\begin{array}{cc}-m& m\\ m& -m\end{array}\right].$$ (23)

The first step requires the calculation of the probability that the two lineages are in the same population (P_together). This probability is the sum of probabilities that both lineages are in population 1 and that both lineages are in population 2:

$$P_{\text{together}}\left(t,m\right)=e_{\left(1,1\right)}^{Q_{m}t}{e}_{\left(1,2\right)}^{Q_{m}t}+e_{\left(2,1\right)}^{Q_{m}t}{e}_{\left(2,2\right)}^{Q_{m}t}.$$ (24)

This is a function of m because Q depends on m. The rate of coalescence then becomes

$$\lambda \left(t,N,m\right)=\frac{P_{\text{together}}\left(t,m\right)}{N}.$$ (25)

Finally we can compute the probability density of a coalescent event. Again this is analytically tractable, but the equation is rather long, and we have included it as a Mathematica worksheet in File S1:

$$p\left(t_{\text{coal}}\right)=\lambda \left(t,N,m\right)e^{-{\displaystyle {\int }_0^x\lambda \left(x,N,m\right)dx}}.$$ (26)

We have plotted Equations 26 and 22 for various values of Nm in Figure 4. Although both N and m can vary independently, the shapes of these curves depend only on the ratio of N to m.

Asymmetric model:

In the first analytic example we created a symmetric model. In this section we explore another simplified model, one with unidirectional rather than symmetric migration.

We simplify the model from Figure 2 and consider only a two-parameter model. The parameters are the population size of population 1, $N_{\text{e}}^{\left(1\right)}$, and the immigration rate m_1→2; the immigration rate m_2→1 is zero. The population size of population 2 is inconsequential. This model is shown in Figure 3.

Figure 3.

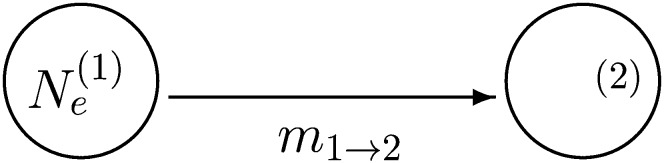
Population model with two parameters.

Just as before, two individuals were sampled, one in each population. We are interested in calculating the probability density of time until coalescence. This simple scenario can be modeled by a continuous-time Markov process. The state probabilities can be calculated exactly, using a continuous-time Markov model with a three-state Q matrix:

$$Q_f=\left[\begin{array}{ccc}0& 0& 0\\ \frac{1}{N_{\text{e}}}& -\frac{1}{N_{\text{e}}}& 0\\ 0& m& -m\end{array}\right].$$ (27)

Here state 1 represents the coalesced state. This is an absorbing state. State 3 is the initial state with each sample in a different population. Since migration is a one-way state the Markov chain will go from state 3 to state 2 at the migration rate. State 2 represents both lineages being in the same population. These will coalesce at a rate that is the inverse of the population size.

The exact probability density of the time to coalescence can be calculated as

$$p\left(t_{\text{coal}}\right)=\frac{d}{dt}P\left(t_{\text{coal}}<t\right)=\frac{d}{dt}{\left(e^{Q_{f}t}\right)}_{\left(3,1\right)}=\frac{m{e}^{-mt}-m{e}^{-(t/N_{\text{e}})}}{1-m{N}_{\text{e}}}.$$ (28)

Using TPSC, first we compute the probability that these two populations are in the same population. This is governed by a simple exponential distribution, because there is an exponential waiting time until the lineage that is able to migrates:

$$P_{\text{together}}=1-e^{-mt}.$$ (29)

The rate of coalescence can be computed:

$$\lambda \left(t\right)=\frac{1-e^{-mt}}{N_{\text{e}}}$$. (30)

This is the probability of both lineages being in the same population. Then the probability density function becomes

$$\begin{array}{c}p\left(t_{\text{coal}}\right)=\lambda \left(t\right)e^{-{\displaystyle {\int }_0^t\lambda }\left(x\right)dx}\\ =\left(1-e^{-mt}\right)e^{-\hspace{0.5em}(1/N_{\text{e}})\left[(e^{-mt}-1)/m+t\right]}\frac{1}{N_{\text{e}}}.\end{array}$$ (31)

Comparisons between the exact method and TPSC, shown in Figure 4 for a symmetric migration model, reveal that the approximation works well in scenarios when the migration rate is high (Nm ≥ 1.0) and poorly when the migration rate is low (Nm ≤ 1.0). Graphs for the asymmetric case reveal the same general pattern (not shown, but included in File S2).

Simulated genealogies

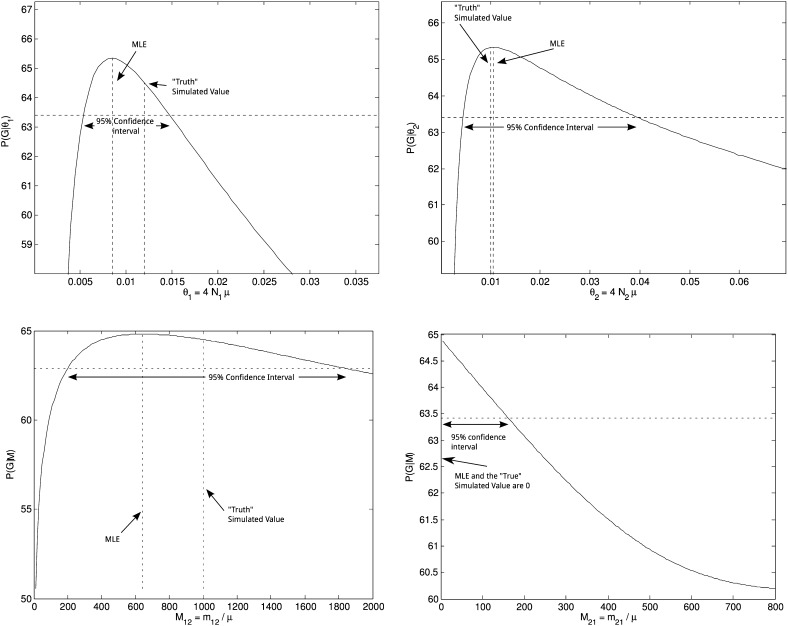
To test our method we simulated genealogies from known population parameters. Using the true genealogy is equivalent to assuming that there is an infinite amount of sequence data to define the genealogy; therefore we can find the maximum-likelihood estimate of Equation 18 (cf. Felsenstein 1992). An example of such an analysis is shown in Figure 5. Each panel presents the profile-likelihood curve for each of the four parameters of a two-population model: Θ₁, Θ₂, M₂₁, and M₁₂. The genealogy was generated using the structured coalescent with parameters Θ₁ = 0.012, Θ₂ = 0.01, M₂₁ = 0, and M₁₂ = 1000. The 95% confidence intervals bracket the true parameter value for all parameters. The profile likelihood curves are strongly peaked for the mutation-scaled population sizes, but the migration parameters have wide confidence intervals.

Figure 5.

Plots of profile-likelihood curves. Data were simulated from a two-population model with migration in one direction. Labels indicate the maximum-likelihood estimate, the “true” parameter value used to generate the genealogy, and the 95% confidence interval of the estimate.

We calculated several statistics over the maximum-likelihood estimates (MLEs) from 1000 simulated genealogies of 40 individuals, 20 per population (Table 1).

Table 1. Accuracy of TPSC.

	M
Statistic	2.5	25	250
Average $\widehat{\Theta }$	0.048	0.043	0.047
Median $\widehat{\Theta }$	0.045	0.041	0.045
Average $\widehat{M}$	10.265	31.874	365.95
Median $\widehat{M}$	4.448	19.845	237.67
Coverage of Θ	86%	91%	85%
Coverage of M	81%	92%	86%

Shown are maximum-likelihood estimates of mutation-scaled migration rates M and mutation-scaled population size Θ assuming the genealogy is known. For each M, 1000 genealogies were simulated using “true” parameter values Θ = Θ₁ = Θ₂ = 0.04 and M = M₁₂ = M₂₁ = [2.5, 25, 250]. The true number of migrants 4N_em = ΘM is [0.1, 1, 10].

Simulated DNA sequence data

To test the effectiveness of the TPSC we simulated DNA sequence data from two populations for a total of 40 individuals. We examined all nine combinations of three mutation-scaled population sizes Θ of 0.001, 0.01, and 0.1 and three mutation-scaled immigration rates of 10, 100, and 1000. The smallest population size is typical for nuclear data in human populations whereas the largest population size seems appropriate for species with very large effective population sizes, such as viruses or bacteria. The number of migrants 4N_em per generation ranged from 0.01 to 100, covering many potential natural scenarios. For each of the nine scenarios we simulated 100 data sets, using the simulation software MIGTREE and MIGDATA (available at http://people.sc.fsu.edu/∼pbeerli/software). DNA sequences with lengths of 500 bp were simulated using the F84 model (Hasegawa et al. 1985; Felsenstein and Churchill 1996). We chose for our simulations a DNA sequence length short enough so that even in natural populations we could expect few or no recombination events to occur.

These data sets were then run in TPSC and MIGRATE. Comparison with other programs that estimate migration rates (IMa and LAMARC) failed because of run-time constraints. Either programs did not converge within 48 hr or memory requirements were prohibitive to run 900 simulations.

TPSC and MIGRATE were run on the high-performance computing cluster at Florida State University. The run time of each separate data set was on the order of a few hours. Convergence was assessed by running TPSC multiple times from random starting genealogies on the same data to check for similar results. This procedure was then repeated using MIGRATE. Convergence of the runs of MIGRATE was assessed by repeated runs; there were potential convergence problems for data sets generated with high numbers of migrants (4N_em = 100).

Table 2 summarizes standardized mean square errors (MSE) [$\left(1/n\right){\displaystyle {\sum }_i^n{\left({\widehat{x}}_i-x_t\right)}^2/x_t^2}$] for TPSC and MIGRATE of n = 100 replicates for each set of Θ and M. Although we used a symmetric model of migration for simulation, the inference used a model with two population sizes and two migration rates that were allowed to vary independently. We report all four estimated parameters ${\widehat{\Theta }}_1$, ${\widehat{\Theta }}_2$, ${\widehat{M}}_{2\to 1}$, and ${\widehat{M}}_{1\to 2}$ for each combination of the true parameters, resulting in 36 comparisons of TPSC and MIGRATE. Because the true values for these parameters are symmetric, we expect that ${\widehat{\Theta }}_1={\widehat{\Theta }}_2={\Theta }_t$ and ${\widehat{M}}_{2\to 1}={\widehat{M}}_{1\to 2}=M_t$.

Table 2. Mean square errors of TPSC and MIGRATE.

	True values		MSE
Parameter	ΘT	MT	Mean		Median		Mode
			T	M	T	M	T	M
Θ1	0.001	10	3.034	1.258	2.094	0.860	0.972	0.542
		100	3.033	1.814	2.141	1.244	1.095	0.639
		1000	4.531	4.078	2.981	2.630	1.476	1.585
	0.01	10	0.609	0.312	0.463	0.245	0.301	0.158
		100	0.714	0.440	0.461	0.289	0.196	0.178
		1000	4.451	4.256	2.110	2.260	0.223	0.440
	0.1	10	0.154	0.128	0.114	0.104	0.083	0.072
		100	3.352	2.935	1.928	1.838	2.516	2.354
		1000	4.164	6.259	0.835	4.966	0.111	4.903
Θ2	0.001	10	3.947	1.591	2.875	1.091	1.472	0.596
		100	3.153	2.146	2.289	1.610	1.172	0.917
		1000	4.539	3.823	3.127	2.657	2.053	1.631
	0.01	10	0.411	0.269	0.310	0.220	0.211	0.161
		100	1.029	0.709	0.728	0.469	0.292	0.254
		1000	4.180	4.116	2.054	2.256	1.070	1.494
	0.1	10	0.151	0.121	0.111	0.095	0.084	0.074
		100	2.227	1.832	1.046	0.937	0.146	0.195
		1000	4.281	6.160	0.941	4.733	0.088	3.201
M2→1	0.001	10	3.454	8.819	2.757	7.998	1.730	11.001
		100	7.346	7.458	6.170	6.298	7.616	8.502
		1000	10.089	11.410	8.751	10.786	11.034	17.790
	0.01	10	5.244	5.259	3.787	3.920	3.260	2.268
		100	4.794	4.607	3.491	3.574	2.159	3.124
		1000	12.180	12.759	10.732	11.660	7.941	9.279
	0.1	10	4.086	3.207	3.051	2.287	1.881	1.211
		100	10.492	11.636	8.986	10.507	13.187	12.015
		1000	14.950	6.581	14.484	6.145	14.305	6.827
M1→2	0.001	10	4.082	8.313	3.398	7.295	2.997	8.058
		100	6.473	8.478	5.247	7.554	6.590	13.072
		1000	9.942	10.835	8.650	9.865	8.616	11.703
	0.01	10	4.510	5.918	3.232	4.753	1.697	4.584
		100	4.832	5.295	3.790	4.101	3.540	2.746
		1000	12.708	12.476	11.385	11.398	9.535	10.421
	0.1	10	2.919	4.100	2.024	3.122	1.095	2.005
		100	11.357	10.410	10.106	9.300	15.358	9.477
		1000	14.937	6.621	14.458	6.673	11.943	4.296

For each Θ_T, M_T pair, 100 simulations were performed.

TPSC and MIGRATE performed similarly on the estimation of mutation-scaled effective population sizes; differences of the MSE were mostly small, although TPSC estimates usually with slightly higher MSE values. The standardized MSEs for M are larger than those for Θ for both programs. TPSC outperforms MIGRATE in the estimation of mutation-scaled migration most of the time (37 of 54). In particular TPSC’s MSE of the median of M with low true effective population size and high true migration rates is smaller than the corresponding MSEs of MIGRATE. With large population sizes (Θ = 0.1) and large migration rates (M = 1000), TPSC seems to have difficulties achieving good estimates. These are cases in which the number of migrants is so high that distinguishing large from very large values becomes difficult. The likelihood surface becomes very flat, making it difficult to get accurate estimates. Although MIGRATE seems to work better in these cases, convergence to a unique solution for a particular data set becomes difficult.

Discussion

Recently, several researchers have described similar methods to TPSC. Takahata (1988) and Hobolth et al. (2011) integrated out migration events similarly to the method described in this article, but their formulation requires much larger transition probability matrices to calculate all potential interactions among lineages. This makes it difficult to employ their methods for large numbers of individuals k. TPSC, in contrast, depends only on the number of populations n in the analysis and work increases on the order O(n³k²) instead of O((kn)^k). Usually, k >> n. The program BEAST (Lemey et al. 2009) contains a phylogeographic model that may relate distantly to our method in that it presents probabilities of origin for particular pathogen strains or populations. The model of Lemey et al. (2009) similarly uses a continuous-time Markov chain to calculate location probabilities of past events. In this model, however, migration and coalescence are not intertwined. Instead a coalescent prior with a single population is used for the entire genealogy. Afterward, the locations of past states are computed on this tree. This does not take into account that individuals in small populations coalesce faster than those in large populations. In contrast, TPSC takes into account multiple population sizes, which gives information on spatial location of coalescent events.

TPSC is an approximation; it assumes independence of lineages for the calculation of the population assignment probability for the nodes in the genealogy. This leads to biased estimates for low migration rates (Figure 5, Table 1); however, TPSC outperforms event-based methods such as MIGRATE in scenarios with high immigration rates and moderate population sizes (Table 2). In such scenarios immigration events happen similarly as often as coalescence events (cf. Nordborg and Krone 2002) . With moderate immigration numbers (Nm ∼ 1) the TPSC approximation and the full solution lead to similar distributions, suggesting that TPSC can replace event-based methods for all data sets except those that include isolated populations.

We distribute our method in a stand-alone program (http://people.sc.fsu.edu/∼pbeerli/software) and will incorporate it into our program MIGRATE, allowing for switching between event-based and transition-probability structured coalescence methods.

Appendix

An Adaptive Scheme

The Metropolis–Hastings algorithms in this program adapt themselves to the data to ensure faster convergence. For Metropolis–Hastings the ideal acceptance rate can differ from 20% to 60% (Gelman et al. 1997; Roberts and Rosenthal 1998; Roberts and Rosenthal 2009). In a typical MCMC algorithm relatively small updates to a parameter will be accepted at a high rate. If a parameter does not change much, a likelihood and prior value will vary by only a small amount. On the other hand, a large change in a parameter when the value is already close to optimal is much more likely to be rejected.

We use the following scheme to adjust the variance of proposal distributions to adjust our acceptance ratio to a theoretical ideal. During burn-in, whenever a value is accepted for a parameter, the variance is increased by multiplying it by a value B that is slightly >1.0,

$${\sigma }_{t+1}^2=B{\sigma }_t^2,$$ (A1)

with t as the step number. Whenever a value is rejected, the proposal variance is decreased by a small value b that is slightly smaller than 1.0:

$${\sigma }_{t+1}^2=b{\sigma }_t^2$$. (A2)

If we assume that σ² has converged to some value, then we can formulate a relation of B, b, and the acceptance rate R. This relation is

$$B^{1-R}=b^R$$. (A3)

In our algorithm we choose to tune our acceptance ratio as closely as possible to the ideal R = 0.44 proposed by Roberts and Rosenthal (2009). We use an arbitrary value of b = 0.99, thus ensuring that our variance is at most 1% away from the ideal variance, and solve for B. Values of b close to 1 will converge to a value closer to the ideal, although they will converge more slowly. Conversely, values of b that are farther away from 1 will converge more quickly but the final variance could be farther from the ideal. The convergence rate is exponential and thus the desired acceptance ratio can be found quickly during the burn-in.

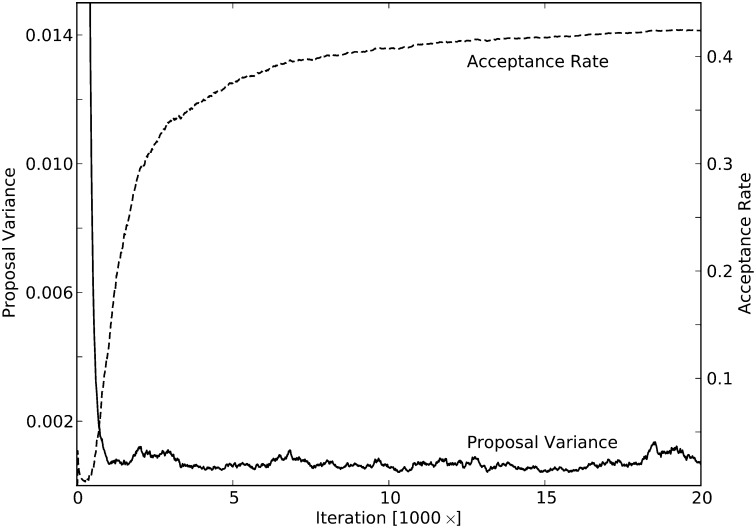
In Figure A1 we show the convergence of a typical run to the ideal variance. We have not seen any examples where the convergence did not happen less quickly. The variance converged very early in the burn-in. It should also be noted that any errors in convergence do not result in an incorrect algorithm. Instead the result would be worse mixing and a longer run time required during the MCMC chain.

Figure A1.

An example of the proposal variance adapting to an ideal. The acceptance rate is cumulative and has an asymptote at 0.44.