Dissecting High-Dimensional Phenotypes with Bayesian Sparse Factor Analysis of Genetic Covariance Matrices

Abstract

Quantitative genetic studies that model complex, multivariate phenotypes are important for both evolutionary prediction and artificial selection. For example, changes in gene expression can provide insight into developmental and physiological mechanisms that link genotype and phenotype. However, classical analytical techniques are poorly suited to quantitative genetic studies of gene expression where the number of traits assayed per individual can reach many thousand. Here, we derive a Bayesian genetic sparse factor model for estimating the genetic covariance matrix (G-matrix) of high-dimensional traits, such as gene expression, in a mixed-effects model. The key idea of our model is that we need consider only G-matrices that are biologically plausible. An organism’s entire phenotype is the result of processes that are modular and have limited complexity. This implies that the G-matrix will be highly structured. In particular, we assume that a limited number of intermediate traits (or factors, e.g., variations in development or physiology) control the variation in the high-dimensional phenotype, and that each of these intermediate traits is sparse – affecting only a few observed traits. The advantages of this approach are twofold. First, sparse factors are interpretable and provide biological insight into mechanisms underlying the genetic architecture. Second, enforcing sparsity helps prevent sampling errors from swamping out the true signal in high-dimensional data. We demonstrate the advantages of our model on simulated data and in an analysis of a published Drosophila melanogaster gene expression data set.

QUANTITATIVE studies of evolution or artificial selection often focus on a single or a handful of traits, such as size, survival, or crop yield. Recently, there has been an effort to collect more comprehensive phenotypic information on traits such as morphology, behavior, physiology, or gene expression (Houle 2010). For example, the expression of thousands of genes can be measured simultaneously (Gibson and Weir 2005; Ayroles et al. 2009; McGraw et al. 2011), together capturing complex patterns of gene regulation that reflect molecular networks, cellular stresses, and disease states (de la Cruz et al. 2010; Xiong et al. 2012). Studying the quantitative genetics of multiple correlated traits requires a joint modeling approach (Walsh and Blows 2009). However, applying the tools of quantitative genetics to high-dimensional, highly correlated data sets presents considerable analytical and computational challenges (Meyer and Kirkpatrick 2010). In this article we formulate a modeling framework to address these challenges for a common quantitative genetic analysis: estimating the matrix of additive genetic variances and covariances, or G-matrix (Lynch and Walsh 1998). The G-matrix encodes information about responses to selection (Lande 1979), evolutionary constraints (Kirkpatrick 2009), and modularity (Cheverud 1996) and is important for predicting evolutionary change (Schluter 1996).

The challenge in scaling classic methods to hundreds or thousands of traits is that the number of modeling parameters grows rapidly. An unconstrained G-matrix for p traits requires p(p + 1)/2 parameters, and modeling environmental variation and measurement error (Kirkpatrick and Meyer 2004) requires at least as many additional parameters. Such large numbers of parameters can lead to instability in parameter estimates—analyses that are highly sensitive to outliers and have high variance. Previous methods for overcoming this instability include (1) “bending” or smoothing unconstrained estimates of G-matrices, such as from pairwise estimates of genetic covariation (Ayroles et al. 2009; Stone and Ayroles 2009) or moments estimators (Hayes and Hill 1981), and (2) estimating a constrained G-matrix that is low rank and is thus specified with fewer parameters (e.g., Kirkpatrick and Meyer 2004). Constraining the G-matrix has computational and analytical advantages: fewer parameters results in more robust estimates and lower computational requirements (Kirkpatrick and Meyer 2004). Constrained estimators of G-matrices include methods based on moments estimators (Hine and Blows 2006; McGraw et al. 2011) and mixed-effects models [e.g., the “animal model” and other related models (Henderson 1984; Kruuk 2004; Kirkpatrick and Meyer 2004; de los Campos and Gianola 2007)]. Mixed-effects models are particularly powerful for studies in large breeding programs and wild populations. These methods perform well on moderate-dimensional data. However, they are computationally costly and not sufficiently robust to analyze high-dimensional traits.

Our objective in this article is to develop a model for estimating G-matrices that is scalable to large numbers of traits and is applicable to a variety of experimental designs, including both experimental crosses and pedigreed populations. We build on the Bayesian mixed-effects model of de los Campos and Gianola (2007) and model the G-matrix with a factor model. But, we add additional constraints by using a highly informative, biologically motivated, prior distribution on the G-matrix. The key idea that allows us to scale to large numbers of traits is that we believe the vast majority of the space of covariance matrices does not contain matrices that are biologically plausible as a G-matrix. In particular, we expect the G-matrix to be sparse, by which we mean that we favor G-matrices that are modular and low rank. Sparsity in statistics refers to models in which many parameters are expected to be zero (Lucas et al. 2006). By modular, we mean that small groups of traits will covary together. By low rank, we mean that there will be few (important) modules. We call a G-matrix with these properties sparse because there exists a low-rank factorization (most of the possible dimensions are zero) of the matrix with many of its values equal to (or close to) zero. This constrains the class of covariance matrices that we search over, a necessary procedure for inference of covariance matrices from high-dimensional data (Bickel and Levina 2008a,b; Carvalho et al. 2008; El Karoui 2008; Meyer and Kirkpatrick 2010; Hahn et al. 2013). Under these assumptions, we can also interpret the modules underlying our factorization without imposing additional constraints such as orthogonality (Engelhardt and Stephens 2010), something not possible with earlier mixed-effect factor models (Meyer 2009).

The biological argument behind our assumption of a sparse G-matrix is that the traits we measure on an organism arise from developmental processes of limited complexity, and developmental processes tend to be modular (Cheverud 1996; Wagner and Altenberg 1996; Davidson and Levine 2008). For gene expression, regulatory networks control gene expression, and variation in gene expression can often be linked to variation in pathways (Xiong et al. 2012; de la Cruz et al. 2010). For a given data set, we make two assumptions about the modules (pathways): (1) a limited number of modules contribute to trait variation and (2) each module affects a limited number of traits. There is support and evidence for these modeling assumptions in the quantitative genetics literature as G-matrices tend to be highly structured (Walsh and Blows 2009) and the majority of genetic variation is contained in a few dimensions regardless of the number of traits studied (Ayroles et al. 2009; Mcgraw et al. 2011). Note that while we focus on developmental mechanisms underlying trait covariation, ecological or physiological processes can also lead to modularity in observed traits and our prior may be applied to these situations as well.

Based on these assumptions, we present a Bayesian sparse factor model for inferring G-matrices for hundreds or thousands of traits which we call Bayesian sparse factor analysis of genetic covariance matrices or BSFG. We demonstrate the advantages of the model on simulated data and reanalyze gene expression data from a published study on Drosophila melanogaster (Ayroles et al. 2009). Although high-dimensional sparse models have been widely used in genetic association studies (Cantor et al. 2010; Engelhardt and Stephens 2010; Stegle et al. 2010; Parts et al. 2011; Zhou and Stephens 2012) to our knowledge, sparsity has not yet been applied to estimating a G-matrix.

Methods

In this section, we derive the BSFG model, by extending the classic multivariate animal model to the high-dimensional setting, where hundreds or thousands of traits are simultaneously examined. A factor model posits that a set of unobserved (latent) traits called factors underly the variation in the observed (measured) traits. For example, variation in gene expression might be the downstream output of variation in the activity of a gene regulatory network. Here, the activity of this gene network is a latent trait, and gene expression is a very high-dimensional set of observed traits. We use the animal model framework to partition variation in the observed traits and the latent factor traits into additive genetic variation and residuals. We encode our two main biological assumptions on the G-matrix as priors on the factors: sparsity in the number of factors that are important, and sparsity in the number of observed traits related to each factor. These priors constrain our estimation to realistic G-matrices and thus prevent sampling errors from swamping out the true signal in high-dimensional data.

Model

For a single trait the following linear mixed-effects model is commonly used to explain phenotypic variation (Henderson 1984),

$$y_i=X{b}_i+Z{u}_i+e_i,$$ (1)

where y_i is the vector of observations of the trait on n individuals; b_i is the vector of coefficients for fixed effects and environmental covariates such as sex or age with design matrix X; $u_i\sim \text{N}\left(\mathbf{0},{\sigma }_{{\text{G}}_i}^{2}A\right)$ is the random vector of additive genetic effects with incidence matrix Z, and $e_i\sim \text{N}\left(\mathbf{0},{\sigma }_{{\text{R}}_i}^2{I}_n\right)$ is the residual error caused by nonadditive genetic variation, random environmental effects, and measurement error. The residuals are assumed to be independent of the additive genetic effects. Here, A is the known r × r additive relationship matrix among the individuals; r generally equals n, but will not if there are unmeasured parents, or if several individuals are clones and share the same genetic background (e.g., see the Drosophila gene expression data below).

In going from one trait to p traits we can align the vectors for each trait in (1) to form the following multivariate model,

$$Y=XB+ZU+E,$$ (2)

where Y = [y₁ … y_p], B = [b₁ … b_p], U = [u₁ … u_p] and E = [e₁ … e_p]. U and E are therefore random variables drawn from matrix normal distributions (Dawid 1981),

$$U\sim {\text{MN}}_{r,p}\left(\mathbf{0};A,G\right),\hspace{1em}E\sim {\text{MN}}_{n,p}\left(\mathbf{0};I_n,R\right),$$ (3)

where the subscripts r, p and n, p specify the dimensions of the matrices, 0 is a matrix of zeros, A and I_n specify the covariances of each trait among individuals, and G and R specify the additive genetic and residual covariances among traits.

We estimate the covariance matrices G and R. To do so, we assume that any covariance among the observed traits is caused by a number of latent factors. Specifically, we model k latent traits that each linearly relate to one or more of the observed traits. We specify U and E via the following hierarchical factor model,

$$\begin{array}{c}U=F_{\text{a}}{\mathbf{\Lambda }}^T+E_{\text{a}},\hspace{1em}E=F_{\text{r}}{\Lambda }^T+E_{\text{r}}\\ F_{\text{a}}\sim {\text{MN}}_{r,k}\left(\mathbf{0};A,{\Sigma }_{\text{a}}\right),\hspace{1em}{F}_{\text{r}}\sim {\text{MN}}_{n,k}\left(\mathbf{0};I_n,{\Sigma }_{\text{r}}\right)\\ E_{\text{a}}\sim {\text{MN}}_{r,p}\left(\mathbf{0};A,{\mathbf{\Psi }}_{\text{a}}\right),\hspace{1em}{E}_{\text{r}}\sim {\text{MN}}_{n,p}\left(\mathbf{0};I_n,{\mathbf{\Psi }}_{\text{r}}\right)\\ \mathbf{\Lambda }\sim \pi \left(\theta \right),\end{array}$$ (4)

where Λ is a p × k matrix called the “factor loadings” matrix. Each column specifies the relationship between one latent trait and all observed traits. Just as U and E partition the among-individual variation in the observed traits into additive genetic effects and residuals in (2), the matrices F_a and F_r partition the among-individual variation in the latent traits into additive genetic effects and residuals. Σ_a and Σ_r model the among-factor (within-individual) covariances of F_a and F_r, which we assume to be diagonal $\left({\Sigma }_{\text{a}}=\text{Diag}\left({\sigma }_{{\text{a}}_j}^2\right),{\Sigma }_{\text{r}}=\text{Diag}\left({\sigma }_{{\text{r}}_j}^2\right)\right)$. Ψ_a and Ψ_r are the idiosyncratic (trait-specific) variances of the factor model and are assumed to be diagonal.

In model (4), as in any factor model (e.g., West 2003), Λ is not identifiable without adding extra constraints. In general, the factors in Λ can be rotated arbitrarily. This is not an issue for estimating G itself, but prevents biological interpretations of Λ and makes assessing MCMC convergence difficult. To solve this problem, we introduce constraints on the orientation of Λ through our prior distribution π(θ) specified below. However, even after fixing a rotation, the relative scaling of corresponding columns of F_a, F_r, and Λ are still not well defined. For example, if the jth column of F_a and F_r are both multiplied by a constant c, the same model is recovered if the jth column of Λ is multiplied by 1/c. To fix c, we require the column variances (${\sigma }_{{\text{a}}_j}^2$ and ${\sigma }_{{\text{r}}_j}^2$) to sum to one, i.e., Σ_a+Σ_r = I_k. Therefore, the single matrix ${\Sigma }_{h^2}={\Sigma }_{\text{a}}=I_k-{\Sigma }_{\text{r}}$ is sufficient to specify both variances. The diagonal elements of this matrix specify the narrow-sense heritability $\left(h_j^2={\sigma }_{{\text{a}}_j}^2/({\sigma }_{{\text{a}}_j}^2+{\sigma }_{{\text{r}}_j}^2)={\sigma }_{{\text{a}}_j}^2\right)$ of latent trait j.

Given the properties of the matrix normal distribution (Dawid 1981) and models (3) and (4) we can recover G and R as

$$\begin{array}{l}G=\Lambda {\Sigma }_{h^2}{\Lambda }^{\text{T}}+{\Psi }_{\text{a}},\\ R=\Lambda \left(I_k-{\Sigma }_{h^2}\right){\Lambda }^{\text{T}}+{\Psi }_{\text{r}}.\end{array}$$ (5)

Therefore, our model for the total phenotypic covariance P = G + R is

$$P=\Lambda {\Lambda }^{\text{T}}+{\Psi }_{\text{a}}+{\Psi }_{\text{r}}.$$ (6)

Our specification of the BSFG model in (4) differs from earlier methods such as the Bayesian genetic factor model of de los Campos and Gianola (2007) in two key respects. First, in classic factor models, the total number of latent traits is assumed to be small (k ≪ p). Therefore, Equation 5 would model G with only pk + k + p parameters instead of p(p + 1)/2. However, choosing k is a very difficult, unsolved problem, and inappropriate choices can result in biased and unstable estimates of G and R (e.g., Meyer and Kirkpatrick 2008). In our model we allow many latent traits but assume that the majority of them are relatively unimportant. This subtle difference is important because it removes the need to accurately choose k, instead emphasizing the estimation of the magnitude of each latent trait. This model is based on the work by Bhattacharya and Dunson (2011), which they term an “infinite” factor model. In our prior distribution on the factor loadings matrix Λ (see section Priors), we order the latent traits (columns of Λ) in terms of decreasing influence on the total phenotypic variation and assume that the variation explained by these latent traits decreases rapidly. Therefore, rather than attempt to identify the correct k we model the decline in the influence of successive latent traits. As in other factor models, to save computational effort we can truncate Λ to include only its first k* < k columns because we require the variance explained by each later column to approach zero. The truncation point k* can be estimated jointly while fitting the model and is flexible (we suggest truncating any columns of Λ defining modules that explain <1% of the phenotypic variation in any observed trait). Note that k* conveys little biological information and does not have the same interpretation as k in classic factor models. Since additional factors are expected to explain negligible phenotypic variation, including a few extra columns to ${\mathbf{\Lambda }}_{k*}$ to check for more factors is permissible (e.g., Meyer and Kirkpatrick 2008).

Second, we assume that the residual covariance R has a factor structure and that the same latent traits underly both G and R. Assuming a constrained space for R is uncommon in multivariate genetic estimation. For example, de los Campos and Gianola (2007) fit an unconstrained R, although they used an informative inverse Wishart prior (Gelman 2006) and only consider five traits. The risk of assuming a constrained R is that poorly modeled phenotypic covariance (P = G + R) can lead to biased estimates of genetic covariance in some circumstances (Jaffrezic et al. 2002; Meyer and Kirkpatrick 2008).

However, constraining R is necessary in high-dimensional settings to prevent the number of modeling parameters from increasing exponentially, and we argue that modeling R as we have done is biologically justified. Factor models fitting low numbers of latent factors are used in many fields because they accurately model phenotypic covariances. Reasonable constraints on R have been applied successfully in previous genetic models. One example is in the direct estimation of genetic principle components model of Kirkpatrick and Meyer (2004). These authors model only the first m_E eigenvectors of the residual covariance matrix. Our model for R is closely related to models used in random regression analysis of function-valued traits (e.g., Kirkpatrick and Heckman 1989; Pletcher and Geyer 1999; Jaffrezic et al. 2002; Meyer 2005). In those models, R is modeled as a permanent environmental effect function plus independent error. The permanent environmental effect function is given a functional form similar to (or more complex than) the genetic function. In Equation 4, F_r is analogous to this permanent environmental effect (but across different traits rather than the same trait observed through time), with its functional form described by Λ, and E_r is independent error. Since both F_a and F_r relate to the observed phenotypes through Λ, the functional form of the model for the residuals (e_i) is at least as complex as the genetic functional form (and more complex whenever $h_j^2=0$ for some factors).

The biological justification of our approach is that the factors represent latent traits, and just like any other trait their value can partially be determined by genetic variation. For example, the activity of developmental pathways is determined by the internal and external environment but can also have a genetic basis. The latent traits determine the phenotypic covariance of the observed traits, and their heritability determines the genetic covariance. In genetic experiments, some of these latent traits (e.g., measurement biases) might be variable, but not have a genetic component. We expect that some factors will contribute to R but not G, so R will be modeled with more factors than G (Meyer and Kirkpatrick 2008).

We examine the impact of our prior on R through simulations below, including cases when the true R is not low rank. When our assumptions regarding R do not hold, the prior may lead to biased estimates. For example, measurement biases might be low dimensional but not sparse, and some studies have estimated the phenotypic covariance P to be full rank (e.g., McGuigan and Blows 2007). However, we expect that for many general high-dimensional biological data sets this model will be useful and can provide novel insights. In particular, by directly modeling the heritability of the latent traits, we can predict their evolution.

Priors

Modeling high-dimensional data requires some prior specification or penalty/regularization for accurate and stable parameter estimation (Hastie et al. 2003; West 2003; Poggio and Smale 2003). For our model this means that constraints on G and R are required. We impose constraints through a highly informative prior on Λ. Our prior is motivated by the biological assumption that variation in underlying developmental processes such as gene networks or metabolic pathways gives rise to genetic and residual covariances. This implies:

1. The biological system has limited complexity: a small number of latent traits are relevant for trait variation. This means that the number of important factors is low (k* ≪ p).

2. Each underlying latent trait affects a limited number of the observed traits. This means the factor loadings (columns of Λ) are sparse (mostly near zero).

We formalize the above assumptions by a prior on Λ that imposes sparsity (formally, shrinkage toward zero) and low effective rank (Bhattacharya and Dunson 2011). This prior is specified as a hierarchical distribution on each element λ_ij of Λ:

$$\begin{array}{c}{\lambda }_{ij}|{\phi }_{ij},{\tau }_j\sim \text{N}\left(0,{\phi }_{ij}^{-1}{\tau }_j^{-1}\right),\hspace{1em}i=1\dots p,\hspace{1em}j=1\dots k\\ {\phi }_{ij}\sim \text{Ga}\left(\nu /2,\nu /2\right),\\ {\tau }_j={\displaystyle \prod _{l=1}^m{\delta }_l}\hspace{1em}{\delta }_1\sim \text{Ga}\left(a_1,b_1\right),\hspace{1em}{\delta }_l\sim \text{Ga}\left(a_2,b_2\right)\text{for}l=2\dots k.\end{array}$$ (7)

The hierarchical prior is composed of three levels:

1. We model each λ_ij (specifying how observed trait i is related to latent trait j) with a normal distribution.

2. Based on assumption 2, we expect most λ_ij ≈ 0. A normal distribution with a fixed variance parameter is not sufficient to impose this constraint. We model the the precision (inverse of the variance) of each loading element λ_ij with the parameter φ_ij drawn from a gamma distribution. This normal–gamma mixture distribution (conditional on τ_j) is commonly used to impose sparsity (Neal 1996; Tipping 2001) as the marginal distribution on λ_ij takes the form of Student’s t-distribution with v degrees of freedom and is heavy tailed. This forces the λ_ij’s to be concentrated near zero, but permits occasional large magnitude values. This prior specification is conceptually similar to the widely used Bayesian Lasso (Park and Casella 2008).

3. The parameter τ_j controls the overall variance explained by factor j by shrinking the variance toward zero as m → ∞. The decay in the variance is enforced by increasing the precision of λ_ij as j increases so that |λ_ij| → 0. The sequence {τ_j, j = 1 … k} is formed from the cumulative product of the sequence {δ_j, j = 1 … k}, where each element is modeled with a gamma distribution, and will be stochastically increasing as long as a₂ > b₂. This means that the variance of λ_ij will stochastically decrease and higher-indexed columns of Λ will be less likely to have any large magnitude elements. This decay ensures that it will be safe to truncate Λ at some sufficiently large k* because columns k > k* will (necessarily) explain less variance.

The prior distribution on τ_j (and therefore the sequence {δ₁, …, δ_j}) is a key modeling decision as τ_j controls how much of the total phenotypic variance we expect each successive factor to explain. Based on assumption 1, we expect that few factors will be sufficient to explain total phenotypic variation, and thus {τ_j} will increase rapidly. However, relatively flat priors on δ_m, m = 2 … k (e.g., a₂ = 3, b₂ = 1), which allow some consecutive factors to be of nearly equal magnitude, appear to work well in simulations.

The prior on the heritability of each of latent factor trait is a discrete set of values in the unit interval. This specification was selected for computational efficiency and to give $h_j^2=0$ positive weight in the prior. We find the following discrete distribution works well,

$${\pi }_{h_j^2}\left(0\right)=0.5,\hspace{1em}{\pi }_{h_j^2}\left(l/n_h\right)=\frac{1}{2\left(n_h-1\right)},\text{for}l=1\dots \left(n_h-1\right)$$, (8)

where n_h is the number of points to evaluate $h_j^2$. In analyses reported here, we set n_h = 100. This prior gives equal weight to $h_j^2=0$ and $h_j^2>0$ because we expect several factors (in particular, those reflecting measurement error) to have no genetic variance. In principle, we could place a continuous prior on the interval [0, 1], but no such prior would be conjugate, and developing a MCMC sampler would be more difficult.

We place inverse gamma priors with parameters a_a, b_a and a_r, b_r on each diagonal element of Ψ_a and Ψ_r, respectively. Priors on each element of B are normal distributions with very large (>10⁶) variances.

Implementation

Inference in the BSFG model uses an adaptive Gibbs sampler for which we provide detailed steps in the appendix. The code has been implemented in Matlab and can be found at the website (http://www.stat.duke.edu/∼sayan/bfgr/index.shtml) together with code to replicate the simulations and gene expression analyses reported here.

Simulations

We present a simulation study of high-dimensional traits observed in the offspring of a balanced paternal half-sib breeding design. We examined 10 scenarios (Table 1), each corresponding to different parameters for the matrices G and R to evaluate the impact of the modeling assumptions specified by our prior. For each scenario we simulated trait values of individuals from Equation (2) with Z = I_n, B = 0_p, and X a single column of ones representing the trait means.

Table 1. Simulation parameters.

	No. factors			R type		No. traits		Sample size
	a	b	c	d	e	f	g	h	i	j
G and R
No. traits	100	100	100	100	100	20	1000	100	100	100
Residual type	SFa	SF	SF	Fb	Wishartc	SF	SF	SF	SF	SF
No. factors	10	25	50	10	5	10	10	10	10	10
h2 of factorsd	0.5 (5)	0.5 (15)	0.5 (30)	0.5 (5)	1.0 (5)	0.5 (5)		0.9–0.1 (5)
	0.0 (5)	0.0 (10)	0.0 (20)	0.0 (5)		0.0 (5)		0.0 (5)
Sample size
No. sires	100	100	100	100	100	100	100	50	100	500
No. offspring/sire	10	10	10	10	10	10	10	5	10	10

Eight simulations were designed to demonstrate the capabilities of BSFG. Scenarios a–c test genetic and residual covariance matrices composed of different numbers of factors. Scenarios d–e test residual covariance matrices that are not sparse. Scenarios f–g test different numbers of traits. Scenarios h–j test different sample sizes. All simulations followed a paternal half-sib breeding design. Each simulation was run 10 times.

^aSparse factor model for R. Each simulated factor loading (λ_ij) had a 75–97% chance of equaling zero.

^bFactor model for R. Residual factors (those with $h_j^2=0$) were not sparse (λ_ij ≠ 0).

^cR was simulated from a Wishart distribution with p + 1 degrees of freedom and inverse scale matrix $\frac{1}{p}{I}_p$. Five additional factors were each assigned a heritability of 1.0.

^dIn each column, factors are divided between those h² > 0 and those with h² = 0. The number in parentheses provides the number of factors with the given heritability.

Scenarios a–c tested the accuracy of the model given increasing numbers of latent traits. G and P were simulated based on 10, 25, or 50 important factors, respectively, for 100 traits. Heritabilities $\left(h_j^2\right)$ of latent factors j = 1 … 5, 1 … 15, or 1 … 30, respectively, were set to 0.5 and contributed to both G and R. Heritabilities of the remaining factors (j = 6 … 10, 16 … 25, or 31 … 50, respectively) were set to 0.0 and contributed only to R. For each latent factor, loadings λ_ij were drawn from independent standard normal distributions. To make the covariance matrices biologically reasonable, we forced each factor to be sparse: 75–97% of the λ_ij were set to zero. The idiosyncratic variances Ψ_a and Ψ_e were set to 0.2 × I_p. Therefore, trait-specific heritabilties ranged from 0.0 to 0.5, with the majority toward the upper limit. Each simulation included 10 offspring from 100 unrelated sires.

Scenarios d–e tested the accuracy of the model when the true R was neither sparse nor low rank, since inappropriately modeled residual variances can lead to biased estimates of G (e.g., Jaffrezic et al. 2002; Meyer and Kirkpatrick 2007). Scenarios were identical to a except the R matrix did not have a sparse factor form. In scenario d, R was constructed with a factor structure with 10 factors, but 5 of these factors (j = 6 … 10, i.e., those with $h_j^2=0.0$) were not sparse (i.e., all factor loadings were nonzero). This might occur, for example, if the nongenetic factors were caused by measurement error. In scenario e, R was drawn from a central Wishart distribution with p + 1 degrees of freedom and therefore was full rank and did not follow a factor structure at all.

Scenarios f–g tested the accuracy of the model given increasing numbers of observed traits. Both scenarios were identical to scenario a except scenario f had 20 observed traits and scenario g had 1000.

Scenarios h–j tested the accuracy of the model given experiments of different size and given different latent trait heritabilities. Simulations were identical to scenario a except that the five genetic factors in each simulation were assigned $h_j^2=0.9,0.7,0.5,0.3$, and 0.1 for j = 2, 4, 6, 8, 10, the number of sires was set to 50, 100, or 500, and the number of offspring per sire was set to 5 (for simulation h only).

To fit the simulated data, we set the hyperparameters in the prior to: ν = 3, a₁ = 2, b₁ = 1/20, a₂ = 3, b₂ = 1. We ran our Gibbs sampler for 12,000 iterations, discarded the first 10,000 samples as burn-in, and collected 1000 posterior samples with a thinning rate of two.

We calculated a number of statistics from each simulation to quantify the estimation error of the BSFG model. For each statistic, we compared the posterior mean of a model parameter to the true value specified in the simulation.

First, as a sanity check, we compared the accuracy of our method to a methods of moments estimate of G calculated as G_m = 4(B − W)/n, where B and W are the between- and within-sire matrices of mean squares and cross products and n is the number of offspring per sire. We compared the accuracy of the moments estimator G_m to the posterior mean $\widehat{\mathbf{G}}$ from our model by calculating the Frobenius norm of the errors: |G_m − G|_F and ${\left|\widehat{\mathbf{G}}-G\right|}_{\text{F}}$.

The Frobenius norm measure above quantifies the total sum of square error in each pairwise covariance estimate. However, the geometry of G is more important for predicting evolution (Walsh and Blows 2009). We evaluated the accuracy of each estimated G matrix by comparing the k-dimensional subspace of ℝ^p with the majority of the variation in G to the corresponding subspace for the posterior mean estimate $\widehat{\mathbf{G}}$. We used the Krzanowski subspace comparison statistic (Krzanowski 1979; Blows et al. 2004), which is the sum of the eigenvalues of the matrix $S={\widehat{G_k}}^{\text{T}}{G}_k{G}_k^{\text{T}}\widehat{G_k}$, where $\widehat{G_k}$ is the subspace spanned by the eigenvectors with the k largest eigenvalues of the posterior mean of G, and G_k is the corresponding subspace of the true (simulated) matrix. This statistic will be zero for orthogonal (nonoverlapping) subspaces and will equal k for identical subspaces. The accuracy of the estimated P was calculated similarly. For each comparison, k was chosen as the number of factors used in the construction of the simulated matrix (Table 1), except in scenario e with the Wishart-distributed R matrix. Here, we set the k for P at 19, which was sufficient to capture >99% of the variation in most simulated P matrices.

We evaluated the accuracy of latent factor estimates in two ways. First, we calculated the magnitude of each factor as |λ_j|² where |⋅| is the L₂-norm. This quantifies the phenotypic variance across all traits explained by each factor. We then counted the number of factors that explained >0.1% of total phenotypic variance. Such factors were termed “large factors.” Second, for each simulated factor j, we calculated the error in estimated factor identity by finding the estimated factor j* with trait loadings vector ${\mathit{\lambda }}_{j^{*}}$ that had the smallest vector angle with the true factor trait loadings vector λ_j. Smaller angles correspond to more accurately identified factors. For scenarios d and e, error angles could be calculated only for the genetically variable factors (factors 1–5) because the residual factors for these scenarios were not well defined. In scenario d, factors 6–10 were not sparse and thus were identifiable only up to an arbitrary rotation by any matrix H such that HH^T = I (Meyer 2009). In scenario e, the residual matrix did not have a factor form.

Gene expression analysis

We downloaded gene expression profiles and measures of competitive fitness of 40 wild-derived lines of Drosophila melanogaster from ArrayExpress (accession E-MEXP-1594) and the Drosophila Genetic Reference Panel (DGRP) website (http://dgrp.gnets.ncsu.edu/) (Ayroles et al. 2009). A line’s competitive fitness (Knight and Robertson 1957; Hartl and Jungen 1979) measures the percentage of offspring bearing the assay line’s genotype recovered from vials seeded with a known proportion of adults from a reference line. We used the BSFG model to infer a set of latent factor traits underlying the among-line gene expression covariance matrix for a subset of the genes and the among-line covariance between each gene and competitive fitness. These latent factors are useful because they provide insight into what genes and developmental or molecular pathways underlie variation in competitive fitness.

We first normalized the processed gene expression data to correspond to the analyses of Ayroles et al. (2009) and then selected the 414 genes identified in that article as having a plausible among-line covariance with competitive fitness. In this data set, two biological replicates of male and female fly collections from each line were analyzed for whole-animal RNA expression. The competitive fitness measurements were the means of 20 competitive trials performed with sets of flies from these same lines, but not the same flies used in the gene expression analysis. Gene expression values for the samples measured for competitive fitness and competitive fitness values for the samples measured for gene expression were treated as missing data (see Appendix). We used our model to estimate the covariance of line effects. Following the analyses of Ayroles et al. (2009), we included a fixed effect of sex and independent random effects of the sex:line interaction for each gene. No sex or sex:line effects were fit for competitive fitness itself as this value was measured at the level of the line, not on individual flies.

We set the prior hyperparameters as above and ran our Gibbs sampler for 40,000 iterations, discarded the first 20,000 samples as a burn-in period, and collected 1000 posterior samples of all parameters with a thinning rate of 20.

Results

Simulation example

The BSFG model’s estimates of genetic covariances were considerably more accurate than estimates based on unbiased methods of moments estimators. In scenario a, for example, the mean Frobenius norm was 13.9 for the moments estimator and 6.3 for the Bayesian genetic sparse factor model’s posterior mean, a 54% improvement.

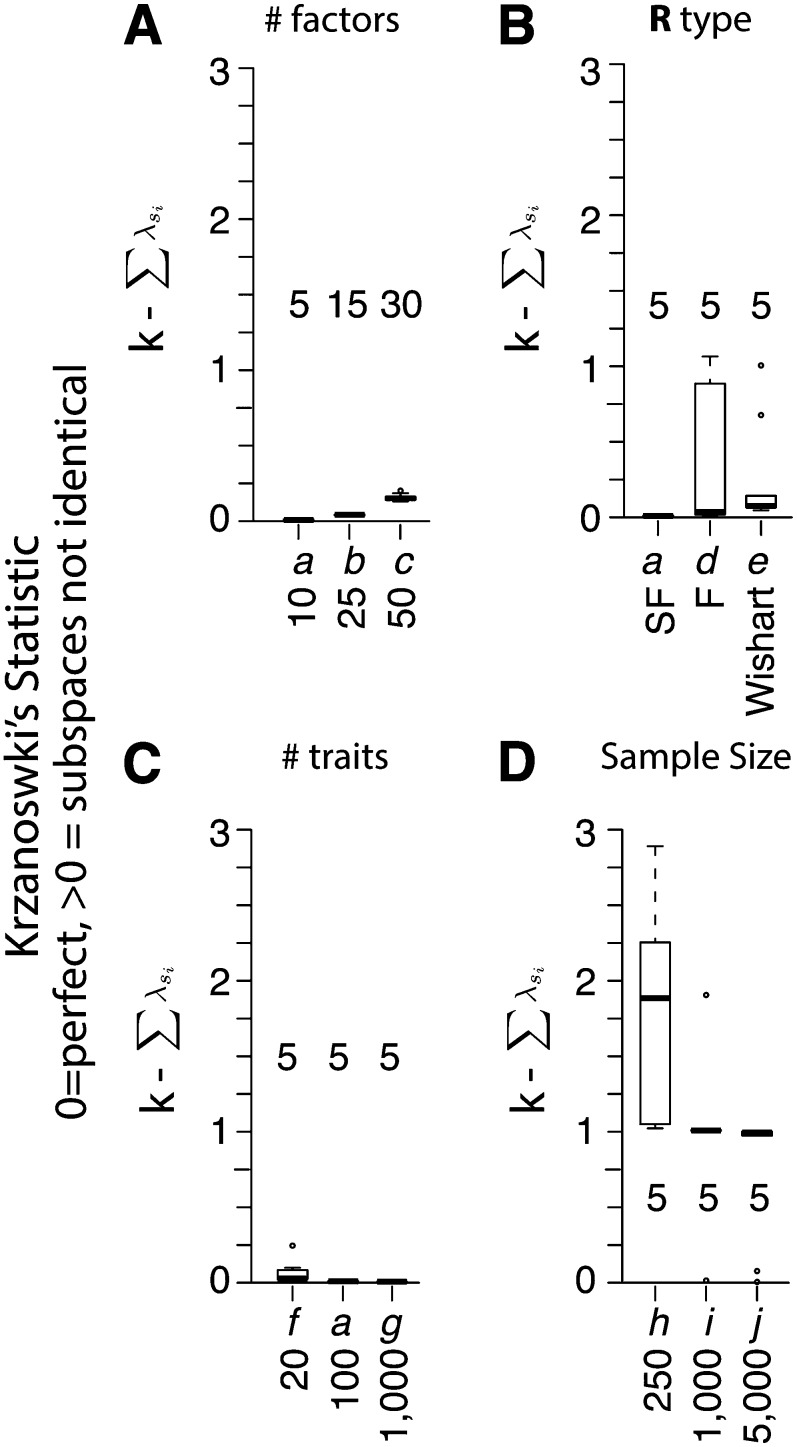
The BSFG model accurately estimated subspaces containing the majority of variation in both G and P. Figure 1 shows the distribution of Krzanowski’s subspace similarity statistics $\left({\displaystyle \sum {\lambda }_{{\text{s}}_i}}\right)$ for G in each scenario (subspace statistics for P are shown in supporting information, Figure S1). Krzanowski’s statistic corresponds approximately to the number of eigenvectors of the true subspace recovered in the estimated subspace and in our simulations rarely differed even one unit from the true value of k for either G and P. The exceptions for G were mostly in scenarios h–j, where the fifth genetic factor (factor 10) was assigned a heritability of 0.1 and the subspace spanned by the first five eigenvectors of estimated G matrices often did not include this vector. This effect was exacerbated at low sample sizes. The Krzanowski error for G (relative to k) also increased slightly for larger numbers of factors (Figure 1A), if R was full rank (Figure 1B), if few traits were observed (Figure 1C), or if the sample size was small (Figure 1D). Some simulations with nonsparse latent factors of R also caused slight subspace errors (scenario d, Figure 1B). Krzanowski’s statistics for P followed a similar pattern to those for G (Figure S1), except that the errors for full-rank R or for different numbers of traits were more pronounced (Figure S1B).

Figure 1.

BSFG recovers the dominant subspace of high-dimensional G-matrices. Each subplot shows the distribution of Krzanowski’s statistics (${\displaystyle \sum {\lambda }_{{\text{s}}_i}}$, Krzanowski 1979; Blows et al. 2004) calculated for posterior mean estimates of G across a related set of scenarios. Plotted values are $k-{\displaystyle \sum {\lambda }_{{\text{s}}_i}}$ so that statistics are comparable across scenarios with different subspace dimensions. On this scale, identical subspaces have a value of zero and values increase as the subspaces diverge. The value of k used in each scenario is listed inside each box plot. The difference from zero roughly corresponds to the number of eigenvectors of the true subspace missing from the estimated subspace. Different parameters were varied in each set of simulations as listed below each box. (A) Increasing numbers of simulated factors. (B) Different types of R matrices. SF, a sparse-factor form for R. F, a (nonsparse) factor form for R. Wishart, R was sampled from a Wishart distribution. (C) Different numbers of traits. (D) Different numbers of sampled individuals. Note that in scenarios h–j, factor h²’s ranged from 0.0 to 0.9. Complete parameter sets describing each simulation are described in Table 1.

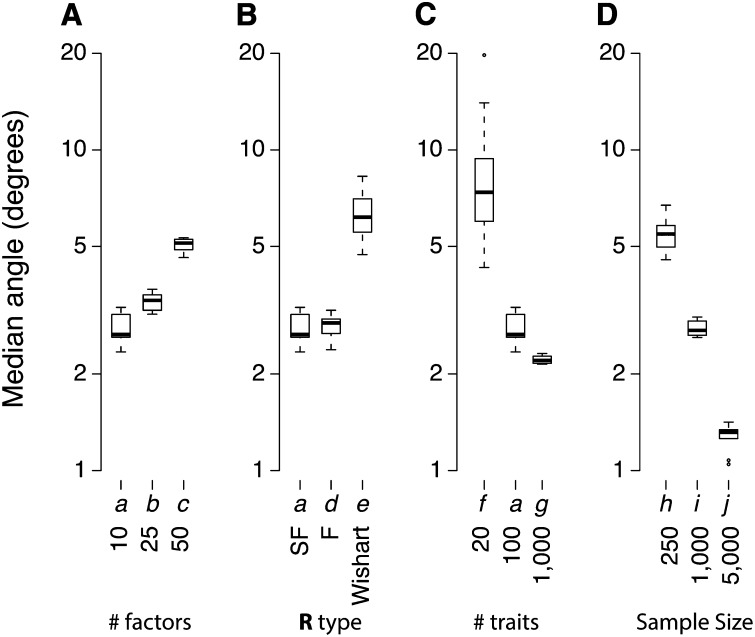
Even though the number of latent factors is not an explicit parameter in the BSFG model, the number of “large factors” fit in each scenario was always close to the true number of simulated factors (Table 2, except in scenario e where R was full rank). Factor identity estimates were also accurate. Figure 2 shows the distribution of error angles between the true factors and their estimates for each scenario. Median error angles were generally around 3°, but occasionally as large 5°–10° when there were more true latent factors (Figure 2A), if R was full rank (scenario e, Figure 2B), or if the sample size was small (small numbers of individuals or small numbers of traits, scenarios f and h; Figure 2, C and D).

Table 2. Number of large factors recovered in each scenario.

Scenario	Expected		Median	Range
No. factors	a	10	10	(10,10)
	b	25	25	(23,25)
	c	50	49	(48,50)
R type	d	10	10	(10,10)
	e	NAa	56	(44,66)
No. traits	f	10	9	(8,11)
	g	10	10	(10,10)
Sample size	h	10	10	(10,10)
	i	10	10	(10,10)
	j	10	10	(10,10)

Each scenario was simulated 10 times. Factor magnitude was calculated as the L₂-norm of the factor loadings, divided by the total phenotypic variance across all traits. Factors explaining >0.1% of total phenotypic variance were considered large.

^aIn scenario e, the residual matrix did not have a factor form.

Figure 2.

BSFG successfully fits trait loadings on latent factors. The estimated factors were matched to the true latent traits in each simulation by calculating the vector angle between the trait loadings of each true factor and the most similar estimated factor (column of Λ). The median error angle across factors was calculated for each simulation. Box plots show the distribution of median error angles by scenario. Two identical vectors have an angle of zero. Completely orthogonal vectors have an angle of 90°. (A) Increasing numbers of simulated factors. (B) Different types of R matrices. Angles are shown only for the genetically variable factors in scenarios d and e (factors 1–5, see Methods). (C) Different numbers of traits. (D) Different numbers of sampled individuals.

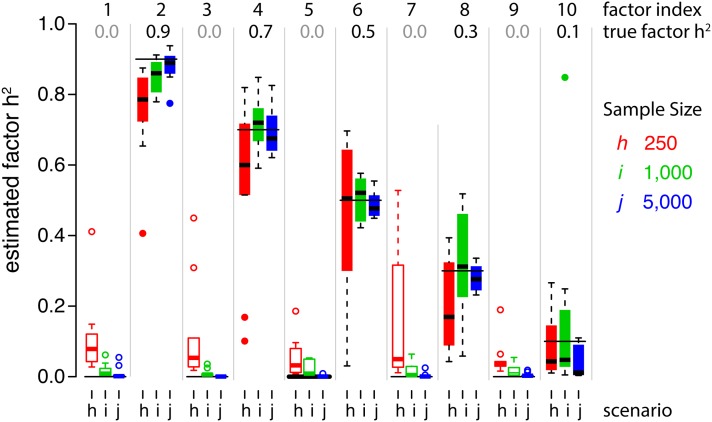
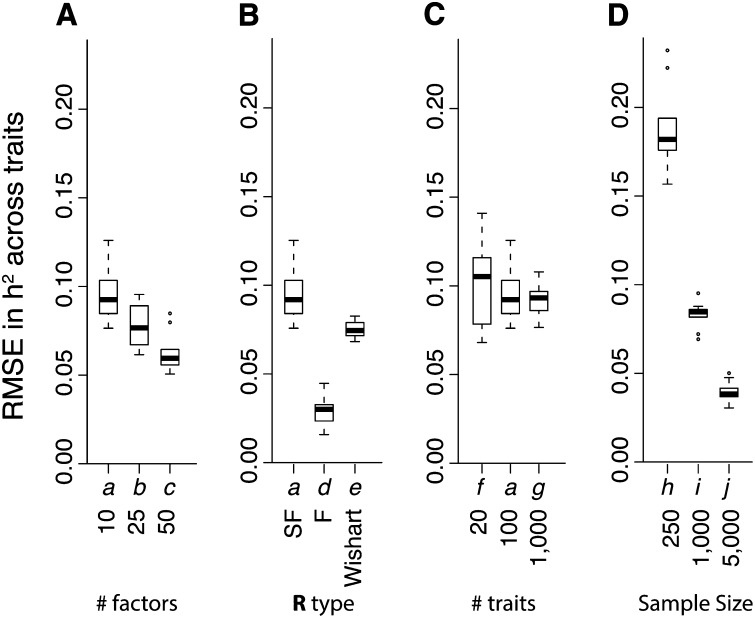
Finally, the genetic architectures of the unobserved latent traits (factors) and the observed traits were accurately estimated. As expected, latent factor heritability estimates were more accurate for scenarios with larger sample sizes (Figure 3), but there was little difference in h² estimates for factors with nonzero heritability across scenarios with different numbers of factors, different residual properties, or different numbers of traits (Figure S2). With small sample sizes (scenario h), larger numbers of factors (scenarios b–c), or fewer traits (scenario f), there was increasing error in h² for factors with true h² = 0 (Figures 3 and Figure S2). Similarly, sample size had the greatest effect on the quality of h² estimates for the 20–1000 traits in each scenario (Figure 4). Surprisingly, the most accurate trait heritability estimates were recovered when R had a factor structure but was not sparse (scenario d, Figure 4B), probably because the true range of h² values was greater. Heritability estimates were also more accurate with increasing complexity of G and R (Figure 4A), but were not strongly affected by the number of traits studied (Figure 4C), or by full-rank R (Figure 4B).

Figure 3.

BSFG accurately estimates the heritability of latent traits. Distributions of factor h² estimates for scenarios h–j. These scenarios differed in the number of individuals sampled. Ten latent traits with h²’s between 0.0 and 0.9 were generated in each simulation. After fitting our factor model to each simulated data set, the estimated factors were matched to the true latent traits based on the trait-loading vector angles. Each box plot shows the distribution of h² estimates for each simulated factor across 10 simulations. Note that the trait loadings for each factor differed in each simulation; only the h² values remained the same. Thin horizontal lines in each column show the simulated h² values. Colors correspond to the scenario, and solid boxes/circles are used for factors with h² > 0.0.

Figure 4.

BSFG estimates of individual trait heritability are accurate. The heritability of each individual trait was calculated as $h_i^2=G_{ii}/P_{ii}$. $\text{RSME}=\sqrt{\left(1/p\right){\displaystyle {\sum }_{i=1}^p{\left({\widehat{h}}_i^2-h_i^2\right)}^2}}$ was calculated for each simulation. Box plots show the distribution of RMSE values for each scenario. (A) Increasing numbers of simulated factors. (B) Different types of R matrices. (C) Different numbers of traits. (D) Different numbers of sampled individuals.

Gene expression example

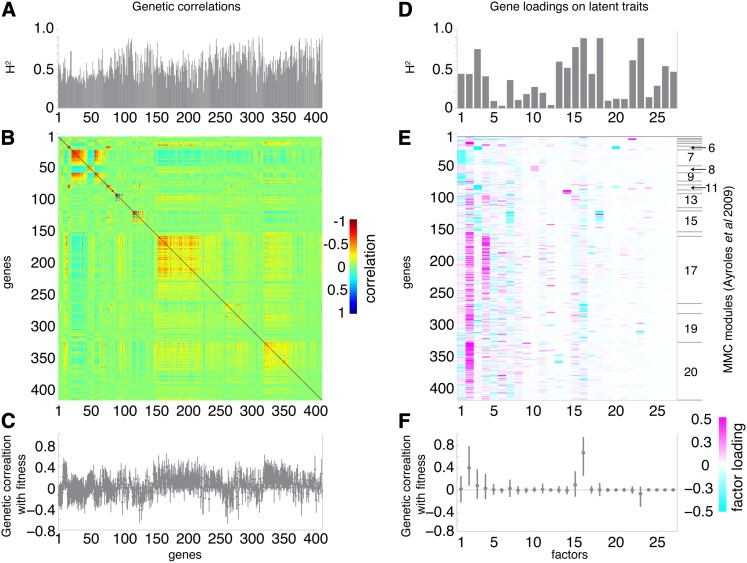
Our estimate of the G-matrix from the Drosophila gene expression data was qualitatively similar to the original estimate (Figure 5B, and compare to Figure 7a in Ayroles et al. 2009). Estimates of the broad-sense heritability of each gene were also similar (r = 0.74). While a direct comparison of the dominant G-matrix subspace recovered by our model and the estimate by Ayroles et al. (2009) was not possible because individual covariances were not reported, we could compare the two estimates of the underlying structure. Using the modulated modularity clustering (MMC) algorithm (Stone and Ayroles 2009), Ayroles et al. (2009) identified 20 modules of genetically correlated transcripts post hoc. Our model identified 27 latent factors (Figure 5, D–F), of which 13 were large factors (explaining >1% variation in 2⁺ genes). The large factors were consistent (r > 0.95) across three parallel chains of the Gibbs sampler. Many factors were similar to the modules identified by MMC (Figure 5E). Some of the factors were nearly one-to-one matches to modules (e.g., factor 10 with module 8, and factor 14 with module 12). However, others merged together two or more modules (e.g., factor 1 with modules 7 and 9, and factor 2 with modules 4, 13, 16–20). And some entire modules were part of two or more factors (e.g., module 17 was included in factors 2 and 4, and module 18 was included in factors 2 and 16).

Figure 5.

Among-line covariance of gene expression and competitive fitness in Drosophila is modular. (A–C) Genetic (among-line) architecture of 414 gene expression traits measured in adult flies of 40 wild-caught lines (Ayroles et al. 2009). (A) Posterior mean broad-sense heritabilities (H²) of the 414 genes. (B) Heat map of posterior mean genetic correlations among these genes. (C) Posterior mean estimates and 95% highest posterior density (HPD) intervals for genetic correlations between each gene and competitive fitness. For comparison, see Ayroles et al. (2009, Figure 7a). (D–F) Latent trait structure underlying gene expression covariances. (D) Posterior mean H² for each estimated latent trait. (E) Heat map of posterior mean Λ matrix showing gene loadings on each latent trait. (F) Posterior mean estimates and 95% HPD intervals for genetic correlations between each latent trait and competitive fitness. The right axis of E groups genes into modules inferred using modulated modularity clustering (Ayroles et al. 2009; Stone and Ayroles 2009).

Each factor represents a sparse set (or “module”) of genes that may be coregulated by a common developmental process. Using the Database for Annotation, Visualization and Integrated Discovery (DAVID) v. 6.7 (Huang et al. 2009a,b), we identified several factors that were individually enriched (within this set of 414 genes) for defense and immunity, nervous system function, odorant binding, and transcription and cuticle formation. Similar molecular functions were identified among the modules identified by Ayroles et al. (2009). By inferring factors at the level of phenotypic variation, rather than the among-line covariances, we could directly estimate the broad-sense heritability (H²) of these latent traits themselves. Figure 5D shows these H² estimates for each latent trait. Several of the factors have very low (<0.2) or very high (>0.75) H² values. Selection on the later latent traits would likely be considerably more efficient than the former.

Finally, we estimated the among-line correlation between the expression of each gene and competitive fitness (Figure 5C). Roughly 15% (60/414) of the 95% highest posterior density (HPD) interval estimates of the among-line correlations did not included zero. We also estimated the genetic correlation between competitive fitness and each of the latent traits defined by the 27 factors (Figure 5F). Most factors were not genetically correlated with competitive fitness. However, the genetic correlations between competitive fitness and factors 2 and 16 were large and highly significant, suggesting intriguing genetic relationships between these two latent traits and fitness.

Discussion

The BSFG model performs well on both simulated and real data and opens the possibility of incorporating high-dimensional traits into evolutionary genetic studies and breeding programs. Technologies for high-dimensional phenotyping are becoming widely available in evolutionary biology and ecology so methods for modeling such traits are needed. Gene expression traits in particular provide a way to measure underappreciated molecular and developmental traits that may be important for evolution, and technologies exist to measure these traits on very large scales. Our model can be applied to other molecular traits (e.g., metabolites or protein concentrations), high-dimensional morphological traits (e.g., outlines of surfaces from geometric morphometrics), or gene–environment interactions (e.g., the same trait observed in multiple environments).

Scalability of the method

The key advantage of the BSFG model over existing methods is its ability to provide robust estimates of covariance parameters for data sets with large numbers of traits. In this study, we demonstrated high performance of the model for 100–1000 simulated traits and robust results on real data with 415. Similar factor models (without the genetic component) have been applied to gene expression data sets with thousands of traits (Bhattacharya and Dunson 2011), and we expect the genetic model to perform similarly. The main limitation will be computational time, which scales roughly linearly with the number of traits analyzed (assuming the number of important factors grows more slowly). As an example, analyses of simulations from scenario g with 1000 traits and 1000 individuals took about 4 hr to generate 12,000 posterior samples on a laptop computer with a 4-core 2.4-GHz Intel Core i7, while analyses of scenario a with 100 traits took ∼45 min. Parallel computing techniques may speed up analyses in cases of very large (e.g., 10,000+) numbers of traits.

The main reason that our model scales well in this way is that under our prior, each factor is sparse. Experience with factor models in fields such as gene expression analysis, economics, finance, and social sciences (Fan et al. 2011), as well as with genetic association studies (e.g., Engelhardt and Stephens 2010; Stegle et al. 2010; Parts et al. 2011) demonstrates that sparsity (or shrinkage) is necessary to perform robust inference on high-dimensional data (Bickel and Levina 2008a,b; El Karoui 2008; Meyer and Kirkpatrick 2010). Otherwise, sampling variability can overwhelm any true signals, leading to unstable estimates. Here, we used the t-distribution as a shrinkage prior, following Bhattacharya and Dunson (2011), but many other choices are possible (Armagan et al. 2011).

Applications to evolutionary quantitive genetics

The G-matrix features prominently in the theory of evolutionary quantitative genetics, and its estimation has been a central goal of many experimental and observational studies (Walsh and Blows 2009). Since the BSFG model is built on the standard “animal model” framework, it is flexible and can be applied to many experimental designs. And since the BSFG model is Bayesian and naturally produces estimates within the parameter space, posterior samples provide convenient credible intervals for the G-matrix itself and for many evolutionarily important parameters, such as trait-specific eritabilities or individual breeding values (Sorensen and Gianola 2010).

An important use of the G-matrix is to predict the response of a set of traits to selection (Lande 1979). Applying Robertson’s second theorem of natural selection, the response in $\overline{\mathbf{y}}$ will equal the additive genetic covariance between the vector of traits and fitness $\left(\Delta \overline{\mathbf{y}}={\sigma }_{\text{A}}\left(y,\overline{w}\right)\right)$ (Rausher 1992; Walsh and Blows 2009). This quantity can be estimated directly from our model if fitness is included as the p* = (p + 1)th trait,

$$\Delta \overline{\mathbf{y}}={\Lambda }_{/p^{*}}{\Lambda }_{p^{*}}^{\text{T}},$$

where ${\Lambda }_{/p^{*}}$ contains all rows of Λ except the row for fitness, and ${\Lambda }_{p^{*}}$ contains only the row of Λ corresponding to fitness. Similarly, the quantity $1-{\psi }_{{\text{a}}_{p^{*}}}/G_{p^{*},p^{*}}$ equals the percentage of genetic variation in fitness accounted for by variation in the observed traits (Walsh and Blows 2009), which is useful for identifying other traits that might be relevant for fitness.

On the other hand, our model is not well suited to estimating the dimensionality of the G-matrix. A low-rank G-matrix means that there are absolute genetic constraints on evolution (Lande 1979). Several methods provide statistical tests for the rank of the G-matrix (e.g., Kirkpatrick and Meyer 2004; Mezey and Houle 2005; Hine and Blows 2006). We use a prior that shrinks the magnitudes of higher index factors to provide robust estimates of the largest factors. This will likely have a side effect of underestimating the total number of factors, although this effect was not observed in our simulations. However, absolute constraints appear rare (Houle 2010), and the dimensions of the G-matrix with the most variation are likely those with the greatest effect on evolution in natural populations (Schluter 1996; Kirkpatrick 2009). Our model should estimate these dimensions well. From a practical standpoint, preselecting the number of factors has plagued other reduced-rank estimators of the G-matrix (e.g., Kirkpatrick and Meyer 2004; Hine and Blows 2006; Meyer 2009). Our prior is based on an infinite factor model (Bhattacharya and Dunson 2011), and so no a priori decision on k is needed. Instead, the parameters of the prior distribution on {τ_j} become important modeling decisions. In our experience, a relatively diffuse prior on δ_l with a₂ = 3, b₂ = 1 tends to work well.

Biological interpretation of factors

Genetic modules are sets of traits likely to evolve together. We assume that the developmental process is modular and model a set of latent traits that each affect a limited number of observed traits. A unique feature of the BSFG model is that the genetic and environmental factors are estimated jointly, instead of separately as in classic multilevel factor models (e.g., Goldstein 2010). If each factor represents a true latent trait (e.g., variation in a developmental process), it is reasonable to decompose variation in this trait into genetic and environmental components. We directly estimate the heritability of the latent traits and, therefore, can use our model to predict their evolution.

Other techniques for identifying genetic modules have several limitations. The MMC algorithm (Stone and Ayroles 2009; Ayroles et al. 2009) does not infer modules in an explicit quantitative genetic framework and constrains each observed trait to belong to only one module. A common strategy (e.g., McGraw et al. 2011) is to treat each major eigenvector of G or P itself as a module. These eigenvectors can be modeled directly (e.g., Kirkpatrick and Meyer 2004), but their biological interpretation is unclear because of the mathematical constraint that the eigenvectors be orthogonal (Hansen and Houle 2008). Classic factor models (such as proposed by Meyer 2009 or de los Campos and Gianola 2007) assume a form of modularity, but since the latent factors are not identifiable (Meyer 2009), the identity of the underlying modules is unclear. In contrast, under our sparsity prior, the modules we identify are identifiable (up to a sign-flip: the loadings on each factor can be multiplied by −1 without affecting its probability under the model, but this does not change which traits are associated with each factor). In simulations and with the Drosophila gene expression data, independent MCMC chains consistently identify the same dominant factors. Therefore the observed traits associated with each factor can be used to characterize a developmental module.

Extensions

Our model is built on the classic mixed effect model in quantitative genetics (Henderson 1984). It is straightforward to extend to models with additional fixed or random effects (e.g., dominance or epistatic effects) for each trait. The update equation for $h_j^2$ in the Gibbs sampler described in the Appendix does not allow additional random effects in the model for the latent factors themselves, although other formulations are possible. A second extension relates to the case in which the relationship matrix among individuals (A) is unknown. Here, relationship estimates from genotype data can be easily incorporated. As such, our model is related to a recently proposed sparse factor model for genetic associations with intermediate phenotypes (Parts et al. 2011). These authors introduced prior information on genetic modules from gene function and pathway databases, which could be incorporated in our model in a similar way.

Conclusions

The BSFG model we propose provides a novel approach to genetic estimation with high-dimensional traits. We anticipate that incorporating many diverse phenotypes into genetic studies will provide powerful insights into evolutionary processes. The use of highly informative but biologically grounded priors is necessary for making inferences on high-dimensional data and can help identify developmental mechanisms underlying phenotypic variation in populations.

Appendix: Posterior sampling

We estimate the posterior distribution of the BSFG model with an adaptive partially collapsed Gibbs sampler (van Dyk and Park 2011) based on the procedure proposed by Bhattacharya and Dunson (2011). The value k* at which columns in Λ are truncated is set using an adaptive procedure (Bhattacharya and Dunson 2011). Given a truncation point, the following conditional posterior distributions are sampled in order:

1. The full conditional posterior distribution of the truncated factor loading matrix ${\Lambda }_{k^{*}}$ is dependent on the parameters B, E_a, F = F_a + F_r, and ${\Psi }_{\text{r}}=\text{Diag}\left({\psi }_{{\text{r}}_j}\right)$. The full density factors into independent multivariate normal densities (MVNs) for each row of ${\Lambda }_{k^{*}}$:

   $$\pi \left({\mathit{\lambda }}_j|y_j,b_j,e_{{\text{a}}_j},F,{\psi }_{{\text{r}}_j}\right)\sim \text{N}\left({\psi }_{{\text{r}}_j}^{-1}{C}^{-1}{F}^T\left(y_j-X{b}_j-Z{e}_{{\text{a}}_j}\right),C^{-1}\right),$$

   where

   $$C={\psi }_{{\text{r}}_j}^{-1}{F}^{\text{T}}F+\text{Diag}\left({\phi }_{ij}{\tau }_j\right)$$.
   To speed up the MCMC mixing, we partially collapse this Gibbs update step by marginalizing over E_a ∼ N(0, A, Ψ_a). Let ${\Psi }_{\text{a}}=\text{Diag}\left({\psi }_{{\text{a}}_j}\right)$,

   $${\pi }_{/e_{a_j}}\left({\mathit{\lambda }}_j|y_j,\hspace{0.17em}{b}_j,\hspace{0.17em}F,\hspace{0.17em}{\psi }_{{\text{a}}_j},\hspace{0.17em}{\psi }_{{\text{r}}_j}\right)\sim \text{N}\left(C^{*-1}{F}^{\text{T}}{\left({\psi }_{{\text{r}}_j}{I}_n+{\psi }_{{\text{a}}_j}ZA{Z}^{\text{T}}\right)}^{-1}\left(y_j-X{b}_j\right),C^{*-1}\right),$$

   where $C^{*}=F^{\text{T}}{\left({\psi }_{{\text{r}}_j}{I}_n+{\psi }_{{\text{a}}_j}ZA{Z}^{\text{T}}\right)}^{-1}F+\text{Diag}\left({\phi }_{ij}{\tau }_j\right)$.

   The matrix sum ${\psi }_{{\text{r}}_j}{I}_n+{\psi }_{{\text{a}}_j}ZA{Z}^{\text{T}}$ can be efficiently inverted each MCMC iteration by precalculating a unitary matrix U and a diagonal matrix S such that ZAZ^T = USU^T. Thus, ${\left({\psi }_{{\text{r}}_j}{I}_n+{\psi }_{{\text{a}}_j}ZA{Z}^{\text{T}}\right)}^{-1}=U\hspace{0.5em}\text{Diag}\left(1/\left({\psi }_{{\text{r}}_j}{s}_{ii}+{\psi }_{{\text{a}}_j}\right)\right)U^{\text{T}}$, which does not require a full matrix inversion.

2. The full conditional posterior distribution of the joint matrix ${\left[B^{\text{T}}\hspace{0.17em}{E}_{\text{a}}^{\text{T}}\right]}^{\text{T}}$ is dependent on the parameters F, Λ, Ψ_a, and Ψ_r. The full density factors into independent MVNs for each column of the matrix,

   $$\pi \left(\left[\begin{array}{c}{b}_j\\ e_{{\text{a}}_j}\end{array}\right]|y_j,{\mathit{\lambda }}_j,\hspace{0.17em}F,{\psi }_{{\text{a}}_j},{\psi }_{{\text{r}}_j}\right)\sim \text{N}\left({\psi }_{{\text{r}}_j}^{-1}{C}^{-1}{W}^{\text{T}}\left(y_j-F{\mathit{\lambda }}_j^{\text{T}}\right),C^{-1}\right),$$

   whereW and C are defined as

   $$\begin{array}{l}\mathbf{W}=\left[\mathbf{X}\hspace{0.5em}\mathbf{Z}\right]\\ C=\left[\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\psi }_{{\text{a}}_j}^{-1}{A}^{-1}\end{array}\right]+{\psi }_{{\text{r}}_j}^{-1}{W}^{\text{T}}W.\end{array}$$

   The precision matrix C can be efficiently inverted each MCMC iteration by precalculating the unitary matrix U and diagonal matrices S₁ and S₂ as the generalized singular value decomposition of the Cholesky decomposition of the two components of C such that $C^{-1}=U\hspace{0.5em}\text{Diag}\left(1/\left({\psi }_{{\text{a}}_j}{s}_{1_{ii}}+{\psi }_{{\text{r}}_j}{s}_{2_{ii}}\right)\right)U^{\text{T}}$, which does not require a full matrix inversion.

3. The full conditional posterior distribution of the latent factor heritabilities, ${\Sigma }_{h^2}=\text{Diag}\left(h_j^2\right)$, is dependent on F and F_a. The density factors into independent distributions for each $h_j^2$, each of which has the form of a multinomial distribution since the prior on this parameter is discrete. This update step can be partially collapsed by marginalizing over $F_{\text{a}}\sim \text{N}\left(\mathbf{0},A,{\Sigma }_{\text{a}}\right)$. The partially collapsed density is normalized by summing over all possibilities of $h_j^2$,

   $${\pi }_{/f_{a_j}}\left(h_j^2=h^2|f_j\right)=\frac{\text{N}\left(f_j|\mathbf{0},h^{2}ZA{Z}^{\text{T}}+\left(1-h^2\right)I_n\right){\pi }_{h_j^2}\left(h^2\right)}{{\displaystyle {\sum }_{l=1}^{n_h}\text{N}\left(f_j|\mathbf{0},h_l^{2}ZA{Z}^{\text{E}}+\left(1-h_l^2\right)I_n\right){\pi }_{h_j^2}\left(h_l^2\right)}}$$

   where N(x|μ, Σ) is the MVN with mean μ and variance Σ, evaluated at x, $h_l^2=l/n_h$, and ${\pi }_{h_j^2}\left(h^2\right)$ is the prior probability that $h_j^2=h^2$. Given this conditional posterior, $h_j^2$ is sampled from a multinomial distribution. The MVN densities can be calculated efficiently with the diagonalization matrices given in step 1.

4. The full conditional posterior distribution of the genetic effects on the factors, F_a, depends on F and Σ_a. This distribution factors into independent MVNs for each column $f_{a_j},j=1\dots k^{*} \text{st} h_j^2\ne 0$,

   $$\pi \left(f_{a_j}|f_j,h_j^2\right)\sim \text{N}\left({\left(1-h_j^2\right)}^{-1}{C}^{-1}Z{F}_j,C^{-1}\right)$$,

   where $C={\left(1-h_j^2\right)}^{-1}Z{Z}^{\text{T}}+{\left(h_j^2\right)}^{-1}{A}^{-1}$.

   The precision matrix C can be efficiently inverted each MCMC iteration in the same manner as in step 2.

5. The residuals of the genetic effects on the factor scores, F_r, can be calculated as F − F_a. The full conditional posterior distribution of F is a matrix variate normal distribution that depends on $\Lambda ,\hspace{0.17em}B,\hspace{0.17em}{E}_{\text{a}},{\Sigma }_{h^2}$ and Ψ_r:

   $$\pi \left(F|Y,\Lambda ,B,E_{\text{a}},{\Sigma }_{h^2},{\Psi }_{\text{r}}\right)\sim {\text{MN}}_{n,k^{*}}\left(\left(\left(Y-XB-Z{E}_{\text{a}}\right){\Psi }_{\text{r}}^{-1}{\Lambda }_{k^{*}}+Z{F}_{\text{a}}{\left(I_{k^{*}}-{\Sigma }_{h^2}\right)}^{-1}\right)C^{-1},I_n,C^{-1}\right),$$

   where

   $$C={\Lambda }_{k^{*}}^{\text{T}}{\Psi }_{\text{r}}^{-1}{\Lambda }_{k^{*}}+{\left(I_{k^{*}}-{\Sigma }_{h^2}\right)}^{-1}$$.
6. The conditional posterior of the factor loading precision parameter φ_ij for trait i on factor j is

   $$\pi \left({\phi }_{ij}|{\tau }_j,{\lambda }_{ij}\right)\sim \text{Ga}\left(\frac{\nu +1}{2},\frac{\nu +{\tau }_j{\lambda }_{ij}^2}{2}\right).$$
7. The conditional posterior of δ_m, m = 1 … k* is as follows. For δ₁,

   $$\pi \left({\delta }_1|\phi ,{\tau }_l^{\left(1\right)},\mathbf{\Lambda }\right)\sim \text{Ga}\left(a_1+\frac{p{k}^{*}}{2},b_1+\frac{1}{2}{\displaystyle \sum _{l=1}^{k^{*}}{\tau }_l^{\left(1\right)}}{\displaystyle \sum _{j=1}^p{\phi }_{jl}{\lambda }_{jl}^2}\right)$$

   and for

   $${\delta }_h,\hspace{1em}h\ge 2,$$

   $$\pi \left({\delta }_h|\phi ,{\tau }_l^{\left(h\right)},\mathbf{\Lambda }\right)\sim \text{Ga}\left(a_2+\frac{p}{2}\left(k^{*}-h+1\right),b_2+\frac{1}{2}{\displaystyle \sum _{l=h}^{k^{*}}{\tau }_l^{\left(h\right)}}{\displaystyle \sum _{j=1}^p{\phi }_{jl}{\lambda }_{jl}^2}\right),$$

   where

   $${\tau }_l^{\left(h\right)}={\displaystyle {\sum }_{t=1,t\ne h}^l{\delta }_t}$$.

   The sequence {τ_j} is calculated as the cumulative product: $\left\{{\displaystyle {\prod }_{m=1}^j{\delta }_m}\right\}$.

8. The conditional posterior of the precision of the residual genetic effects of trait j is

   $$\pi \left({\psi }_{{\text{a}}_j}^{-1}|e_{{\text{a}}_j}\right)\sim \text{Ga}\left(a_{\text{a}}+\frac{r}{2},b_{\text{a}}+\frac{1}{2}{e}_{{\text{a}}_j}^{\text{T}}{e}_{{\text{a}}_j}\right).$$
9. The conditional posterior of the residual precision of model residuals for trait j is

   $$\pi \left({\psi }_{e_j}^{-1}|-\right)\sim \text{Ga}\left(a_{\text{r}}+\frac{n}{2},b_{\text{r}}+\frac{1}{2}\stackrel{n}{{\displaystyle \sum }_{i=1}}{\left(y_{ij}-x^{\left(i\right)}{b}_j-f^{\left(i\right)}{\mathit{\lambda }}_j^{\text{T}}-z^{\left(i\right)}{e}_{{\text{a}}_j}\right)}^2\right).$$
10. If missing observations are present, values are drawn independently from univariate normal distributions parameterized by the current values of all other parameters,

    $$\pi \left(y_{ij}|-\right)\sim \text{N}\left(x^{\left(i\right)}{b}_j+f^{\left(i\right)}{\mathit{\lambda }}_j^{\text{T}}+z^{\left(i\right)}{e}_{{\text{a}}_j},{\psi }_j\right),$$

    where y_ij is the imputed phenotype value for the jth trait in individual i. The three components of the mean are: x⁽ⁱ⁾, the row vector of fixed effect covariates for individual i times b_j, the jth column of the fixed effect coefficient matrix; f⁽ⁱ⁾, the row vector of factor scores on the k* factors for individual i times ${\mathit{\lambda }}_j^{\text{T}}$, the row of the factor loading matrix for trait j; and z⁽ⁱ⁾, the row vector of the random (genetic) effect incidence matrix for individual i times $e_{{\text{a}}_j}$, the vector of residual genetic effects for trait j not accounted for by the k* factors. Finally, ψ_j is the residual variance of trait j. All missing data are drawn in a single block update.

    Other random effects, such as the line × sex effects modeled in the gene expression example of this article can be incorporated into this sampling scheme in much the same way that the residual genetic effects, E_a, are included here.