Electron spin resonance studies of trityl OX063 at optimal concentration for DNP

Abstract

We have performed temperature-dependent electron spin resonance (ESR) measurements of the stable free radical trityl OX063, an efficient polarizing agent for dissolution dynamic nuclear polarization (DNP), at the optimum DNP concentration (15 mM). We have found that (i) when compared to the W-band electron spin-lattice relaxation rate T_1e⁻¹ of other free radicals used in DNP at the same concentration, trityl OX063 has slower T_1e⁻¹ than BDPA and 4-oxo-TEMPO. At T> 20 K, the T_1e⁻¹ vs T data of trityl OX063 appears to follow a power law dependence close to the Raman process prediction whereas at T<10 K, electronic relaxation slows and approaches the direct process behaviour. (ii) Gd³⁺ doping, a factor known to enhance DNP, of trityl OX063 samples measured at W-band resulted in monotonic increases of T_1e⁻¹ especially at temperatures below 20–40 K while the ESR lineshapes remained essentially unchanged. (iii) The high frequency ESR spectrum can be fitted with an axial g-tensor with a slight g-anisotropy: g_x=g_y=2.00319(3) and g_z=2.00258(3). Although the ESR linewidth D monotonically increases with field, the temperature-dependent T_1e ⁻¹ is almost unchanged as the ESR frequency is increased from 9.5 GHz to 95 GHz, but becomes faster at 240 GHz and 336 GHz. The ESR properties of trityl OX063 reported here may provide insights into the efficiency of DNP of low-γ nuclei performed at various magnetic fields, from 0.35 T to 12 T.

1 Introduction

The carbon-centered tris{8-carboxyl-2,2,6,6-benzo(1,2-d:4,5-d)-bis(1,3)dithiole-4-yl}methyl sodium salt or trityl OX063 (see structure in Fig. 1) belongs to a family of triarylmethyl free radicals that has been used in Overhauser-enhanced magnetic resonance imaging (OMRI),¹ proton-electron double resonance imaging (PEDRI),^2,3 as a dual pH and oxygen electron spin resonance (ESR) probe,⁴ and recently as a polarizing agent in dissolution dynamic nuclear polarization (DNP).⁵ Trityl OX063 has a highly symmetric structure which reduces g-anisotropy and the carbon center is surrounded mainly by spin-less nuclei which minimizes hyperfine interaction; thus it has one of the narrowest ESR line widths (D) among all free radicals.^6,7 In this work, we describe ESR investigations of the relaxation properties of trityl OX063 at the optimum concentration for DNP and discuss the results in the context of maximal transferred polarization to the coupled nuclear spins.

Fig. 1.

The structures of the free radical polarising agents and the Gd³⁺ complex discussed in this work.

DNP enhances the NMR signal by transferring the high electron thermal polarization of paramagnetic centers to the target nuclear spins via microwave irradiation at low temperature and high magnetic field.^8–11 This NMR signal amplification technique has been used for the production of polarised targets in particle and nuclear physics experiments since the 1960s.^8–11 DNP has recently received renewed interest in chemistry^12,13 and biomedical research^14–16 with the invention of the rapid dissolution method in 2003.⁵ Central to the DNP process is the source of paramagnetic electrons, typically provided by doping the sample with stable free radicals, the ESR properties of which have a dramatic effect on the efficiency of the DNP process.^7–11 Mounting evidence has shown that the narrow ESR linewidth trityl OX063 is a more efficient polarising agent for low-γ nuclei such as ¹³C, ²H, and ⁸⁹Y compared to broader linewidth free radicals such as TEMPO in the regime of 2–5 T and 1 K.^7,17,18 In the context of the thermal mixing DNP process, narrow ESR linewidths correspond to lower specific heat of the electron dipolar system, which eventually leads to a lower spin temperature of the nuclear Zeeman system.^7,19 Aside from the ESR linewidth D, the electron spin-lattice relaxation time T_1e of the paramagnetic center has also been implicated as a factor in achieving a lower spin temperature of the nuclear Zeeman system in DNP.^7,19,20 Thus, the ESR properties, namely the ESR linewidth and relaxation play a crucial role in attaining high nuclear polarization in DNP. In this light, we have measured these two important ESR parameters of trityl OX063 at an optimum concentration for DNP (15 mM)²¹ under various perturbations: temperature, magnetic field or ESR frequency (9.5 GHz, 95 GHz, 240 GHz, and 336 GHz), and in the presence of Gd³⁺, an electron T_1e relaxation agent known to enhance DNP, at 95 GHz.^{17,18,22–24} Furthermore, the W-band ESR results of trityl OX063 are compared with the ESR properties of two other well-known free radical polarizing agents in dissolution DNP, the carbon-centered BDPA and the nitroxide-based 4-oxo-TEMPO.

2 Materials and Methods

Sample preparations

Trityl OX063 (tris{8-carboxyl-2,2,6,6-benzo(1,2-d:4,5-d)-bis(1,3)dithiole-4-yl}methyl sodium salt) was obtained from Oxford Instruments Molecular Biotools (Tubney Woods, UK) while BDPA (1,3-bisdiphenylene-2-phenylallyl) and 4-oxo-TEMPO (4-oxo-2,2,6,6-tetramethyl-1-piperidinyloxy) were purchased from Sigma Aldrich (St. Louis, MO). These free radicals (see the structures in Fig. 1) and the corresponding solvents were used without further purification. The following samples were prepared for ESR measurements: (a) 4.28 mg trityl OX063 was dissolved in a 200 μL solution containing 1:1 (v/v) glycerol:water. The final concentration of trityl OX063 in the solution was 15 mM. (b) 3 mg BDPA was dissolved in 100 μL sulfolane solution via sonication as described previously,²⁵ then mixed with equal volume of DMSO. The final concentration of BDPA in the solution was 15 mM. (c) 1 mg 4-oxo-TEMPO was dissolved in 400 μL solution containing 1:1 (v/v) glycerol:water. The final concentration of 4-oxo-TEMPO in the solution was 15 mM. (d) Trityl OX063 samples as described in (a) were prepared separately and then doped with different concentrations (0, 1, 5 mM) of the Gd³⁺ complex of 2-[4-(2-hydroxypropyl)-7,10-bis(2-oxido-2-oxoethyl)-1,4,7,10-tetrazacyclododec-1-yl]acetate or Gd-HP-DO3A (commercially known as ProHance®, Bracco Diagnostics, NJ; see structure in Fig. 1). These aforementioned samples were not degassed.

ESR Measurements

The ESR experiments were performed at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee, FL. The X (9.5 GHz) and W-band (95 GHz) measurements were done on a Bruker E680 ESR spectrometer (Bruker, Billerica, MA) using a dielectric resonator for X-band (Bruker, ER 4118X-MD5), and a cylindrical cavity for W-band (Bruker E-600-1021 HE). On the other hand, the ESR experiments at 240 GHz and 336 GHz were performed on homebuilt quasi-optical superheterodyne ESR spectrometers where a configuration without a cavity was used.^26,27 The trityl OX063 samples were measured at 9.5 GHz, 95 GHz, 240 GHz, and 336 GHz, whereas the BDPA, 4-oxo-TEMPO, and the Gd³⁺-doped trityl OX063 samples were only measured in the W-band. The ESR spectra were recorded by an echo-detected field sweep method, except for Gd³⁺-doped trityl OX063 samples where a continuous wave field sweep technique was used to ensure proper ESR intensity detection over a wide field range covering both the ESR spectra of trityl OX063 and the Gd³⁺-complex. Temperature-dependent spin-lattice relaxation time T_1e data were recorded by saturation recovery technique. Temperature control and readout was done by a Lakshore Model 336 temperature controller (Lakeshore Cryotronics Inc., Westerville, OH).

Data analyses

Analyses of the electron T_1e magnetization recovery curves and fitting of the temperature-dependent relaxation data were done using Igor Pro version 6 (Wavemetrics Inc., Portland, OR). The estimation of the ESR parameters were done using a homebuilt program EPRCalc.²⁸ A Si:P reference with a concentration 10¹⁶ P spins/cm³ (g=1.99852) was used to estimate the high field ESR parameters.

3 Results and Discussion

A key element to achieving the maximum nuclear polarization in the context of thermodynamic model of DNP is to minimize the spin temperature T_s of the nuclear spin system defined by T_s=(2D/ω_e)T_L[η(1+f)]^1/2, where D is the ESR linewidth, ω_e is the electron Larmor frequency, T_L is the lattice temperature or the operating temperature of the polarizer, f is the nuclear relaxation leakage factor, and η is the ratio of the electron Zeeman relaxation time T_1e,Z over electron dipolar relaxation time T_1e,D.^7,19 Based on this equation, a minimum T_s of the nuclear spin system and henceforth higher nuclear polarization in the thermal mixing regime can be achieved by: (i) using a free radical with small ESR linewidth D (ii) lower lattice temperature T_L (lower operating temperature of the polarizer) (iii) higher microwave frequency/increased magnetic field (iv) low nuclear relaxation “leakage” factor f, which refers to relaxation pathways other than through the electron dipolar system and (v) having a minimal value of η. It should be noted that these trends are expected for DNP of low-γ nuclear spins where the dominant DNP mechanism is thermal mixing,^7,17,18,29 a condition achieved when the ESR linewidth D is greater than or comparable to the nuclear Larmor frequency ω_n. This is the case for dissolution DNP of low-γ nuclear spins such as ¹³C where the microwave source power close to 100 mW is sufficient for the efficient polarization transfer. On the other hand, DNP of high-γ nuclei such as protons using narrow ESR linewidth free radicals such as trityl OX063 or BDPA is expected to proceed predominantly via the solid effect, which necessitates higher microwave power on the order of 1–10 W for efficient DNP.³⁰ In both cases, ESR parameters play a central role in achieving highly polarized NMR signals at conditions typically used for dissolution DNP.

The ESR samples measured here were already frozen at the temperature range measured, thus molecular tumbling affects are removed and the spin-lattice relaxation rate T_1e⁻¹ typical for S=1/2 molecular species in glassy matrices can be written as a sum of contributions predominantly from the direct T_1,dir⁻¹, Raman T_1,ram⁻¹ processes, and the Orbach process T_1,orb⁻¹.^31,32 In the direct proces, T_1,dir⁻¹=acoth(ħω_e/2kT) where an electron spin is flipped with the emission or absorption of a phonon with energy equal to the electron Zeeman energy ħω_e. In the high temperature limit ħω_e/kT≪1, the relaxation rate has a linear dependence with temperature and in the low temperature limit ħω_e/kT≫1, the relaxation rate becomes independent of temperature.³² In the case of Raman processes, two phonons are involved where the difference (less than the Debye temperature θ_D) of the absorbed and emitted energies for an excited state is transferred to the lattice.³² In the high temperature limit for Raman processes, the relaxation rate follows a T² dependence. The Orbach process also involves two phonons and is given by T_1,dir⁻¹~(Δ_orb)³/[e^Δorb/T−1] where Δ_orb is the energy separation between the ground and excited states.³²

Before discussing the temperature dependence of the electron relaxation rate T_1e⁻¹, we note that a single-exponential buildup equation M_z(t)=M₀[1−exp(−t/T_1e)] yields a good fit for the trityl OX063 T_1e magnetization recovery curve in the temperature region above 100 K. However in the low temperature regime, the recovery curves deviate from a single exponential fit. In this case, a stretched exponential buildup equation M_z(t)=M₀[1−exp(−(t/T_1e)^β)] where β is a stretching parameter ranging from 0 to 1, seems to be the appropriate fitting equation. The stretched exponential relaxation behavior is not unusual in magnetic resonance. In NMR, it is usually interpreted as a distribution of relaxation components³³ or glassy dynamics in general.³⁴ Another alternative is a double-exponential buildup equation which also gives good fits for the low temperature recovery curves as well as the high temperature data. This was observed in high concentrations of TEMPO (40 mM) at high magnetic fields³⁵ where the longer relaxation time component is attributed to purely T_1e relaxation contribution and the shorter component is ascribed to cross relaxation effects due to high free radical concentration. It should be pointed out that regardless of which equation (single, double, or stretched exponential) is used to fit the data, the general pattern or trend observed in the temperature dependence of the electron relaxation is the same. The similarity of the T_1e⁻¹ vs T trends using either of the three fitting parameters was also observed in previous studies.³⁶ For consistency, we opted to use the stretched exponential fitting equation, which is more widely used in ESR, and we have allowed the stretching parameter β to vary from 0.5 to 0.6.

A. Comparison of trityl OX063 T_1e⁻¹ vs T with other free radical polarizing agents at W-band

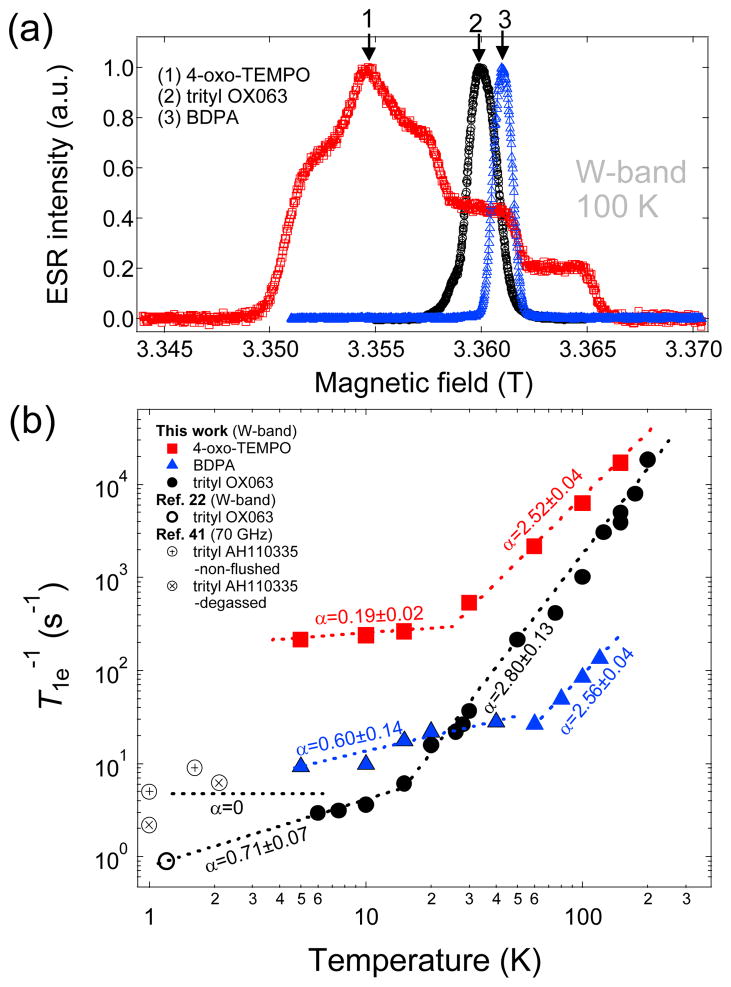
The concentration of trityl OX063 that yields the maximum nuclear polarization for low temperature DNP was found to be around 15 mM.²¹ The relatively high optimum concentration of free radical is needed to maintain enough electron dipolar interactions for fast cross relaxation of the electron spin system, allowing the establishment of a single spin-temperature for the entire sample. It has been shown in a previous ESR study under DNP conditions that the ESR spectra of trityl and TEMPO at optimum concentrations are roughly saturated by continuous microwave irradiation.³⁷ The concentration corresponds to electron spin density of approximately 9x10¹⁸ e-/cm³ with inter-electron spin distance of ~50 Å. Other free radical polarizing agents used in low temperature DNP for dissolution include the carbon-centered BDPA and the nitroxide-based 4-oxo-TEMPO (see structures in Fig. 1). The optimum concentrations of these free radicals for ¹³C DNP are relatively high compared to trityl OX063—approximately 20–40 mM for BDPA^18,25 and 30–50 mM for TEMPO.^18,38,39 To properly compare the electronic relaxation of trityl OX063 with that of BDPA and 4-oxo-TEMPO, we have performed the electron relaxation measurements of the aformentioned free radical polarizing agents at the same concentration (15 mM). The water-soluble free radicals trityl OX063 and 4-oxo-TEMPO were dissolved in 1:1 (v/v) glycerol:water glassing matrix, whereas the hydrophobic free radical BDPA was prepared in a 1:1 (v/v) sulfolane:DMSO glassing matrix as described previously.²⁵ Fig. 2a shows the W-band ESR spectra of trityl OX063 and the other two polarizing agents taken at 100 K. It can be seen that the ESR spectra of the carbon-centered free radicals BDPA and trityl OX063 are more symmetric and narrower than the nitroxide-based 4-oxo-TEMPO. The ESR linewidth of BDPA, trityl OX063, and 4-oxo-TEMPO, in this case defined as the width from 2 % height from the base, are 62 MHz, 115 MHz, and 465 MHz, respectively. The principal values of the g-tensor (g_x, g_y, g_z) and ¹⁴N hyperfine splitting (A_x, A_y, A_z) for 4-oxo-TEMPO have values close to the published results, (2.0094, 2.0065, 2.0017) and (0.73, 0.63, 3.60) mT, respectively.³⁹ The BDPA and trityl OX063 free radicals have no resolved hyperfine splitting and a relative g-anisotropy Δg/g of the order of 1.5x10⁻⁴ and 2x10⁻⁴, respectively. These values are close to the estimated relative g-anisotropy data reported earlier.⁷

Fig. 2.

(a) Field-swept W-band ESR spectra of trityl OX063 (15 mM in 1:1 v/v glycerol:water), BDPA (15 mM in 1:1 v/v sulfolane:DMSO), and 4-oxo-TEMPO (15 mM in 1:1 v/v glycerol:water) measured at 100 K. The down arrows indicate the location on the spectra where the corresponding relaxation measurements were taken. (b) Temperature-dependent electron relaxation rate T_1e⁻¹ of the aformentioned free radicals at different ESR frequencies/magnetic fields from this work and a data point for trityl OX063 at 1.2 K from Ref. 22. Low temperature NEDOR T_1e⁻¹ data points of a trityl derivative AH10335 (dissolved in butanol) at 70 GHz from Ref. 41 were also plotted for comparison. The dashed lines are fits/extrapolations using power law equations where α is the extracted power law exponent.

The temperature dependence of the electron relaxation T_1e⁻¹ of the aforementioned free radicals at W-band is shown in Fig. 2b. Saturation recovery T_1e measurements were done at the locations on the ESR spectra indicated by the down arrows in Fig. 2a in the temperature range from 200 K to 5 K. We note that the electron T_1e⁻¹ of a trityl free radical has been measured before at X-band at a lower concentration (0.2 mM) in 1:1 (v/v) glycerol:water glassing matrix; the relaxation data from 100 K to 22 K can be fitted to a predominantly Raman process with θ_D=105 K and some contribution from the local mode.³¹ A similar trend was observed for dilute concentrations (0.2–0.5 mM) of chlorinated trityl derivatives measured at X-band in the temperature range 25–295 K.⁴⁰ In our case where trityl OX063 concentration is higher (15 mM) at W-band, the relaxation data in the temperature range 200 K to 20 K can be empirically fitted with a power law dependence T_1e⁻¹~T^α where α=2.80±0.13, a value close to the Raman process prediction. Below 20 K, the electron relaxation of trityl OX063 slows to a near linear dependence with α=0.71±0.07, indicative of the one-phonon direct process. The W-band ESR spectrometer was capable of experiments only down to 5 K whereas DNP is usually performed at temperatures close to 1 K. A previous ESR investigation of 15 mM trityl OX063 in 1:1 (v/v) glycerol:water measured at DNP conditions (3.35 T, 1.2 K) reported a T_1e close to 1 s using a stretched-exponential fit (β=0.6) of the electron magnetization recovery curve.²² This single data point was incorporated in Fig. 2b and it seems to agree with the linear dependence extrapolation of our T_1e⁻¹ data at T<20 K. In addition, a recent NEDOR (Nuclear-Electron Double Resonance) measurement, an ESR technique which uses the NMR line shift to monitor electron magnetisation recovery, on a trityl derivative AH110335 (which has the same structure as trityl OX063 except that the R=CH₂CH₂OH group is replaced by R=CD₃) yielded a T_1e of 392 ms at 2.5 T and 1 K for a concentration of ~10 mM in butanol.⁴¹ Some of the NEDOR data points between 1–2 K from this previous study⁴¹ were also plotted in Fig. 2b and revealed some dispersion of relaxation data points. This slight scattering of relaxation data points may be attributed to the differences in sample preparation (e.g. glassing solvents, sample degassing), ESR conditions, and the choice of fitting parameters. Nevertheless, the overall results suggest that the trityl relaxation rate below 10 K slowed, yielding a temperature dependence (whether linear or constant) close to the one-phonon direct process behavior.

Similar trends were observed for the W-band relaxation data of the nitroxide-based 4-oxo-TEMPO at 15 mM concentration as shown in Fig. 2b. In the high temperature region above ~30 K, the relaxation data can be fitted empirically with a power law exponent α=2.52±0.04, which is close to the Raman process prediction. These relaxation data seem to agree with the previously reported electron relaxation data of dilute concentrations of TEMPO derivatives.^31,42 In the low temperature region below 20 K, the electron relaxation slows and displays an almost temperature-independent behaviour with α=0.19±0.02, suggesting that the direct process is the predominant relaxation mechanism. Despite the fact that the ESR relaxation measurements of 4-oxo-TEMPO were performed in the same glassing matrix and concentration as that of trityl OX063, it can be seen in Fig. 2b that 4-oxo-TEMPO generally relaxes faster than trityl OX063, an observation that may be ascribed to the larger spin-orbit interaction in the nitroxide radical. It is expected that increasing the TEMPO concentration to the actual optimum value for DNP (33 or 40 mM)^18,38 would lead to even shorter electron relaxation times.

Fig. 2b also displays the temperature-dependent relaxation data of 15 mM BDPA in the W-band. We first revisit a previous ESR investigation³⁶ of dilute concentrations of BDPA (1.1 or 0.1 mM) in sucrose octaacetate at Q-band: the log-log T_1e⁻¹ vs T plot in the temperature range 80 K to 250 K yielded a slope close to 2, which is in the high temperature limit of the Raman process. In addition, it was shown that increasing the BDPA concentration to 44 mM increases the relaxation rate and the slope of the log-log plot approaches 1, which is an indication of the direct process.³⁶ However, for 15 mM BDPA concentration in 1:1 (v/v) sulfolane:DMSO, the log-log plot yielded a slope of 2.56 in the temperature range 100 K to 60 K with relaxation rates slower than that of trityl OX063. At temperatures below 20 K, the relaxation rates are slightly higher than that of trityl OX063 and exhibit an almost linear dependence with temperature. This somewhat different behavior might also be due to the differences in the glassing matrix itself, as it plays a role in the phonon spectrum. The actual optimum concentration of BDPA for DNP is around 20–40 mM,^17,18 and at such concentration we anticipate that the relaxation rate of BDPA would increase further due to the shorter inter-electron spin distances. Therefore, when these three free radicals are prepared at their optimum concentration for DNP, it is clear that trityl OX063 (15 mM) has a slower relaxation rate compared to BDPA (20–40 mM) and 4-oxo-TEMPO (30–50 mM).

B. The effect of Gd³⁺ on the ESR spectra and relaxation of trityl OX063 at W-band

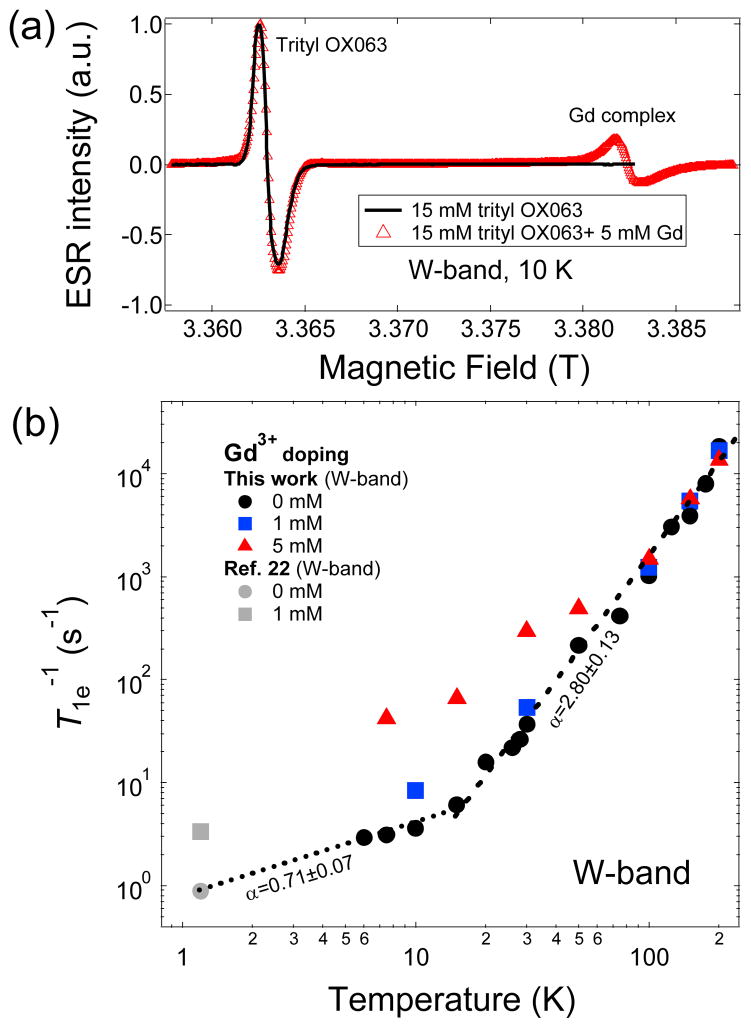
The inclusion of trace amounts of Gd³⁺ (1–2 mM) and other lanthanides in trityl-doped DNP samples has been shown to improve the nuclear polarization of the frozen DNP samples.^{17,18,22–24} Consequently, the liquid-state DNP-NMR enhancement ε is also improved in dissolution DNP experiments with slight decreases in nuclear T₁ due to the paramagnetic effect of Gd³⁺ in the hyperpolarized solution. In addition, it has been shown in a previous work that concomitant with the improvement in DNP-enhanced nuclear polarization, there is a slight narrowing of the ¹³C microwave DNP spectrum of trityl-doped [1-¹³C]sodium pyruvate samples with the addition of Gd³⁺ and a question arises whether the ESR spectrum of trityl OX063 is affected by Gd³⁺ doping.¹⁸ To elucidate this behavior, we have performed an ESR investigation of the influence of Gd³⁺ doping on the ESR spectra and relaxation of trityl OX063 at the W-band. Fig. 3a shows that the addition of 5 mM Gd³⁺ complex Gd-HP-DO3A (see structure in Fig. 1) has no apparent effect on the trityl ESR lineshape. Continuous wave (CW) ESR spectra were taken in this case instead of the field-swept electron spin echo (ESE) technique to properly track the ESR intensity over a wide frequency range encompassing both the trityl OX063 and Gd³⁺ ESR signals. The sharp peak on the right shown in Fig. 3a is due to the S=+1/2<—>S=−1/2 transition of the Gd³⁺ (S=7/2) complex; the higher-order transitions form a broad background peak which dominates in the low temperature region as more electron spins reside in the higher energy levels with increasing electron thermal polarization.^43–45 Although Gd³⁺ doping in the optimum concentration range does not significantly alter the trityl OX063 ESR spectrum as shown in Fig. 3a and even the nuclear relaxation at cryogenic temperatures,^18,22 Gd³⁺ doping shortens the electron T_1e of trityl OX063 in the low temperature regime as shown in Fig. 3b. The reduction in T_1e with Gd³⁺ doping correlates to the decrease of the parameter η, which theoretically results in lower spin temperature T_s of the electron dipolar system and higher polarization of the nuclear Zeeman system.^17,18 The T_1e-shortening behavior of trityl OX063 with Gd³⁺ doping has been reported previously in ESR studies done at 1.2 K, albeit at limited concentration range only up to 2 mM.²² The temperature dependence of trityl OX063 electron relaxation doped with Gd³⁺ (0 mM, 1 mM, 5 mM) over a wider temperature range is shown in Fig. 3b. Gd³⁺ doping does not seem to significantly affect the electron relaxation rate above 100 K, where the relaxation data for different Gd³⁺ concentrations (0, 1, 5 mM) almost overlap. On the other hand, the effect of Gd³⁺ is strongly manifested at lower temperature where at approximately 20 K and lower the electron relaxation slows down close to a linear temperature dependence and becomes faster with Gd³⁺ doping. Moreover, the data in Fig. 3b suggest that the one-phonon direct process relaxation mechanism still seems to be preserved in the low temperature region even in the presence of Gd³⁺.

Fig. 3.

(a) CW W-band ESR spectra of trityl OX053 (15 mM in 1:1 v/v glycerol:water) in the absence and presence of Gd³⁺ (5 mM Gd-HP-DO3A) at 10 K. The overlapping left peaks are the trityl OX063 spectra and the sharp peak on the right emanates from the central transition of Gd³⁺ complex. (b) Temperature-dependent spin-lattice relaxation rate T_1e⁻¹ at different Gd³⁺ doping concentrations from this work and two low temperature T_1e⁻¹ data points from Ref. 22. The dashed lines are fits/extrapolations using power law equations where α is the extracted power law exponent.

C. ESR properties of trityl OX063 at various ESR frequencies

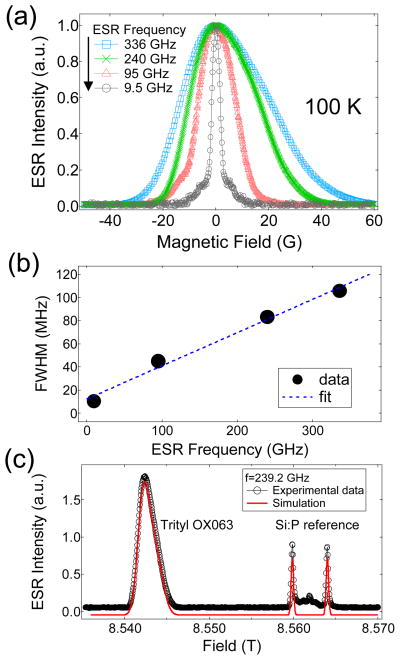
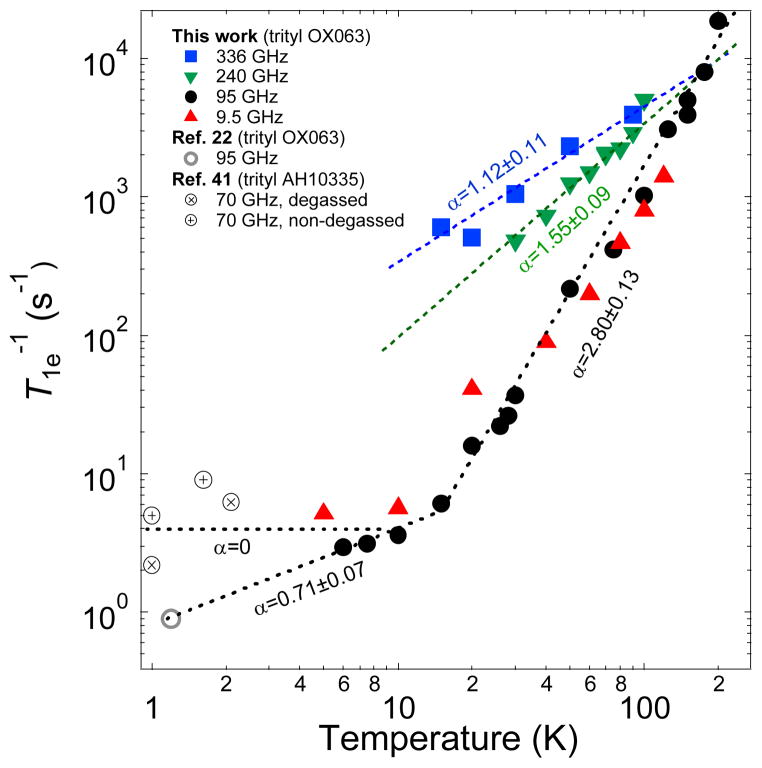
Recent experiments have shown the beneficial effect of DNP performed at higher magnetic fields:^46–49 higher nuclear polarizations were achieved when the operating field of the polarizer is increased, for instance, from 3.35 T to 5–7 T. It remains to be seen whether this trend would continue at much higher fields. We have measured the DNP-relevant ESR parameters, ESR spectra and relaxation rate, of trityl OX063 at various ESR frequencies from 9.5 GHz (0.35 T) to 336 GHz (12 T) using pulsed ESR spectrometers available at NHMFL in Tallahassee, Florida. Fig. 4a displays the normalized field-swept ESR spectra of trityl OX063 taken at 100 K, showing a monotonic increase of the ESR lineshapes as the frequency is increased from 9.5 GHz to 336 GHz. Fig. 4b shows the calculated full-width at half maximum (FWHM) of the ESR spectra using a Voigt fitting function where the data points appear to increase with field in a linear-like fashion. Of special note is the X-band ESR lineshape where broad shoulders at the base of the ESR spectrum are visible. This feature in the X-band spectrum is attributed to proton spin flip effects⁵⁰ which are known to manifest at low magnetic fields and high free radical concentration. The proton spin flip satellites are not visible in the W-band and higher magnetic fields. The implications of a wider ESR linewidth may not be favorable for DNP via thermal mixing because this translates to higher electron heat capacity of the electron spin-spin interaction reservoir. However, also included in the equation for the minimization of the spin temperature T_s of the electron dipolar system is higher electron Larmor frequency ω_e.^7,19 Fig. 4c displays the field-swept ESR spectrum of trityl OX063 and a reference sample of Si:P ([P]~10¹⁶/cm³) with g=1.99852 measured at 339.2 GHz. This high-frequency spectrum can be fitted with an axial g-tensor with a slight anisotropy: g_x=g_y=2.00319(3) and g_z=2.00258(3). In addition, the inherent linewidth also increases with frequency due to considerable g-strain, which corresponds to an approximate gaussian g-value distribution with a FWHM of 0.00035 around these average g-values.⁵¹ Fig. 5 shows the field dependence of trityl OX063 electron relaxation. It is interesting to note that although there is a significant ESR linewidth broadening from 0.35 T (X-band) to 3.35 T (W-band), the temperature dependence of their electron relaxation rates are very similar. The similarity of the relaxation rate values of trityl OX063 (15 mM) at X- and W-bands was also previously observed in an earlier work⁵² on a more dilute trityl radical concentration (0.2 mM). This relaxation behavior was ascribed to the field-independent Raman process and local mode being the dominant relaxation processes at a wide temperature range for trityl radical.⁵² On the other hand, increasing the magnetic field to 8.5 T (240 GHz) and 12 T (336 GHz) shortens the electron relaxation time. This is in line with the expected frequency dependence of the direct process. No data were obtained for the lowest temperatures, as the saturation recovery is dominated by spectral diffusion, due to the narrow excitation bandwidth at these frequencies (~1 MHz). Nevertheless, the log-log plot of electron relaxation rate vs temperature shown in Fig. 5 shows a monotonic decrease in slope in the high temperature region (T>15 K) as the field is increased from X or W-band, suggesting deviation from the Raman process. As DNP is pushed to higher fields, the ESR properties of the free radical polarizing agent (e.g. linewidth D and spin-lattice T_1e relaxation) play an important role in the performance of DNP. The current results seem to suggest that higher field and lower temperatures will continue to provide increases in nuclear polarization which will approach the theoretical limit without serious hindrance from the free radical relaxation properties.

Fig. 4.

(a) Normalized field-swept ESR spectra of trityl OX063 (15 mM in 1:1 v/v glycerol:water) at multiple ESR frequencies: 9.5 GHz, 95 GHz, 240 GHz, and 336 GHz measured at 100 K. (b) The corresponding full-width at half-maximum (FWHM) of the ESR spectra at different magnetic fields. The solid line is a fit to a linear equation. (c) Field-swept ESR spectrum at 239.2 GHz showing the signals emanating from trityl OX063 and the Si:P reference sample. The solid curve represents the simulated spectrum where the g-tensor values were extracted.

Fig. 5.

Temperature-dependent electron relaxation rate T_1e⁻¹ of trityl OX063 at different ESR frequencies/magnetic fields from this work and a data point at 1.2 K from Ref. 22. Low temperature NEDOR T_1e⁻¹ data points of a trityl derivative AH10335 (dissolved in butanol) at 70 GHz from Ref. 41 were also plotted for comparison. The dashed lines are fits/extrapolations using power law equations where α is the extracted power law exponent.

Conclusions

In conclusion, we have measured the ESR properties of trityl OX063, one of the most efficient free radical polarizing agents in dissolution DNP-NMR spectroscopy, at the optimal concentration for DNP. W-band data have shown that, at temperatures above ~15 K, the electron relaxation rate T_1e⁻¹ vs T can be fitted empirically to a power-law dependence close to the T² curve predicted by the two-phonon Raman relaxation process. Below 10 K, the relaxation rate slows down close to the linear or temperature-independent behaviour indicative of the one-phonon direct process. When compared at the same concentration (15 mM), trityl OX063 has longer T_1e than the other DNP free radical polarizing agents BDPA and 4-oxo-TEMPO in the low temperature region. In addition, we have also shown that addition of a trace amount of a Gd³⁺ complex into the trityl-doped sample, a practice known to improve DNP-enhanced nuclear polarization, shortens the electron T_1e but does not affect the trityl OX063 ESR spectrum. Finally, the ESR lineshape of trityl OX063 monotonically increases as the field is increased from 0.35 T to 12 T. While the X- and W-band electron relaxation of trityl OX063 are very similar, T_1e⁻¹ increases as the field is increased to 12 T. The relaxation data in this work may be important in elucidating the behavior of DNP performed at different magnetic field strengths.