Use of genotype × environment interactions to understand rooting depth and the ability of wheat to penetrate hard soils

Abstract

Background

Root systems are well-recognized as complex and a variety of traits have been identified as contributing to plant adaptation to the environment. A significant proportion of soil in south-western Australia is prone to the formation of hardpans of compacted soil that limit root exploration and thus access to nutrients and water for plant growth. Genotypic variation has been reported for root-penetration ability of wheat in controlled conditions, which has been related to field performance in these environments. However, research on root traits in field soil is recognized as difficult and labour intensive. Pattern analysis of genotype × environment (G × E) interactions is one approach that enables interpretation of these complex relationships, particularly when undertaken with probe genotypes with well-documented traits, in this case, for the ability to penetrate a wax layer. While the analytical approach is well-established in the scientific literature, there are very few examples of pattern analysis for G × E interactions applied to root traits of cereal crops.

Scope

In this viewpoint, we aim to review the approach of pattern analysis for G × E interaction and the importance of environment and genotype characterization, with a focus on root traits. We draw on our research on G × E interaction for root depth and related studies on genotypic evaluation for root-penetration ability. In doing so, we wish to explore how pattern analysis can aid in the interpretation of complex root traits and their interaction with the environment and how this may explain patterns of adaptation and inform future research.

Conclusions

With appropriate characterization of environments and genotypes, the G × E approach can be used to aid in the interpretation of the complex interactions of root systems with the environment, inform future research and therefore provide supporting evidence for selecting specific root traits for target environments in a crop breeding programme.

INTRODUCTION

Our interest in the application of pattern analysis tools for genotype × environment (G × E) interactions for root depth grew from a desire to (a) validate research we were conducting on evaluating wheat (Triticum aestivum) genotypes for variation in the ability to penetrate a wax layer; and (b) integrate and relate this to field performance in soils with contrasting soil hardness in the Western Australian wheatbelt. Soils in this region are geologically old, weathered, and, in addition to a range of other physical and chemical subsoil constraints, around 24 % are highly susceptible to subsurface compaction or hardpans (Davies and Lacey, 2011). Western Australian soils are hardly unique in this regard, hardpans or, more broadly, soils with high penetration resistance, e.g. due to high clay content, being a common feature of many agricultural soils (Hamza and Anderson, 2005). Such soil physical properties constrain root growth and access to nutrients and water for crop growth. As little as 2 MPa of resistance is sufficient to limit root growth (Hamblin et al., 1982) and, instead, the majority of roots, particularly in subsoils with high bulk density explore the soil profile through biopores (White and Kirkegaard, 2010).

Our previous research had shown that genotypic variation existed in bread wheat cultivars and breeding lines for the ability to penetrate thin wax layers when grown in controlled conditions in soil columns (Botwright Acuña et al., 2007). Field trials were undertaken in a low-rainfall environment in Western Australia on two soil types in 2005, one containing a hardpan and another that increased in soil strength with depth, to validate our observations from soil columns. Root depth was targeted as a simple integrative trait, but one which has been associated with greater resource capture and hence yield (Kirkegaard and Lilley, 2007). Early results were encouraging, with root depth on a Calcic Lixisol with a hardpan at 0·25 cm showing a positive relationship with above-ground biomass at anthesis (Fig. 1). Furthermore, cultivars differed in root depth between the two soil types (Fig. 2), indicating possible differences in adaptation to soil characteristics that warranted further investigation. Subsequent field trials were undertaken and the field sites expanded to include a medium rainfall environment, again on a Calcic Lixisol where half the site had been ripped to a depth of 50 cm the previous season. In the meantime, research in the controlled environment in soil columns containing wax layers had expanded to include phenotyping of two wheat cultivars, Cranbrook and Halberd, known to differ in root-penetration ability (Botwright Acuña et al., 2007), and their doubled-haploid population, for identification of quantitative trait loci (QTL).

Fig. 1.

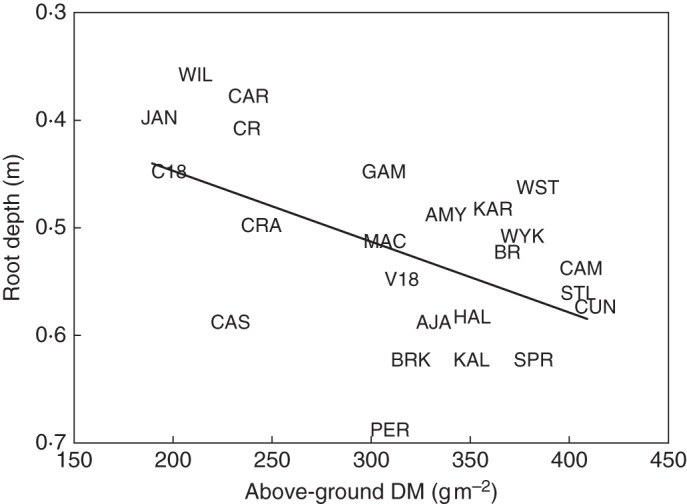
Relationship between root depth and above-ground dry matter (DM) at maturity on a Calcic Lixisol (P = 0·02; r² = 0·28) at Merredin in 2005. Soil sampled for root depth at 75 and 89 d after sowing, respectively. Abbreviations of cultivar and breeding lines: AJA, Ajana; AMY, Amery; BRK, Brookton; CAM, Camm; CAR, Carnamah; CAS, Cascades; C18, Chaun Mai 18; CBK, Cranbrook; CUN, Cunderdin; BR, Bonnie Rock; CR, Castle Rock; GAM, Gamenya; HAL, Halberd; JAN, Janz; KAL, Kalannie; KAR, Karlgarin; MAC, Machete; PER, Perenjori; SPR, Spear; STL, Stiletto; V18, Vigour 18; WST, Westonia; WIL, Wilgoyne; WYK, Wyalkatchem. Modified from Botwright Acuña et al. (2007).

Fig. 2.

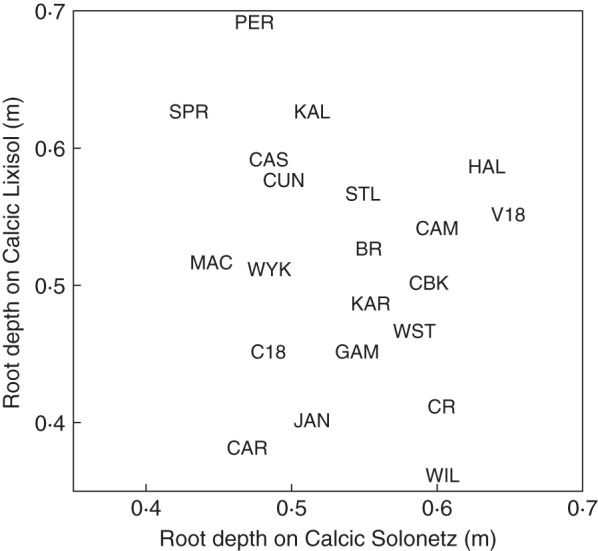
Site × entry interaction for root depth at two sites in Merredin in 2005. LSD = 0·15 at P = 0·05. The line represents the 1 : 1 ratio. Refer to Fig. 1 legend for explanation of abbreviations. Modified from Botwright Acuña et al. (2007).

Pattern analysis of G × E interactions for root depth was subsequently used as one approach to integrating the field and controlled environment observations, based on our understanding of the soil physical characteristics and evaluation of genotypes for the ability of roots to penetrate wax layers. While pattern analysis of G × E interactions is not new and is widely reported in the scientific literature, the approach has been applied to few root traits and specifically not for wheat. This is likely to be a reflection of the difficulty in obtaining the necessary data from a range of genotypes and field trials. In this viewpoint, we aim to review the approach of pattern analysis for G × E interaction and the importance of environment and genotype characterization, with a focus on root traits. We draw on our research on G × E interaction for root depth (Botwright Acuña and Wade, 2012) and other research on genotypic evaluation for root-penetration ability.

G × E APPROACH

G × E interactions are common in agricultural research and describe the association between the environment and the phenotypic expression of a genotype (Allard and Bradshaw, 1964). The presence of G × E interaction indicates that both environmental factors and the genotype influence the phenotypic expression of a trait. The approach is typically used in plant and animal breeding to identify and select genotypes for a target environment. Genotypes are usually tested across a diverse range of environments, including locations, years and seasons, and often involve a large number of genotypes. For plants, the most common trait routinely targeted using the G × E approach is yield, but other examples have been reported for other traits including quality (Aucamp et al., 2006) and biomass production (Bradbury et al., 2011). The G × E approach has been used to describe variation in root traits in tuberous plant species such as sweet potato (e.g. Grüneberg et al., 2005) and cassava (Benesi et al., 2004). There are few published papers on G × E for root traits in cereals (e.g. Kondo et al., 2003) and none to our knowledge on wheat.

A range of statistical approaches have been published for the analysis of the G × E interaction. Examples include analysis of variance, regression (Finlay and Wilkinson, 1963), nonparametric methods (Kang, 1988; Fox et al., 1990) and pattern analysis of multivariate analytical methods such as the additive main effects and multiplicative interaction (AMMI) model (Zobel et al., 1988), and genotype plus G × E interaction (GGE) biplots (Yan et al., 2000). For the latter two approaches, biplots jointly display genotypes and environments on the one plot and are derived from the G and E means. The relationship among these attributes is affected by the scale of measurement, which is eliminated by data transformation (Kroonenburg, 1995). There are several approaches to data transformation, such as environment-centred or -standardized that result in a family of pattern analyses (Kroonenburg, 1995). The appropriate transformation depends on the purpose of the analysis as reviewed by DeLacy et al. (1996). For example, the environment-standardized transformation is implied when the correlation matrix is used and is recommended for plant breeding. In contrast, the environment-centred model is implied when an ordination on genotypes is performed using the covariance matrix and is recommended for adaptation studies. Transformation is then followed by ordination using singular value decomposition on the residuals (Eckart and Young, 1936) to produce biplots and cluster analysis using the hierarchical agglomerative clustering strategy.

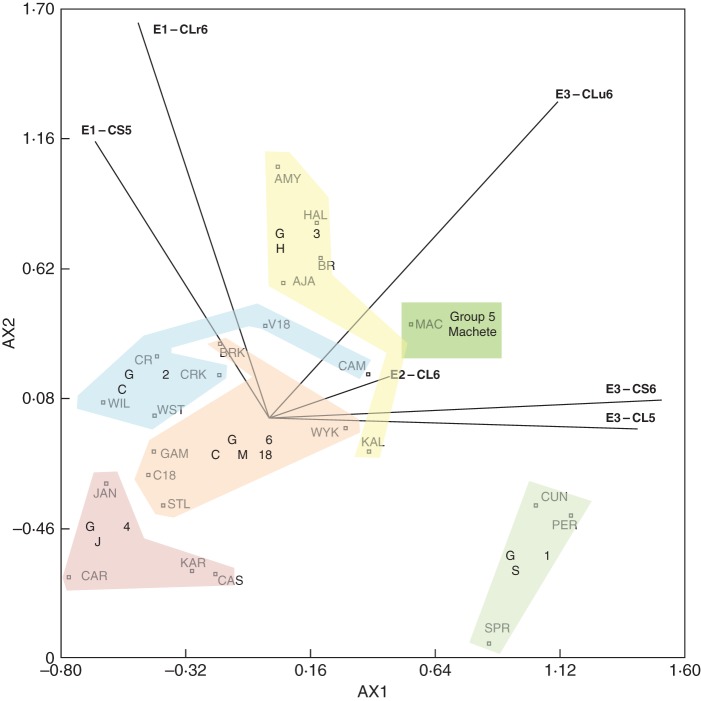
The pattern analysis to evaluate G × E for root depth in wheat (Botwright Acuña and Wade, 2012) uses the GGE approach with environment-standardized data, which were extracted from replicated field trials in six environments (2005–2006) and 24 genotypes (wheat cultivars and breeding lines). Note that while datasets for GGE analysis of multiple-environment trials are often large, Gauch and Zobel (1989) state that at a minimum the matrix of means should be larger than 3 × 3, requiring more than three genotypes in three or more environments. Thus, the number of genotypes and environments used in our study meet these criteria. In our study, the transformed data from the GGE analysis were clustered using the agglomerative hierarchical algorithm of Ward (1963) based on minimizing incremental sums of squares. Scores for both genotypes and environments from the two-component interaction principal components model were computed for AX1, AX2 and AX3 and plotted as bi-plots (Botwright Acuña and Wade, 2012).

G × E INTERACTIONS FOR ROOT DEPTH

In our analysis for G × E interactions for root depth, genotype main-effects accounted for 12 %, environment 48 %, and the G × E interactions 40 % of the total sum of squares. The key point from this analysis of root depth is that the sum of squares for G × E (G × E-SS) was more than three times that for G. Cluster analysis on the environment-standardized residuals was used to identify three environment and six genotype groups, which preserved 72 % of the G × E-SS among groups. The ordination analysis of the environment-standardized residuals indicated that interaction principal component axes AX1, AX2 and AX3 accounted for 30, 24 and 18 % of the G × E-SS, respectively. The relationship between AX1 and AX2 is shown in Fig. 3. An additional bi-plot (AX2 vs. AX3) and full description of main effects and G × E interactions for root depth are presented in Botwright Acuña and Wade (2012).

Fig. 3.

Principal component analysis (environment standardized) for the environment × genotype interaction for AX1 and AX2 for root depth for 6 environments and 24 wheat genotypes. Probe genotypes are identified. The G × E interaction for AX1 and AX2 accounted for 54·2 % of the sum of squares. Modified from Botwright Acuña and Wade (2012) with permission from the publisher.

The biplot shown in Fig. 3 should be interpreted with respect to the environment-standardized transformation used in the analysis. The biplot displays genotype plus G × E interaction effects, consistent with Yan (2002), where the genotype values are standard deviations from the average of the environments. The origin is the average value of the environments and it represents the genotype that has an average value in each environment (Kroonenburg, 1995). The lines that connect the biplot origin and the markers for the environments are called environment vectors. Thus, the larger the projection of a genotype on an environment vector, the more the genotype deviates from the average in the environment and has reduced stability (Yan, 2002).

For broad selection, ideal genotypes have both high mean root depth and are close to the origin. For specific selection, ideal genotypes with high mean root depth but low stability will respond best to particular environments (Yan, 2002). The three environment groups (Fig. 3) were clearly separated by the two principal component axes AX1 and AX2. The six genotype groups were also separated by the two principal component axes shown in Fig. 3, although these relationships were variously positive, neutral or negative.

The biplot is an effective tool for identifying genotypes adapted to specific environments and their mean performance and stability (Yan, 2002). Here we have focused on root depth as an integrative trait, as a simple measure of genotype success from penetration and other strategies, including adaptation to soil conditions. Results from the biplot and principal component analyses could potentially be used by plant breeders to inform the so-called ‘which-won-where’ scenario for recommending cultivar choices with respect to root depth in different environments. On the other hand, pattern analysis of G × E interactions has a broader application in contributing to our understanding of the physiological basis of these differences in root depth among genotypes and their adaptation to environment (Byth, 1981). Given the recognized complexity in root systems, their structure and function, the ability to explore root data from a holistic perspective may lead to new hypotheses worthy of further study. Integral to this aim is characterization of environments and genotypes.

CHARACTERIZATION OF ENVIRONMENTS

The importance of and approaches to environmental characterization for understanding G × E interactions was reviewed by Wade et al. (1996). As would be expected, this can include a range of characteristics, from climate and biological factors, to soil morphology, chemistry and physics. One of the issues with large, multi-environment trials is the time and expense required for full characterization of environments. Under these circumstances, alternative approaches to characterization of environments include the measurement of key data and the use of so-called ‘probe’ genotypes (Cooper and Fox, 1996). Given the lack of papers on pattern analysis for G × E in root traits in the literature, here we will instead briefly refer to an example from Wade et al. (1999) in which G × E interactions were analysed for grain yield of 37 lowland rice cultivars across 36 environments in south and south-east Asia. Environments were characterized according to data on planting method, the duration of flowering, the hydrological environment during key stages of crop development, soil texture and pH. This combination of data was sufficient to characterize environment groups that differed in the onset of drought and submergence and adaptation of genotypes to these conditions.

Beyond the G × E theme of this paper, there have been examples in the scientific literature on root research with broad characterization of environments that has led to the identification of constraints to root growth. For example, research by Valentine et al. (2012) used regression analysis to relate variation in root elongation rate of a barley cultivar to a wide range of soil chemical and physical properties measured in topsoil across 59 sites in Scotland. In this case, soil strength and porosity were identified as key soil attributes that constrained root elongation of barley. For our study on root depth, the environments were characterized for climate and soil physical characteristics, including soil morphology, gravimetric water content and soil hardness (Fig. 4), as part of field validation of genotypic variation in root penetration through wax layers in controlled conditions (Botwright Acuña et al., 2007). Of the six environments, four were on a Calcic Lixisol, the remainder on a Calcic Solonetz (Isbell, 1996). Environments on the Calcic Lixisol were split between two sites at Merredin (lat. –31·483333, long. 118·266667) and Buntine (lat. –29·983333, long. 116·566667) in the low and medium rainfall zones of Western Australia, which receive 223- and 292-mm growing-season rainfall, respectively. These environments, with the exception of one site on the Calcic Lixisol at Buntine which had been ripped to a depth of 50 cm, had hardpans of approx. 4 MPa in strength at around 0·10–0·25 m. In contrast, the Calcic Solonetz at Merredin increased in soil strength to 4 MPa at a depth of 0·6 m and, while the site was co-located in the low rainfall zone, the clay soil texture resulted in a greater drained upper and lower limit than the sandier Calcic Lixisol (Botwright Acuña et al., 2007).

Fig. 4.

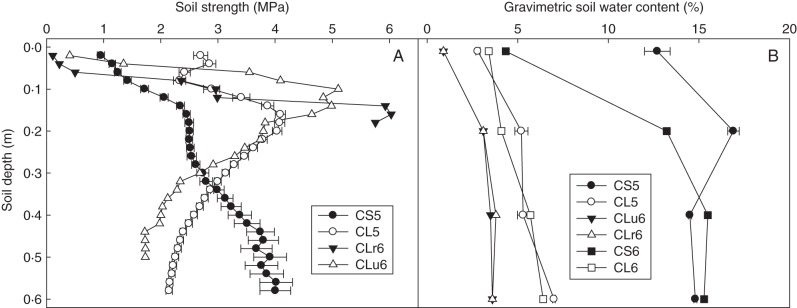
Change in soil hardness and gravimetric soil moisture content with soil depth on a: Calcic Solonetz 2005 (CS5); Calcic Lixisol 2005 (CL5); Calcic Lixisol, ripped 2006 (Clu6); Calcic Lixisol, unripped 2006 (CLr6); Calcic Solonetz 2006 (CS6); and Calcic Lixisol 2006 (CL6). Bars are the standard error. Modified from Botwright Acuña and Wade (2012) with permission from the publisher.

To understand fully the response of roots to their environment, there are a number of other soil biological, chemical and physical factors that must be considered, to assist in the interpretation of the G × E analysis at the specific locations of the environments. Furthermore, there has also been a growing use of crop simulation models such as APSIM (Keating et al., 2003) in Australia, which by their nature require characterization of environments. As such, there is a growing database of soils in the Australian Soil Resource Information System (ASRIS; CSIRO, 2012) in addition to previously published research available in the literature, which variously includes soil physical and chemical properties that can be drawn upon to aid interpretation. For example, the Calcic Lixisol has a neutral to moderately acidic pH (Tang et al., 2002), while the Calcic Solonetz has a neutral to acidic pH (Hamza and Anderson, 2002). Both soils have low organic carbon levels in the top soil of around 1 %. Furthermore, boron toxicity occurs in around 15 % of Western Australian soils, particularly those with a high clay content in the low rainfall areas of the eastern wheatbelt (Lacey and Davies, 2009) and, based on a similar soil type in ASRIS, was likely to be at low concentrations in the top soil of the Calcic Solonetz, but reaching around 30 mg kg⁻¹ at depths of around 0·7 m. Genotypic variation in boron sensitivity was proposed as a possible cause of separation for AX3 in Botwright Acuña and Wade (2012).

Returning to the G × E analysis, three environment groups are shown in Fig. 3. Cluster analysis revealed that E1 (CS5 and CLr6) separated first, and then E2 (CL6) separating from the rest (E3) (Botwright Acuña and Wade, 2012). The next step is to compare and contrast characteristics of the environments so as to develop hypotheses on the key attributes driving the separation into groups of environments. In this case, these included the hardness of the soil profile, which was in turn related to soil moisture content (Rickert et al., 1987) and, therefore, influenced by rainfall events. Using this approach, group E3 included three sites that tended to have high soil penetration resistance (Fig. 4). In contrast, group E1 was proposed to have lower resistance to penetration, which we linked with the higher rainfall at CS5 and soil ripping at CLr6. The CL6 site did not have a significant hardpan, so formed singleton group E2. The next step is to relate the vectors for the environments and their groups to statistically significant principal component axes identified through the G × E-SS analysis, which are represented as biplots. For root depth, the three environment groups were clearly separated by the two principal component axes AX1 and AX2 (Fig. 3). For, AX1, for example, the high soil strength group (E3) was strongly positive, the low soil strength group (E2) mildly positive or neutral, and the medium soil strength group (E1) negative (Fig. 3). For AX2, the medium soil strength group (E1) and the unripped Calcic Lixisol in 2006 were strongly positive, while the remaining environments and sites were neutral.

CHARACTERIZATION OF GENOTYPES

Phenotypic characterization of genotypes for cereal root traits, particularly in situ, is labour intensive and therefore often limited to only a few traits or genotypes within a plant species. Thus there are relatively few examples in the literature (e.g. Samson et al., 2002; Cairns et al., 2004; Botwright Acuña and Wade, 2012). Instead, researchers have used a range of approaches in controlled conditions, in soil columns, lysimeters and root boxes and so on, using repacked or intact soil cores or other artificial growth media. There have also been recent developments in the use of remote technologies, such as X-ray microtomography (Gregory et al., 2009) and genetic markers (e.g. Courtois et al., 2009). The G × E approach can augment these by ex situ measurements of genotypic variation by providing comparative analysis of identified phenotypes against their performance in situ.

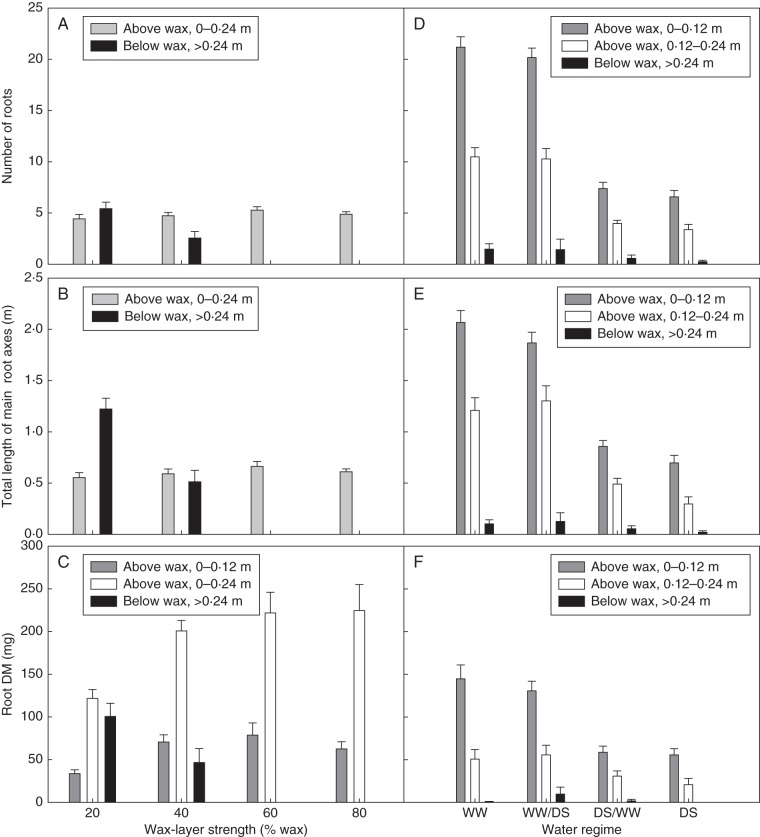
Take, for example, the results of the pattern analysis of main effects of genotypes in the G × E analysis, which identified six genotype groups that were separated by the principal component axes shown in Fig. 3. A full description of these interrelationships is provided in Botwright Acuña and Wade (2012). From our analysis of root depth across environments, we have reported that the Spear (G1), Machete (G5) and Halberd (G3) groups all had deeper roots than the Janz (G4), C18 (G6) or Cranbrook (G2) groups. These same or a subset of contrasting genotypes were included in screening (Botwright Acuña and Wade, 2005) or more detailed experiments (Botwright Acuña et al., 2007) for root-penetration ability through thin wax layers in controlled conditions in pots under contrasting conditions of soil water availability. Briefly, a thin wax layer (3 mm deep) of known strength was placed half-way in a soil column 0·5 m in depth and 0·12 m wide, packed with a sandy loam. The wax layer was sealed to the side of the pot to compartmentalize the soil so that the soil moisture above and below the wax layer could be manipulated. Placement of the wax-layer at this depth, which is similar to that of a hardpan in field soil, allows for slow soil drying under drought conditions, which has enabled us to examine the interaction between root-penetration ability and soil water deficit (Botwright Acuña and Wade, 2005). Using this approach, we have shown that seminal number, total length of the main root axes and dry matter sharply declined as the wax-layer strength increased, with a strong interaction between wax-layer strength and depth of the wax layer (Fig. 5). In contrast, nodal root axes are produced later in plant development, making it impossible to observe their capacity to penetrate the wax layer; hence their total length and dry matter instead interacted strongly with water availability (Fig. 5).

Fig. 5.

Effect of wax-layer strength on (A) seminal root number, (B) total length of main axes and (C) root dry matter (DM), and effect of water regime on (D) nodal root number, (E) total length of main axes and (F) dry matter. Bars represent the standard error. Water regimes: WW, well-watered; WD, water-deficit. Modified from Botwright Acuña and Wade (2005).

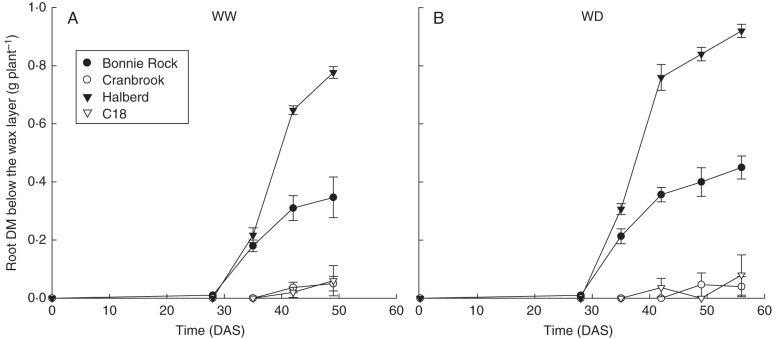
Genotypic variation has been reported using the thin-wax layer technique in rice (e.g. Clark et al., 2000) and bread (Botwright Acuña and Wade, 2005) and durum (Kubo et al., 2004) wheat, which was related to field performance (Samson et al., 2002; Botwright Acuña et al., 2007). From these combined analyses, we have reported that few seminal to no roots of wheat cultivars C18 and Cranbrook penetrated thin wax layers in pots and vice versa for Bonnie Rock and Halberd (Fig. 6). Further research is required to discern whether this response is related to specific classes of the seminal or primary root system, which consists of tap, basal and lateral roots (Zobel, 2011). Finally, penetration of the wax layer in Bonnie Rock and Halberd was, as expected, linked with improved soil water extraction under water deficit (Fig. 7).

Fig. 6.

Variation in root dry matter (DM) according to genotype and sampling time (days after sowing, DAS) in pots containing a wax layer at a depth of 0·25 m for: (A) below the wax layer in well-watered conditions; (B) below the wax layer in water-deficit conditions. Bars represent the standard error. Modified from Botwright Acuña et al. (2012) with permission from the publisher.

Fig. 7.

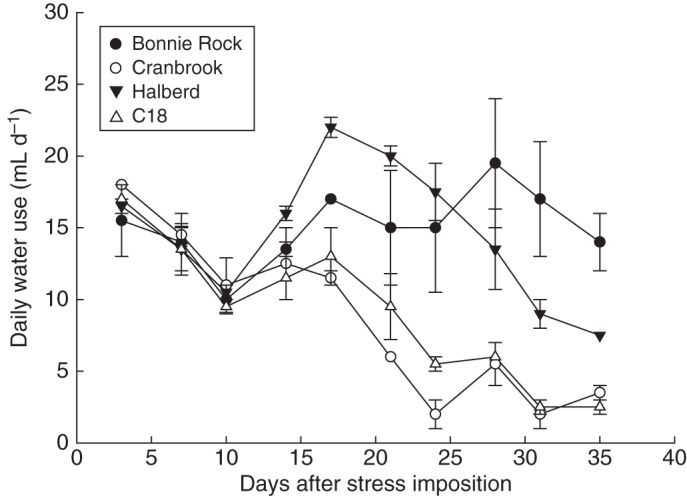
Daily water use over time of selected entries under water deficit in controlled conditions. Modified from Botwright Acuña et al. (2007).

In addition, QTL have been identified for two of the wheat genotypes with contrasting ability to penetrate a wax layer and their doubled haploid line (DHL) progeny grown in well-watered conditions. For example, a total of seven and five QTL for seminal dry weight above and below the wax layer, respectively, have been identified (Table 1). Of these, two QTL on chromosomes 3DL and 4AL each accounted for 12 % of the variance. There is very little published literature on QTL for root traits in wheat linked with the ability to penetrate hard soil or, more specifically, wax layers. While Kubo et al. (2007) found QTL for durum wheat for root dry matter on 1B, and penetrating root number and RP index on 6A, these did not correspond with the QTL we identified for bread wheat. In contrast, QTL for root traits in rice and other crops have been extensively studied (de Dorlodot et al., 2007), with some 28 traits collated from a range of publications in a meta-analysis (Courtois et al., 2009), which included several QTL for the number of roots penetrating hard soil. Comparative genomics between wheat and rice reveals a reasonable degree of synteny (Sorrells et al., 2003), so there may be opportunity to relate root QTL across species.

Table 1.

Estimated genetic (additive) effects for root trait QTL measured on random progeny from the Cranbrook/Halberd wheat population evaluated across well-watered and water-deficit environments as described in Botwright Acuña and Wade (2005) and Botwright Acuña et al. (2007)

Population/chromosome	LOD	a genetic effect (°C)*	Percentage variance (σ2)†
Above-wax seminal dry weight
1BS	4·6	–0·038	7
1DS	4·5	–0·042	8
3AL	3·8	0·036	5
3BS	3·7	–0·020	4
3DL	5·4	0·049	12
5AL	3·2	–0·029	6
7DS	4·8	0·047	9
Below-wax seminal dry weight
1BS	3·8	–0·019	5
1DS	4·5	–0·026	8
2BS	4·6	–0·027	9
3BS	3·3	–0·016	5
4AL	5·3	0·032	12

* Positive additive effects indicate that the Cranbrook allele with ‘a’ the additive effect estimated as one-half the difference in homozygotes carrying either parental allele.

^† Distance from the tip of the short arm of the chromosome.

An understanding of the G × E interactions can allow the identification of a reference set to represent the germplasm in a breeding programme and thought to respond differently (Fox and Rosielle, 1982), or a set of probe genotypes with known adaptations to specific constraints (Cooper and Fox, 1996). Outputs from the G × E analysis with support from our understanding of the underlying physiology and genetics can be used to identify a set of probe genotypes for hardpan penetration ability drawing from the identified genotype groups.

INTERPRETING THE G × E INTERACTION FOR ROOT DEPTH

The characterization of environments and genotypes then forms the basis of interpreting the G × E analysis for root depth of wheat, which is discussed in full in Botwright Acuña and Wade (2012), but the approach for interpreting the biplot is described here. As noted previously, from a plant-breeding perspective, the relationship of genotype to an environment vector can provide information on the expression of the target trait, in this case root depth, for a particular environment in the ‘which-won-where’ scenario.

In addition, the G × E biplot can aid interpretation of the physiological mechanisms associated with rooting depth of wheat in the target environment, by integrating our interpretation of the cluster analysis into environment and genotype groups, detailed characteristics of probe genotypes, and their relative projection in the G × E biplot. For root depth, most genotype groups aligned from negative for AX1 and AX2 in the lower left to positive for AX1 and AX2 in the upper right (Fig. 3), which we have proposed to represent soil physical conditions ranging from friable to very hard (Botwright Acuña and Wade, 2012). Genotype groups containing the probe genotype, Halberd (G3), were better adapted to soil physical constraint, and this was consistent with Halberd having a greater capacity for root penetration of wax layers under controlled conditions (Botwright Acuña et al., 2007). In contrast, groups containing Cranbrook (G2) and C18 (G6) were less able to cope with soil physical constraint, again consistent with the poor ability of roots to penetrate wax layers under controlled conditions. The two Calcic Solonetz soils were likely to contain high levels of boron at depth (Lacey and Davies, 2009), which may have influenced separation of sensitive genotypes, such as Machete (Jefferies et al., 2000). Therefore six probe genotypes can be chosen to represent each of the six genotype groups: Spear, Cranbrook, Halberd, Janz, Machete and C18. There is a need for broader adoption of the probe genotypes in screening populations in controlled and field conditions and further experimentation to understand if the root traits associated with the probe genotypes are constitutive or adaptive in response to stress, which may implicate root signals for stress perception and signalling for trait expression (Siopongco et al., 2008, 2009).

FUTURE RESEARCH

The application of pattern analysis of G × E interactions for root depth is a new scientific approach to aid in the interpretation of complex root traits in a range of environments, and this warrants further attention. While we have focused on root depth in our study, pattern analysis is likely to be amenable to a range of root traits. Validation of the approach will require further datasets with well-characterized environments and genotypes. With specific reference to our research, we have provided some evidence on genotype responses of representatives from the Halberd (G3) and Cranbrook (G2) groups, and, to some extent, the Spear (G1) and C18 (G6) groups, but no data are available on representatives from the Janz group (G4) and Machete (G5) in relation to soil physical constraint. Further research is needed to document better the dynamics of root responses of such probe genotypes, which these analyses imply, may be preferentially adapted to contrasting soil physical conditions, in order to confirm trait identity and contribution, and confirm robust screening procedures.

Particularly promising is the link between field performance of parental lines and identification of QTL for traits such as root dry matter using the wax layer technique, which provides support for future research utilizing this genetic material. We have a validated a technique for evaluating the ability of roots to penetrate a wax layer under contrasting water regimes, which we have related to the field. We now know of QTL of chromosome segments associated with root traits using these techniques, albeit under well-watered conditions. Future research could identify QTLs under contrasting conditions of water availability using the wax-layer technique, given that this has been shown to allow for slow soil drying under drought conditions and examination of the interaction between root-penetration ability and soil water deficit (Botwright Acuña and Wade, 2005). DHLs contrasting in these traits could then be used as probe genotypes to investigate further the expression of these root traits in field conditions, in an unbiased genetic background, without the confounding effects of other traits such as plant height, flowering and plant type. There may be potential to use QTLs or even candidate genes for marker-assisted selection of these root traits in plant breeding (de Dorlodot et al., 2007).

Finally, recently there has been refinement of 3-D root architectural models to study the interaction between plant roots and objects or barriers in soil (Dunbabin et al., 2011). Modelling can play an important role in upscaling from pot to field studies and, in investigating the complexity of root–soil interactions (de Dorlodot et al., 2007) and trait contribution. Root growth in soil containing a hardpan restricts access to water and nutrients at depth. Modelling the root architecture of probe genotypes contrasting in their ability to penetrate wax layers in different soil types and available soil water and nutrients would complement QTL studies under controlled conditions in pots and in the field and assist in the interpretation and proof of concept of these complex interactions.

CONCLUSIONS

Pattern analysis of G × E interactions is an approach that has been largely neglected in the study of root systems and their adaptation to environment. With appropriate characterization of environments and genotypes, this approach can be used to aid in the interpretation of the complex interactions of root systems with the environment, inform future research and therefore provide supporting evidence for selecting specific root traits for target environments in a crop breeding programme. In the example presented in this paper, we have focussed on pattern analysis of G × E for root depth, which we have linked with phenotypic characterization undertaken in controlled conditions in pots containing a wax layer and evidence for genetic control, including QTLs. Future research will focus on additional phenotyping of the DHL population in pots containing a wax layer under contrasting water regimes, which allows for slow soil drying under drought conditions so that we can examine the interaction between root-penetration ability and soil water deficit. DHLs identified with contrasting root traits will be used to further our understanding and proof of concept of root growth of wheat in soils containing a hardpan, through a combination of detailed studies in controlled environments, in the field and using root architectural models.