Abstract
The molecular basis of adaptation—and, in particular, the relative roles of protein-coding versus gene expression changes—has long been the subject of speculation and debate. Recently, the genotyping of diverse human populations has led to the identification of many putative “local adaptations” that differ between populations. Here I show that these local adaptations are over 10-fold more likely to affect gene expression than amino acid sequence. In addition, a novel framework for identifying polygenic local adaptations detects recent positive selection on the expression levels of genes involved in UV radiation response, immune cell proliferation, and diabetes-related pathways. These results provide the first examples of polygenic gene expression adaptation in humans, as well as the first genome-scale support for the hypothesis that changes in gene expression have driven human adaptation.
The molecular mechanisms of adaptive mutations have long been a topic of great interest (King and Wilson 1975). In particular, the relative roles of protein-coding versus cis-regulatory changes have been much debated (King and Wilson 1975; Hoekstra and Coyne 2007; Prud'homme et al. 2007; Stern and Orgogozo 2008). However, no systematic comparisons between the two classes have been reported for humans; previously reported evidence supporting either mechanism has been either indirect, theoretical, or anecdotal (King and Wilson 1975; Hoekstra and Coyne 2007; Prud'homme et al. 2007; Stern and Orgogozo 2008). Many genome-wide scans for positive selection in humans have been conducted (Akey 2009; Pickrell et al. 2009; Torgerson et al. 2009; Hancock et al. 2011), but none have compared the prevalence of these two classes of human adaptations.
Adaptations that have arisen in recent human evolution are likely to be present only in a subset of human populations. For example, the sickle-cell mutation in beta hemoglobin, which confers resistance to malaria, is present at high frequency only in populations where malaria is endemic (Kwiatkowski 2005). Likewise, alleles causing lactase persistence—the continued expression of the lactase enzyme beyond childhood, allowing lactose to be metabolized—are at high frequency primarily in populations that have historically practiced dairy farming (Harris and Meyer 2006). These represent “local adaptations,” since they are specific to the local environments of a subset of human populations.
Recently, many other candidate local adaptations have been detected as correlations between population-specific allele frequencies and factors reflecting the climates or geographies of those populations (e.g., temperature, latitude, etc.) (Hancock et al. 2011). These associations are present even after controlling for genome-wide covariation due to population structure, and are enriched for nonsynonymous variants, suggesting the action of natural selection and not simply neutral drift (Hancock et al. 2011). Although the allele frequencies of these putatively adaptive variants typically differ only slightly between populations, presumably affecting phenotypes in a highly polygenic manner, collectively they may account for a significant fraction of recent human adaptation (Hancock et al. 2010, 2011; Pritchard et al. 2010).
To what extent human polygenic adaptations may act via changes in gene expression levels has not been investigated. Despite many examples of polygenic gene expression adaptations in model organisms (Fraser et al. 2010, 2011, 2012; Fraser 2011), the handful of known human gene expression adaptations all involve changes at only single genes, such as lactase (Harris and Meyer 2006). Therefore I sought to address two questions: (1) How important is gene expression in recent human adaptation, relative to changes in protein sequences? and (2) What specific functional classes have been targets of gene expression adaptations?
Results
Comparing nonsynonymous versus cis-regulatory adaptation
A recent genome-wide catalog of candidate local adaptations (Hancock et al. 2011) provides an ideal resource for comparing the roles of changes in protein sequences versus expression in recent human adaptation, since the approach used is agnostic with respect to the molecular mechanisms of the adaptations. In this study, nine climate variables were compared with allele frequencies of ∼623,000 autosomal SNPs in 61 diverse human populations. The resulting putative local-adaptation SNPs show a small but significant enrichment for nonsynonymous (NS) SNPs (Hancock et al. 2011), as expected if amino acid changes have played a role in recent adaptation.
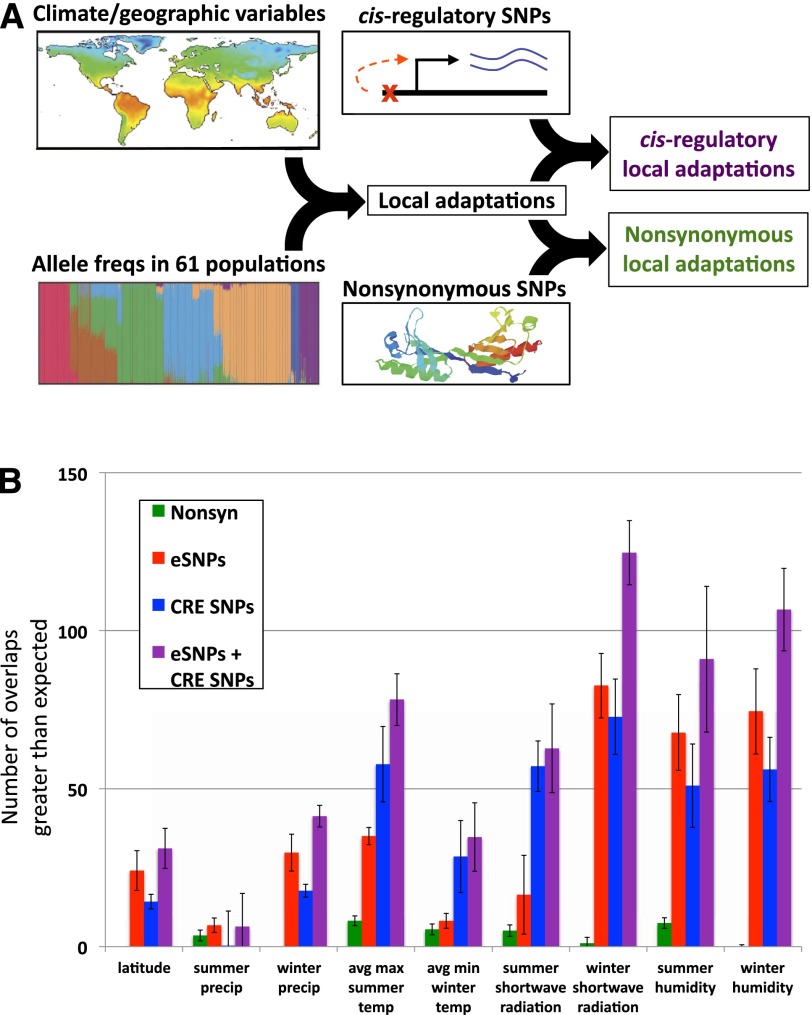
To assess the prevalence of cis-regulatory variants in local adaptation, a catalog of such variants can be combined with the putative local-adaptation SNPs. The size of their intersection (correcting for the number expected to overlap by chance) is a lower-bound estimate of how many local adaptations have likely been driven by cis-regulatory changes; this can be directly compared with the analogous intersection of NS SNPs (Fig. 1A; see Methods). While the catalog of putative local adaptations surely contains false positives and negatives, as long as these are not systematically biased toward one of the two classes (cis-regulatory or NS), they will not bias the comparison (other potential biases are discussed below). Although this statistical approach to understanding the molecular mechanisms of local adaptation cannot definitively implicate the mechanism of any single adaptation, it is well suited to assess the relative importance of different classes of genetic variation.
Figure 1.
(A) Outline of the data sets integrated to identify putative local adaptations (Hancock et al. 2011) and to assess the relative importance of cis-regulatory variants compared with nonsynonymous variants among these adaptations. (B) The estimated number of putative local adaptations associated with each of nine climate/geographic variables that are explicable by either a nonsynonymous SNP (green), eSNP (red), CRE SNP (blue), or combined eSNP/CRE SNP (purple). Error bars indicate the standard deviations when randomly sampling negative control SNPs (see Methods). Various controls are shown in Supplemental Figures 1–5.
Gene expression-associated SNPs (eSNPs) have been identified in several human tissues, with most occurring near their target gene because they act in cis (Cheung and Spielman 2009). I compiled a compendium of cis-eSNPs from 15 studies of seven human cell types (see Methods), and quantified their overlap with local-adaptation LD blocks (correcting for the overlap expected by chance). Across the nine climate variables tested, the eSNPs showed a median of 11.3-fold greater overlap than the analogous NS/local adaptation overlap (Fig. 1B, green vs. red bars), suggesting that they constitute a greater fraction of local adaptations.
SNPs located within cis-regulatory elements (CREs), e.g., promoters and enhancers, may contain additional cis-regulatory variants not captured by known eSNPs. Applying the same overlap analysis to SNPs within CREs identified by genome-wide chromatin state profiling in nine human cell types (Ernst et al. 2011), again a significant excess was implicated in local adaptation (Fig. 1B, blue bars). Finally, combining eSNPs and CRE SNPs into an integrated predictor (see Methods) yielded the greatest overlap (Fig. 1B, purple bars; median 12.4-fold above NS SNPs). In sum, these results suggest that local adaptations are far more likely to impact gene expression than protein sequence.
To test the robustness of these results, I carried out two types of controls. First, the local adaptation SNPs were randomly permuted, and the same analyses were run on the randomized data. No significant enrichments were observed for any category (Supplemental Fig. 1), indicating that the analysis itself does not lead to false-positive enrichments. Second, I varied each of the three adjustable parameters in the analysis (see Methods) and found the results to be robust to all three (Supplemental Figs. 2–4).
It is also important to consider factors that may bias this comparison. Specifically, (1) local-adaptation SNPs are enriched in genic regions (Hancock et al. 2011), which (by definition) include all NS SNPs, but only some cis-regulatory SNPs; (2) essentially all common NS SNPs are known, but many cis-regulatory SNPs have not yet been identified; (3) the precise locations of NS SNPs are known, whereas eSNPs are identified at the level of linkage-disequilibrium (LD) blocks often containing dozens of SNPs (only one of which is likely to be causal); and (4) the genotyping microarray used was designed to be highly enriched for NS SNPs (Eberle et al. 2007). Because all of these biases favor NS SNPs, they could only make the current results conservative, by underestimating the relative contribution of cis-regulatory variants (see Methods).
Detecting examples of local adaptations driven by gene expression
Functional enrichments among the genes associated with eSNPs/local-adaptation SNPs can provide insight into the types of genes affected by recent gene expression adaptations. Such enrichments are most likely to be found in the intersections of eSNP sets and local-adaptation SNPs with the highest overlap (and thus the fewest false positives overlapping due to chance). Therefore, I identified the five pairs of eSNP sets/environmental variables with the highest overlap (greater than twofold above expected, and with enrichment p < 10−5) (Supplemental Table 1), for further investigation.
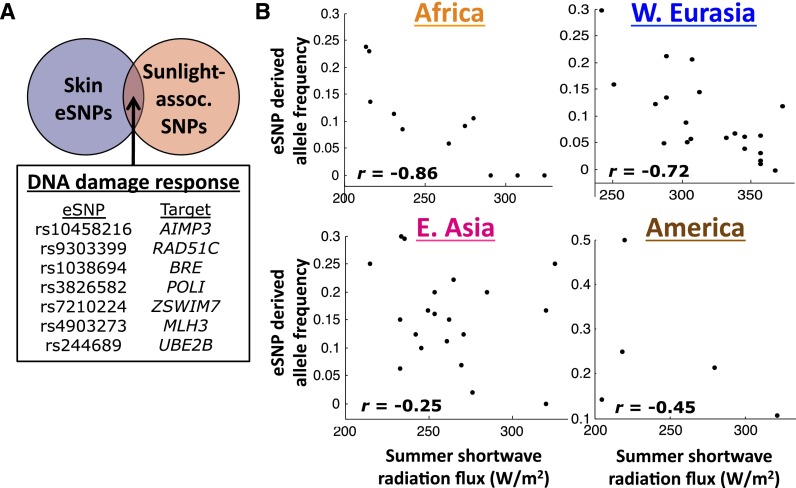
Two of the most significant overlaps were between skin eSNPs and local adaptations associated with winter precipitation and summer shortwave radiation flux (P < 1.3 × 10−6 for each) (Supplemental Table 1). The latter was particularly intriguing because skin is greatly affected by sunlight and shows many population-specific attributes (Jablonski and Chaplin 2010). Testing the skin eSNPs associated with summer shortwave solar radiation flux for enrichment among 281 GO terms (see Methods), “DNA damage response” was by far the most significantly enriched functional category among eSNP targets (7.2-fold over expected, P = 2 × 10−5) (Fig. 2A), suggesting that one way in which human populations may have adapted to local levels of sunlight is by altering the expression levels of genes involved in repairing DNA damage—consistent with the known population specificity of the response to UV-induced DNA damage in melanocytes (Barker et al. 1995). Interestingly, for many of these eSNPs the association with sunlight was replicated in multiple geographic regions (Fig. 2B), implying that these eSNPs have likely been targets of selection in diverse human populations.
Figure 2.
(A) Venn diagram showing DNA damage response as the most highly enriched functional category in the intersection between skin eSNPs and summer shortwave radiation (sunlight)–associated local-adaptation SNPs. The seven DNA damage response genes in this intersection are listed, with eSNPs that affect their expression levels in skin. Circles and overlap are not to scale. (B) The derived allele frequencies of one SNP in the skin eSNP/summer sunlight–associated SNP intersection (rs10458216) plotted against summer shortwave radiation flux in 58 worldwide human populations, split into four geographic regions. The derived allele is associated with lower expression of EEF1E1 (also known as AIMP3) (a tumor-suppressor gene that activates the DNA damage response in response to UV exposure and other DNA-damaging agents) (Kwon et al. 2011) in skin. Population names and additional data are shown in Supplemental Figure 6.
While a simple enrichment analysis such as above can lead to important insights, it ignores a valuable aspect of eSNPs: their directionality. For gene sets where most gene products have the same direction of effect on a process or phenotype—such as enzymes promoting flux through a pathway, or subunits of a protein complex contributing to a common molecular function—many genes may be coordinately up- or down-regulated in response to selection acting on their shared output. Indeed, this signature of polygenic gene expression adaptation is widespread in both yeast and mice (Fraser et al. 2010, 2011, 2012; Fraser 2011).
To take advantage of this additional information inherent in eSNPs, I developed an approach for identifying sets of eSNPs under selection by relating eSNP directionality to any population-specific variable of interest (Fig. 3A). In this framework, the mean frequency of all eSNP alleles up-regulating the members of a given gene set is calculated for each population of interest, resulting in a single aggregate “expression score” for that gene set in each population. The Pearson correlation (denoted r) between the expression score and a variable such as population latitude reflects the strength of association. Because such associations can be greatly affected by human population structure, a rigorous null model is essential. A simple yet effective control is to test how often the expression score of N randomly chosen eSNPs (where N is the number of eSNPs regulating the gene set of interest) has a correlation with latitude of at least |r|. Because the eSNPs are all sampled from a single eSNP data set, any ascertainment biases introduced by eSNP mapping are accounted for. Furthermore, no assumptions or models concerning population structure or demographic history are required, since these again are precisely captured by the randomly sampled eSNPs. This procedure results in a P-value reflecting the probability that the observed association could arise by chance, given the population structure and any other biases present among the eSNPs. By comparing to this null model, the method can identify sets of eSNPs whose allele frequencies are inconsistent with random drift, and therefore imply the action of natural selection (in contrast to nearly all previous genome-wide “selection scans,” which identify outlier SNPs in the absence of a neutral null model [Akey 2009], and thus cannot reject neutrality for any loci; see Supplemental Note).
Figure 3.
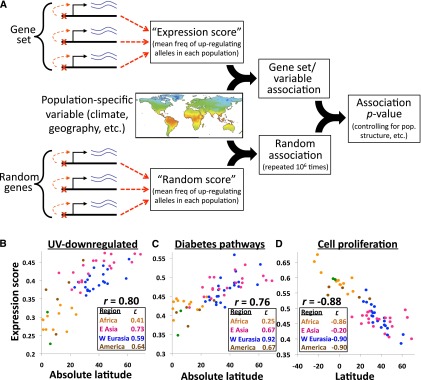
(A) Outline of the approach for identifying polygenic gene expression adaptations. (B–D) The three gene sets with significant associations (after correction for multiple tests; see Methods). Plots show their expression scores in each population versus the most strongly associated variable. Points are colored according to geographical regions listed in the insets; the two green points in each plot represent populations from Oceania. (B) Expression scores for the “UV down-regulation” gene set compared with absolute latitude. (C) Expression scores for the “Diabetes pathways” gene set compared with absolute latitude. (D) Expression scores for the “Positive regulation of cell proliferation” gene set (of which most eSNP target genes were immune-related) (Supplemental Table 2) compared with latitude.
Applying this approach revealed three striking cases of local adaptations involving the expression of entire gene sets. In one example, genes previously observed to be down-regulated in response to UV radiation (Gentile et al. 2003) constituted a gene set, containing genes involved in diverse functions such as apoptosis, angiogenesis, and transcriptional regulation. The correlation between this gene set's expression scores (the mean up-regulating allele frequencies of 12 eSNPs in each of 60 populations) and population absolute latitudes (distance from equator) was r = 0.80 (Fig. 3B; P = 2 × 10−6), the strongest association in this analysis. A strong correlation was also observed with winter shortwave radiation flux (r = −0.68). Separating the analysis into four major geographic regions showed that the association is replicated within all four (Fig. 3B, inset). Populations that receive more UV radiation have lower frequencies of the up-regulating alleles (Fig. 3B)—i.e., genetically encoded down-regulation—consistent with their dynamic down-regulation in response to UV (Gentile et al. 2003). Because random gene sets so rarely resulted in such a strong association, the null hypothesis of neutrality can confidently be rejected in favor of natural selection acting on these eSNPs—suggesting an adaptive “hard-wiring” of a transient transcriptional response.
The next most significant association highlights the relevance of this methodology to understanding how natural selection has affected population-specific disease prevalence. This association was between eSNPs in “Diabetes pathways” (primarily pathways related to insulin, ghrelin, and insulin-like growth factors) and distance from the equator (Fig. 3C; r = 0.76, P = 2 × 10−5). This association was strongly replicated in three out of the four major geographic regions (Fig. 3C, inset). Many hypotheses have been proposed to explain the marked population specificity of type 2 diabetes (T2D), including selection for “thrifty genes” (Neel 1962) or cold-tolerance genes (Fridlyand and Philipson 2006). The latitudinal gradient of eSNP frequencies is most clearly consistent with the latter, which posits that alleles originally selected for cold tolerance may now confer protection against T2D (Fridlyand and Philipson 2006). To further test this idea, I compared T2D risk allele frequencies with equatorial distance and found a negative association (r = −0.54, i.e., greater risk close to the equator; see Methods), as expected if alleles that are advantageous in cold climates confer protection against T2D.
To increase the signal in this analysis, I recalculated the associations after excluding SNPs with little population differentiation (global FST < 0.1). The strongest new association was for the gene set “Positive regulation of cell proliferation” with population latitude (Fig. 3D; r = −0.88, P = 1 × 10−6; Supplemental Fig. 7). Again the association was strongly replicated across three out of four geographic regions (Fig. 3D, inset) and was also present for absolute latitude (r = −0.77) and winter shortwave radiation flux (r = 0.74). Among the 16 eSNP target genes in this gene set, nine were directly related to immune cell proliferation (Supplemental Table 2), including six cytokines, strongly suggesting a relationship with immune system function. Because the diversity of human pathogens decreases with latitude (Guernier et al. 2004) and is known to impact natural selection on the human immune system (Qutob et al. 2012; Sanchez-Mazas et al. 2012), it is possible that the higher expression of immune cell proliferation genes near the equator is driven by selection for survival in the face of the high diversity of pathogens endemic to the tropics.
Conclusions
These results suggest that changes in gene expression regulation have been more prevalent in recent human adaptation than have changes in protein sequences, supporting King and Wilson's hypothesis (King and Wilson 1975). Although further work will be required to understand the selection pressures and phenotypic effects of the specific adaptations reported here, it is clear that natural selection in humans has acted in a distributed fashion on the expression of many genes in parallel, as it has in yeast and mice (Fraser et al. 2010, 2011, 2012; Fraser 2011).
The gene-set-based test of local adaptation introduced here represents a departure from previous “selection scans.” Because of its simple yet accurate neutral null model, it can distinguish natural selection from neutral drift—a surprisingly rare quality among published selection scans (Akey 2009). Although only three gene sets were significant in this initial analysis, variations of the method may reveal many more. For example, different correlation metrics can be used; contributions of each gene to the expression score could be weighted by the eSNP effect size or importance of each gene's expression level within a gene set; associations could be calculated separately in different geographic regions and then combined into a single score; or some regions could be excluded entirely in order to detect selection operating in only some parts of the world. The approach could also be applied directly to SNPs implicated by genome-wide association studies (with directionality provided by increase/decrease in the associated trait or disease risk, as opposed to up-/down-regulation of gene expression). Finally, the test is applicable to any species for which (1) allele frequency data are available from many populations (of known geographic coordinates), and (2) eSNPs have been mapped. Finally, applying this approach to the most evolutionarily relevant gene sets and population-specific selection pressures may also reveal many more cases of polygenic adaptation.
Because eSNPs have been mapped in only a handful of human cell types and populations, it is likely that their importance in local adaptation has been underestimated in this analysis. As the number of known eSNPs continues to grow, the power of population-genetic analyses of eSNPs will grow as well, and may eventually lead us to a comprehensive understanding of the role of gene expression in human adaptation.
Methods
eSNPs and CRE SNPs
eSNPs were collected from studies of the following cell types: lymphoblastoid cell lines (Kwan et al. 2008; Fraser and Xie 2009; Ge et al. 2009; Montgomery et al. 2010; Pickrell et al. 2010; Stranger et al. 2012), monocytes (Zeller et al. 2010; Fairfax et al. 2012), B cells (Fairfax et al. 2012), whole blood (Fehrmann et al. 2011), liver (Schadt et al. 2008; Innocenti et al. 2011), brain (Myers et al. 2007; Gibbs et al. 2010), and skin (Ding et al. 2010). (Some eSNP studies were not included because their results could not be obtained.) Four of the cell line studies included eSNPs affecting splicing and alternative transcription start/stop sites (Kwan et al. 2008; Fraser and Xie 2009; Montgomery et al. 2010; Pickrell et al. 2010). In addition, I included the “consensus eQTLs” for lymphoblastoid cells from the seeQTL database (Xia et al. 2012). For all data sets, only local (likely cis-acting) eSNPs were included, typically defined as eSNPs located within 1 Mb of their target gene.
Putative cis-regulatory elements (CREs) were determined previously, using combinations of histone modifications measured in nine human cell types (Ernst et al. 2011). Using the coordinates for those annotated as promoters, enhancers, or insulators (numbered types 1–8 in Ernst et al. 2011), all HapMap SNPs within each region were designated as CRE SNPs.
Calculating the observed number of overlaps
A straightforward approach would be to choose a particular number of the top-scoring local-adaptation SNPs and calculate the observed overlap with eSNPs/CRE SNPs/NS SNPs by matching dbSNP rs-IDs. However, because of linkage disequilibrium (LD), most eSNPs and local-adaptation SNPs are only proxies that tag the causal variants. If an eSNP study used a different genotyping array from the local-adaptation study, then many overlapping LD blocks might be missed if only single SNPs were checked for overlap, because different arrays use different tag SNPs. (For CRE SNPs and NS SNPs, even though the exact locations are known, a local-adaptation SNP may still be in LD with one of them, even if it is not itself a CRE SNP or NS SNP.) Therefore, I performed this analysis at the level of LD blocks, instead of single SNPs. I expanded each local-adaptation SNP into an LD block by including all other HapMap SNPs above a certain r2 cutoff in one HapMap population (see below). If two local-adaptation SNPs were in LD with one another or with a third SNP, they were collapsed into a single LD block. Then eSNPs/CRE SNPs/NS SNPs were intersected with these LD blocks; if multiple eSNPs/CRE SNPs/NS SNPs were contained in a single LD block, they were only counted as one overlap, to avoid double counting. Although the HapMap does not contain all common SNPs, it is a superset of those in the array platforms used for eSNP and local-adaptation SNP mapping, so using a more complete SNP list (e.g., from the 1000 Genomes Project) would not affect the results.
Because not all eSNP data sets are equally relevant to local adaptation (due to different cell types, false-positive rates, etc.), the overlap analysis described above was applied separately to each eSNP set (similarly, the eight CRE types, measured in nine cell types, yielded 72 CRE sets). A stepwise regression framework was then applied, to exclude those eSNP/CRE SNP sets not able to discriminate between the real versus negative control sets. It is important to note that exclusion of any eSNP/CRE SNP sets can only decrease the total number of overlaps with local adaptations. Each climate-associated LD block (defined as those containing at least one SNP in the top 0.5% of Bayes factors, with each of the nine environmental variables [Hancock et al. 2011] tested separately) or negative control LD block was represented by a 1 or 0, respectively; any eSNPs on these same LD blocks were then used as binary predictors of the climate association. Stepwise regression was used to identify those eSNP sets adding significant (P < 0.01) predictive power not provided by other sets. The number of independent eSNP/local adaptation SNP overlaps was estimated as the number of local-adaptation LD blocks containing at least one eSNP from an eSNP set that was significant in the stepwise regression. For the combined eSNP/CRE SNP predictor (purple bars in Fig. 1B), the regression procedure was applied to the eSNPs and CRE SNPs jointly, to account for any redundancy between them. Note that excluding those eSNP/CRE SNP sets not providing significant predictive power reduces the number of eSNPs/CRE SNPs overlapping with local-adaptation SNPs.
Calculating the expected number of overlaps
In this analysis, it is critical to estimate the expected number of overlaps accurately between different SNP catalogs. The expected overlap can be found by randomly drawing “non-local-adaptation” SNPs from the lower half of climate-association scores and repeating the overlap analysis (performed 100 times for each bar in Fig. 1B). To minimize stochastic variation in these randomly sampled SNP sets, 10-fold more SNPs were included in each negative control set than in the positive set (the resulting number of expected overlaps was thus divided by 10 to be comparable to the real SNP set). Because the negative control SNPs are drawn from the same genotyping array (Illumina Infinium HumanHap 650Y), they share all the same ascertainment biases as the real local-adaptation SNPs (including over-representation of nonsynonymous SNPs on the 650Y array) (Eberle et al. 2007).
However, two important factors may affect the overlap: LD block length (in number of SNPs) and minor allele frequency (MAF). LD blocks containing many SNPs will have more overlaps with any other SNP catalog simply by chance, and if both eSNPs and local-adaptation SNPs are biased toward high MAF, then they will also overlap more than expected by chance. Therefore, negative control SNPs were chosen to match the local-adaptation SNPs for these two factors. The number of local-adaptation SNPs in each of 50 global MAF (mean MAF across all 61 populations) bins (0–0.01; 0.01–0.02; etc.) was counted, and negative control SNPs were selected from the low-scoring tail in exactly the same proportions. The LD block length of each negative-control candidate was then calculated and matched to the most similar local-adaptation SNP. As a result, negative control SNPs were matched for both MAF and LD block length. Because the negative controls were sampled from a list 100× larger than the number of putative local adaptations, each randomly sampled negative control list was mostly independent (composed of different SNPs) from all others.
Expected overlaps were subtracted from the observed overlaps and averaged over 100 randomly sampled negative control sets, to yield the number of overlaps above expected (shown in Fig. 1B). Error bars are calculated from the variation between randomly sampled negative control sets; empirical error bars were used (as opposed to theoretical, Poisson-based error bars) because they capture any deviations from the theoretical expectations of overlap variation. Median fold-differences of the estimated numbers of adaptive eSNPs or CRE SNPs compared with NS SNPs were calculated by taking the median ratio of overlaps above expected for the two SNP classes being compared, across the nine climate variables.
Potential biases
Four potentially biasing factors are listed in the main text:
Local adaptation SNPs are enriched in genic regions (Hancock et al. 2011), which (by definition) include all NS SNPs but only some regulatory SNPs. I did not attempt to correct for this because its cause is not known; e.g., if it is caused mainly by NS SNPs, then correcting for it would be unfairly penalizing those SNPs. If, instead, it is caused largely by other genic SNPs (such as synonymous or intronic SNPs) and inflates the NS SNP enrichment due to LD between NS SNPs and the causal SNPs, this bias would lead to overestimation of the role of NS SNPs in local adaptation.
Essentially all common NS SNPs are known, but many regulatory SNPs have not yet been identified. I did not attempt to correct for this because it is not known how many regulatory SNPs remain to be discovered.
The precise locations of NS SNPs are known, whereas regulatory SNPs are identified at the level of LD blocks often containing dozens of SNPs (only one of which is likely to be causal). If LD was the same across all human populations, this might have been accounted for by the LD block-based overlap analysis described above. However, because LD patterns differ between populations, a SNP that tags a causal variant in the population where an eSNP was discovered may not tag the causal variant in another population, which could decrease the signal in this analysis. A precise correction for this is not possible without detailed LD data from all populations studied.
The genotyping microarray used was designed to be highly enriched for NS SNPs (Eberle et al. 2007). This bias may lead to preferential detection of local adaptations involving NS SNPs, since a greater fraction of regulatory SNPs will not be genotyped by the microarray. Compounding this, LD is stronger in genic than intergenic regions (Eberle et al. 2006), meaning that even NS SNPs not directly genotyped by the array are more likely to be indirectly measured by another variant in strong LD.
As stated in the main text, because all four of these biases act in favor of relatively more overlap with NS SNPs, they make the current results (an excess of regulatory SNPs overlapping with putative local adaptations) conservative.
Factors that may exaggerate the observed results include any unknown bias that could preferentially increase the density of putative local adaptation SNPs in CREs or eSNP LD blocks, compared with NS SNP LD blocks. For example, if climate-related background selection led to associations with various climate variables, and this affected regulatory regions more than coding regions, this could lead to an excess of regulatory SNPs among putative local adaptation SNPs. However, I am not aware of any evidence suggesting that this is the case.
Randomization control
In randomized data, the number of observed overlaps should approximately equal the expected overlaps; therefore, to test the accuracy of this regression approach, I randomized the local adaptation scores of the 623,318 SNPs 100 times, and performed the same enrichment analysis for NS SNPs, eSNPs, and CRE SNPs. The results show no significant enrichment for any test (Supplemental Fig. 1), suggesting that the analysis does not lead to false positives.
Results with other parameter values
There are several adjustable parameters in this analysis, so the results were calculated using different values of each, to assess the robustness of the results shown in Figure 1B. These parameters are the r2 cutoff for defining LD blocks; in which HapMap population LD blocks were defined; and what fraction of SNPs assessed for local adaptation were considered “putative local-adaptation SNPs” for overlap analysis. In Figure 1B, these are r2 = 0.9, Yoruban, and 0.5%, respectively. Supplemental Figures 2–4 show the results of changing each parameter; in each case the results are qualitatively unchanged. In addition, a parameter used in calculating the climate association Bayes factors is the number of MCMC “burn-in” iterations (Hancock et al. 2011). Supplemental Figure 5 shows the results of the analysis using climate associations generated with 15,000 burn-ins (burn-ins were not used in Hancock et al. 2011), again not qualitatively affecting the results.
Functional enrichment analysis (ignoring eSNP directionality)
For each eSNP set/climate variable combination, I calculated the fold-enrichment compared with the random expectation (as determined by the negative control SNPs described above). Five combinations yielded a greater than twofold enrichment and enrichment P-value < 10−5 (Supplemental Table 1, boldface). To determine if any functions were enriched in these intersections, I tested the eSNP target genes from all five intersections for enrichments with 281 GO terms (with >100 members each). The only GO term to remain significant after correction for multiple testing was “DNA damage response” in the skin eSNP/summer solar radiation intersection (281 GO terms tested in five overlaps = 1405 tests; P = 0.03 after Bonferroni correction; note, however, that the Bonferroni correction is overly conservative because many gene sets and climate variables are not independent—e.g., temperature is correlated with latitude, etc.). There were seven DNA damage-related genes in this intersection (Fig. 2A), compared with fewer than one expected by chance. While solar radiation is a plausible explanation for the selection pressure leading to changes in expression levels of these genes, it is not possible to rule out the possibility that another factor (correlated with solar radiation) is the agent of selection.
Scan for selection on expression levels of gene sets using eSNP directionality
To leverage the additional specificity gained by searching for gene sets that show coordinated changes in their gene expression levels between human populations, I carried out the following test. For five of the published eSNP sets listed above, information about the directionality of allelic effects (i.e., which allele was up-regulating) could be extracted from the supplemental data or obtained from the authors. These five sets were from four tissues: LCLs (Montgomery et al. 2010; Stranger et al. 2012), whole blood (Fehrmann et al. 2011), brain (Myers et al. 2007), and liver (Innocenti et al. 2011). Because the goal of this approach is identifying polygenic gene expression adaptations, regardless of whether those are cis- or trans-acting (unlike the analyses described above where the focus was on cis-regulation), both cis- and trans-acting eSNPs were included but analyzed separately when available. Since the effects of splicing changes are not easily inferred (e.g., inclusion of an exon may either increase or decrease a particular activity of a protein), splicing-related eSNPs were not included in this analysis.
For each eSNP set, all eSNPs not in LD (r2 > 0.9 in the HapMap YRI population) with an Illumina 650Y SNP were excluded, so that the up-regulating allele (or proxy allele) frequency in 60 populations could be calculated. YRI was chosen for the LD mapping since this shows less LD than non-African populations and therefore tends to lead to a conservative mapping; cases in which SNPs in LD in YRI are not in LD in other populations will add noise and make the present results conservative. If multiple eSNPs from the same study were regulating a single gene and were in LD with 650Y SNPs, the one with the most significant eSNP was chosen.
The set of eSNPs with worldwide up-regulating allele frequency data was then grouped by gene sets. (Although eSNPs could be analyzed individually, this would simply identify empirical outliers [as described for previous “selection scans” by Akey 2009], with no indication of how likely they are to be evolving neutrally or non-neutrally.) Gene sets were downloaded from the GSEA website (http://www.broadinstitute.org/gsea/msigdb/collections.jsp), using all GO, Reactome, and KEGG gene sets, as well as all chemical/genetic perturbation gene sets containing “UV” in the description (since UV exposure is a plausible selection pressure correlated with climate/geography). Only gene sets regulated by at least 10 distinct eSNPs from a single eSNP data set were considered for analysis in conjunction with that eSNP set (i.e., a gene set could be analyzed with one eSNP set but not with another). Furthermore, one out of any pair of eSNPs within 1 Mb of each other was excluded, to ensure that each eSNP represents an independent signal. (This filter also applied to cases in which a single eSNP regulated multiple genes within a single gene set.) For gene sets with at least 10 eSNPs passing this filter, the mean up-regulating allele frequency in each population (“Expression score”) was calculated and compared (using Pearson correlation) with 10 variables: the nine used by Hancock et al. (2011), plus absolute latitude.
These correlation values represent the effects of both natural selection and neutral demographic processes. To correct for the latter, I reasoned that the demographic effects in a gene set of size N eSNPs would be well-captured by N eSNPs randomly chosen from the same eSNP data set (and subjected to the same process of mapping proxies to the Illumina 650Y microarray; see above). These are expected to reflect not only the varying relatedness of the 60 human populations, but also any effects of ascertainment bias in the original eSNP study (e.g., due to the genotyping platform used, bias toward high MAF, etc.). Therefore, because multiple eSNPs are present in each gene set, the effects of demography and other confounders can be accounted for, without resorting to complex/questionable models of human demographic history. To achieve this, up to 107 randomly drawn sets of eSNPs were compared with each real set (only sets that were significant with smaller numbers of randomizations were tested with the full 107, to increase computational efficiency). The number of random sets with an association to a climate variable that was at least as strong as that of the real set, divided by the number of random sets tested, represented the P-value estimate. Absolute values of correlation coefficients were used, to make the test two-sided.
Within most gene sets, it is likely that not every eSNP has been subject to the same selective pressures; in particular, some may be effectively neutral. To enrich eSNPs in the analysis for those that are subject to selection, I re-ran the analysis using only eSNPs with global FST > 0.1. Although this reduced the number of eSNPs being analyzed, those remaining were specifically those showing at least moderate population differentiation.
It is critical to correct for the number of statistical tests performed in this analysis. Across all five eSNP sets, a total of 2201 gene sets were tested in the all-FST analysis, and 837 in the FST > 0.1 analysis (fewer were tested at FST > 0.1 because fewer gene sets had more than 10 eSNPs with FST > 0.1). With 10 climate variables being compared, there were nominally 10 × (2201 + 837) = 30,380 tests performed; however, because of the highly redundant nature of many gene sets and climate variables, a simple Bonferroni correction is not appropriate. To estimate more accurately the effect of these nonindependent tests, I recorded how often any gene set (out of all tested) reached a given significance level when gene labels were randomly shuffled, so that all of the gene set assignments for gene X were assigned to the same randomly chosen gene. Among 1000 of these randomizations (each involving the complete collection of gene sets used in the real analysis), nine yielded a single gene set/climate variable pair with P = 2 × 10−6 or lower, yielding a multiple test-corrected P = 9/1000 = 0.009 for the UV-down-regulated gene set. Analogous calculations yielded a corrected P = 0.035 for the “Diabetes pathways” gene set, and P = 0.002 for the “Positive regulation of cell proliferation” gene set. No other gene sets were significant at a corrected P < 0.05.
Correlation between type 2 diabetes risk allele frequencies and distance from the equator
This result was calculated using the SNPs reported to be associated with T2D in the NHGRI GWAS Database (http://www.genome.gov/26525384; downloaded in September 2012). For the 20 T2D-associated SNPs with non-negligible population differentiation (FST > 0.1) present on (or in r2 > 0.9 with a SNP on) the Illumina 650Y microarray, risk-allele frequency was calculated in each of the 60 populations, and the mean of these frequencies was compared with the absolute latitude of each population. This approach is justified by the observation that T2D-associated SNPs discovered in European cohorts are nearly all replicated in diverse worldwide populations (Waters et al. 2010). Since GWAS power increases with MAF, the T2D SNPs could potentially be biased toward high MAF in Europeans (the study population for nearly all of the T2D GWAS); however, this would not be expected to introduce any correlation between the risk allele (which is about evenly split between major and minor) frequency and latitude. The association between mean risk allele frequency and absolute latitude is consistent with the known population differentiation of T2D-associated variants (Pickrell et al. 2009; Chen et al. 2012).
Acknowledgments
I thank M. Feldman, D. Petrov, J. Pritchard, N. Rosenberg, A. Ting, and members of the Fraser laboratory for helpful feedback. The work was supported by NIH grant 1R01GM097171-01A1. H.B.F. is an Alfred P. Sloan Fellow and a Pew Scholar in the Biomedical Sciences.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.152710.112.
References
- Akey JM 2009. Constructing genomic maps of positive selection in humans: Where do we go from here? Genome Res 19: 711–722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barker D, Dixon K, Medrano EE, Smalara D, Im S, Mitchell D, Babcock G, Abdel-Malek ZA 1995. Comparison of the responses of human melanocytes with different melanin contents to ultraviolet B irradiation. Cancer Res 55: 4041–4046 [PubMed] [Google Scholar]
- Chen R, Corona E, Sikora M, Dudley JT, Morgan AA, Moreno-Estrada A, Nilsen GB, Ruau D, Lincoln SE, Bustamante CD, et al. 2012. Type 2 diabetes risk alleles demonstrate extreme directional differentiation among human populations, compared to other diseases. PLoS Genet 8: e1002621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung VG, Spielman RS 2009. Genetics of human gene expression: Mapping DNA variants that influence gene expression. Nat Rev Genet 10: 595–604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding J, Gudjonsson JE, Liang L, Stuart PE, Li Y, Chen W, Weichenthal M, Ellinghaus E, Franke A, Cookson W, et al. 2010. Gene expression in skin and lymphoblastoid cells: Refined statistical method reveals extensive overlap in cis-eQTL signals. Am J Hum Genet 87: 779–789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberle MA, Rieder MJ, Kruglyak L, Nickerson DA 2006. Allele frequency matching between SNPs reveals an excess of linkage disequilibrium in genic regions of the human genome. PLoS Genet 2: e142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberle MA, Ng PC, Kuhn K, Zhou L, Peiffer DA, Galver L, Viaud-Martinez KA, Lawley CT, Gunderson KL, Shen R, et al. 2007. Power to detect risk alleles using genome-wide tag SNP panels. PLoS Genet 3: e1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ernst J, Kheradpour P, Mikkelsen TS, Shoresh N, Ward LD, Epstein CB, Zhang X, Wang L, Issner R, Coyne M, et al. 2011. Mapping and analysis of chromatin state dynamics in nine human cell types. Nature 473: 43–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairfax BP, Makino S, Radhakrishnan J, Plant K, Leslie S, Dilthey A, Ellis P, Langford C, Vannberg FO, Knight JC 2012. Genetics of gene expression in primary immune cells identifies cell type-specific master regulators and roles of HLA alleles. Nat Genet 44: 502–510 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fehrmann RS, Jansen RC, Veldink JH, Westra HJ, Arends D, Bonder MJ, Fu J, Deelen P, Groen HJ, Smolonska A, et al. 2011. Trans-eQTLs reveal that independent genetic variants associated with a complex phenotype converge on intermediate genes, with a major role for the HLA. PLoS Genet 7: e1002197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser HB 2011. Genome-wide approaches to the study of adaptive gene expression evolution. Bioessays 33: 469–477 [DOI] [PubMed] [Google Scholar]
- Fraser HB, Xie X 2009. Common polymorphic transcript variation in human disease. Genome Res 19: 567–575 [DOI] [PubMed] [Google Scholar]
- Fraser HB, Moses A, Schadt EE 2010. Evidence for widespread adaptive evolution of gene expression in budding yeast. Proc Natl Acad Sci 107: 2977–2982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser HB, Babak T, Tsang J, Zhou Y, Zhang B, Mehrabian M, Schadt EE 2011. Systematic detection of polygenic cis-regulatory evolution. PLoS Genet 7: e1002023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser HB, Levy S, Chavan A, Shah HB, Perez JC, Zhou Y, Siegal ML, Sinha H 2012. Polygenic cis-regulatory adaptation in the evolution of yeast pathogenicity. Genome Res 22: 1930–1939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fridlyand LE, Philipson LH 2006. Cold climate genes and the prevalence of type 2 diabetes mellitus. Med Hypoth 67: 1034–1041 [DOI] [PubMed] [Google Scholar]
- Ge B, Pokholok DK, Kwan T, Grundberg E, Morcos L, Verlaan DJ, Le J, Koka V, Lam KC, Gagné V, et al. 2009. Global patterns of cis variation in human cells revealed by high-density allelic expression analysis. Nat Genet 41: 1216–1222 [DOI] [PubMed] [Google Scholar]
- Gentile M, Latonen L, Laiho M 2003. Cell cycle arrest and apoptosis provoked by UV radiation–induced DNA damage are transcriptionally highly divergent responses. Nucleic Acids Res 31: 4779–4790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbs JR, van der Brug MP, Hernandez DG, Traynor BJ, Nalls MA, Lai SL, Arepalli S, Dillman A, Rafferty IP, Troncoso J, et al. 2010. Abundant quantitative trait loci exist for DNA methylation and gene expression in human brain. PLoS Genet 6: e1000952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guernier V, Hochberg ME, Guégan JF 2004. Ecology drives the worldwide distribution of human diseases. PLoS Biol 2: e141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock AM, Alkorta-Aranburu G, Witonsky DB, Di Rienzo A 2010. Adaptations to new environments in humans: The role of subtle allele frequency shifts. Phil Trans R Soc B 365: 2459–2468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock AM, Witonsky DB, Alkorta-Aranburu G, Beall CM, Gebremedhin A, Sukernik R, Utermann G, Pritchard JK, Coop G, Di Rienzo A 2011. Adaptations to climate-mediated selective pressures in humans. PLoS Genet 7: e1001375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris EE, Meyer D 2006. The molecular signature of selection underlying human adaptations. Am J Phys Anthropol 49: 89–130 [DOI] [PubMed] [Google Scholar]
- Hoekstra HE, Coyne JA 2007. The locus of evolution: Evo devo and the genetics of adaptation. Evolution 61: 995–1016 [DOI] [PubMed] [Google Scholar]
- Innocenti F, Cooper GM, Stanaway IB, Gamazon ER, Smith JD, Mirkov S, Ramirez J, Liu W, Lin YS, Moloney C, et al. 2011. Identification, replication, and functional fine-mapping of expression quantitative trait loci in primary human liver tissue. PLoS Genet 7: e1002078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jablonski NG, Chaplin G 2010. Human skin pigmentation as an adaptation to UV radiation. Proc Natl Acad Sci (Suppl 2) 107: 8962–8968 [DOI] [PMC free article] [PubMed] [Google Scholar]
- King MC, Wilson AC 1975. Evolution at two levels in humans and chimpanzees. Science 188: 107–116 [DOI] [PubMed] [Google Scholar]
- Kwan T, Benovoy D, Dias C, Gurd S, Provencher C, Beaulieu P, Hudson TJ, Sladek R, Majewski J 2008. Genome-wide analysis of transcript isoform variation in humans. Nat Genet 40: 225–231 [DOI] [PubMed] [Google Scholar]
- Kwiatkowski DP 2005. How malaria has affected the human genome and what human genetics can teach us about malaria. Am J Hum Genet 77: 171–192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon NH, Kang T, Lee JY, Kim HH, Kim HR, Hong J, Oh YS, Han JM, Ku MJ, Lee SY, et al. 2011. Dual role of methionyl-tRNA synthetase in the regulation of translation and tumor suppressor activity of aminoacyl-tRNA synthetase-interacting multifunctional protein-3. Proc Natl Acad Sci 108: 19635–19640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montgomery SB, Sammeth M, Gutierrez-Arcelus M, Lach RP, Ingle C, Nisbett J, Guigo R, Dermitzakis ET 2010. Transcriptome genetics using second generation sequencing in a Caucasian population. Nature 464: 773–777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers AJ, Gibbs JR, Webster JA, Rohrer K, Zhao A, Marlowe L, Kaleem M, Leung D, Bryden L, Nath P, et al. 2007. A survey of genetic human cortical gene expression. Nat Genet 39: 1494–1499 [DOI] [PubMed] [Google Scholar]
- Neel JV 1962. Diabetes mellitus: A thrifty genotype rendered detrimental by progress. Am J Hum Genet 14: 353–362 [PMC free article] [PubMed] [Google Scholar]
- Pickrell JK, Coop G, Novembre J, Kudaravalli S, Li JZ, Absher D, Srinivasan BS, Barsh GS, Myers RM, Feldman MW, et al. 2009. Signals of recent positive selection in a worldwide sample of human populations. Genome Res 19: 826–837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell JK, Marioni JC, Pai AA, Degner JF, Engelhardt BE, Nkadori E, Veyrieras JB, Stephens M, Gilad Y, Pritchard JK 2010. Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature 464: 768–772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Pickrell JK, Coop G 2010. The genetics of human adaptation: Hard sweeps, soft sweeps, and polygenic adaptation. Curr Biol 20: R208–R215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prud'homme B, Gompel N, Carroll SB 2007. Emerging principles of regulatory evolution. Proc Natl Acad Sci (Suppl 1) 104: 8605–8612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qutob N, Balloux F, Raj T, Liu H, Marion de Procé S, Trowsdale J, Manica A 2012. Signatures of historical demography and pathogen richness on MHC class I genes. Immunogenetics 64: 165–175 [DOI] [PubMed] [Google Scholar]
- Sanchez-Mazas A, Lemaître JF, Currat M 2012. Distinct evolutionary strategies of human leucocyte antigen loci in pathogen-rich environments. Philos Trans R Soc Lond B Biol Sci 367: 830–839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schadt EE, Molony C, Chudin E, Hao K, Yang X, Lum PY, Kasarskis A, Zhang B, Wang S, Suver C, et al. 2008. Mapping the genetic architecture of gene expression in human liver. PLoS Biol 6: e107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern DL, Orgogozo V 2008. The loci of evolution: How predictable is genetic evolution? Evolution 62: 2155–2177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stranger BE, Montgomery SB, Dimas AS, Parts L, Stegle O, Ingle CE, Sekowska M, Smith GD, Evans D, Gutierrez-Arcelus M, et al. 2012. Patterns of cis regulatory variation in diverse human populations. PLoS Genet 8: e1002639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torgerson DG, Boyko AR, Hernandez RD, Indap A, Hu X, White TJ, Sninsky JJ, Cargill M, Adams MD, Bustamante CD, et al. 2009. Evolutionary processes acting on candidate cis-regulatory regions in humans inferred from patterns of polymorphism and divergence. PLoS Genet 5: e1000592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waters KM, Stram DO, Hassanein MT, Le Marchand L, Wilkens LR, Maskarinec G, Monroe KR, Kolonel LN, Altshuler D, Henderson BE, et al. 2010. Consistent association of type 2 diabetes risk variants found in Europeans in diverse racial and ethnic groups. PLoS Genet 6: e1001078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia K, Shabalin AA, Huang S, Madar V, Zhou YH, Wang W, Zou F, Sun W, Sullivan PF, Wright FA 2012. seeQTL: A searchable database for human eQTLs. Bioinformatics 28: 451–452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeller T, Wild P, Szymczak S, Rotival M, Schillert A, Castagne R, Maouche S, Germain M, Lackner K, Rossmann H, et al. 2010. Genetics and beyond—the transcriptome of human monocytes and disease susceptibility. PLoS ONE 5: e10693. [DOI] [PMC free article] [PubMed] [Google Scholar]