Non-ideal Solution Thermodynamics of Cytoplasm

Abstract

Quantitative description of the non-ideal solution thermodynamics of the cytoplasm of a living mammalian cell is critically necessary in mathematical modeling of cryobiology and desiccation and other fields where the passive osmotic response of a cell plays a role. In the solution thermodynamics osmotic virial equation, the quadratic correction to the linear ideal, dilute solution theory is described by the second osmotic virial coefficient. Herein we report, for the first time, intracellular solution second osmotic virial coefficients for four cell types [TF-1 hematopoietic stem cells, human umbilical vein endothelial cells (HUVEC), porcine hepatocytes, and porcine chondrocytes] and further report second osmotic virial coefficients indistinguishable from zero (for the concentration range studied) for human hepatocytes and mouse oocytes.

Introduction

As well as playing a role in many biological processes, passive water transport across cell membranes (cellular osmotic response) is central to cryopreservation¹ and desiccation,² which are necessary for cell therapy, tissue engineering, biotechnology, and biological research with cell lines. Passive water transport is governed by intracellular and extracellular water chemical potentials (i.e., solution thermodynamics), in addition to membrane permeability and area. “Solution thermodynamics” is the term used to describe the thermodynamics of molecular mixtures. Such mixtures need not be ideal, or dilute, or devoid of molecular order, or even liquid. While ideal, dilute solution thermodynamics are ubiquitously applied in biology, the application of ideal dilute solution behavior to concentrated solutions, such as those that occur during cryopreservation or desiccation, will introduce errors—sometimes severe, and may be misleading even in physiological conditions such as for the complex solution containing macromolecules that contributes to the cytoplasm.³ The relationship between osmolality and concentration is well described for a variety of solutions, including the cytoplasm of erythrocytes.^3,4 However, other than the simplest proposition of osmolality depending linearly on concentration, this relationship has not been available for the cytoplasm of a nucleated mammalian cell.

Nucleated mammalian cells have many intracellular components, such as water, organelles, electrolytes, and proteins of varying concentrations.⁵ The intracellular milieu can be viewed through its biochemical behavior, its mechanical behavior, or its osmotic behavior. As the cytoplasm typically loses the majority of its water during cryobiological processing, and this osmotic response is typically the process most correlated with cell outcome, the osmotic behavior of the cell is very important in cryobiological applications. This is why it has been a focus of cryobiological modeling efforts, albeit until recently only through ideal dilute solution thermodynamics. Most mathematical models in cryobiology use solution thermodynamics;^6–22 however, these models treat the cytoplasm as an ideal, dilute solution. Karlsson, Toner, and co-workers have improved certain aspects of modeling by coupling ice nucleation, crystal growth, and water transport models.^6,14,20 This approach allows for better predictions of intracellular ice formation; however, the solution thermodynamics of the intracellular milieu has been largely ignored and is based on an ideal, dilute solution assumption. Herein, we use the osmotic virial equation, a non-ideal solution thermodynamics model, being applied with success in cryobiological modeling of the extracellular solution.^23–29

While the solution properties are known for some individual components (e.g., hemoglobin^3,30) and combinations of known single-solute components using, for example, the osmotic virial equation,^3,26 the cytoplasm is too complex to make general use of the individual solute solution properties feasible. It is precisely because of the requirement to incorporate thermodynamics of a wide variety of molecules that we have chosen the osmotic virial approach. The osmotic virial equation has been shown by many researchers over decades to apply to a vast number of types of solutes in aqueous systems, including sugars, electrolytes, cryoprotectants, macromolecules, proteins, alcohols, and starches.^{3,24,26,27,31–44}

Osmolality describes the concentration dependence of the chemical potential of water in a solution and is the solution thermodynamics quantity that appears directly in equations describing freezing point depression of a solution (see Eq. 12) or the driving force for passive osmotic transport.^28,29 Osmolality, π, is defined by its relationship to the chemical potential of water in a solution μ₁:

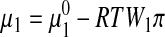(Eq. 1)

where 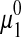is the chemical potential of pure water, R is the universal gas constant, T is the absolute temperature, and W₁ is the molar mass of water. Osmolality is related to the osmotic pressure, Π, of the solution by the following relationship:

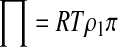(Eq. 2)

where ρ₁ is the density of water (kg/m³).

The simplest relationship between osmolality and concentration is the ideal, dilute assumption

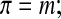(Eq. 3)

where π is osmolality (osmol/kg solvent) and m is molality (mole/kg solvent).^45–47 Equation 1 can also be considered the dilute relation for electrolytes if one considers m to be the molality of all distinct entities per kilogram of solvent (i.e., for salts m is considered to be the undissociated salt molality multiplied by a constant called the van't Hoff factor that accounts for dissociation).²⁷

In an attempt to allow for some more complexity, another linear model is commonly used

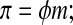(Eq. 4)

where φ is the osmotic coefficient,²⁶ which may be determined from an equilibrium measurement. In many studies, φ is assumed to be unity as in Equation 3, and in other studies, φ is assumed to be a constant. If a measured dependence of φ on molality is used then the equation is a nonlinear theory equivalent to those described below.

After the two linear models of Equations 3 and 4, the most widely used thermodynamic solution model in biology is the osmotic virial equation^3,31,48 (Eq. 5), which describes the osmolality as a polynomial function of concentration.

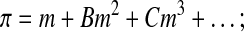(Eq. 5)

where B is the second osmotic virial coefficient ((mole/kg solvent)⁻¹) and C is the third osmotic virial coefficient ((mole/kg solvent)⁻²), which define the quadratic and cubic corrections to the linear ideal, dilute theory, respectively. Equation 5 can be applied to electrolytes if the values of m are considered to be salt molal multiplied by an additional fitting constant.²⁷ For a full description of the relationship between the electrolyte osmotic virial equation and more rigorous electrolyte theories, see Prickett et al.²⁷ Taking a value of zero for all virial coefficients results in the ideal dilute solution assumption (Eq. 3).

The osmotic virial approach is very successful when the molecular components and their thermodynamic contribution to the solution are known.^3,26 However, there has been no way to apply the osmotic virial approach for the cytoplasm of a living cell where the molecular constituents and their contributions to the cytoplasmic chemical potential are unknown. We have proposed a form of the osmotic virial equation that combines effects of multiple solutes (even of different types) without neglecting inter species interactions.^3,26

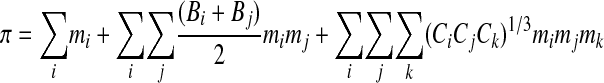(Eq. 6)

where subscripts i, j and k refer to the individual solutes. We have shown through a series of articles, that our equation (Eq. 6) accurately predicts multi-solute osmolalities of aqueous solutions containing: i) two permeating cryoprotectants;^3,26 ii) a permeating cryoprotectant and a salt;²⁷ iii) a macromolecule and a salt;²⁷ and iv) two proteins.²⁶ This equation is able to predict directly the osmolality of the cytoplasmic solution of red blood cells in agreement with measurements.³ Other research groups have applied our equation to v) a quaternary system of water–CPA–sugar–salt,⁴³ and vi) aqueous solutions of two micelle-forming non-ionic surfactants.⁴⁴ Although there have been other multi-solute solution theories able to make predictions directly from single solute information that apply accurately to specific examples,⁴⁹ our osmotic virial approach is the most broadly applied.^{3,26,27,42–44}

It is important to point out that some nonlinear relationships have been presented for osmolality of cytoplasm in bacteria (i.e., Escherichia coli);^50,51 however, in those studies the nonlinearity arose from different phenomena than those being studied here. Specifically the nonlinear function in these works^50,51 described the dependence of osmolality on the molality of the growth medium in adaptation studies, while the osmotic coefficient was assumed to be independent of the solution osmolality in passive osmotic response studies. Herein we propose to describe the non-ideality arising from only the solution thermodynamics of the cytoplasm of osmotically-responding mammalian cells over short times during which no adaptation takes place.

To obtain an estimate of the cytoplasm second osmotic virial coefficient, we report herein a technique requiring only measurements of cell volume as a function of externally imposed osmolality. Volume measurements are easily obtained for mammalian cells by a variety of standard methods. In one of the most common methods, electronic particle counters⁵² have been used to determine cell volumes for a variety of cell types including: human lymphocytes;⁵³ bovine chondrocytes;⁵⁴ pancreatic islet cells;^55,56 human corneal endothelial, stromal, and epithelial cells;⁷ several African mammalian spermatozoa;⁵⁷ and hematopoietic stem cells.^58–61 This method has been shown to produce results comparable with volumes calculated from optical microscope measurements of cell diameters.⁶²

Herein we report measurements of equilibrium cell volume as a function of osmolality for a human hematopoietic stem cell line TF-1, human umbilical vein endothelial cells (HUVEC), porcine articular cartilage chondrocytes, and human hepatocytes. For this study, we also obtained equilibrium cell volume data from the literature for additional cell types, including mouse embryonic stem cells,¹⁶ mouse ova,⁶³ mouse embryos,⁶⁴ mouse blastocysts,⁶⁴ porcine hepatocytes,⁶⁵ human erythrocytes,⁶⁶ human keratinocytes,⁶⁷ mouse oocytes,⁶⁸ porcine islets,⁶⁹ and hamster ova.¹⁷

Traditionally, data for equilibrium cell volume in solutions of impermeant solutes are analyzed using the Boyle van't Hoff relationship,^45,46,70 (which contains ideal, dilute solution assumptions⁴⁷):

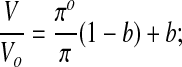(Eq. 7)

where V is the equilibrium cell volume (μm³) at osmolality π (osmoles/kg water), V_o is the isotonic cell volume (μm³) at isotonic osmolality π^o, and b is the osmotically-inactive fraction of the cell volume. The osmotically-inactive fraction is found by fitting Equation 7 to data of V at different values of π.

Since the cytoplasm contains many different solutes in varying concentrations, we used the osmotic virial equation^3,48 (here truncated to second order) to model the thermodynamics of the cytoplasm by treating all cytoplasmic solutes together as one “grouped solute”⁴⁷ with a second osmotic virial coefficient defined by:

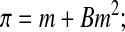(Eq. 8)

where m is the effective molal concentration of all intracellular solutes combined into one grouped solute (mole/kg solvent) and B is the second osmotic virial coefficient ((mole/kg solvent)⁻¹) of this grouped solute. In this study, it was required to truncate the osmotic virial equation to second order because the data were only sufficient to obtain the second osmotic virial coefficient and not higher order osmotic virial coefficients.

We have shown that the grouped solute approach used in the osmotic virial equation can model the osmolality of the red blood cell cytoplasm as accurately as direct predictions from the osmotic virial equation of hemoglobin and salt and in agreement with measurements.⁴⁷ It was also shown that one need not have an actual value of m for the grouped solute to evaluate the performance of the virial coefficients since experimental data were analyzed with respect to the isotonic molality of the grouped solute.⁴⁷ Osmotic virial coefficients take into account the interactions between the solutes in the solution, with the second osmotic virial coefficient for a particular solute directly related to the energy of interaction of two molecules of that solute, and the mixing rules introduced in Equation 6 allowing the equation to account for energies of interaction between different solutes. In this study, using the grouped solute approach, all solutes are treated as one solute type with effective properties, and in this case the second osmotic virial coefficient is representative of an average interaction energy between solute molecules but is probably best thought of as an empirical parameter describing the osmotic behavior of the cell.

The modified Boyle van't Hoff equation (Eq. 9) and the osmotic virial equation (Eq. 8) can be combined to determine the non-ideal osmotically-inactive fraction and the second osmotic virial coefficient of the cytoplasm from measurements of cell volume as a function of osmolality. The Boyle van't Hoff equation has been modified by Prickett et al.⁴⁷ to eliminate the ideal, dilute solution assumptions implicit in Equation 7 and express equilibrium cell volume in non-dilute solutions of impermeant solutes:

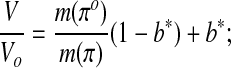(Eq. 9)

where m(π) is the molality as a function of osmolality and b* is the osmotically-inactive fraction of the cell volume, a parameter found by fitting Equation 9 to data (the * indicating that the value is inferred from data without making ideal, dilute assumptions).

The modified Boyle van't Hoff equation requires m(π); therefore, the osmotic virial equation (Eq. 8) was inverted choosing the positive root:

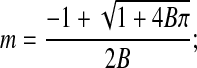(Eq. 10)

Equation 10 was substituted into Equation 9 to yield:

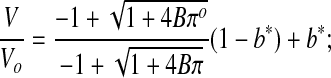(Eq. 11)

so that the modified osmotically-inactive fraction (b*), and the second osmotic virial coefficient (B) could be found simultaneously by fitting Equation 11 to data of V at different values of π (obtained as described below in the Experimental Methods section).

Experimental Methods

Cell preparations

TF-1 cells ((Lot #2056376) ATCC, Manassas, VA) were cultured at 37°C in 5% CO₂ in Modified RPMI 1640 Medium (ATCC) with 10% fetal bovine serum (ATCC), and supplemented with 2 ng/ml recombinant human GM-CSF (Stemcell Technologies, Vancouver, BC, Canada). Cells were centrifuged and re-suspended in media (4×10⁶ cells/ml) for experiments. Cells from different passages were used for experiments.

Human umbilical vein endothelial cells (HUVEC) ((Lot #7F3659) LONZA, Walkersville, MD) were cultured at 37°C in 5% CO₂ in EBM-2 Bulletkit (LONZA), which includes Endothelial Cell Basal Medium-2 supplemented with human fibroblast growth factor-B, hydrocortisone, vascular endothelial growth factor, R3-insulin-like growth factor, ascorbic acid, heparin, fetal bovine serum, and human endothelial growth factor. Prior to experiments, cells were trypsinized using trypsin-EDTA (LONZA) once they had reached ∼70% confluency. Cells were then centrifuged and re-suspended in media (4×10⁶ cells/ml) for experiments. Cells from different passages were used for experiments.

Ethical approval was obtained from the University of Alberta, Faculty of Medicine Research Ethics Board, and informed consent was obtained from all erythrocyte and hepatocyte donors. Human whole blood (7 ml) was collected from healthy donors into vacutainer tubes containing citrate anticoagulant (BD, Fanklin Lakes, NJ) using standard phlebotomy. The sample was centrifuged at 1500 g for 10 min at 4°C (Eppendorf Centrifuge 5810R, Westbury, NY). Plasma supernatant and buffy coat were removed and the erythrocyte pellet was washed three times with phosphate buffered saline (PBS; GIBCO Invitrogen Corp., Carlsbad, CA). Erythrocytes were then resuspended in 5 ml of PBS buffer and immediately used in experiments. Hepatocytes were isolated from resected liver by technician J.T. Lewis in the University of Alberta laboratory of Dr. N.M. Kneteman (as previously described^71,72). Hepatocytes in suspension (4×10⁶ cells/ml) were used for experiments immediately following isolation.

Porcine chondrocytes were isolated by A. Weiss from the laboratory of Dr. N.M. Jomha (University of Alberta), as previously described.⁷³ Briefly, intact stifle joints were harvested from six sexually mature pigs sacrificed for meat consumption (Sturgeon Valley Pork, St. Albert, AB, Canada). Portions of full thickness cartilage (3–4 g per joint) were removed from the femoral chondyles and placed in a 100 mm petri dish containing 1X Dulbecco's phosphate buffered saline solution (PBS; GIBCO Invitrogen Corp.). The PBS was removed and supplemented with 20 ml of Dulbecco's modified Eagle's medium with F-12 nutritional supplement and 1% penicillin-streptomycin (DMEM/F-12, GIBCO) containing 1 mg/ml of collagenase 1A (Sigma-Aldrich Canada, Oakville, ON, Canada). The chondrocytes were then incubated in DMEM/F-12 with 10% fetal bovine serum (FBS, GIBCO) at 37°C and 5% CO₂ for 24 h. Prior to experiments, cells were trypsinized using 0.25% Trypsin-EDTA (GIBCO). Cells were then centrifuged and re-suspended in media (4×10⁶ cells/ml) for experiments. Cells from different pigs were used for experiments.

Cell volume measurements

Methods used to obtain cell volume as a function of osmolality have been described previously in more detail.⁵⁸ Briefly, a Coulter electronic particle counter (ZB1, Coulter Inc., Hialeah, FL), fitted with a pulse-height analyzer (The Great Canadian Computer Company, Spruce Grove, AB, Canada) was used to monitor cell volume of individual cells as the cells passed through the 50 μm (erythrocytes) or 100 μm (TF-1, HUVECs, chondrocytes, hepatocytes) aperture.^52,74–76 The cell suspension of 4×10⁶ cells/ml (150–200 μL) was injected into well-mixed hypertonic experimental solutions (10 ml). Pulse heights, proportional to the cell volumes, were digitized and the time recorded as each cell traversed the aperture of the Coulter counter.⁵² Once the cells reached equilibrium, the mean cell volume was calculated. There was approximately 2% coincidence correction for the cell density used in the experiments.⁷⁷ Latex beads (5 μm diameter (erthryocytes); 10 μm diameter (chondrocytes); 15 μm diameter (TF-1 and HUVEC); 20 μm diameter (hepatocytes), Beckman Coulter, Miami, FL) were used as calibrators to convert pulse heights to actual volumes in 1X PBS and in the experimental solutions. In addition for erythrocytes, the calibration factor from the beads was multiplied by a shape factor (1.18).⁷⁵ PBS solutions of various osmolalities were prepared by diluting 10X PBS (GIBCO) with distilled water to final osmolalities ranging from 0.3 Osm/kg (1X) to 2.7 Osm/kg (9X). Osmolalities were measured using a freezing-point depression Osmometer (Precision Systems Inc., Natick, MA). For each experiment, 3 replicate measurements were performed for each experimental solution (∼1.2–1.6×10⁵ cells counted for each measurement). The Coulter counter measurements were conducted at 4 temperatures ranging from 2°C to 37°C and the maximum time required for a measurement was less than 3 minutes before dilution back to isotonic. Thus, we assume that passive transport would dominate transport across the membrane and the contributions of active transport would be minimal. The experiments were repeated with cells from three different passages for TF-1 and HUVECs, 6 different erythrocyte donors three times each, 3 different hepatocyte donors once each, and 3 different pigs once each. Cell volume data obtained using the Coulter counter method were independently verified using optical measurements for TF-1 cells and HUVECs (data not shown).

Cell volume as a function of osmolality data for various cell types of interest in cryobiology were also obtained from the literature and used in the analysis, including TF-1 cells (0.3–1.5 Osm/kg data),⁵⁸ human erythrocytes,⁶⁶ mouse blastocysts,⁶⁴ mouse eight-cell embryos,⁶⁴ mouse embryonic stem cells,¹⁶ porcine hepatocytes,⁶⁵ mouse ova,⁶³ human keratinocytes,⁶⁷ mouse oocytes,⁶⁸ porcine islets,⁶⁹ and hamster ova.¹⁷

Results and Discussion

Modified osmotically inactive fraction and the second osmotic virial coefficient

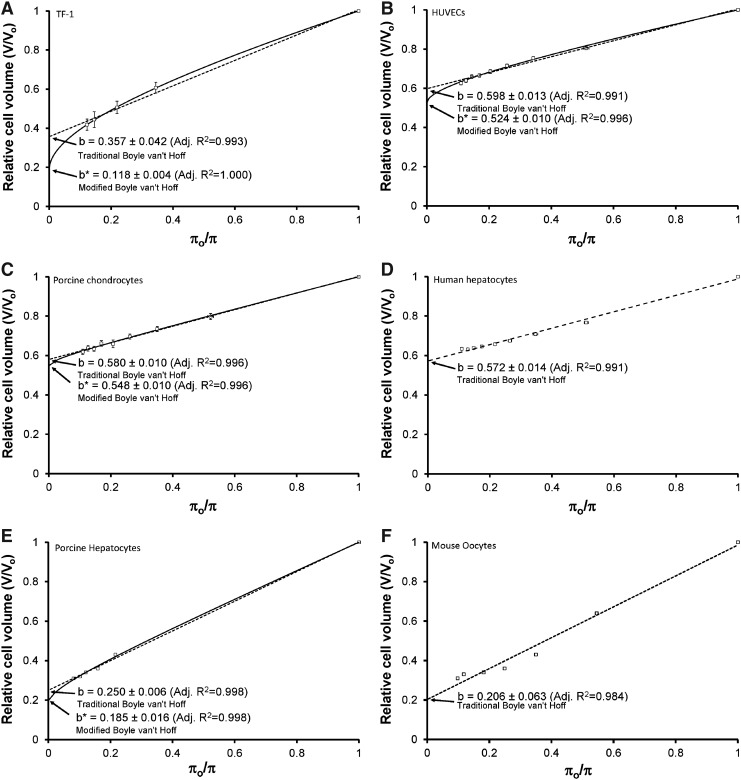
The osmotic equilibrium data were plotted on a traditional Boyle van't Hoff plot, which is equilibrium cell volume as a function of inverse osmolality (Fig. 1 (A) TF-1 cells, (B) HUVECs, (C) porcine chondrocytes, (D) human hepatocytes, (E), porcine hepatocytes, and (F) mouse oocytes). The traditional ideal, dilute osmotically-inactive fraction is found by fitting Equation 7 to data of V at different values of π (LINEST function, EXCEL, Microsoft, Mississauga, ON, Canada), shown as b (mean±95% confidence intervals) on the four panels of Figure 1. The coefficient of determination,⁷⁸ R², was calculated to assess the goodness of fit of the data to the traditional Boyle van't Hoff equation.

FIG. 1.

Osmotic equilibrium plots for cells in phosphate buffered saline. (A) TF-1 cells, (B) HUVECs, (C) porcine chondrocytes, (D) human hepatocytes, (E) porcine hepatocytes, and (F) mouse oocytes. The symbols represent the experimental relative equilibrium cell volumes (V/Vo) in hypertonic solutions as a function of osmolality (π) (mean±SEM). The dashed line is the Boyle van't Hoff equation and represents the linear regression fit of Equation 7 to the data. The solid line represents the nonlinear regression fit of Equation 11 to the data. The y-intercepts (mean±95 % confidence intervals) give the ideal osmotically-inactive fraction, b, and the non-ideal osmotically-inactive fraction, b*. The respective adjusted R² values are also shown. In the modified Boyle van't Hoff equation, inverse relative molality is the independent variable; however we have included the modified Boyle van't Hoff on the traditional Boyle van't Hoff graph for direct comparison.

Next, we used nonlinear regression to fit Equation 11 to the data using the Matrix method in EXCEL.²⁶ This resulted in a non-ideal osmotically-inactive fraction (b*) (mean±95% confidence intervals), shown on the panels of Figure 1, and an osmotic virial coefficient (B) (mean±95% confidence intervals), shown in Table 1. The standard R² does not take into account the number of parameters in the model and may increase erroneously with increasing number of parameters in the equation. However, the adjusted coefficient of determination,⁷⁸ adjusted R², is a measure of the goodness of fit of an equation to a data set, which also takes into account the number of parameters in the fitted equation. The adjusted R² was used to assess the necessity of adding additional parameters to the model. The adjusted R² of the nonlinear regression is shown on the panels of Figure 1. If the adjusted R² is greater for the nonlinear fit than the linear fit and the confidence intervals of B do not include zero (for TF-1 cells and HUVECs, see Table 1), we conclude that the non-ideal model of the cytoplasm more accurately describes the equilibrium data than the ideal model. For some of the cell types [porcine chondrocytes (Fig. 1C) and porcine hepatocytes⁶⁵ (Fig. 1E)], the adjusted R² remained the same for the non-ideal model of the cytoplasm, so the non-ideal model is at least as accurate as the ideal model, and since the confidence intervals for B did not include zero, we assert that the non-ideal model is a better description than assuming B=0 (ideal).

Table 1.

Obtained Values for Ideal Osmotically-Inactive Fractions (b), the Second Osmotic Virial Coefficients (B), and the Non-ideal Osmotically-Inactive Fractions (b^*) for Various Cell Types and the Temperatures (T) at which the Data Were Obtained

Cell type	b±95 % C.I.	B, (mole/kg)−1±95 % C.I.	b*±95 % C.I.	T, °C
TF-1	0.357±0.042	7.6±1.9	0.188±0.004	2 to 37
HUVEC	0.598±0.013	2.4±1.9	0.524±0.010	2 to 37
Porcine hepatocyte65	0.250±0.006	0.61±0.48	0.185±0.016	−1 to −6
Porcine chondrocyte	0.580±0.010	0.43±0.39	0.548±0.010	2 to 37
Human hepatocyte	0.572±0.014	0.00±0.23	0.569±0.016	2 to 20
Mouse oocyte63	0.206±0.063	0.00±0.52	0.198±0.053	20

The non-ideal model of the cytoplasm did not more accurately represent the data for the other cell types analyzed: human hepatocytes (Fig. 1D) and mouse oocytes⁶⁸ (Fig. 1F). The obtained osmotic virial coefficients were zero (Table 1) and the adjusted R² decreased, with the nonlinear fit. Therefore, the osmotic equilibrium data was better described by the traditional Boyle van't Hoff equation, and an ideal, dilute solution description over the range of osmolalities investigated is the best we have.

For several cell types with existing data for equilibrium volume as a function of osmolality, including mouse embryonic stem cells,¹⁶ mouse ova,⁶³ mouse embryos,⁶⁴ and human erythrocytes⁶⁶ (and our unpublished data), the shape of the data was different from ideal, even in the low range of osmolalities where the solution should be ideal, indicating the presence of other effects than thermodynamic solution nonideality, such as mechanical properties. In these cases, the non-ideal model did not converge and so this data cannot be used to estimate the second osmotic virial coefficients for these cells. For mouse blastocysts, the data converged and a B value was obtained (4.8±15); however, the adjusted R² stayed the same (0.976) and the confidence intervals were large and contained zero.

Since the majority of Boyle van't Hoff analysis in the literature was done using data obtained from hypertonic solutions only up 1.5 Osm/kg, we also compared the ideal and non-ideal models of the cytoplasm for this lower range of osmolalities. The ideal model of the cytoplasm accurately represented this limited data for many of the cell types analyzed (i.e., the adjusted R² decreased when using the non-ideal model), including HUVECs, TF-1 cells, porcine chondrocytes, human hepatocytes, human keratinocytes,⁶⁷ mouse oocytes,⁶⁸ porcine islets,⁶⁹ and hamster ova.¹⁷ Also, with data obtained from hypertonic solutions only up 1.5 Osm/kg, the osmotically-inactive fraction did not change significantly with the modified Boyle van't Hoff equation and the osmotic virial equation. Therefore, data up to only 1.5 Osm/kg is not sufficient to determine estimates of the second osmotic virial coefficient for any of the cell types analyzed. Although these data appear linear when plotted on a traditional Boyle van't Hoff plot, they are limiting as they result in erroneously large values for the osmotically-inactive fraction,⁴⁷ as the osmotically-inactive fraction is obtained from an extrapolation of the linear fit to infinite osmolality.

All of the second osmotic virial coefficients and the non-ideal osmotically-inactive fractions and their 95% confidence intervals resulting from our analysis of our data and literature data are given in Table 1.

Phase diagram of the cytoplasm

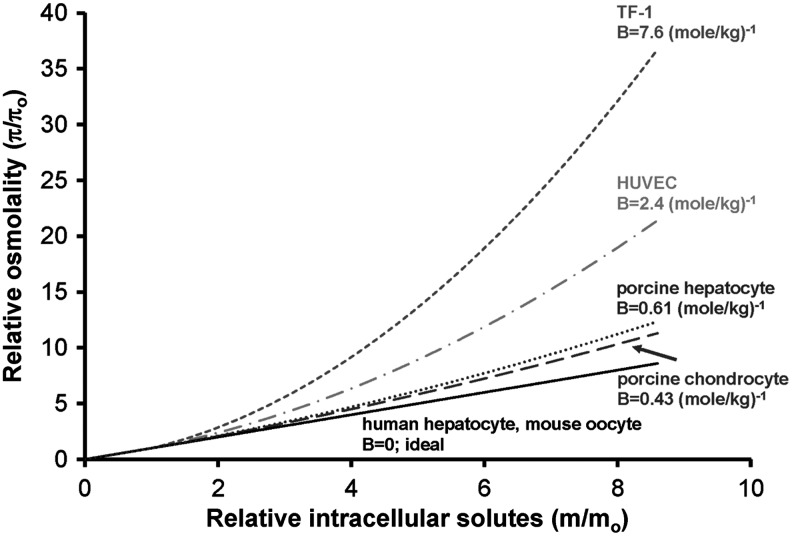
Using the second osmotic virial coefficient, osmolality as a function of molality can be calculated, visually indicating the extent of the deviation from ideality as demonstrated in Figure 2. Since this function determines the chemical potential and may thus be used to compute the phase diagram directly, this function is sometimes colloquially called simply the “phase diagram”. Like many solutes (as per the CRC tables⁷⁹), the osmolality increases faster than the molality at high concentrations, reflecting the non-ideal behavior of solutes.

FIG. 2.

Relative osmolality as a function of intracellular solute concentration for the cytoplasms of TF-1 cells, HUVECs, porcine chondrocytes, human hepatocytes, porcine hepatocytes, and mouse oocytes. The solid line is predicted assuming the cytoplasm behaves as an ideal solution (π=m). The dashed lines are predicted assuming non-ideality of the cytoplasm using the osmotic virial equation (Equation 8) and the measured second osmotic virial coefficients (B).

Comparison with human erythrocytes

The phase diagram of the cytoplasm of human erythrocytes has been measured using ESR.^3,4,47,80 It has been shown that the solution thermodynamics of human erythrocytes' cytoplasm are highly non-ideal^3,47 and can be accurately described by a multisolute cubic osmotic virial equation,³ assuming the cytoplasm is made up of hemoglobin (with independently determined coefficients B=49.3 (mole/kg)⁻¹, C=3.07×10⁴ (mole/kg)⁻¹) and an ideal solute.³ In addition, the solutes in the cytoplasm could be accurately represented with a grouped solute, using a slightly different version of a cubic osmotic virial equation.⁴⁷ To compare these previous predictions with the results from this study, we fit the hemoglobin-and-ideal solute model of the cytoplasm with a quadratic osmotic virial equation to estimate an effective overall second osmotic virial coefficient for the erythrocyte resulting in B=3.75 (mole/kg)⁻¹. TF-1 cells were more non-ideal (B>3.75 (mole/kg)⁻¹) than the erythrocytes, while the other cell types (HUVECs, porcine hepatocytes, porcine chondrocytes, human hepatocytes, and mouse oocytes) were more ideal (B<3.75 (mole/kg)⁻¹) within the range of osmolalities investigated in this study.

Impact of the cytoplasm model in the context of cryobiology

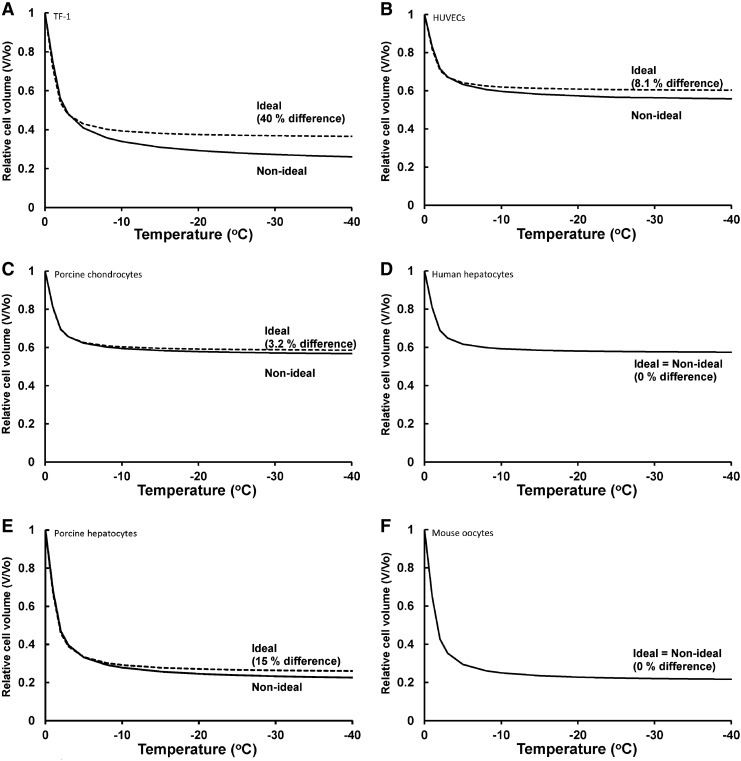
The range of osmolalities used in this study corresponds to freezing a cell in suspension to −3°C (1.5 Osm/kg) or −5°C (2.7 Osm/kg), and it is not surprising that cellular osmotic responses can be adequately described using ideal solutions over this range. For all cell types: TF-1 cells, HUVECs, porcine chondrocytes, human hepatocytes, porcine hepatocytes, and mouse oocytes, we also investigated the impact of the improved cytoplasm model in the context of cryobiology.

Relative equilibrium volumes were predicted as a function of subzero temperatures using the two models: (i) the ideal solution thermodynamics model B=0 combined with the traditional Boyle van't Hoff equation, Equation 7, which contains ideal, dilute solution assumptions; and (ii) a non-ideal solution thermodynamics model utilizing the osmotic virial equation, Equation 8 combined with the modified Boyle van't Hoff equation,⁴⁷ Equation 9, resulting in Equation 11. For both models, osmolality was calculated from temperature (0°C to −40°C) using:

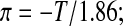(Eq. 12)

where T is in °C.²⁶

Figure 3 shows the relative equilibrium cell volume as a function of subzero temperature for both ideal and non-ideal models of the cytoplasm at temperatures down to −40°C for these six cell types. (Note that calculations shown are equilibrium calculations at specific temperatures and therefore no cooling rate was used; however, if cells are cooled slowly enough, they will follow this line.) The two models begin to diverge at −5°C, with the greatest difference being at lower subzero temperatures. Using the ideal model, the calculated relative equilibrium cell volume was higher than with the non-ideal model. For example at −40°C, the relative equilibrium cell volume of TF-1 cells using the ideal model was 0.366 compared to the non-ideal model relative equilibrium cell volume of 0.261. Hence, there was a 40 % error in using the ideal model versus the non-ideal model. Our ideal/non–ideal comparisons quantify the magnitude of error in using ideal, dilute solution descriptions which could have consequences when simulating effects of low temperatures on cellular osmotic responses.

FIG. 3.

The predicted relative equilibrium cell volume as a function of subzero temperature for cells using ideal and non-ideal models of the cytoplasm. (A) TF-1 cells, (B) HUVECs, (C) porcine chondrocytes, (D) human hepatocytes, (E) porcine hepatocytes, and (F) mouse oocytes. The dashed lines are predicted using the ideal osmotic equilibrium equation (Eq. 7) to determine the cell volume as a function of temperature. The solid lines are predicted using the non-ideal osmotic equilibrium equation (Eq. 11) to determine the cell volume as a function of temperature. The percent error was calculated at −40°C.

A limitation of this study is that the temperature dependence of the second osmotic virial coefficient was not addressed. While this dependence may be small,⁸¹ it would be prudent to exercise caution when relying quantitatively on these values outside of the temperature range of the measurements. We hope that, as well as providing values for several cell types for use in biophysical modeling, this demonstration of the non-ideality of the cytoplasm for mammalian cell types in addition to red blood cells will provide impetus to extend this type of measurement and develop novel methods for obtaining more precise estimates.

Conclusions

A method has been provided for quantifying the non-ideal solution thermodynamics of the cytoplasm of a living mammalian cell using the osmotic virial equation. In this work, we do not consider cell volumes above isotonic osmolality (physiological osmolality, which is approximately 300 mmolal). We consider only cell measurements for which the deviation from linearity can be explained by the thermodynamics and we use statistics to determine when the second order polynomial is a better description of measurements than the first order model currently in use in the field. Data presented in this study demonstrate that the cytoplasm of TF-1 cells, HUVEC, porcine hepatocytes, and porcine chondrocytes do not behave as ideal dilute solutions. This is only evident when the cells are shrunken in high osmolality solutions (i.e., small values of π_o/π).⁴⁷ If cells are only exposed to lesser hypertonic solutions, the osmotic equilibrium data appear linear. The second osmotic virial coefficients could be obtained where data were available; however to obtain third osmotic virial coefficients would require data at higher concentrations. Nevertheless, the obtained second osmotic virial coefficients will allow mathematical predictions of osmotic behavior without relying on the ideal, dilute assumption for the cytoplasm. In addition, these measurements introduce a new means of characterizing mammalian cells. In the same way that thermodynamics mathematically describes the collective behavior arising from detailed molecular behavior, measurement of cytoplasmic solution thermodynamics allows one to probe the molecular behavior of the cell as a whole—thermodynamics is systems molecular biology. We expect this new tool to lead to insight into the fundamental behavior, similarities, and differences of biological cells.

Acknowledgments

We are grateful to Y. Shardt for his assistance with our statistical analysis and M. Yu for his assistance with TF-1 cell volume measurements. We are also grateful to J.T. Lewis (Dr. NM Kneteman's laboratory) and A. Weiss (Dr. NM Jomha's laboratory) for the isolation of human hepatocytes and porcine chondrocytes, respectively.

Author Disclosure Statement

No potential conflicts of interest for any of the authors.

This research was supported financially by the Canadian Institutes of Health Research (CIHR MOP 86492, 85068, CPG 75237) and the Natural Sciences and Engineering Research Council (NSERC) of Canada. JAWE holds a Canada Research Chair in Thermodynamics.