Three-dimensional Čerenkov tomography of energy deposition from ionizing radiation beams

Abstract

Since its discovery during the 1930’s, the Čerenkov effect (light emission from charged particles traveling faster than the local speed of light in a dielectric medium) has been paramount in the development of high-energy physics research. The ability of the emitted light to describe a charged particle’s trajectory, energy, velocity, and mass has allowed scientists to study subatomic particles, detect neutrinos, and explore the properties of interstellar matter. However, all applications of the process to date have focused on identification of particle’s themselves, rather than their effect upon the surroundings through which they travel. Here, we explore a novel application of the Čerenkov effect for the recovery of the spatial distribution of ionizing radiation energy deposition in a medium, and apply it to the issue of dose determination in medical physics. By capturing multiple projection images of the Čerenkov light induced by a medical linear accelerator (LINAC) x-ray photon beam, we demonstrate the successful three-dimensional (3D) tomographic reconstruction of the imparted dose distribution for the first time.

Interest into the concept of dose (i.e., the energy deposited in a medium by ionizing radiation) began in 1895 following the discovery of x-rays [1]. The importance of accurate dose assessment was elevated with the introduction of the medical LINAC and the general clinical adoption of external beam radiation therapy (EBRT), which requires routine dose calibration and quality assessment [2]. To date, several methods have been developed to spatially resolve the dose distribution from therapeutic electron and photon beams for quality assurance (QA) and dosimetry purposes. Of the several available techniques, the most commonly used and widely accepted method relies on using ionization chambers in which the dose to the surrounding medium (conventionally a water volume due to its similarity in atomic composition to human tissue) is related to the recorded electrical signal [3]. However, the time-consuming raster-scanning point measurement nature of ionization chamber systems limits measurements to sparsely spaced one-dimensional (1D) and two-dimensional (2D) data. Additionally, many correction factors are necessary to account for perturbation of the radiation by the chamber itself, and the measurement resolution is limited by the finite size of the detectors [4].

Alternative modalities to overcome the prohibitive spatial profiling capabilities of ionization chambers have been proposed, including plastic or liquid scintillation and gel dosimetry, in which the number of emitted scintillation photons or a chemical change in a polymer gel is assumed to scale with imparted dose [5–7]. Although the techniques offers several advantages, each requires a material other than water to record the deposited dose, an unfavorable requirement which introduces dosimetric inaccuracies due to material property differences. Therefore, there is immediate interest in a simple, fast, high-resolution, and noninvasive modality capable of reconstructing full 3D dose distributions originating from the native water volume itself.

Herein, we present a method to recover volumetric dose distributions in pure water by tomographically capturing optical projection images of the induced Čerenkov radiation from a megavoltage x-ray photon LINAC beam using an intensified charge-coupled device (ICCD). Fig. 1(a) presents a schematic of the experimental optical dosimetry system. X-ray photons generated by electron bombardment of a target within a medical LINAC form a pulsed radiation beam (5 µs in duration at 180 Hz) and travel downward into a perpendicularly placed water-filled glass tank, where either the primary collimator (capable of providing rectangular shapes), or the multileaf collimator (capable of producing irregular shapes), dictates the cross section of the propagating radiation beam. The two beam configurations used in the current study, Field A and Field B, were chosen to explore the ability of the modality to reconstruct axis symmetric and asymmetric distributions. The current produced at the target during electron irradiation is converted into a trigger voltage suitable for opening the shutter, which subsequently closes at the end of the pulse. The process repeats iteratively as signal accumulates on the camera (PI-MAX3: 1024i, Princeton Instruments, Acton, MA).

Fig.1.

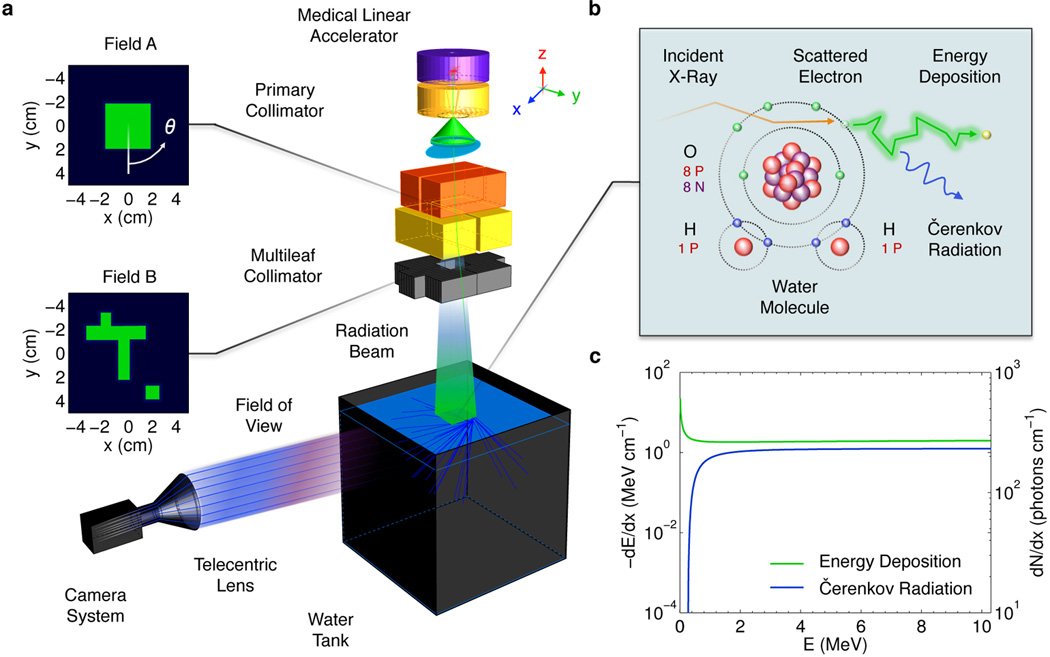
In (a) Experimental schematic of the proposed optical dosimetry system. The telecentric lens captures optical rays emerging from the transparent water tank that are near parallel to the optical axis and focuses them onto the ICCD. The two field shapes corresponding to the primary and multileaf collimator are shown in green. In (b) the atomic diagram of the radiation transport interactions governing electron energy loss in water. In (c) the electron energy loss per unit path length resulting in local energy deposition and emitted Čerenkov photons as a function of electron energy.

As each radiation pulse enters the tank, secondary electrons are liberated from water molecules via Compton scattering, which dissipate their energy through electromagnetic interactions with neighboring water molecules, see Fig. 1(b). During propagation, a small fraction of each electron’s energy is emitted as optical photons due to the Čerenkov effect, which is focused by a peripherally placed telecentric lens (0.06X Gold Series, Edmund Optics, Barrington, NJ). Due to the approximate proportionality between the electron energy loss due to ionizing events leading to energy deposition and the energy released in the form of Čerenkov photons, see Fig. 1(c), the imaged light serves as a surrogate to indirectly determine the imparted dose distribution (i.e., the number of Čerenkov photons captured is directly correlated to the electron energy deposition at any spatial location in the irradiated medium), see Ref. 8 for background theory and definition of equations used in Fig. 1(c).

To demonstrate tomographic reconstruction of 3D dose distributions, images of the induced Čerenkov radiation (10×10 cm field of view) from a 6 MeV x-ray photon beam for both field sizes shown in Fig1a are recorded by rotating the LINAC collimators through an angle (0° ≤ θ ≤ 180° in 2° increments) to provide the telecentric lens with a number of angled projections (91 total), see supplemental material for full projection image data. Each projection is acquired by imaging individual pulses over 18 seconds and processed for noise induced by indirect irradiation of the ICCD using a 5×5 pixel median filter, resulting in a 1 mm resolution (0.2 mm native image resolution), and total scan time less than 30 minutes. Once all projections are captured, a sinogram is constructed at each depth, z, in the irradiated water volume corresponding to a single row of pixels in each captured projection. Representative sinograms for Field A and B are shown in Figs 2(a,d) at a depth of z = 1.5 cm. The resulting sinograms are then used to reconstruct 2D cross sections of the induced light volume using a parallel beam back projection algorithm and cosine filter to prevent high spatial frequency noise amplification in the reconstruction. The recovered cross sections for the sinograms in Figs. 2(a,d) are shown in Figs. 2(b,e). Finally, the full 3D distributions are created by parsing together the 2D reconstructions from each depth. The results for Field A and B are displayed in Figs. 2(c,f), see supplemental material for additional 3D reconstruction results.

Fig. 2.

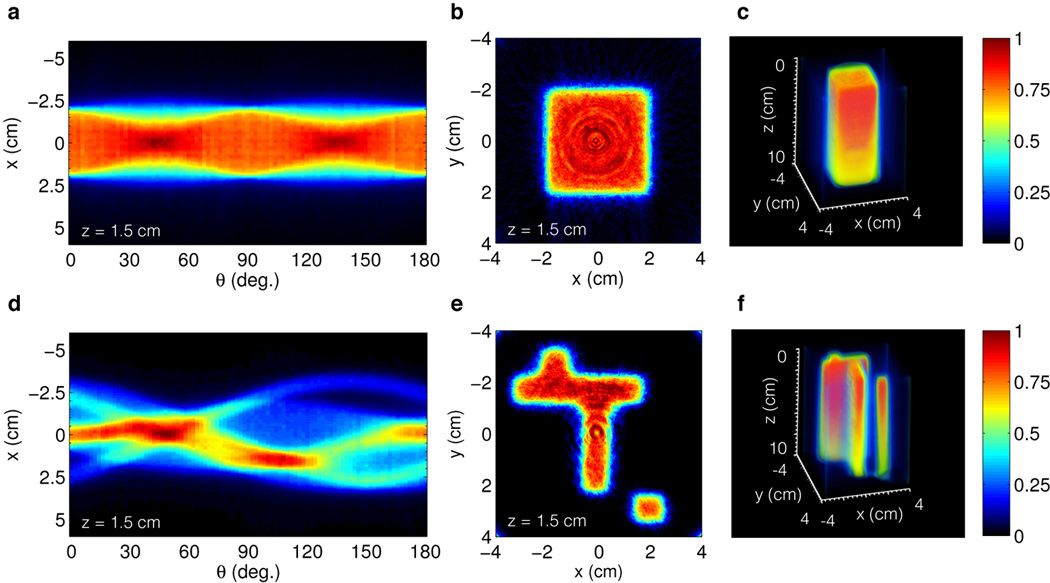
In (a,b) and (d,e) the sinogram and reconstructed cross section for Field A and B respectively. In (c) and (f) the full 3D reconstruction of Field A and B to a depth of z = 10 cm. The intensity decreases with depth due to exponential attenuation of the primary x-ray photon beam.

To examine the accuracy of the proposed system, a well-characterized and known dose profile along the central depth axis (i.e., x = 0 cm, y = 0 cm) of Field A from a treatment planning system was compared to the experimentally reconstructed distribution based on the captured Čerenkov light. The results are plotted in Fig. 3 where the recovered light profile decays exponentially and is indicative of the known dose at all depths (within ±3%) beyond the dose maximum, before which the difference is higher due to the large dose gradient. An alternative accuracy metric in the buildup region is the distance to agreement (i.e. shortest distance to equivalence between the two curves), which is less than 1 mm for the curves presented in Fig. 3.

Fig. 3.

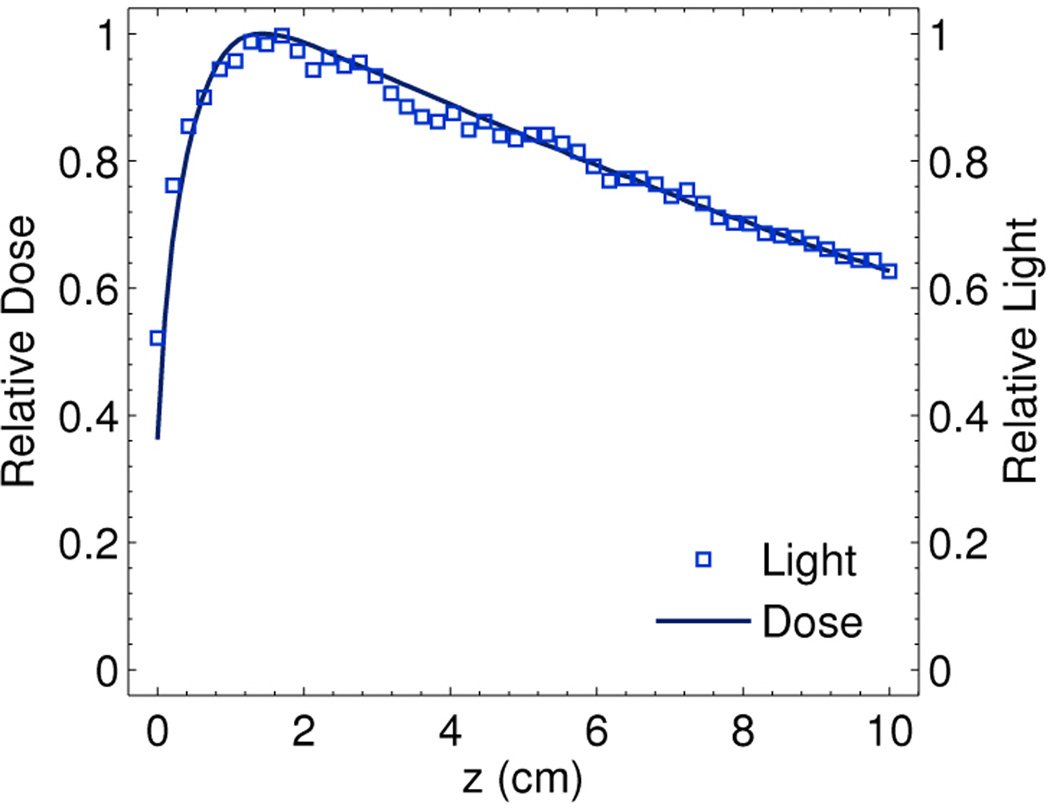
Comparison of the reconstructed central axis light profile for Field A to the known dose profile.

In contrast to initial reports investigating the capture of a single 2D projection, the results in the present study extend the concept to optical tomography, a significant advancement providing full 3D distributions [8, 9]. We introduce a critical innovation by using a telecentric lens to establish a constant magnification at all imaging distances and thereby avoid parallax (i.e., objects closer appear larger and vice versa), a technique used previously for bubble chamber photography [10]. By eliminating the perspective error associated with all conventional imaging lenses, true orthographic projections of the imparted 3D light volume suitable for optical tomography are captured. The use of a telecentric lens also provides a novel solution to the main challenge in quantitatively imaging the anisotropic light volume, an issue which was previously resolved using a Monte Carlo derived correction factor, or a fluorophore to convert the anisotropic Čerenkov light to isotropic fluorescence [8, 9]. However, by only accepting rays parallel to the optical axis of the detection system, the telecentric lens samples the same solid angle of the anisotropic phase function of Čerenkov emission from each spatial location within the image, inherently providing accurate results, see Ref. 8.

In conclusion, we report full 3D optical tomography of ionizing radiation beams using only the induced Čerenkov radiation in a pure water volume, at a high speed, and with a resolution of 1.0 mm per pixel. With the ability to non-invasively interrogate energy deposition of energetic charged particles, the technique could be applied to additional fields utilizing high-energy ionizing radiation.