The Effects of Maternity Leave on Children's Birth and Infant Health Outcomes in the United States

Abstract

This paper evaluates the impacts of unpaid maternity leave provisions of the 1993 Family and Medical Leave Act (FMLA) on children's birth and infant health outcomes in the United States. My identification strategy uses variation in pre-FMLA maternity leave policies across states and variation in which firms are covered by FMLA provisions. Using Vital Statistics data and difference-in-difference-in-difference methodology, I find that maternity leave led to small increases in birth weight, decreases in the likelihood of a premature birth, and substantial decreases in infant mortality for children of college-educated and married mothers, who were most able to take advantage of unpaid leave. My results are robust to the inclusion of numerous controls for maternal, child, and county characteristics, state and year fixed effects, and state-year interactions, as well as across several different specifications.

1 Introduction

Maternity leave policies are designed to address the challenges faced by working mothers and their newborn children. Before 1993, only thirteen U.S. states and Washington, D.C. had enacted maternity leave provisions, which enable women to take time off during pregnancy and the first months of their child's infancy while maintaining their health insurance and their right to resume work at the conclusion of the leave. The length of leave varied between six and sixteen weeks, and was unpaid except for some women in a few states, who received about half-pay with a benefit cap.¹ In 1993, President Bill Clinton signed into law the Family and Medical Leave Act (FMLA), which mandated a minimum of twelve weeks of unpaid maternity leave for the slightly more than half of working women who were eligible. Since 1993, only California (in 2004) and New Jersey (in 2008) have mandated paid maternity leave, so by law the vast majority of eligible working women are only entitled to unpaid maternity leave.² In this study, I measure how unpaid maternity leave affected children's outcomes at birth and infancy, and whether this policy has differential impacts on children from different socio-economic backgrounds. This is the first study to analyze the causal effects of the existing maternity leave provisions on children in the United States.

There are several mechanisms through which unpaid maternity leave may exert opposing impacts on child outcomes. The guarantee of maternity leave may reduce maternal stress during pregnancy. However, if a woman is forced to work more hours during pregnancy than she otherwise would have in order to qualify for the leave, then her stress level may be heightened. Given that stress during pregnancy adversely impacts birth outcomes (Copper et al., 1996), the net effects of maternity leave on birth outcomes are theoretically ambiguous. After birth, maternity leave may affect the amount of time a child spends with his mother rather than in non-maternal care. Maternity leave will also affect the quality of time the child spends with the mother, depending on changes to her stress level and her satisfaction with the trajectory of her career. The quantity and quality of time a mother spends with her child in his first year of life matter for the child's well-being (Baum, 2003; Berger et al., 2005). For example, a mother may have more time to take care of her ill child, to breastfeed, or to seek prompt medical care when she is able to take time off work. Further, the effect of maternal time depends on the quality of non-maternal care relative to the quality of maternal time. There exists substantial variation in the quality levels of non-parental care options available for children of working parents in the U.S., and the quality level plays an important role in child development (Lefebvre et al., 2006; Loeb et al., 2007; Gormley and Gayer, 2005). Finally, unpaid maternity leave may exert an effect on the mother's income and therefore the family's material resources available for child rearing. Hence, not all new mothers may be able to take advantage of unpaid leave, and it may have different implications for the welfare of children depending on whether they grow up in low-income and low-educated one-parent households or high-income and high-educated two-parent households, as these families likely face different constraints.

I examine the effects of unpaid maternity leave due to FMLA on birth outcomes and infant mortality rates using Vital Statistics natality and mortality data in difference-in-difference (DD) and difference-in-difference-in-difference (DDD) frameworks. My identification strategy relies on the facts that some states enacted maternity leave policies prior to FMLA, and that FMLA eligibility rules only apply to women who work in firms with 50 or more employees. Women employed by firms with fewer than 50 employees, and women living in states that had maternity leave prior to FMLA should not be affected by the policy, and can serve as a comparison group. Unfortunately, there does not exist a dataset that combines information on mother's firm size and children's outcomes during the relevant time period. To approximate maternity leave eligibility based on firm size, I use data from the County Business Patterns (CBP) for 1989–1997 to estimate the likelihood that a resident of a particular county is employed in a firm with 50 or more employees in each year. I link this information to the Vital Statistics data by county and year, and then split the sample into likely eligible and likely ineligible mothers. I compare the likely eligible and likely ineligible groups before and after FMLA and across states. I also conduct sub-sample analysis on children of college-educated and married mothers and children of less-educated and single mothers to test my theoretical predictions.

My results suggest that unpaid maternity leave due to FMLA led to small improvements in birth outcomes and substantial reductions in infant mortality rates for children of college-educated and married mothers, and had much smaller or non-existent effects on children of less-educated and single mothers. I also find effects on parity at birth that indicate that more previously childless women gave birth, while fewer women had later parity births. The effects on parity are especially present for the less-educated and single mothers, suggesting that these women were most constrained in their childbearing ability before a guarantee of maternity leave. However, given that these women are more likely to be low-income, the lack of effects on their children's health suggests that they could not afford to take the full twelve weeks of unpaid leave.³ Further, the results on parity imply that any favorable effects of FMLA may be slightly understated, given that higher-parity children are likely to have better health at birth (Gluckman and Hanson, 2005). I find no consistent effects on risk factors or complications during pregnancy or at birth or on overall fertility. My findings of larger effects on infant mortality rates than on health at birth for children of college-educated and married mothers suggest that the effects of FMLA are concentrated on the care of children after birth.

My results are robust to a number of different specifications that especially test the validity of the eligibility approximation. Further, the robustness checks suggest that the results are not driven by differential selection into motherhood based on observable characteristics or by changes to county-level firm size distributions. Additionally, the magnitudes of the effects on parity are too small to produce substantial selection bias in the main results on infant mortality, suggesting that FMLA truly affected the likelihood of survival in infancy for children of mothers who were likely eligible for and able to take the full length of leave.

Recent studies on the effects of maternity leave policies in Canada (Baker et al., 2008), Germany (Dustmann and Schönberg, forthcoming), and Sweden (Liu and Skans, 2010) find no effects on children's outcomes at various ages throughout their lives. However, the effect of U.S. maternity leave policies on children has not been previously examined, and my findings suggest that the institutions and available alternatives where these policies are enacted can determine the degree of their effectiveness. Additionally, a recent study on the long-term effects of a maternity leave expansion in Norway finds that children of mothers who were eligible for the leave (and thus likely affected by the expansions) are less likely to drop out of high school (Carneiro et al., 2010). Thus, properly accounting for eligibility is important for identifying effects of maternity leave.

The paper proceeds as follows. Section 1.2 discusses FMLA. Section 1.3 reviews the relevant background literature. Section 1.4 describes the data. Section 1.5 discusses the empirical methods and presents summary statistics. Section 1.6 presents the results on the effects of unpaid maternity leave. Section 1.7 presents some robustness checks. Finally, section 1.8 concludes.

2 The Family and Medical Leave Act of 1993

FMLA affected the lives of women as mothers and workers by being the first federal law to grant unpaid maternity leave to women in every state in the U.S. Signed in January of 1993, the law actually went into effect on August 5, 1993. The federal government mandated that all eligible new mothers receive 12 weeks of unpaid leave with guaranteed health insurance coverage.⁴ Eligibility requirements include having worked for at least 1,250 hours in the past 12 months for an employer with at least 50 employees, and approximately half of all private sector workers are estimated to be eligible for leave under FMLA (Han et al., 2009; Ruhm, 1997).⁵ As a result of FMLA, the share of full-time workers employed by firms with more than 100 employees that were covered by leave policies rose from 35% in 1988 to 86% in 1995, while the share of full-time workers in firms with less than 100 employees covered by leave policies rose from 19% in 1990 to 47% in 1995 (Waldfogel, 1999). The link between FMLA and child outcomes relies on the assumption that FMLA actually increased maternity leave-taking among women with infants. There is evidence that supports this assertion: in medium-sized firms, leave-taking increased by 23% due to FMLA for women with children under age 1 (Waldfogel, 1999). Other research shows that women took about 6 more weeks of unpaid leave due to FMLA (Ross, 1998). In more recent work, Han et al. (2009) find that US maternity leave policies are associated with a 13% increase in maternal leave-taking during the birth month, 16% increase during the month after birth, and a marginally significant 20% increase during the second month after birth. Further, they find that these policies only had an effect on leave-taking for college-educated and married mothers, and had no effect for less-educated and single mothers.

3 Background Literature

Much of the existing literature on effects of parental leave policies on childhood outcomes is somewhat limited in scope and suffers from endogeneity concerns arising in cross-sectional and cross-country regression methods. Several of such studies suggest a significant negative association between parental leave and post-neonatal mortality, as well as child mortality between ages one and five in European countries (Ruhm, 2000; Tanaka, 2005).

Three more recent studies use plausibly exogenous policy changes to identify the effects of maternity leave polices on children. Baker and Milligan (2010) find no statistically significant impacts of a recent expansion in paid maternity leave from six months to a year in Canada on early childhood development indicators for children up to 29 months old. Dustmann and Schönberg (forthcoming) find no statistically significant impacts of expansions in unpaid and paid maternity leave policies in Germany on any long-run child outcomes, including wages, employment, selective high school attendance, grade retention, and attendance.⁶ Liu and Skans (2010) examine the effects of an expansion in paid leave from 12 to 15 months in Sweden, and find no impact on children's scholastic performance at age 16, or on intermediate outcomes such as mothers' subsequent earnings, measures of child health, parental fertility, divorce rates, and the mothers' mental health. They do find positive effects on age-16 educational achievement of children of well-educated mothers. Carneiro et al. (2010) analyze the long-term effects of a reform in Norway, which increased paid leave entitlements from 0 to 4 months, and unpaid entitlements from 3 to 12 months. Unlike in the other three studies, the authors are actually able to observe eligibility for maternity leave in administrative data. They find that children of mothers who were affected by the leave expansions are less likely to drop out of high school. However, to my knowledge, there has been no rigorous evaluation of the effects of maternity leave policies in the United States on children's outcomes at birth and in infancy.

While the existing evidence suggests that maternity leave policies in Canada, Germany, and Sweden may not have much impact on children's outcomes at various ages, the context where the policy is enacted matters. For example, a policy that expands paid leave from 12 to 15 months in a setting where the alternative is good-quality subsidized child care and universal health insurance (as is the case in Sweden) is quite different from one that provides maternity leave for the first time on a national level in a setting where neither child care nor health insurance is guaranteed (as is the case in the United States). So while the FMLA provides unpaid maternity leave that only lasts for 12 weeks, it may have impacts on children because of the lack of existing supports in the U.S. Further, effects may be heterogeneous across children from different backgrounds, as only mothers with sufficient income from their job and/or spouse may be able to afford to take unpaid leave. Among the several studies that examine the effects of maternity leave policies in other countries, only two have considered such heterogeneous effects (Liu and Skans, 2010; Carneiro et al., 2010). I contribute to this literature by addressing these questions for mothers and children in the United States, where the institutions and unpaid leave policy may augment the importance of mother heterogeneity. Additionally, Carneiro et al. (2010) provide evidence that properly accounting for eligibility for maternity leave is important. In my analysis, I attempt to proxy for eligibility to the best of my ability given the data limitations.

Maternity leave policies can impact child outcomes through several mechanisms. First, a legal maternity leave policy that forbids employers to fire women due to pregnancy or childbirth potentially affects the stress levels of working women during pregnancy.⁷ There is some medical evidence that maternal stress during pregnancy is associated with spontaneous pre-term birth (Copper et al., 1996). Further, the fetal origins literature provides ample evidence for the importance of the prenatal environment on later child and adult outcomes. Aizer et al. (2009) find adverse effects of maternal cortisol levels during pregnancy on their children's educational attainment. Studies by Almond and Mazumder (2005), Almond (2006), and Almond et al. (2009) illustrate the harmful impacts of poor prenatal conditions on adult health, educational, and labor market outcomes. More relevant to my study on childhood outcomes, Kelly (2011) documents that in utero exposure of British children to the Asian flu in 1957 had detrimental effects on birth weight and cognitive outcomes at ages 7 and 11.

Maternity leave policies also affect child outcomes by increasing the amount of time a mother can spend with her child, especially in the first year of life. Several studies examine the relationship between maternal employment and child outcomes, but many suffer from omitted variables bias due to simple cross-sectional regression methodology. Maternal return to work within the first 12 weeks of her child's life is associated with reduced breastfeeding and immunizations and increased behavior problems in early childhood (Berger et al., 2005). Although the negative effects of maternal work are partially offset by the positive effects of increases in income, conditioning on income, maternal work in the first year of life is associated with decreases in reading and math test scores at ages 3–11 (Baum, 2003). Han et al. (2001) find a negative association between maternal employment in the first year of life and white children's cognitive test scores at ages 3–8, but no effects on black children's scores.

A common side effect of early maternal employment is an increase in non-parental care for the child. Studies on the effects of non-parental childcare show mixed results for child outcomes. Full-day publicly provided childcare in Quebec has been shown to have substantial adverse effects on children's vocabulary scores at age 5, and motor and social development skills, emotional disorders, aggression, and overall health at ages 2–3 (Lefebvre et al., 2006; Baker et al., 2008).⁸ For children below age 1 in the U.S., entry to non-parental care can have detrimental effects on cognitive and behavioral outcomes (Loeb et al., 2007). Additionally, there is some evidence that the effects of non-parental care depend greatly on its quality, especially for the most disadvantaged children (Karoly et al., 1998; Blau, 1999).⁹

My focus on early childhood outcomes is supported by a wealth of literature pointing to the importance of early childhood factors in predicting later-life educational, labor market, and health outcomes. Case and Paxson (2008) document a positive link between early childhood health (proxied by adult height) and cognitive test scores at ages 7, 10, and 11, which are in turn positively related to earnings and occupational status in the labor market in adulthood. Currie et al. (2010) find lasting impacts of birth weight and health at various ages throughout childhood on the likelihood of being on welfare, of being in grade 12 by age 17, on literacy, and on the likelihood of taking a college-preparatory math course in high school. Further, early childhood health accounts for 18% of the gap in cognitive ability and 65% of the gap in language ability between children of college-educated and children of less-educated parents in Germany (Salm and Schunk, 2008).

Given the importance of childhood factors for later life outcomes, and the different potential mechanisms through which maternity leave can affect childhood outcomes, a careful study of the impact of FMLA on children born to working mothers is warranted. To my knowledge, no other study has rigorously considered the causal impacts of maternity leave policies generated by FMLA on child outcomes. My research will reveal whether or not the unpaid maternity leave policies generated by FMLA were in fact sufficient for actually affecting child outcomes, and whether there were heterogeneous impacts across children of different types of mothers.

4 Data

To measure birth outcomes I use data from the National Center for Health Statistics Vital Statistics natality data. I collapse the universe of birth records in the United States for 1989–1997 into birth-year/birth-month/county/mother-education/mother-race/mother-age/mother-marital-status cells.¹⁰ This results in 5,806,669 cells, with an average of 6.2 births per cell. Data on infant mortality comes from Vital Statistics mortality data for children under 1 year of age for 1989–1998.¹¹. I collapse this data into county/year/birth-month cells using the exact age at the time of death to calculate the birth month, and merge it to the natality data (also collapsed into county/year/birth-month cells) by county, year, and birth month. On average, there are 137.7 births in each cell. I calculate the infant mortality rate by dividing the number of deaths for each birth month by the number of births in that birth month. The implicit assumption is that the out-of-county mobility between birth and the end of the first year of life is negligible.¹² Since this infant mortality rate approximation may be less valid for very small cells, I limit infant mortality analysis to cells with more than 25 observations to make sure that small cells do not drive my results.¹³ I am left with 185,431 cells for infant mortality rate analysis.

I then merge the natality and infant mortality rate data with data from the CBP for 1989–1997 by county and year to construct a county-by-year measure of the likelihood of maternal employment in a firm with 50 or more employees (as only these firms are covered by the FMLA mandate). The CBP provides information on the total employment in each county and year, as well as the number of firms in different size categories. I estimate the conditional probability that a person in a given county and year is employed by a firm with at least 50 employees:

$$\text{Prob}(\text{Employed in firm with}50+\mid \text{Employed})=\frac{\mu (50-99)\times n(50-99)+\mu (100-249)\times n(100-249)+\mu (250-499)\times n(250-499)+\dots }{\text{Total Employment}}$$

where n(i − j) = number of firms with firm size between i and j, and μ(i − j) is the median number of employees in each firm-size category.

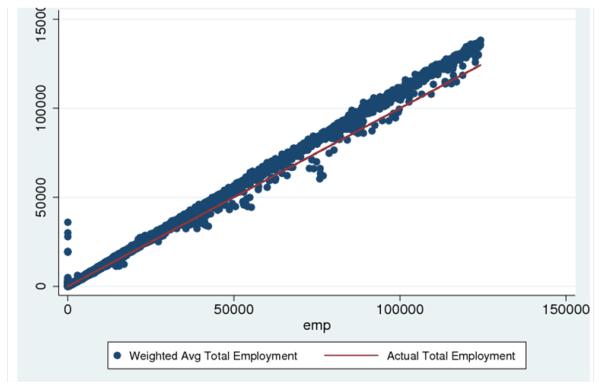
For lack of better information on average firm size in each firm-size category, I use the median of each firm-size category to approximate the number of workers. To check the validity of this method, I plot the total employment calculated this way versus actual employment in Appendix Figure 1. It seems like my method overestimates total employment somewhat, but slightly decreasing the number used to approximate average firm size in each firm-size category does not alter my results.

As a further check of the firm-size approximation, I use data from the Quarterly Work-force Indicators (QWI) database. This database is part of the U.S. Census Bureau's Labor Employment Dynamics database, which combines information from unemployment wage records and businesses on various labor force indicators, including average establishment size for every county and year. I do not use these data in my main analysis because only seven states (California, Colorado, Florida, Idaho, Oregon, Washington, and Wisconsin) have data before 1993. However, I can check whether my calculation of the conditional probability of working in a firm with 50 or more employees is consistent with QWI data for available counties and years. Reassuringly, across counties and years for which I calculate the conditional probability of employment in a firm with 50 or more employees to be greater than 0.5, the minimum average establishment size in the QWI is 60.

It is important to note that my approximation of eligibility based on firm size abstracts away from several issues. In particular, counties with lower total employment may by construction have higher conditional probabilities of employment in a firm with 50 or more employees. However, constructing unconditional probabilities of employment necessitates the use of yearly county-level population estimates which can be very unreliable, especially for small counties.¹⁴ Further, female employment differs by industry, and industries differ by average firm size. Additionally, certain industries are more likely to have unionized occupations, which may have been more likely to offer maternity leave benefits prior to FMLA enactment.¹⁵ Ideally, I would like to estimate the probability that a woman in a given county would have been affected by the FMLA based on her employment status, occupation or industry, and firm size. However, given the lack of information on any of these variables in the natality and mortality data, and the lack of information on maternity leave provisions among different industries and occupations, I am forced to rely on crude approximations of eligibility using county-year level firm size information in the CBP. Nevertheless, my results are robust to a number of specification checks that test this eligibility approximation (presented in section 1.7), and my identification strategy is an improvement over existing analyses that attempt to estimate the causal effects of maternity leave provisions and maternal employment on child outcomes in the U.S.¹⁶

As a result, I obtain a range of conditional probabilities across the cells that vary on a county-year level. Because of the way they are calculated, these probabilities can potentially be greater than 1, but only 1,521 out of 5,806,669 cells (0.02%) have this problem in the natality data and 239 out of 185,431 cells (0.1%) have this problem in the infant mortality rate data. Omitting them from the analysis does not alter the main findings. I then compute the median probability. Cells that have a probability higher than the median belong to the likely eligible group and the rest to the likely ineligible group.¹⁷ Section 1.7 presents several specification checks that test the validity of this eligibility approximation.

Since my eligibility approximation is made at the county level, I include a number of county-level controls in my estimation. In particular, I merge the natality and infant mortality data to county-level summary data from the 1990 Census by county of birth. For each county, I calculate the proportion of the population that is white, black, urban, living below poverty, and female aged 18 to 44. I also calculate the proportion of the female population aged 15 and older that is employed and the proportion that is married, and the proportion of the female population aged 25 and older that has a college degree.

Finally, I merge the natality and infant mortality rate data with data on the monthly state-level unemployment rates from the Bureau of Labor Statistics by state, year, and month of birth to control for labor market conditions that may affect a mother's decision to work immediately after childbirth.

5 Estimation and Summary Statistics

In the DD specification, I use the fact that some states had maternity leave policies in place prior to FMLA and compare outcomes between children born in states that had maternity leave and states that did not, before and after FMLA. Hereafter, I will call the group of states that had some kind of maternity leave policies before FMLA as the control states, and the group with no maternity leave policies as the treatment states. I use information from Han et al. (2009) to determine which states to put into the treatment and control groups based on whether the states had maternity leave policies in 1989–1992. Table 1 presents information on the length of leave provided in the control states.¹⁸

Table 1.

Maternity Leave Policies Prior to FMLA in Control States

State	Number of Weeks of Maternity Leave Under State Laws in 1989–1992
California	12
Connecticut	12
District of Columbia	16
Hawaii	6
Maine	10
Massachusetts	8
Minnesota	6
New Jersey	6
New York	6
Oregon	12
Rhode Island	6
Tennessee	16
Washington	12
Wisconsin	6

Source: Han, Ruhm, and Waldfogel (2009).

I first estimate the following equation:

$$Y_{\mathit{iscmy}}={\beta }_0+{\beta }_1\ast {\mathit{POST}}_{\mathit{my}}+{\beta }_2\ast {\mathit{TREATMENT}}_s+{\beta }_3\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{TREATMENT}}_s+{\gamma }^{\prime }{X}_{\mathit{iscmy}}+{\rho }^{\prime }{C}_c+{\theta }_m+{\lambda }_y+{\delta }_s+{\delta }_s\ast y+\psi \ast {\eta }_{\mathit{smy}}+{∊}_{\mathit{iscmy}}$$ (1)

for each cell i in state s, county c, for birth month m, and birth year y. Y_iscmy is the outcome of interest, and POST_my is an indicator equal to 1 if i's birth date is in or after August, 1993 and 0 otherwise. TREATMENT_s is an indicator equal to 1 if the birth occurred in a state that had no maternity-leave policies prior to FMLA. X_iscmy is a vector of cell-specific control variables for maternal and child characteristics, C_c is a vector of county-level controls, θ_m is a month-of-birth fixed effect, λ_y is a year-of-birth fixed effect, δ_s is a state fixed effect, δ_s * y is a state-specific time trend, and η_smy is the unemployment rate in the state, year and month of birth. ∊_iscmy is a cell-specific error term. The key coefficient of interest is β₃, which measures the DD estimate of the effect of FMLA on children born in treatment states.

Table 2 presents summary statistics for selected variables in the Vital Statistics data, for the whole sample and split according to the four groups in the DD specification. In the whole sample, average birth weight is about 3,300 grams, and about 7% of babies are born low birth weight (<2,500g). About 11% of all births are considered premature (born after less than 37 weeks of gestation). The total infant mortality rate over 1989–1997 is about 8 deaths per 1,000 births. Most mothers are between 25 and 34 years old and have a high school degree. About 40% of all mothers are unmarried at the time of giving birth. The differences between the four groups are quite negligible for most variables, although the large sample size will provide me with sufficient power to detect small effects on outcomes.¹⁹ The control state mothers are more likely to be college-educated and either white or Hispanic, while the treatment state mothers are on average less educated and more likely to be black.

Table 2.

Summary Statistics for Selected Variables in Vital Statistics Data

	WHOLE SAMPLE			CONTROL STATE AND PRE-FMLA		CONTROL STATE AND POST-FMLA		TREATMENT STATE AND PRE-FMLA		TREATMENT STATE AND POST-FMLA
	N (whole sample)	mean	sd	mean	sd	mean	sd	mean	sd	mean	sd
OUTCOMES
Birth weight in grams	5,806,085	3324.915	455.045	3318.071	456.333	3298.097	492.859	3282.944	495.475	3297.621	485.849
5-min Apgar Score	5,109,176	8.970	0.684	8.949	0.665	8.958	0.738	8.940	0.709	8.951	0.714
Gestation in weeks	5,787,698	39.078	2.059	38.976	2.013	39.019	2.309	38.870	2.253	38.963	2.229
Low birth weight (<2500g)	5,806,085	0.074	0.192	0.075	0.194	0.079	0.216	0.083	0.221	0.079	0.213
Total infant mortality rate	185,431	0.008	0.012	0.007	0.010	0.006	0.009	0.009	0.012	0.008	0.012
Low Apgar score (<8)	5,109,176	0.035	0.139	0.033	0.137	0.036	0.150	0.034	0.146	0.035	0.146
Born premature (<37 weeks of gestation)	5,787,698	0.110	0.230	0.110	0.232	0.120	0.261	0.122	0.263	0.118	0.255
Parity 1	5,787,041	0.348	0.393	0.351	0.373	0.348	0.376	0.345	0.397	0.350	0.399
Parity 2	5,787,041	0.271	0.341	0.261	0.312	0.260	0.315	0.274	0.348	0.274	0.350
Parity 3	5,787,041	0.176	0.295	0.171	0.269	0.169	0.271	0.180	0.302	0.176	0.301
CONTROLS
Child is male	5,811,445	0.512	0.385	0.513	0.357	0.512	0.361	0.512	0.392	0.511	0.394
Mom <19 yrs old	5,811,445	0.138	0.345	0.133	0.340	0.127	0.333	0.143	0.350	0.137	0.344
Mom 19–24 yrs old	5,811,445	0.340	0.474	0.318	0.466	0.312	0.463	0.349	0.477	0.346	0.476
Mom 25–34 yrs old	5,811,445	0.362	0.481	0.356	0.479	0.352	0.478	0.368	0.482	0.362	0.481
Mom 35–44 yrs old	5,811,445	0.157	0.363	0.187	0.390	0.200	0.400	0.138	0.345	0.153	0.360
Mom 45+ yrs old	5,811,445	0.003	0.056	0.005	0.074	0.008	0.086	0.002	0.041	0.002	0.049
Mom < HS education	5,569,391	0.281	0.449	0.278	0.448	0.263	0.441	0.294	0.455	0.273	0.445
Mom has HS education	5,569,391	0.341	0.474	0.324	0.468	0.320	0.467	0.350	0.477	0.342	0.475
Mom has some college	5,569,391	0.227	0.419	0.230	0.421	0.242	0.428	0.217	0.412	0.232	0.422
Mom has college degree or more	5,569,391	0.151	0.358	0.167	0.373	0.175	0.380	0.139	0.346	0.153	0.360
Mom is non-Hispanic white	5,716,135	0.623	0.466	0.583	0.464	0.564	0.465	0.642	0.465	0.633	0.465
Mom is black	5,716,135	0.212	0.409	0.174	0.380	0.170	0.375	0.231	0.422	0.217	0.412
Mom is Hispanic	5,716,135	0.080	0.232	0.103	0.246	0.122	0.269	0.062	0.210	0.077	0.233
Mom is unmarried	5,811,445	0.406	0.491	0.421	0.494	0.439	0.496	0.381	0.486	0.416	0.493
Unemployment rate in state, year, and month of birth	5,811,445	5.784	1.420	6.300	1.647	5.884	1.420	6.213	1.409	5.169	1.093

Notes: The units of observation for the summary statistics presented here are county/year/birth month/mother age/mother race/mother education/mother marital status cells. Analysis is based on the universe of birth records in the United States for 1989–1997. Treatment state = birth occurred in a state that had no maternity leave laws prior to FMLA. Control state = birth occurred in a state that had some kind of maternity leave law prior to FMLA. Post-FMLA = birth occurred in or after August, 1993. Pre-FMLA = birth occurred before August, 1993.

A key assumption in DD analysis is that the underlying trends of the two groups being considered are similar. In particular, we must assume that in the absence of FMLA, the trends in birth outcomes and infant mortality rates between the treatment and control states would have been the same, and that no other factors that might affect these outcomes occurred at the same time as FMLA. If this assumption is violated, then the DD estimates will be biased. I include state-specific linear time trends in the DD specifications to partially address this issue. However, placebo checks for differential time trends presented in Section VII suggest that some of the DD results may still be slightly biased. Additionally, the DD specifications might produce inaccurate results because they do not take into account that many new mothers were not affected by the FMLA. In particular, the DD specification does not account for the fact that women working in firms with less than 50 employees are ineligible for maternity leave under FMLA. To address these issues, I employ a DDD technique by comparing children born to mothers who were likely eligible for FMLA benefits with children born to mothers who were likely ineligible, in the two groups of states, before and after FMLA went into effect. This specification also allows me to include a full set of state-year interactions to control for any other factors that are changing at the state-year level that may affect my outcomes of interest. The triple-difference estimation is my preferred specification.

More precisely, I estimate the following DDD model with state, year, and month of birth fixed effects, as well as state-year interactions:

$$Y_{\mathit{iscmy}}={\beta }_0+{\beta }_1\ast {\mathit{POST}}_{my}+{\beta }_2\ast {\mathit{TREATMENT}}_s+{\beta }_3\ast {\mathit{ELIG}}_{\mathit{cy}}+{\beta }_4\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{TREATMENT}}_s+{\beta }_5\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{ELIG}}_{\mathit{cy}}\ast +{\beta }_6\ast {\mathit{ELIG}}_{\mathit{cy}}\ast {\mathit{TREATMENT}}_s+{\beta }_7\ast {\mathit{ELIG}}_{\mathit{cy}}\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{TREATMENT}}_s+{\gamma }^{\prime }{X}_{\mathit{iscmy}}+{\rho }^{\prime }{C}_c+{\theta }_m+{\lambda }_y+{\delta }_s+{\mu }_{\mathit{sy}}+\psi \ast {\eta }_{\mathit{smy}}+{∊}_{\mathit{iscmy}}$$ (2)

where ELIG_cy is an indicator equal to 1 if i's county and year of birth place i into the likely eligible group (estimated using CBP) and 0 otherwise. μ_sy is a state-year interaction effect. The rest of the variables and parameters are as defined before. The key coefficient of interest is β₇, which measures the estimate of the DDD effect of FMLA.

To get a better sense of the firm size variation used to identify the triple difference effects, I present some county-level summary statistics split by treatment and control states and by likely eligible and likely ineligible county-years in Appendix Table 1. In both the treatment and control states, likely eligible county-years are more urban, have a lower proportion of whites and a higher proportion of blacks, and have a lower proportion of married females and a higher proportion of employed females. Interestingly, the likely eligible county-years also tend to have more college-educated females and fewer people living below poverty.

However, although there are clear differences between the likely eligible and likely ineligible counties, the validity of the DDD model relies on the assumption that in the absence of FMLA, the difference in outcomes between likely eligible and likely ineligible counties in treatment states after FMLA would have been similar to the difference in outcomes between these counties in control states and before FMLA went into effect. While I cannot rule out that there are other unobservable factors that have a divergent effect on this difference, a series of robustness checks suggests that this is unlikely. First, there are no changes to the difference in observable maternal characteristics between likely eligible and likely ineligible counties in treatment states after FMLA relative to the difference in control states and before FMLA went into effect. This suggests that my results are not driven by FMLA-induced selection into motherhood based on observable characteristics (for instance, the observed reduction in infant mortality is not a result of more educated women being more likely to have a child once FMLA went into effect). Second, the FMLA did not affect the county-year level firm size distribution. Thus, my results are not driven by endogenous selection of firms into firm-size categories (for example, this means that the observed reduction in infant mortality is not a result of lower-quality firms changing firm-size categories to be below the 50-employee cut-off and thus mothers with a higher probability of employment in a firm with 50 or more employees being employed in higher-quality firms). Section 1.7 discusses these issues in more detail.

6 Results on the Effects of FMLA

6.1 Effects on Birth Outcomes and Infant Mortality Rates

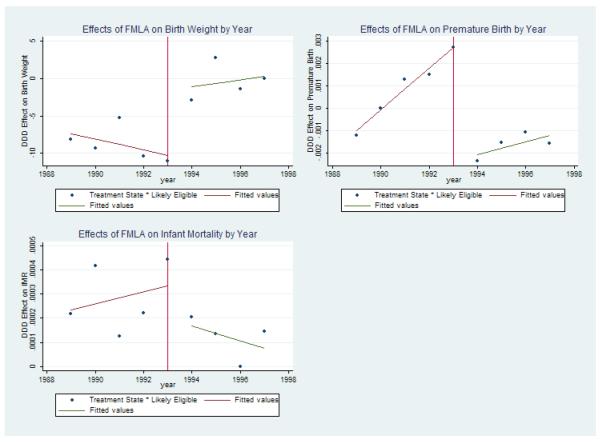
Figure 1 depicts a graphical representation of some of the key results from my analysis. In particular, for three outcomes (birth weight, an indicator for a premature birth, and the total infant mortality rate) I plot the yearly coefficients from the DDD model - each point represents the coefficient on the interaction between an indicator for a birth in a treatment state, an indicator for a birth in a likely-eligible county-year, and an indicator for the year on the x-axis. I include all the controls, fixed effects, and state-year interactions listed in equation (1.2) in the regressions used to estimate these coefficients. The graphs suggest that after 1993, there is a positive effect on birth weight and negative effects on the likelihood of a premature birth and on the infant mortality rate of being born in a treatment state and in a likely-eligible county-year. Thus, these graphs present suggestive evidence that FMLA may have improved infant health for children of mothers who were most likely affected by FMLA provisions.

Figure 1.

The Effects of FMLA by Year

Notes: These figures plot the yearly DDD coefficients on the interaction between an indicator for a birth in a treatment state, an indicator for a birth in a likely-eligible county-year, and an indicator for the year on the x-axis. I include all the controls, fixed effects, and state-year interactions listed in equation (2) in the regressions used to estimate these coefficients.

Table 3 presents the regression results on the effects of FMLA on birth outcomes in the natality data. The first four columns list the coefficients from the DD specification based on treatment and control states, while the last three columns present the coefficients from the DDD specification. The regressions with controls include maternal and child cell-level characteristics (four dummies for mother's age category, three dummies for mother's education, three dummies for mother's race, a dummy for mother's marital status at the time of childbirth, and the proportion of male births), county-level characteristics (percent white population, percent black population, percent urban population, percent population below poverty, percent female aged 18–44 population, percent females employed, percent females married, and percent females aged 25+ with a college degree), and the unemployment rate in the state, year, and month of birth.²⁰ Robust standard errors are clustered on the state level, and all regressions are weighted by cell size. Notably, the coefficients of interest do not change significantly as fixed effects and control variables are added to the specifications, thus providing some validation of the identification strategy. While the DD results suggest that there are no effects on birth outcomes for the whole sample, the more reliable DDD results show small but statistically significant effects on birth weight and likelihood of a premature birth. The magnitudes of the coefficients imply that the FMLA is associated with a 0.2% increase in birth weight, a 0.04% increase in the gestation length, a 3% decrease in the likelihood of a low-birth-weight birth, and a 3% decrease in the likelihood of a premature birth.²¹ There seem to be larger and more statistically significant effects on births by college-educated and married mothers, who were more likely to be eligible for FMLA and able to afford unpaid leave, than on births by less-educated and unmarried mothers. This is also consistent with evidence that U.S. maternity leave policies only affect the leave-taking of college-educated and married mothers (Han et al., 2009).²² I also conducted analysis on the five-minute Apgar score, risk factors, labor complications, and births with congenital anomalies, and found no statistically significant effects for the whole sample or for the sub-samples.

Table 3.

Effects of FMLA Maternity Leave on Birth Outcomes

OUTCOMES:	DD WHOLE SAMPLE				DDD WHOLE SAMPLE	DDD COLLEGE-ED AND MARRIED	DDD LESS THAN COLLEGE AND SINGLE
Birth weight in grams	−3.4727 (2.0805)	−2.7452 (1.9993)	1.0079 (1.8492)	1.1151 (1.8974)	6.5037*** (1.7878)	9.1972** (3.7886)	7.1445+ (3.5631)
N	5,806,085	5,806,085	5,806,085	5,488,302	5,483,611	671,425	2,053,113
Gestation in weeks	−0.0230+ (0.0118)	−0.0211+ (0.0115)	0.0012 (0.0113)	0.0034 (0.0113)	0.0173** (0.0085)	0.0246+ (0.0143)	0.0065 (0.0139)
N	5,787,698	5,787,698	5,787,698	5,478,550	5,473,862	670,866	2,048,140
Low birth weight	0.0010 (0.0007)	0.0011 (0.0007)	−0.0000 (0.0005)	0.0001 (0.0006)	−0.0020** (0.0006)	−0.0020+ (0.0010)	−0.0023+ (0.0012)
N	5,806,085	5,806,085	5,806,085	5,488,302	5,483,611	671,425	2,053,113
Premature	0.0011 (0.0012)	0.0010 (0.0011)	−0.0010 (0.0006)	−0.0010 (0.0006)	−0.0019** (0.0009)	−0.0029** (0.0014)	−0.0012 (0.0015)
N	5,787,698	5,787,698	5,787,698	5,478,550	5,473,862	670,866	2,048,140
Controls	No	No	No	Yes	Yes	Yes	Yes
Year of birth fixed effects	No	Yes	Yes	Yes	Yes	Yes	Yes
Month of birth fixed effects	No	Yes	Yes	Yes	Yes	Yes	Yes
State fixed effects	No	Yes	Yes	Yes	Yes	Yes	Yes
State-specific time trends	No	No	Yes	Yes	No	No	No
State-year interactions	No	No	No	No	Yes	Yes	Yes

Notes: The results presented here list the DD and DDD effects on each of the outcomes listed in the first column. The units of analysis are county/year/birth month/mother's education/mother's race/mother's age/mother's marital status cells. The DD regressions compare births in states with and without maternity leave policies prior to FMLA, before and after August 1993. The DDD regressions compare likely eligibles with likely ineligibles (see text for description of how eligibility was calculated using County Business Patterns data), before and after August 1993, across states that had maternity leave policies prior to FMLA and states that did not. Controls include: 1) maternal and child cell-level characteristics — four dummies for mother's age, three dummies for mother's education, three dummies for mother's race, a dummy for mother's marital status at time of childbirth, the proportion of male births; 2) county-level characteristics — percent white population, percent black population, percent urban population, percent population below poverty, percent female aged 18–44 population, percent females employed, percent females married, percent females aged 25+ with a college degree; and 3) the unemployment rate in state, year, and month of birth. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

Table 4 presents the results on the effects of FMLA on infant mortality rates. Again, the first four columns of this table list the coefficients from the DD specification based on treatment and control states, while the last three columns present the coefficients from the DDD specification. The controls are the same as in Table 3, robust standard errors are clustered on the state level, and all regressions are weighted by cell size. There is a statistically significant and negative effect of FMLA on infant mortality for the college-educated and married sub-sample.²³ The results suggest that for this sub-sample, FMLA reduced the overall infant mortality rate by 6 deaths per 10,000 births (10% decline at the sub-sample mean), the post-neonatal mortality rate by 2 deaths per 10,000 births (10% decline at the sub-sample mean), and the neonatal mortality rate by 3 deaths per 10,000 births (7.5% decline at the sub-sample mean). Since there is no effect on the overall number of births,²⁴ these results are not mechanically driven by an increase in the denominator of the infant mortality rate. While these effects may seem large, it is important to note that they are only present for a specific sub-sample that was most likely to be eligible for FMLA and able to take unpaid leave, and in which the mean infant mortality rates are relatively low. There are no statistically significant effects on infant mortality in the less-educated and unmarried sub-sample, suggesting that the children of these mothers were unaffected by FMLA's unpaid leave.

Table 4.

Effects of FMLA Maternity Leave on Infant Mortality

OUTCOMES:	DD WHOLE SAMPLE				DDD WHOLE SAMPLE	DDD COLLEGE-ED AND MARRIED	DDD LESS THAN COLLEGE AND SINGLE
Total Infant Mortality	−0.0002 (0.0001)	−0.0001 (0.0001)	−0.0003** (0.0001)	−0.0003** (0.0001)	−0.0002+ (0.0001)	−0.0006*** (0.0002)	0.0000 (0.0003)
N	185,431	185,431	185,431	183,054	182,997	59,668	50,330
Mean of dep. var.	0.008	0.008	0.008	0.008	0.008	0.006	0.009
Infant Mortality: 28 days – 1 year	−0.0000 (0.0001)	−0.0000 (0.0001)	−0.0001** (0.0001)	−0.0001 (0.0001)	−0.0001 (0.0001)	−0.0002+ (0.0001)	0.0000 (0.0002)
N	185,431	185,431	185,431	183,054	182,997	59,668	50,330
Mean of dep. var.	0.003	0.003	0.003	0.003	0.003	0.002	0.003
Infant Mortality: <28 days	−0.0001 (0.0001)	−0.0001 (0.0001)	−0.0002** (0.0001)	−0.0002+ (0.0001)	−0.0001 (0.0001)	−0.0003** (0.0002)	0.0000 (0.0003)
N	185,431	185,431	185,431	183,054	182,997	59,668	50,330
Mean of dep. var.	0.005	0.005	0.005	0.005	0.005	0.004	0.005
Controls	No	No	No	Yes	Yes	Yes	Yes
Year of birth fixed effects	No	Yes	Yes	Yes	Yes	Yes	Yes
Month of birth fixed	No	Yes	Yes	Yes	Yes	Yes	Yes
State fixed effects	No	Yes	Yes	Yes	Yes	Yes	Yes
State-specific time trends	No	No	Yes	Yes	No	No	No
State-year interactions	No	No	No	No	Yes	Yes	Yes

Notes: The results presented here list the DD and DDD effects on each of the outcomes listed in the first column. The units of analysis are county-year-birth month cells. Cells with fewer than 25 births are omitted from the analysis. Please refer to notes under Table 3 for details about controls and estimation methods. The college-educated and married sample includes cells where the proportion of college-educated and married mothers is greater than the median in that state and year, while the less than college and single sample considers cells with proportions below the median. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

Appendix Table 2 presents the DDD results on birth weight, premature births, and the total infant mortality rate for college-educated and married mothers in more detail across different specifications and with coefficients for the main effects and double interactions. As in the DD specifications, the DDD key coefficients of interest do not vary significantly as the various controls and fixed effects are added.

To further understand the mechanisms through which maternity leave might affect infant deaths, I estimate the triple-difference models for the number of deaths per 1,000 births separately by cause of death for the whole sample and the college-educated and married sub-sample. Table 5 presents the results from these regressions. For the whole sample, the decline in the infant mortality rate seems to be driven by deaths from ill-defined causes (which include deaths from the Sudden Infant Death Syndrome), while for the college-educated and married sub-sample it is also driven by deaths from congenital anomalies. In particular, at the sub-sample mean, the estimates suggest there is a 16% decline in deaths from congenital anomalies, and a 16% decline in deaths from ill-defined causes for the college-educated and married sub-sample.

Table 5.

Effects of FMLA Maternity Leave on Infant Mortality — By Cause

	Deaths per 1000 births from disease	Deaths per 1000 births from congenital anomalies	Deaths per 1000 births from causes originating in the perinatal period	Deaths per 1000 births from ill-defined causes	Deaths per 1000 births from accidents	Deaths per 1000 births from homicide	Deaths per 1000 births from other causes
Whole Sample DDD	−0.0316 (0.0401)	−0.0244 (0.0568)	−0.0120 (0.0889)	−0.1587** (0.0545)	0.0202 (0.0244)	0.0177 (0.0158)	0.0335 (0.0280)
N	182,997	182,997	182,997	182,997	182,997	182,997	182,997
Mean of Dep. Var	0.725	1.890	3.267	1.460	0.296	0.068	0.441
College-Ed and Married DDD	−0.0825 (0.0559)	−0.2826** (0.0933)	−0.0177 (0.1201)	−0.1962** (0.0647)	−0.0451 (0.0364)	0.0328 (0.0280)	0.0124 (0.0459)
N	59,668	59,668	59,668	59,668	59,668	59,668	59,668
Mean of Dep. Var	0.572	1.640	2.841	1.057	0.205	0.063	0.352

Notes: The results presented here list the DDD effects on each of the outcomes listed in the top row. The units of analysis are county-year-birth month cells. Cells with fewer than 25 births are omitted from the analysis. Please refer to notes under Table 3 for details about controls and estimation methods. The college-educated and married sample includes cells where the proportion of college-educated and married mothers is greater than the median in that state and year, while the less than college and single sample considers cells with proportions below the median. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

To put this in context, we can consider that these estimates represent reduced-form or intent-to-treat (ITT) effects, given that I do not observe leave-taking. To calculate the treatment-on-the-treated (TOT) effects on women who actually take up maternity leave, consider that Han et al. (2009) estimate that about 36% of college-educated and married women take leave as a result of FMLA.²⁵ Using this as an estimate of the “first-stage” effect of FMLA on leave-taking among college-educated and married women, my results suggest that FMLA led to a 47% reduction in the likelihood that a child born to one of these women dies from a congenital anomaly in infancy.²⁶ To calculate a confidence interval for this TOT effect size, I use the delta method to estimate a standard error of 0.15. With these estimates, I can conclude that the 95% confidence interval for the TOT effect size for infant mortality from congenital anomalies ranges from 18% to 76%. For overall infant mortality among children of college-educated and married mothers, the implied TOT effect size is 27% with a 95% confidence interval that ranges from 8% to 44%. Unfortunately, since, to my knowledge, this is the first paper to estimate the causal effect of U.S. maternity leave policies on infant mortality, there is no benchmark effect size for comparison. However, literature on the effects of air pollution on infant mortality in the U.S. reports relatively comparable effect sizes. In particular, Chay and Greenstone (2003) find that a 1% reduction in total suspended particulates (TSP) exposure leads to a 0.5% decrease in infant mortality. They write that TSP concentrations decreased from 95 $\frac{\mu }{m^3}$ to 60 $\frac{\mu }{m^3}$ over the 1970s and 1980s — a 37% decline. This means that the reductions in TSP exposure over this time period led to an 18% decline in total infant mortality. Currie and Neidell (2005) and Currie et al. (2009) estimate that a 1-unit increase in carbon monoxide exposure leads to a 2.5–5% increase in total infant mortality in California and New Jersey. Given they find that the effects of air pollution exposure on infant health are 2–6 times bigger for smokers and older mothers, their estimated effect sizes for these subgroups would overlap with the confidence intervals that I present. Thus, while seemingly large, the magnitudes that I estimate are not unreasonable especially at the lower end of the implied range of effect sizes and given the low incidence of infant deaths for the sample of interest.

The observed pattern of results suggests that FMLA allowed new mothers to take better care of their ill children by spending more time with them at home, by seeking prompt medical care (with their guaranteed health insurance), and by breastfeeding them.²⁷ In particular, the American Academy of Pediatrics highlights the importance of prompt professional medical care for infants who have different kinds of congenital anomalies. For instance, parents of children with spina bifida, a congenital anomaly of the spine, should be very alert for signs of infection and ensure that their children receive immediate medical treatment (Harstad and Albers-Prock, 2011). It seems that mothers who are able to spend time at home with their newborns as a result of FMLA are less constrained in their ability to immediately respond to such signs, and thus potentially save their children's lives. While data limitations prevent me from analyzing these particular mechanisms empirically, the findings suggest that maternal time at home after birth may be a key factor for preventing infant deaths among ill newborns.

It is important to note that I find no statistically significant effects on risk factors during pregnancy, incidence of complications during labor, or on births with congenital anomalies. In fact, it appears that FMLA did not affect the number of births of ill children or children with birth defects, rather, mothers with more leave were better able to take care of their children and keep them alive. Finally, some may conclude that the fact that FMLA did not have an impact on deaths from external causes (such as homicides and traffic accidents) and causes originating in the perinatal period suggests that the policy had little net effect on mothers' stress levels or well-being during pregnancy and after childbirth (and this is also consistent with the very small effects on birth outcomes). However, evolving research on fetal origins suggests that in-utero conditions, including maternal stress during pregnancy, have lasting causal effects on adult health and well-being, and that these effects may not operate through impacts on birth weight and infant health (Gluckman and Hanson, 2005). Thus, while my results point to increased maternal time at home after childbirth following FMLA as being a crucial factor for improving infant health, I cannot rule out the possibility of effects on later-life health and other outcomes as a result of reductions in maternal stress during pregnancy due to FMLA enactment.

6.2 Effects on Parity of Birth

Given that maternity leave provisions may affect women's decisions to have children, it is important to determine whether the policy impacted selection into the birth sample. In particular, there is evidence that higher-parity births have healthier birth outcomes because of a better in-utero environment (Gluckman and Hanson, 2005).²⁸ So, if FMLA affects the ratio of first-parity births to later-parity births, one must account for the selection effects due to a change in the composition of the birth sample to isolate the true effect of FMLA on birth outcomes and infant mortality rates.

Table 6 presents the results on the effects of FMLA on parity. The DDD results suggest that overall there was an increase in first-parity births and a decrease in later parity births in the whole sample. Interestingly, this effect is rather persistent, and still present when one compares 1996–1997 outcomes to those pre-FMLA (results available upon request). However, there are no effects on overall fertility as measured by the number of births in each cell.²⁹ Further, unlike any of the other outcomes, the positive effects on first-parity births are driven by the less-than-college-educated and single mothers. One explanation for these findings may be that the guarantee of maternity leave (and the employers' inability to fire new mothers for taking time off) lowered the costs of childbirth for some working mothers, and hence encouraged previously childless women to give birth.³⁰ Less-educated, single, and childless working women likely faced higher costs of childbirth prior to guaranteed maternity leave than college-educated and married women because they are less likely to have a safety net of savings, family support or a secondary income that can support them in case they lose their jobs. Hence, by eliminating the risk of unemployment due to childbirth, FMLA affected the decision to have a first child for this group of women. However, given that prior evidence suggests that these new mothers did not take much of the maternity leave (Han et al., 2009), there are no noticeable effects of FMLA on their children's outcomes. In contrast, FMLA did not affect the decision to have a first child for college-educated and married women, but their children benefited from their mothers' ability to take advantage of the twelve weeks of unpaid leave.

Table 6.

Effects of FMLA Maternity Leave on Parity

OUTCOMES:	DDD WHOLE SAMPLE	DDD COLLEGE-ED AND MARRIED	DDD LESS THAN COLLEGE AND SINGLE
Parity 1	0.0092** (0.0038)	−0.0006 (0.0022)	0.0149** (0.0064)
N	5,476,003	670,659	2,050,009
Parity 2	−0.0047** (0.0017)	−0.0047** (0.0019)	−0.0062** (0.0028)
N	5,476,003	670,659	2,050,009
Parity 3	−0.0031** (0.0011)	0.0013 (0.0016)	−0.0035 (0.0030)
N	5,476,003	670,659	2,050,009

Notes: The results presented here list the DDD effects on each of the outcomes listed in the first column Please refer to notes under Table 3 for details about the sample, controls, and estimation methods. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

The decline in later-parity births can be potentially explained by a change in the work-place culture for women after FMLA. Since a large fraction of women giving birth to higher-parity children gave birth to their firstborn children prior to FMLA, it is likely that these women face different costs of childbirth than the women giving birth for the first time after FMLA. Prior to guaranteed maternity leave, it may have been customary for these women to stop working for some time (or quit the labor force entirely) to care for their newborn child. With the advent of FMLA, the standard changed to just taking twelve weeks of leave, and this may be seen as inadequate by women who already have children, thus reducing the rate of later-parity births.³¹

Regardless of the exact explanation for the parity effects, these results suggest that my findings of FMLA's favorable effects on birth outcomes and infant mortality rates may be slightly understated, given that the fraction of later-parity births declines. However, given that FMLA only increased the likelihood of a first-parity birth by 2.6%, decreased the likelihood of a second-parity and third-parity birth by 1.7%, and that the first-parity effects are not apparent in the college-educated and married sub-sample, the understatement of the true effects on infant mortality rates for this sub-sample is likely negligible.

7 Robustness Checks

My first specification check tests for differential time trends in the DD analysis. I include placebo interactions between indicators for years 1992 and 1991 and an indicator for treatment states into the DD model. If there are any differential time trends between treatment and control states, then we may see spurious effects in the years prior to FMLA enactment. Appendix Table 3 presents the results of this specification check for college-educated and married mothers, as this is the sample for which I find the most results. The results for infant mortality rates suggest that there are mostly no spurious effects prior to FMLA (except for an increase in the treatment state post-neonatal mortality rate in 1992), thereby strengthening the validity of my findings for these outcomes. However, there seems to be a downward trend in birth outcomes for treatment states prior to FMLA. This suggests that the lack of DD effects for birth outcomes may be driven by a downward bias due to these differential trends. Hence, the DDD model is a necessary improvement upon the DD specification, as it does not rely on an assumption of similar time trends between treatment and control states. The remainder of this section tests the robustness of the DDD model.

First, since the split into likely eligible and likely ineligible groups across the median probability of employment in a firm with 50 or more employees is somewhat arbitrary, I also estimate a model using the continuous measure of the probability rather than a binary indicator. In particular, the effect of FMLA is measured by the coefficient on the interaction between the conditional probability that a mother is employed in a firm with 50 or more employees, an indicator for a birth occurring after August 1993, and an indicator for the state being in the treatment group. This coefficient represents the effect of the FMLA for a given conditional probability of being eligible. One can multiply this coefficient by the conditional probability to get the true treatment effect.

Table 7 presents the results on birth outcomes and infant mortality rates from estimating this model. In the natality data, the mean probability is 0.56, while the median is 0.58, the 25th percentile is 0.49, the 75th percentile is 0.65, and the 99th percentile is 0.80. The results are qualitatively consistent with those in Tables 3 and 4, suggesting small effects on birth weight and likelihood of a premature birth, and large negative effects on the infant mortality rate for the college-educated and married sub-sample only. The coefficients here can be interpreted as the effects for those mothers whose conditional probability of eligibility based on firm size equals 1, and so they are much larger than those in the triple-difference specifications. At the mean probability, the results suggest a 22g increase in birth weight, a 0.8 percentage point decrease in the likelihood of a premature birth, and a reduction in 1.6 deaths per 1,000 births for the college-educated and married sub-sample. However, these magnitudes should be interpreted with caution, as they are based only on calculations of conditional probability of employment in a firm with 50 or more employees using the year and county of birth, and cannot assess individual mothers' actual eligibility for FMLA.

Table 7.

Effects of FMLA Using Continuous Probability Measure

	Birth Weight (g)	Gestation (weeks)	LBW	Premature	Total Infant Mortality	Infant Mortality: 28 days – 1 year	Infant Mortality: <28 days
WHOLE SAMPLE	27.8990 (23.7618)	0.0284 (0.0571)	−0.0068 (0.0062)	−0.0068 (0.0045)	−0.0007 (0.0007)	0.0000 (0.0003)	−0.0007 (0.0006)
N	5,483,611	5,473,862	5,483,611	5,473,862	182,997	182,997	182,997
COLLEGE-ED AND MARRIED SAMPLE	38.4834** (14.1071)	0.1039 (0.0813)	−0.0067 (0.0046)	−0.0148** (0.0069)	−0.0029** (0.0012)	−0.0015** (0.0006)	−0.0014 (0.0011)
N	671,425	670,866	671,425	670,866	59,668	59,668	59,668
LESS THAN COLLEGE AND SINGLE SAMPLE	29.1966 (32.1345)	−0.0482 (0.1000)	−0.0045 (0.0108)	−0.0032 (0.0100)	−0.0004 (0.0021)	0.0002 (0.0010)	−0.0006 (0.0014)
N	2,053,113	2,048,140	2,053,113	2,048,140	50,330	50,330	50,330

Notes: The results presented here list the coefficients on the DD effects of the FMLA scaled by the conditional probability of employment in a firm with 50 or more employees (as a proxy for FMLA eligibility). In particular, the coefficients represent the effect of the FMLA for any given conditional probability. Please refer to notes under Tables 3 and 4 for details about the samples, controls, and estimation methods. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

As another robustness check, I conduct my analysis on “small-firm” counties where the likelihood of employment in a firm with 50 or more employees is less than 0.30, and “big-firm” counties where it is greater than 0.70.³² If my analysis truly captures the effects of FMLA, then all the effects should be concentrated among the “big-firm” counties, and we should not see any effects for the “small-firm” counties, where mothers were likely ineligible for FMLA. More precisely, I estimate:

$$Y_{\mathit{iscmy}}={\beta }_0+{\beta }_1\ast {\mathit{POST}}_{\mathit{my}}+{\beta }_2\ast {\mathit{TREATMENT}}_s+{\beta }_3\ast {\mathit{SMALL}}_{\mathit{cy}}+{\beta }_4\ast {\mathit{BIG}}_{\mathit{cy}}+{\beta }_5\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{TREATMENT}}_s+{\beta }_6\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{SMALL}}_{\mathit{cy}}+{\beta }_7\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{BIG}}_{\mathit{cy}}+{\beta }_8\ast {\mathit{SMALL}}_{\mathit{cy}}\ast {\mathit{TREATMENT}}_s+{\beta }_9\ast {\mathit{BIG}}_{cy}\ast {\mathit{TREATMENT}}_s+{\beta }_{10}\ast {\mathit{SMALL}}_{\mathit{cy}}\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{TREATMENT}}_s+{\beta }_{11}\ast {\mathit{BIG}}_{\mathit{cy}}\ast {\mathit{POST}}_{\mathit{my}}\ast {\mathit{TREATMENT}}_s+{\gamma }^{\prime }{X}_{\mathit{iscmy}}+{\rho }^{\prime }{C}_c+{\theta }_m+{\lambda }_y+{\delta }_s+{\mu }_{\mathit{sy}}+\psi \ast {\eta }_{\mathit{smy}}+{∊}_{\mathit{iscmy}}$$ (3)

where SMALL_cy equals 1 if the birth occurred in a “small-firm” county, and 0 otherwise, and BIG_cy equals 1 if the birth occurred in a “big-firm” county, and 0 otherwise. If there are any effects of FMLA, then we should expect β₁0 to be zero, and β₁1 to be statistically different from zero.

Table 8 presents the results from estimating this specification for birth outcomes and infant mortality rates.³³ Notably, the estimate of the coefficient on the DDD effect for “small-firm” counties (β₁₀ in equation (1.3)) is only statistically significant at the 5% level in one out of the 24 specifications. However, there are statistically significant effects for the “big-firm” counties (as measured by β₁₁ in equation (1.3)) on the likelihood of a low-birth-weight birth, the likelihood of a premature birth, the overall infant mortality rate, and the post-neonatal mortality rate in the college-educated and married sample. These effects are consistent with those found in the main results, and suggest that FMLA had some impacts on the health of children of eligible women who could afford to take leave.

Table 8.

Comparing Effects of FMLA on Birth Outcomes and Infant Mortality in Big-Firm and Small-Firm Counties

	Birth Weight (g)	Gestation (weeks)	LBW	Premature	Total Infant Mortality	Infant Mortality: 28 days – 1 year	Infant Mortality: <28 days
WHOLE SAMPLE
Small County * Post * Treatment State	0.7149 (4.3459)	−0.0037 (0.0264)	−0.0013 (0.0010)	0.0009 (0.0025)	0.0020+ (0.0011)	0.0010 (0.0008)	0.0009 (0.0007)
Big County * Post * Treatment State	2.0436 (6.2221)	0.0206 (0.0337)	−0.0008 (0.0024)	−0.0027 (0.0029)	−0.0002 (0.0003)	0.0001 (0.0001)	−0.0002 (0.0003)
N	5,806,400	5,788,023	5,806,400	5,788,023	185,431	185,431	185,431
COLLEGE-ED AND MARRIED SAMPLE
Small County* Post * Treatment State	11.8667 (14.8911)	0.0611 (0.0802)	−0.0054 (0.0039)	0.0015 (0.0065)	0.0027 (0.0022)	−0.0011 (0.0012)	0.0038** (0.0018)
Big County * Post * Treatment State	14.9578+ (8.8581)	0.0408 (0.0247)	−0.0040** (0.0019)	−0.0043** (0.0019)	−0.0008** (0.0004)	−0.0004** (0.0002)	−0.0004 (0.0003)
N	680,940	679,539	680,940	679,539	50,651	50,651	50,651
LESS THAN COLLEGE AND SINGLE SAMPLE
Small County* Post * Treatment State	−6.5206 (17.1318)	0.1024 (0.0611)	−0.0034 (0.0057)	0.0002 (0.0044)	−0.0001 (0.0015)	−0.0004 (0.0009)	0.0004 (0.0012)
Big County * Post * Treatment State	5.0248 (7.4235)	0.0305 (0.0347)	0.0010 (0.0021)	−0.0014 (0.0028)	0.0003 (0.0003)	−0.0000 (0.0003)	0.0003 (0.0004)
N	2,085,200	2,079,522	2,085,200	2,079,522	60,026	60,026	60,026

Notes: The results presented here list the coefficients on the difference-in-difference-in-difference effects of the FMLA, separately for “big-firm” and “small-firm” counties. “Big-firm” counties are those that have a conditional probability of employment in a firm with 50+ employees greater than 0.70. “Small-firm” counties are those that have a conditional probability of employment in a firm with 50+ employees less than 0.30. Please refer to notes under Tables 3 abd 4 for details about the sample, controls, and estimation methods. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

To further check the robustness of the eligibility approximation, I limit my analysis to counties that have zero firms with more than 50 employees and to counties that have fewer than 75 firms with less than 50 employees, but at least one firm with more than 50 employees.³⁴ Mothers in the former group of counties cannot be eligible for FMLA, while mothers in the latter group are much more likely to be eligible. Because there are only about 150 counties per year that fall into each group, I conduct the DDD analysis on individual-level births data (instead of cell data) in these two groups of counties. The results from this robustness check are generally consistent with my main results on birth outcomes despite substantial reductions in sample sizes that limit test power, and are available upon request.

An additional issue with the conditional probability measure is that it relies on total county-year employment. It is possible that differential changes in county-level employment that do not affect eligibility for FMLA are driving the results. To alleviate this concern, I use county-year population projections from the U.S. Census to estimate unconditional probabilities of employment in a firm with 50 or more employees. In particular, I use the county-year population estimates of individuals aged 15–64 instead of county-year total employment from the CBP as the denominator of the eligibility measure. To reduce measurement error, I drop counties that have ever had a year with a population of less than 1000 people over 1989–1997. Table 9 presents the results from these DDD models. Reassuringly, these results are quite similar to those in Tables 3 and 4.

Table 9.

Effects of FMLA Using Unconditional Probability of Eligibility

	Birth Weight (g)	Gestation (weeks)	LBW	Premature	Total Infant Mortality	Infant Mortality: 28 days – 1 year	Infant Mortality: <28 days
WHOLE SAMPLE	4.9278** (2.0877)	0.0252+ (0.0149)	−0.0021*** (0.0005)	−0.0028+ (0.0015)	−0.0005** (0.0002)	−0.0001 (0.0001)	−0.0005** (0.0002)
N	5,474,178	5,464,434	5,474,178	5,464,434	182,895	182,895	182,895
COLLEGE-ED AND MARRIED SAMPLE	6.0616** (2.6420)	0.0214+ (0.0107)	−0.0026** (0.0011)	−0.0024** (0.0010)	−0.0006** (0.0003)	−0.0002 (0.0002)	−0.0004+ (0.0002)
N	669,830	669,270	669,830	669,270	59,877	59,877	59,877
LESS THAN COLLEGE AND SINGLE SAMPLE	5.6331+ (3.2004)	0.0063 (0.0119)	−0.0012 (0.0008)	−0.0025+ (0.0014)	−0.0003 (0.0004)	−0.0001 (0.0002)	−0.0001 (0.0003)
N	2,050,765	2,045,790	2,050,765	2,045,790	50,458	50,458	50,458

Notes: The results presented here list the coefficients on the DDD effects of the FMLA on each of the outcomes listed in the top row. Likely eligibility is calculated using the unconditional probability of employment in a firm with 50 or more employees for a given county and year. This probability equals the ratio of approximate employment in all firms with 50 or more employees to the population aged 15–64 in each county and year. Counties that have ever had a year with population less than 1000 people over 1989–1997 are omitted. Please refer to notes under Tables 3 and 4 for details about the samples, controls, and estimation methods. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

Another concern is that the large effects on infant mortality are driven by selection into motherhood based on maternal characteristics. For instance, if more college-educated and married mothers choose to give birth as a result of FMLA, then the pool of healthier babies born to these mothers might increase, hence driving down the infant mortality rate. Similarly, selection based on other maternal characteristics may be driving the results. To check, I run regression (1.2) with all available maternal characteristics as dependent variables. Appendix Table 4 presents the results of this exercise. None of the coefficients is statistically significant except for the one in the regression of an indicator for the mother having a high school degree. However, there are no effects on any of the other educational categories, or the age, race, or marital status categories. These results suggest that the effects of FMLA are not driven by selection into motherhood based on observable characteristics, thus providing more support for the validity of my identification strategy.

One more important concern is that FMLA led to endogenous selection of firms into firm-size categories. For instance, one might suppose that lower-quality firms or firms with less financial capital may choose to lower employment and move below the 50-employee firm-size cut-off to avoid bearing the costs of providing FMLA leave. As a result, after the FMLA, women in counties with a higher probability of employment in a firm with 50 or more employees would also be more likely employed in a better or wealthier firm. Thus, there could potentially be omitted variables that drive the results on birth outcomes and infant mortality for mothers in likely-eligible counties, in treatment states after FMLA.

While I cannot observe firm characteristics or firm behavior, I can test whether the FMLA induced changes to the county-year firm size distribution. I estimate equation (1.1) with my measure of the conditional probability of employment in a firm with 50 or more employees as the dependent variable. If women giving birth in treatment states after FMLA did not experience a different likelihood of employment in a firm with 50 or more employees, then there is evidence that FMLA did not lead to any changes in the firm size distribution during the time period of my analysis, thus making it unlikely that my results are driven by endogenous sorting of firms. Appendix Table 5 presents the estimates of the key coefficient of interest for the whole sample, and for the two sub-samples that I analyze. Notably, this coefficient is not statistically significant at any conventional level in any of the samples. Given that my main results rely on this measure of conditional probability, it is reassuring that it is unlikely to suffer from endogenous selection issues.

8 Conclusion

High female labor force participation rates in the United States call attention to the importance of maternity leave policies. Unlike men, women who have children must take at least some time off from working during childbirth. Hence policies that ensure their job security during this time period are crucial for women's careers, health, and overall well-being. These benefits alone provide support for the enactment and continuation of maternity leave policies in this country.

The effects of maternity leave on children, however, are not well established. Existing studies in Canada, Germany, and Sweden do not find significant effects of maternity leave on either early childhood or later outcomes. Studies in the U.S. find some negative effects of maternal work during a child's first year of life, but do not evaluate current maternity leave policies. My study contributes to this literature as the first to analyze the causal effects of unpaid maternity leave due to FMLA on children's birth and infant outcomes. I use difference-in-difference and difference-in-difference-in-difference methodology and consider numerous outcomes. I also conduct sub-group analyses on children of college-educated and married women, as these are the women who are likely to be eligible under FMLA and able to take unpaid leave, and on children of less-educated and single mothers.

I find that for the college-educated and married sub-sample of mothers, FMLA led to small increases in birth weight, decreases in the likelihood of a premature birth, and considerable decreases in infant mortality rates that are driven by decreases in deaths from congenital anomalies and ill-defined causes. I also find the policy affected parity — there is an increase in first-parity births, which is offset by a decrease in later-parity births among all mothers. However, the effects on parity are too small to produce meaningful selection bias for the main results on infant health. Notably, there are no effects on birth outcomes or infant mortality rates for children of less-educated and single mothers.

These results suggest that for mothers who were able to take advantage of the full length of leave, the policy's effects on infant mortality are largely driven through increases in maternal time at home, and ability to provide and seek prompt care for an ill child during the first few months of life. Maternal stress and mental health during pregnancy and after childbirth are not affected, at least as measured by child outcomes that are likely impacted by maternal well-being.

The consistent finding of significant effects for the sub-sample of college-educated and married mothers and no effects for the sub-sample of less-educated and single mothers implies that FMLA may have increased disparities in early childhood health between children from different socio-economic backgrounds. Further, back-of-the-envelope cost-benefit calculations suggest that unpaid maternity leave may not be the most cost-effective way to help working mothers and their children. In particular, businesses and their employees bear the costs of FMLA's unpaid leave because of lost productivity, provision of health benefits while workers are on leave, foregone wages and benefits for employees, and administrative burdens. In 2004, FMLA cost approximately $21 billion (Neese et al., 2009). However, the benefits of FMLA are only concentrated among mothers and children from high socio-economic backgrounds. In 2004, my results suggest that among the 1,011,125 births by college-educated and married mothers in the U.S., 607 of these babies were saved by FMLA. This implies that FMLA costs almost $35 million per life saved. Given that the incidence of poor birth outcomes and infant mortality is higher among women from lower socio-economic backgrounds, maternity leave policies that cover mothers and children from all backgrounds may result in much greater benefits that could outweigh the extra costs from covering more working women.

Children of poor, single and low-educated working mothers are a key vulnerable population that was not reached by the FMLA. However, these children and their families may benefit the most from policies that enable their mothers to take time off work during their early life without substantial losses in income. These mothers are often forced to work immediately after childbirth, and their newborn children are then placed in low-quality childcare. Their children already stand at a disadvantage for their later-life opportunities as they are born into low socio-economic status families, and lack of maternal time during their first few months of life may exacerbate this disadvantage. Thus, if policymakers are concerned with decreasing disparities in child health and well-being between children of different backgrounds, they need to consider the fact that an unpaid maternity leave policy may actually increase disparities because it only benefits those mothers who can afford to take it. On the other hand, paid maternity leave policies (such as those in California and New Jersey) may allow poor, single and working mothers to care for their newborn children at home, to seek prompt medical care when needed, and to develop a closer bond with them, thereby saving their lives and improving their life chances from the start.

Appendix Table 1.

Summary Statistics by County-Year Eligibility Status

County Characteristics:	CONTROL STATE AND LIKELY INELIGIBLE	CONTROL STATE AND LIKELY ELIGIBLE	TREATMENT STATE AND LIKELY INELIGIBLE	TREATMENT STATE AND LIKELY ELIGIBLE
Percent White	88.73%	82.85%	85.01%	80.72%
Percent Black	2.69%	9.18%	9.80%	15.87%
Percent Female Aged 18–44	20.02%	21.82%	19.63%	21.22%
Percent Females Aged 18–44 Employed	50.79%	54.96%	47.82%	52.29%
Percent Females Married	57.30%	51.68%	57.71%	53.65%
Percent Urban	30.59%	63.51%	16.35%	43.39%
Percent Females Aged 25+ College-Educated	15.26%	18.63%	12.69%	14.69%
Percent Below Poverty Line	12.75%	11.76%	17.96%	15.13%
Unemployment Rate	6.25%	5.95%	5.76%	5.63%

Notes: Data on county characteristics is from the 1990 US Census, while data on the unemployment rate is from the BLS. Treatment states that had no maternity leave laws prior to FMLA. Control states had some kind of maternity leave law prior to FMLA. In every year, likely ineligible counties have the likelihood of employment in a firm with 50 or more employees at or below the median, while likely eligible counties have the likelihood of employment in a firm with 50 or more employees above the median.

Appendix Table 2.

Effects of FMLA on Birth Outcomes and Infant Mortality Among College-Educated and Married Mothers: Different Specifications

	Birth Weight (g)					Premature Birth					Infant Mortality Rate
	(1)	(2)	(3)	(4)	(5)	(1)	(2)	(3)	(4)	(5)	(1)	(2)	(3)	(4)	(5)
Post	−12.3795+ (6.4978)	−11.9781+ (6.2551)	−13.4920** (5.9244)	2.0537 (2.9542)	4.6993 (3.0845)	0.0081*** (0.0013)	0.0077*** (0.0012)	0.0075*** (0.0013)	0.0010 (0.0009)	−0.0000 (0.0009)	−0.0009*** (0.0001)	−0.0006*** (0.0001)	−0.0006*** (0.0001)	−0.0003** (0.0001)	−0.0003** (0.0001)
Treatment State	−26.1627+ (13.0256)	−30.8211** (11.4788)	−33.1880** (11.5572)	−43.7308*** (5.0283)	−15.5693 (23.8961)	0.0073*** (0.0015)	0.0074*** (0.0012)	0.0043** (0.0015)	0.0056** (0.0025)	−0.0148*** (0.0037)	0.0015*** (0.0003)	0.0002 (0.0002)	0.0004+ (0.0002)	0.0005+ (0.0003)	−0.0008** (0.0003)
Likely Eligible	−45.6306*** (4.9272)	−26.4112*** (2.7280)	−15.8827*** (3.6000)	−8.9766** (3.4590)	−8.2797** (3.7318)	0.0030** (0.0010)	0.0008 (0.0009)	0.0019+ (0.0011)	0.0011** (0.0005)	0.0012** (0.0006)	−0.0008*** (0.0002)	−0.0005** (0.0002)	−0.0002 (0.0002)	−0.0003+ (0.0002)	−0.0003** (0.0001)
Post*Likely Eligible	−6.6550 (4.5149)	−4.7946 (5.1525)	−3.8746 (4.8740)	0.2427 (2.6041)	−1.4702 (3.4632)	0.0013 (0.0012)	0.0010 (0.0013)	0.0012 (0.0014)	0.0002 (0.0010)	0.0002 (0.0011)	0.0000 (0.0001)	0.0002 (0.0002)	0.0001 (0.0001)	0.0001 (0.0001)	0.0001 (0.0001)
Post*Treatment State	−12.9054+ (6.7856)	−12.5691+ (6.6324)	−11.6487+ (6.3241)	−9.9532** (3.4239)	−14.3728*** (3.8499)	0.0028+ (0.0014)	0.0028** (0.0013)	0.0028+ (0.0015)	0.0018+ (0.0010)	0.0038** (0.0014)	0.0002 (0.0002)	0.0002 (0.0002)	0.0001 (0.0002)	0.0002 (0.0002)	0.0003 (0.0003)
Post*Treatment State*Likely Eligible (DDD)	6.1276 (5.2102)	6.2719 (5.7143)	6.8207 (5.4416)	6.1781+ (3.2086)	9.1972** (3.7886)	−0.0029+ (0.0015)	−0.0030+ (0.0016)	−0.0032+ (0.0017)	−0.0026** (0.0013)	−0.0029** (0.0014)	−0.0005** (0.0002)	−0.0006** (0.0002)	−0.0005** (0.0002)	−0.0004** (0.0002)	−0.0006*** (0.0002)
N	679,557	671,556	671,425	671,425	671,425	678,902	670,997	670,866	670,866	670,866	60,011	59,668	59,668	59,668	59,668
R-squared	0.0072	0.1264	0.1297	0.1491	0.1500	0.0041	0.0265	0.0275	0.0306	0.0315	0.0312	0.0601	0.0642	0.0836	0.0895
Maternal and child controls	No	Yes	Yes	Yes	Yes	No	Yes	Yes	Yes	Yes	No	Yes	Yes	Yes	Yes
County controls	No	No	Yes	Yes	Yes	No	No	Yes	Yes	Yes	No	No	Yes	Yes	Yes
Year of birth fixedeffects	No	No	No	Yes	Yes	No	No	No	Yes	Yes	No	No	No	Yes	Yes
Month of birth fixed effects	No	No	No	Yes	Yes	No	No	No	Yes	Yes	No	No	No	Yes	Yes
State fixed effects	No	No	No	Yes	Yes	No	No	No	Yes	Yes	No	No	No	Yes	Yes
State-year interactions	No	No	No	No	Yes	No	No	No	No	Yes	No	No	No	No	Yes

Notes: Each column is a separate regression. Please refer to Tables 3 and 4 for details about units of analysis, controls, and samples. Robust standard errors are clustered on the state. All regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

Appendix Table 3.

Placebo Effects in Difference-in-Difference Model for College-Educated and Married Mothers

	Birth Weight (g)	Gestation (weeks)	LBW	Premature	Total Infant Mortality	Infant Mortality: 28 days – 1 year	Infant Mortality: <28 days
Treatment State * 1991 (placebo 1)	−4.0925 (2.7573)	−0.0300** (0.0089)	0.0014+ (0.0008)	0.0021** (0.0007)	−0.0000 (0.0001)	0.0000 (0.0001)	−0.0001 (0.0001)
Treatment State * 1992 (placebo 2)	−3.6875 (2.2018)	−0.0195** (0.0083)	0.0009 (0.0006)	0.0007 (0.0008)	−0.0000 (0.0002)	0.0002** (0.0001)	−0.0002 (0.0002)
Treatment State * 1993+ (DD effect)	−5.3511+ (2.8381)	−0.0222 (0.0163)	0.0018** (0.0008)	0.0002 (0.0011)	−0.0002** (0.0001)	−0.0000 (0.0001)	−0.0001 (0.0001)
N	672,850	672,290	672,850	672,290	59,683	59,683	59,683

Notes: The results presented here list the coefficients on the DD specifications which include placebo tests for treatment effects in the two years prior to FMLA. Please refer to notes under Tables 3 and 4 for details about controls and estimation methods. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

Appendix Table 4.

Selection into Motherhood

	Mom <19 yrs old	Mom 19–24 yrs old	Mom 25–34 yrs old	Mom 35–44 yrs old	Mom has < HS education	Mom has HS education	Mom has some college	Mom is non- Hispanic white	Mom is black	Mom is Hispanic	Mom is unmarried
DDD	0.0009 (0.0020)	−0.0022 (0.0036)	−0.0017 (0.0036)	0.0031 (0.0023)	0.0063 (0.0116)	−0.0114** (0.0053)	−0.0008 (0.0050)	0.0030 (0.0056)	0.0032 (0.0052)	−0.0029 (0.0155)	0.0015 (0.0067)
N	185,374	185,374	185,374	185,374	184,070	184,070	184,070	185,374	185,374	185,374	185,374
Year of birth fixed effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Month of birth fixed effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
State fixed effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
State-year interactions	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

Notes: The coefficients listed here are from DDD regressions that use the variables listed in the top row as dependent variables. The units of analysis are county-year-birth month cells. Cells with fewer than 25 births are omitted from the analysis. All regressions control for the unemployment rate in the state, year, and month of birth. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

Appendix Table 5.

Effects of FMLA on County-Level Firm Size Distribution

Outcome: Conditional Probability of Employment in Firm with 50+ Employees
	WHOLE SAMPLE	COLLEGE-ED AND MARRIED	LESS THAN COLLEGE AND SINGLE
Treatment State *
Post-FMLA	0.0008 (0.0022)	0.0007 (0.0017)	0.0004 (0.0030)
N	5,487,100	671,783	2,054,466

Notes: The results presented here list the coefficients on the DD effects on the county-year level conditional probability of employment in a firm with 50 or more employees estimated using the CBP. Please refer to notes under Table 3 for details about the sample, controls, and estimation methods. Robust standard errors are clustered on the state. All the regressions are weighted by the cell population.

Significance levels:

⁺p<0.10

^**p<0.05

^***p<0.001

Appendix Figure 1.

Comparing Weighted Average Total Employment with Total Employment

Notes: This figure plots the total employment in each county and year calculated using the formula in the text in Section 1.4 versus the actual total employment in the data.