Load-bearing properties of minimal-invasive monolithic lithium disilicate and zirconia occlusal onlays: finite element and theoretical analyses

Abstract

Objectives

The aim of this study was to test the hypothesis that monolithic lithium disilicate glass-ceramic occlusal onlay can exhibit a load-bearing capacity that approaches monolithic zirconia, due to a smaller elastic modulus mismatch between the lithium disilicate and its supporting tooth structure relative to zirconia.

Methods

Ceramic occlusal onlays of various thicknesses cemented to either enamel or dentin were considered. Occlusal load was applied through an enamel-like deformable indenter or a control rigid indenter. Flexural tensile stress at the ceramic intaglio (cementation) surface—a cause for bulk fracture of occlusal onlays—was rigorously analyzed using finite element analysis and classical plate-on-foundation theory.

Results

When bonded to enamel (supported by dentin), the load-bearing capacity of lithium disilicate can approach 75% of that of zirconia, despite the flexural strength of lithium disilicate (400 MPa) being merely 40% of zirconia (1000 MPa). When bonded to dentin (with the enamel completely removed), the load-bearing capacity of lithium disilicate is about 57% of zirconia, still significantly higher than the anticipated value based on its strength. Both ceramics show slightly higher load-bearing capacity when loaded with a deformable indenter (enamel, glass-ceramic, or porcelain) rather than a rigid indenter.

Significance

When supported by enamel, the load-bearing property of minimally invasive lithium disilicate occlusal onlays (0.6 to 1.4 mm thick) can exceed 70% of that of zircona. Additionally, a relatively weak dependence of fracture load on restoration thickness indicates that a 1.2 mm thin lithium disilicate onlay can be as fracture resistant as its 1.6 mm counterpart.

1. Introduction

Esthetics and preservation of tooth structure are the primary driving forces in modern restorative dentistry [1, 2]. Bonded feldspathic porcelain and glass-ceramic veneers have become the treatment of choice for restorations of anterior teeth, with proven long-term success [3]. Superior esthetics, diminished gingival inflammation, and reduced risk for secondary caries are cited as the benefits of these restorations [4, 5]. However, fracture of bonded ceramics becomes a concern when considering the same treatments for posterior teeth. This is particularly the case with restorations covering the entire occlusal surface. To meet the load-bearing requirements, the current recommendation for posterior porcelain restoration thickness is 1.5 mm to 2.0 mm [6, 7]. With the development of stronger ceramics, thinner more conservative restorations can be made to meet the posterior load requirements.

The rehabilitation of patients with increased chewing forces due to bruxism or parafunctions represent a particular challenge in restorative dentistry [8]. In most studies on all-ceramic restorations, patients with parafunctions were excluded due to the increased risk of fracture. Restorations with metal occulsal surfaces were the standard of care for these patients; however, these restorations did not meet the esthetic demands of patients [9].

Zirconia, the strongest and toughest of all dental ceramics, with a flexural strength of 800 MPa to 1200 MPa [10, 11] and a fracture toughness of 6 MPa·m^1/2 to 8 MPa·m^1/2 [10], meets the mechanical requirements for high stress-bearing posterior restorations. Zirconia, however, is a non-adhesive restoration and has limited translucency and shade options. Lithium disilicate glass-ceramics, the strongest and toughest of the glass-ceramics available, have moderate flexural strength (360 MPa to 440 MPa) [12] and fracture toughness (2.5 MPa·m^1/2 to 3 MPa·m^1/2) [13], yet have excellent translucency and shade matching options [14, 15]. These glass ceramics can be bonded to enamel and dentin through hydrofluoric acid etching and silanization. Additionally, glass ceramics prevent excessive wear of the opposing dentition due to their similar modulus and hardness to enamel. Therefore, it would be most desirable if lithium disilicate glass-ceramics could be found to have similar load-bearing capacities to zirconia through fine tuning of application parameters such as ceramic thickness, bonding substrate, and cement modulus and thickness.

The thickness of the restoration is dictated by the amount of tooth preparation required to remove disease, obtain natural looking contours, rehabilitate occlusion, promote periodontal health, and/or to meet the physical requirements of the restorative material. Thinner, conservative occlusal veneers provide the advantage of enamel bonding which offers superior bond strength as compared to dentin [16, 17]. However, thin ceramics have low fracture resistance. One way to overcome this is to reduce the modulus ratio between the ceramic and tooth support (enamel and/or dentin) [18, 19]. Thus, there exists an optimal ceramic thickness and ceramic/substrate modulus ratio that yields excellent load-bearing capacity of ceramic restorations. This study compares the load-bearing capacity of monolithic lithium disilicate veneers of various thicknesses to their zirconia counterparts, when bonded onto enamel or dentin, and loaded with a deformable or rigid indenter using finite element stress analysis and the classical plate-on-foundation theory.

2. Materials and methods

2.1. Ex vivo occlusal model

We shall first establish an occlusal model for stress analysis in posterior ceramic restorations using classical plate-on-foundation theory and finite element analyses (FEA). Ceramic occlusal veneers and onlays are bonded to and supported by enamel or dentin (Fig. 1). While chewing, high flexural tensile stresses may develop on the ceramic intaglio (cementation) surface directly below the loaded area (Fig. 1b) [20]. When these tensile stresses exceed the flexural strength of the ceramics, radial fracture occurs in the ceramic subsurface, at its interface with the cement. Clinically, this radial fracture can cause the bulk failure of all-ceramic restorations [20, 21]. The stress solution in a ceramic restoration is complex and is best solved by finite element methods. Thus, FEA utilizing axis-symmetrical models of multilayer structures loaded with a blunt indenter (Figs. 1c and d) have been widely used to determine the flexural tensile stresses in the ceramic restorations [21-24]. The accuracy and reliability of such FEA simulation have been validated by experimentation and theory [20, 24-27]. Below we outline the key points of the plate-on-foundation theory and describe the details of the FEA method utilized in this study. But first, we define the parameters of the multilayer models used for our FEA and theoretical analyses.

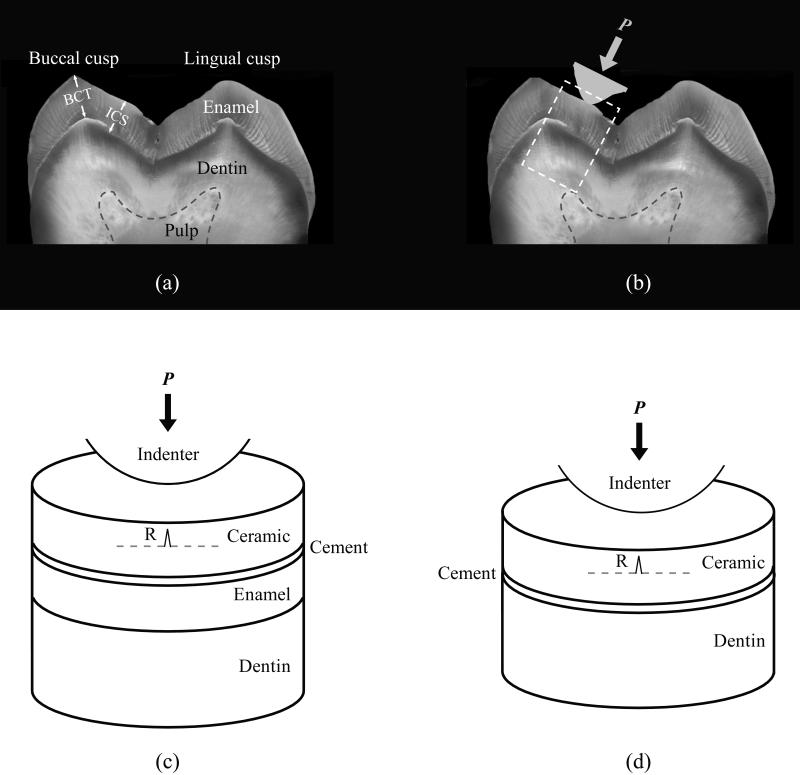
Figure 1.

Ex vivo occlusal model. (a) Optical image of a cross-section through the mesial cusp region of a human mandibular second molar indicating the enamel thickness used in this study. BCT: Buccal cusp thickness (2.1 mm); ICS: Enamel thickness in the internal cusp slope region (1.8 mm). (b) Occlusal contact on the functional cusps of a mandibular molar. (c) and (d) Schematic representations of the box highlighted area in (b), used in finite element and analytical stress analyses for blunt loading of ceramic veneer bonded to enamel and dentin, respectively. The symbol P represents load, and R represents cementation surface radial cracks.

2.2 Defining the parameters

The distribution of enamel thickness in posterior molars is known to correspond to the functional demands of a given cusp [28]. Functional cusps (maxillary lingual cusps and mandibular buccal cusps) possess thicker enamel than corresponding nonfunctional cusps (maxillary buccal cusps and mandibular lingual cusps). The nominal thicknesses of the cusp tip and internal cusp slope for maxillary lingual cusps [29] and mandibular buccal cusps [30] of posterior molars are approximately 2.1 mm and 1.8 mm, respectively. For our FEA and theoretical analyses, we specified the enamel thickness at the internal cusp slope (ICS) of a posterior molar to be 1.8 mm (Fig. 1a).

The elastic modulus of enamel varies within a molar. In general, enamel modulus increases from about 65 GPa near the enamel-dentin junction to 91 GPa at the occlusal surface [31, 32]. The elastic modulus also varies with the orientation of enamel owing to its anisotropic nature. Careful investigations using nanoindentations with a Berkovich indenter revealed the values of elastic modulus as 72.71 ± 2.01 GPa and 77.73 ± 1.39 GPa for enamel sectioned in the directions perpendicular and parallel, respectively, to the long axis of a tooth [33]. These findings suggested that a nominal enamel modulus of 70 GPa may be utilized for our current FEA models. Other researchers have also used a single elastic modulus value (65 GPa) in a similar range for FEA stress analysis of ceramic crowns supported by nature teeth [23].

We designated the modulus and thickness of dentin to be 18 GPa [20] and 4 mm, respectively. We defined the modulus and thickness of the adhesive cement to be 8.6 GPa (Variolink II, Ivoclar Vivadent, Schaan Liechtenstein) [19] and 50 μm [34, 35], respectively.

Since a typical radius of an antagonistic enamel cusp tip is several millimeters [36], we set our indenter radius r = 3.2 mm. We utilized a deformable indenter with the elastic modulus of 95 GPa to simulate glass-ceramics, porcelain, or enamel (at the occlusal surface) for FEA simulation. To elucidate the effect of indenter modulus on the remote flexural tensile stresses at the ceramic cementation surface and to validate our analysis, we also conducted FEA stress analysis using a rigid indenter.

We applied the occlusal load at the top surface of ceramic restorations through a spherical indenter and determined the flexural tensile stress at the ceramic cementation surface. The thickness range of the ceramic restorations examined was 0.2 mm to 2.0 mm, covering a typical thickness range of 0.4 mm to 1.6 mm for occlusal veneers and onlays [7, 16]. Critical loads for cementation flexural radial fracture, also known clinically as bulk fracture [19, 20], were recorded. Relevant material properties and various layer thickness combinations used for elastic plate analysis and FEA simulation are listed in Table I.

Table I.

Material properties and various layer thicknesses used for FEA simulation and analytical analysis.

	Lithium Disilicate (IPS e.max Press)	Zirconia (3Y-TZP)	Cement (Variolink II)	Enamel	Dentin
Elastic modulus, E (GPa)	95	210	8.6	70	18
Flexural strength, σ (MPa)	400	1000	110	–	–
Poisson's ratio	0.23	0.30
Layer thickness (mm)	0.20	0.20	0.05	1.55	4.00
	0.30	0.30	0.05	1.45	4.00
	0.40	0.40	0.05	1.35	4.00
	0.50	0.50	0.05	1.25	4.00
	.	.	.	.	.
	.	.	.	.	.
	.	.	.	.	.
	1.70	1.70	0.05	0.05	4.00
	1.80	1.80	0.05	0	3.95
	1.90	1.90	0.05	0	3.85
	2.00	2.00	0.05	0	3.75

2.3. Theory of plate-on-foundation

Consider a ceramic plate of thickness d cemented to dentin, and loaded on top with a rigid sphere (Fig. 1d). Since, clinically, bulk fracture is deemed as one of the most common failure modes of all-ceramic restorations [20, 21], we concentrate on the flexural radial fracture originating from the ceramic intaglio surface. Near-contact, occlusal surface cone cracking is not considered as a critical failure mode. The critical load, P_R, for cementation surface flexural radial fracture is given by [37, 38]:

$$P_{\mathrm{R}}=B\sigma d^2∕\text{log}(CE∕E^{\ast })$$ (1)

where σ and E are the flexural strength and elastic modulus, respectively, of the ceramic, and B (= 1.35) and C (≈ 1) are dimensionless constants [26]. E* is the effective modulus of the cement/dentin layers, and can be described by a simple, empirical function that has a basis in contact mechanics [37, 39, 40]:

$$E^{\ast }=E_{\mathrm{c}}{(E_{\mathrm{s}}∕E_{\mathrm{c}})}^L$$ (2)

where E_c and E_s are the modulus of cement and dentin respectively. L is an experimentally determined dimensionless function [37]:

$$L=\text{exp}\{-{[\alpha +\beta \text{log}(h∕d)]}^{\gamma }\}$$ (3)

where α = 1.18, β = 0.33, γ = 3.13. d and h are thicknesses of the ceramic and cement layer, respectively. Utilizing Eqs. 1 to 3, we can compute the critical loads for ceramic plates of various thicknesses cemented to dentin. Eqns. 1 and 3 have been validated by extensive experimentation [37].

2.4. Finite element modeling

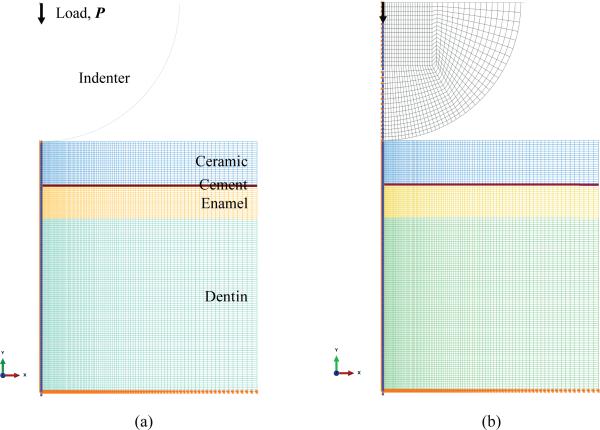
FEA modeling of the frictionless normal contact of multilayered mediums by rigid and deformable spheres of radius 3.2 mm was performed using a commercial code ABAQUS. Taking advantage of axis-symmetry of both the indenter and the specimen, only a cross section of a ball and specimen was modeled. The deformable indenter was modeled with a flat rigid plate at the top. A cylindrical multilayer specimen model of radius 5 mm was selected (Figs. 1c and d). The interface between the connected layers was modeled by assuming that the adjacent layers were tied together. Both the deformable indenter and the specimen mesh were constructed with quadrilateral four-node axisymmetric elements, CAX4. A fine mesh was used in the vicinity of the contact region, insuring that at least 4 elements with linear shape functions were in contact with the indenter. The meshes were then gradually coarsened as the distance from the contact region increased. However, for the thin cement layer, a fine mesh was used throughout. Examples of detailed FE mesh and boundary conditions for a four-layer (ceramic/cement/enamel/dentin) model loaded with a rigid or deformable indenter are shown in Figs. 2a and b. The bottom of the specimen was restricted from moving downward; the centerline of the specimen and deformable indenter was restricted from moving horizontally. An indentation depth was added to the reference point of either the rigid spherical indenter or the rigid plate atop the deformable indenter.

Figure 2.

Details of the FE mesh generated from a ceramic/cement/enamel/dentin four-layer model loaded with a (a) rigid and (b) deformable indenter.

In the current analysis, all the materials represented in the FEA models were considered homogeneous, linearly elastic and isotropic, assumptions that are regularly applied with continuum mechanics models [41, 42]. All material components were assumed to only undergo elastic deformation. This is because ceramic veneers undergo only very limited flexural plastic deformation prior to fracture. The stress shielding effect of the overlay ceramic veneers prevents the enamel and dentin from entering the plastic domain. The bond between various layers was assumed to stay intact with no sliding or delamination before the ceramic fracture. This is because our in situ observations of experimentation on Hertzian indentation radial fracture in ceramic plates cemented to compliant substrates revealed that delamination never occurs before the ceramic fracture, rather it arises after the fracture and upon unloading [43-45].

We focused on flexural tensile stress at the cementation surface of the ceramic and normal to the load direction rather than the Von Mises stress. The latter is an equivalent stress value computed by combining three principal stresses, which is most applicable to ductile materials. This was done because flexural tensile stress is the sole determinant of the load-bearing property of ceramics, and because failure cracks arising from the cementation surface of ceramic restorations remain one of the primary failure modes observed clinically [21, 46, 47].

3. Results

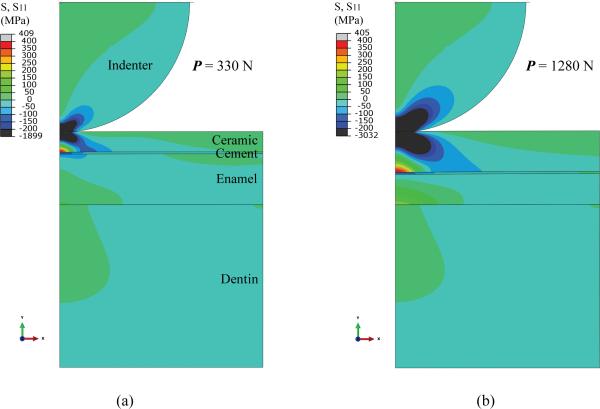
Fig. 3 shows the contour of FEA calculated stresses in lithium disilicate onlay/cement/enamel/dentin assemblies, loaded with a deformable indenter of radius r = 3.2 mm and elastic modulus E = 95 GPa. The indentation depth was increased stepwise until the maximum tensile stress in the lithium disilicate onlay exceeded its flexural strength of 400 MPa. Two examples were selected: ultrathin (0.5 mm) and thin (1.0 mm) lithium disilicate onlays cemented to enamel supported by dentin. In both cases, a large component of compression was observed in the ceramic layer under the contact area (shaded in blue or black); only a modest tension was perceived outside the contact area (shaded in green). The maximum tensile stress was, however, located in the ceramic intaglio surface at the cement interface, directly below the loaded area (shaded in red or grey). It is important to note that stresses in the cement layer were predominantly compressive in nature, owing to the stress shielding effect of the ceramic overlay and the low elastic modulus of cement relative to enamel. Some tensile stresses were also revealed in the enamel subsurface. However, the magnitude of these tensile stresses was much smaller relative to that observed in the ceramic onlay, due to the stress shielding effect of the ceramic overlay.

Figure 3.

FEA-generated stresses in lithium disilicate onlays of thicknesses (a) 0.5 mm and (b) 1.0 mm cemented to enamel backed by dentin, loaded with a deformable indenter of radius, r = 3.2 mm, and elastic modulus, E = 95 GPa.

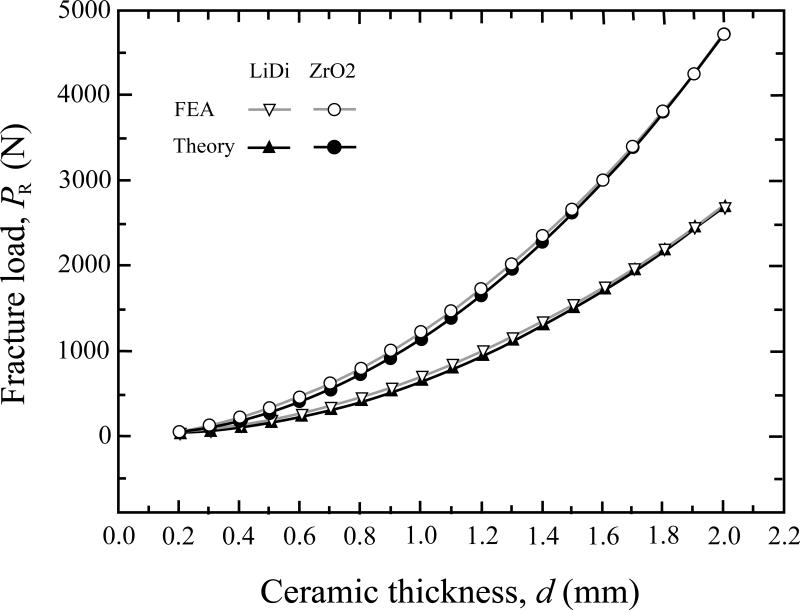
Critical fracture load, P_R, for the onset of cementation radial fracture (bulk fracture) of ceramic occlusal veneers is plotted in Fig. 4 as a function of ceramic thickness, d. Ceramic plates (lithium disilicate or zirconia) were bonded to enamel (Fig. 1c) or dentin (Fig. 1d), and loaded with a rigid indenter. Fig. 4 compares the P_R – d curve generated by FEA (open symbols) with that predicted by theory (solid symbols) using Eqs. 1 to 3 for ceramic plates luted to dentin; an excellent match between the two data sets lends confidence to the accuracy of the FEA.

Figure 4.

Comparison of ceramic fracture load versus thickness relationship generated by FEA simulation and theoretical analysis. Ceramic plates of various thicknesses were bonded to dentin and loaded at the top surface with a rigid indenter. Open symbols: FEA generated data; solid symbols: theoretical predictions. Triangles: lithium disilicate (LiDi); circles: zirconia (ZrO₂).

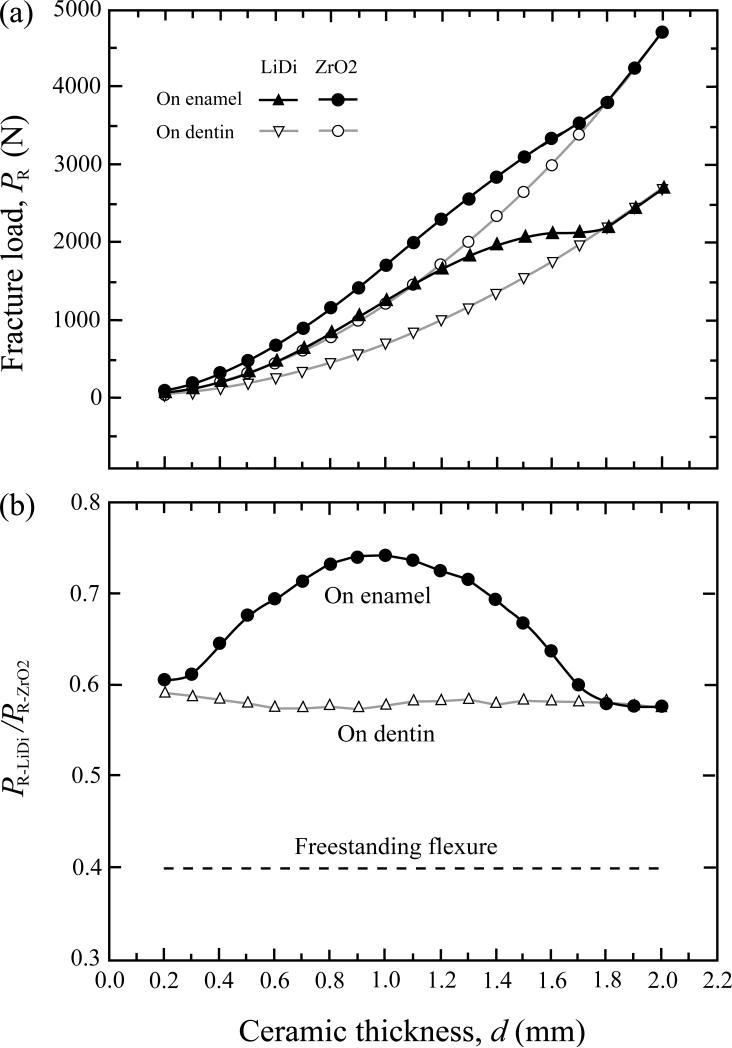
To elucidate the effect of elastic modulus of substrate material on the load-bearing property of ceramics, FEA P_R – d data for ceramic/cement/dentin (open symbols) is compared with that for ceramic/cement/enamel/dentin (solid symbols) in Fig. 5a. In the latter case, the initial enamel thickness was assumed to be 1.8 mm and an occlusal reduction was prepared to accommodate the thicknesses of ceramic plate and cement layer; details of thickness combinations for various constituents are summarized in Table I. For a given thickness, the fracture load was significantly higher for ceramics supported by enamel relative to those supported by dentin. However, such a strengthening effect diminished as the ceramic thickness increased to 1.6 mm or thicker, due to concurrent reduction of enamel thickness. The two P_R – d curves for ceramic/cement/enamel/dentin and ceramic/cement/dentin eventually coincided just as the ceramic thickness reached 1.8 mm, upon which the enamel layer had been completely removed. In addition, the dependence of fracture load on ceramic thickness is less pronounced for lithium disilicate and zirconia onlays supported by enamel relative to their dentin-supported counterparts (Fig. 5a). This decrease in fracture load dependence on thickness is especially the case for lithium disilicate onlays in thicknesses ranging from 0.8 mm to 1.7 mm.

Figure 5.

Load-bearing capacity of ceramics bonded to and supported by dentin loaded with a rigid indenter. (a) Ceramics luted to enamel backed by dentin (solid symbols) relative to those bonded to dentin alone (open symbols). Triangles: lithium disilicate (LiDi); circles: zirconia (ZrO₂). (b) Fracture load ratio between lithium disilicate and zirconia as a function of ceramic thickness and substrate materials. P_R-LiDi and P_R-ZrO2 denote fracture loads for lithium disilicate and zirconia, respectively. Solid circles: ceramics luted to enamel backed by dentin. Open triangles: ceramics luted to dentin. Dashed line: ceramics in freestanding flexure.

To elucidate the effect of elastic modulus mismatch between ceramic and the substrate on the load-bearing property of ceramics, the fracture load ratio, P_R-LiDi/P_R-ZrO2, is plotted as a function of ceramic layer thickness for ceramics supported by enamel, dentin, or without support (i.e. freestanding flexure, such as a 4-point-bend or biaxial test) in Fig 5b. Fracture load for lithium disilicate increased from about 40 % of that for zirconia in freestanding flexure, to about 57 % for supported by dentin, and to about 75 % for supported by enamel.

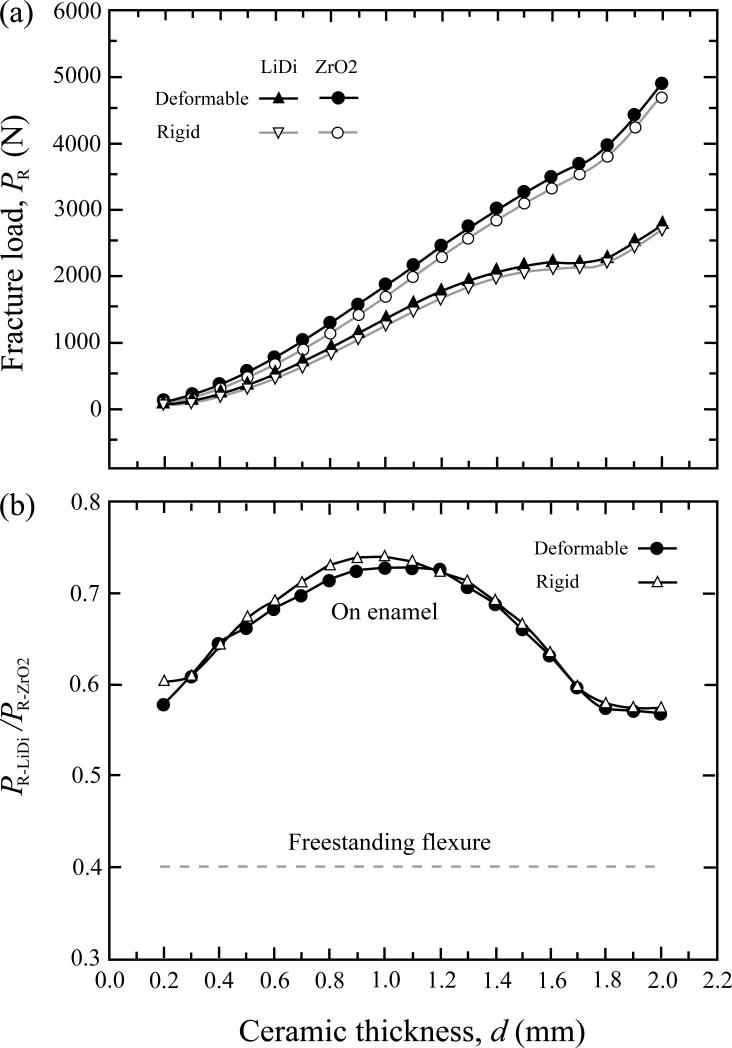
In a clinical setting, onlays and occlusal veneers are occluding against natural dentition, porcelain, or glass-ceramics alike. These materials all have finite elastic modulus values (Table I). Thus, the real-life indenters (antagonist cusps) are non-rigid and deformable. FEA generated P_R – d data for ceramics supported by enamel loaded with a deformable indenter are compared with those produced by a rigid indenter (Fig. 6a). A small increase in fracture load was observed for specimens loaded with a deformable indenter relative to its rigid counterpart.

Figure 6.

Load-bearing capacity of ceramics on enamel backed by dentin loaded with a deformable indenter (solid symbols) relative to a rigid indenter (open symbols). (a) Fracture loads for lithium disilicate (triangles) and zirconia (circles), and (b) fracture load ratio between lithium disilicate and zirconia as a function of ceramic thickness. Dashed line represents fracture load ratio for the two ceramics in freestanding flexure.

The fracture load ratio, P_R-LiDi/P_R-ZrO2, is plotted as a function of ceramic thickness for ceramics/cement/enamel/dentin systems loaded with a deformable indenter (Fig. 6b). The load-bearing capacity of lithium disilicate reached 70 % to 75 % of that of zirconia when thickness was in the range between 0.7 mm and 1.4 mm. Analogous data generated by a rigid indenter from Fig. 2c are re-plotted here for comparison (open symbols). No significant difference in relative fracture load between lithium disilicate and zirconia was observed for a deformable indenter compared to a rigid one. This is because the high elastic modulus of the rigid indenter would increase the near-contact Hertzian stresses at the occlusal surface, but have less influence on the far-field flexural stress at the ceramic cementation surface.

4. Discussion

Posterior restorations are subjected to high stresses as a result of masticatory loading. Zirconia and lithium disilicate glass-ceramics have become the materials of choice for posterior all-ceramic restorations due to their superior mechanical properties [48, 49]. Flexural strength or fracture load (for a given specimen thickness) of zirconia is 2.5 times higher than lithium disilicate glass-ceramics, suggesting that zirconia is much more suitable for freestanding stress-bearing applications, such as multi-unit or long span fixed partial prostheses. However, only a little information is currently available on these all-ceramic materials and their application in minimally invasive treatment concepts [50]. When ceramic restorations are bonded to and supported by tooth structures, the relative load-bearing capacity between zirconia and lithium disilicate changes. Our study demonstrates that when supported by dentin, the fracture load of zirconia restorations is about 1.8 times greater than lithium disilicate glass-ceramics. More dramatically, when supported by enamel backed by dentin, the fracture load of zirconia is only 1.3 to 1.4 times greater than lithium disilicate. This is true for ceramic restoration thickness of 0.6 mm to 1.4 mm, suggesting that lithium disilicate is especially suited for use in conservative restorations in which the preparation can be confined to enamel.

The current study also reveals that when supported by enamel, the resistance to flexural fracture of both lithium disilicate and zirconia onlays is much greater relative to their dentin-backed counterparts. This is in agreement with previous experimental studies, reporting that the fracture resistance of ceramic restorations bonded with resin to enamel was higher than those bonded to dentin [17, 51]. The difference between the enamel and dentin backings becomes more pronounced in lithium disilicate onlays due to a smaller mismatch in elastic modulus between lithium disilicate and enamel relative to zirconia and enamel. For example, a 1.0 mm thick lithium disilicate onlay supported by enamel exhibits a load-bearing property similar to that of its 1.4 mm thick counterpart supported by dentin, again demonstrating the advantage of using thin lithium disilicate for minimally invasive treatments.

In addition, when supported by enamel, the fracture load of lithium disilicate onlay becomes less sensitive to its thickness, especially in the thickness range between 0.8 mm and 1.7 mm. A recent experimental study on the fracture resistance of lithium disilicate (IPS e.max Press, Ivoclar Vivadent, Schaan Liechtenstein) occlusal onlays of various thicknesses adhesively luted to maxillary premolars confirmed the present results [52]. Three onlay thicknesses, 0.5 mm (ultra-thin), 1.0 mm (thin), and 2.0 mm (standard), were examined. It was found that the fracture loads for minimally invasive 0.5 mm thin lithium disilicate onlays supported by enamel were comparable to their dentin-backed 2.0 mm thick counterparts.

Lithium disilicate glass-ceramics have a number of advantages over zirconia, including better esthetics, similar wear behavior to enamel [53], ability to be etched and salinized (to promote an adhesive bond), and lower processing temperatures. Additionally, low temperature degradation of zirconia are a matter of controversial discussion in the dental literature for monolithic zirconia ceramic restorations [54, 55]. Lithium disilicate ceramics appear more suitable than zirconia for ultra-thin onlays, large occlusal veneers, and even partial-coverage crowns. The long-term success of posterior lithium disilicate partial coverage restorations has been reported [56].

Posterior ceramic onlays and occlusal veneers are particularly useful for patients who may need a slight increase in occlusal height to harmonize with the adjacent occlusal plane [57]. In many of these cases, only the enamel surface needs to be prepared to accept the adhesively bonded occlusal onlay. The traditional restorative approach with full-coverage crowns would require a much greater removal of sound enamel [2]. CAD/CAM ceramic occlusal veneers with conservative defect-orientated tooth preparation have also been recently demonstrated as an effective treatment for rehabilitation of severe dental erosion [16].

The key to the long-term stability of ceramic structures is the ability to effectively utilize the properties of restorative materials and supporting structures. Based on the plate-on-foundation theory and finite element analysis, the elastic modulus mismatch between ceramic and the substrate influences the fracture load of uniformly supported and bonded ceramic restorations. For a given thickness, theory predicts that the fracture load is governed by ceramic strength and the log of the ceramic to substrate modulus ratio (Eq. 1). Although the elastic modulus mismatch has only a secondary effect (logarithm to base 10) on fracture load compared to ceramic strength, in cases in which the ceramic modulus approaches enamel, the modulus mismatch contribution can be significant.

It is important to note that the elastic modulus of the substrate is an effective (or combined) modulus, including cement, enamel, and dentin layers. Since cement has a much lower modulus compared to enamel, inclusion of any cement layer can have a detrimental effect on ceramic load-bearing capacity. A detailed analysis of the effect of cement modulus and thickness on ceramic load-bearing property has been conducted in a previous study [19]. In order to increase the load-bearing properties, a high modulus and thin cement layer is most desirable.

Finally, several limitations of the current theoretical model need to be addressed: (i) The current theoretical analysis does not account for the effect of indenter radius on flexural stress at the intaglio surface of ceramic onlays. However, our FE stress analysis does include the indenter radius. Our findings have shown that the theoretical predictions agree with the FEA simulations very well (Fig. 4). (ii) The accuracy of predicting critical load for radial fracture decreases as the thickness of the ceramic layer diminishes. Previous studies have systemically compared the analytical results derived from this theoretical model with experimental data for critical load as a function of ceramic thickness for a wide range of dental ceramics bonded to compliant substrates, including zirconia, alumina, glass-infiltrated zirconia, glass-infiltrated alumina, lithium disilicate, and porcelain [27, 58]. It was found that the theoretical predictions agree very well with the experimental data for ceramic thickness ranging from 0.15 mm to 1.5 mm and for all ceramic systems examined. At large ceramic thickness (>1.5 mm), however, cone fracture may occur at the ceramic occlusal surface before radial fracture. Under the current configuration, single-cycle indentation loads for cone fracture in zirconia and lithium disilicate are 4000 N [59] and 1100 N [19], respectively. Such high levels of load are far beyond the maximum masticatory force recorded in humans [20]. Thus, cone cracking is not considered as a critical failure mode in this study. (iii) Our model assumes that the multilayer system only undergoes elastic deformation. In the current configuration, the stiff ceramic onlay provides stress-shielding of the underlying cement and tooth support, preventing the substrate from significant plastic deformation. In addition, the brittle nature of ceramics only allows the overlay ceramic to undergo minimal flexural deformation prior to fracture. This, and other evidence, suggests that the current theoretical model, although it is based on the linear elasticity theory and is rather simple, serves very well in predicting the critical fracture loads of tooth-supported ceramic veneers and onlays.

5. Conclusion

The resistance to bulk fracture of ceramic occlusal onlays is governed by their flexural strength as well as the elastic modulus mismatch between the ceramic and tooth support. A smaller mismatch in elastic modulus can significantly increase the load-bearing capacity of ceramic restorations, even though the effect of elastic modulus mismatch on fracture load is secondary (logarithm to base 10) compared to ceramic strength. Our FEA simulation and theoretical analysis demonstrate that despite the flexural strength of lithium disilicate (400 MPa) being merely 40 % of zirconia (1000 MPa), the load-bearing capacity of lithium disilicate can approach 75 % of that of zirconia when bonded to enamel. This is particularly true for ceramic restoration thicknesses of 0.6 mm to 1.4 mm, which is most pertinent to the occlusal veneers and onlays. In addition, the load-bearing property of lithium disilicate onlay becomes less sensitive to its thickness when supported by enamel, signifying its great potential for applications in minimally invasive dentistry.