Wave-breaking-extended fiber supercontinuum generation for high compression ratio transform-limited pulse compression

Abstract

Wave-breaking often occurs when a short intense optical pulse propagates in a long normally dispersive optical fiber. This effect has conventionally been avoided in fiber (super-)continuum-based pulse compression because the accumulated frequency chirp of the output pulse cannot be fully compensated by a standard prism (or grating) pair. Thus, the spectral extending capability of the wave-breaking has not been utilized to shorten the compressed pulse. We demonstrate that wave-breaking-free operation is not necessary if a 4f pulse shaper-based compressor is employed to remove both the linear and nonlinear chirp of the output pulse. By propagating a 180 fs (FWHM) input pulse in a nonlinear photonic crystal fiber beyond the wave-breaking limit, we compress the wave-breaking-extended supercontinuum output pulse to the bandwidth-limited duration of 6.4 fs (FWHM). The combination of high compression ratio (28×) and short pulse width represents a significant improvement over that attained in the wave-breaking-free regime.

Optical wave-breaking (WB) is a well-documented effect that dramatically distorts the temporal and spectral properties of a short optical pulse propagating along a normally dispersive optical fiber [1–3]. In the temporal domain, both the leading and trailing edges of the pulse break into interference-type oscillations, analogous to the breaking of water waves under shock formation [2]. Concurrently, two sidelobes emerge from the shortand long-wavelength ends of the pulse spectrum [1]. WB degrades the fiber continuum-based pulse compression by a standard prism or grating pair (termed a quadratic compressor) [1,4] and therefore negatively affects the pulse dechirping of ultrafast fiber lasers. Thus, it has long been treated as a harmful factor to be avoided in practice, e.g., by the use of parabolic pulse shaping [5]. However, two recent studies have indicated the benefit of WB in generating spectrally smooth fiber continuum [6] and supercontinuum [7]. In this Letter, we demonstrate an additional benefit of WB in high compression ratio [1,4] ultrashort (<10 fs) pulse compression.

Supercontinuum can be generated in a photonic crystal fiber with its full bandwidth falling into a normal dispersion regime of the fiber. This highly coherent supercontinuum [8] allows high-quality pulse compression, even though the pulse spectrum is typically modulated by the characteristic fringes of self-phase modulation (SPM) [9–14]. SPM is responsible for the spectral broadening of the input pulse and dictates the spectral edges (bandwidth) of the output supercontinuum pulse. If the supercontinuum is generated beyond the WB limit by using a larger input pulse energy and/or a longer fiber length [6], the spectral edges of the SPM-extended supercontinuum are further extended by WB through four-wave mixing [1–3,7,8]. Thus, the resulting WB-extended supercontinuum may lead to a shorter pulse at a higher compression ratio. However, prior studies have not taken full advantage of this spectral extending capability of WB [9–14], partially because the widely used quadratic compressor has difficulty dechirping the nonlinear frequency chirp introduced by WB [9–12], as pointed out theoretically [4]. We note that this limitation is not intrinsic if a 4f pulse shaper, termed an ideal compressor [4], is employed to remove both the linear and nonlinear chirps of the supercontinuum pulse [13–15]. By using this ideal compressor and invoking WB, we obtain a short pulse width of 6.4 fs at a high compression ratio of 28×, which greatly improves the performance (9.6 fs at a compression ratio of 24×) reported in a similar study operated in the WB-free regime [14,16].

Our experimental setup resembles that reported previously [16], except that a longer (14 cm) but straight mounted photonic crystal fiber (NL-1050-NEG-1, NKT Photonics) was used to promote the WB effect, and a more compact solid-state Yb:KYW laser oscillator (Model-Z, High-Q laser) was used as the pump source. An aspheric lens coupled the linearly polarized 1041 nm, 180 fs (FWHM), 80 MHz pulses of the laser to the fiber, with a coupling efficiency of ~60% and a coupling (average) power up to 0.27 W. The coupling power was varied by attenuating the incident laser power [16]. A half-wave plate was used to align the incident polarization along the slow-axis of this weakly birefringent fiber [16], so that the polarization extinction ratio (PER) of the supercontinuum was maximized to > 10 dB. This procedure is necessary for successfully modeling the fiber supercontinuum by the scalar generalized nonlinear Schrödinger equation (S-GNLSE) [16]. Higher coupling powers are permitted by the laser power (up to 2.5 W), but these undesirably decrease the PER.

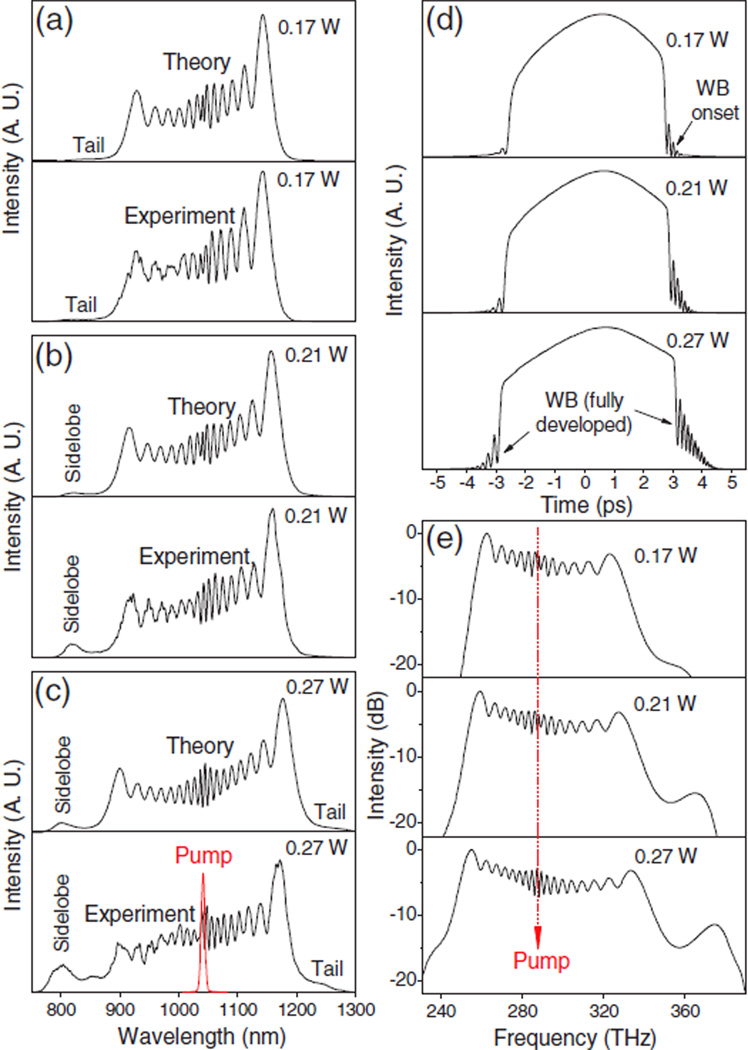
An optical spectrum analyzer was used to record the spectra of the fiber supercontinuum at three coupling powers [Figs. 1(a)–1(c)]. Interestingly, at the lowest power, a long tail emerges from the pulse spectrum at the short-wavelength end of the characteristic SPM fringes [Fig. 1(a)]. At the intermediate power, the tail develops into a well-defined sidelobe [Fig. 1(b)]. This is a dramatic effect in a dark optical laboratory because the sidelobe reveals the otherwise invisible supercontinuum as a bright red beam. At the highest power, the sidelobe begins to merge with the SPM fringes, while a second tail emerges from the long-wavelength end of the supercontinuum [Fig. 1(c)]. These spectral changes at both edges of the SPM fringes strongly suggest the occurrence of WB [1].

Fig. 1.

(Color online) (a)–(c) Comparison of experimental and theoretical spectra of fiber supercontinuum at three coupling powers; (d) corresponding theoretical pulse profiles in time; (e) corresponding theoretical spectra (log-scale) in optical frequency.

To confirm this assumption, we perform the S-GNLSE-based simulation reported before [16]. Because the Yb laser emits soliton-type pulses by design, the envelope of the pulses is a secant hyperbolic function defined by the pulse width T₀, which is 0.567 times the FWHM pulse width. The recorded pump laser spectrum [Fig. 1(c)] corresponds to T₀ = 102 ± 5 fs, or an FWHM width of 180 fs. Also, we assume the laser pulses accumulated a linear chirp of 5500 fs² (due to an isolator and other dispersive optics) before incident on the 14 cm fiber. The other parameters of the simulation follow Table 2 of [16]. The simulated spectra at the three coupling powers are found to be in good agreement with the observed spectra [Figs. 1(a)–1(c)]. In particular, the spectral tails and sidelobes at the edges of the SPM fringes, which are not present in our previous simulation [16], have all been reproduced.

The origin of these tails or sidelobes can be clarified if the simulated supercontinuum pulses are presented in the time domain [Fig. 1(d)] and the optical frequency domain [Fig. 1(e)]. At the lowest coupling power, the trailing edge of the pulse experiences a more pronounced steepening effect than the leading edge [Fig. 1(d)], an effect known as self-steepening [17]. Consistently, the SPM spectral fringes are asymmetrically broadened toward the high-frequency end [Fig. 1(e)] [17]. This effect produces an optical shock that precedes WB [Fig. 1(d)] [1,2], evidenced by the temporal oscillations immediately following the trailing edge. These oscillations reflect the interference between the short-wavelength components of the pulse, leading to the short-wavelength tail in the pulse spectrum [Fig. 1(a)] through four-wave mixing [1–3]. At elevated coupling powers, the oscillations following the trailing edge strengthen so that the short-wavelength tail develops into an intense sidelobe [Figs. 1(b) and 1(c)]. By a similar mechanism, WB occurs on the steepened leading edge of the pulse [Fig. 1(d)] to produce the long-wavelength tail in the pulse spectrum [Fig. 1(c)] [1–3]. The simultaneous appearance of the temporal oscillations and spectral tail corresponding to either the trailing or leading pulse edge unambiguously confirms the occurrence of WB and the WB origin of the spectral tails or sidelobes [3].

Without the self-steepening, the onsets of the shortand long-wavelength tails would occur simultaneously, and the spectral extension of WB would be rather symmetric toward the high- and low-frequency ends [1–3]. Thus, the self-steepening is responsible for the biased spectral extension of WB toward the high-frequency end [Fig. 1(e)]. The observed disparate onsets of the WB-induced short- and long-wavelength tails with increasing coupling power echo those predicted with increasing fiber length at a constant coupling power [7,8]. These results are consistent because WB can be equivalently induced by increasing the coupling power of the input pulses or the fiber length of pulse propagation [6]. To review, WB is responsible for the emerging spectral tail at the short- or long-wavelength end of the supercontinuum, while the self-steepening is responsible for the earlier onset of the short-wavelength tail and the biased spectral extension of WB toward the high-frequency (short-wavelength) end.

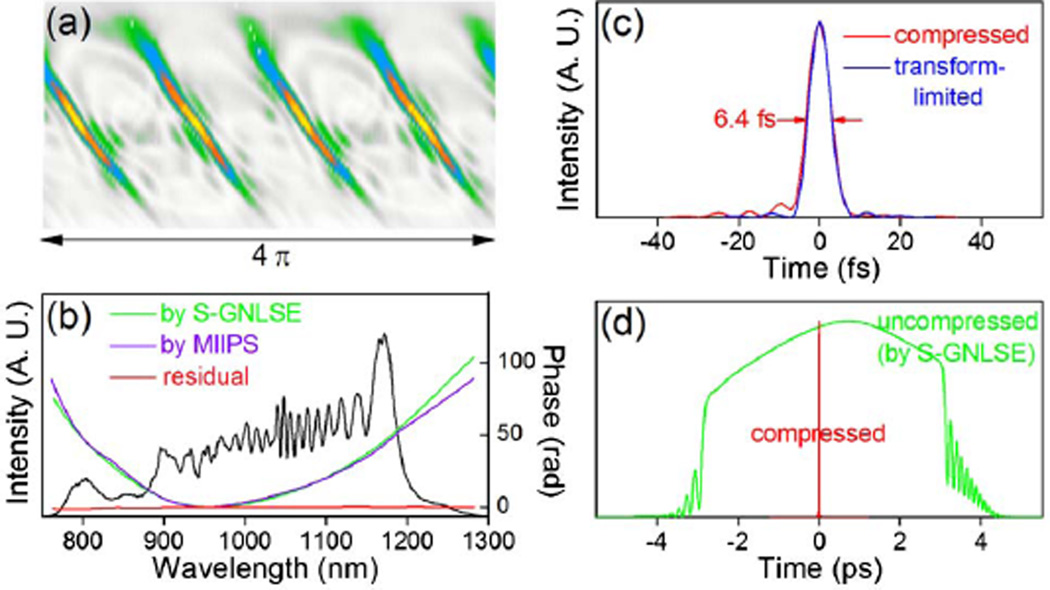
Because the fully developed WB occurs on both edges of the pulse [Fig. 1(d)], the spectral extension of WB is maximized [Fig. 1(e)]. Thus, the S-GNLSE-quantified supercontinuum of Fig. 1(c) was used for subsequent pulse compression. The supercontinuum was collimated by a parabolic mirror and sent to a 4f pulse shaper (Box 640, BioPhotonic Solutions). The compression was performed by multiphoton intrapulse interference phase scans (MIIPSs) [18] with a typical MIIPS trace of four parallel lines separated by π horizontally [Fig. 2(a)], which is indicative of high-quality transform-limited pulse compression [13]. Consistently, the compressed pulse calculated according to the residual spectral phase [Fig. 2(b)] has an FWHM width of 6.4 fs with no strong pedestal, and approximates the corresponding transform-limited pulse of flat spectral phase [Fig. 2(c)]. In contrast to the earlier studies [1,2], the compressed pulse is much shorter than the half period of the simulated WB oscillations (~80 fs) [Fig. 2(d)].

Fig. 2.

(Color online) (a) Typical MIIPS trace after pulse measurement and compression; (b) comparison of measured (violet curve) and calculated (green curve) spectral phases, along with residual spectral phase (red curve) and pulse spectrum (black curve); (c) temporal intensity profiles of compressed pulse (red curve) and the corresponding transform-limited pulse (blue curve); (d) temporal intensity profiles of uncompressed (green curve) and compressed (red curve) pulses.

Since the pulse shaper was carefully calibrated [14], the measured spectral phase of the pulse can be compared with that predicted from the S-GNLSE simulation associated with Fig. 1(c). The good agreement between the two [Fig. 2(b)], termed as a cross-validation [14], strongly validates the MIIPS-assisted pulse measurement and compression. WB does not negatively affect the full phase compensation of this ideal compressor because the spectral phase of the corresponding spectral features is smooth [Fig. 2(b)]. The discrepancy at the edges of the spectral phase [Fig. 2(b)] is likely linked to the discrepancy occurring in the spectrum [Fig. 1(c)], which may be due to the neglect of the frequency dependence of the fiber nonlinear coefficient in the simulation [8].

The throughput of the 4f pulse shaper permits the generation of 0.1 W, 80 MHz, 6.4 fs (FWHM), near transformlimited compressed pulses from the 0.5W180 fs (FWHM) laser pulses incident on the moderately long (14 cm) fiber. This performance can be compared to the two extremes of coherent fiber continuum-based pulse compression. In one extreme, a high compression ratio (80×) is obtained from a long (93.5 m) fiber at the cost of a long compressed pulse width (460 fs) [1]. In the other extreme, a short compressed pulse width (3.64 fs, FWHM) is obtained from a short (13 mm) fiber at the cost of a low compression ratio (2×) [15]. Similar studies [9–14] have attempted to improve both aspects. By operating under fully developed WB, we simultaneously achieve a short compressed pulse width (6.4 fs) and a high compression ratio (28×). This strategy capitalizes on the reliability of commercial ~200 fs lasers and the controllability of the related fiber supercontinuum generation [Figs. 1(c) and 2(b)], and might therefore find wide applications in ultrafast spectroscopy and nonlinear microscopy. Shorter pulse widths at higher compression ratios may be attained well above the WB limit [7,8] by avoiding a limiting factor of nonlinear depolarization [19]. It can be argued that some early compression attempts might have been operated at the onset of the trailing edge WB [Fig. 1(a)], as evidenced by the presence of a “mysterious” short-wavelength tail in the supercontinuum spectrum [9,11,13]. However, the contribution of this single-edged WB onset to high compression ratio pulse compression is limited in comparison to that of the fully developed WB [Fig. 1(c)].

In conclusion, WB is not an intrinsic barrier for high-quality pulse compression, as often assumed for the fiber supercontinuum generated in a normally dispersive optical fiber. To the contrary, the supercontinuumgeneration beyond the WB limit is beneficial for pulse compression, with both a short compressed pulse width and a high compression ratio.