Cross-validation of interferometric synthetic aperture microscopy and optical coherence tomography

Abstract

Computationally reconstructed interferometric synthetic aperture microscopy is coregistered with optical coherence tomography (OCT) focal plane data to provide quantitative cross validation with OCT. This is accomplished through a qualitative comparison of images and a quantitative analysis of the width of the point-spread function in simulation and experiment. The width of the ISAM point-spread function is seen to be independent of depth, in contrast to OCT.

Optical coherence tomography (OCT) is a modality for optical and near-IR three-dimensional imaging [1–3]. Several methods, e.g., axicon lenses, adaptive optics, and multiple acquisitions, have been used to capture high-resolution OCT images over extended axial distances [4–7]. Interferometric synthetic aperture microscopy (ISAM) is a modality based on a solution of the inverse scattering problem for low-coherence imaging that provides spatially invariant resolution. It has been demonstrated in simulation [8–12] and in experiments with tissue phantoms and human tissue [12]. The instrumentation is similar to OCT with augmentation to achieve phase stability. ISAM images may be obtained over many confocal lengths in depth without scanning the focus. Thus, there is no need to compromise between depth of field and transverse resolution as in OCT.

In this Letter, it is verified that ISAM produces spatially invariant resolution equal to the focal-plane resolution obtained in a similar OCT system. In ISAM, the spatially invariant transverse resolution limit is set by the NA of the lens, and the axial resolution limit is determined by the bandwidth of the system. An en face ISAM reconstruction of a tissue phantom in a plane far from the focus is compared with OCT in the same arrangement and an OCT image refocused to the same plane. A sample consisting of subresolution particles was imaged with both modalities, and the FWHM of the transverse point-spread function (PSF) is shown as a function of depth. It may be seen that the ISAM FWHM is spatially uniform, whereas the OCT FWHM increases nearly linearly with distance outside the confocal region. These results are in agreement with simulation and theory. Measurements in rat adipose tissue demonstrate that ISAM reconstruction of an en face plane far from focus correlates well with coregistered focal-plane OCT.

In OCT and ISAM, a beam of light is projected into a semitransparent sample, and the backscattered light is collected and measured in an interferometer. The center of the beam, in a plane perpendicular to the beam axis, is denoted by the position vector r_||. At each r_||, data are collected interferometrically as a function of frequency, ω, by using a fiber-based spectral-domain OCT system. The data are written as a function S(r_||,k) of position and wavenumber, k=n(ω)ω/c, where n(ω) is a generally dispersive background index of refraction [13]. In OCT, the data from distinct axial scans are treated as independent, and an image is obtained by taking the one-dimensional inverse Fourier transform of the data with respect to k. ISAM takes into account a more complete model that includes scattering and beam diffraction effects. Data in different axial scans are related. Phase and position stability between scans must be preserved. In this work, a common path reflector and triggered acquisition provide the needed stability and precision [14]. Taking the two-dimensional Fourier transform of S (indicated by a tilde) with respect to r_||, it may be found that [10,12]

$$\stackrel{\sim }{S}(\mathbf{Q},k)=K(\mathbf{Q},k)\stackrel{\sim }{\stackrel{\sim }{\eta }}[\mathbf{Q},-2\sqrt{k^2-Q^2/4}],$$ (1)

where Q represents the transverse frequency coordinates, $\stackrel{\sim }{\stackrel{\sim }{\eta }}$ is the three-dimensional Fourier transform of the scattering potential, which describes the structure of the sample, Q represents the magnitude of Q, and the specifics of K(Q,k) are described by Eq. (9) of [10]. The object structure may be recovered by solving Eq. (1). Since the relationship between the data and the object structure is expressible entirely in the Fourier domain, there is no resolution advantage gained by longitudinal movement of the focus relative to the sample. The resolution is expected to be uniform throughout the illuminated volume and equal to the resolution of the conventional OCT data in the focal plane.

Several factors limit the signal-to-noise ratio (SNR) and reconstruction fidelity for both ISAM and OCT. An analysis of the system PSF shows that far from focus the expected signal power in ISAM falls off as the inverse of the distance from focus [12,15], while the noise power remains constant. Second, as the light propagates deeper into the sample, the signal power is attenuated by scattering and absorption. Consequently, when the beam focus is placed within the sample, the reconstruction SNR is superior above the focus. Third, multiple scattering reduces reconstruction quality for larger depths in both ISAM and OCT.

A source with a center wavelength of 810 nm and a bandwidth of 100 nm was used to illuminate a sample consisting of roughly 1 μm diameter TiO₂ particles suspended in silicone. These particles are well below the resolution of the system and therefore are represented by the PSF of the system. The interference signal was collected with a spectrometer-based system. The optics produced a focal-plane resolution of Δx=9.3 μm (FWHM, where the waist radius is 5.6 μm), a confocal parameter of 240 μm, and an NA of 0.05. The reference path length was matched at 1.4 mm above the focus. En face images were obtained with the focus fixed 450 μm below the plane being imaged using both OCT and ISAM. The sample was then moved 450 μm so that the focus now coincided with the en face plane, and OCT imaging was performed again. This translation corresponds to an optical path length change of 640 μm, since the index of refraction for silicone is 1.42. The results are shown in Fig. 1, where the A-scan rate was 29 kHz in the fast scanning direction and about 2 Hz in the slow scanning direction for 400×400 A-scans in the transverse plane. The resolution appears the same in the ISAM and coregistered OCT. It may also be observed in Figs. 1(a) and 1(b) that the SNR is worse for the data outside the focal plane, for reasons described above.

Fig. 1.

(a) En face OCT of a plane 450 μm above the focal plane. (b) ISAM reconstruction of the same en face plane. (c) En face OCT with the focal plane moved to the plane of interest in (a). The field of view in each panel is 360 μm × 360 μm. All images are displayed on a linear scale. The gray scales indicate the displayed range of relative signal amplitudes.

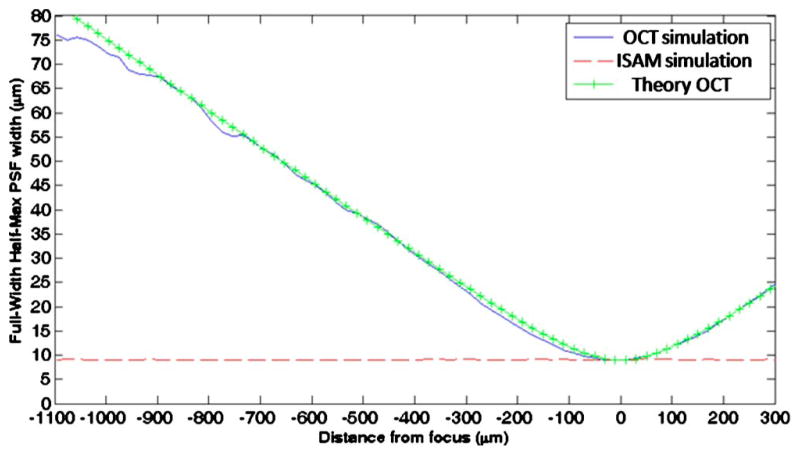
A simulation of the PSF FWHM was made for OCT and for ISAM. By the method in [10], 100 point scatterers were located by a Monte Carlo method, and the data for the forward and inverse problems were calculated. The FWHM focal-plane resolution of the simulated beam is 9.3 μm (FWHM) to match the experimental data. To measure the average FWHM of each point at each depth, the transverse Fourier transform of the amplitude of the image was taken and averaged over 40 realizations of the Monte Carlo scatterer distributions. A Gaussian profile was fitted to the average Fourier transform, and the width of this Gaussian was taken to be the reciprocal of the FWHM of the PSF. The normalized sum-of-square error [16] indicates an average goodness of fit per Gaussian of 97.5%. Figure 2 shows the average PSF FWHM as a function of distance from the focus for OCT and ISAM. ISAM exhibits a uniform PSF width for all depths, while the PSF width for the OCT data increases approximately linearly at distances of more than one Rayleigh range from the focus. In comparison, the theoretical PSF FWHM for the optical field is plotted, $\mathrm{\Delta }x(z)=(2\sqrt{ln2})w_0\sqrt{1+{(z/z_{\text{R}})}^2}$, where z is the distance from the focus, w₀ is the waist radius, and z_R is the Rayleigh range. At larger distances from the focus, coherent interference between scatterers produces what appears as well-localized structure. This may explain why the simulated OCT data exhibit a narrower PSF at larger distances from the focus than predicted by theory.

Fig. 2.

(Color online) Simulation of scatterers in OCT and ISAM. The plot shows the PSF (FWHM) versus distance from focus for simulated OCT (solid curve), simulated ISAM (dashed curve), and the corresponding theoretical PSF of OCT (crosshair curve).

In both modalities, the bandwidth of the complex analytic signal, in principle, is invariant with depth. What might mistakenly be called blurring in the OCT data is actually defocus. This is why ISAM is feasible: the defocusing observed in OCT is the result of a changing phase relationship between plane wave components of the field, and this can be corrected when one has access to the complex signal.

By the same method as in the simulations, the average PSF width of the imaged TiO₂ particles in the tissue phantom was measured as a function of depth for OCT and ISAM. The results are shown in Fig. 3. In agreement with the simulations, ISAM exhibits a relatively uniform PSF width for all depths, while the PSF width of OCT increases approximately linearly outside the confocal region.

Fig. 3.

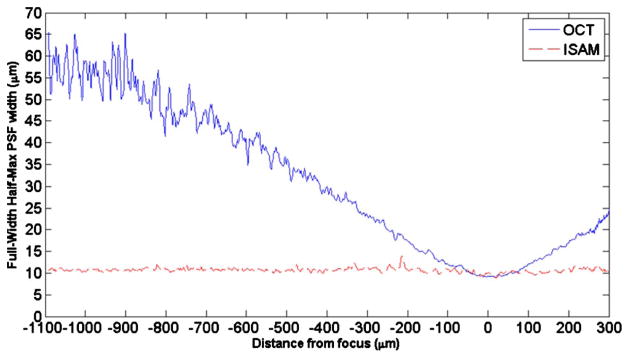
(Color online) Experimental measurement of the PSF (FWHM) versus distance from the focus for OCT (solid curve) and ISAM (dashed curve).

In Fig. 4, ISAM reconstruction of rat adipose tissue is compared with focal-plane OCT. The measurements were made by using an achromatic doublet of focal length 12 mm, producing a theoretical focal-plane resolution of 4.4 μm (FWHM) and a (free-space) Rayleigh range of 52 μm. Three-dimensional data were acquired at an A-scan rate of 1 kHz in the fast scanning direction and 0.6 Hz in the slow scanning direction for 1000×600 transverse positions with 1 μm spacing. Data were acquired first with the focus 443 μm (optical depth) below the sample surface and subsequently with the sample translated along the optical axis by 270 μm by use of a precision translation stage, so that the beam focus was near the sample surface. The en face plane shown is 24 μm (optical depth) below the tissue surface and is approximately eight Rayleigh ranges (419 μm) above the focus. Improvement in resolution is observed between the above-focus OCT [Fig. 4(a)] and ISAM reconstruction [Fig. 4(b)]. The ISAM image reveals tissue morphology that is unresolved in the above-focus OCT and that correlates well with the focal-plane OCT data [Fig. 4(c)].

Fig. 4.

(Color online) ISAM and OCT in ex vivo rat adipose tissue. (a) En face OCT of a plane 419 μm (optical depth) above the focal plane. (b) ISAM reconstruction of the same en face plane. (c) En face OCT with the focal plane moved to the plane of interest in (a). The field of view in each panel is 500 μm×500 μm. All images have gamma correction (γ =0.5). Gray scales indicate the displayed range of relative signal amplitudes.

Our results demonstrate that ISAM produces spatially uniform resolution regardless of the placement of the focus, within the context of the single-scattering model. That is, deviations from uniform resolution are attributable to refraction and multiple scattering, the same effects that degrade OCT image quality. In ISAM, there is no trade-off between depth of field and resolution. There are two immediately apparent benefits. First, an ISAM instrument may be made mechanically simpler than a similar OCT system, because there is no need to scan the focus. Second, data may be acquired much more rapidly than in OCT, namely, by a factor of the number of focal positions needed in the OCT. At large distances from the focus, the SNR degrades in ISAM as compared to the focus scanning in the axial direction in OCT.

Implementation of ISAM with an existing OCT system requires relatively straightforward modifications, and the computational efficiency of this technique makes possible real-time processing for clinical applications.