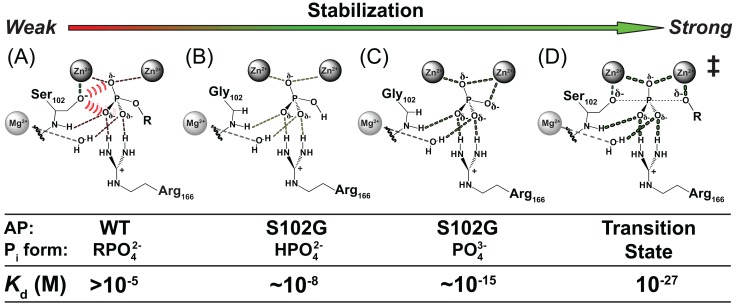
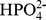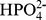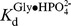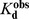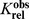Enhanced phosphate binding by phosphatases upon removal of their anionic nucleophiles suggests that these enzymes use ground state destabilization by anionic active site nucleophiles as part of their catalytic arsenal.
Abstract
Enzymes stabilize transition states of reactions while limiting binding to ground states, as is generally required for any catalyst. Alkaline Phosphatase (AP) and other nonspecific phosphatases are some of Nature's most impressive catalysts, achieving preferential transition state over ground state stabilization of more than 1022-fold while utilizing interactions with only the five atoms attached to the transferred phosphorus. We tested a model that AP achieves a portion of this preference by destabilizing ground state binding via charge repulsion between the anionic active site nucleophile, Ser102, and the negatively charged phosphate monoester substrate. Removal of the Ser102 alkoxide by mutation to glycine or alanine increases the observed Pi affinity by orders of magnitude at pH 8.0. To allow precise and quantitative comparisons, the ionic form of bound Pi was determined from pH dependencies of the binding of Pi and tungstate, a Pi analog lacking titratable protons over the pH range of 5–11, and from the 31P chemical shift of bound Pi. The results show that the Pi trianion binds with an exceptionally strong femtomolar affinity in the absence of Ser102, show that its binding is destabilized by ≥108-fold by the Ser102 alkoxide, and provide direct evidence for ground state destabilization. Comparisons of X-ray crystal structures of AP with and without Ser102 reveal the same active site and Pi binding geometry upon removal of Ser102, suggesting that the destabilization does not result from a major structural rearrangement upon mutation of Ser102. Analogous Pi binding measurements with a protein tyrosine phosphatase suggest the generality of this ground state destabilization mechanism. Our results have uncovered an important contribution of anionic nucleophiles to phosphoryl transfer catalysis via ground state electrostatic destabilization and an enormous capacity of the AP active site for specific and strong recognition of the phosphoryl group in the transition state.
Author Summary
Enzymes use a variety of tools and strategies to enhance (catalyze) biological reactions; these include the use of general acids and bases, cofactors, and the employment of remote binding interactions to position substrates near reactive chemical groups. Phosphatases are some of Nature's best enzymes, affording exceptional rate enhancements to the biologically ubiquitous removal of a phosphate group from a substrate (dephosphorylation). The apparent challenge faced by nonspecific phosphatases is that their wide substrate specificity precludes the efficient use of remote binding interactions. Previous work suggested that phosphatases could use negatively charged chemical groups (anionic nucleophiles) at the active site to destabilize substrate binding without simultaneously destabilizing the transition state barrier—an elusive catalytic strategy known as preferential ground state destabilization. In this work, we test this ground state destabilization model of catalysis by removing the anionic active site nucleophile of alkaline phosphatase and observing the effects on the enzyme's affinity for a phosphate ligand. We find that alkaline phosphatase has an exceptionally strong affinity for phosphate, and provide clear evidence for ground state destabilization by the anionic active site nucleophile that, when present, forestalls substrate saturation and product inhibition, and enhances catalysis by at least a thousand fold.
Introduction
Enzymes are central to biology, allowing chemical processes to be carried out rapidly and specifically. A range of enzymatic catalytic efficiencies of 106–1029 fold have been observed [1],[2], with the more difficult chemical reactions generally exhibiting higher rate enhancements such that k cat/K M values tend to cluster around 104–105 M−1 s−1 [3].
Decades of mechanistic enzymology have revealed several general strategies used by enzymes to achieve their prodigious rate enhancements, including the use of general acids and bases to facilitate proton transfers, coenzymes and metal cofactors to broaden the enzymatic reaction repertoire, and positioned hydrogen bond donors and acceptors and metal ions to stabilize rearranged charges in transition states. An additional hallmark of enzymes is the use of binding interactions with portions of their substrates that are not directly involved in the chemical transformation to position the reacting groups favorably for that transformation [4]–[14].
Nonspecific phosphatases, however, have little or no binding interactions with remote portions of the phosphate monoester substrates they hydrolyze, enabling them to liberate inorganic phosphate (Pi) from any available monosubstituted phosphate source. Remarkably, these same phosphatases that do not use remote binding interactions for catalysis nonetheless exhibit some of the largest rate enhancements known. For example, alkaline phosphatase (AP) from Escherichia coli provides estimated rate enhancements of up to 1027-fold for the hydrolysis of a wide range of alkyl phosphates [15],[16]. According to transition state theory, this rate enhancement represents a stabilization energy of 37 kcal/mol 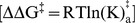 [16]. This energy, if expressed as binding energy in a ground state, would correspond to a dissociation constant of 10−12 fM, a trillion fold stronger than the affinity of avidin for biotin (K
d≈1 fM, [17]).
[16]. This energy, if expressed as binding energy in a ground state, would correspond to a dissociation constant of 10−12 fM, a trillion fold stronger than the affinity of avidin for biotin (K
d≈1 fM, [17]).
Some of the interactions that contribute to AP's enormous transition state stabilization are readily assigned based on structural inspection, chemical insight, and functional studies (Figure 1B) [18],[19]. For example, in the transition state substantial negative charge builds up on the leaving group oxygen atom of the phosphoryl group such that the Zn2+ ion interacting with this group likely provides substantial stabilization [20]–[22]. Activation of the Ser102 nucleophile via Zn2+ coordination to give the serine alkoxide anion presumably also accelerates the enzyme-catalyzed reaction relative to the solution reaction that uses neutral water as the nucleophile [15], and further acceleration likely arises from positioning of the serine alkoxide nucleophile with respect to the reactive phosphoryl group within the active site.
Figure 1. Active site models for the AP ground and transition state.
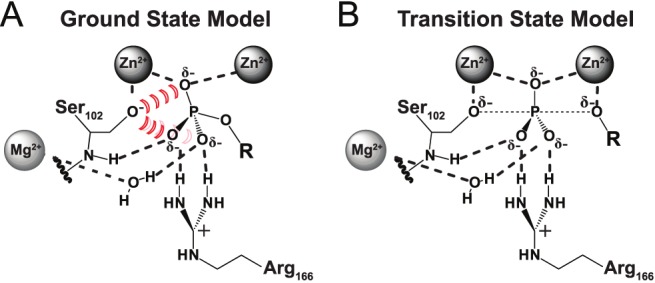
AP ground state (A) and transition state (B) models based on previously solved X-ray crystal structures (PDB Codes 3TGO and 1B8J, respectively). Proposed active site contacts are illustrated with dashed lines. The proposed electrostatic destabilization from Ser102 in the ground state model is illustrated by the red hash marks.
Despite these recognizable strategies, the ability of AP to provide this enormous overall rate enhancement is not understood, and this rate enhancement is especially remarkable considering that, unlike in the avidin-biotin complex and in many enzymes that make extensive interactions with their entire substrates, the transition state interactions in AP appear to involve only five atoms—the oxygen atoms of the transferred phosphoryl group and of the incoming and outgoing groups (Figure 1B). These observations suggest that the AP active site could, in principle, provide exceptionally strong binding to simple phosphoryl compounds, a prediction that we test herein.
These considerations raise a further perplexing question that is also addressed herein. Transition state recognition involves the central phosphoryl group, a group also present in the ground state: How does AP distinguish so profoundly between its transition state and these same atoms in the ground state? The actual ground state affinity of AP for its substrate (K d>10 µM [20]; Figure 1A) is more than 1022-fold lower than the formal transition state affinity.
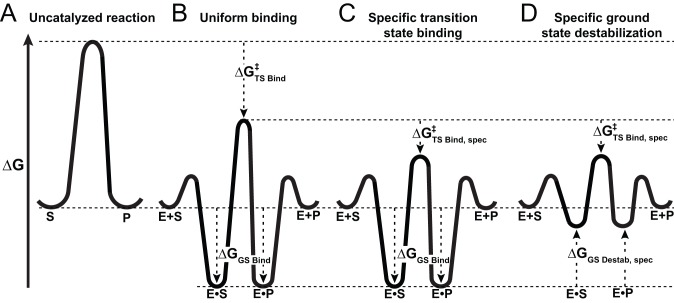
Most generally, differential transition state versus ground state recognition is a requirement for any catalyst, as illustrated in Figure 2 (cf. A versus B). The simplest way to provide specific transition state stabilization (Figure 2C) is to introduce a group that can provide chemical catalysis—for example, the introduction of a base that can abstract a proton more efficiently than can water [23],[24]. A second common way to provide needed differential stabilization is to use binding interactions to position reacting groups within the active site, thereby entropically destabilizing the ground state (in terms of conformational entropy) but not equivalently destabilizing the transition state (Figure 2D), as these groups are, by definition, positioned with respect to one another in the transition state [4],[5],[25]–[27].
Figure 2. Free energy reaction profiles illustrating preferential E•S ground state destabilization.
(A) Hypothetical uncatalyzed reaction profile. (B) Hypothetical enzyme that stabilizes the ground and transition states equally (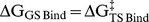 ) so that the resulting reaction barrier is equal to the uncatalyzed reaction barrier under saturating conditions. This enzyme is not a catalyst as stabilization of the transition state without parallel stabilization of the ground state is required for catalysis. (C) Hypothetical enzyme that makes additional, specific transition state stabilizing interactions,
) so that the resulting reaction barrier is equal to the uncatalyzed reaction barrier under saturating conditions. This enzyme is not a catalyst as stabilization of the transition state without parallel stabilization of the ground state is required for catalysis. (C) Hypothetical enzyme that makes additional, specific transition state stabilizing interactions, 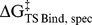 so that the reaction barrier between E.S and E.P is lower than that for the uncatalyzed barrier. This enzyme is a catalyst. (D) Hypothetical enzyme that makes specific ground state destabilizing interactions,
so that the reaction barrier between E.S and E.P is lower than that for the uncatalyzed barrier. This enzyme is a catalyst. (D) Hypothetical enzyme that makes specific ground state destabilizing interactions, 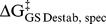 , to further enhance the catalytic properties of the enzyme relative to that in panel (C). This destabilization is discussed in the text.
, to further enhance the catalytic properties of the enzyme relative to that in panel (C). This destabilization is discussed in the text.
In addition to addressing the ability of AP to engage in remarkably strong ligand interactions, we provide evidence for electrostatic repulsion in AP that likely contributes to this critical discrimination against the ground state. We further show that there is analogous ground state destabilization in a structurally unrelated phosphatase that also contains an anionic nucleophile.
Results and Discussion
Model for Ground State Destabilization from the Ser102 Alkoxide Nucleophile
The AP active site contains three divalent metal ions and additional positively charged side chains in position to interact with the negatively charged phosphate monoester substrate (Figure 1A). The exception to this preponderance of positive charge is the active site nucleophile Ser102, which is Zn2+-coordinated and presumably negatively charged in the free enzyme with a pK
a of ≤5.5 [20]. Isotope-edited vibrational spectroscopy [16] and the pH dependence of binding of Pi and other ligands [20] indicated that when the Pi dianion 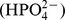 binds WT AP, its proton is lost to give bound Pi trianion
binds WT AP, its proton is lost to give bound Pi trianion 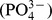 , and a proton is taken up by a group on the enzyme so that there is no net proton loss to solution (Equation 1).
, and a proton is taken up by a group on the enzyme so that there is no net proton loss to solution (Equation 1).
| (1) |
Based on the close positioning of the anionic Ser102, the negative charge of 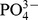 , and the protonation of an enzymatic group upon Pi binding, we proposed Ser102 as the proton acceptor [16]. This model further predicts that the Ser102 anion substantially destabilizes binding of the phosphate ester dianion substrate in the ground state, as the substrate has no proton to transfer to Ser102 to eliminate the repulsion (Figure 1A). By limiting the stability of the E•S complex, ground state destabilization from Ser102 could prevent saturation at low substrate concentrations and reduce the barrier for reaction of bound substrate. This scenario is shown schematically in Figure 2D. A direct test of this proposal is that removal of Ser102 via mutagenesis should lead to stronger ground state binding, a test we carry out herein.
, and the protonation of an enzymatic group upon Pi binding, we proposed Ser102 as the proton acceptor [16]. This model further predicts that the Ser102 anion substantially destabilizes binding of the phosphate ester dianion substrate in the ground state, as the substrate has no proton to transfer to Ser102 to eliminate the repulsion (Figure 1A). By limiting the stability of the E•S complex, ground state destabilization from Ser102 could prevent saturation at low substrate concentrations and reduce the barrier for reaction of bound substrate. This scenario is shown schematically in Figure 2D. A direct test of this proposal is that removal of Ser102 via mutagenesis should lead to stronger ground state binding, a test we carry out herein.
Ideally, to directly determine the effect of Ser102 on the E•S ground state stability, the affinity of a phosphate monoester would be compared in the presence and absence of Ser102. However, in the absence of Ser102, the affinity cannot be measured because trace Pi contamination in phosphate ester stocks (>0.1% as determined by 31P NMR) dominates binding due to the strong affinity of Pi (vide infra). In addition, trace contaminating phosphatase activity in the Ser102 mutant preparations generates Pi from any added phosphate ester (see Text S1). Thus, we turned to measurements of Pi affinities (the E•Pi ground state). Investigation of Pi interactions can provide a wealth of information, as Pi also serves as a substrate in an 18O-exchange reaction [28]–[32], several structures of Pi-bound AP are available (e.g., [33]–[36]), its affinity is readily determined, and comparisons of the relative affinities of its di- and tri-anionic forms provide additional information.
Observed Binding Affinity of Pi to Ser102 Mutants
To test if Ser102 destabilizes ground state binding, Ser102 was mutated to Gly or Ala, and the Pi binding affinity was compared to the Pi affinity of AP with Ser102 intact. We used a new 32P equilibrium-binding assay (see Materials and Methods) to measure the Pi affinity of the Ser102 AP mutants as the Ser102 mutants lack detectable activity, preventing the use of a kinetic inhibition assay to determine the Pi affinity that was previously used for WT AP and mutants with detectable activity ([20],[35],[37]; see Text S1). To test the validity and range of this assay we first determined the Pi affinity for WT AP. A 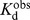 value of 0.26±0.07 µM was determined at pH 8.0 (Table 1; Text S2; Figure S1A), in reasonable agreement with values from prior kinetic inhibition assays (K
i = 0.5–1 µM) [16],[20],[38]. From a previous pH-dependent characterization of WT AP, the Pi affinity is expected to decrease as the pH is raised from 8.0 [20] and this result was also accurately reproduced with the equilibrium-binding assay (Figure S1D and E; see also Figure S1F and G). Controls carried out with mutant APs, described below and in the Supporting Information section, provide additional support for the accuracy of this assay.
value of 0.26±0.07 µM was determined at pH 8.0 (Table 1; Text S2; Figure S1A), in reasonable agreement with values from prior kinetic inhibition assays (K
i = 0.5–1 µM) [16],[20],[38]. From a previous pH-dependent characterization of WT AP, the Pi affinity is expected to decrease as the pH is raised from 8.0 [20] and this result was also accurately reproduced with the equilibrium-binding assay (Figure S1D and E; see also Figure S1F and G). Controls carried out with mutant APs, described below and in the Supporting Information section, provide additional support for the accuracy of this assay.
Table 1. Binding of Pi to active site nucleophile mutants of AP.
| Residue 102 | Residue 166 |
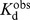 (nM)a (nM)a
|
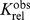 b
b
|
| Ser | Arg | 260±74 | (1) |
| Gly | Arg | ≤0.2 | ≥1,000 |
| Ala | Arg | ≤0.02 | ≥1×104 |
| Ser | Ser | (3.6±1.6)×105 | (1) |
| Gly | Ser | 66±8 | 5,500 |
| Ala | Ser | 77±6 | 4,700 |
The observed dissociation constants were determined at pH 8.0 in 100 mM NaMOPS, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2 at 4°C.
K
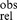 is the ratio of the observed Pi dissociation constant in the presence of Ser102 compared to the dissociation constant in the absence of Ser102: K
d(Ser102)/K
d(Gly or Ala102). Numbers greater than 1 represent stronger binding.
is the ratio of the observed Pi dissociation constant in the presence of Ser102 compared to the dissociation constant in the absence of Ser102: K
d(Ser102)/K
d(Gly or Ala102). Numbers greater than 1 represent stronger binding.
Mutation of Ser102 to either Gly or Ala led to binding of Pi that was so strong that, subsequent to uptake of 32Pi, no significant dissociation of 32Pi bound to S102G or S102A AP could be observed following the addition of an excess of unlabeled Pi (see Materials and Methods), even after 100 h (Text S3; Figure S2A; see also Figure S3). These results provided upper limits for the dissociation rate constant, k
off, of 2×10−7 s−1 for both S102G and S102A AP. This dissociation rate constant was too slow to allow equilibration prior to protein loss (presumably from irreversible denaturation) and thus prevented measurement of the Pi dissociation constants. Nevertheless, we could estimate the rate of uptake of 32Pi (Text S3 and figures therein) to obtain an upper limit for the equilibrium dissociation constant from this value and the above upper limit for k
off (Table 1; K
d = k
off/k
on). This dissociation constant is at least 103-fold lower than that observed for Pi with WT AP, indicating stabilization of Pi binding upon removal of Ser102 (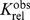 ; Table 1).
; Table 1).
To reduce the Pi affinity of the Ser102 mutants to a measurable range, an additional mutation was introduced. Previous studies showed that mutation of Arg166, which interacts with two of the phosphoryl oxygen atoms (Figure 1), reduces Pi binding affinity by ∼103-fold at pH 8.0 (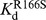 = 460 µM and
= 460 µM and 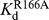 = 640 µM, [35],[39];
= 640 µM, [35],[39]; 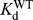 = 0.5–1 µM, [16],[20],[38]). Pi binding by the R166S AP single mutant could not be detected using the equilibrium-binding assay, as the concentrations of R166S AP needed to achieve binding in this assay are not readily obtained (Figure S7B). We therefore used the prior kinetic inhibition assay (Figure S7A) and repeated the Pi affinity measurement of R166S AP (Table 1) [35]. When Ser102 was mutated in the R166S AP background, Pi binding was observed using the equilibrium-binding assay (Text S4; Figure S8A and E) with dissociation constants of 66 and 77 nM for S102G/R166S and S102A/R166S AP, respectively, at pH 8.0 (Table 1). Measurements of the rate constants for Pi association and dissociation gave dissociation constants in reasonable agreement with the values determined in the equilibrium-binding assay (Text S4; Figure S8; Table S1). The mutations that remove Ser102 increase affinity by ∼103-fold (
= 0.5–1 µM, [16],[20],[38]). Pi binding by the R166S AP single mutant could not be detected using the equilibrium-binding assay, as the concentrations of R166S AP needed to achieve binding in this assay are not readily obtained (Figure S7B). We therefore used the prior kinetic inhibition assay (Figure S7A) and repeated the Pi affinity measurement of R166S AP (Table 1) [35]. When Ser102 was mutated in the R166S AP background, Pi binding was observed using the equilibrium-binding assay (Text S4; Figure S8A and E) with dissociation constants of 66 and 77 nM for S102G/R166S and S102A/R166S AP, respectively, at pH 8.0 (Table 1). Measurements of the rate constants for Pi association and dissociation gave dissociation constants in reasonable agreement with the values determined in the equilibrium-binding assay (Text S4; Figure S8; Table S1). The mutations that remove Ser102 increase affinity by ∼103-fold (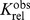 ; Table 1), providing additional strong support for a destabilizing influence of Ser102.
; Table 1), providing additional strong support for a destabilizing influence of Ser102.
Structural Analysis of Pi Bound to AP With and Without Ser102 Present
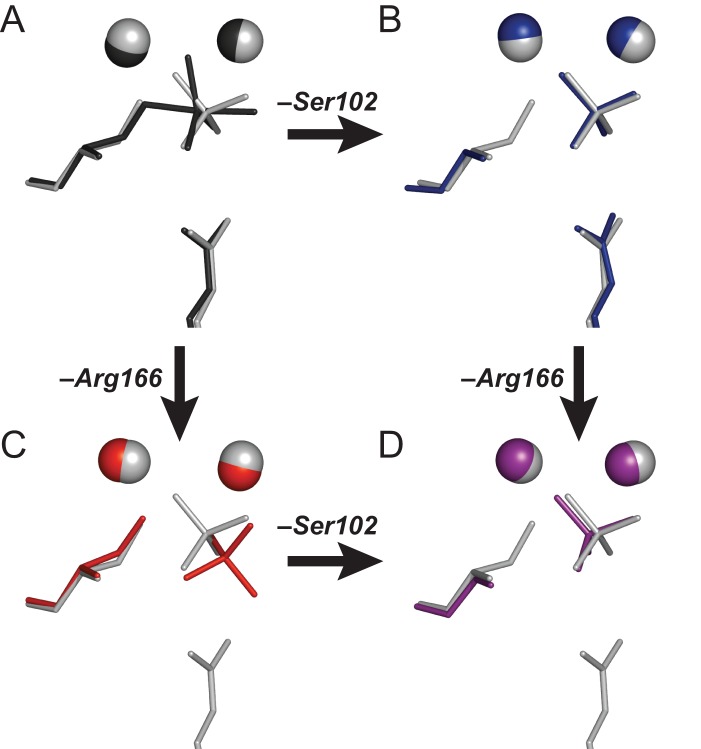
The observed increase in Pi binding affinity of AP without Ser102 is expected to arise, according to our ground state destabilization model (Figure 1A), from the removal of the Ser102 negative charge. The Gly and Ala mutations give Pi binding affinities within 2-fold of one another, showing that the binding increase is not highly dependent on the steric properties of the group replacing the Ser102 side chain, but both side chain substitutions could allow bound Pi to rearrange to an alternative, more favorable, binding conformation. If this were the case, the weaker binding with Ser102 present could arise, at least in part, from steric hindrance rather than from electrostatic repulsion. However, the orientation of Pi bound to WT AP and the Ser102Gly and Ala mutants is indistinguishable (Figure 3B; [34]). The Pi binding geometry in the S102G/R166S AP double mutant (Figure 3D), solved herein (see Table S2 for refinement statistics), is also indistinguishable from that in WT AP. The structural analysis described in this section suggests that this alternative model does not hold and provides additional insights into active site features that contribute to alignment and positioning.
Figure 3. Structural comparisons of noncovalently bound Pi in AP and Ser102 mutants.
(A) Overlay of WT AP with vanadate transition state analog covalently bound to Ser102 (black, 1PDB code 1B8J) and Pi noncovalently bound (gray, PDB code 3TGO). (B) Overlay of WT AP (grey) and S102G AP (blue, PDB code 1ELZ), both with bound Pi. (C) Overlay of WT AP (grey) and R166S AP (red, PDB code 3CMR). Mutation of Arg166 to Ser results in rotation and 1.0 Å translation of the bound Pi. (D) Overlay of WT AP (grey) and S102G/R166S AP (purple). Removal of the Arg166 side chain (R166S AP) results in a rearrangement of the bound Pi with Ser102 present (A→C) but not with Ser102 mutated (B→D) (see Text S5). While it is likely, based on the results herein and previously [16], that Pi is bound as the trianion in all cases and Ser102 is protonated when present, the X-ray data lack the resolution needed to identify protons.
A comparison of our newly obtained S102G/R166S AP structure to a previously obtained structure of R166S AP [35] also reveals another active site property, an interplay between Ser102 and Arg166 in positioning bound Pi that underscores the role of Arg166 in specifically stabilizing the transition state. This interplay is depicted in Figure 3 and described in Text S5.
Intrinsic Binding Affinities of Specific Ionic Pi Species to AP With and Without Ser102
The Pi binding results described above show that removing the Ser102 side chain increases the observed affinity by more than 103-fold at pH 8.0. However, understanding the energetics of Pi binding and destabilization requires determination of equilibrium binding constants for individual Pi species to specified forms of WT and mutant APs. Pi has multiple ionic forms, whose relative populations depend on the solution pH (Equation 2) [40], and the form bound depends on these relative populations and the enzyme's binding preferences for each ionic form:
| (2) |
The following quantitative analyses reveal that removal of Ser102 unmasks an active site capable of very strong ground state binding of ∼1 fM and suggest a substantial role for Ser102 in destabilizing both substrate and product ground state binding by several orders of magnitude. Immediately following we describe the results underlying these conclusions, and their implications are addressed in the subsequent sections.
pH-dependent Pi binding to AP containing the Ser102 nucleophile
The pH dependence for the binding of Pi and other ligands can provide information about protonation events required for binding, which can in turn be used to distinguish between binding models. As previously reported for WT AP [20], and shown here for R166S AP, the pH dependence for binding of Pi follows a bell-shaped curve (Figure 4A, open symbols). At acidic pH, the observed Pi affinity decreases log-linearly with a slope of 1, indicating that a single protonation event greatly weakens or prevents binding. This protonation could prevent binding by either inactivating the enzyme or by forming a Pi species that does not bind. As the data are consistent with a pK
a of 6.9, which is the pK
a of 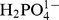 (at ionic strength, I = 0.1), these results suggest that R166S AP does not bind appreciably to
(at ionic strength, I = 0.1), these results suggest that R166S AP does not bind appreciably to 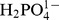 .
.
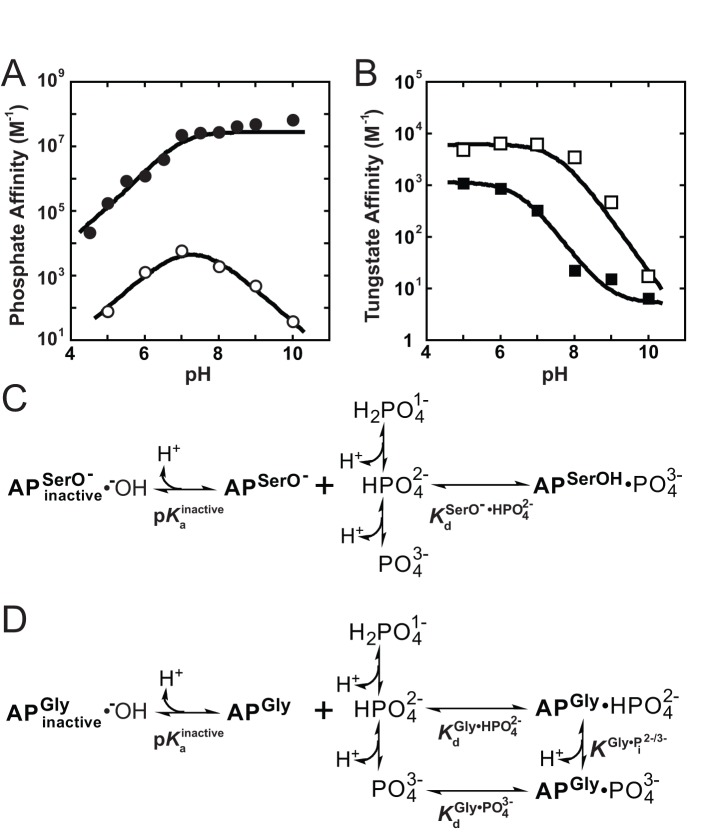
Figure 4. The pH dependence of Pi and tungstate binding for AP with and without Ser10.
(A) The pH-dependent binding of Pi to R166S AP (open circles) and S102G/R166S AP (closed circles). See Methods for assay details. Weighted, nonlinear least-squares fits of Equations S1 and S2 (see Text S9) derived from the binding models in parts (C) and (D) for R166S and S102G/R166S AP, respectively, are shown as solid lines. For R166S AP, 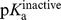 = 7.6±0.1 and
= 7.6±0.1 and 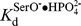 = 110±20 µM. For S102G/R166S AP,
= 110±20 µM. For S102G/R166S AP, 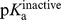 was fixed at 6.5 based on the tungstate binding data in part (B) and
was fixed at 6.5 based on the tungstate binding data in part (B) and 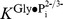 was fixed at 10−6.1 M based on the 31P NMR data in Figure 6. Fits yielded
was fixed at 10−6.1 M based on the 31P NMR data in Figure 6. Fits yielded 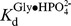 = 93±8 nM, and
= 93±8 nM, and 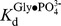 = 210±20 fM. (B) The pH-dependent binding of tungstate to R166S (open squares) and S102G/R166S AP (closed squares). A weighted, nonlinear least-squares fit of
= 210±20 fM. (B) The pH-dependent binding of tungstate to R166S (open squares) and S102G/R166S AP (closed squares). A weighted, nonlinear least-squares fit of 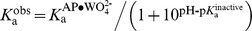 derived from a two-state tungstate binding model (
derived from a two-state tungstate binding model (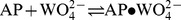 ) yielded a fit of the R166S AP data with
) yielded a fit of the R166S AP data with 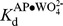 = 170±25 µM and
= 170±25 µM and 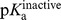 = 7.6±0.1. The corresponding fit to the observed tungstate affinity of S102G/R166S AP yielded a
= 7.6±0.1. The corresponding fit to the observed tungstate affinity of S102G/R166S AP yielded a 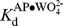 = 890±90 µM and
= 890±90 µM and 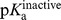 = 6.5±0.1. The tungstate affinity of S102G/R166S AP is weaker than R166S AP, indicating that Ser102 plays a favorable role in tungstate binding, possibly by allowing formation of octahedral tungstate as observed in other proteins that bind tungstate [73],[74]. At pH values ≥8 where the Pi affinity is strongest, the observed competition of 32Pi binding is likely influenced by competition from contaminating, unlabeled Pi in the tungstate stock rather than tungstate (see Materials and Methods). The dashed portion of the S102G/R166S AP tungstate fit line illustrates where the observed affinity can be accounted for by 0.5 ppm Pi contamination. Omitting the pH 9 and 10 points in the fit did not significantly change the fitted
= 6.5±0.1. The tungstate affinity of S102G/R166S AP is weaker than R166S AP, indicating that Ser102 plays a favorable role in tungstate binding, possibly by allowing formation of octahedral tungstate as observed in other proteins that bind tungstate [73],[74]. At pH values ≥8 where the Pi affinity is strongest, the observed competition of 32Pi binding is likely influenced by competition from contaminating, unlabeled Pi in the tungstate stock rather than tungstate (see Materials and Methods). The dashed portion of the S102G/R166S AP tungstate fit line illustrates where the observed affinity can be accounted for by 0.5 ppm Pi contamination. Omitting the pH 9 and 10 points in the fit did not significantly change the fitted 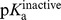 or
or 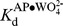 values. (C) Binding model used to fit the pH-dependent Pi affinity of R166S (and WT) AP. (D) Binding model used to fit the pH-dependent Pi affinity of S102G/R166S AP.
values. (C) Binding model used to fit the pH-dependent Pi affinity of R166S (and WT) AP. (D) Binding model used to fit the pH-dependent Pi affinity of S102G/R166S AP.
A prediction of this model—that the pK
a of 6.9 is associated with the ligand and not the enzyme—is that this pK
a would be absent in the binding profile for a ligand that lacks a pK
a in this range. As predicted, the observed acidic limb with pK
a of 6.9 was not observed with tungstate (Figure 4B, open symbols), which has a pK
a below the pH range of our assays (pK
a∼4 for 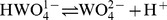 [40],[41]).
[40],[41]).
We next considered the basic limb of the bell-shaped pH-dependent profile for binding of Pi to R166S AP. The slope of −1 suggests that the loss of a single proton with a pK a of 7.6 also prevents binding, and this result mirrors the behavior of WT AP [20]. Considering that Pi does not have a pK a near 7.6 and that Pi and tungstate binding both have the basic limb with the same pK a values of 7.6 (cf., R166S AP basic limbs in Figure 4A and B), this pK a very likely represents an enzymatic deprotonation. One possible model for this binding deactivation involves deprotonation of a water molecule to leave a Zn2+-associated hydroxide ion blocking the bimetallo site of AP as suggested previously to account for the analogous pH-dependent loss of catalytic activity [20].
The above results are consistent with binding of 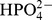 from solution. To determine whether there is additional binding from trianionic
from solution. To determine whether there is additional binding from trianionic 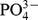 (
(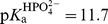 ), binding assays were extended to higher pH values. Binding of
), binding assays were extended to higher pH values. Binding of 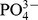 would manifest as an upturn in the basic limb of the pH dependence, but this limb remains linear with a slope of −1 in the highest pH region of 10–11.4 (Figure S9). These results provide no indication of AP binding
would manifest as an upturn in the basic limb of the pH dependence, but this limb remains linear with a slope of −1 in the highest pH region of 10–11.4 (Figure S9). These results provide no indication of AP binding 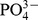 from solution and establish upper limits for the Pi dissociation constant
from solution and establish upper limits for the Pi dissociation constant 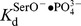 of 100 nM and 2.5 µM for WT AP and R166S AP, respectively (Table 2; Text S6; Figure S9).
of 100 nM and 2.5 µM for WT AP and R166S AP, respectively (Table 2; Text S6; Figure S9).
Table 2. Summary of pH-independent Pi dissociation constants for AP active site nucleophile mutants.
| Residue 102 | Residue 166 |
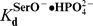 (M)a (M)a
|
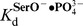 (M)b (M)b
|
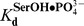 (M)c (M)c
|
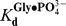 (M)d (M)d
|
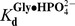 (M)e (M)e
|
| Ser | Arg | 4.6×10−7 | ≥1×10−7 | ≤2.9×10−13 | — | — |
| Gly | Arg | — | — | — | (∼1×10 −15 ) | (∼1×10 −8 ) |
| Ser | Ser | 1.1×10−4 | ≥2.5×10−6 | ≤6.9×10−11 | — | — |
| Gly | Ser | — | — | — | 2.1×10−13 | 9.3×10−8 |
—, not applicable.
Dissociation constant for 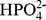 binding to deprotonated Ser102 as defined in Figure 4C from the measured pH-dependent Pi affinity in Figure 4A for R166S AP and Figure S9C for WT AP. Note that binding of
binding to deprotonated Ser102 as defined in Figure 4C from the measured pH-dependent Pi affinity in Figure 4A for R166S AP and Figure S9C for WT AP. Note that binding of 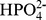 results in a proton transfer to the enzyme as illustrated in Equation 1;
results in a proton transfer to the enzyme as illustrated in Equation 1; 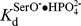 represents the observed overall binding.
represents the observed overall binding.
Lower limit of the dissociation constant for 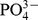 binding to deprotonated Ser102 AP determined as described in Text S6 and Figure S9.
binding to deprotonated Ser102 AP determined as described in Text S6 and Figure S9.
Upper limit for the dissociation constant for 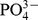 binding to protonated Ser102 AP as described in the main text and Figure 5.
binding to protonated Ser102 AP as described in the main text and Figure 5.
Dissociation constant for 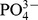 binding to S102G AP estimated from the measured
binding to S102G AP estimated from the measured 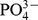 affinity of S102G/R166S AP and the expected contribution of Arg166 of 240-fold to the
affinity of S102G/R166S AP and the expected contribution of Arg166 of 240-fold to the 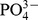 affinity (cf.,
affinity (cf., 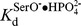 for WT and R166S AP). The dissociation constant for
for WT and R166S AP). The dissociation constant for 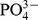 binding to S102G/R166S AP was determined from the pH-dependent binding data in Figure 4A and is defined in the model in Figure 4D.
binding to S102G/R166S AP was determined from the pH-dependent binding data in Figure 4A and is defined in the model in Figure 4D.
The above results rule out significant binding of 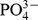 directly to AP with Ser102 intact. However, as noted above, our prior isotope-edited IR studies provide strong evidence for a proton transfer within the E•Pi complex to give bound
directly to AP with Ser102 intact. However, as noted above, our prior isotope-edited IR studies provide strong evidence for a proton transfer within the E•Pi complex to give bound 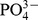 accompanied by protonation of a group on WT AP that was suggested to be Ser102 [16]. While analogous vibrational spectra could not be obtained for R166S AP due to signal-to-noise limitations, the observed 31P NMR chemical shift of Pi bound to WT and R166S AP is the same within error (3.8±0.2 and 3.7±0.2 ppm for R166S and WT AP, respectively; Text S7 and Figure S10), suggesting that the same Pi species is bound to both enzymes and allowing us to extend the assignment of bound
accompanied by protonation of a group on WT AP that was suggested to be Ser102 [16]. While analogous vibrational spectra could not be obtained for R166S AP due to signal-to-noise limitations, the observed 31P NMR chemical shift of Pi bound to WT and R166S AP is the same within error (3.8±0.2 and 3.7±0.2 ppm for R166S and WT AP, respectively; Text S7 and Figure S10), suggesting that the same Pi species is bound to both enzymes and allowing us to extend the assignment of bound 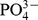 from WT AP to R166S AP.
from WT AP to R166S AP.
The pH-dependent Pi and tungstate binding results, together with the previous vibrational spectroscopy measurements and 31P NMR comparison, lead to the model for Pi binding to R166S AP (and WT AP) shown in Figure 4C. A fit of this model to the pH-dependent Pi binding data for R166S AP shown in Figure 4A yields a pH-independent dissociation constant for 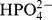 binding of
binding of 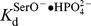 = 110 µM (Table 2) and a
= 110 µM (Table 2) and a 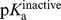 describing the basic limb of 7.6. This model further allowed us to assign intrinsic binding constants, as described below.
describing the basic limb of 7.6. This model further allowed us to assign intrinsic binding constants, as described below.
The thermodynamic cycle in Figure 5A can be used to compute a limit for the dissociation constant between 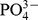 and the protonated form of Ser102, as binding of
and the protonated form of Ser102, as binding of 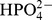 involves a formal internal proton transfer from
involves a formal internal proton transfer from 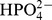 to Ser102 to give bound
to Ser102 to give bound 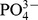 . The relationship of Figure 5B, derived from Figure 5A, and the observed binding affinity of
. The relationship of Figure 5B, derived from Figure 5A, and the observed binding affinity of 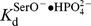 = 110 µM, the pK
a of 11.7 for
= 110 µM, the pK
a of 11.7 for 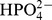 , and the pK
a of ≤5.5 for deprotonation of Ser102 [20] give the affinity of R166S AP with protonated Ser102 for
, and the pK
a of ≤5.5 for deprotonation of Ser102 [20] give the affinity of R166S AP with protonated Ser102 for 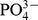 ,
, 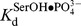 ≤69 pM [ = ((110 µM)×(10−11.7 M))/(≥10−5.5 M); Table 2]. The calculation for WT AP was carried out analogously using the thermodynamic cycle in Figure 5A with the value of
≤69 pM [ = ((110 µM)×(10−11.7 M))/(≥10−5.5 M); Table 2]. The calculation for WT AP was carried out analogously using the thermodynamic cycle in Figure 5A with the value of 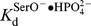 = 0.46 µM (Table 2) obtained by fitting the pH-dependent Pi affinity (Figure S9C; [16]) to the model in Figure 4C. Using this value and the relationship of Figure 5B yields the value for WT AP of
= 0.46 µM (Table 2) obtained by fitting the pH-dependent Pi affinity (Figure S9C; [16]) to the model in Figure 4C. Using this value and the relationship of Figure 5B yields the value for WT AP of 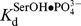 ≤290 fM [ = ((0.46 µM)×(10−11.7 M))/(≥10−5.5 M)]; Table 2].
≤290 fM [ = ((0.46 µM)×(10−11.7 M))/(≥10−5.5 M)]; Table 2].
Figure 5. Thermodynamic cycle for 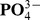 binding AP with Ser102 protonated.
binding AP with Ser102 protonated.
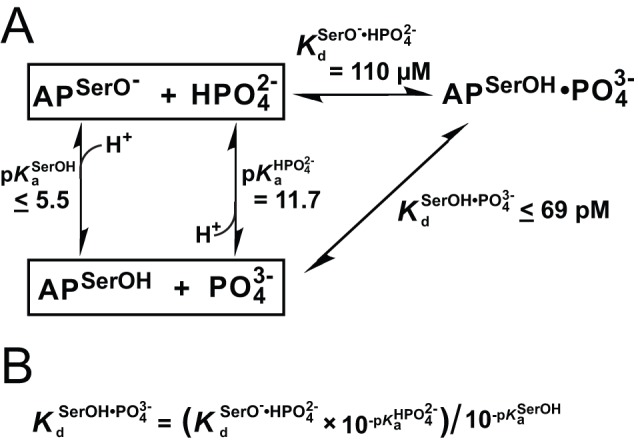
(A) The value of 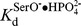 for R166S AP is from a fit of the model in Figure 4C to the pH-dependent Pi binding affinity in Figure 4A. The Ser102 pK
a is an upper limit [20], and thus, the dissociation constant between protonated Ser102 and
for R166S AP is from a fit of the model in Figure 4C to the pH-dependent Pi binding affinity in Figure 4A. The Ser102 pK
a is an upper limit [20], and thus, the dissociation constant between protonated Ser102 and 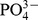 (
(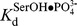 ) is also an upper limit (≤69 pM). The same cycle was used to establish an upper limit for the dissociation constant between WT AP with Ser102 protonated and
) is also an upper limit (≤69 pM). The same cycle was used to establish an upper limit for the dissociation constant between WT AP with Ser102 protonated and 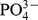 ,
, 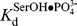 ≤290 fM, from the following values:
≤290 fM, from the following values: 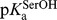 ≤5.5,
≤5.5, 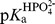 = 11.7, and
= 11.7, and 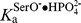 = 0.46 µM (Table 2). (B) Relationship derived from the thermodynamic cycle of part (A).
= 0.46 µM (Table 2). (B) Relationship derived from the thermodynamic cycle of part (A).
pH-dependent Pi binding to AP without the Ser102 nucleophile
We conducted pH-dependent Pi binding measurements with S102G/R166S AP using the 32Pi binding assay described above, as we could measure equilibrium binding constants with this AP mutant and not just limits as for S102G AP. The Pi affinity of S102G/R166S AP (Figure 4A) decreases log-linearly with a slope of 1 at acidic pH, indicating that a single protonation event prevents binding, as observed for R166S AP with Ser102 present. As 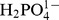 has a pK
a in the pH range of the observed acidic limb, it is likely that S102G/R166S AP does not have measurable affinity for
has a pK
a in the pH range of the observed acidic limb, it is likely that S102G/R166S AP does not have measurable affinity for 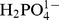 , just like WT and R166S AP. Furthermore, as observed for R166S AP here and for WT AP previously [20], the pH dependence for S102G/R166S AP binding to tungstate, which does not have a pK
a in this range, lacks the acidic limb pK
a (Figure 4B), strongly supporting this interpretation.
, just like WT and R166S AP. Furthermore, as observed for R166S AP here and for WT AP previously [20], the pH dependence for S102G/R166S AP binding to tungstate, which does not have a pK
a in this range, lacks the acidic limb pK
a (Figure 4B), strongly supporting this interpretation.
The observed Pi binding affinity of S102G/R166S AP remains constant above pH 7 (Figure 4A). This dependence is different than that for WT and R166S AP, indicating that the protonation event(s) involved in Pi binding to S102G/R166S AP differ from those when Ser102 is present. The simplest model to account for the lack of an apparent basic limb for S102G/R166S AP would be that 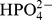 binds and the protein does not undergo the deprotonation that prevents binding as observed for WT and R166S AP. This model predicts that tungstate binding to S102G/R166S AP should also lack a basic limb. However, as shown in Figure 4B, tungstate binding decreases log linearly with a slope of 1 as the pH is raised, strongly suggesting that, like WT and R166S AP, S102G/R166S AP undergoes a pH-dependent loss of binding. The lower pK
a for S102G/R166S AP of 6.5, relative to 7.6 measured for R166S AP (Figure 4B), is consistent with more favorable formation of a Zn2+-associated hydroxide ion in the absence of the Ser102 anion. Nevertheless, our interpretations herein do not depend on the validity of this particular model for loss of binding at higher pH.
binds and the protein does not undergo the deprotonation that prevents binding as observed for WT and R166S AP. This model predicts that tungstate binding to S102G/R166S AP should also lack a basic limb. However, as shown in Figure 4B, tungstate binding decreases log linearly with a slope of 1 as the pH is raised, strongly suggesting that, like WT and R166S AP, S102G/R166S AP undergoes a pH-dependent loss of binding. The lower pK
a for S102G/R166S AP of 6.5, relative to 7.6 measured for R166S AP (Figure 4B), is consistent with more favorable formation of a Zn2+-associated hydroxide ion in the absence of the Ser102 anion. Nevertheless, our interpretations herein do not depend on the validity of this particular model for loss of binding at higher pH.
The absence of weaker binding of Pi as pH is increased indicates that the deactivating deprotonation of S102G/R166S AP revealed via tungstate binding is countered by a favorable deprotonation associated with Pi binding. This scenario is depicted in Figure 4D in which pH-independent binding arises from two counterbalancing deprotonation events, generation of inactive AP (at higher pH values), as noted above, and generation of the tighter binding species 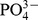 via deprotonation of the predominant
via deprotonation of the predominant 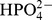 species at pH 7–10. Thus, S102G/R166S AP binds
species at pH 7–10. Thus, S102G/R166S AP binds 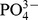 preferentially to
preferentially to 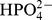 , presumably by virtue of the increased negative charge of
, presumably by virtue of the increased negative charge of 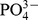 and the stronger net interactions with the positively charged AP active site. As elaborated below, this binding is much stronger than binding to R166S AP due to the absence of the negatively charged Ser102. These results also support our proposal that Ser102 acts as the proton acceptor in WT and R166S AP, because in its absence there is no internal proton transfer to the protein.
and the stronger net interactions with the positively charged AP active site. As elaborated below, this binding is much stronger than binding to R166S AP due to the absence of the negatively charged Ser102. These results also support our proposal that Ser102 acts as the proton acceptor in WT and R166S AP, because in its absence there is no internal proton transfer to the protein.
While the above results indicate stronger binding of 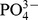 than
than 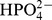 , we considered whether S102G/R166S AP also has measurable binding of
, we considered whether S102G/R166S AP also has measurable binding of 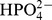 . If
. If 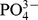 were the only species to detectably bind, we would expect to observe a single and constant 31P NMR chemical shift associated with S102G/R166S-bound
were the only species to detectably bind, we would expect to observe a single and constant 31P NMR chemical shift associated with S102G/R166S-bound 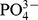 across all observable pH values. Instead, we observe that the chemical shift of Pi bound to S102G/R166S AP migrates as the solution pH is varied (Figure 6A), supporting a general model in which more than one Pi species binds with the bound species in fast exchange. Additional 31P NMR measurements with Pi in excess of AP demonstrated that the observed chemical shift variation does not reflect exchange between unbound and bound Pi (Text S8 and Figure S11). The observed chemical shift cannot be used to directly assign the ionic Pi form—the chemical shift does not correspond to that of any of the ionic forms in solution (Table S3), presumably due to active site interactions that are distinct from those in solution. Isotope-edited vibrational spectroscopy with Pi bound to S102G/R166S AP, as was carried out previously for WT AP [16], gave complex spectra (Figure S12) that could not be interpreted, presumably also due to the effects from the active site environment.
across all observable pH values. Instead, we observe that the chemical shift of Pi bound to S102G/R166S AP migrates as the solution pH is varied (Figure 6A), supporting a general model in which more than one Pi species binds with the bound species in fast exchange. Additional 31P NMR measurements with Pi in excess of AP demonstrated that the observed chemical shift variation does not reflect exchange between unbound and bound Pi (Text S8 and Figure S11). The observed chemical shift cannot be used to directly assign the ionic Pi form—the chemical shift does not correspond to that of any of the ionic forms in solution (Table S3), presumably due to active site interactions that are distinct from those in solution. Isotope-edited vibrational spectroscopy with Pi bound to S102G/R166S AP, as was carried out previously for WT AP [16], gave complex spectra (Figure S12) that could not be interpreted, presumably also due to the effects from the active site environment.
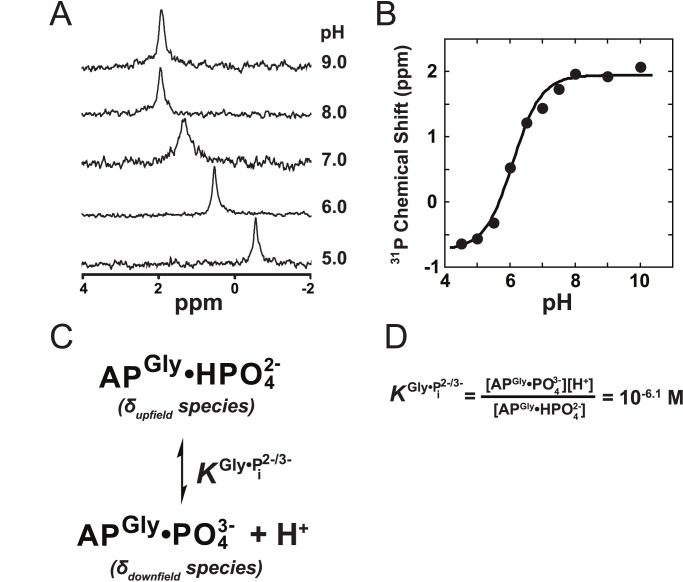
Figure 6. The pH-dependence of the 31P chemical shift of Pi bound to S102G/R166S AP.
(A) 31P NMR spectra of Pi bound to S102G/R166S AP at various pH values. See Materials and Methods for conditions. (B) The chemical shift of Pi-bound to S102G/R166S AP versus the solution pH. A nonlinear least-squares fit to an equation (see Materials and Methods) derived from the binding model in (C) yields δupfield and δdownfield values of −0.74 and 1.94 ppm, respectively, and a value for 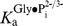 of 10−6.1 M as defined in (D).
of 10−6.1 M as defined in (D).
Although the bound Pi species could not be directly assigned via NMR or IR measurements, the pH dependence of binding provides strong evidence for the identity of the bound species. As noted above, the differential pH dependence of Pi and tungstate binding described above (Figure 4) strongly suggests that 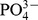 binds predominantly at pH values above 6.5. Further, the 2.7 ppm 31P chemical shift decrease for Pi bound to S102G/R166S AP upon going from high to low pH (Figure 6B) is similar to the decrease of 2.5 ppm upon protonation of
binds predominantly at pH values above 6.5. Further, the 2.7 ppm 31P chemical shift decrease for Pi bound to S102G/R166S AP upon going from high to low pH (Figure 6B) is similar to the decrease of 2.5 ppm upon protonation of 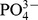 to give
to give 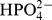 in aqueous solution [42]. Thus, the chemical shift at the lower pH likely arises from predominant binding of
in aqueous solution [42]. Thus, the chemical shift at the lower pH likely arises from predominant binding of 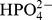 . A fit to the pH dependence of the chemical shift migration yields a pH-dependent equilibrium constant (
. A fit to the pH dependence of the chemical shift migration yields a pH-dependent equilibrium constant (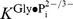 ) between S102G/R166S-bound
) between S102G/R166S-bound 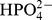 and
and 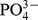 of 10−6.1 M (p
of 10−6.1 M (p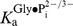 = 6.1; Figure 6B). This S102G/R166S AP-bound pK
a of
= 6.1; Figure 6B). This S102G/R166S AP-bound pK
a of 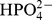 is 5.6 units lower than its solution pK
a of 11.7, reflecting the ability of the protein active site to strongly favor formation of
is 5.6 units lower than its solution pK
a of 11.7, reflecting the ability of the protein active site to strongly favor formation of 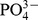 relative to solution.
relative to solution.
Pi bound to S102G AP gives a constant 31P chemical shift from pH 4.5–10.2 with a value that is the same within error as the high-pH chemical shift of Pi bound to S102G/R166S AP (Figure S11A). This observation supports the above model and suggests, as expected, that Arg166 (S102G versus S102G/R166S AP) provides additional, preferential stabilization of bound 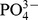 over
over 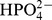 .
.
Figure 4D shows the Pi binding model for S102G/R166S AP that incorporates all of the features noted above: an inactivating pK
a, binding of 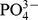 and
and 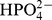 , and protonation equilibria between both free and bound
, and protonation equilibria between both free and bound 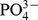 and
and 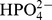 . The equilibrium constants in this scheme were determined from the above-noted pH-dependent binding and NMR data (Figures 4 and 6), as described in the figure legend.
. The equilibrium constants in this scheme were determined from the above-noted pH-dependent binding and NMR data (Figures 4 and 6), as described in the figure legend.
Our data also indicate that S102G AP binds Pi stronger than S102G/R166S AP, as expected from the additional interaction of Arg166 with the phosphoryl group (Figure 1). We could only obtain a lower limit for this affinity, but we could crudely estimate this value. Arg166 stabilizes 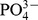 binding by 240-fold when Ser102 is present [(
binding by 240-fold when Ser102 is present [(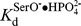 )R166S/(
)R166S/(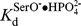 )WT = 110 µM/0.46 µM = 240; Table 2] and a similar stabilization would be expected when Ser102 is absent because the same interactions can form. We thus estimate a dissociation constant of ∼1 fM [(
)WT = 110 µM/0.46 µM = 240; Table 2] and a similar stabilization would be expected when Ser102 is absent because the same interactions can form. We thus estimate a dissociation constant of ∼1 fM [(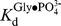 )S102G/R166S/240 = 210 fM/240 = 0.9 fM] for
)S102G/R166S/240 = 210 fM/240 = 0.9 fM] for 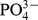 binding to S102G AP (Table 2). While this is a crude estimate, the affinity is clearly in the range of the strongest measured in biology [17],[43]. In addition, while known ligands with femtomolar binding affinities contain at least 16 atoms [43],
binding to S102G AP (Table 2). While this is a crude estimate, the affinity is clearly in the range of the strongest measured in biology [17],[43]. In addition, while known ligands with femtomolar binding affinities contain at least 16 atoms [43], 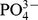 has just five atoms, albeit with high charge density, and only four directly interacting with the AP active site.
has just five atoms, albeit with high charge density, and only four directly interacting with the AP active site.
The enormous rate enhancement that AP provides by interacting with the transferred phosphoryl group transition state suggests that this enzyme is capable of making very strong interactions. Indeed, the ∼1 fM binding of 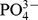 shown here illustrates that a substantial portion of the transition state stabilization energy can be unmasked and manifested in the ground state by removing the Ser102 alkoxide. The substantial additional affinity for the transition state presumably arises from positioning of the reacting Ser102 and phosphoryl group as well as optimized positioning of interacting groups to better complement the trigonal bipyramidal geometry of the transition state versus the tetrahedral geometry of the
shown here illustrates that a substantial portion of the transition state stabilization energy can be unmasked and manifested in the ground state by removing the Ser102 alkoxide. The substantial additional affinity for the transition state presumably arises from positioning of the reacting Ser102 and phosphoryl group as well as optimized positioning of interacting groups to better complement the trigonal bipyramidal geometry of the transition state versus the tetrahedral geometry of the 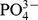 ground state (cf., models for the
ground state (cf., models for the 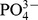 ground state and the transition state in Figure 7).
ground state and the transition state in Figure 7).
Figure 7. Models for AP binding Pi dianion and trianion and summary of AP binding energetics.
(A) The dissociation constant limit for dianionic phosphate monoester binding to WT AP was determined in ref. [20]. This limit is also expected to hold for R166S AP where an interacting residue is removed. (B) Removing Ser102 strengthens binding of a dianion by ≥103-fold, as 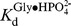 was estimated to be ∼10 nM (Table 2). (C) Trianion binding (
was estimated to be ∼10 nM (Table 2). (C) Trianion binding (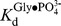 ; Table 2) was estimated to be ∼1 fM and is 107-fold stronger than dianion binding. (D) The AP rate enhancement is 1027-fold (for methyl phosphate dianion hydrolysis: k
cat/K
M = 1.2×106 M−1 s−1
[20] and k
uncat∼4×10−22 M−1 s−1
[75]), corresponding to a theoretical dissociation constant for transition state binding of 10−12 fM (derived in Figure S1 of ref. [16]). This theoretical affinity reflects binding of the enzyme to the transition state while accompanied by replacement of water by the active site Ser102 nucleophile. The energetics of these two processes cannot be separated and the formal dissociation constant reflects contributions from both binding interactions and positioning of the Ser102 nucleophile and substrate.
; Table 2) was estimated to be ∼1 fM and is 107-fold stronger than dianion binding. (D) The AP rate enhancement is 1027-fold (for methyl phosphate dianion hydrolysis: k
cat/K
M = 1.2×106 M−1 s−1
[20] and k
uncat∼4×10−22 M−1 s−1
[75]), corresponding to a theoretical dissociation constant for transition state binding of 10−12 fM (derived in Figure S1 of ref. [16]). This theoretical affinity reflects binding of the enzyme to the transition state while accompanied by replacement of water by the active site Ser102 nucleophile. The energetics of these two processes cannot be separated and the formal dissociation constant reflects contributions from both binding interactions and positioning of the Ser102 nucleophile and substrate.
Destabilization of 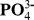 Binding by the Ser102 Nucleophile
Binding by the Ser102 Nucleophile
With the binding affinities determined for individual Pi species (Table 2), we were able to determine a minimum amount for the destabilization of 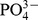 binding caused by the Ser102 alkoxide. We compared the
binding caused by the Ser102 alkoxide. We compared the 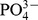 affinity in AP lacking Ser102 to AP with the deprotonated Ser102 alkoxide intact. In the absence of the Ser102 alkoxide, the
affinity in AP lacking Ser102 to AP with the deprotonated Ser102 alkoxide intact. In the absence of the Ser102 alkoxide, the 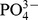 dissociation constant is 210 fM and ∼1 fM for S102G/R166S and S102G AP, respectively. Limits for the
dissociation constant is 210 fM and ∼1 fM for S102G/R166S and S102G AP, respectively. Limits for the 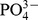 affinity of AP with deprotonated Ser102 (+/− Arg166) were estimated from the absence of detectable Pi binding at high pH (Figure S9), as described above, and give lower limits for the
affinity of AP with deprotonated Ser102 (+/− Arg166) were estimated from the absence of detectable Pi binding at high pH (Figure S9), as described above, and give lower limits for the 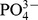 dissociation constant (
dissociation constant (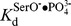 ) of ≥2.5 µM and ≥100 nM for R166S and WT AP, respectively, and thus, upper limits for the affinity. Comparing these affinity limits to the
) of ≥2.5 µM and ≥100 nM for R166S and WT AP, respectively, and thus, upper limits for the affinity. Comparing these affinity limits to the 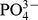 affinity in the absence of Ser102 reveals a destabilization from the Ser102 alkoxide of at least 107–108 fold (for S102G/R166S AP, K
rel = ≥2.5 µM/210 fM; for S102G AP, K
rel = ≥100 nM/∼1 fM). (For a further comparison of the
affinity in the absence of Ser102 reveals a destabilization from the Ser102 alkoxide of at least 107–108 fold (for S102G/R166S AP, K
rel = ≥2.5 µM/210 fM; for S102G AP, K
rel = ≥100 nM/∼1 fM). (For a further comparison of the 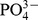 affinity in the presence of protonated Ser102 and with Ser102 mutated to Gly, see Text S10 and Figure S13 therein.)
affinity in the presence of protonated Ser102 and with Ser102 mutated to Gly, see Text S10 and Figure S13 therein.)
Destabilization of Dianion Substrate Binding by the Ser102 Nucleophile
Our ability to measure the 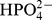 affinity of S102G/R166S AP, with a dissociation constant of 90 nM, allows us to estimate the Ser102 destabilization to a dianionic phosphate monoester substrate, as
affinity of S102G/R166S AP, with a dissociation constant of 90 nM, allows us to estimate the Ser102 destabilization to a dianionic phosphate monoester substrate, as 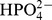 and a phosphate ester have the same overall charge and tetrahedral geometry. (See Text S11 for discussion of a previous [16] estimation of the Ser102 destabilization of dianion binding.) In comparison to WT AP with Ser102 intact, which has a dissociation constant for dianionic substrate binding of >10 µM [20], S102G/R166S AP binds a dianion at least 102-fold more strongly (>10 µM versus 90 nM), suggesting a destabilization of substrate (E•S) binding from the Ser102 alkoxide of at least 102-fold. Analogous considerations lead to a suggested destabilization of at least 103-fold with Arg166 present (WT versus S102G AP) as the
and a phosphate ester have the same overall charge and tetrahedral geometry. (See Text S11 for discussion of a previous [16] estimation of the Ser102 destabilization of dianion binding.) In comparison to WT AP with Ser102 intact, which has a dissociation constant for dianionic substrate binding of >10 µM [20], S102G/R166S AP binds a dianion at least 102-fold more strongly (>10 µM versus 90 nM), suggesting a destabilization of substrate (E•S) binding from the Ser102 alkoxide of at least 102-fold. Analogous considerations lead to a suggested destabilization of at least 103-fold with Arg166 present (WT versus S102G AP) as the 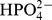 affinity of S102G is expected to be ∼10-fold stronger than the
affinity of S102G is expected to be ∼10-fold stronger than the 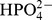 affinity of S102G/R166S AP (see Text S12). From a practical perspective, if Ser102 did not provide this destabilization, the enzyme would saturate with substrate concentrations of ∼10 nM, at least 103-fold lower than the K
M with destabilization from Ser102 present. Such a low K
M would greatly limit turnover and function any time substrate concentrations exceeded the K
M.
affinity of S102G/R166S AP (see Text S12). From a practical perspective, if Ser102 did not provide this destabilization, the enzyme would saturate with substrate concentrations of ∼10 nM, at least 103-fold lower than the K
M with destabilization from Ser102 present. Such a low K
M would greatly limit turnover and function any time substrate concentrations exceeded the K
M.
The 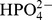 affinity in the absence of Ser102 is very strong, but the
affinity in the absence of Ser102 is very strong, but the 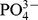 affinity is much stronger—at least 107 fold stronger (Table 2;
affinity is much stronger—at least 107 fold stronger (Table 2; 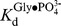 /
/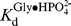 for S102G AP). In Text S13 we discuss potential origins of this enhanced affinity.
for S102G AP). In Text S13 we discuss potential origins of this enhanced affinity.
In addition to destabilizing substrate binding, Ser102 also destabilizes the binding of the reaction product, Pi, by ∼103-fold at pH 8.0 (Table 1), thereby preventing subnanomolar product inhibition. This consideration, along with the analysis of substrate destabilization above, strongly suggests that ground state destabilization from an anionic nucleophile can make a substantial catalytic contribution and suggests that other phosphatases with anionic nucleophiles may also exhibit ground state electrostatic repulsion.
Active Site Nucleophile Destabilization in a Protein Tyrosine Phosphatase
To test whether the results in AP generalize to other phosphatases with negatively charged active site nucleophiles, we compared the Pi affinity of a protein tyrosine phosphatase (PTP) with and without its active site nucleophile. The PTP Stp1 is a member of the low-molecular weight PTP family, which uses a negatively charged cysteine nucleophile [44]. With its Cys11 nucleophile intact, we measured a dissociation constant for Pi binding by Stp1 of 18 mM at pH 6.0 (Table 3; Figure S14), in reasonable agreement with a previous measurement [45]. Measurements were carried out at pH 6.0 because this is the pH of maximal catalytic activity [46]. When Cys11 is mutated to Gly, Pi binding gets stronger, with a dissociation constant of 10 µM, demonstrating a 103-fold destabilizing influence from the Cys11 nucleophile. The observed destabilization effect of Ser102 in AP (R166S) at pH 6 is also ∼103-fold (cf., data points at pH 6 in Figure 4A). In the absence of extensive pH-dependent binding studies, we cannot assign the ionic form of Pi that binds Stp1 as was done for AP and mutants thereof. Nevertheless, our findings of analogous increases in affinity upon removal of Cys11 from Stp1 supports a model in which this anionic active site nucleophile destabilizes ground state binding, and raises the possibility that ground state destabilization is a general strategy among phosphatases with anionic nucleophiles.
Table 3. Binding of Pi to a PTP with and without its active site Cys anionic nucleophile.
See Materials and Methods for assay conditions.
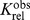 is the ratio of the observed Pi dissociation constant in the presence of Cys11 compared to the dissociation constant in the absence of Cys11: K
d(Cys11)/K
d (Gly11).
is the ratio of the observed Pi dissociation constant in the presence of Cys11 compared to the dissociation constant in the absence of Cys11: K
d(Cys11)/K
d (Gly11).
Preferential Ground State Destabilization from Ser102
We propose that the destabilization from electrostatic repulsion by Ser102 is present in the substrate (E•S) and product (E•Pi) ground states and is absent, or nearly so, in the reaction's transition state. Recall that in order for ground state destabilization to play a role in catalysis, the destabilization must not be present in the transition state (as illustrated in Figure 2D). Specific destabilization of the ground state results in a lowering of the transition state barrier and catalysis of the chemical step is thereby accelerated.
Previous studies of phosphoryl transfer reactions in solution [47]–[49] provide strong evidence against substantial electrostatic repulsion in the transition state, suggesting that electrostatic repulsion in the enzymatic ground state does not carry over into the transition state as required for ground state destabilization to be catalytic. Text S14 provides a summary of these studies.
Summary and Implications
To accelerate chemical reactions, enzymes must provide stabilization to the reaction's transition state yet limit binding to ground states—i.e., substrates and products. As noted in the Introduction, AP imparts an exceptional rate enhancement to the hydrolysis of phosphate monoesters, corresponding to a formal stabilization of the transition state of 1027-fold. The same active site that provides this enormous transition state stabilization limits ground state binding to an affinity of at most 10 µM, which is more than 1022-fold weaker than the formal transition state stabilization (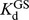 >10−5 M versus
>10−5 M versus 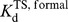 = 10−27 M; Figure 1).
= 10−27 M; Figure 1).
The similarity of the transition and ground states of the AP-catalyzed reaction (Figure 1) raises the question of how AP distinguishes so profoundly between these states and, in particular, how AP specifically limits ground state binding. Our results support a model in which electrostatic repulsion from the anionic active site Ser102 nucleophile plays an important role in limiting ground state binding.
The most common source of preferential ground state destabilization in enzyme active sites, as described in the Introduction, is presumably the ubiquitous entropic cost incurred upon binding free substrates and positioning them with respect to catalytic residues in the enzyme active site (and to each other for multisubstrate reactions). Other sources of ground state destabilization have also been suggested when binding energy, in addition to paying for the entropic penalty of binding, is used to impart geometrical distortion (typically referred to as “strain”) or electrostatic destabilization to the bound ground state. Approaches including X-ray crystallography (e.g., [50]–[52]), vibrational spectroscopy (for review, see [53]), and binding isotope effect measurements (e.g., [54]–[59]) have identified enzyme-bound substrates (or analogs thereof) in alternative, or distorted, conformations relative to the corresponding structures in solution. These distortions in the ground state tend to approach the conformation thought to be present in the transition state, leading to the proposal that such distortions contribute to catalysis. While our understanding of transition state structures and properties are well enough advanced that many of these proposals are likely correct, they do not reveal the underlying energetics of the destabilizing distortion or the specific residues responsible for imparting the distortion (see also [60]).
We have combined binding, structural, and spectroscopic studies of AP to obtain a quantitative energetic estimate of ground state destabilization and have assigned this effect to a particular active site residue, the active site nucleophile Ser102. Similar destabilization was shown for an unrelated phosphatase, PTP, and is likely present in the many other classes of phosphoryl transfer enzymes that use anionic nucleophiles or metal-coordinated anionic hydroxide.
The ≥103-fold electrostatic ground state destabilization from anionic nucleophiles ascribed herein is one component of the overall transition state stabilization conferred by AP and other phosphatases. As illustrated in Figure 7, even after removing the ≥103-fold destabilization from Ser102, binding is still much weaker compared to the formal transition state stabilization implied by the 1027-fold rate enhancement that AP provides relative to the corresponding reaction in water. Thus, destabilization from Ser102 is just one component that, together with other active site features and properties of AP, imparts the overall observed catalysis, as is consistent with the general view that enzymes catalyze reactions through multiple mechanisms and interactions, each with a relatively modest contribution [4],[23]. Text S15 presents further discussion of these other catalytic mechanisms and provides additional context for the observations herein.
Materials and Methods
AP Expression and Purification
Mutant and WT AP were purified using an N-terminal maltose binding protein (MBP) fusion construct (AP-MBP) in the pMAL-p2X vector (New England Biolabs), as previously described [37]. Purity was estimated to be >95% as judged visually by band intensities on Coomassie blue-stained SDS-polyacrylamide gels. Protein concentrations were determined by absorbance at 280 nm (background subtracted by absorbance at 330 nm) in 8 M guanidine hydrochloride (Gdn•HCl) using a calculated extinction coefficient for the AP monomer of 31,390 M−1 cm−1 [61]. Concentrations of active WT AP and R166S AP were confirmed by activity assays using 1 mM p-nitrophenyl phosphate (pNPP) and agreed with previously reported k cat values [35] to within 20%.
Following purification, the ratio of AP to Pi present was approximately 0.6 for WT AP and 0.95–1 for the Ser102 AP mutants. The fractional Pi content was reduced to below 0.1 by dialysis in 6 M Gdn•HCl at 25°C for several days, as previously described [16]. R166S AP did not have associated Pi after purification but was still subjected to the same dialysis procedure as the other AP variants. For WT and R166S AP, activity assays using pNPP demonstrated that at least 90% of the pre-dialyzed activity was retained. For the Ser102 mutants, which lacked measurable activity, the post-dialyzed samples were capable of stoichiometric binding of Pi, similarly indicating that there was no significant loss in Pi binding activity from the dialysis procedure.
Pi Binding Affinity Measurements
AP•Pi affinities were previously determined using kinetic inhibition assays, typically by inhibition of pNPP activity or promiscuous p-nitrophenyl sulfate (pNPS) activity (e.g., [16],[20],[62]). The observed low level of activity of the Ser102 mutant preparations is likely due to contaminating phosphatase activity (Text S1), and thus, inhibition of this activity would not reflect binding to the Ser102 mutants. Consequently, a new equilibrium-binding assay was developed that enabled the determination of Pi dissociation constants. For this assay, 32Pi (∼200 pM or less; Perkin Elmer NEX053002MC) was added to samples containing varying concentrations of AP (with less than 0.1 fraction pre-bound Pi) in the standard buffer conditions of 100 mM buffer, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2 at 4°C. The following buffers were used over the indicated pH ranges: NaAcetate (4.5–5.5), NaMES (5.5), NaMaleate (6.0–6.5), Tris•HCl (7.0–7.5), NaMOPS (7.0–8.0), NaCHES (8.5–9.0), and NaCAPS (10–10.5).
For equilibrium measurements, after a period sufficient to allow equilibration as demonstrated by achieving constant binding over time, each AP sample was subjected to brief filtration through a 10 kDa molecular weight cutoff centrifugal filter (VWR centrifugal filters, modified PES, 10K, 500 µL) by centrifugation at 3,600 g for ∼90 s. (Binding of Pi to S102G and S102A AP likely does not reach equilibration within the time course of the assay; limits for their Pi affinities were estimated using the kinetics of Pi uptake and dissociation as described in Text S3 and figures therein.) The filtrate volume (10–50 µL), which was much smaller than the retentate volume (400 µL) so as to avoid significant changes in the protein concentration in the retentate, is expected to contain free 32Pi. The retentate is expected to contain both free and bound 32Pi. No significant AP (<0.1%) passed through the filter as assessed by activity assays of the filtrate of WT and R166S AP samples. Variation of the filtration time and volume did not result in significant differences in the concentration of 32Pi passing through the filter, suggesting that bound 32Pi is not significantly lost over the time of centrifugation. Scintillation counting of both the filtrate and retentate was used to measure the concentrations of free and bound 32Pi at the various AP concentrations, and the fraction 32Pi bound dependence on the AP concentration was used to determine dissociation constants using a modified binding equation, f
bound = (C)×([AP]/([AP]+K
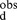 ))+(1–C), where C allows for background levels of apparent binding in the absence of protein. Samples containing no protein usually gave fraction 32Pi values very close to 0, although background levels ranging from −0.02 to 0.15 were observed in some instances (see Figures S1A, S8A, S8C, and S8E).
))+(1–C), where C allows for background levels of apparent binding in the absence of protein. Samples containing no protein usually gave fraction 32Pi values very close to 0, although background levels ranging from −0.02 to 0.15 were observed in some instances (see Figures S1A, S8A, S8C, and S8E).
An alternative assay was used in some instances to lower background levels of apparent Pi binding and thereby provide greater sensitivity to small amounts of bound Pi. Filtration units that contained G-25 Sephadex (USA Scientific) in the top portion to trap unbound 32Pi and allow bound 32Pi to pass through always trapped ∼100% of the unbound 32Pi so that when no protein is present the background fraction binding observed is very close to 0. However, very high protein concentrations did not reach 100% binding as expected, but only approached 85%–90% bound—presumably from loss of 32Pi bound to AP as the bound complex passes through the Sephadex resin during the filtration. The uptake and dissociation of 32Pi measured with these filters (vide infra) give results in agreement with the uptake and dissociation of 32Pi results obtained using the membrane filtration method described above (see Figure S8I–L).
To measure the uptake of 32Pi by the AP sample, the fraction of 32Pi bound was measured over time starting just after the addition of 32Pi to the AP samples. The uptake was fit to the single exponential equation 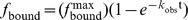 . Plotting k
obs versus the AP concentration allowed k
on and k
off values to be determined by fitting the data to the equation for bimolecular binding rates of
. Plotting k
obs versus the AP concentration allowed k
on and k
off values to be determined by fitting the data to the equation for bimolecular binding rates of 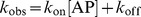 (see Table S1 for kinetic values determined for each AP mutant). For S102G and S102A AP, the amount of 32Pi uptake observed was much less than expected, potentially reflecting a protein inactivation process. Fitting of a model allowing for irreversible protein inactivation to the Pi binding kinetics for these mutants was conducted using the KinTek Global Explorer program [63],[64] as described in the Text S3 and Figure S4 (see also Figures S5 and S6).
(see Table S1 for kinetic values determined for each AP mutant). For S102G and S102A AP, the amount of 32Pi uptake observed was much less than expected, potentially reflecting a protein inactivation process. Fitting of a model allowing for irreversible protein inactivation to the Pi binding kinetics for these mutants was conducted using the KinTek Global Explorer program [63],[64] as described in the Text S3 and Figure S4 (see also Figures S5 and S6).
Although k
off values can in principle be determined from the uptake assays, these values, determined by the y-intercept of plots of the observed uptake rate constant versus the concentration of protein, are highly sensitive to small errors in the slope (k
on). We used chase assays to independently determine k
off for Pi binding, which were conducted by first incubating 32Pi with concentrations of AP sufficient to result in near complete 32Pi binding, and then after incubation times long enough to allow equilibration, saturating levels of unlabeled Pi well above the AP and 32Pi concentrations were added. The concentration of the unlabeled Pi addition was varied (2–20 mM) to ensure saturation and the absence of any secondary effects. Immediately following the addition of unlabeled Pi, the filtration procedure was used to determine the fraction 32Pi bound. As 32Pi dissociates from the protein it is replaced by unlabeled Pi and the observed fraction of 32Pi decreases. The time-dependent loss of the fraction 32Pi bound was fit to a single exponential decay equation 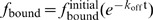 .
.
The WT Stp1•Pi affinity was determined using a kinetic inhibition assay. The pNPP hydrolysis activity of Stp1 was measured in 20 mM NaMaleate, 100 µM Na2EDTA, and 0.15 M NaCl at pH 6.0 and 4°C in the absence and presence of Pi inhibitor. A range of Pi concentrations was added to the kinetic assays from at least 5-fold below to 5-fold above the inhibition constant. The concentration of Stp1 was 20 nM and the concentration of pNPP was 50 µM (5-fold below the K
M under these conditions so that the K
i essentially equals the K
d for Pi binding). Nonlinear least-squares fits of the equation for competitive inhibition [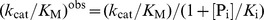 ] gave fits with standard errors of less than 10% (Figure S14B).
] gave fits with standard errors of less than 10% (Figure S14B).
The C11G Stp1•Pi affinity was determined using the equilibrium-binding assay that was used for AP described above. The buffer conditions, pH, and temperature were the same as those for the WT Stp1 kinetic inhibition assays (Figure S14A).
Tungstate Affinity Measurements
The binding of tungstate to the S102G/R166S AP mutant was measured using a variation of the equilibrium-binding assay described above in which observed 32Pi binding is competed with tungstate. Various concentrations of tungstate (at least 5-fold above and below the expected binding dissociation constant) were first incubated with a concentration of S102G/R166S AP needed to achieve ∼0.5 fraction 32Pi binding with no tungstate present under the standard buffer conditions at 4°C. Variation of the incubation time of S102G/R166S AP with tungstate from 1–6 h did not affect the observed competition binding. After this first incubation, trace 32Pi was added and the sample was incubated further to allow 32Pi binding to complete. The resulting dependence of the tungstate concentration on the observed fraction 32Pi bound was well fit to the simple binding isotherm, 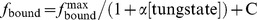 , where α is the K
a of tungstate binding in the limit that the free tungstate concentration is equal to the total tungstate concentration and C is the background fractional 32Pi binding as the tungstate concentration approaches infinity (<0.15). The tungstate competition assays had 0.5–10 µM S102G/R166S AP, the concentration needed to achieve ∼0.5 fraction 32Pi binding depending on the pH; at most, 20% of the total tungstate concentration is bound over all conditions so that [tungstate]free≈[tungstate]total. This competition assay reproduced well the pH-dependent tungstate affinity of WT AP that was previously measured using kinetic inhibition methods (Figure S15; [20]).
, where α is the K
a of tungstate binding in the limit that the free tungstate concentration is equal to the total tungstate concentration and C is the background fractional 32Pi binding as the tungstate concentration approaches infinity (<0.15). The tungstate competition assays had 0.5–10 µM S102G/R166S AP, the concentration needed to achieve ∼0.5 fraction 32Pi binding depending on the pH; at most, 20% of the total tungstate concentration is bound over all conditions so that [tungstate]free≈[tungstate]total. This competition assay reproduced well the pH-dependent tungstate affinity of WT AP that was previously measured using kinetic inhibition methods (Figure S15; [20]).
As noted in the legend of Figure 4B, the observed tungstate affinity of S102G/R166S AP at pH values ≥8 deviates from the log-linear affinity decrease expected for a protein inactivation with pK a∼6.5. The observed competition measured at these pH values likely originates from contaminating levels of unlabeled Pi in the tungstate stock. The deviation is consistent with the constant Pi affinity in this pH range (Figure 4A) with Pi present in only one part in ∼106 (i.e., the observed tungstate affinity of S102G/R166S AP in Figure 4B at pH values ≥8 is approximately 106-fold lower than the Pi affinity over the same pH values in Figure 4A). Assays of the tungstate stock for Pi, using malachite green [65], resulted in a very high absorbance signal, likely because tungstate itself can form a complex with malachite green and mask the signal from relatively very low levels of Pi contamination.
The tungstate affinity for R166S AP was determined by inhibition of pNPP hydrolysis as was done previously with WT AP [20], but under the standard buffer conditions used in this work. A range of tungstate concentrations was used from at least 5-fold below and above the inhibition constant at each pH.
Crystallization, Structure Determination, and Refinement
S102G/R166S AP (23.5 mg/mL in 10 mM NaMOPS, pH 8.0, and 50 mM NaCl) was crystallized at 18°C by the sitting-drop method using a mother liquor of 0.2 M NH4F, 17%–21% PEG (polyethylene glycol) 3350, and 500 µM ZnCl2 (conditions adapted from [37]). Crystals were passed through a 30% glycerol solution in mother liquor before direct immersion in liquid nitrogen.
Diffraction data were collected at the Stanford Synchrotron Radiation Lightsource on beamline 11-1. Data were integrated and scaled using DENZO and SCALEPACK, respectively [66], and 5% of data were set aside for cross-validation [67]. Data statistics are summarized in Table S2.
Initial phases were determined by molecular replacement with Phaser [68] using R166S AP (PDB entry 3CMR; [35]) as a search model, with Ser102 truncated to a glycine. Subsequently, σA-weighted 2F o–F c and F o–F c maps were inspected, and a complete model comprising residues 4–449 and three Zn2+ ions per monomer. Model building was performed using Coot [69].
In most structures of AP, two Zn2+ ions occupy the bimetallo site and a Mg2+ ion occupies the third metal site. The high ZnCl2 concentrations used in the crystallization conditions here apparently allow Zn2+ to outcompete Mg2+ for the third metal site. Mg2+ was not included in the crystallization conditions. An alignment with a previously determined AP structure with Mg2+ bound in the third metal site showed no significant structural differences of the coordinating ligands at the metal site regardless of whether Zn2+ or Mg2+ is occupying the site, suggesting that Zn2+ replacement of Mg2+ has very limited structural consequences on residues beyond this metal ion coordination sphere (see Figure S16 for structural overlay). This metal ion is 4.6 Å from the closest oxygen atom of the bound Pi in WT AP (3TGO; [36]).
Noncovalently bound phosphate was modeled in the active site of S102G/R166S AP to account for the appearance of tetrahedral electron density there, as in prior structures 1ALK [33] and 3TGO [36]. Although no Pi was added during the crystallization, Pi copurifies with S102G/R166S AP, binds the protein tightly, and contaminates commercial PEG solutions (Hampton Research) used for the crystallization [37].
From this model, maximum-likelihood amplitude-based refinement was carried out using refmac [70], resulting in an R-factor of 23.0% and R free of 31.0%. Final stages of refinement were carried out with Force Field X [71]. Each stage of refinement was interspersed with manual corrections and model adjustments using Coot. The R and R free values for the final refined model were 23.2% and 29.6%, respectively. All structural figures were prepared using MacPyMol [72].
31P NMR
Samples for 31P NMR measurements had 1–2 mM AP, 100 mM buffer, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. Sub-stoichiometric and excess levels of Pi were added to the samples to identify peaks that were associated with bound-Pi and free-Pi in solution. 31P NMR spectra were recorded at 161.97 MHz on a Varian Mercury spectrometer equipped with a broadband tunable probe. Protein samples of ∼350 µL were contained in 5 mm tubes fitted with a coaxial capillary insert (Wilmad Lab Glass) containing D2O for the external field-frequency lock. Spectra were recorded at 37°C with a sweep width of 50,000 Hz, pulse delay of 2 s, and an acquisition time of 0.8 s. Proton decoupling was employed and S/N of >10 could usually be obtained after ∼10,000 transients (∼11 h). A line broadening of 5–10 Hz was typically applied and all spectra were referenced to a 1% phosphoric acid external standard.
The observed 31P chemical shift data for S102G/R166S AP-bound Pi as a function of pH (Figure 6) was fit to δobs = (δupfield−δdownfield)/(1+ )+δdownfield, which was derived from a two-state model in which an upfield and downfield species bind in a ratio dependent on the solution pH (Figure 6C). The
)+δdownfield, which was derived from a two-state model in which an upfield and downfield species bind in a ratio dependent on the solution pH (Figure 6C). The  value is the pK
a of the equilibrium between
value is the pK
a of the equilibrium between 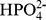 -bound S102G/R166S AP and
-bound S102G/R166S AP and 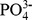 -bound S102G/R166S AP (as defined in Figure 6C and D).
-bound S102G/R166S AP (as defined in Figure 6C and D).
Accession Numbers
Protein Data Bank Code for the S102G/R166S AP X-ray crystal structure: 4KM4.
Supporting Information
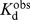 = 0.20±0.02 µM (diamonds, dashed line), 0.24±0.05 µM (circles, solid line), and 0.34±0.06 µM (triangles, dotted line). The average K
d value from the three assays is 0.26±0.07 µM (Table 1 and Table S1). Samples of WT AP and 32Pi were incubated for >1 h before the fraction 32Pi bound was measured and no dependence on the incubation time was observed (not shown). (B) Inhibition of pNPP hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 0.4 µM pNPP. Activity was normalized by dividing the observed rate constant in the presence of inhibitor by the rate constant in the absence of inhibitor. Two replicate assays yielded individual, nonlinear least-squares fits for competitive inhibition with K
d values of 0.67±0.04 µM (circles) and 0.67±0.06 µM (diamonds); the combined fit is shown with K
d = 0.67±0.04 µM. (C) Inhibition of pNPS hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 21 mM pNPS. To achieve activity significantly above background, a much higher concentration of AP (0.2 µM) is needed than for the pNPP inhibition assays. As a result, the simplifying assumption that [inhibitor]free = [inhibitor]total does not hold; [AP] is similar to the expected K
i and the commonly used form of the Michaelis–Menten equation with competitive inhibition could not be used. Instead, a quadratic equation (below) was used to relate the observed fractional activity to the total inhibitor and AP concentrations used in the assay and a nonlinear least-squares fit of this equation gave K
d = 0.50±0.14 µM. (D) The equilibrium-binding assay at pH 8.0, 9.5, and 10.5 with
= 0.20±0.02 µM (diamonds, dashed line), 0.24±0.05 µM (circles, solid line), and 0.34±0.06 µM (triangles, dotted line). The average K
d value from the three assays is 0.26±0.07 µM (Table 1 and Table S1). Samples of WT AP and 32Pi were incubated for >1 h before the fraction 32Pi bound was measured and no dependence on the incubation time was observed (not shown). (B) Inhibition of pNPP hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 0.4 µM pNPP. Activity was normalized by dividing the observed rate constant in the presence of inhibitor by the rate constant in the absence of inhibitor. Two replicate assays yielded individual, nonlinear least-squares fits for competitive inhibition with K
d values of 0.67±0.04 µM (circles) and 0.67±0.06 µM (diamonds); the combined fit is shown with K
d = 0.67±0.04 µM. (C) Inhibition of pNPS hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 21 mM pNPS. To achieve activity significantly above background, a much higher concentration of AP (0.2 µM) is needed than for the pNPP inhibition assays. As a result, the simplifying assumption that [inhibitor]free = [inhibitor]total does not hold; [AP] is similar to the expected K
i and the commonly used form of the Michaelis–Menten equation with competitive inhibition could not be used. Instead, a quadratic equation (below) was used to relate the observed fractional activity to the total inhibitor and AP concentrations used in the assay and a nonlinear least-squares fit of this equation gave K
d = 0.50±0.14 µM. (D) The equilibrium-binding assay at pH 8.0, 9.5, and 10.5 with 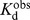 values of 0.24 µM (circles), 1.7 µM (diamonds), and 23 µM (triangles), respectively. (E) Comparison of the pH-dependent
values of 0.24 µM (circles), 1.7 µM (diamonds), and 23 µM (triangles), respectively. (E) Comparison of the pH-dependent 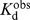 values from the new equilibrium-binding assay [closed circles; part (D)] with values measured by kinetic inhibition (open circles; from Figure S9C). The line shown is the combined fit of both data sets and gives a protein inactivation pK
a value of 8.7, in agreement with the inactivation pK
a value determined over the full pH range (Figure S9C). (F) The fraction 32Pi bound determined by the filtration assay after addition of unlabeled Pi (2 mM) to AP•32Pi (assay in standard buffer conditions with 10 µM WT AP), giving a limit for k
off of ≥0.01 s−1. (G) The uptake of 32Pi after addition of 32Pi to Pi-free AP and following the fraction bound using the filtration assay in standard buffer conditions with 0.1–10 µM WT AP; k
values from the new equilibrium-binding assay [closed circles; part (D)] with values measured by kinetic inhibition (open circles; from Figure S9C). The line shown is the combined fit of both data sets and gives a protein inactivation pK
a value of 8.7, in agreement with the inactivation pK
a value determined over the full pH range (Figure S9C). (F) The fraction 32Pi bound determined by the filtration assay after addition of unlabeled Pi (2 mM) to AP•32Pi (assay in standard buffer conditions with 10 µM WT AP), giving a limit for k
off of ≥0.01 s−1. (G) The uptake of 32Pi after addition of 32Pi to Pi-free AP and following the fraction bound using the filtration assay in standard buffer conditions with 0.1–10 µM WT AP; k ≥0.03 s−1 for all concentrations of WT AP.
≥0.03 s−1 for all concentrations of WT AP. |
(EPS)
Equilibrium-binding assay with S102G and S102A AP. All assays were carried out at pH 8.0 under the standard buffer conditions described in Materials and Methods. (A) Dissociation of 32Pi from S102G and S102A AP. Excess unlabeled Pi (2 mM) was added to 1 µM samples of S102G (open diamonds) or S102A (closed circles) AP with maximal 32Pi bound. After the addition of unlabeled Pi, the fraction 32Pi bound was measured over time. The line shows the expected behavior for a dissociation rate constant of 2×10−7 s−1 (t1/2∼1,000 h), which provides the upper limit used in the text. (B, C) Uptake of 32Pi over time by S102G (B) or S102A (C) AP. (Pi-free proteins were generated as described in Materials and Methods.) Nonlinear least-squares fits to the equation  at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. The observed background (at 0 min) fraction 32Pi bound is different for the two uptake assays because different filtration devices were used for each assay (see Materials and Methods). (D, E) The observed uptake rate constants versus each S102G (D) or S102A (E) AP concentration. For simple two-state binding, k
obs = k
on[AP]+k
off
[23]. The weighted, nonlinear least-squares fits shown as solid lines give slope values (k
on) of 1,300 and 1.6×104 M−1 s−1 for S102G and S102A AP, respectively. The y-intercept values for these plots are strongly influenced by small errors in the slope fit and are not typically interpreted for this reason. Fixing the y-intercept value at the limit for k
off suggested by the chase assays (2×10−7 s−1) nevertheless yields reasonable fits to the data as shown by the dashed lines. Note the log scale in (D) but not in (E).
at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. The observed background (at 0 min) fraction 32Pi bound is different for the two uptake assays because different filtration devices were used for each assay (see Materials and Methods). (D, E) The observed uptake rate constants versus each S102G (D) or S102A (E) AP concentration. For simple two-state binding, k
obs = k
on[AP]+k
off
[23]. The weighted, nonlinear least-squares fits shown as solid lines give slope values (k
on) of 1,300 and 1.6×104 M−1 s−1 for S102G and S102A AP, respectively. The y-intercept values for these plots are strongly influenced by small errors in the slope fit and are not typically interpreted for this reason. Fixing the y-intercept value at the limit for k
off suggested by the chase assays (2×10−7 s−1) nevertheless yields reasonable fits to the data as shown by the dashed lines. Note the log scale in (D) but not in (E).
(EPS)
Dilution of S102G AP after uptake of 32Pi. S102G AP (1 µM at pH 8.0 in standard buffer conditions) was incubated with ∼200 pM 32Pi for 400 min. The sample was serially diluted 2-fold by addition of buffer at t = 400, 1,430, and 1,810 min (as indicated by the vertical dashed lines) to give the S102G AP concentrations indicated at the top of the figure, and the fraction 32Pi bound was measured after each dilution using the filtration assay.
(EPS)
Model and fits for uptake of 32Pi by S102G and S102A AP. (A) The model for uptake of 32Pi with both reversible binding of 32Pi and irreversible inactivation of the free protein. k off was fixed at the limit measured with the chase assay [the fits in parts (B) and (C) were insensitive to lowering k off below the upper limit of 2×10−7 s−1]. (B) The uptake of 32Pi by S102G AP (data from Figure S2B) fit to the model in part (A). For fitting, the data were normalized to correct for the ∼0.1 fraction 32Pi loss during centrifugation for the filtration units used in these assays (see Materials and Methods). The lines show a global, nonlinear fit for k on and k inactive and yielded values of ∼1,000 M−1 s−1 and ∼3×10−4 s−1, respectively. (C) The uptake of 32Pi by S102A AP (data from Figure S2C) fit to the model in part (A). For model fitting, the data were normalized to correct for the background fraction binding at time zero of ∼0.1, as observed for the type of filtration units used in this assay (see Materials and Methods). The global fit shown to the model in (A) yielded a poor fit, particularly to the data at lower concentrations of S102A AP.
(EPS)
Initial uptake rate constant analysis for S102G and S102A AP. (A) The uptake of 32Pi by S102G AP (data from Figure S2B). The dashed lines are the single exponential fits to the entire uptake time course, as shown in Figure S2B. The solid lines estimate the rate of initial 32Pi uptake. (B) The estimated initial uptake rate constants from the slopes of the lines in (A) at each concentration of S102G AP. The nonweighted, linear fit shown gives a slope of k on 740 M−1 s−1 (with the y-intercept, k off, fixed at 2×10−7 s−1). Note the logarithmic x-axis scale. (C) The uptake of 32Pi by S102A AP (data from Figure S2C). The dashed lines are the single exponential fits to the entire uptake time course, as shown in Figure S2C. The solid lines estimate the rate of initial 32Pi uptake. (D) The estimated initial uptake rate constants from the slopes of the lines in (C) at each concentration of S102A AP. The nonweighted, linear fit shown gives a slope for k on of 1.2×104 M−1 s−1 (with the y-intercept, k off, fixed at 2×10−7 s−1).
(EPS)
Equilibrium-binding assays for S102G and S102A AP. Samples of various concentrations of S102G (A) or S102A (B) AP were incubated with ∼200 pM 32Pi at pH 8.0 in the standard buffer conditions. The samples were incubated ≥24 h before the fraction 32Pi bound was measured. Independent replicate assays are depicted by different symbols. Fits to a simple two-state binding isotherm yielded a variable midpoint of the fraction bound values and yielded a steeper binding dependence than expected for simple 1∶1 binding. As noted in Text S3, these and other results suggest complications for protein inactivation over the long times of these assays and led us to use weaker binding and faster equilibrating mutants for quantitative comparisons.
(EPS)
Inhibition by Pi and equilibrium-binding assay for R166S AP. (A) Inhibition of R166S AP pNPP hydrolysis activity by Pi at pH 8.0 under the standard reaction conditions (see Materials and Methods) with [pNPP] = 0.8 µM. Three independent replicate assays are shown. Activity was normalized by the observed rate constant in the absence of inhibitor. The lines are nonlinear least-squares fits for competitive inhibition and give an average K i value of 360±160 µM. (B) Equilibrium-binding assay conducted for R166S AP at pH 8.0 (closed circles) and 9.0 (open diamonds) under the standard reaction conditions. The dashed line shows the predicted fraction 32Pi bound for a dissociation constant of 360 µM.
(EPS)
Pi equilibrium-binding assay for S102G/R166S and S102A/R166S AP. (A) Three independent equilibrium-binding assays for 32Pi binding to S102G/R166S AP at pH 8.0 (in standard buffer conditions). Nonlinear least-squares fits for fractional 32Pi binding give an average 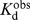 value of 66±8 nM. Incubation times were >300 min. (B) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102G/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (
value of 66±8 nM. Incubation times were >300 min. (B) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102G/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (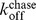 ) of 1.2±0.05×10−4 s−1. (C) Uptake of 32Pi over time by S102G/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (D) The observed uptake rate constants versus S102G/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line yields a k
on value of 1,190±120 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.2×10−4 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations from this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars (assuming symmetrical error). (E) Three independent equilibrium-binding assays for 32Pi binding to S102A/R166S AP at pH 8.0. Nonlinear least-squares fits for fractional 32Pi binding give an average
) of 1.2±0.05×10−4 s−1. (C) Uptake of 32Pi over time by S102G/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (D) The observed uptake rate constants versus S102G/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line yields a k
on value of 1,190±120 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.2×10−4 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations from this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars (assuming symmetrical error). (E) Three independent equilibrium-binding assays for 32Pi binding to S102A/R166S AP at pH 8.0. Nonlinear least-squares fits for fractional 32Pi binding give an average 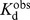 value of 77±6 nM. Incubation times were >4 d. (F) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102A/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (
value of 77±6 nM. Incubation times were >4 d. (F) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102A/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (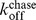 ) of 1.6±0.06×10−6 s−1, assuming a background fraction-bound at t = ∞ of 0.05, as was observed for the S102G/R166S AP chase assay. (G) Uptake of 32Pi over time by S102A/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (H) The observed uptake rate constants versus S102A/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 51±4 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (I) Uptake of 32Pi over time by S102G/R166S AP followed using a filtration device containing G-25 Sephadex resin (see Materials and Methods). These filtration devices give very low background 32Pi fraction binding (but note that the maximum 32Pi bound that could be observed only approaches 0.85–0.90, presumably from loss of 32Pi bound to AP as the bound complex passes through the Sephadex resin during the filtration). Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (J) The observed uptake rate constants versus S102G/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 1,420±520 M−1 s−1, within error of the value obtained with the filtration method used in part (C). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (K) Uptake of 32Pi over time by S102A/R166S AP followed using filtration devices containing G-25 Sephadex resin. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (L) The observed uptake rate constants versus S102A/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 36±14 M−1 s−1 within error of the value obtained with the filtration devices used in part (G). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. The fit error for the 0.2 µM S102A/R166S AP uptake sample is exceptionally large, reflecting the influence of an outlier data point collected during the time course.
) of 1.6±0.06×10−6 s−1, assuming a background fraction-bound at t = ∞ of 0.05, as was observed for the S102G/R166S AP chase assay. (G) Uptake of 32Pi over time by S102A/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (H) The observed uptake rate constants versus S102A/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 51±4 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (I) Uptake of 32Pi over time by S102G/R166S AP followed using a filtration device containing G-25 Sephadex resin (see Materials and Methods). These filtration devices give very low background 32Pi fraction binding (but note that the maximum 32Pi bound that could be observed only approaches 0.85–0.90, presumably from loss of 32Pi bound to AP as the bound complex passes through the Sephadex resin during the filtration). Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (J) The observed uptake rate constants versus S102G/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 1,420±520 M−1 s−1, within error of the value obtained with the filtration method used in part (C). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (K) Uptake of 32Pi over time by S102A/R166S AP followed using filtration devices containing G-25 Sephadex resin. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (L) The observed uptake rate constants versus S102A/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 36±14 M−1 s−1 within error of the value obtained with the filtration devices used in part (G). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. The fit error for the 0.2 µM S102A/R166S AP uptake sample is exceptionally large, reflecting the influence of an outlier data point collected during the time course.
(EPS)
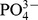 affinity to AP with Ser102 deprotonated. Assays in standard conditions of 100 mM NaAcetate (pH 4.5–5.5), NaMaleate (pH 6.0–6.5), NaMOPS (pH 7–8.0), NaCHES (pH 8.5–9.5), NaCAPS (pH 10–11.2), or NaCABS (pH 11.0–11.4), with 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. (A) The model used to estimate the
affinity to AP with Ser102 deprotonated. Assays in standard conditions of 100 mM NaAcetate (pH 4.5–5.5), NaMaleate (pH 6.0–6.5), NaMOPS (pH 7–8.0), NaCHES (pH 8.5–9.5), NaCAPS (pH 10–11.2), or NaCABS (pH 11.0–11.4), with 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. (A) The model used to estimate the 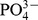 binding affinity. (B) The pNPP hydrolysis activity of R166S AP from pH 7–10. The line shows the expected trend for a single enzymatic inactivation given by
binding affinity. (B) The pNPP hydrolysis activity of R166S AP from pH 7–10. The line shows the expected trend for a single enzymatic inactivation given by  with
with  = 7.6 and (k
cat/K
M)max = 8×104 M−1 s−1. (C) The pH-dependent Pi affinity of WT AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed values of K
= 7.6 and (k
cat/K
M)max = 8×104 M−1 s−1. (C) The pH-dependent Pi affinity of WT AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed values of K
 are shown.
are shown. 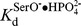 was fixed at 0.46 µM and
was fixed at 0.46 µM and 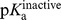 was fixed at 8.6, which are the values from the optimal fits assuming no
was fixed at 8.6, which are the values from the optimal fits assuming no 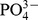 affinity. The fit using a fixed K
affinity. The fit using a fixed K
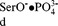 of 100 nM deviated 4-fold from the data above pH 11.0. (D) The pH-dependent Pi affinity of R166S AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed K
of 100 nM deviated 4-fold from the data above pH 11.0. (D) The pH-dependent Pi affinity of R166S AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed K
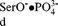 values are shown. K
values are shown. K
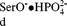 was fixed at 110 µM and
was fixed at 110 µM and 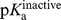 was fixed at 7.6, which are the values from the optimal fits assuming no
was fixed at 7.6, which are the values from the optimal fits assuming no 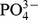 affinity. The fit with a K
affinity. The fit with a K
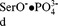 = 2.5 µM deviates from the data at pH 10 with greater than the expected error of these measurements (<50%).
= 2.5 µM deviates from the data at pH 10 with greater than the expected error of these measurements (<50%).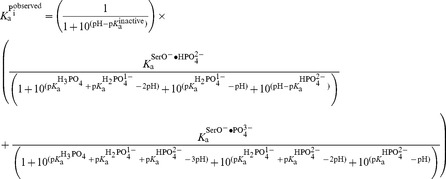 |
(Equation S3) |
(EPS)
31P NMR of Pi with R166S AP. (A) Samples contained ∼1.3 mM R166S AP, 10 mM NaTris, pH 7.5, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. The concentration of Pi was initially very low to achieve the highest fraction bound. The concentration of Pi was subsequently increased by adding small volumes of concentrated Pi to achieve the lower fraction bound values listed. The fraction Pi bound was computed using the measured R166S AP dissociation constant for Pi binding of 360 µM. 31P NMR parameters are as described in Materials and Methods. The chemical shift approaches the shift of the bound Pi shift observed in WT AP (bottom spectrum). (B) Extrapolation of the 31P NMR chemical shift as the fraction Pi bound increases yields a chemical shift for bound Pi of ∼3.8 ppm.
(EPS)
31P NMR spectra of S102G (A) and S102G/R166S (B) AP with excess Pi. Solution conditions for all 31P NMR measurements are described in Materials and Methods. Protein concentrations were typically 1–2 mM and Pi concentrations were approximately 2-fold in excess. When Pi is not in excess, only the chemical shift peaks demarcated with red arrows remain present (spectra not shown). The additional peaks present with Pi in excess correspond to the chemical shifts expected for the unbound species of Pi at each pH (see Table S3).
(EPS)
[18O]-Pi edited FTIR difference spectra of Pi in solution and Pi bound to WT, S102G, and S102G/R166S AP. (A) FTIR difference spectrum between 16O-Pi and 18O-Pi at pH 4.5 (green), 9.5 (blue), or 13 (red). (B) FTIR difference spectra between AP•16O-Pi and AP•18O-Pi for WT AP (2.6 mM AP/2.3 mM Pi) in 140 mM NaMOPS, pH 8.0, 680 mM NaCl, 1.4 mM MgCl2, and 140 µM ZnCl2 (from ref. [16]); S102G AP (3.4 mM AP/1 mM Pi) in 110 mM NaCHES, pH 9.5, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2; and S102G/R166S AP (2.2 mM AP/1 mM Pi) in 50 mM NaCHES, pH 9.0, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. All samples and spectra were prepared and acquired as described in [16].
(EPS)
Comparison of 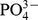 binding of AP with and without Ser102. Comparison of
binding of AP with and without Ser102. Comparison of 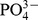 binding AP with Ser102 either mutated to Gly, deprotonated or protonated. Black bars show the
binding AP with Ser102 either mutated to Gly, deprotonated or protonated. Black bars show the 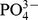 affinity measured for S102G/R166S AP and estimated for S102G AP (
affinity measured for S102G/R166S AP and estimated for S102G AP (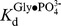 values in Table 2 of the main text). Red bars show the upper limits for the
values in Table 2 of the main text). Red bars show the upper limits for the 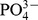 affinity (denoted by downward arrows) measured for R166S and WT AP with Ser102 deprotonated (
affinity (denoted by downward arrows) measured for R166S and WT AP with Ser102 deprotonated (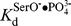 values in Table 2 of the main text). Grey bars show the lower limits for the
values in Table 2 of the main text). Grey bars show the lower limits for the 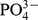 affinity for R166S and WT AP with Ser102 protonated (
affinity for R166S and WT AP with Ser102 protonated (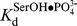 values in Table 2 of the main text).
values in Table 2 of the main text).
(EPS)
Binding of Pi to a protein tyrosine phosphatase with and without its nucleophilic cysteine present. (A) Equilibrium-binding assay of the PTP, Stp1, with Cys11 intact (open circles) and three independent assays of C11G Stp1 (closed symbols) at pH 6.0 in 20 mM NaMaleate, 100 µM Na2EDTA, and 0.15 M NaCl at 4°C. Fits to the data for C11G Stp1 gave K d values of 4.9±0.5 µM (inverted triangles), 9.6±1.7 µM (squares), and 15±2.3 µM (triangles). The average K d value from the three assays is 10±5 µM. The observed fraction 32Pi bound did not depend on incubation times of C11G Stp1 with 32Pi greater than 60 min. No significant Pi binding of WT Stp1 could be detected within the protein concentration limits of the assay (500 µM). [In contrast to the observations with R166S AP at pH 8.0, concentrations of Stp1 >25 µM did not result in a significant decrease in flow rate through the filtration unit (see Text S4).] (B) Inhibition of WT Stp1 pNPP hydrolysis activity by Pi at pH 6.0 in 20 mM NaMaleate, 100 µM Na2EDTA, and 0.15 M NaCl for three independent assays. Fits yield K i values of 14±4 mM (circles), 19±2 mM (open triangles), and 20±2 mM (open diamonds) with an average K i value of 18±3 mM. WT and C11G Stp1 were purified as reported previously [44].
(EPS)
The pH dependence of tungstate binding to WT AP. (A) Fraction 32Pi bound to AP as a function of tungstate concentration. A competition-binding assay at pH 8.0 for WT AP (see Materials and Methods for assay details) under the standard buffer conditions. A nonlinear least-squares fit to the competition equation shown in Materials and Methods yields a dissociation constant value for tungstate binding (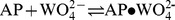 ) of
) of 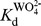 = 0.9±0.2 µM in good agreement with the dissociation constant at this pH reported previously (
= 0.9±0.2 µM in good agreement with the dissociation constant at this pH reported previously (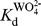 = 1.1 µM; [20]) at pH 8.0. (B) The pH-dependent tungstate affinity for WT AP determined by kinetic inhibition measurements (circles) and by the equilibrium-binding assay via competition with 32Pi binding (squares). The fits shown yield inactivating pK
a values of 7.82±0.13 (solid line) and 8.07±0.16 (dashed line) and pH-independent dissociation constants for tungstate dianion binding of 0.57±0.11 µM (solid line; data from [20]) and 2.06±0.48 µM (dashed line).
= 1.1 µM; [20]) at pH 8.0. (B) The pH-dependent tungstate affinity for WT AP determined by kinetic inhibition measurements (circles) and by the equilibrium-binding assay via competition with 32Pi binding (squares). The fits shown yield inactivating pK
a values of 7.82±0.13 (solid line) and 8.07±0.16 (dashed line) and pH-independent dissociation constants for tungstate dianion binding of 0.57±0.11 µM (solid line; data from [20]) and 2.06±0.48 µM (dashed line).
(EPS)
Structural overlay of AP Mg2+ site. The WT AP crystal structure (PDB code 3TGO, [36]) is shown in grey with the crystal structure reported here for S102G/R166S AP in magenta. In the S102G/R166S AP structure, a Zn2+ ion occupies the Mg2+ site. The position of the coordinating residues and the metal ion are the same within error in the two structures.
(EPS)
Summary of Pi binding kinetics for WT, S102G, S102A, R166S, S102G/R166S, and S102A/R166S AP. a
k
on for S102G and S102A AP is the estimated association rate constant from a fit analysis of the 32Pi uptake assay results described in Text S2. k
on for S102G/R166S and S102A/R166S AP is from the fit of the k
obs values from the uptake assay versus the [AP] shown in Figure S8D and H.
b
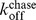 is the dissociation rate constant measured by the 32Pi chase assay (Figure S1F; Figure S2A; Figure S8B and F). c
is the dissociation rate constant measured by the 32Pi chase assay (Figure S1F; Figure S2A; Figure S8B and F). c
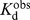 is the dissociation constant for Pi binding at pH 8.0 measured from the fraction 32Pi bound after an incubation time sufficient to reach equilibrium (Figure S1A for WT AP; Figure S8A for S102G/R166S; Figure S8D for S102A/R166S AP), except for the value reported for R166S AP, which is from kinetic inhibition assays (Figure S7A). dThe
is the dissociation constant for Pi binding at pH 8.0 measured from the fraction 32Pi bound after an incubation time sufficient to reach equilibrium (Figure S1A for WT AP; Figure S8A for S102G/R166S; Figure S8D for S102A/R166S AP), except for the value reported for R166S AP, which is from kinetic inhibition assays (Figure S7A). dThe 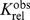 value is calculated by dividing the dissociation constant for AP with Ser102 intact by the dissociation constant (
value is calculated by dividing the dissociation constant for AP with Ser102 intact by the dissociation constant (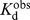 ) for the Ser102 mutants in either the context of WT or R166S AP; larger values represent stronger binding of the Ser102 mutant relative to proteins with Ser102 intact.
) for the Ser102 mutants in either the context of WT or R166S AP; larger values represent stronger binding of the Ser102 mutant relative to proteins with Ser102 intact.
(DOC)
Crystallographic data and model statistics.
(DOC)
31P NMR chemical shift summary of free Pi and Pi bound to WT, R166S, S102G, and S102G/R166S AP. aChemical shifts reported for unbound Pi species were measured here under conditions identical to those used for protein-containing samples and referenced to a 1% phosphoric acid standard. These shifts are within error of those reported previously [42]. At intermediate pH values the observed chemical shift represents a weighted average of the ionic forms present.
(DOC)
Observed activity of Ser102 mutants likely arises from WT AP contamination.
(DOC)
Tests of the new equilibrium-binding assay with WT AP.
(DOC)
Equilibrium-binding assay results with S102G and S102A AP.
(DOC)
Equilibrium binding of Pi to R166S, S102G/R166S, and S102A/R166S AP.
(DOC)
Interplay between Ser102 and Arg166 revealed by structural comparison.
(DOC)
Estimation of 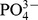 affinity for AP with Ser102 deprotonated.
affinity for AP with Ser102 deprotonated.
(DOC)
31P NMR of the R166S AP•Pi complex suggests bound 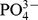 .
.
(DOC)
31P NMR of Pi-bound to S102G and S102G/R166S AP with excess Pi.
(DOC)
Equations derived from the models in Figure 4C and D to fit the pH-dependent Pi binding data for R166S (Equation S1) and S102G/R166S (Equation S2) AP in Figure 4A.
(DOC)
Comparison of AP•Pi affinities with AP Ser102 protonated, deprotonated, or mutated to Gly.
(DOC)
Previous estimation for the destabilization from Ser102 on the binding of a dianionic phosphate.
(DOC)
Estimation of the contribution of Arg166 to binding of Pi dianion.
(DOC)
Comparison of 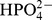 and
and 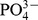 binding by S102G AP.
binding by S102G AP.
(DOC)
Evidence against electrostatic repulsion in phosphoryl transfer transition states.
(DOC)
Extended implications for phosphoryl transfer catalysis.
(DOC)
Acknowledgments
We thank members of the Herschlag lab for critical discussions and comments on the manuscript. We thank Steve Lynch for assistance with NMR experiments and Hua Deng for assistance with isotope-edited vibrational spectroscopy measurements.
Abbreviations
- AP
alkaline phosphatase
- Pi
inorganic phosphate
- PTP
protein tyrosine phosphatase
Funding Statement
This work was supported by a grant from the US National Institutes of Health to DH (GM64798). LDA was supported in part by an NIH training grant (R1GM064798), and TDF was supported by NIH Grant U54 GM072970. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Edwards DR, Lohman DC, Wolfenden R (2011) Catalytic proficiency: the extreme case of S-O cleaving sulfatases. J Am Chem Soc 134: 525–531. [DOI] [PubMed] [Google Scholar]
- 2. Wolfenden R, Snider MJ (2001) The depth of chemical time and the power of enzymes as catalysts. Acc Chem Res 34: 938–945. [DOI] [PubMed] [Google Scholar]
- 3. Bar-Even A, Noor E, Savir Y, Liebermeister W, Davidi D, et al. (2011) The moderately efficient enzyme: Evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 50: 4402–4410. [DOI] [PubMed] [Google Scholar]
- 4. Jencks WP (1975) Binding energy, specificity, and enzymic catalysis: Circe effect. Adv Enzymol Relat Areas Mol Biol 43: 219–410. [DOI] [PubMed] [Google Scholar]
- 5. Jencks WP (1987) Economics of enzyme catalysis. Cold Spring Harb Symp Quant Biol 52: 65–73. [DOI] [PubMed] [Google Scholar]
- 6. Wells TN, Fersht AR (1986) Use of binding energy in catalysis analyzed by mutagenesis of the tyrosyl-tRNA synthetase. Biochemistry 25: 1881–1886. [DOI] [PubMed] [Google Scholar]
- 7. Narlikar GJ, Herschlag D (1998) Direct demonstration of the catalytic role of binding interactions in an enzymatic reaction. Biochemistry 37: 9902–9911. [DOI] [PubMed] [Google Scholar]
- 8. Thompson RC, Blout ER (1973) Dependence of the kinetic parameters for elastase-catalyzed amide hydrolysis on the length of peptide substrates. Biochemistry 12: 57–65. [DOI] [PubMed] [Google Scholar]
- 9. Fersht AR (1987) Dissection of the structure and activity of the tyrosyl-tRNA synthetase by site-directed mutagenesis. Biochemistry 26: 8031–8037. [DOI] [PubMed] [Google Scholar]
- 10. Day PJ, Shaw WV, Gibbs MR, Leslie AG (1992) Acetyl coenzyme A binding by chloramphenicol acetyltransferase: Long-range electrostatic determinants of coenzyme A recognition. Biochemistry 31: 4198–4205. [DOI] [PubMed] [Google Scholar]
- 11. Fisher BM, Grilley JE, Raines RT (1998) A new remote subsite in ribonuclease A. J Biol Chem 273: 34134–34138. [DOI] [PubMed] [Google Scholar]
- 12. Fisher BM, Schultz LW, Raines RT (1998) Coulombic effects of remote subsites on the active site of ribonuclease A. Biochemistry 37: 17386–17401. [DOI] [PubMed] [Google Scholar]
- 13. Amyes TL, O'Donoghue AC, Richard JP (2001) Contribution of phosphate intrinsic binding energy to the enzymatic rate acceleration for triosephosphate isomerase. J Am Chem Soc 123: 11325–11326. [DOI] [PubMed] [Google Scholar]
- 14. Barnett SA, Amyes TL, Mckay Wood B, Gerlt JA, Richard JP (2010) Activation of R235A mutant orotidine 52-monophosphate decarboxylase by the guanidinium cation: Effective molarity of the cationic side chain of Arg-235. Biochemistry 49: 824–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Lassila JK, Zalatan JG, Herschlag D (2011) Biological phosphoryl transfer reactions: Understanding mechanism and catalysis. Annu Rev Biochem 80: 669–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Andrews LD, Deng H, Herschlag D (2011) Isotope-edited FTIR of alkaline phosphatase resolves paradoxical ligand binding properties and suggests a role for ground-state destabilization. J Am Chem Soc 133: 11621–11631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Green NM (1990) Avidin and streptavidin. Methods Enzymol 184: 51–67. [DOI] [PubMed] [Google Scholar]
- 18. Coleman JE (1992) Structure and mechanism of alkaline phosphatase. Annu Rev Biophys Biomol Struc 21: 441–483. [DOI] [PubMed] [Google Scholar]
- 19. Holtz K, Kantrowitz E (1999) The mechanism of the alkaline phosphatase reaction: Insights from NMR, crystallography and site-specific mutagenesis. FEBS Letters 462: 7–11. [DOI] [PubMed] [Google Scholar]
- 20. O'Brien PJ, Herschlag D (2002) Alkaline phosphatase revisited: Hydrolysis of alkyl phosphates. Biochemistry 41: 3207–3225. [DOI] [PubMed] [Google Scholar]
- 21. Nikolic-Hughes I, Rees DC, Herschlag D (2004) Do electrostatic interactions with positively charged active site groups tighten the transition state for enzymatic phosphoryl transfer? J Am Chem Soc 126: 11814–11819. [DOI] [PubMed] [Google Scholar]
- 22. Catrina I, O'Brien PJ, Purcell J, Nikolic-Hughes I, Zalatan JG, et al. (2007) Probing the origin of the compromised catalysis of E. coli alkaline phosphatase in its promiscuous sulfatase reaction. J Am Chem Soc 129: 5760–5765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fersht A (1999) Structure and mechanism in protein science. New York: W. H. Freeman and Company.
- 24. Albery WJ, Knowles JR (1976) Evolution of enzyme function and the development of catalytic efficiency. Biochemistry 15: 5631–5640. [DOI] [PubMed] [Google Scholar]
- 25. Jencks WP (1981) On the attribution and additivity of binding energies. Proc Natl Acad Sci USA 78: 4046–4050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Page MI, Jencks WP (1971) Entropic contributions to rate accelerations in enzymic and intramolecular reactions and the chelate effect. Proc Natl Acad Sci USA 68: 1678–1683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Jencks WP, Page MI (1974) “Orbital steering”, entropy, and rate accelerations. Biochem Biophys Res Commun 57: 887–892. [DOI] [PubMed] [Google Scholar]
- 28. Stein SS, Koshland DE (1952) Mechanism of action of alkaline phosphatase. Arch Biochem Biophys 39: 229–230. [DOI] [PubMed] [Google Scholar]
- 29. Schwartz JH (1963) The phosphorylation of alkaline phosphatase. Proc Natl Acad Sci U S A 49: 871–878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Applebury M, Johnson B, Coleman J (1970) Phosphate binding to alkaline phosphatase: Metal ion dependence. J Biol Chem 245: 4968–4976. [PubMed] [Google Scholar]
- 31. Bock J, Cohn M (1978) Metal dependence of the phosphate (oxygen)-water exchange reaction of Escherichia coli alkaline phosphatase. Kinetics followed by 31P (18O) NMR. J Biol Chem 253: 4082–4085. [PubMed] [Google Scholar]
- 32. Caswell M, Caplow M (1980) Correlation of thermodynamic and kinetic properties of the phosphoryl-enzyme formed with alkaline phosphatase. Biochemistry 19: 2907–2911. [DOI] [PubMed] [Google Scholar]
- 33. Kim EE, Wyckoff HW (1991) Reaction mechanism of alkaline phosphatase based on crystal structures. Two-metal ion catalysis. J Mol Biol 218: 449–464. [DOI] [PubMed] [Google Scholar]
- 34. Stec B, Hehir MJ, Brennan C, Nolte M, Kantrowitz ER (1998) Kinetic and X-ray structural studies of three mutant E. coli alkaline phosphatases: Insights into the catalytic mechanism without the nucleophile Ser102. J Mol Biol 277: 647–662. [DOI] [PubMed] [Google Scholar]
- 35. O'Brien PJ, Lassila JK, Fenn TD, Zalatan JG, Herschlag D (2008) Arginine coordination in enzymatic phosphoryl transfer: Evaluation of the effect of Arg166 mutations in Escherichia coli alkaline phosphatase. Biochemistry 47: 7663–7672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Bobyr E, Lassila JK, Wiersma-Koch HI, Fenn TD, Lee JJ, et al. (2012) High-resolution analysis of Zn2+ coordination in the alkaline phosphatase superfamily by EXAFS and X-ray crystallography. J Mol Biol 415: 102–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Zalatan J, Fenn T, Herschlag D (2008) Comparative enzymology in the alkaline phosphatase superfamily to determine the catalytic role of an active-site metal ion. J Mol Biol 384: 1174–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Snyder SL, Wilson IB (1972) Phosphoramidic acids. A new class of nonspecific substrates for alkaline phosphatase from Escherichia coli . Biochemistry 11: 1616–1623. [DOI] [PubMed] [Google Scholar]
- 39. Holtz KM, Catrina IE, Hengge AC, Kantrowitz ER (2000) Mutation of Arg-166 of alkaline phosphatase alters the thio effect but not the transition state for phosphoryl transfer. Implications for the interpretation of thio effects in reactions of phosphatases. Biochemistry 39: 9451–9458. [DOI] [PubMed] [Google Scholar]
- 40.Martell AE, Smith RM (1989) Critical Stability Constants, Vol 1–6 Plenum Press, New York.
- 41. Cruywagen J (2000) Protonation, oligomerization, and condensation reactions of vanadate (V), molybdate (VI), and tungstate (VI). Adv Inorg Chem 49: 127–182. [Google Scholar]
- 42. Yoza N, Ueda N, Nakashima S (1994) pH-dependence of 31P-NMR spectroscopic parameters of monofluorophosphate, phosphate, hypophosphate, phosphonate, phosphinate and their dimers and trimers. Fresenius J Anal Chem 348: 633–638. [Google Scholar]
- 43. Kuntz ID, Chen K, Sharp KA, Kollman PA (1999) The maximal affinity of ligands. Proc Natl Acad Sci USA 96: 9997–10002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Zhang ZY, Zhou G, Denu JM, Wu L, Tang X, et al. (1995) Purification and characterization of the low molecular weight protein tyrosine phosphatase, Stp1, from the fission yeast Schizosaccharomyces pombe. Biochemistry 34: 10560–10568. [DOI] [PubMed] [Google Scholar]
- 45. Wu L, Zhang ZY (1996) Probing the function of Asp128 in the lower molecular weight protein-tyrosine phosphatase-catalyzed reaction. A pre-steady-state and steady-state kinetic investigation. Biochemistry 35: 5426–5434. [DOI] [PubMed] [Google Scholar]
- 46. Hengge AC, Zhao Y, Wu L, Zhang ZY (1997) Examination of the transition state of the low-molecular mass small tyrosine phosphatase 1. Comparisons with other protein phosphatases. Biochemistry 36: 7928–7936. [DOI] [PubMed] [Google Scholar]
- 47. Herschlag D, Jencks W (1989) Evidence that metaphosphate monoanion is not an intermediate in solvolysis reactions in aqueous solution. J Am Chem Soc 111: 7579–7586. [Google Scholar]
- 48. Herschlag D, Jencks W (1989) Phosphoryl transfer to anionic oxygen nucleophiles. Nature of the transition-state and electrostatic repulsion. J Am Chem Soc 111: 7587–7596. [Google Scholar]
- 49. Herschlag D, Jencks W (1990) Nucleophiles of high reactivity in phosphoryl transfer reactions: Alpha-effect compounds and fluoride ion. J Am Chem Soc 112: 1951–1956. [Google Scholar]
- 50. Milic D, Demidkina TV, Faleev NG, Phillips RS, Matkovic-Calogovic D, et al. Crystallographic snapshots of tyrosine phenol-lyase show that substrate strain plays a role in C-C bond cleavage. J Am Chem Soc 133: 16468–16476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Xiang S, Short SA, Wolfenden R, Carter CW Jr (1997) The structure of the cytidine deaminase-product complex provides evidence for efficient proton transfer and ground-state destabilization. Biochemistry 36: 4768–4774. [DOI] [PubMed] [Google Scholar]
- 52. Strynadka NC, James MN (1991) Lysozyme revisited: crystallographic evidence for distortion of an N-acetylmuramic acid residue bound in site D. J Mol Biol 220: 401–424. [DOI] [PubMed] [Google Scholar]
- 53. Carey PR (2006) Spectroscopic characterization of distortion in enzyme complexes. Chem Rev 106: 3043–3054. [DOI] [PubMed] [Google Scholar]
- 54. Griswold WR, Castro JN, Fisher AJ, Toney MD (2012) Ground-state electronic destabilization via hyperconjugation in aspartate aminotransferase. J Am Chem Soc 134: 8436–8438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Zhang Y, Schramm VL (2011) Ground-state destabilization in orotate phosphoribosyltransferases by binding isotope effects. Biochemistry 50: 4813–4818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Lewis BE, Schramm VL (2003) Glucose binding isotope effects in the ternary complex of brain hexokinase demonstrate partial relief of ground-state destabilization. J Am Chem Soc 125: 4672–4673. [DOI] [PubMed] [Google Scholar]
- 57. Anderson VE (2005) Quantifying energetic contributions to ground state destabilization. Arch Biochem Biophys 433: 27–33. [DOI] [PubMed] [Google Scholar]
- 58. Lewis BE, Schramm VL (2003) Binding equilibrium isotope effects for glucose at the catalytic domain of human brain hexokinase. J Am Chem Soc 125: 4785–4798. [DOI] [PubMed] [Google Scholar]
- 59. Silva RG, Kipp DR, Schramm VL (2012) Constrained bonding environment in the michaelis complex of Trypanosoma cruzi uridine phosphorylase. Biochemistry 51: 6715–6717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Cheng H, Nikolic-Hughes I, Wang JH, Deng H, O'Brien PJ, et al. (2002) Environmental effects on phosphoryl group bonding probed by vibrational spectroscopy: implications for understanding phosphoryl transfer and enzymatic catalysis. J Am Chem Soc 124: 11295–11306. [DOI] [PubMed] [Google Scholar]
- 61. Gill SC, von Hippel PH (1989) Calculation of protein extinction coefficients from amino acid sequence data. Anal Biochem 182: 319–326. [DOI] [PubMed] [Google Scholar]
- 62. O'Brien PJ, Herschlag D (1998) Sulfatase activity of E. coli alkaline phosphatase demonstrates a functional link to arylsulfatases, and evolutionarily related enzyme family. J Am Chem Soc 120: 12369–12370. [Google Scholar]
- 63. Johnson KA, Simpson ZB, Blom T (2009) Global Kinetic Explorer: A new computer program for dynamic simulation and fitting of kinetic data. Anal Biochem 387: 20–29. [DOI] [PubMed] [Google Scholar]
- 64. Johnson KA, Simpson ZB, Blom T (2009) FitSpace Explorer: An algorithm to evaluate multidimensional parameter space in fitting kinetic data. Anal Biochem 387: 30–41. [DOI] [PubMed] [Google Scholar]
- 65. Lanzetta PA, Alvarez LJ, Reinach PS, Candia OA (1979) An improved assay for nanomole amounts of inorganic phosphate. Anal Biochem 100: 95–97. [DOI] [PubMed] [Google Scholar]
- 66. Otwinowski Z, Minor W (1997) Processing of X-ray diffraction data collected in oscillation mode. Methods Enzymol 276: 307–326. [DOI] [PubMed] [Google Scholar]
- 67. Brunger AT (1992) Free R value: A novel statistical quantity for assessing the accuracy of crystal structures. Nature 355: 472–475. [DOI] [PubMed] [Google Scholar]
- 68. McCoy AJ, Grosse-Kunstleve RW, Storoni LC, Read RJ (2005) Likelihood-enhanced fast translation functions. Acta Crystallogr D Biol Crystallogr 61: 458–464. [DOI] [PubMed] [Google Scholar]
- 69. Emsley P, Cowtan K (2004) Coot: Model-building tools for molecular graphics. Acta Crystallogr D Biol Crystallogr 60: 2126–2132. [DOI] [PubMed] [Google Scholar]
- 70. Murshudov GN, Vagin AA, Dodson EJ (1997) Refinement of macromolecular structures by the maximum-likelihood method. Acta Crystallogr D Biol Crystallogr 53: 240–255. [DOI] [PubMed] [Google Scholar]
- 71. Fenn TD, Schnieders MJ (2011) Polarizable atomic multipole X-ray refinement: weighting schemes for macromolecular diffraction. Acta Crystallogr D Biol Crystallogr 67: 957–965. [DOI] [PubMed] [Google Scholar]
- 72.DeLano W (2007) MacPyMOL: A PyMOL-based molecular graphics application for MacOS X. DeLano Scientific LLC, Palo Alto, CA.
- 73. Hollenstein K, Comellas-Bigler M, Bevers LE, Feiters MC, Meyer-Klaucke W, et al. (2009) Distorted octahedral coordination of tungstate in a subfamily of specific binding proteins. J Biol Inorg Chem 14: 663–672. [DOI] [PubMed] [Google Scholar]
- 74. Lu Z, Dunaway-Mariano D, Allen KN (2008) The catalytic scaffold of the haloalkanoic acid dehalogenase enzyme superfamily acts as a mold for the trigonal bipyramidal transition state. Proc Natl Acad Sci USA 105: 5687–5692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Lad C, Williams NH, Wolfenden R (2003) The rate of hydrolysis of phosphomonoester dianions and the exceptional catalytic proficiencies of protein and inositol phosphatases. Proc Natl Acad Sci U S A 100: 5607–5610. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
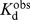 = 0.20±0.02 µM (diamonds, dashed line), 0.24±0.05 µM (circles, solid line), and 0.34±0.06 µM (triangles, dotted line). The average K
d value from the three assays is 0.26±0.07 µM (Table 1 and Table S1). Samples of WT AP and 32Pi were incubated for >1 h before the fraction 32Pi bound was measured and no dependence on the incubation time was observed (not shown). (B) Inhibition of pNPP hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 0.4 µM pNPP. Activity was normalized by dividing the observed rate constant in the presence of inhibitor by the rate constant in the absence of inhibitor. Two replicate assays yielded individual, nonlinear least-squares fits for competitive inhibition with K
d values of 0.67±0.04 µM (circles) and 0.67±0.06 µM (diamonds); the combined fit is shown with K
d = 0.67±0.04 µM. (C) Inhibition of pNPS hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 21 mM pNPS. To achieve activity significantly above background, a much higher concentration of AP (0.2 µM) is needed than for the pNPP inhibition assays. As a result, the simplifying assumption that [inhibitor]free = [inhibitor]total does not hold; [AP] is similar to the expected K
i and the commonly used form of the Michaelis–Menten equation with competitive inhibition could not be used. Instead, a quadratic equation (below) was used to relate the observed fractional activity to the total inhibitor and AP concentrations used in the assay and a nonlinear least-squares fit of this equation gave K
d = 0.50±0.14 µM. (D) The equilibrium-binding assay at pH 8.0, 9.5, and 10.5 with
= 0.20±0.02 µM (diamonds, dashed line), 0.24±0.05 µM (circles, solid line), and 0.34±0.06 µM (triangles, dotted line). The average K
d value from the three assays is 0.26±0.07 µM (Table 1 and Table S1). Samples of WT AP and 32Pi were incubated for >1 h before the fraction 32Pi bound was measured and no dependence on the incubation time was observed (not shown). (B) Inhibition of pNPP hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 0.4 µM pNPP. Activity was normalized by dividing the observed rate constant in the presence of inhibitor by the rate constant in the absence of inhibitor. Two replicate assays yielded individual, nonlinear least-squares fits for competitive inhibition with K
d values of 0.67±0.04 µM (circles) and 0.67±0.06 µM (diamonds); the combined fit is shown with K
d = 0.67±0.04 µM. (C) Inhibition of pNPS hydrolysis activity by Pi under the standard reaction conditions at pH 8.0 with 21 mM pNPS. To achieve activity significantly above background, a much higher concentration of AP (0.2 µM) is needed than for the pNPP inhibition assays. As a result, the simplifying assumption that [inhibitor]free = [inhibitor]total does not hold; [AP] is similar to the expected K
i and the commonly used form of the Michaelis–Menten equation with competitive inhibition could not be used. Instead, a quadratic equation (below) was used to relate the observed fractional activity to the total inhibitor and AP concentrations used in the assay and a nonlinear least-squares fit of this equation gave K
d = 0.50±0.14 µM. (D) The equilibrium-binding assay at pH 8.0, 9.5, and 10.5 with 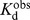 values of 0.24 µM (circles), 1.7 µM (diamonds), and 23 µM (triangles), respectively. (E) Comparison of the pH-dependent
values of 0.24 µM (circles), 1.7 µM (diamonds), and 23 µM (triangles), respectively. (E) Comparison of the pH-dependent 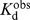 values from the new equilibrium-binding assay [closed circles; part (D)] with values measured by kinetic inhibition (open circles; from Figure S9C). The line shown is the combined fit of both data sets and gives a protein inactivation pK
a value of 8.7, in agreement with the inactivation pK
a value determined over the full pH range (Figure S9C). (F) The fraction 32Pi bound determined by the filtration assay after addition of unlabeled Pi (2 mM) to AP•32Pi (assay in standard buffer conditions with 10 µM WT AP), giving a limit for k
off of ≥0.01 s−1. (G) The uptake of 32Pi after addition of 32Pi to Pi-free AP and following the fraction bound using the filtration assay in standard buffer conditions with 0.1–10 µM WT AP; k
values from the new equilibrium-binding assay [closed circles; part (D)] with values measured by kinetic inhibition (open circles; from Figure S9C). The line shown is the combined fit of both data sets and gives a protein inactivation pK
a value of 8.7, in agreement with the inactivation pK
a value determined over the full pH range (Figure S9C). (F) The fraction 32Pi bound determined by the filtration assay after addition of unlabeled Pi (2 mM) to AP•32Pi (assay in standard buffer conditions with 10 µM WT AP), giving a limit for k
off of ≥0.01 s−1. (G) The uptake of 32Pi after addition of 32Pi to Pi-free AP and following the fraction bound using the filtration assay in standard buffer conditions with 0.1–10 µM WT AP; k ≥0.03 s−1 for all concentrations of WT AP.
≥0.03 s−1 for all concentrations of WT AP. |
(EPS)
Equilibrium-binding assay with S102G and S102A AP. All assays were carried out at pH 8.0 under the standard buffer conditions described in Materials and Methods. (A) Dissociation of 32Pi from S102G and S102A AP. Excess unlabeled Pi (2 mM) was added to 1 µM samples of S102G (open diamonds) or S102A (closed circles) AP with maximal 32Pi bound. After the addition of unlabeled Pi, the fraction 32Pi bound was measured over time. The line shows the expected behavior for a dissociation rate constant of 2×10−7 s−1 (t1/2∼1,000 h), which provides the upper limit used in the text. (B, C) Uptake of 32Pi over time by S102G (B) or S102A (C) AP. (Pi-free proteins were generated as described in Materials and Methods.) Nonlinear least-squares fits to the equation 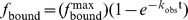 at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. The observed background (at 0 min) fraction 32Pi bound is different for the two uptake assays because different filtration devices were used for each assay (see Materials and Methods). (D, E) The observed uptake rate constants versus each S102G (D) or S102A (E) AP concentration. For simple two-state binding, k
obs = k
on[AP]+k
off
[23]. The weighted, nonlinear least-squares fits shown as solid lines give slope values (k
on) of 1,300 and 1.6×104 M−1 s−1 for S102G and S102A AP, respectively. The y-intercept values for these plots are strongly influenced by small errors in the slope fit and are not typically interpreted for this reason. Fixing the y-intercept value at the limit for k
off suggested by the chase assays (2×10−7 s−1) nevertheless yields reasonable fits to the data as shown by the dashed lines. Note the log scale in (D) but not in (E).
at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. The observed background (at 0 min) fraction 32Pi bound is different for the two uptake assays because different filtration devices were used for each assay (see Materials and Methods). (D, E) The observed uptake rate constants versus each S102G (D) or S102A (E) AP concentration. For simple two-state binding, k
obs = k
on[AP]+k
off
[23]. The weighted, nonlinear least-squares fits shown as solid lines give slope values (k
on) of 1,300 and 1.6×104 M−1 s−1 for S102G and S102A AP, respectively. The y-intercept values for these plots are strongly influenced by small errors in the slope fit and are not typically interpreted for this reason. Fixing the y-intercept value at the limit for k
off suggested by the chase assays (2×10−7 s−1) nevertheless yields reasonable fits to the data as shown by the dashed lines. Note the log scale in (D) but not in (E).
(EPS)
Dilution of S102G AP after uptake of 32Pi. S102G AP (1 µM at pH 8.0 in standard buffer conditions) was incubated with ∼200 pM 32Pi for 400 min. The sample was serially diluted 2-fold by addition of buffer at t = 400, 1,430, and 1,810 min (as indicated by the vertical dashed lines) to give the S102G AP concentrations indicated at the top of the figure, and the fraction 32Pi bound was measured after each dilution using the filtration assay.
(EPS)
Model and fits for uptake of 32Pi by S102G and S102A AP. (A) The model for uptake of 32Pi with both reversible binding of 32Pi and irreversible inactivation of the free protein. k off was fixed at the limit measured with the chase assay [the fits in parts (B) and (C) were insensitive to lowering k off below the upper limit of 2×10−7 s−1]. (B) The uptake of 32Pi by S102G AP (data from Figure S2B) fit to the model in part (A). For fitting, the data were normalized to correct for the ∼0.1 fraction 32Pi loss during centrifugation for the filtration units used in these assays (see Materials and Methods). The lines show a global, nonlinear fit for k on and k inactive and yielded values of ∼1,000 M−1 s−1 and ∼3×10−4 s−1, respectively. (C) The uptake of 32Pi by S102A AP (data from Figure S2C) fit to the model in part (A). For model fitting, the data were normalized to correct for the background fraction binding at time zero of ∼0.1, as observed for the type of filtration units used in this assay (see Materials and Methods). The global fit shown to the model in (A) yielded a poor fit, particularly to the data at lower concentrations of S102A AP.
(EPS)
Initial uptake rate constant analysis for S102G and S102A AP. (A) The uptake of 32Pi by S102G AP (data from Figure S2B). The dashed lines are the single exponential fits to the entire uptake time course, as shown in Figure S2B. The solid lines estimate the rate of initial 32Pi uptake. (B) The estimated initial uptake rate constants from the slopes of the lines in (A) at each concentration of S102G AP. The nonweighted, linear fit shown gives a slope of k on 740 M−1 s−1 (with the y-intercept, k off, fixed at 2×10−7 s−1). Note the logarithmic x-axis scale. (C) The uptake of 32Pi by S102A AP (data from Figure S2C). The dashed lines are the single exponential fits to the entire uptake time course, as shown in Figure S2C. The solid lines estimate the rate of initial 32Pi uptake. (D) The estimated initial uptake rate constants from the slopes of the lines in (C) at each concentration of S102A AP. The nonweighted, linear fit shown gives a slope for k on of 1.2×104 M−1 s−1 (with the y-intercept, k off, fixed at 2×10−7 s−1).
(EPS)
Equilibrium-binding assays for S102G and S102A AP. Samples of various concentrations of S102G (A) or S102A (B) AP were incubated with ∼200 pM 32Pi at pH 8.0 in the standard buffer conditions. The samples were incubated ≥24 h before the fraction 32Pi bound was measured. Independent replicate assays are depicted by different symbols. Fits to a simple two-state binding isotherm yielded a variable midpoint of the fraction bound values and yielded a steeper binding dependence than expected for simple 1∶1 binding. As noted in Text S3, these and other results suggest complications for protein inactivation over the long times of these assays and led us to use weaker binding and faster equilibrating mutants for quantitative comparisons.
(EPS)
Inhibition by Pi and equilibrium-binding assay for R166S AP. (A) Inhibition of R166S AP pNPP hydrolysis activity by Pi at pH 8.0 under the standard reaction conditions (see Materials and Methods) with [pNPP] = 0.8 µM. Three independent replicate assays are shown. Activity was normalized by the observed rate constant in the absence of inhibitor. The lines are nonlinear least-squares fits for competitive inhibition and give an average K i value of 360±160 µM. (B) Equilibrium-binding assay conducted for R166S AP at pH 8.0 (closed circles) and 9.0 (open diamonds) under the standard reaction conditions. The dashed line shows the predicted fraction 32Pi bound for a dissociation constant of 360 µM.
(EPS)
Pi equilibrium-binding assay for S102G/R166S and S102A/R166S AP. (A) Three independent equilibrium-binding assays for 32Pi binding to S102G/R166S AP at pH 8.0 (in standard buffer conditions). Nonlinear least-squares fits for fractional 32Pi binding give an average 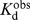 value of 66±8 nM. Incubation times were >300 min. (B) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102G/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (
value of 66±8 nM. Incubation times were >300 min. (B) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102G/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (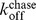 ) of 1.2±0.05×10−4 s−1. (C) Uptake of 32Pi over time by S102G/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (D) The observed uptake rate constants versus S102G/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line yields a k
on value of 1,190±120 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.2×10−4 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations from this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars (assuming symmetrical error). (E) Three independent equilibrium-binding assays for 32Pi binding to S102A/R166S AP at pH 8.0. Nonlinear least-squares fits for fractional 32Pi binding give an average
) of 1.2±0.05×10−4 s−1. (C) Uptake of 32Pi over time by S102G/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (D) The observed uptake rate constants versus S102G/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line yields a k
on value of 1,190±120 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.2×10−4 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations from this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars (assuming symmetrical error). (E) Three independent equilibrium-binding assays for 32Pi binding to S102A/R166S AP at pH 8.0. Nonlinear least-squares fits for fractional 32Pi binding give an average 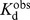 value of 77±6 nM. Incubation times were >4 d. (F) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102A/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (
value of 77±6 nM. Incubation times were >4 d. (F) The fraction 32Pi bound followed by the filtration assay after addition of unlabeled Pi (2 mM) to 1 µM S102A/R166S AP pre-bound with 32Pi (assay in standard buffer conditions). The line shows a nonlinear least-squares fit with a first-order decay constant (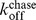 ) of 1.6±0.06×10−6 s−1, assuming a background fraction-bound at t = ∞ of 0.05, as was observed for the S102G/R166S AP chase assay. (G) Uptake of 32Pi over time by S102A/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (H) The observed uptake rate constants versus S102A/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 51±4 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (I) Uptake of 32Pi over time by S102G/R166S AP followed using a filtration device containing G-25 Sephadex resin (see Materials and Methods). These filtration devices give very low background 32Pi fraction binding (but note that the maximum 32Pi bound that could be observed only approaches 0.85–0.90, presumably from loss of 32Pi bound to AP as the bound complex passes through the Sephadex resin during the filtration). Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (J) The observed uptake rate constants versus S102G/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 1,420±520 M−1 s−1, within error of the value obtained with the filtration method used in part (C). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (K) Uptake of 32Pi over time by S102A/R166S AP followed using filtration devices containing G-25 Sephadex resin. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (L) The observed uptake rate constants versus S102A/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 36±14 M−1 s−1 within error of the value obtained with the filtration devices used in part (G). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. The fit error for the 0.2 µM S102A/R166S AP uptake sample is exceptionally large, reflecting the influence of an outlier data point collected during the time course.
) of 1.6±0.06×10−6 s−1, assuming a background fraction-bound at t = ∞ of 0.05, as was observed for the S102G/R166S AP chase assay. (G) Uptake of 32Pi over time by S102A/R166S AP followed by the filtration assay. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (H) The observed uptake rate constants versus S102A/R166S AP concentration. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 51±4 M−1 s−1. Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (I) Uptake of 32Pi over time by S102G/R166S AP followed using a filtration device containing G-25 Sephadex resin (see Materials and Methods). These filtration devices give very low background 32Pi fraction binding (but note that the maximum 32Pi bound that could be observed only approaches 0.85–0.90, presumably from loss of 32Pi bound to AP as the bound complex passes through the Sephadex resin during the filtration). Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (J) The observed uptake rate constants versus S102G/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 1,420±520 M−1 s−1, within error of the value obtained with the filtration method used in part (C). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102G/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. (K) Uptake of 32Pi over time by S102A/R166S AP followed using filtration devices containing G-25 Sephadex resin. Nonlinear least-squares fits at each protein concentration were used to estimate the observed uptake rate constant and the endpoint 32Pi fraction bound. (L) The observed uptake rate constants versus S102A/R166S AP concentration using filtration devices containing G-25 Sephadex resin. The weighted, nonlinear least-squares fit shown as a solid line gives a k
on value of 36±14 M−1 s−1 within error of the value obtained with the filtration devices used in part (G). Fixing the y-intercept value at the k
off determined in the chase assay (1.6×10−6 s−1) yields the fit shown by the dashed line and does not significantly change the k
on value obtained. The largest deviations of this fit occur at the lowest concentrations of S102A/R166S AP, which have the highest k
obs fit error as illustrated by the error bars. The fit error for the 0.2 µM S102A/R166S AP uptake sample is exceptionally large, reflecting the influence of an outlier data point collected during the time course.
(EPS)
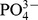 affinity to AP with Ser102 deprotonated. Assays in standard conditions of 100 mM NaAcetate (pH 4.5–5.5), NaMaleate (pH 6.0–6.5), NaMOPS (pH 7–8.0), NaCHES (pH 8.5–9.5), NaCAPS (pH 10–11.2), or NaCABS (pH 11.0–11.4), with 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. (A) The model used to estimate the
affinity to AP with Ser102 deprotonated. Assays in standard conditions of 100 mM NaAcetate (pH 4.5–5.5), NaMaleate (pH 6.0–6.5), NaMOPS (pH 7–8.0), NaCHES (pH 8.5–9.5), NaCAPS (pH 10–11.2), or NaCABS (pH 11.0–11.4), with 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. (A) The model used to estimate the 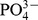 binding affinity. (B) The pNPP hydrolysis activity of R166S AP from pH 7–10. The line shows the expected trend for a single enzymatic inactivation given by
binding affinity. (B) The pNPP hydrolysis activity of R166S AP from pH 7–10. The line shows the expected trend for a single enzymatic inactivation given by 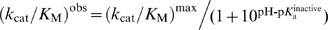 with
with 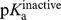 = 7.6 and (k
cat/K
M)max = 8×104 M−1 s−1. (C) The pH-dependent Pi affinity of WT AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed values of K
= 7.6 and (k
cat/K
M)max = 8×104 M−1 s−1. (C) The pH-dependent Pi affinity of WT AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed values of K
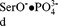 are shown.
are shown. 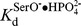 was fixed at 0.46 µM and
was fixed at 0.46 µM and 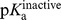 was fixed at 8.6, which are the values from the optimal fits assuming no
was fixed at 8.6, which are the values from the optimal fits assuming no 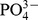 affinity. The fit using a fixed K
affinity. The fit using a fixed K
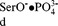 of 100 nM deviated 4-fold from the data above pH 11.0. (D) The pH-dependent Pi affinity of R166S AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed K
of 100 nM deviated 4-fold from the data above pH 11.0. (D) The pH-dependent Pi affinity of R166S AP. Weighted, nonlinear least-squares fits of Equation S3 with various fixed K
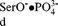 values are shown. K
values are shown. K
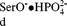 was fixed at 110 µM and
was fixed at 110 µM and 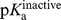 was fixed at 7.6, which are the values from the optimal fits assuming no
was fixed at 7.6, which are the values from the optimal fits assuming no 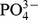 affinity. The fit with a K
affinity. The fit with a K
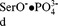 = 2.5 µM deviates from the data at pH 10 with greater than the expected error of these measurements (<50%).
= 2.5 µM deviates from the data at pH 10 with greater than the expected error of these measurements (<50%). |
(Equation S3) |
(EPS)
31P NMR of Pi with R166S AP. (A) Samples contained ∼1.3 mM R166S AP, 10 mM NaTris, pH 7.5, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. The concentration of Pi was initially very low to achieve the highest fraction bound. The concentration of Pi was subsequently increased by adding small volumes of concentrated Pi to achieve the lower fraction bound values listed. The fraction Pi bound was computed using the measured R166S AP dissociation constant for Pi binding of 360 µM. 31P NMR parameters are as described in Materials and Methods. The chemical shift approaches the shift of the bound Pi shift observed in WT AP (bottom spectrum). (B) Extrapolation of the 31P NMR chemical shift as the fraction Pi bound increases yields a chemical shift for bound Pi of ∼3.8 ppm.
(EPS)
31P NMR spectra of S102G (A) and S102G/R166S (B) AP with excess Pi. Solution conditions for all 31P NMR measurements are described in Materials and Methods. Protein concentrations were typically 1–2 mM and Pi concentrations were approximately 2-fold in excess. When Pi is not in excess, only the chemical shift peaks demarcated with red arrows remain present (spectra not shown). The additional peaks present with Pi in excess correspond to the chemical shifts expected for the unbound species of Pi at each pH (see Table S3).
(EPS)
[18O]-Pi edited FTIR difference spectra of Pi in solution and Pi bound to WT, S102G, and S102G/R166S AP. (A) FTIR difference spectrum between 16O-Pi and 18O-Pi at pH 4.5 (green), 9.5 (blue), or 13 (red). (B) FTIR difference spectra between AP•16O-Pi and AP•18O-Pi for WT AP (2.6 mM AP/2.3 mM Pi) in 140 mM NaMOPS, pH 8.0, 680 mM NaCl, 1.4 mM MgCl2, and 140 µM ZnCl2 (from ref. [16]); S102G AP (3.4 mM AP/1 mM Pi) in 110 mM NaCHES, pH 9.5, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2; and S102G/R166S AP (2.2 mM AP/1 mM Pi) in 50 mM NaCHES, pH 9.0, 100 mM NaCl, 1 mM MgCl2, and 100 µM ZnCl2. All samples and spectra were prepared and acquired as described in [16].
(EPS)
Comparison of 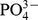 binding of AP with and without Ser102. Comparison of
binding of AP with and without Ser102. Comparison of 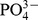 binding AP with Ser102 either mutated to Gly, deprotonated or protonated. Black bars show the
binding AP with Ser102 either mutated to Gly, deprotonated or protonated. Black bars show the 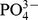 affinity measured for S102G/R166S AP and estimated for S102G AP (
affinity measured for S102G/R166S AP and estimated for S102G AP (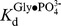 values in Table 2 of the main text). Red bars show the upper limits for the
values in Table 2 of the main text). Red bars show the upper limits for the 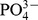 affinity (denoted by downward arrows) measured for R166S and WT AP with Ser102 deprotonated (
affinity (denoted by downward arrows) measured for R166S and WT AP with Ser102 deprotonated (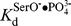 values in Table 2 of the main text). Grey bars show the lower limits for the
values in Table 2 of the main text). Grey bars show the lower limits for the 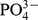 affinity for R166S and WT AP with Ser102 protonated (
affinity for R166S and WT AP with Ser102 protonated (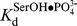 values in Table 2 of the main text).
values in Table 2 of the main text).
(EPS)
Binding of Pi to a protein tyrosine phosphatase with and without its nucleophilic cysteine present. (A) Equilibrium-binding assay of the PTP, Stp1, with Cys11 intact (open circles) and three independent assays of C11G Stp1 (closed symbols) at pH 6.0 in 20 mM NaMaleate, 100 µM Na2EDTA, and 0.15 M NaCl at 4°C. Fits to the data for C11G Stp1 gave K d values of 4.9±0.5 µM (inverted triangles), 9.6±1.7 µM (squares), and 15±2.3 µM (triangles). The average K d value from the three assays is 10±5 µM. The observed fraction 32Pi bound did not depend on incubation times of C11G Stp1 with 32Pi greater than 60 min. No significant Pi binding of WT Stp1 could be detected within the protein concentration limits of the assay (500 µM). [In contrast to the observations with R166S AP at pH 8.0, concentrations of Stp1 >25 µM did not result in a significant decrease in flow rate through the filtration unit (see Text S4).] (B) Inhibition of WT Stp1 pNPP hydrolysis activity by Pi at pH 6.0 in 20 mM NaMaleate, 100 µM Na2EDTA, and 0.15 M NaCl for three independent assays. Fits yield K i values of 14±4 mM (circles), 19±2 mM (open triangles), and 20±2 mM (open diamonds) with an average K i value of 18±3 mM. WT and C11G Stp1 were purified as reported previously [44].
(EPS)
The pH dependence of tungstate binding to WT AP. (A) Fraction 32Pi bound to AP as a function of tungstate concentration. A competition-binding assay at pH 8.0 for WT AP (see Materials and Methods for assay details) under the standard buffer conditions. A nonlinear least-squares fit to the competition equation shown in Materials and Methods yields a dissociation constant value for tungstate binding (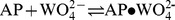 ) of
) of 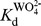 = 0.9±0.2 µM in good agreement with the dissociation constant at this pH reported previously (
= 0.9±0.2 µM in good agreement with the dissociation constant at this pH reported previously (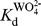 = 1.1 µM; [20]) at pH 8.0. (B) The pH-dependent tungstate affinity for WT AP determined by kinetic inhibition measurements (circles) and by the equilibrium-binding assay via competition with 32Pi binding (squares). The fits shown yield inactivating pK
a values of 7.82±0.13 (solid line) and 8.07±0.16 (dashed line) and pH-independent dissociation constants for tungstate dianion binding of 0.57±0.11 µM (solid line; data from [20]) and 2.06±0.48 µM (dashed line).
= 1.1 µM; [20]) at pH 8.0. (B) The pH-dependent tungstate affinity for WT AP determined by kinetic inhibition measurements (circles) and by the equilibrium-binding assay via competition with 32Pi binding (squares). The fits shown yield inactivating pK
a values of 7.82±0.13 (solid line) and 8.07±0.16 (dashed line) and pH-independent dissociation constants for tungstate dianion binding of 0.57±0.11 µM (solid line; data from [20]) and 2.06±0.48 µM (dashed line).
(EPS)
Structural overlay of AP Mg2+ site. The WT AP crystal structure (PDB code 3TGO, [36]) is shown in grey with the crystal structure reported here for S102G/R166S AP in magenta. In the S102G/R166S AP structure, a Zn2+ ion occupies the Mg2+ site. The position of the coordinating residues and the metal ion are the same within error in the two structures.
(EPS)
Summary of Pi binding kinetics for WT, S102G, S102A, R166S, S102G/R166S, and S102A/R166S AP. a
k
on for S102G and S102A AP is the estimated association rate constant from a fit analysis of the 32Pi uptake assay results described in Text S2. k
on for S102G/R166S and S102A/R166S AP is from the fit of the k
obs values from the uptake assay versus the [AP] shown in Figure S8D and H.
b
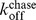 is the dissociation rate constant measured by the 32Pi chase assay (Figure S1F; Figure S2A; Figure S8B and F). c
is the dissociation rate constant measured by the 32Pi chase assay (Figure S1F; Figure S2A; Figure S8B and F). c
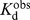 is the dissociation constant for Pi binding at pH 8.0 measured from the fraction 32Pi bound after an incubation time sufficient to reach equilibrium (Figure S1A for WT AP; Figure S8A for S102G/R166S; Figure S8D for S102A/R166S AP), except for the value reported for R166S AP, which is from kinetic inhibition assays (Figure S7A). dThe
is the dissociation constant for Pi binding at pH 8.0 measured from the fraction 32Pi bound after an incubation time sufficient to reach equilibrium (Figure S1A for WT AP; Figure S8A for S102G/R166S; Figure S8D for S102A/R166S AP), except for the value reported for R166S AP, which is from kinetic inhibition assays (Figure S7A). dThe 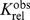 value is calculated by dividing the dissociation constant for AP with Ser102 intact by the dissociation constant (
value is calculated by dividing the dissociation constant for AP with Ser102 intact by the dissociation constant (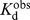 ) for the Ser102 mutants in either the context of WT or R166S AP; larger values represent stronger binding of the Ser102 mutant relative to proteins with Ser102 intact.
) for the Ser102 mutants in either the context of WT or R166S AP; larger values represent stronger binding of the Ser102 mutant relative to proteins with Ser102 intact.
(DOC)
Crystallographic data and model statistics.
(DOC)
31P NMR chemical shift summary of free Pi and Pi bound to WT, R166S, S102G, and S102G/R166S AP. aChemical shifts reported for unbound Pi species were measured here under conditions identical to those used for protein-containing samples and referenced to a 1% phosphoric acid standard. These shifts are within error of those reported previously [42]. At intermediate pH values the observed chemical shift represents a weighted average of the ionic forms present.
(DOC)
Observed activity of Ser102 mutants likely arises from WT AP contamination.
(DOC)
Tests of the new equilibrium-binding assay with WT AP.
(DOC)
Equilibrium-binding assay results with S102G and S102A AP.
(DOC)
Equilibrium binding of Pi to R166S, S102G/R166S, and S102A/R166S AP.
(DOC)
Interplay between Ser102 and Arg166 revealed by structural comparison.
(DOC)
Estimation of 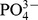 affinity for AP with Ser102 deprotonated.
affinity for AP with Ser102 deprotonated.
(DOC)
31P NMR of the R166S AP•Pi complex suggests bound 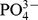 .
.
(DOC)
31P NMR of Pi-bound to S102G and S102G/R166S AP with excess Pi.
(DOC)
Equations derived from the models in Figure 4C and D to fit the pH-dependent Pi binding data for R166S (Equation S1) and S102G/R166S (Equation S2) AP in Figure 4A.
(DOC)
Comparison of AP•Pi affinities with AP Ser102 protonated, deprotonated, or mutated to Gly.
(DOC)
Previous estimation for the destabilization from Ser102 on the binding of a dianionic phosphate.
(DOC)
Estimation of the contribution of Arg166 to binding of Pi dianion.
(DOC)
Comparison of 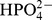 and
and 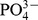 binding by S102G AP.
binding by S102G AP.
(DOC)
Evidence against electrostatic repulsion in phosphoryl transfer transition states.
(DOC)
Extended implications for phosphoryl transfer catalysis.
(DOC)