Plant Water Use Efficiency over Geological Time – Evolution of Leaf Stomata Configurations Affecting Plant Gas Exchange

Abstract

Plant gas exchange is a key process shaping global hydrological and carbon cycles and is often characterized by plant water use efficiency (WUE - the ratio of CO₂ gain to water vapor loss). Plant fossil record suggests that plant adaptation to changing atmospheric CO₂ involved correlated evolution of stomata density (d) and size (s), and related maximal aperture, a_max. We interpreted the fossil record of s and d correlated evolution during the Phanerozoic to quantify impacts on gas conductance affecting plant transpiration, E, and CO₂ uptake, A, independently, and consequently, on plant WUE. A shift in stomata configuration from large s-low d to small s-high d in response to decreasing atmospheric CO₂ resulted in large changes in plant gas exchange characteristics. The relationships between gas conductance, g_ws, A and E and maximal relative transpiring leaf area, (a_max⋅d), exhibited hysteretic-like behavior. The new WUE trend derived from independent estimates of A and E differs from established WUE-CO₂ trends for atmospheric CO₂ concentrations exceeding 1,200 ppm. In contrast with a nearly-linear decrease in WUE with decreasing CO₂ obtained by standard methods, the newly estimated WUE trend exhibits remarkably stable values for an extended geologic period during which atmospheric CO₂ dropped from 3,500 to 1,200 ppm. Pending additional tests, the findings may affect projected impacts of increased atmospheric CO₂ on components of the global hydrological cycle.

Introduction

Aspects of plant gas exchange operating at the stomatal scale may exert significant influences on global hydrological and carbon cycles with about 40% of terrestrial precipitation evaporating back to the atmosphere through plant leaves [1]–[6]. The extent of plant influence on hydrological and carbon cycles is directly linked with plant water use efficiency (WUE) defined as the ratio of CO₂ gain by assimilation, A [mol L⁻² T⁻¹], to water vapor loss by transpiration, E [mol L⁻² T⁻¹]:

(1)

Stomata and impervious leaf cuticle have originated some 400 Myr ago as crucial adaptations enabling plant proliferation in water-limited terrestrial habitats [5], [7]–[9]. Plant CO₂ uptake for photosynthesis and concurrent water loss by transpiration are dynamically regulated by stomata perforating leaf surfaces. The intertwined control of CO₂ uptake and water loss obscures the primary driving process, prompting a century-long debate concerning the primary regulating factor [10], [11].

A widely-used approach for the evaluation of plant WUE in Eq. (1) is based on (i) estimating maximal water vapor diffusive leaf conductance, g_w [mol m⁻² s⁻¹], considering diffusion through an ensemble of non-interacting individual pores [12]–[16]; and (ii) invoking similarity between water vapor conductance, g_w, and CO₂ conductance, g_c [1], [12], [14], [15], [17]–[19], resulting in a convenient and widely used relation for gas conductance:

(2)

The factor 1.6 is the ratio of binary diffusivities of CO₂ and water vapor in air. The gas fluxes based on Fickian diffusion are expressed as [11], [20]:

(3)

(4)

with p_i and p_a are the leaf interior and atmospheric partial pressures of CO₂; and similarly e_i and e_a are the leaf interior and atmospheric water vapor pressures, with Δe = (e_a–e_i) often expressed in units of [mol gas mol⁻¹ air]. For low respiration rates relative to A, Eqs. 3 and 4 are similar to the model of Von Caemmerer and Farquhar [21]. According to Eqs. 1–2–3–4, plant WUE is reduced to the simple expression [20], [22], [23]:

(5)

where a constant 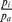value is generally applied [20]. Tanner and Sinclair [24] reviewed water use in crop production and found a relatively constant value of  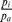= 0.7 for C3 species. For relatively constant values of Δe and 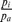, the resulting plant WUE based on Eq. 5 is proportional to atmospheric CO2 partial pressure, p_a.

Noting that information concerning plant stomatal configuration cancels out in Eq. 5, we show in the following that considering the two key diffusion processes separately while accounting for the effects of specific stomatal configurations yields a significantly different relationship between plant WUE and CO₂ that deviates from the simple linear expression in Eq. 5.

During the 400 million years (Myr) of plant evolution (the Phanerozoic eon), atmospheric CO₂ concentrations (CO₂) decreased by one order of magnitude from 4,000 ppm to present day levels [25]-[28]. The plant fossil record for the same period revealed that plant gas exchange adaptation involved significant variations in stomatal density, d [mm⁻²], and size (stomatal area), s [µm²] [14], [15], [29], [30]. Stomatal size, s, estimated by multiplying guard cell length by the width of guard cell pair [14], [15], is used to estimate stomatal maximal aperture, a_max, approximated as 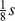[14], [31]. The correlated evolution of s and d is in line with theoretical and experimental evidence demonstrating that stomata a_max and d jointly determine gas diffusive resistance, a nonlinear function of these two variables [32]–[42].

We hypothesize that improved description of diffusive resistances by consideration of specific stomatal configurations deduced from plant fossil record could provide new insights on the independent responses of A and E to variations in atmospheric CO₂ during the Phanerozoic. The primary objectives of this study were to: (i) analyze the impact of independent estimates of A and E on historical trends in plant WUE relative to the coupled estimates based on Eq. 5; and (ii) infer the role of stomata configuration evolution on plant gas exchange and WUE estimates during the Phanerozoic. A wide range of stomatal adaptation to decreasing CO₂ during the Phanerozoic is deduced from the fossil record of s [µm²] and d [mm⁻²] evolution [14], [15], [29], [30], providing a unique opportunity to investigate trends in plant gas exchange characteristics across geological time scales during significant changes in atmospheric CO₂.

Methodology

Environmental Conditions During the Phanerozoic

The CO₂ time series for the Phanerozoic provided by Berner and Kothvala [27] were used in this study. In contrast with large variations in CO₂ during plant evolutiong_wevidence suggests that fluctuations in solar radiation and air temperature during the Phanerozoic were relatively minor, with the estimated mean air temperature varying only between 15°C and 23°C [25]. Consequently, variations in potential evaporation, E_p, during plant evolution remained relatively moderate as noted by Sperry [43]: “the maximum gradient for plant water loss to the atmosphere has remained constant during plant evolution”. A simple approximation based on the Penman-Monteith equation for E_p [44] suggests that for reported variation in mean air temperature, E_p would vary by 15%. For simplicity, we assumed a constant E_p value of 7,500 [µmol m⁻² s⁻¹] (corresponding to a mean daily potential evaporation rate of 3 mm d⁻¹ and boundary layer thickness δ = 2.0 mm for a mean wind speed of 1 m/s, in accordance with the assumptions in Beerling et al. [12]).

In addition to CO₂ levels, the concentration of atmospheric oxygen exhibited fluctuations throughout the Phanerozoic [45], which could affect stomatal function [46]. Nevertheless, we neglected the impact of such fluctuations, which photosynthesis models have shown to have a minor impact on inferences concerning WUE [15].

Evolution of Stomata Size and Density during the Phanerozoic

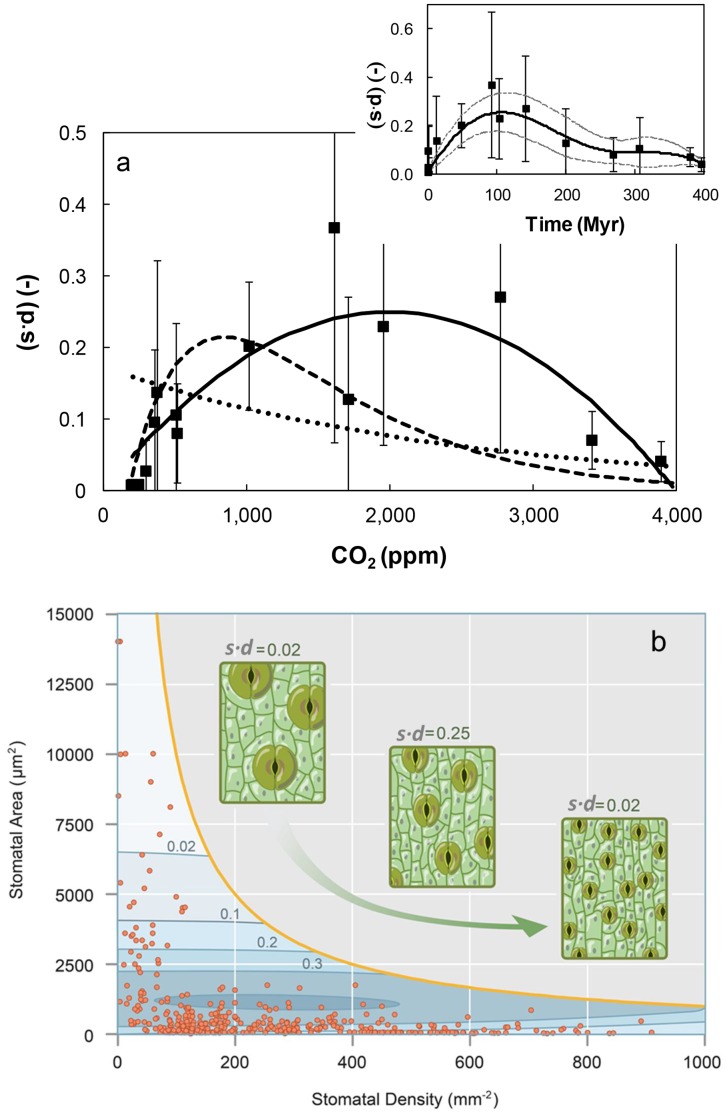
Fossil record data on the evolution of s and d for a wide range of C3 plants were reported by Franks and Beerling [14]. The s and d values were averaged for time intervals ranging from 5 to 85 Myr and related to corresponding atmospheric CO₂ concentrations. The product (s⋅d) [−], deduced from average values of s and d for each time interval determines the maximal relative leaf transpiring area, (a_max⋅d) [−], and thus strongly influences plant gas exchange. The resulting (s⋅d) evolution during the Phanerozoic is depicted in Fig. 1a and the fitted expression (solid line) is given in Eq. S1 in Appendix S1. Low values of (s⋅d) characterize both the beginning of the eon with high CO₂ (∼4,000 ppm), and present day values with low CO₂ (∼350 ppm). Plant adaptation to decreasing CO₂ may be reflected by increasing (s⋅d) from initial (∼4,000 ppm) to mid-range CO₂ levels (∼2,000 ppm), followed by decreasing (s⋅d) to present day values [30]. The chronological sequence of (s⋅d) variation during the Phanerozoic is depicted in the inset in Fig. 1a, indicating that approximately 100 Myr ago (corresponding CO₂ between 1500 to 2000 ppm) the trend in (s⋅d) was reversed, and decreased with decreasing CO₂. Statistical analysis including fitting a general additive model (GAM) showed that the trend (solid curve) was highly significant.

Figure 1. Fossil record-based plant leaf stomatal size and density, (s ⋅d), during the Phanerozoic.

(a) Variations in mean (s⋅d) with changes in atmospheric CO₂ concentrations; black symbols represent mean values for different time intervals based on data reported by Franks and Beerling [15]; the solid line is a fitted polynomial to the data (Eq. S1 in Appendix S1); the dashed line represent (s⋅d) values estimated by the product of Eqs. S3 and S4 from Franks and Beerling [14]; the dotted line represent (s⋅d) values estimated by the product of Eqs. S5 and S6 from Franks and Beerling [15]. The inset depicts the corresponding change of (s⋅d) with time (the solid line is the curve fitted using GAM and the upper and lower dashed curves indicate the 95% confidence intervals). (b) Correlated evolution of stomata density d [mm⁻²] and area s [µm²] (symbols) over the Phanerozoic bounded by geometrical maximum (solid line), based on Fig. 1 of Franks and Beerling [14]. Contours of equal (s⋅d) values highlight the non-monotonic evolution of (s⋅d) as stomata size decreased and their density increased.

Franks and Beerling [14] have used larger time intervals (50 or 100 Myr)for data averaging (resulting in less data points but similar trend), and have fitted regression equations to s and d individually as functions of CO₂ (Eqs. S3 and S4 in Appendix S1). The resulting evolution of (s⋅d) computed according to their regression equations (Eqs. S3 and S4) is depicted by the dashed line in Fig. 1a. Interestingly, in a related study, Franks and Beerling [15] have reported different trends of s and d vs. CO₂ that yield a monotonously increasing (s⋅d) with CO₂ decrease (dotted line in Fig. 1a). In that analysis of the fossil record, they have used a 10-Myr averaging time interval. The resulting regression equations for s and d as individual functions of CO₂ are presented in Eqs. S5 and S6 in Appendix S1.

The correlated evolution of plant stomata s and d over the Phanerozoic reflects general transition from large s-low d configuration (in the early Phanerozoic) to a present day small s-high d configuration (Fig. 1b). The range of admissible values of d and s is geometrically limited by the continuous line in Fig. 1b [14], forcing the evolution of s and d across a non-monotonous (s⋅d) trajectory (as depicted in Fig. 1a).

Based on Franks and Farquhar [37] and Franks and Beerling [14], the maximal relative transpiring leaf area, (a_max⋅d), is proportional to (s⋅d) (approximated as 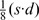. Consequently, the correlated evolution of s and d is expected to significantly influence plant gas exchange and related attributes A, E, and WUE.

Stomatal Configurations Effects on Diffusive Resistances and Transpiration Rate

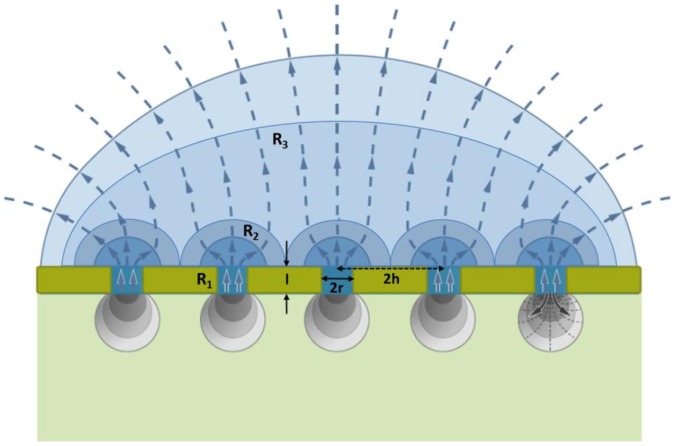
Diffusion theory predicts formation of a three-dimensional water vapor concentration field over individual stomata as depicted in Fig. (2) [33], [36], [41], [42]. These local vapor “shells” are confined within the boundary layer induced by convective air flow and introduce an additional diffusion resistance term to commonly-used gas exchange models and give rise to nonlinear relationship between evaporative fluxes, E [µmol m⁻² s⁻¹], and stomata aperture and density configurations. Studies have distinguished three primary resistances to vapor diffusion from perforated surfaces or plant leaves that operate in series as depicted in Fig. (2) [33]. The first resistance term, R₁, corresponds to the classical single pore resistance [32]; R₂, represents the resistance due to local vapor “shells” forming over pores and reflect interactions among neighboring pores; and R ₃, corresponds to the resistance of the boundary layer over the entire membrane or leaf surface. The resistance R ₃ is identical to standard resistance, R_p, characterizing vapor diffusion from a reference system (typically free water surface) that represents the potential evaporation, E_p. Several diffusion models have been proposed to quantify these resistances [33], [36], [37], [40]. In this study we adopted the model of Bange [33] based on its modest input parameter requirements and the explicit account for stomatal interactions affecting vapor diffusive fluxes. The model expresses evaporation rate, E, across a diffusion barrier perforated by identical pores of radius r relative to a potential evaporation rate from uncovered free water surface (under similar conditions), E_p. The first diffusion resistance term, R ₁, is defined as:

(6)

Where l is the thickness of the diffusion barrier or membrane [mm], approximated in the case where it represents the stomatal depth by 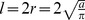; k, the ratio of water vapor diffusivity to air molar volume; 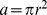, the pore area [mm²]; and d, the pore density [mm⁻²]. In terms of conductance, Eq. 6 is identical to the classical expression employed to estimation of stomatal conductance to water vapor, g_ws [13], [15]:

(7)

where a_max is the stomata maximum aperture. The second diffusive resistance term, R₂, represents the effect of interactions between neighboring pores or stomata, and it is defined in the model of Bange [33]:

(8)

Where r is the pore radius [L] and h, half mean distance between pores or stomata [L], approximated by . Alternative expressions for R₂ proposed by Cooke [37] and Schlünder [40] were compared and yield similar results for the range of (a_max⋅d) values of plant leaves (results not shown).

Figure 2. Gas exchange resistances and diffusion fields for water vapor and CO₂ over plant leaves.

Diffusion flow lines (dashed lines) and equal concentrations lines (solid lines) for water vapor in the boundary layer over the leaf (blue areas) and for atmospheric CO₂ within the substomatal cavities (grey areas) are shown. The figure depicts the consecutive three diffusive resistances resulting from the interactions between neighboring stomata, as expressed in Eqs. (6–9). The schematic representation is adapted from Bange [33].

Finally, the third resistance term, R ₃, is expressed by

(9)

where δ is the thickness of the boundary layer [L] (referred to as viscous sublayer, the region above the surface where the flow is laminar [42]). The three diffusive resistances defined in Eqs. 6 to 9 are expressed per unit of perforated leaf area.

The resulting relative transpiration rate, 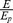, from a leaf surface accounting for the three diffusive resistances is thus:

(10)

The expression in Eq. 10 has been evaluated using relative transpiration rates from Zebrina pendula leaves (for a range of stomatal apertures ranging from 1 to 20 µm and similar stomatal density of 1,625 cm⁻²) measured by Bange [33]. The results are depicted in Fig. 3 as a function of the relative transpiring area of the leaf, (a⋅d). The corresponding boundary layer thickness δ was set to 7.5 mm, well within the range of viscous sub-layer thicknesses expected for air flows according to the Blasius relationship δ∼2v_∞ ^−1/2 with mean air velocity v_∞ in [m/s], and δ in [mm] [42], [47]. The relative transpiration rate estimated by Eq. 10 that accounts for all three resistance terms was in excellent agreement with measurements for the entire range of experimental values (Fig. 3). In Fig. 3, we also present the relative transpiration rates estimated without consideration of resistances R₂ and R₃. The results demonstrate that the resistance R₃ due to the boundary layer is the most important component of overall resistance to gas diffusion. An important aspect from plant gas exchange point of view, is that consideration of stomatal resistance only, R₁ (Eq. 6) does not capture measured fluxes for (a⋅d) values exceeding 0.001. Neglecting the contribution of interactions between neighboring stomata expressed by R₂ resulted in overestimation of gas fluxes by 65% for low (a⋅d) values down to 15% for higher (a⋅d) values. This suggests that including stomatal interactions systematically reduces gas fluxes with significant effects for certain a and d combinations, hence such interactions cannot be generally disregarded as suggested by Waggoner and Zetlich [1].

Figure 3. Relative evaporation as a function of relative evaporating area (a⋅d) from Zebrina pendula leaves.

The symbols depict relative transpiration rates for several stomata apertures ranging from 1 to 20 µm and a mean density of 1625 cm⁻² based on measurements of Bange [33] in still air. The short-dashed line corresponds to estimates that consider diffusive resistance from single pores only (Eq. 6). The large-dashed line corresponds to estimates that neglect interactions between neighboring stomata. The solid line corresponds to estimates based on Eq. 10 that express the effect of all three resistances depicted in Fig. 2.

The model in Eq. 10 was applied to estimate the evolution of relative transpiration flux, during the Phanerozoic (assuming E_p remained constant as discussed above). For estimation of absolute values of E, we have used a constant E_p = 7,500 [µmol m⁻² s⁻¹] equivalent to mean daily potential evaporation rate of 3 mm d⁻¹ and boundary layer thickness δ = 2.0 mm that corresponds to mean wind speed of 1 m/s, in accordance with the assumptions in Beerling et al. [12]. A sensitivity analysis indicated that the basic trend deduced in this study was not sensitive to fluctuation in E_p related to variations in mean air temperature (results not shown).

Estimation of Plant Net CO₂ Assimilation Rate, A

Plant CO₂ assimilation rate, A [µmol m⁻² s⁻¹], is more difficult to estimate than E, due to additional assumptions concerning uncertain biochemical processes. We considered two different methods for estimation of A as a function of CO₂ during the Phanerozoic. Both methods rely on the widely-used photosynthesis model of Farquhar et al. [48] where A is expressed as:

(11)

with the constants a₁ [µmol m⁻² s⁻¹] and a₂ [µmol mol⁻¹] whose values depend on light or Rubisco limitations; c_p [µmol mol⁻¹] is the CO₂ compensation point, and c_i the intercellular CO₂ concentration. For light-saturated conditions, a₁ represents the maximum carboxylation capacity, and a₂ accounts for both carboxylation rate and the impact of air oxygen concentration on CO₂ fixation [11]. Following Katul et al. [11], A is expressed in terms of leaf conductance to CO₂, g_c, and atmospheric CO₂ concentration, c_a:

(12)

We invoke similarity between diffusive conductance to CO₂ uptake and water vapor loss (Eq. 2), hence, the leaf conductance g_c considering all diffusive resistances described previously is:

(13)

Method 1: V_cmax Estimated Following de Boer et al. [16]

Katul et al. [49] proposed parameters and temperature adjustments for the model in Eq. 12, assuming a constant maximal carboxylation capacity at 25°C, V_cmax, [µmol m⁻² s⁻¹] to obtain a₁ values. However, evidence suggests that the maximal Rubisco carboxylation rate, V_cmax, decreased with increasing CO₂ [50]. Therefore, we adopted the model parameters presented in Katul et al. [11] except the assumption concerning a constant V_cmax. Instead we followed de Boer et al. [16] expression of V_cmax as a function of CO₂:

(14a)

where V_R is the reference value of V_cmax for a CO₂ concentration of 385 ppm, and CO₂ is expressed in [ppm]. Hence, the first method for estimating plant A was based on Eqs. 11, 12, 13 and 14a.

Method 2: V_cmax Estimated Following Franks & Beerling [15]

Beerling and Woodward [29] and Franks & Beerling [15] have developed a coupled photosynthesis-stomatal conductance-energy balance model that also employs the biochemical model of Farquhar et al. [48] for C3 plants. To better account for changes in plant gas conductance (stemming from the evolution of s and d), Franks and Beerling [15] proposed an empirical relationship expressing V_cmax as a function of gas diffusion conductance g_w:

(14b)

where g_w is expressed in [mmol m⁻² s⁻¹]. The second method for estimating A was based on Eqs. 11, 12, 13 and 14b.

Within the unavoidable uncertainties of reconstructing plant A for the Phanerozoic, we considered A estimates from the reconstruction of Franks and Beerling [15] (symbols), to determine the values of the constants in Eqs. (14a) and (14b). The best agreement for A-CO₂ relationships was obtained for the following parameter values: V_R = 120 µmol m⁻² s⁻¹; κ = 2.8 10⁻⁴ ppm⁻¹; α = 82 µmol m⁻² s⁻¹; β = 0.974. The A-CO₂ relationships resulting from the two methods applied are depicted in Fig. 4 (curves) as functions of atmospheric CO₂ concentrations, along with the estimates of A as reported in figure 7A (symbols) of Franks and Beerling [15]. The time course of A estimates is similar to that described in that figure in Franks and Beerling [15].

Figure 4. Photosynthetic assimilation rate A as a function of atmospheric CO₂ levels for C3 plants.

The curves represent the results from the model of Katul et al. [11, 49] based on [48] (Eq. 12) with V_cmax-g_w given in Eq. 14b (solid line) and V_cmax-CO₂ given in Eq. 14a (dashed line). The symbols represent values resulting from the reconstruction of Franks and Beerling [15] (based on results corresponding to the “Upper bound L, variable Temp. and O₂” case in their Fig. 7A).

Results and Discussion

Evolution of Plant WUE during the Phanerozoic

Plant WUE (Eq. 1) was evaluated from independent estimates of A and E (Eqs. 12 and 10), and is expressed as a function of CO₂ in Fig. 5 (solid and dashed lines for the two methods for A estimation described above). The resulting WUE-CO₂ trends were compared with the conventional approach (Eq. 5; dotted line in Fig. 5), and with modeled WUE by Franks and Beerling ([15] (symbols in Fig. 5). The latter two depict a quasi-linear decreasing trend for WUE-CO₂. In contrast, the estimated plant WUE trend resulting from independent estimates of E and A exhibit a complex behavior. Results suggest that plant gas exchange adaptation resulted in a steep decrease in WUE in response to the initial drop in CO₂, followed by leveling off to CO₂ values of ∼1,200 ppm; and subsequently WUE decreased as CO₂ declined to present day values. Interestingly, for the last period of plant WUE evolution, all models converge and yield a similar WUE decreasing trend.

Figure 5. Reconstructed WUE-CO₂ relationship for C3 plants during the Phanerozoic.

The curves result from the independent estimates of A based on Eq. 12 with Eq. 14a (dashed line) and Eq. 14b (solid line), and E (Eq. 10; with E_p = 7500 [µmol m⁻² s⁻¹] and δ = 2.0 mm) for the parabolic (s⋅d)-CO₂ relationship (Eq. A1).The dotted line corresponds to WUE estimates based on Eq. 5, with p_i/p_a = 0.7 and Δe = 0.03. The symbols represent values resulting from the model of Franks and Beerling [15] (based on their Fig. 10).

At first glance, the interpretation of the conventional nearly-linear decreasing WUE with declining CO₂ would imply that improving CO₂ uptake was the primary driver for plant gas exchange evolution. However, consideration of the new WUE trend (Fig. 5; solid line) shows that plant WUE remained practically constant despite the large decrease in CO₂ (from 3,500 to 1,200 ppm). This trend lends support to an alternate interpretation whereby regulation of water losses and not improving CO₂ uptake could have served as the primary driver for plant gas exchange evolution, especially during a period where plants have gradually adapted to life in dryer terrestrial environments [5], [8].

Estimating Plant Transpiration, E, during the Phanerozoic

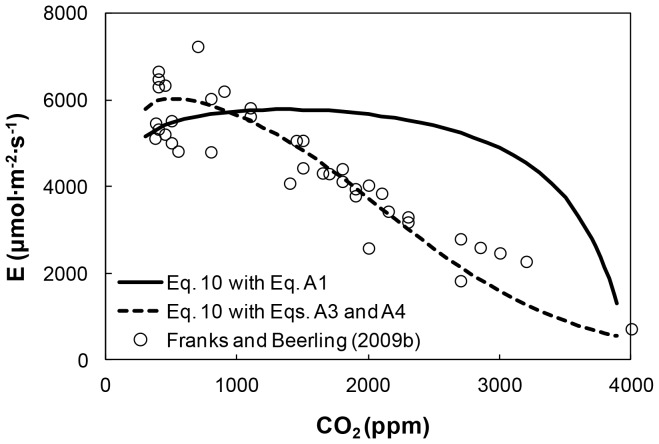
Plant transpiration rate, E, was estimated based on Eq. 10, considering resistive terms (Eqs. 6–9) computed for specific a_max–d configurations at each CO₂ level corresponding to the s-d patterns in Fig. 1a (solid and dashed lines). The respective E-CO₂ relationships are depicted in Fig. 6 (solid line and dashed line). The symbols in Fig. 6 represent E values deduced from the ratio of WUE and A values (represented by the symbols in Figs. 5 and 4, respectively) from the model results in [15]. The E-CO₂ relationship for the skewed (s⋅d)-CO₂ function based on Franks and Beerling [14] empirical relations (dashed line in Fig. 1a ), and the values extracted from the model of Franks and Beerling [15] both exhibit a nearly-linear increase in E with decreasing CO₂. In contrast, the E-CO₂ relationship based on Eq. 10 (with the solid (s⋅d)-CO₂ line in Fig. 1a ) yields nearly constant plant transpiration rates for most of the range of CO₂ changes during the Phanerozoic. The initial steep increase of E is associated with increasing (s⋅d) as CO₂ decreased early in the Phanerozoic (Fig. 1a). These results suggest that evolutionary refinements in s-d configurations enabled plants to maintain a relatively constant transpiration rate for a wide range of CO₂ levels.

Figure 6. Relationship between transpiration rate E and CO₂ for C3 plants during the Phanerozoic.

The solid line corresponds to Eq. 10 using the parabolic (s⋅d)- CO₂ relationship in Eq. S1, and the dashed line corresponds to the skewed (s⋅d)- CO₂ relationship resulting from Eqs. S3 and S4. The symbols are computed from the ratio of modeled values of WUE and A in [15].

The results in Fig. 6 highlight the role of stomatal configuration in shaping plant E. The gradual increase in (s⋅d) with decreasing CO₂ for the rising limb of the skewed (s⋅d)-CO₂ relationship (Fig. 1a; dashed line) resulted in a nearly-linear increase in E, whereas for the parabolic-shaped relation (Fig. 1a; solid line), E increased nonlinearly. Interestingly, the falling limbs of both (s⋅d)-CO₂ relationships exerted only a small impact on the E-CO₂ trend. The largest influence on plant gas exchange seems to be associated with the early increase in (s⋅d) reflecting a gradual shift from large s-low d to small s-high d configuration (Fig. 1b), that correspond to large a_max-low d and small a_max-high d configuration. The resulting small a_max-high d configuration represents a more robust configuration that greatly reduced sensitivity of diffusive gas exchange to reduced leaf evaporating area (a_max⋅d).

We note that in contrast with the steep decrease in A for CO₂ concentrations below 1,200 ppm (Fig. 4), E remained practically constant for the same period (and for the corresponding changes in CO₂) as seen in Fig. 6. These diverging responses of A and E suggest that total resistances for plant CO₂ uptake and water loss are different. Part of this difference are attributed to additional biochemical/photosynthetic resistance that affect CO₂ uptake but not water loss, and to other factors not explored here such as mesophyll resistance [51], [52] and cell walls resistances [12]. Consequently, plant response to environmental changes in terms of A may be different and decoupled from the response in plant E. Additional factors involving asymmetry in diffusion fields for water vapor and CO2 have been discussed by Parkhurst [53].

Variations in Plant A and E with Evolution of Stomata s and d

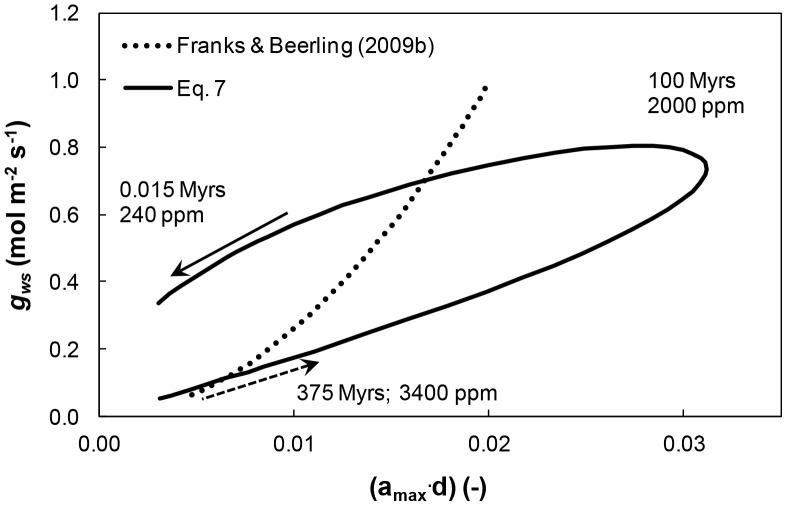
The impact of s and d evolution on maximal conductance to water vapor, g_ws [mol m⁻² s⁻¹], was estimated based on Eq. 7, using the a_max and d values corresponding to the s and d values in Eqs. S1 and S2, and those of Franks and Beerling [15] in Eqs. S5 and S6. The evolution of g_ws as a function of (a_max⋅d) variations during the Phanerozoic is depicted in Fig. 7. The resulting hysteretic-like behavior of g_ws-(a_max⋅d) reflects the parabolic (s⋅d)-CO₂ relationship (Fig. 1a; solid line), and differs from the monotonously increasing g_ws-(a_max⋅d) relation resulting from the monotonous (s⋅d)-CO₂ relationship (Fig. 1a; dotted line). The non-monotonous behavior suggests that plant adjustment of stomatal configuration by selection for small a_max-high d resulted in higher g_ws for similar (a_max⋅d) values. The two trends in Fig. 7 suggest that stomatal evolution has led to increased diffusive gas conductance. Hence, the shift towards small a_max-high d configuration not only enabled lower diffusive gas resistance with lower (a_max⋅d), it also reduced gas exchange sensitivity to leaf evaporating area (as evidenced by maintenance of nearly constant transpiration rates). It may have also contributed to improved leaf thermal management [8], [12].

Figure 7. Relationship between maximal vapor diffusive conductance of a stoma and maximal leaf partial transpiring area.

Estimated variations in maximal vapor diffusive conductance of a stoma, g_ws (Eq. 7) [mol m⁻² s⁻¹] and maximal leaf partial transpiring area (a_max⋅d) based on values from Eqs. (S1) and (S2) (solid line). The dotted line corresponds to g_ws-(a_max⋅d) computed according to Eq. 7 with the regression equations of Franks and Beerling [15] (Eqs. S5 and S6). Arrows depict chronology (dashed arrows represent early Phanerozoic; solid arrows represent late Phanerozoic).

Figure 8 depicts the evolution of transpiration rates (Eq. 10) and CO₂ assimilation rates (Eq. 12) as functions of leaf partial evaporative area (a_max⋅d) for the parabolic (s⋅d)-CO₂ relationships estimated in this study (Fig. 1a; solid line). The hysteretic-like behavior of g_ws-(a_max⋅d) (Fig. 7) is reflected in both E-(a_max⋅d) and A-(a_max⋅d) (Fig. 8). Surprisingly, the trends exhibited by the hysteretic-like behavior of E-(a_max⋅d) and A-(a_max⋅d) differ significantly after the hysteretic apex. Following the joint initial increase in E and A with increasing plant (a_max⋅d) (see Figs. 4 and 6), a subsequent decrease in (a_max⋅d) resulted in a virtually stable E whereas A exhibited a consistent decrease. The decrease in (a_max⋅d) was accompanied by the selection for smaller and denser stomata (Fig. 1b), which reduced gas resistance for lower leaf evaporating area (Fig. 7). Consequently, E remained constant as (a_max⋅d) decreased to present day values. These improvements in diffusive gas exchange were insufficient to compensate for the decrease in CO₂, hence A continually decreased with decreasing (a_max⋅d).

Figure 8. Non-unique relationships between transpiration and CO₂ assimilation rates and maximal leaf partial evaporative area.

Computed relationships between maximal leaf partial evaporative area (a_max⋅d) and transpiration rate, E, according to Eq. (10) (solid line), and between (a_max⋅d) and CO₂ assimilation rate, A, according to Eq. (12) (dashed line) for the parabolic (s⋅d)-CO₂ function (Eq. S1). Arrows depict chronology (dashed arrows represent early Phanerozoic; solid arrows represent late Phanerozoic).

Summary and Conclusions

We have considered s and d data from plant fossil record spanning the Phanerozoic eon to investigate effects of stomatal configuration on plant CO₂ uptake, A, on transpiration, E, rates, and on plant water use efficiency, WUE. Plant transpiration rates were estimated based on the diffusion resistance model of Bange [33], whereas CO₂ uptake rates were estimated based on the model of Farquhar et al. [48]. Both gas fluxes considered stomata interactions in the leaf gas resistance formulation. Different (s⋅d)-CO₂ patterns resulting from different analyzes of the fossil record were considered. Stomata configuration, expressed in terms of maximal relative leaf evaporating area, (a_max⋅d), was found to affect mostly the gas exchange rates during the first phase of the Phanerozoic when large s-low d configuration prevailed. It is likely that the drastic drop in atmospheric CO₂ induced a shift from large s-low d configuration to small s-high d configuration. This shift enabled lower diffusive gas resistance with lower (a_max⋅d), decreased gas exchange sensitivity to leaf evaporating area and may has also contributed to improved leaf thermal management.

The estimated plant WUE during the Phanerozoic reveals a significantly different trend than the conventional WUE postulating proportionality with atmospheric CO₂ concentration. In contrast with the linear decrease in WUE with decreasing CO₂, the estimated WUE was relatively stable during a significant part of the eon. This new trend results from decoupled response of plant A and E to the correlated evolution of s and d and their related product (a_max⋅d). We observed that the shape of A exerts a stronger influence on the WUE pattern than the shape of E. Uncertainties in past plant biochemical photosynthetic response introduces complexities into the estimation of A, and thus in estimates of WUE. Nevertheless, the new WUE trend was relatively robust using two variations in the model for A. This trend suggests that regulation of water losses could have served as the primary driver for plant gas exchange evolution, thus contributing to the invasion of dryer terrestrial environments [5], [8].

Supporting Information

Appendix S1

Detailed presentation of the three different methods used to quantify the changes in stomatal density, d , and size, s with atmospheric CO₂ concentrations during the Phanerozoic eon based on fossil record. These three methods led to the three curves depicted in Fig. 1a describing the resulting (s⋅d) evolution during the Phanerozoic.

(DOCX)

Funding Statement

Supported by Chief Scientist of the Israeli Ministry of Agriculture Fund. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.