Physical Models of Mesoderm Invagination in Drosophila Embryo

Abstract

The invagination of the mesoderm in the Drosophila melanogaster embryo is an intensely studied example of epithelial folding. Several theoretical studies have explored the conditions and mechanisms needed to reproduce the formation of the invagination in silico. Here we discuss the aspects of epithelial folding captured by these studies, and compare the questions addressed, the approaches used, and the answers provided.

Introduction

The ability to describe a biological process in mathematical terms is often considered an indication of having a good understanding of its underlying biochemical and physical mechanisms. Successful models provide predictions that in turn suggest experiments that test whether the process is fully understood. If needed, they also provide corrections and refinements. Modeling has moved beyond the description of biochemical processes and is increasingly being used to study complex behaviors of cells, including their shape changes, motions, and spatial rearrangements. These transformations are described by a theoretical framework based on the mechanics of cells, subcellular structures, and cell-cell interactions. In the recent past, the development of mechanical models has been supported and guided by advances in live-cell imaging. The formation of the ventral furrow in the early Drosophila embryo, which involves controlled folding of a cell sheet of ≈500 cells, is an example of a process that is often studied theoretically. The genetic control of this process and many of its cellular biological parameters are well understood, and since it occurs in a geometrically simple system, it is particularly well suited for theoretical analysis.

The formation of the ventral furrow is the first step of gastrulation. Gastrulation, which occurs in all multicellular animals, is a series of processes that transform the early compact cell mass or single-cell-layer embryo into a multilayered organism. The cells that form the gut and its appendages (the endoderm) and those that form the tissues lying between the gut and the outer body wall, including muscles, blood, and heart (the mesoderm), translocate from the surface of the embryo into the interior. The endoderm and mesoderm are covered up by the cells that develop into skin or epidermis and nervous system (the ectoderm). The early Drosophila embryo consists of ≈6000 morphologically similar cells that form a columnar epithelium. The cells are attached to each other by adherens junctions encircling their apical sides (the side of the cell that faces the surface of the embryo). The cells that form the future mesoderm, the mesoderm primordium (which we will simply call the mesoderm here), reside on the ventral side of the blastoderm (the pregastrulation embryo) in an ≈20-cell-wide band encompassing ∼70° of the circumference of the embryo. The epithelium encloses a central yolk mass consisting of cytosol filled with organelles, lipid droplets, and additional nuclei, and the whole embryo is enclosed by a shell-like vitelline membrane.

The mesoderm is moved into the interior of the embryo by changes in cell shape. The ventral epithelium first makes an inward fold called the ventral furrow, which then deepens and sinks into the embryo until the initially separate sides of the furrow touch each other. Formation of the furrow involves the constriction of the apical surfaces of the centrally located mesodermal cells. Cells in the ventralmost band transform from a columnar to a wedge shape, creating the initial indentation. However, even when they are fully constricted on their apical sides, cells in the furrow have not been moved into their final position in the interior of the embryo. It is not known whether the further deepening of the furrow and the translocation of the cells to the interior is a consequence of apical constriction alone. The mesodermal cells lengthen along their apical-basal axis at the beginning of furrow formation, and during the late phase of furrow formation they shorten again. It is not known whether these late shape changes also play an active role. Some of the models discussed below address these issues (1–3). Eventually the cells adjacent to the mesoderm on each side come together and seal off the internalized mesodermal tube.

The invagination of the future mesoderm occurs very rapidly, over a period of ∼20 min. During invagination, the participating cells retain their epithelial connections and they neither divide nor exchange their neighbors. Moreover, the epithelium consists of a single cell layer of columnar cells. All of these properties make the process very suitable for modeling.

The proposed mechanical models can be divided into two classes. One class explores the principles and conditions under which a furrow forms, paying less attention to how precisely the resulting shape of the model epithelium resembles the furrow seen in a given animal. The advantage of these models is that they are transparent and can identify the minimal requirements and mechanisms for formation of a furrow. On the other hand, the predictions rarely resemble the in vivo furrow closely, so it is hard to conclude whether the mechanisms explored indeed operate in vivo, either alone or in conjunction with others. The more-complex models aim to reproduce the exact in vivo cell shapes, describing the complete mesoderm internalization as closely as possible. The downside to this approach is that these models are fairly complicated and it is difficult to pinpoint the mechanism responsible for a given transformation.

In this review, we compare the results obtained with the various models of ventral furrow formation. From this well-studied example, we can begin to learn which mechanisms contribute to epithelial folding, and although the insights provided are primarily important for understanding gastrulation in Drosophila, they also shed light on the mechanisms of epithelial morphogenesis in general.

Concepts

The mechanical theories of ventral furrow formation are based on various assumptions that can be categorized into several groups. Not all of them are equally important, so it is instructive to list those that are most prominent:

• •Subdivided epithelium. In most models, it is assumed that mesoderm cells are mechanically distinct from endoderm cells, and the epithelium consists of two dissimilar parts (1–7). Yet, invagination is also seen in a subdivision-free model in which the mechanical properties of all cells are identical (8).
• •Active deformation. A major conceptual difference among the models is how they define the invagination-inducing processes. Deformations whereby the shape of cells is changed in a prescribed way are referred to as active (1,2,5,6), with the main modes being apical constriction and apical-basal elongation. In an active deformation, the cell-shape change is given but the underlying forces are not specified. Active deformations that are manually imposed (1,2,5,6) or suggested by experimental observations (7) are considered prescribed, whereas those that depend on specific mechanisms are considered controlled (9–12). A passive deformation results from given forces (mostly thought to be driven by actomyosin contractility) and force balance (1–8). Active deformations are thus kinematic descriptions, whereas passive ones are dynamic. In models devoid of active deformations, the change of cell shape leading to invagination is triggered by an imposed local or global variation of the appropriate parameter, such as the surface tension (3,8).
• •3D geometry. Most models consider the 2D transverse cross section of the embryo (2–4,6–8) based on the fact that mesoderm invagination takes place along the dorsoventral axis of the embryo. The 3D models better reflect the full shape of the Drosophila embryo (1,3,5), including its finite length and deviations from axisymmetric shape prior to invagination. In addition, they can also account for the dynamics and the spatial variation of cell properties along the anteroposterior axis during furrow formation. However, no major differences between the results of 2D and 3D models have been reported so far.
• •Viscous dissipation. Living cells behave as solid elastic materials on short timescales and as viscous fluids on longer timescales (reviewed in Lecuit and Lenne (13)). In the dynamic models of ventral furrow formation, the viscosity of the tissue and the corresponding dissipation is taken into account in purely viscous models (3,7,8), whereas in others they are neglected (1,2,5,6). In this case, the various stages of furrow formation are represented by a sequence of equilibrium shapes corresponding to a suitable continuous variation of model parameters.
• •Bulk versus surface elasticity. The forces responsible for passive deformation are associated either with bulk elasticity, where the epithelium is considered an isotropic elastic body (1,2,5,6), or with surface tension of the cell wall (3,8), which also leads to a finite shear modulus as long as the cytosol compressibility is larger than zero. A mixed model in which the surface-elasticity-based shear modulus of cells is increased by diagonal struts has also been explored (4).
• •Vitelline membrane. Almost all models take into account the vitelline membrane (1–3,5–8), which is represented by either a deformable (8) or a rigid (1–3,5–7) shell enclosing the epithelium. Vitelline membrane-free models (2,4,8) also predict invagination, although in most cases the overall round shape of the embryo is not reproduced (2,8).

The remaining differences among the models are less prominent and lead to subdominant effects. Yolk compressibility is usually neglected, such that during invagination its volume remains constant (1–4,6,8); however, in some cases the yolk is considered compressible (5,7), which imposes a soft rather than a hard constraint on the epithelium. All models share one property: in all cases, a local invagination is based on a local inhomogeneity, with the type of inhomogeneity resulting from differences in stress or constriction (1,2,4–6), or differences in surface on the basal and apical sides of the cell (3,8). All models are solved numerically, with some accounting for the discreteness of cells (3,4,7,8) and others (1,2,5,6) treating the epithelium as a continuous medium. A summary of the features of these models is presented in Fig. 1 along with representative examples of the furrows.

Figure 1.

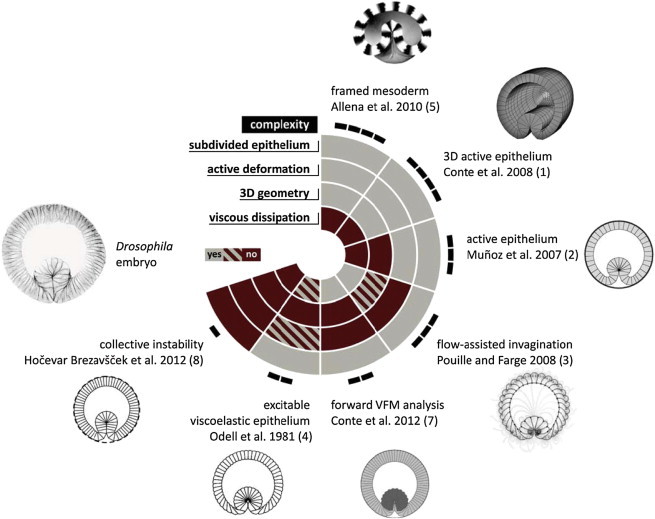
Overview of the main features of the models and their outcomes. The color-coded circular diagram in the center indicates whether a given feature is included in each of the eight models discussed. The level of complexity of the models is encoded by the number of black rectangles on the perimeter. Each model is illustrated by a representative predicted cross section of the embryo. The image on the left is a cross section of a gastrulating Drosophila embryo stained with antibodies against neurotactin, which labels the cell membrane (the inverted grayscale image of a fluorescent micrograph was kindly provided by Dr. G. Schäfer, University of Cologne).

The Models

Here we review the models in the order in which they were published, describing the hypotheses, assumptions, and conditions, as well as the conclusions reached. To emphasize their most characteristic features and facilitate the comparison, we refer to them by their respective keywords, although these designations are neither complete nor established.

Most models distinguish between the prospective mesoderm (ventral epithelium) and the prospective ectoderm, but none of them make further distinctions within the nonmesodermal cell population. We follow this simple principle, and although most dorsal cells in reality do not give rise to ectodermal structures, we denote all cells that are not mesodermal as ectodermal.

Excitable viscoelastic epithelium

The model of epithelial folding proposed by Odell et al. (4) in 1981 is based on identical viscoelastic cells and an elaborate model of propagation of a wave of cell contractions. The cross section of the embryo consists of trapezoidal cells, each composed of several spring-and-dashpot viscoelastic mechanical units representing the basal, lateral, and apical sides. A grouped subset of cells (approximately half of the total number of cells present in the system) possess an excitable apical side. At small deformations, the apical sides behave as an elastic material, but if they are stretched beyond a certain threshold, their rest length is suddenly decreased, which gives rise to an active contraction. This leads to the propagation of a wave of contractions from a randomly deformed cell in either direction along the epithelium, resulting in an invagination (4). The implementation of this model closely reproduce the in vivo starting geometry, cell number, and final cell geometry. Both the yolk cross-sectional area and the area of the epithelial cell population were assumed to be constant; the vitelline membrane was not included.

This model shows that a wave of apical constrictions starting from a single cell is sufficient to drive ventral furrow formation. Whereas the final shape of the gastrula resembles that observed in vivo, the intermediate stages do not. One possibility is that this is due to the absence of the vitelline membrane. In vivo, the cells that will form the furrow begin to constrict in a stochastic pattern. As a result, the whole region is first flattened and then progressively bent inward, and eventually the cells are internalized. In the model, a sharp indentation is caused by the very first single constriction of the contraction wave. The indentation then develops into a wide bend and finally the epithelium is internalized. Although it is a novel and conceptually interesting idea, such a constriction wave has not been observed in vivo. However, the idea that apical constriction is sufficient to create a furrow has remained very influential and is probably correct.

Rather than addressing molecular details, this model relies on the mechanics of the cytoskeleton. Building on an old idea of a contractile gel at the cortex of the embryonic epithelium (14), it postulates the presence of a contractile meshwork of actin and myosin filaments underlying the apical surface of cells. At the time the model was published, such a meshwork in the Drosophila embryo had not yet been described. Only later was it found that myosin is indeed concentrated on the apical sides of constricting cells (15,16), and recently it was demonstrated that myosin is part of a medial contractile meshwork (17). The idea that this meshwork would contract upon being stretched was inspired by the stretch activation of smooth muscle cells (18). In stretch-activated contraction in muscle cells, the actin-myosin network undergoes cycles of contraction, relaxation, and stabilization. A similar situation was discovered for the medial actomyosin network in contracting ventral furrow cells (17).

Active epithelium

The excitable-cell model of Odell et al. (4) combines passive elastic response below the threshold of apical stretching with active contraction beyond this threshold. This behavior can be referred to as conditional activity. Twenty-six years after Odell et al.’s pioneering work, Muñoz et al. (2) proposed a new 2D model for the formation of the ventral furrow. In this framework, the cell activity mechanism modeled by Odell et al. (4) is stripped of the threshold and dynamics. The main ingredients of the model are subdivision of the epithelium into mesoderm and ectoderm, and unconditional active cell deformation involving apical constriction and apical-basal elongation/shortening. Superimposed on these two active modes with prescribed kinematics is the elastic deformation of the epithelial sheet, which is considered a hyperelastic, nonviscous continuum rather than a series of individual cells. The equilibrium shape of the embryo is obtained by minimizing the neo-Hookean elastic energy after the active deformations have been imposed. The yolk is considered incompressible and the vitelline membrane is represented by an infinitely rigid, friction-free circular shell.

The active deformations assigned to mesoderm and ectoderm are different. Whereas only the mesoderm undergoes apical constriction, the change in the length of the apical-basal axis is applied to both the mesoderm and the ectoderm. The mesodermal cells elongate by a given length and the ectodermal cells shorten by the same length. Because the overall cross-sectional area of each cell is constrained, an apical-basal shortening of the epithelium results in its lateral widening and vice versa for apical-basal lengthening. In contrast to several subsequent studies, the model of Muñoz et al. (2) does not account for the causes of the active deformations, and instead relies on the experimentally observed cell-shape changes as an input.

The advantage of this model is that it can be used to test a range of combinations of active apical constrictions and changes in overall cell length, each leading to a different invaginated or noninvaginated epithelium. Among the parameter sets discussed here, moderate mesoderm lengthening and ectoderm shortening combined with a sufficiently large apical constriction is the only one that gives a furrow shape similar to that seen in vivo, although it is not tubular (see Fig. 1). In addition, Muñoz et al. (2) explored the impact of the vitelline membrane and the yolk, and concluded that both are important for furrow formation in this model.

In 2009, Conte et al. (6) explored the model of Muñoz et al. (2) in a more systematic fashion. In this study, the shapes generated by a given active deformation are represented in a phase diagram. This work also introduces explicit criteria for a successful invagination: 1), the mesoderm must bend inward; 2), cells must not penetrate one another; and 3), the two initially distant ectodermal cells at either side of the mesoderm must come to lie next to each other at the site of invagination (meaning that the buckling epithelium should finally form a tube).

The range of shapes generated by this model is broad, and it includes shapes that have no resemblance to the cross section of an embryo. For example, there may be more than one invagination, the invaginations may be very shallow, or they may not occur at all. Conte et al. (6) reached three main conclusions: first, according to the above criteria, successful invaginations only occur when the active component of ectoderm apical-basal shortening (which leads to ectodermal cell widening) is included. Conversely, the only single-mode active deformation that produces successful invaginations is ectoderm apical-basal shortening, which is thus both necessary and sufficient to create a furrow. Second, mesoderm apical constriction results in only a shallow furrow, and only by adding at least one other active component does the mesoderm become completely internalized. Third, the invaginations that are least sensitive to fluctuations in the amplitude of the active processes are those that contain the three active components in approximately equal weights.

Unfortunately, because the active deformations are not independent of each other, a particular combination seen in vivo (mesodermal apical-basal lengthening followed by shortening) cannot be implemented in this model. Not all of its predictions agree with experiments. For example, the interpretation of the requirement for ectodermal shortening as a pushing force of the ectoderm allegedly contributing a decisive force in vivo is not in line with experimental data. In embryos in which the lateral cells do not behave like ectoderm because their cell fate has been changed, a deep invagination can nevertheless be formed (19), which suggests that mesoderm shape changes are sufficient to produce a furrow.

3D active epithelium

The framework of Muñoz et al. (2) was also implemented in a 3D model by Conte et al. (1) in 2008. The results obtained are qualitatively and quantitatively similar to those of Muñoz et al. (2), suggesting that the transverse 2D cross section is fairly representative. An interesting inherently 3D effect reported by Conte et al. (1) is that the area of the yolk cross section at different positions along the anteroposterior axis changes during invagination, which indicates yolk flux from the center toward the poles of the embryo.

Flow-assisted invagination

Like the active epithelium model of Muñoz et al. (2), the framework developed and examined by Pouille and Farge (3) in 2008 also relies partly on the postulates of Odell et al. (4). The main differences compared with Odell et al.’s model are the absence of the conditional elastic/active behavior of the apical surfaces and a detailed description of the hydrodynamics of invagination. As in Odell et al.’s work (4), the model epithelium represented by the cross section consists of individual cells, but it contains 36 cells rather than 80 as seen in a real embryo. The cells are filled with incompressible fluid and their apical, lateral, and basal sides are under a given cortex tension. In addition, the apical adherens junctions are connected by springs representing actomyosin apical rings. The epithelium is immersed in an incompressible viscous fluid. The furrow formation is triggered by a gradual 100-fold increase of the apical tension in seven ventral cells representing the mesoderm, and the evolution of the epithelium is governed by the hydrodynamic motion of yolk, cells, and the surrounding fluid in the low-Reynolds-number regime.

Despite the large increase of the apical tension in the seven ventral cells and the ensuing apical constriction, this model does not generate a complete mesoderm invagination, either with or without the semi-hard vitelline membrane. Instead, the mesoderm forms a shallow furrow that does not fully close. The depth of the groove increases after the introduction of an additional radial force mimicking the effect of curvature of the ventral surface along the anteroposterior axis in real 3D embryos, but it still does not reach that of the in vivo configuration.

Despite this discrepancy, the study by Pouille and Farge (3) provides interesting predictions for cell-scale processes. In this model, subcellular structures are taken into consideration, and processes such as the relocation of apical junctions in mesoderm cells and mesoderm cell elongation and shortening are shown to be purely passive. They emerge from the apical constrictions and the physical properties of the system rather than being explicitly imposed as in other studies (1,2,5,6). It also predicts the bending of ventrolateral cells toward the furrow midline as observed in vivo (20), and it reproduces the gradient of apical-basal cell length along the dorsoventral axis reported by Odell et al. (4). Finally, the disagreement between the shapes produced by this model, where only a few ventral cells provide the driving force for invagination, and the shapes of a real Drosophila embryo cross section may also suggest that both the ectoderm and the mesoderm are involved in furrow formation in some way.

Framed mesoderm

In 2010, Allena et al. (5) presented a variant of the 3D analysis by Conte et al. (1) involving only mesodermal cells, with the ectoderm and vitelline membrane essentially acting as constraints. The mesoderm undergoes an active deformation comprising apical constriction and apical-basal elongation complemented by a passive deformation. The rigidity of the ectoderm is compensated for by the compressibility of the inner yolk. The results obtained are similar to those described by Conte et al. (1). The obtained furrow is wide and does not invaginate to produce a tube. The overall shape of the embryo is abnormally distorted in the dorsoventral axis, which is most likely due to the compressibility of the yolk. These models have been further developed (9,21), but the resulting shape of the embryo that they yield has not improved significantly. A comparison of the shapes presented by Allena et al. (5) and those of a real embryo suggests that treating the ectoderm as a rigid structure that holds the mesoderm perimeter is a poor approximation. The disagreement between the shapes obtained in this model and in vivo may indicate that all parts of the epithelium are involved in invagination.

Forward video force microscopy analysis

In 2010, Brodland et al. (22) introduced video force microscopy (VFM) as a way to deduce the forces that drive morphogenetic movements from live imaging. Images of biological specimens are discretized into polygonal fields and the deformation of polygons, as defined by segments and nodes, is tracked in time. By assuming a given viscosity of the tissue, the inverse VFM algorithm calculates the net forces on the nodes needed to achieve the observed changes. The VFM analysis of a gastrulating Drosophila embryo shows that in the mesoderm the greatest forces are present apically and laterally, whereas in the ectoderm they are greater at the basal side.

In the forward model developed by Conte et al. (7) in 2012, VFM forces inferred from live images are used as input for a numerical analysis of the overdamped dynamics of an embryo cross section, which obviously recreates the observed in vivo epithelial deformation. The goal of Conte et al. (7) was to modify these forces in amplitude and timing so that they could explore their roles in different regions of the mesoderm and ectoderm. Instead of using the exact measured forces, they considered four active contributions separately: 1), mesoderm apical constriction; 2), mesoderm radial shortening; 3), ectoderm basal constriction; and 4), ectoderm radial shortening. They probed the function of ectodermal forces by simulating the absence of ectodermal basal constriction and lateral shortening, both one by one and simultaneously, and also varied the timing of mesoderm radial shortening.

Using observation-based forces, Conte et al. (7) found that although ectodermal shortening slightly affects the shape of the furrow and the speed at which it forms, it is not essential for furrow formation. They also found other differences compared with their earlier model (1,2,6). By deleting radial ectodermal shortening or advancing the time point of mesoderm shortening, one can produce a more tubular invagination, whereas previously this was achieved more efficiently by increasing mesoderm lengthening. Delaying the onset of mesodermal radial shortening increases the depth of the invagination and makes it more tubular. Similar results are obtained by decreasing or increasing the amplitude of mesoderm shortening. Finally, reducing or increasing the intensity of mesoderm apical constriction has almost no effect on the height, thickness, or overall shape of the furrow. In this model, the radial shortening of the mesoderm has the strongest effect on the depth of the furrow.

Collective instability

After the original demonstration that apical constriction of a subset of cells is sufficient to create an invagination (4), most models attempted to simulate the process in more detail by focusing on the influence of additional mechanisms on the final shape. In 2012, Hočevar Brezavšček et al. (8) explored a different approach: instead of looking for a detailed explanation for the in vivo folding behavior, they aimed to elucidate the minimal requirements for furrow formation.

In the 2D model proposed by Hočevar Brezavšček et al. (8), the epithelium is made of discrete cells with identical mechanical properties. The energy of the cells consists exclusively of surface energy and is parametrized by the tensions of the apical, basal, and lateral sides. The three tensions are independent and the equilibrium shapes of the epithelium are those that minimize the overall energy. The cell and yolk area are set constant and the vitelline membrane is treated as an elastic shell of varying stiffness. The phase diagram of stable shapes shows that for large relative apical-to-lateral and basal-to-lateral tensions, the epithelium maintains a circular shape. However, at small relative apical-to-lateral and basal-to-lateral tensions, the overall length of the epithelium is longer, and since the epithelium is constrained by the vitelline membrane, it buckles. In the absence of the vitelline membrane, the epithelium deviates from the circular shape, extending beyond the circumference of the circular shape, but it still features one or multiple furrows if the difference between the apical and the basal tensions is large enough. In this model, the vitelline membrane thus plays a dual role: it contains the tissue within a circular shape and it ensures the formation of a single groove. When the stiffness of the vitelline membrane is increased, a smaller apical-to-lateral or basal-to-lateral tension ratio is needed to obtain a furrow.

Because buckling is a collective effect involving all cells, no epithelium subdivision or specific behavior of individual cells is needed. This makes the surface-tension-based model appealing, but it also means that invagination will result from spontaneous symmetry breaking at a random angular position. To ensure that the furrow is formed on the ventral side, as it is in vivo, it is necessary to introduce some asymmetry into the epithelium. Measurements of embryos show that just before mesoderm invagination occurs, the cross-sectional area of cells in the mesoderm is on average 30% larger than that in ectoderm cells. Imposing such a difference in the model results in a furrow positioned in the region with the largest cells.

In this model, the furrow is induced by a decrease of the relative apical-to-lateral and basal-to-lateral tensions uniformly throughout the epithelium rather than by a specific activity of subsets of cells. Embryos in which all cells along the dorsoventral axis have identical fates can be created experimentally. In extreme cases, these embryos do not form a furrow (23), but in some cases they do.

By making a step away from the in vivo system and starting from a minimal set of assumptions, this study provided evidence of possible unexplored physical mechanisms that may govern epithelial folding. Further experimental tests are needed to confirm the validity of the collective-instability hypothesis.

Conclusions

The theoretical studies on Drosophila mesoderm invagination differ in their working hypotheses and conclusions. Some of them show that certain minimal conditions or mechanisms are sufficient to generate furrows or complete invaginations. Such models are useful to biologists because they show which mechanisms may potentially work and are worth considering as explanations for in vivo behavior, with their viability being determined by experimentally established biochemical and cell-biological processes. One mechanism that is sufficient to create an indentation is apical constriction (3,4), and this mechanism is indeed observed in vivo. The model proposed by Odell et al. (4) uses a wave of constrictions rather than simultaneous or stochastic constrictions in a predefined subset of cells. It does not address whether simultaneous constriction would also achieve a full internalization of the constricting part of epithelium, but waves of constriction have not been observed during gastrulation in vivo. Apical constriction in the Drosophila ventral furrow proceeds in a stochastic fashion, though with higher probability for cells near the ventral midline to constrict early (24). Another single-mechanism model is that of Hočevar Brezavšček et al. (8), which refrains from using cell-specific processes and shows that an epithelium of mechanically identical cells with surface-tension-based energy is also sufficient to produce tissue internalization. Geometrically, this leads to cell shortening/widening throughout the epithelium in conditions where a furrow is formed. Importantly, this model identifies a cell-level mechanism that achieves this geometry, and partly confirms the conclusion of Conte et al. (6) that this change in geometry is sufficient to drive tissue internalization. It also correlates with the conclusion of several studies (3,5,7) that all of the epithelium is involved in invagination.

Based partly on the recognition that a single process is unlikely to be responsible for furrow formation in vivo and that the single-mechanism theories do not recapitulate the shape of the furrow in the embryo, more elaborate models, including combinations of active processes to achieve tissue internalization, were proposed (1,2,5,6). Models that rely on simple hypotheses often involve forces (3,4,8), whereas the complex ones usually impose the experimentally reported cell-shape changes, avoiding the use of complex sets of forces for which no direct experimental data are available. In some cases, these forces are based on in vivo observations (e.g., changes in the apical-basal length of cells), but they are not always deployed in a manner that is consistent with conditions reported in the real embryo. For example, although shortening of ectodermal cells does occur, it only begins after the furrow has almost completely invaginated and thus cannot be considered the cause of furrow formation. Lengthening and shortening of mesodermal cells are not alternatives, but they occur in succession in vivo (20).

On the theoretical side, the main lessons learned from the comparison of the various models of ventral furrow formation in Drosophila may be summarized as follows: Although it is difficult to measure the quality of these models objectively, it appears that the full 3D analysis (1) does not give rise to a qualitatively distinct behavior, and that 2D models are adequate (2). Second, although it is clear that the cells and thus the tissue must be characterized by a certain shear rigidity to resist shape change, both surface-tension-based effective shear modulus of incompressible cells (3,8) and bulk elasticity (2) seem to work equally well. Third, the results of the models, including the full hydrodynamic description of invagination (3,7), do not depart very much from those based on energy minimization (1,2,5,8), suggesting that the effect of a complete account of the flow pattern is limited. This implies that energy-minimizing models in which the furrow formation is represented by a sequence of equilibrium shapes are suitable. Finally, the resemblance of results obtained within the different models suggests that the furrow formation may be driven by several mechanisms simultaneously. From the cell-biological perspective, a morphogenetic process such as mesoderm invagination is unlikely to rely on only one physical mechanism, and even if a single mechanism were able to mediate the process in vivo, it could be backed up by others acting in a partially or fully redundant manner to ensure successful completion every single time.

The theories reviewed here illustrate that similar predictions may be obtained by approaches of very different levels of complexity, both in terms of the mechanisms at work and in terms of the number of parameters. A comparison of these approaches may help define the physical forces in the embryo that can drive processes of cell and tissue shape change. Among the force-based models, the forward VFM analysis (22) is the first to apply forces deduced from in vivo observations to an in silico model. However, the available body of experimental information is still insufficient for this approach to be fully exploited. Additional in vivo experimental measurements are needed to reveal the force fields and suggest as yet unidentified driving processes that will allow the development of more refined and predictive in silico models, thereby advancing our biophysical understanding of morphogenesis.