Confidence intervals for two sample means: Calculation, interpretation, and a few simple rules

Abstract

Valued by statisticians, enforced by editors, and confused by many authors, standard errors (SEs) and confidence intervals (CIs) remain a controversial issue in the psychological literature. This is especially true for the proper use of CIs for within-subjects designs, even though several recent publications elaborated on possible solutions for this case. The present paper presents a short and straightforward introduction to the basic principles of CI construction, in an attempt to encourage students and researchers in cognitive psychology to use CIs in their reports and presentations. Focusing on a simple but prevalent case of statistical inference, the comparison of two sample means, we describe possible CIs for between- and within-subjects designs. In addition, we give hands-on examples of how to compute these CIs and discuss their relation to classical t-tests.

If you take care of the means, the end will take care of itself. Mahatma Ghandi

State of Affairs

Recent developments in psychological research methods converge on the notion that each mean is best accompanied by an appropriate confidence interval (CI) and, consequently, CIs are discussed in many contemporary statistical textbooks (e.g., Bortz & Schuster, 2010; Howell, 2012). Interestingly, this mainly holds true for between-subjects designs for which CIs are relatively easy to compute (Cumming & Finch, 2005). In contrast, standard errors (SEs) and CIs for within-subjects designs are still mysterious for many researchers (cf. Belia, Fiedler, Williams, & Cumming, 2005) even though several excellent publications elaborated on appropriate CIs for this situation during the last decades (Loftus & Masson, 1994; see also Cousineau, 2005; Estes, 1997; Franz & Loftus, 2012).

Most of these approaches to CIs for within-subjects desgins, however, are rather difficult to understand because they rely on relatively advanced measures such as the error term of the repeated-measures Analysis of Variance (ANOVA). So, while potentially applicable to a wide range of studies, CIs for within-subjects designs are widely misunderstood (Belia et al., 2005) and rather complicated to calculate (Bakeman & McArthur, 1996). This dilemma is especially relevant for cognitive psychologists who tend to rely heavily on within-subjects designs (e.g., as compared to researchers in personality or social psychology; cf. Erlebacher, 1977; Keren, 1993).

Nonetheless, reporting appropriate CIs has become an essential component of American Psychological Association (APA) style (APA, 2010; Wilkinson & the Task Force on Statistical Inference, 1999), and nowadays many journal editors encourage authors to add CIs or SEs when reporting their data. Further, as teachers we often push students to aid their data presentation with CIs, be it in-class data presentation or for presentations at scientific meetings. Yet, an easy, tutorial-like explanation on how to choose and calculate these CIs is missing. To fill this gap, we focus on a simple and often applied statistical analysis - the comparison of two means from independent groups as well as from dependent groups/conditions - and describe appropriateCIs in an intuitive framework. In this framework, we suggest that using a much simpler approach to within-subjects CIs than suggested in often-referenced papers (e.g., Loftus & Masson, 1994) is preferable in most cases. In particular, this approach simply relies on the CI of the difference between sample means (see Franz & Loftus, 2012, for a more detailed discussion of this approach and its advantages over other approaches). Such CIs are more initimately related to their between-subjects counterparts, are easily obtained with any computer program, and allow for a straightforward interpretation.

In the following section, we outline how different CIs can be computed for the common situation of comparing two sample means (cf. Table 1). These guidelines are intended to simplify graphical data presentation in a unifying framework that is intimately related to the different t-tests in classical hypothesis testing.

Table 1. Fundamental Concepts for the Graphical Data Presentation of Two Means and the Associated Confidence Intervals.

Parameter	A parameter is a fixed, but unknown population value. Sample statistics are used to estimate parameters.
Standard error (SE)	Measure for the standard deviation of a parameter estimator. In case of a sample mean, it is equal to the estimated standard deviation divided by the square root of the underlying sample size.
Confidence interval (CI)	An estimate for plausible population parameters. Several different CIs can be constructed for the comparison of two means, depending on the employed design and the desired interpretation. Still, each CI can be broken down to the simple formula: "Mean ± Standard Error ✕ Coefficient" (CI = M ± SE ✕ tdf;1-1-α/2
Confidence interval for an individual mean (CIM)	This CI is constructed from the standard error of the mean (SEM) and can be used to compare this mean to any fixed parameter. It corresponds to a one-sample t-test and does not yield any precise information about the difference between two sample means.
Confidence interval for the difference between two means from independent samples (CID)	This CI is constructed from the between-subjects standard error of the difference between two means (SED). It thus corresponds to a t-test for independent samples and can be used for inferences about the difference between both means.
Confidence interval for the paired difference between two means (CIPD)	This CI is constructed from the standard error of the difference between two dependent sample means (paired differences). It is thus applicable for within-subjects designs and equivalent to a paired-samples t-test.

A CI is a CI is a CI

Independent of the underlying design, any CI for a sample mean can be broken down to a simple formula that only includes the mean itself, an appropriate SE, and a coefficient that is derived from the t-distribution. In the following, we will use 95% CIs (i.e., = .05) in all examples because of their widespread use in the literature (cf. Equation 1):

$$95\%\mathrm{Cl}=M\pm \mathit{SE}\cdot t_{\mathit{df};1-\frac{0.05}{2}}$$ (1)

All CIs computed with this formula rely on the same assumptions as t-tests in classical hypothesis testing do. More precisely, they assume a normally distributed variable with an unknown population variance that is estimated from the sample (thus implying measurement at the interval scale). Furthermore, these CIs are inherently two-tailed, as reflected by the use of α/2 to determine the coefficient.

Most importantly, particular CIs differ in how the corresponding SE is computed, and the appropriate formula depends on two factors: (1) the experimental design and (2) the intended meaning of the CI. We start by discussing two CIs for between-subject designs before continuing with within-subjects designs. Following these theoretical points, we demonstrate how to compute the three CIs for an exemplary data set.

Between-subjects designs: Two independent samples

For between-subjects designs, two distinct CIs can be computed that differ in meaning and interpretation. At first sight, the most straightforward way might be to compute separate CIs for each individual mean M by simply using the corresponding SE. In fact, this is a valid solution and we will denote the resulting SE as SE_M. Following from the central limit theorem, SE_M is computed by dividing the unbiased estimator of the standard deviation (s) by the square root of the sample size n (see Equation 2):

$${\mathit{SE}}_M=\frac{s}{\sqrt{n}}\mathit{with}s=\sqrt{s^2}=\sqrt{\frac{1}{(n-1)}\cdot \sum _{i=1}^n{(x_i-M_x)}^2}$$ (2)

The corresponding CI for individual means is denoted as CI_M (cf. Equation 3):

$$95\%{\mathrm{Cl}}_M=M\pm {\mathit{SE}}_M\cdot t_{n-1;0.975}$$ (3)

This confidence interval can be used for inferring whether the mean is different from any fixed, hypothesized value (e.g., zero). Thus, the CI_M corresponds to the one-sample t-test. The CI_M, however, does not yield any precise information about the difference between its mean and any other sample mean. To obtain this information, one needs to compute a different SE that captures the (between-subjects) variability of the difference between both means. This measure - SE_D - is composed of both sample sizes (n₁, n₂) and estimated standard deviations (s₁ and s₂, respectively; see Equation 4):

$${\mathit{SE}}_D=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{(n_1+n_2-2)}}\cdot \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$$ (4)

The corresponding CI for the difference between two independent means is denoted as CI_D (cf. Equation 5):

$$95\%{\mathrm{Cl}}_D=M_{1/2}\pm {\mathit{SE}}_D\cdot t_{n_1+n_2-2;0.975}$$ (5)

In addition to the general assumptions mentioned above, CI_D assumes that the standard deviations are estimated from independent samples and that the size of these standard deviations is comparable (i.e., we assume homogeneity of variance)¹. Importantly, conclusions based on the CI_D are valid only for the difference between the means, and the CI_D thus corresponds to the t-test for two independent samples. If centered around one of the means this test is significant if, and only if, the CI_D does not include the other mean. Accordingly, the CI_D can be used for inferences about the statistical significance of the between-subjects difference; and because the difference between sample means is what a researcher will typically be interested in, CI_D is preferable to CI_M in most circumstances.

To conclude, CI_D and CI_M are intimately related to classical t-tests and allow for a straightforward interpretation: A standard t-test is significant if, and only if, the 95% CI does not include the value in question. For the CI_D, this value is the second sample mean, for the CI_M, this is any fixed parameter value.

Within-subjects designs: Two paired samples

For within-subjects designs, matters seem to be more complicated at first sight. In fact, Cumming and Finch (2005) recommended: “For paired data, interpret the mean of the differences and error bars for this mean. In general, beware of bars on separate means for a repeated-measure independent variable: They are irrelevant for inferences about differences“ (p. 180).

Caution is indeed necessary in this situation, because the often-used CI_M obviously is unrelated to the within-subjects difference. Yet, several CIs for within-subjects designs have been proposed in the last decades (Cousineau, 2005; Jarmasz & Hollands, 2009; Loftus & Masson, 1994) with the most prevalent variant being the one of Loftus and Masson. These CIs are typically derived from the error term of the repeated-measures ANOVA and we will come back to these methods in the section What to do with more complex designs. For comparing the means of two paired samples, however, a straightforward and elegant solution seems to be more closely related to meaning and interpretation of CIs for between-subjects designs (see also Franz & Loftus, 2012). This solution simply uses the standard error of the paired differences (SE_PD) to construct the CI. Accordingly, it does not require any ANOVA statistics, but can be computed easily from the standard deviation of individual difference scores s_d (see Equation 6):

$${\mathit{SE}}_{\mathit{PD}}=\frac{s_d}{\sqrt{n}}$$ (6)

The corresponding CI is labelled CI_PD (following Franz & Loftus, 2012; cf. Equation 7

$$95\%{\mathit{Cl}}_{\mathit{PD}}=M_{1/2}\pm {\mathit{SE}}_{\mathit{PD}}\cdot t_{n-1;0.975}$$ (7)

The CI_PD is thus equivalent to the confidence interval of the difference between both paired means and corresponds directly to a paired-samples t-test. When plotted around the actual sample means, this t-test is significant if one mean is not part of the CI_PD around the other mean; consequently CI_PD is a direct within-subjects counterpart of the CI_D for independent samples. Taken together, we suggest that the CI_PD can be computed more easily and seems to be more closely related to interpreting the difference between two dependent means than any other solution.

Affection, pheromones, and CIs: A hands-on example

Table 2 shows the data of a fictitious - and rather arbitrary - study in which participants indicated their affection for the experimenter on a rating scale. This scale ranges from -10 (dislike) to 0 (neutral) to 10 (affection). Condition 1 is a control condition without any specific treatment whereas the experimenter used a healthy dose of pheromones in Condition 2.

Table 2. Example Data.

Reported affection for the experimenter as indicated on a rating scale (-10 to 10).
Observation	Condition 1(control)	Condition 2(pheromones)
1	7	8
2	3	5
3	4	6
4	2	5
5	5	7
M	4.20	6.20
s	1.92	1.30

Note. Condition 1 is a control condition without any specific treatment, whereas the experimenter had used a dose of pheromones in Condition 2. In the following equations, we will use the indices 1 and 2 to refer to the control condition and the pheromone condition, respectively.

Different CIs are possible in this situation, depending on the actual design and the CI’s intended meaning. The most important question, of course, relates to the design: Different CIs are appropriate depending on whether the data result from a between-subjects design (different participants contributed to Condition 1 and Condition 2, respectively) or a within-subjects design (the data in each row belong to a single participant). The three different CIs described above are plotted in Figure 1 and will be discussed in the following (see Appendix A for a short tutorial on how to compute these intervals with common computer programs).

Figure 1.

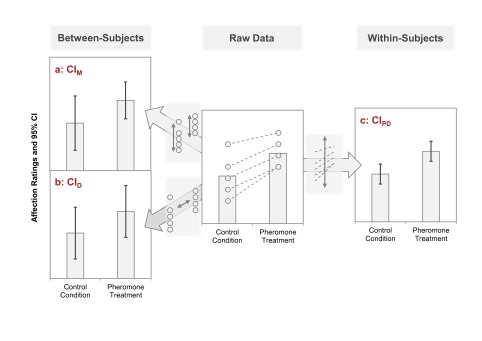
Three different confidence intervals (CIs) for two sample means. The raw data are plotted in the center of the figure; dots represent individual data points (five observations per mean; see also Table 2). Panels A and B show CIs that are appropriate for between-subjects designs; Panel C shows a CI that is appropriate for within-subjects designs (pairs of values are indicated by dashed lines in the raw data). Panel A. CIs for individual means (CI_M) rely on the standard error (SE) of the corresponding mean. The CI_M indicates whether this mean is significantly different from any given (fixed) value. They do not inform about the statistical significance of the difference between the means. Panel B. CI for the difference between the means (CI_D). The means are significantly different (as judged by t-tests for independent samples) if one mean is not included in the CI_D around the other mean. Panel C. Within-subjects CI, constructed from the paired difference scores (CI_PD). Two means from paired samples are significantly different (as judged by a paired-samples t-test) if one mean is not included in the CI_PD around the other mean.

Between-subjects: CIs for individual means

Confidence intervals for individual means can be easily computed based on the two standard deviations in Table 2. Accordingly, the two SEs amount to the following values (Equation 8):

$${\mathit{SE}}_{M(1)}=\frac{s_1}{\sqrt{n_1}}=\frac{1.92}{\sqrt{5}}=0.86{\mathit{SE}}_{M(2)}=\frac{s_2}{\sqrt{n_2}}=\frac{1.30}{\sqrt{5}}=0.58$$ (8)

Both SEs are then multiplied with the critical t-value of t5-1; 0.975 = 2.78 to compute the respective CI (see Equation 9 and 10). These two CI_M are plotted in Figure 1 (Figure 1, Panel A).

$$95\%{\mathrm{Cl}}_{M(1)}=4.20\pm 0.86\cdot 2.78=4.20\pm 2.39$$ (9)

$$95\%{\mathrm{Cl}}_{M(2)}=6.20\pm 0.58\cdot 2.78=6.20\pm 1.62$$ (10)

The two CI_M indicate that the mean affection ratings are significantly different from zero for both conditions, that is, participants were positively biased toward the experimenter even when not affected by pheromones. Importantly, however, the CI_M are not informative for the difference between the affection rating of the control participants and the participants who were exposed to pheromones.

Between-subjects: CIs for the difference

The SE_D is equivalent to the SE that is used for the t-test for independent samples (Equation 11):

$${\mathit{SE}}_D=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{(n_1+n_2-2)}}\cdot \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}=\sqrt{\frac{(5-1)\cdot {1.92}^2+(5-1)\cdot {1.30}^2}{(5+5-2)}}\cdot \sqrt{\frac{1}{5}+\frac{1}{5}}=1.04$$ (11)

Because the difference between both (independent) means involves subjects of both groups, the CI_D is computed by multiplying the SE_D with the appropriate critical t-value of t5 + 5 - 2; 0.975 = 2.31 (see Equation 12):

$$95\%{\mathrm{Cl}}_D=M_{1/2}\pm 1.04\cdot 2.31=M_{1/2}\pm 2.40$$ (12)

This CI_D is plotted around each mean in Figure 1 (Figure 1, Panel B). The mean rating of the control participants is clearly included in the CI_D around the mean of the participants who were exposed to pheromones - both values are thus not significantly different as judged by a t-test for independent samples.

Within-subjects: CI for the difference

In contrast to the previous CIs, we now assume the data in Table 2 to result from a within-subjects design: Participants were first tested in the control condition and then exposed to the pheromones (or vice versa). Accordingly, the two ratings in each row of Table 2 are now assumed to belong to the same individual. The now appropriate CI_PD is based on the pairwise difference scores for the data in Table 2 (Condition 2 - Condition 1). These differences scores are 1, 2, 2, 3, and 2 for the five participants and their standard deviation is s_d = 0.71. The corresponding SE_PD amounts to (see Equation 13):

$${\mathit{SE}}_{\mathit{PD}}=\frac{s_d}{\sqrt{n}}=\frac{0.71}{\sqrt{5}}=0.32$$ (13)

With a critical t-value of t_{5 - 1; 0.975 = 2.78}, we can now compute the CI_PD (Equation 14):

$$95\%{\mathit{Cl}}_{\mathit{PD}}=M_{1/2}\pm 0.32\cdot 2.78=M_{1/2}\pm 0.88$$ (14)

The CI_PD is plotted around each mean in Figure 1 (Figure 1, Panel C). The mean of the control condition is clearly not included in the CI_PD around the mean of the pheromones condition. This is equivalent to a significant effect as revealed by a paired-samples t-test.

Deciding what to plot

As we have seen in the above example, different and equally possible SEs and CIs for a given situation can vary substantially and do convey different information. On closer inspection, the question which one to plot boils down to the question whether the difference between the two means is of major interest or not.

If the difference is indeed of interest, we suggest that each mean is best accompanied by the CI of the difference that is appropriate for the employed design (i.e., either CI_D or CI_PD). As noted above, these intervals allow direct inferences about the difference and have also been labelled inferential CIs for this reason (Tryon, 2001). In addition to plotting these CIs, it is of course equally important to describe what is plotted. Here, a typical description to be used in a figure caption would be “Error bars represent the XY% confidence interval of the difference”. Alternatively, a concise description is also possible with the nomenclature suggested in this article that can be used to specify the plotted CI or SE on the axis of a graph (e.g., “RT ± SE_PD” or “RT and CI_PD” for a within-subjects design using response time as dependent variable).

An additional option to this approach can be used if it is only the difference that counts whereas the actual means are not of interest. In this case, it is also possible to plot only the difference itself, accompanied by the corresponding CI (i.e., CI_D or CI_PD).

If the difference between the two means is not of major interest, however, we suggest to plot the CI_M or SEM for each individual mean. Here, a typical description to be used in a figure caption would be “Error bars represent the XY% confidence interval of the individual means” or, to use the suggested nomenclature, a similar statement on the axis of a graph (e.g., “RT ± SEM” or “RT and CI_M”). These error bars inform about the homogeneity of variance across different samples or conditions and - even though they cannot be used for inferences about the difference between two means - they provide information about the difference of each mean from a fixed parameter.

What to do with more complex designs?

The framework described in the preceding sections provides a straightforward and intuitive approach to CIs for means from two conditions for both, between- and within-subjects designs. These CIs can be mapped directly to the different t-tests in classical hypothesis testing and, as mentioned above, they also rely on the same statistical assumptions as the corresponding test. The described method of plotting the appropriate CI for the difference - CI_D or CI_PD, respectively - can also be applied to more complex designs given that specific pairwise comparisons are crucial for the research question at hand (Franz & Loftus, 2012). If applicable, this method might indeed be the easiest and thus favorable strategy.

Still, this approach has obvious limitations regarding complex stu-dies which include numerous conditions. In such factorial designs, CIs are typically constructed from the error term of the ANOVA omnibus test. For between-subjects designs, appropriate methods are described comprehensively in several publications (e.g., Keppel & Wickens, 2004; cf. also Estes, 1997). As noted above, different methods have been proposed also for factorial within-subjects designs (Cousineau, 2005; Jarmasz & Hollands, 2009; Loftus & Masson, 1994) with the most prevalent variant being the one of Loftus and Masson (1994; see also Baguley, 2012; Bakeman & McArthur, 1996; Masson & Loftus, 2003; Hollands & Jarmasz, 2010; Tryon, 2001). Using these methods, however, requires a precise understanding of what these CIs reveal about the data. For instance, within-subject CIs according to Loftus and Masson (1994) are not directly equivalent to t-tests for paired samples but have to be multiplied by a fixed factor to allow for inferences about possibly significant effects (i.e., in the case of two groups/conditions: CI_PD = 2 × CI_{Loftus& Masson}). Excellent examples on how to compute and interpret these CIs can be found in the corresponding articles.

Concluding Remarks

In the preceding sections, we have summarized three approaches to CIs for one of the most common designs in psychological research, that is, the comparison of two sample means. Clearly, different CIs need to be computed for between- and within-subjects designs (cf. Blouin & Riopelle, 2005; Cumming & Finch, 2005; Estes, 1997; Loftus & Masson, 1994) and the particular CI used in a plot needs to be specified. To this end, we suggested an easy nomenclature for three different CIs to facilitate communication about what exactly a given CI represents (see Table 1). Furthermore, we argue that CIs for the difference between two means (CI_D and CI_PD) are most informative in the majority of cases, because they can be interpreted intuitively. These CIs provide a straightforward approach to the described setting; more complex designs of course call for different approaches to CIs which can be found in a variety of recent articles.

Appendix A

In the following, we show how the different CIs can be computed by common software packages, such as SPSS, MS Excel, and R.

SPSS

CIs for individual means (CI_M) can be computed with the Explore command:

Analyze > Descriptive Statistics > Explore

Here, the menu Statistics allows to set the α level (default: 5%). Alternatively, the CI_M is also contained in the output of the one-sample t-test in a section labelled 95% Confidence Interval of the Difference (with the α level being set in the Options menu). Both ways of computing the CI result in a CI that is specified via lower and upper boundaries which can be easily transformed to the the notation that is used in this article (see Equation A1):

$${\mathit{Cl}}_M=M\pm \frac{\mathit{Upper}-\mathit{Lower}}{2}$$ (A1)

CIs for the difference between independent means (CI_D) and CIs for the difference between paired means (CI_PD) can be obtained by using the same formula on the output of the t-test for independent-samples and the paired-samples t-test, respectively. These outputs also contain the corresponding values for SE_D or SE_PD.

Microsoft Excel

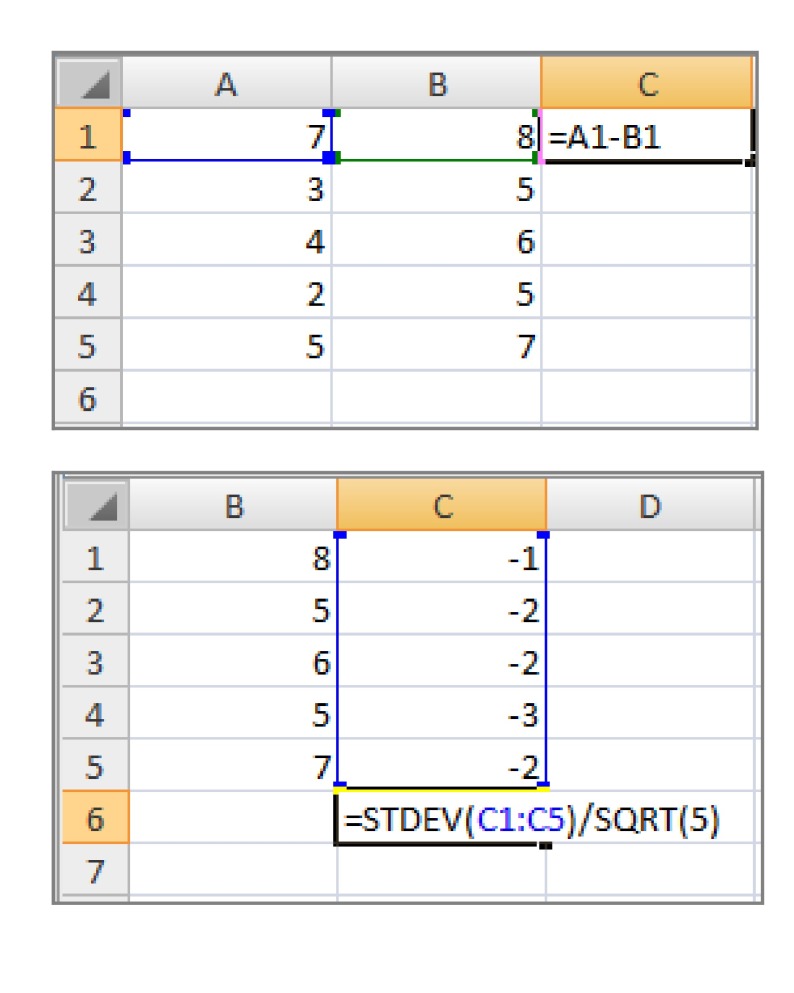
Computing CIs for individual means (CI_M) in MS Excel requires several quick steps. First, the standard deviation s is computed with STDEV function. Dividing this value by √n returns the SE_M. This can be done by using SQRT(n) or by computing n with the COUNT function. Finally, the SE_M is multiplied with the coefficient taken from the t-distribution which can be accessed via the TINV function. Importantly, TINV is inherently two-tailed and takes the intended α level as input. Thus, calling TINV(0.05, n-1) will result in the correct value for t_{n - 1; 0.975}. The CI for the difference of two independent means, CI_D, is computed similarly with two changes. Most importantly, the SE_D is computed using the corresponding formula in the section Between-subjects designs: Two independent samples (using SQRT for the square root and “^2” to denote exponents). Furthermore, the critical t-value has to be requested with the correct number of dfs via TINV(0.05, n₁ + n₂ - 2). In contrast to CI_M and CI_D, the CI for the difference between paired means, CI_PD, requires an additional first step. Assuming that each condition is entered in a separate column, one first needs to compute pairwise differences (Figure A1). The estimated standard deviation of the difference scores d_d can now be computed via the STDEV function. Dividing this value by √n returns the SE_PD. This can again be done by using SQRT(n). CI_PD is then computed by multiplying the SE_PD with the coefficient computed by TINV(0.05, n-1) for t_{n - 1; 0.975}.

Figure A1.

Computing the SE_PD in MSMS Excel. Upper panel: Pairwise differences are computed for each case. Lower panel: The standard deviation of these difference scores is divided by √n to obtain the SE_PD.

R

Confidence intervals are included in the output of the function t.test. As in SPSS, CIs are typically given in terms of lower and upper boundaries. These values can be accessed directly to arrive at the notation that is used in this article:

$${\mathit{Cl}}_M=M\pm \frac{\mathit{Upper}-\mathit{Lower}}{2}$$ (A2)

Accessing the boundaries works similarly for all t-tests and we will demonstrate the general procedure for the one-sample t-test and the corresponding CI_M. First, we enter the data of Condition 1 as a vector and compute the one-sample t-test via t.test. The output is stored in the new variable result:

>cond1 <- c(7,3,4,2,5)

>result <- t.test(cond1)

The boundaries can now be addressed by result$conf.int which returns a vector containing both values. The length of an individual error bar can now be computed in the following way:

>(max(result$conf.int) - min(result$conf.int))/2 [1] 2.388388

Alternatively, R allows for a manual computation of SEs and CIs just as in MS Excel. We demonstrate this procedure for the CI_PD. For the sake of simplicity, we assume the data to be coded in vectors instead of being variables in a data frame.

>cond1 <- c(7,3,4,2,5) >cond2 <- c(8,5,6,5,7)

We then compute a difference vector and its length (i.e., the number of participants):

>diff < -cond1-cond2 >n <-length(diff)

Then, the standard deviation of these difference scores is divided by √n and multiplied by n_{n - 1; 0.975}. The latter coefficient is computed via the function qt.

>errorbar < -sd(diff)/sqrt(n)*qt(0.975, n-1)

The resulting error bar is used to compute upper and lower boundaries of the CI_PD for both condition means:

>ci1 < -c(mean(cond1)-errobar,mean(cond1)+errobar

>ci2 < -c(mean(cond2)-errobar,mean(cond2)+errobar