A Model for the Interfacial Kinetics of Phospholipase D Activity on Long-Chain Lipids

Abstract

The membrane-active enzyme phospholipase D (PLD) catalyzes the hydrolysis of the phosphodiester bond in phospholipids and plays a critical role in cell signaling. This catalytic reaction proceeds on lipid-water interfaces and is an example of heterogeneous catalysis in biology. Recently we showed that planar lipid bilayers, a previously unexplored model membrane for these kinetic studies, can be used for monitoring interfacial catalytic reactions under well-defined experimental conditions with chemical and electrical access to both sides of the lipid membrane. Employing an assay that relies on the conductance of the pore-forming peptide gramicidin A to monitor PLD activity, the work presented here reveals the kinetics of hydrolysis of long-chain phosphatidylcholine lipids in situ. We have developed an extension of a basic kinetic model for interfacial catalysis that includes product activation and substrate depletion. This model describes the kinetic behavior very well and reveals two kinetic parameters, the specificity constant and the interfacial quality constant. This approach results in a simple and general model to account for product accumulation in interfacial enzyme kinetics.

Introduction

Phospholipases are interfacial enzymes that catalyze the hydrolysis of ester bonds in phospholipids. These enzymes play an important role in lipid metabolism, cell signaling, meiosis, and vesicle trafficking (1–5). Due to the amphiphilic nature of their phospholipid substrates, the catalytic reaction of phospholipases proceeds on membrane interfaces and depends strongly on the structure and properties of these interfaces (1). The underlying variables that govern catalysis in heterogeneous environments, such as the physical structure and chemical properties of lipid interfaces, are far more complex than those encountered by soluble enzymes in homogeneous solutions (1–3,6,7). This, in turn, gives rise to a rich kinetic behavior (8) that cannot be described with simple Michaelis-Menten kinetic analysis.

Within the past four decades, several kinetic models have been developed to describe the catalytic reaction of interfacial enzymes. Verger et al. pioneered this field by proposing the first and simplest kinetic model by combining the Michaelis-Menten model with interfacial activation of enzymes (9). Since then, kinetic models have been proposed for various interfacial structures including lipid monolayers, liposomes, and micelles (3,6,10,11). Examples include the surface dilution kinetics developed by Dennis and colleagues, which described catalysis on mixed micelles (3,10,12), and the scooting and hopping modes of enzyme action proposed by Berg and co-workers to describe catalysis on liposomes (6,11). These theoretical models have been frequently employed for analyzing the kinetics of phospholipases on model membranes (1). Most of the previous work in this area has, however, focused on kinetic analysis of phospholipase A (PLA) (3,6,9,11–23). More recently, phospholipase D (PLD) has attracted attention due to its critical role in cellular processes such as signaling, exocytosis, and migration (24–32). Only a limited number of studies have presented any analysis of the interfacial kinetics of PLD from mammalian (2,25,33) and plant (24,34,35) cells, and most of these studies have examined the activity of PLD on mixed micelles and employed the surface dilution model for the kinetic analysis. These models typically assume that the products of the enzyme reaction are soluble in water and do not account for accumulation of phospholipid products with long acyl chains.

Here, we present, to our knowledge, the first quantitative kinetic description of PLD activity on planar lipid bilayers (36–40) composed of long-chain phospholipids in an attempt to mimic the physiological conditions of long-chain phospholipid substrates and products that are associated with cellular membranes. Starting with the kinetic model proposed by Verger et al. (9) for short-chain lipids, we extend this model to account for the interaction between PLD and its reaction product, phosphatidic acid (PA), which is a long-chain lipid and remains in the membrane. This analysis also demonstrates that a recently introduced ion-channel-based assay (41) that reports PLD-induced changes of the ion conductance through gramicidin A (gA) pores (Fig. 1) can be used to determine the kinetics of PLD-catalyzed reactions. It should be noted that in addition to conductance, PLD activity might influence other aspects of gA channel activity, such as lifetime, through changes in membrane physical properties including surface charge, fluidity, thickness, and curvature (42–44). Although these aspects of gA activity might provide further insight into the effect of PLD binding and activity on membranes, the assay introduced here relies solely on PLD-induced changes in membrane surface charge that can be monitored through gA conductance and does not consider other aspects of the gA response to PLD activity.

Figure 1.

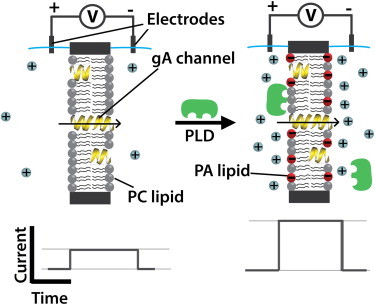
Schematic illustration of the basic concept of the gA-based assay employed to monitor PLD activity (41). Enzymatic activity of PLD (green) on a planar lipid bilayer composed of electrically neutral PC lipids (gray) results in production of negatively charged PA lipids (red); the concomitant accumulation of cations (light blue spheres) near the membrane surface leads to an increase in single-channel conductance, γ, of transient openings of gA pores. The schematic current-versus-time traces below the cartoons depict the PLD-induced increase in the ion current passing through single gA channels.

Materials and Methods

Materials

We purchased cesium acetate, cyclosporin A, and 1-octadecanethiol from Sigma Aldrich (St. Louis, MO); cesium chloride (CsCl) from International Biotechnologies (New Haven, CT); and calcium chloride (CaCl₂), pentane, and hexadecane from Fluka. gA was purchased as gramicidin D from Sigma Aldrich and purified by silica chromatography as described previously (45) to afford a final purity of 97% of gA. We purchased the following phospholipids from Avanti Polar Lipids (Alabaster, AL): 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DiPhyPC), 1,2-diphytanoyl-sn-glycero-3-phosphate (sodium salt) (DiPhyPA). PLD from cabbage (EC 3.1.4.4) was obtained from Sigma Aldrich.

Storage and final concentration of PLD

We received PLD as a lyophilized powder and dissolved it in a buffer solution containing 10 mM CsCl, 0.5 mM CaCl₂, and 10 mM cesium acetate with a pH of 5.5 (the same buffer was used for single-channel recordings with this enzyme) to a final activity of 2500 units × mL⁻¹. We aliquoted and stored this PLD solution at −80°C until usage. According to Sigma Aldrich, 1 unit of PLD liberates 1.0 μmol of choline from L-R-phosphatidylcholine (egg yolk) per hour at pH 5.6 at 30°C. The specific activity of this enzyme, provided by Sigma Aldrich, was >1670 units/mg of protein. Assuming a pure enzyme and considering a molecular weight of ∼92,000 Da (46), a concentration of 1 unit mL⁻¹ corresponds to a PLD concentration of ∼6.5 nM.

Formation of planar lipid bilayers

We formed planar lipid bilayers with the folding technique (38), as described previously (41). Briefly, two compartments (with 3- or 4-mL capacity) of a custom-made Teflon chamber were separated by a thin Teflon film containing a single pore with a diameter of ∼100 μm. To facilitate bilayer formation, we pretreated the area around the pore with 2 μL of 5% (v/v) hexadecane in pentane. Upon addition of a fraction of electrolyte solution (∼1 mL) to each compartment, we spread 3–5 μL of a solution of 25 mg mL⁻¹ DiPhyPC in pentane at the air-water interface. Then we raised the liquid level by adding the rest of the electrolyte solution (2 or 3 mL) to each compartment, which resulted in bilayer formation as described originally by Montal and Mueller (47). We repeated the cycle of raising and lowering the liquid levels until we obtained a bilayer with a minimum capacitance of 70 pF.

Single-channel recordings

After formation of a stable lipid bilayer, we sequentially added small volumes (0.2 μL) of a solution of 10 ng mL⁻¹ gA in isopropanol (Acros Organics, Geel, Belgium) to both compartments of the bilayer setup until one to six active gA channels could be observed in the bilayer at the same time. After each addition of gA, we mixed the bilayer chambers by stirring the solutions in both compartments for at least 3 min with a stir bar (Sun Stir, Warner Instruments, Hamden, CT). In these experiments, the final concentration of gA in the bilayer chamber was in the range 0.1–2.0 pM. This range of gA concentration corresponds to a total amount of 0.3–8 fmol of gA in the chamber with a volume of 3–4 mL; the total amount of lipid in each compartment was ∼150 nmol, leading to a lipid/gA ratio of ∼10⁸. To measure the single-channel conductance of gA pores (48,49), we recorded current-versus-time traces while applying different voltages in the range of ±100 mV across the planar lipid bilayers. We performed these single-channel recordings in voltage-clamp mode using Ag/AgCl pellet electrodes (Warner Instruments) in both compartments of the bilayer setup. Data acquisition and storage were carried out using custom software written in Labview by Dr. J. D. Uram and Dr. D. J. Estes in combination with a Geneclamp 500 amplifier from Axon Instruments (Union City, CA; set to a gain of 100 mV pA⁻¹ and a filter cutoff frequency of 2 kHz). The data acquisition board (National Instruments, Austin, TX) that was connected to the amplifier was set to a sampling frequency of 15 kHz. All recordings were carried out at a temperature of ∼22°C. Recordings could be routinely performed for 15–20 min; due to limited stability of the bilayer, however, recording for longer times became increasingly more challenging as the experiment progressed.

We analyzed single-channel current traces by computing histograms of the currents from the original current-versus-time traces with Clampfit 9.2 software (Axon Instruments) (41). From these histograms, we extracted the mean current amplitude of gA channel opening and closing events. All conductance values were obtained from the slopes of current-amplitude-versus-voltage (I-V) curves. Fig. 1 demonstrates the experimental setup used for this study.

Preparation of small liposomes

We prepared small unilamellar liposomes of DiPhyPC lipids by tip sonication as described previously (50,51). Briefly, we deposited a small droplet of the lipid stock solution (25 mg mL⁻¹ DiPhyPC in pentane) into a clean round-bottom flask with a volume of 5 mL and employed a rotatory evaporator to form a thin lipid film on the wall of the flask. To remove residual traces of pentane, we desiccated the lipid film under vacuum (∼−740 torr) for at least 1 h. We hydrated the lipid film by adding an aqueous solution of 150 mM KCl to reach a final lipid concentration of 6 mM. We formed small liposomes by tip-sonicating the resulting solution using a Branson Sonifier 150 (Branson Ultrasonics, Danbury, CT) for 10–12 min (with ∼5 W output energy). During tip sonication, the flask was immersed in an ice bath to prevent excessive heating of the solution.

Surface plasmon resonance measurements

We prepared glass substrates to use for surface plasmon resonance (SPR) measurements from SF10 glass slides (n = 1.7) (Accurion, Goettingen, Germany). We coated one side of these slides with a 2-nm-thick layer of titanium followed by a 50-nm-thick layer of gold. Immediately after coating the slides, we immersed them overnight in a solution containing 5 mM octadecanethiol to generate a self-assembled monolayer (SAM) of octadecane on the gold surface of the slide. We used a Nanofilm EP³-SPR instrument (Accurion) with an SPR/total-internal-reflection fluid-cell accessory for the SPR measurements. We mounted the SF10 glass slide in the fluid cell with a 60° SF10 prism and index matching fluid (n = 1.7) between the slide and the prism. We set the instrument to direct polarized light (λ = 532 nm) through the prism onto the gold-coated chip at an incident angle of 60°. Before each experiment, we degassed all buffer solutions to prevent air bubbles from forming in the fluid cell. We flowed solutions through the fluid cell and over the octadecane monolayer, proceeding according to the following order: 1), Filling the cell with reaction buffer by flowing a solution of PLD buffer (10 mM CsCl, 0.5 mM CaCl₂, and 10 mM cesium acetate, pH 5.5) at a flow rate of 100 μL min⁻¹ for 5 min; 2) generating a self-assembled lipid monolayer on top of the octadecane SAM by introducing a solution of liposomes containing 2 mM DiPhyPC and 150 mM KCl at 200 μL min⁻¹ for 15 min; 3) removal of excess liposomes by flowing a solution of PLD buffer at 100 μL min⁻¹ for 20 min; 4), measuring the on rate of PLD binding to the lipid layer by introducing PLD buffer that contained the PLD (at a concentration of 20, 41, or 110 nM) at 100 μL min⁻¹ for 20–30 min; and 5), measuring the off rate of PLD from the lipid layer by introducing PLD buffer (without the enzyme) at 100 μL min⁻¹ for 30 min. Fig. S1in the Supporting Material illustrates a representative SPR signal during an experiment. During each experiment, we monitored the change in the Delta signal, ΔD, and the Psi signal, Δψ, from the instrument using the EP3 View Software (Accurion). From these signals, we calculated the exponential rate constant, τ, for each concentration of PLD from: ΔD(t) = ΔD_max × (1 − exp(t/τ)) and Δψ (t) = Δψ_max × (1 − exp(t/τ)) (see Fig. S2 A). The ratio 1/τ is linearly dependent on the bulk concentration of PLD as described by the equation 1/τ = k_on [PLD] + k_off (52). Therefore, we plotted (1/τ) as a function of [PLD] and obtained the on rate (k_on) and off rate (k_off) from the best linear fit to the data in this plot (see Fig. S2 B). The slope of the linear fit to the data corresponded to k_on and the intercept of the linear fit with the y axis corresponded to k_off. We used these values to calculate K_d = k_off /k_on. Note, k_on and k_off in these SPR experiments correspond to k_p and k_d, respectively, in the kinetic analysis.

Results and Discussion

Kinetic model

Verger et al. proposed the first adaptation of the Michaelis-Menten model to describe the interfacial kinetics of PLA (9). Fig. 2 illustrates the general scheme: the basic steps involve reversible adsorption of the soluble enzyme (E) to an interfacial form (E^∗) followed by a 2D Michaelis-Menten reaction where the enzyme binds the interfacial substrate (S^∗) to form the Michaelis complex (E^∗S^∗) and then releases the product(s), which may remain in the membrane (P^∗) and/or be released back into solution (P). By invoking the usual steady-state assumptions, Verger et al arrived at the following equation for the velocity (9)

$$\upsilon \mathrm{\equiv }\frac{d{\Gamma }_{{\text{P}}^{\text{∗}}}}{dt}=\frac{k_2{\Gamma }_{{\text{S}}^{\text{∗}}}}{K_{\text{M}}^{\mathrm{\ast }}\frac{k_{\text{d}}}{k_{\text{p}}}+\left(K_{\text{M}}^{\mathrm{\ast }}+{\Gamma }_{{\text{S}}^{\text{∗}}}\right)\frac{A}{V}}{C}_{{\text{E}}_{\text{o}}},$$ (1)

where K_M^∗ = (k₂ + k₋₁)/k₁ is the interfacial Michaelis-Menten constant, Γ_P^∗ and Γ_S^∗ (mol m⁻²) are the surface concentrations of the product and the substrate, respectively, C_Eo (mol m⁻³) is the total enzyme concentration, A (m²) is the total water/lipid interfacial area (in our setup ∼2.25 × 10⁻⁴ m²), and V (m³) is the volume of the electrolyte solution (in our setup 3 or 4 × 10⁻⁶ m³).

Figure 2.

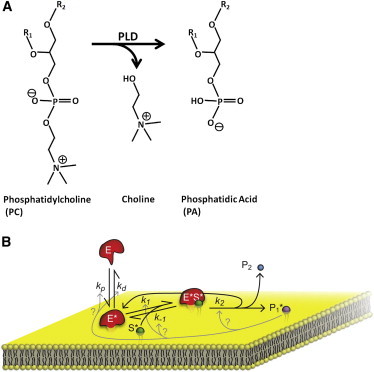
(A) Schematic of the enzymatic reaction catalyzed by PLD. (B) Illustration of an extended version of Verger’s Michaelis-Menten model (9) to describe the interfacial hydrolysis of lipids. Illustrated steps include reversible adsorption of the soluble enzyme (E) to an interfacial form (E^∗) followed by a 2D Michaelis-Menten reaction where the enzyme binds the interfacial substrate (S^∗) to form the Michaelis complex (E^∗S^∗) and then releases the product(s), which may remain in the membrane (P₁^∗) and/or be released back into solution (P₂). Although the reaction products of membrane-active enzymes are often long-chain lipids and therefore not water-soluble, Verger’s model is best suited for short-chain lipids whose hydrolysis products can be treated as soluble species that diffuse away from the lipid membrane into the aqueous bulk solution (1). The cartoon shown here is an extended version of Verger’s original cartoon and depicts the possible mechanisms (gray arrows) by which product accumulation at the interface might modify the kinetics of individual steps along the interfacial catalytic reaction.

This model assumes that the product P^∗ diffuses quickly and does not affect subsequent reactions. This assumption may be valid for water-soluble short-chain phospholipids but is likely not true for natural long-chain phospholipids, which remain in the bilayer (13). In fact, accumulation of reaction products at the interface can dilute the substrate at the surface, inhibit the enzymatic reaction, or even alter the binding of enzyme to the interface and thus affect the hydrolysis reaction (1,9). The gray arrows in Fig. 2 illustrate how these effects could modify the kinetics of various steps in the enzymatic reaction.

In the case of PLD, we find exactly these effects. First, as the product PA accumulates in the membrane, we observe an increase in PLD activity, suggesting that the product is affecting the equilibrium between E and E^∗, represented by k_d/k_p in Eq. 1. A cation-mediated interaction between PA and PLD has been documented (53), and we account for this effect by modeling the adsorption-desorption of the enzyme as a bimolecular association process,

$${\text{P}}^{\text{∗}}+\text{E}\underset{k_{\text{d}}}{\overset{k_{\text{p}}}{\rightleftharpoons }}{\text{E}}^{\text{∗}},$$

where E^∗ represents the membrane-associated enzyme bond to PA lipids. As a result, the equilibrium between E and E^∗ in the denominator of Eq. 1 changes from k_d/k_p to k_d/(k_pΓ_P^∗) (see Appendix for a derivation of a more complete model). The second contribution that we need to account for is substrate depletion and dilution due to product accumulation. The lipid density of the bilayer is fixed (Γ_o) and is simply the sum of the substrate and product densities, assuming that the area/lipid is approximately the same for substrate and product (54)

$${\Gamma }_{\text{o}}={\Gamma }_{{\text{S}}^{\text{∗}}}+{\Gamma }_{{\text{P}}^{\text{∗}}}.$$

One further step can be taken to simplify this model, since for the bilayer system used in this work the A/V ratio is small and the second term in the denominator of Eq. 1 can be ignored. Taken together, we arrive at an extended description for the velocity:

$$\frac{d{\Gamma }_{{\text{P}}^{\text{∗}}}}{dt}=\frac{k_2}{K_{\text{M}}^{\mathrm{\ast }}\frac{k_{\text{d}}}{k_{\text{p}}}}\left({\Gamma }_{\text{o}}-{\Gamma }_{{\text{P}}^{\text{∗}}}\right){\Gamma }_{{\text{P}}^{\text{∗}}}{C}_{{\text{E}}_{\text{o}}}=Q_{\text{m}}\left({\Gamma }_{\text{o}}-{\Gamma }_{{\text{P}}^{\text{∗}}}\right){\Gamma }_{{\text{P}}^{\text{∗}}}{C}_{{\text{E}}_{\text{o}}},$$ (2)

where we have introduced the interfacial quality term Q_m (9). Equation 2 gives the rate of product formation, and integrating this expression gives the product concentration as a function of time,

$${\Gamma }_{{\text{P}}^{\text{∗}}}=\frac{{\Gamma }_{\text{o}}}{1+\mathit{\alpha }\exp \left(-Q_{\text{m}}{\Gamma }_{\text{o}}{C}_{{\text{E}}_{\text{o}}}t\right)},$$ (3)

or, written as a dimensionless mole fraction,

$$X_{\text{PA}}=\frac{{\Gamma }_{{\text{P}}^{\text{∗}}}}{{\Gamma }_{\text{o}}}=\frac{1}{1+\mathit{\alpha }\exp \left(-Q_{\text{m}}{\Gamma }_{\text{o}}{C}_{{\text{E}}_{\text{o}}}t\right)},$$ (4)

where α is an integration constant.

Quantifying PLD activity

We monitored the enzymatic activity of PLD using the previously described gA-based assay (41). Briefly, we formed planar lipid bilayers composed of long-chain PC lipids and added the appropriate concentration of gA (0.1−2.0 pM) to the bulk electrolyte solution to generate only a few, transiently open gA pores at any given time in these bilayers. We added PLD to the electrolyte solutions on both sides of the lipid bilayer and monitored the changes in the single-channel conductance of gA pores, γ, over time. As expected, the enzymatic activity of PLD on the planar lipid bilayer led to a time-dependent increase in the single-channel conductance of gA. This increase is the result of PLD-mediated formation of negatively charged PA lipids in the membrane, which leads to accumulation of cations close to the entrance of gramicidin pores in the membrane. Since monovalent cations are the charge carriers that translocate through gA pores, this local accumulation of ions leads to a measurable increase in γ. Fig. 3 demonstrates this increase in γ as a function of time after the addition of PLD for three different enzyme concentrations.

Figure 3.

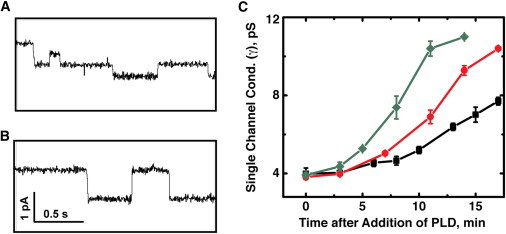
(A and B) Changes in the single-channel conductance of gA, γ, after the addition of PLD. (A and B) Current versus time recordings in the bilayer containing gA before addition of PLD (A) and 13 min after addition of 20.3 nM PLD (B). (C) Time-dependent change in gA conductance after the addition of 15.2 (black ovals), 20.3 (red circles), and 33.3 nM (green diamonds) concentrations of PLD to both sides of the bilayer. Error bars represent the mean ± SE (N ≥ 3).

To quantify the enzymatic activity of PLD, we prepared a calibration curve of γ as a function of the mole fraction of PA lipids as previously described (41). From this calibration curve, which was done in the same buffer as the experiments with PLD (see Supporting Material), we obtained Eq. 5, which describes the relationship between γ (in units of pS = 10⁻¹² Ω⁻¹) and the mole fraction of PA in the bilayer (X_PA)

$$\mathit{\gamma }=3.50\text{pS}+\frac{12.83\text{pS}\times X_{\text{PA}}}{0.23+X_{\text{PA}}}$$ (5)

Using Eq. 5, we converted the time-dependent changes in γ upon addition of PLD to time-dependent changes of the mole fraction of PA lipids, X_PA, in the membrane. Fig. 4 A shows plots of X_PA as a function of time for PLD concentrations of C_Eo = 15.2, 20.3, 27.1, and 33.3 nM. In this figure, data are fit using the novel kinetic model in Eq. 4. Fig. 4 B shows the same data after rescaling the time axis to (C_Eo × time). According to Eq. 4, the kinetic model developed here predicts that this rescaling should result in all of the data collapsing to a single curve, and indeed we find no statistical difference between the data and this theoretical prediction (Kolmogorov-Smirnov test D = 0.1071, p = 0.9971, N = 28).

Figure 4.

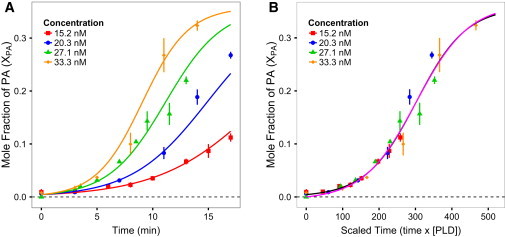
Time dependence of PA production for different concentrations of PLD. (A) The mole fraction of PA (X_PA) for PLD concentrations of 15.2, 20.3, 27.1, and 33.3 nM. (B) The same data as in A after rescaling the time by the PLD concentration. As predicted by Eq. 4, the data points collapse to a single curve. The magenta curve is the full model from Eq. 8 and is indistinguishable from the simplified model given by Eq. 4 (black curve). The error bars in both plots represent the mean ± SD (N ≥ 3) and the curves are best fits to the data using Eq. 4.

Two kinetic parameters, the specificity constant, k₂/K_M^∗, and the interfacial quality constant, Q_m = k₂/ (K_M^∗ × (k_d/k_p)), are commonly used to describe enzymatic reaction rates of phospholipases quantitatively. Q_m has slightly different units in our model since PLD association with the membrane is now lipid dependent, and from curve fitting in Fig. 4, we obtained a value of 14.5 μM⁻¹ s⁻¹ for Q_m Γ_o of the examined PLD activity on long-chain PC lipids. To estimate the specificity constant, we first employed SPR to determine the binding affinity of PLD to PC bilayers and obtained the dissociation constant for this binding event in units of bulk concentrations, K_d = 150 nM. This number, based on the definition of K_d, represents the enzyme concentration (C_Eo) at which half of the available binding sites for enzyme are occupied by bound enzymes. We thus assume that at the enzyme concentration of C_Eo = 150 nM, half of the maximally available surface area of the lipid bilayer is occupied by bound PLD. To determine the surface concentration of the enzyme, Γ_E^∗, when C_Eo = K_d, we approximated the size of individual PLD molecules as described below, and thus, we could determine the equilibrium dissociation constant, k_d/(k_p Γ_o) = C_Eo/Γ_E^∗.

We approximated the size of individual PLD proteins employed in the assay presented here based on the molecular weight of ∼92 kDa (55) and a comparison with another protein with the same molecular weight (a 92-kDa fragment of yeast DNA topoisomerase II) (56), whose molecular volume of 720 nm³ is known. Assuming a spherical shape, each PLD molecule would cover an area of ∼97 nm² on the bilayer. If we consider a square unit area of 1 μm² and a close hexagonal packing (corresponding to a coverage of 90.7%) (57) of the PLD enzyme at the interface, the maximum surface coverage would be ∼9.4 × 10³ enzymes μm⁻² at the interface. This coverage corresponds to the densest possible packing of PLD in the absence of any steric hindrance or thermal motion. If we consider less ideal packing, where each PLD molecule would occupy twice its actual projected area on the membrane, this would reduce the maximal possible coverage to ∼45% or ∼4.7 ×10³ enzymes μm⁻² at the membrane surface. Thus, we assume that maximal PLD coverage on the membrane would be within the range 45–90.7%. At half-maximal binding, therefore, ∼2.3 × 10³ – 4.7 × 10³ enzymes μm⁻² could be bound at the interface, corresponding to an approximate surface concentration of Γ_E^∗ = 3.8 – 7.8 nmol enzyme m⁻². Consequently, the constant C_Eo/Γ_E^∗ and, hence, k_d/(k_p Γ_o) have an estimated value of 19.0 × 10³ – 39.5 × 10³ m⁻¹. Based on this range of values for k_d/(k_p Γ_o), we calculated a range of values from our experimentally determined value of Q_m Γ_o for the specificity constant, k₂/K_M^∗, of 0.77 – 1.6 m² nmol⁻¹ s⁻¹ for the PLD-catalyzed hydrolysis of long-chain PC lipids.

PLD-catalyzed hydrolysis of long-chain PC lipids results in production of long-chain PA lipids, which remain in the membrane. Fig. 4 clearly illustrates that PLD activity on the PC bilayer starts with a relatively slow phase, and as PA accumulates in the membrane, PLD catalytic activity accelerates. Accumulation of PA in the presence of Ca²⁺, which is required for maximal activity of cabbage PLD, leads to the formation of Ca²⁺/PA domains in the membrane (41,53). Kuppe et al. have previously shown that these domains facilitate the binding of PLD to the membrane and hence lead to an increase in the hydrolysis rate of this enzyme (53). Ahyayauch et al. suggested that Ca²⁺/PA complexes bind to an allosteric site of PLD and facilitate its association with the membrane. Moreover, the activity of phospholipases is strongly influenced by physical properties of the interface such as membrane curvature (58). PA is a cone-shaped lipid and is known to induce negative curvatures in bilayers that could contribute to modulation of PLD binding and activity.

A similar initial slow phase, typically referred to as a lag phase, has previously been reported for other phospholipase enzymes (59). As PLD activity further proceeds on the membrane, however, accumulation of product leads to depletion of substrate lipids in the membrane and thus slows the PLD catalytic rate. The kinetic model presented here considers these two effects of PA accumulation and, as demonstrated in Fig. 4, describes the behavior of this enzyme extremely well.

The specificity constant and interfacial quality constant, the two parameters that we determined in this work, are commonly employed to describe the kinetics of interfacial enzymatic reactions (1,9). The specificity constant is a measure of the catalytic efficiency of the enzyme, and the interfacial quality constant accounts for the effect of physiochemical parameters of the interface, such as the orientation and conformation of the molecules, the molecular and charge densities, the water structure, and the viscosity, on the activity of the enzyme (1). The value of 14.5 μM⁻¹ s⁻¹ for the interfacial quality constant obtained for the enzymatic reaction of PLD on the long-chain PC lipid examined here appears reasonable for this enzyme based on a previously reported value of 3 μM⁻¹ s⁻¹ for the hydrolysis of a medium-chain length lipid by a different lipase enzyme, PLA, on a lipid monolayer (60).

Conclusions

This study demonstrates that the gA-based assay employed here can be used for monitoring the kinetics of catalytic reactions of membrane-active enzymes on natural lipid substrates whose net electrical charge changes as a result of enzyme activity. Further, the high-quality data arising from this assay allowed us to develop a novel and quantitative model that describes the activity of interfacial enzymes on physiologically relevant long-chain phospholipids and accounts for the accumulation of product lipids and dilution of substrate lipids in the membrane. Based on this analysis, we were able to determine the specificity constant and interfacial quality constant for the examined reaction. Planar lipid bilayers provide an attractive platform for such studies, since they share many of the advantages of lipid monolayer systems, as compared to the bulk systems such as micelles and liposomes (61), and mimic the lipid bilayer structure of natural cell membranes while providing electrical and chemical access to both sides of the lipid bilayer. In addition, planar lipid bilayers can be prepared from a variety of lipids (62–64). Likewise, the theoretical description of PLD activity introduced here will contribute to the understanding of the collective activity of systems of lipolytic enzymes and their function in cell signaling.

Appendix

The kinetic model we present that results in Eq. 4 is based on the assumption that PA in the membrane attracts more PLD to the surface. We account for this effect by including a bimolecular association reaction where PLD (E) binds to PA (P^∗) to produce a membrane-associated form of PLD (E^∗). This is a simple model, but technically (and mathematically) it has problems if we start with a pure PC membrane, since without any PA no enzyme will ever associate with the membrane. A more correct model would adopt a form for the penetration rate constant like

$$k_{\text{p}}={\tilde{k}}_{\text{p}}\left(1+\mathit{\beta }{\Gamma }_{{\text{P}}^{\text{∗}}}\right),$$ (6)

where we now have some basal rate of PLD association to the membrane $\left({\tilde{k}}_p\right)$ that naturally increases as more PA accumulates $\left({\tilde{k}}_p\mathit{\beta }{\Gamma }_{P^{\mathrm{\ast }}}\right)$. When we adopt this form, we arrive at a more complex form for the velocity,

$$\frac{d{\Gamma }_{P^{\mathrm{\ast }}}}{dt}=Q_m\left({\Gamma }_o-{\Gamma }_{P^{\mathrm{\ast }}}\right)\left(1+\mathit{\beta }{\Gamma }_{P^{\mathrm{\ast }}}\right)C_{E_o}.$$ (7)

If we integrate Eq. 7 and impose the condition that we initially have no PA in the membrane (at t = 0), we arrive at a slightly more complex formula for the product concentration as a function of time,

$${\Gamma }_{{\text{P}}^{\text{∗}}}=\frac{{\Gamma }_{\text{o}}\left(\exp \left[\left(1+\mathit{\beta }{\Gamma }_{\text{o}}\right)Q_{\text{m}}{C}_{{\text{E}}_{\text{o}}}t\right]-1\right)}{\exp \left[\left(1+\mathit{\beta }{\Gamma }_{\text{o}}\right)Q_{\text{m}}{C}_{{\text{E}}_{\text{o}}}t\right]+\mathit{\beta }{\Gamma }_{\text{o}}}.$$ (8)

We fit our scaled data using this more complete model and get the plot shown in Fig. 4 B, where the black line is the original fit from Eq. 4 and the magenta curve is the complete model based on Eq. 8. The difference between the simple and full model is obviously very minimal and only occurs for small values of X_PA. Indeed, the best fit to the data gives a value of β = 178.7, and in the limit of β ≫ 1, we can ignore the 1 in the numerator and Eq. 8 reduces to the same form as Eq. 3.