Receptor Displacement in the Cell Membrane by Hydrodynamic Force Amplification through Nanoparticles

Abstract

We introduce an intrinsically multiplexed and easy to implement method to apply an external force to a biomolecule and thus probe its interaction with a second biomolecule or, more generally, its environment (for example, the cell membrane). We take advantage of the hydrodynamic interaction with a controlled fluid flow within a microfluidic channel to apply a force. By labeling the biomolecule with a nanoparticle that acts as a kite and increases the hydrodynamic interaction with the fluid, the drag induced by convection becomes important. We use this approach to track the motion of single membrane receptors, the Clostridium perfringens ε-toxin (CPεT) receptors that are confined in lipid raft platforms, and probe their interaction with the environment. Under external force, we observe displacements over distances up to 10 times the confining domain diameter due to elastic deformation of a barrier and return to the initial position after the flow is stopped. Receptors can also jump over such barriers. Analysis of the receptor motion characteristics before, during, and after a force is applied via the flow indicates that the receptors are displaced together with their confining raft platform. Experiments before and after incubation with latrunculin B reveal that the barriers are part of the actin cytoskeleton and have an average spring constant of 2.5 ± 0.6 pN/μm before vs. 0.6 ± 0.2 pN/μm after partial actin depolymerization. Our data, in combination with our previous work demonstrating that the ε-toxin receptor confinement is not influenced by the cytoskeleton, imply that it is the raft platform and its constituents rather than the receptor itself that encounters and deforms the barriers formed by the actin cytoskeleton.

Introduction

Single-molecule tracking (SMT) experiments have shown that the motion of biomolecules in the membrane is often non Brownian (1,2). The membrane architecture and underlying cytoskeleton greatly influence the motion of membrane biomolecules during complex cellular processes, such as signaling, trafficking, and transport. Anomalous diffusion of membrane biomolecules has been attributed to lipid rafts or platforms (3–7), cytoskeleton barriers (8–12), tethering to the cytoskeleton (13–15), crowding of molecules (16,17), and intermolecular interactions (18,19). SMT experiments that showed non Brownian diffusion are mostly done without exerting an external force on the tracked biomolecule.

An external force, however, can give access to information about the boundary or the stability of the confinement region. Such experiments, where the external force is applied with optical tweezers, have so far provided values for the barrier-free path length that a receptor can cover in the membrane before encountering a barrier, the spring constant of actin filaments that obstruct the motion of the tracked molecules, and the friction coefficient inside the membrane (13,14,20–24). However, optical tweezers can generally only apply a force on one biomolecule at a time, unless multiple traps are created, e.g., with complex holographic techniques (25), and require technical expertise along with expensive equipment. Furthermore, the high laser intensities of the focused tweezer beam may harm cells (26). Recently, an alternative approach that relies on centripetal force to apply forces on many biomolecules simultaneously has been introduced (27); however, the setup is rather complicated and may not be appropriate for cells.

Here, we propose what we believe is a new technique that can create an in-plane force on single membrane biomolecules to probe the interaction between the biomolecule and its membrane environment. A flow of liquid around the cell membrane creates a drag force that scales with the hydrodynamic radius of the part of the biomolecule that sticks out of the membrane (28). A similar approach is used by the single cell parasite, Trypanosoma brucei. This parasite is known for its ability to evade the human immune system partly by clearance of surface-bound antibodies by using the hydrodynamic drag created by swimming in the blood of the host (29). We here increase the drag force on the membrane receptor through a nanoparticle. The drag force on a micron-sized bead attached to a single molecule has been previously used in experiments on stretching single DNA or RNA strands (30–33) and on the investigation of the Willebrand factor (34,35). In cells, the drag force on unlabeled membrane receptors is negligible, but coupled nanoparticle labels act as kites and amplify the drag force. During standard SMT experiments, the drag force on the fluorescent probe, such as a quantum dot, is neglected because it is much lower than the drag force experienced by the receptor in the membrane. However, in our setup, the flow speed around the nanoparticle in the medium is at least 150 times larger than the flow present due to Brownian diffusion. This approach provides a cheap, easily implementable, and easy to multiplex approach to create an in-plane force on a biomolecule in the cell membrane.

To investigate the cell membrane architecture, we label Clostridium perfringens ε-toxin (CPεT) receptors in the membrane of Madin-Darby Canine kidney (MDCK) cells with Eu-doped oxide (Y_0.6Eu_0.4VO₄) nanoparticles (NPs) of 30−60 nm diameter (36,37). CPεT is a pore-forming toxin (38) that targets a 37-kDa membrane protein receptor (39), potentially the hepatitis A virus cellular receptor 1 (40), which was found localized in detergent-resistant membrane domains (41,42). We have shown that these receptors are preorganized in the membrane and undergo confined Brownian motion in stable lipid platforms (37). In particular, we have shown that cell incubation with cholesterol oxidase and sphingomyelinase drastically decreases the confining potential felt by the receptors, whereas actin depolymerization and microtubule destabilization had no effect on the receptor confinement (37). Given the size of these confinement domains, we attributed them to raft platforms resulting from coalescence of smaller lipid raft entities (7). A controlled flow in a microchannel allows us to generate a constant force on the receptor through the hydrodynamic drag of the nanoparticle. This system allows SMT using a simple wide field microscopy setup, while exerting a force on the tracked receptors in live cells.

In this article, we will first introduce the simple concept used to generate the drag force, and then we will show that it is possible to move receptors over the cell membrane, while the cell does not move. We then discuss the observations made while forcing the CPεT receptor and their confining raft microdomains across the membrane.

Materials and Methods

Cell preparation

Madin-Darby canine kidney (MDCK) cells were cultured in culture medium (Dulbecco’s modified Eagle’s medium, 10% fetal calf serum, 1% penicillin-streptomycin) at 37°C. Cells are not used for more than 10 weeks. Culture medium is injected into the channel two days before cell injection and the channel is incubated overnight at 37°C to remove gas from the polydimethylsiloxane (PDMS) that would interfere with cell growth by forming bubbles in the channel. Cells were trypsinated and resuspended in culture medium. After concentrating the cells by centrifugation to a high concentration (∼8 × 10⁷ cells/mL), they are injected into the channel and incubated at 37°C. Cells are used the next day for experiments. We typically perform experiments on patches of multiple cells. Fig. 1 B shows the simple geometry of the PDMS microchannel. Three syringe-pump driven entries are used to supply liquid flow, NP solution, and any other solution needed.

Figure 1.

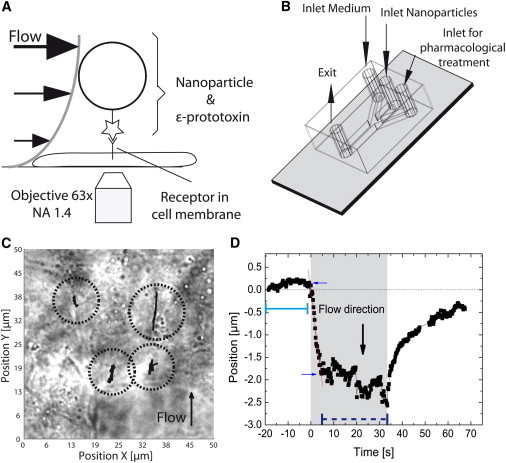
Application of a drag force to a membrane receptor using the drag created by a liquid flow. (A) The nanoparticle amplifies the drag force that acts on a receptor. (B) Geometry of the microfluidic channels used to conduct the experiment. (C) Multiple Clostridium perfringens ε-toxin (CPεT) receptor trajectories can be observed simultaneously. Four different trajectories are shown with black lines superimposed on the white-light transmission image of MDCK cells to highlight the multiplexing capabilities of this technique. (D) Position of a receptor for a cycle of liquid flow. A flow rate of 7.5 μL/min (flow speed: 0.002 m/s) was applied between t = 0 s and 33 s (shading: time range). When the flow is stopped, the receptor returns close to its initial position. (Blue arrows) Receptor is displaced linearly with time between the time points. (Straight red line) Linear fit in this time range.

For the experiments involving incubation with latrunculin B or cholesterol oxidase, we used the third entry to inject minimal medium (MM: HBSS + 10 mM HEPES) with 500 nM latrunculin B (Calbiochem, Millipore, Billerica, MA ) or 20 U/mL cholesterol oxidase (Calbiochem, Millipore), respectively, at a low flow rate of ∼1 μL/min and left to incubate for 30 min. Experiments after incubation with latrunculin B were performed on cells that showed rounding in white-light transmission images.

Preparation of Clostridium perfringens ε-prototoxin (CPεpT) nanoparticle complex

Y_0.6Eu_0.4VO₄ nanoparticles were prepared as described in Masson et al. (36) and Türkcan et al. (37). We then coupled the APTES-coated europium-doped nanoparticles to ε-prototoxin produced by C. perfringens bacteria, via the amine-reactive cross-linker bis (sulfosuccinimidyl) suberate (BS₃), as described in Türkcan et al. (37).

Experimental setup

For the tracking experiments, the microfluidic chip is mounted on a wide-field inverted microscope (Axiovert 100; Carl Zeiss, Jena, Germany) equipped with a 63×, NA = 1.4 oil immersion objective. Three syringe pumps are attached to the three inputs of the chip: one contains observation medium (HBSS + 10 mM HEPES, 1% fetal calf serum), the second contains a solution of ε-prototoxin functionalized nanoparticles at a concentration of 0.05 mM in vanadate ions, and the last contains minimal medium with latrunculin B or cholesterol oxidase. To begin, the channel is rinsed with observation medium through the first input with a low flow rate of ∼1 μL/min. Nanoparticles are then injected through the second input and incubated with the cells for 30 min. The channel is rinsed with observation medium through the first input at a low flow rate of 1 μL/min to remove unbound nanoparticles. The channel design with two or more inputs provides an easy system to remove unbound nanoparticles that would otherwise increase the background fluorescence.

For tracking experiments under external force, images of the receptors are recorded with an electron-multiplying charge-coupled device (QuantEM:512SC; Roper Scientific, Trenton, NJ). The nanoparticles are excited with an Ar⁺-ion laser using the 465.8-nm line. The emission of the NPs is collected through a 617/8M filter (Chroma Technology, Bellows Falls, VT). We record images at frame rates down to 20 Hz and an excitation intensity of 0.25 kW/cm² at room temperature. The motion of the receptor is first recorded without flow to check if it behaves normally (i.e., as documented in Türkcan et al. (37)), then its motion is tracked under external force, by applying a flow through the syringe pump containing observation medium. We regularly verified with white-light transmission images that there was no visible modification of the cell morphology. The toxin receptor position in each frame was determined from a Gaussian fit to the diffraction pattern of the nanoparticles with a homemade MATLAB V8.2 (The MathWorks, Natick, MA) algorithm. The mean total photon number per nanoparticle label in each frame is 70 photons, the average signal/noise ratio is equal to 10, and the average static positioning noise is 30 nm in the absence of flow (for details, see the Supporting Information of Türkcan et al. (37)). We also verified that the motion of a NP-toxin conjugate adsorbed on the glass coverslip is not influenced by the presence of a flow, as expected from the short length of the cross-linker (six carbon atoms) coupling the toxin to the nanoparticle (see Fig. S1 in the Supporting Material).

The error bars on all measured values are standard errors on the mean except for the error bars on the speed measurements in Fig. S2, which are standard deviations.

Actin, microtubule, and raft labeling in microchannels

Transfection with GFP-actin

We used a reduced expression GFP-β actin (Addgene plasmid 31502; Addgene, Cambridge, MA) (43). The plasmid was extracted from the Escherichia coli (DHα) bacterial culture according to the HiSpeed Plasmid Midi Kit protocol by QIAGEN (Venlo, Netherlands) to a final concentration of 0.225 μg/μL determined by the absorption spectrum. A quantity of 5 μL was then diluted in 100 μL observation medium and 3 μL of X-tremeGENE HP DNA Transfection Reagent (Roche Applied Science, Penzberg, Germany) were added. The solution was left to incubate for 15 min at room temperature and was then injected in the microchannels and left to incubate with the cells for 24–28 h.

Actin staining with phalloidin-rhodamine

The labeling process involved five different syringes, each respectively filled with formaldehyde (4%) in phosphate-buffered saline (PBS), marking solution (PBS+0.125% gelatin), Triton (1%) in marking solution, blocking solution (PBS+0.25% gelatin), and staining solution (DAPI (Invitrogen, Carlsbad, CA) and phalloidin-rhodamine (Invitrogen) diluted by 1:200 and 1:40 in PBS, respectively). Injections were performed at low flow rates of ∼1–2 μL/min. We first injected the formaldehyde solution and incubated for 15 min. We then injected the Triton solution. After 4 min, the channels were rinsed with marking solution and flooded with blocking solution for 30–60 min. The channels were then rinsed and flooded with staining solution and incubated for 45–60 min at 37°C. Lastly, the channels were again rinsed with marking solution before observation.

Microtubule labeling by transfection with end-binding protein EB3-GFP

A stock solution of 3-green fluorescent protein (EB3-GFP DNA) in PBS is prepared at a concentration of 0.1 g/L. 3 μL Fugene is diluted in 90 μL PBS and added to 10 μL of the EB3-GFP DNA solution and incubated for 20 min. The solution is added to 750 μL of culture medium and added to the cells for 5 h. After replacing the solution with culture medium, the cells are incubated at 37°C for 24 h to give them time to express the protein.

Raft labeling with cholera toxin-Alexa488

Monosialotetrahexosylgangliosides (GM1) molecules were labeled by adding 100 μL of a 10–100 μg/μL solution of cholera toxin subunit B coupled to Alexa488 (CT-B-Alexa488; Molecular Probes, Eugene, OR) and incubating for 15 min at 37°C. The cells were rinsed to remove excess CT-B-Alexa488 before observation.

Raft labeling with sphingomyelin-BODIPY

We diluted BODIPY FL C12-sphingomyelin (Life Technologies, Carlsbad, CA) in chloroform:(pure)ethanol (19:1) to a final concentration of 1 mM. A quantity of 50 μL of this solution was first dried in an Ar environment and then under vacuum for 1 h. The lipid was then redissolved in 200 μL of pure ethanol. A 50 mL plastic tube was prepared containing 10 mL HBSS + 10 mM HEPES and 0.34 mg/mL BSA (A2058; Sigma, St. Louis, MO). The lipid solution was slowly added, drop by drop, to the plastic tube under N₂ atmosphere, without disrupting the oxygen-free environment, and during vortexing. This solution was then injected in the microchannels containing the cells and incubated at 4°C for 30–60 min. The cells were rinsed before observation.

Preparation of PDMS microchannels

The polydimethylsiloxane (PDMS) was molded using the dry film photoresist soft lithography technique (44). The master mold of thickness 32 ± 2 μm was etched into Laminar E8020 Negative Films (Eternal Chemical, Kaohsiung, Taiwan). The photoresist layer for the master mold was laminated onto a clean glass slide using an office laminator at 100°C. It was then exposed to UV light through a photo mask with the desired channel architecture. The photoresist was developed by immersion in an aqueous bath of carbonate potassium at 1% mass concentration. PDMS (1:10 ratio of curing agent to bulk material, SYLGARD 184; Dow Corning, Midland, MI) is then poured over the master mold and cured for 3 h at 70°C. After peeling off, the cured PDMS was sealed by plasma-bonding onto a microscope glass coverslip. The channels have a width of 400 μm.

Results

Using hydrofluidic drag to exert a force

We functionalize a nanoparticle with a biomolecule that binds to a receptor in the cell membrane. The NP acts as a kite by sticking out in the moving fluid (Fig. 1 A): when a flow is applied, the small particle in solution experiences a drag force. In the small Reynolds number regime, the drag force on a spherical particle can be described by the Stokes law F_d = 6πηrv_flow, where the drag force F_d depends on the fluid viscosity η, the hydrodynamic radius r of the nanoparticle, and the velocity v_flow of the fluid. Here we assume that neither the receptor nor the nanoparticle-conjugated molecule will unfold, as unfolding requires much higher forces.

Determining the force magnitude

To estimate the applied force, the only parameter that needs to be determined besides the material properties η and r is the velocity of the liquid flow around the NP. Note that the nanoparticle radius r can be estimated from the emitted photon number with a precision of 10% (45) and has a mean value of 28 ± 8 nm. The liquid flow should be laminar, in order to easily control the force on the receptor. A microfluidic channel provides adequate conditions, because viscous forces are more important than inertial forces, which leads to a small Reynolds number (0.02–0.5 in our experiments). In this regime, the flow within the channel is laminar and its velocity can be calculated at any point based on the Stokes equation. In a channel longer than wide, the solution is a Poiseuille flow, with a parabolic velocity profile and a maximal flow speed halfway between the bottom and the top of the channel. The velocity depends on the width l and height h of the channel, as well as on the flow rate. However, due to the physical properties of the cell surface, i.e., the fact that the lipid bilayer possesses fluidity (46), the no-slip boundary condition (47) is not fulfilled. In this case, a slip length can be determined and the Poiseuille flow solution can still be applied assuming a broader channel with the virtual zero-flow plane located one slip length below the water-cell interface (48).

We determined the flow speed experimentally using particle velocimetry with unbound nanoparticles (see Fig. S2). The flow speeds we measure at the same height as the nanoparticles bound to receptors are compatible with a slip length of 800 nm. This means that the particles are located multiple particle radii away from the zero-flow plane. As a consequence, modifications of the flow around the nanoparticle can be neglected and the introduction of an effective viscosity η_eff is not required (see the Supporting Material). Although we estimate the drag force F_d with somewhat lower precision than in optical-tweezer experiments, the important advantage is that we can easily measure many trajectories simultaneously (Fig. 1 C).

Nanoparticle-amplified drag force displaces ε-toxin receptors

The hydrodynamic drag force at a flow rate of 7.5 μL/min (flow speed: 0.002 m/s), which is turned on at t = 0 s, is large enough to displace a CPεT receptor by 2.1 ± 0.3 μm in the flow direction in the cell membrane of a live MDCK cell (Fig. 1 D; see Fig. S3 for additional displacement trajectories and see Movie S1 in the Supporting Material). After a displacement phase linear with time (see below), the receptor reaches an equilibrium position. The total displacement is calculated by averaging all recorded positions of the receptor from the frames before the flow started (in the zone indicated with a solid line in Fig. 1 D) and then subtracting the average position after the equilibrium position under flow has been reached (calculated in the zone indicated with a dashed line in Fig. 1 D). In some cases, a small component of displacement is observed in the direction perpendicular to the flow (Fig. 1 C). This is probably due to obstacles in the cell membrane and below it like cell compartments or cytoskeleton bundles. These deviations from displacement along the flow can, in approximately half of the cases, be associated to visible features in the white-light transmission images, mainly the edge of the cell.

The intriguing result is that, after the flow is turned off, the receptor returns close to its initial position. The same behavior is observed for all displaced receptors (see Fig. S3). As documented below, we interpret the forced displacement of the toxin receptors as being hindered by barriers related to the actin cytoskeleton. When the receptors are forced against a flexible barrier, the barrier can deform and generate a restoring force on the receptor. When the flow is switched off, this restoring force brings the receptor back close to its initial position. However, a small fraction of the total displacement is not reversible (Fig. 1 D). This may be due to a nonreversible deformation of the barrier such as a rearrangement of the actin cytoskeleton meshwork. For the first application of flow, this effect may also be due to the fact that the receptor travels a certain distance before encountering a barrier.

The linear displacement phase between t = 0 s and t = 2 s can be fitted with a straight line (red line in Fig. 1 D) whose slope yields the receptor displacement speed v_disp due to the flow (0.52 ± 0.03 μm/s). Using this displacement speed and the total displacement for the equilibrium position L_disp (2.1 ± 0.3 μm), we can evaluate the Péclet number Pe = L_dispv_disp/D of the system, the ratio of the rate of advection due to the flow to the Brownian diffusion coefficient of the biomolecule D (0.16 ± 0.01 μm²/s) (37). The measured Péclet number of 7 indicates that the receptor is indeed displaced by the hydrodynamic drag of the flow and not due to Brownian motion.

Cell stability during flow

It is important to verify that the observed displacement is indeed due to the flow-induced drag force acting on the receptor and not to the displacement of the entire cell due to the induced shear stress. To verify this, three types of experiments were performed with and without a flow of observation medium: observation of the actin, observation of the microtubule cytoskeleton, and observation of rafts labeled with fluorescent cholera toxin or with fluorescent sphingomyelin (Fig. 2, A and B) under the same flow conditions as in the NP experiments. The mean observed displacement of the microtubules is 0.3 ± 0.2 μm (N = 60 measurements on four cells) (average of multiple independent displacement measurements in different locations of the cell indicated by arrowheads in Fig. 2 A and see Fig. S4). Note that the most important microtubule displacements are observed in cell protrusions for isolated cells. The microtubule displacements in the cell body where the receptor displacements under flow are measured are typically smaller than the average value given above.

Figure 2.

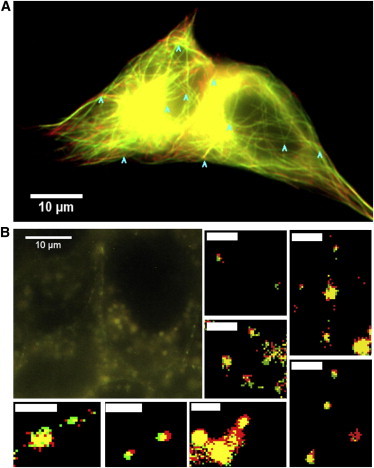
(A) EB3-GFP labeled microtubules of a cell without fluid flow (red) and under a flow rate: 50 μL/min (flow velocity: 0.01 m/s) (green). This flow rate is the maximal flow rate used during single-molecule experiments. (Arrows) Points of measurements of displacement (N = 60 on 4 cells). (B) Position of fluorescently labeled GM1 clusters under flow. (Red image) Recorded without flow; (green image) under a flow rate of 2.5 μL/min (flow velocity: 0.0006 m/s) (N = 21 on 8 cells). The small images zoom in on individual GM1 patches (scale bar is 2 μm).

Labeling of the actin cytoskeleton with GFP-actin reveals that even during the maximum flow rate of 30 μL/min, the actin fibers only move on average 0.36 ± 0.04 μm (N = 30 on three cells) with respect to their position before flow (see Fig. S5). We also stained with phalloidin-rhodamine the cell populations that had and had not undergone the series of flow cycles shown in Fig. 3. The Hough transforms of the recorded images (see Fig. S6) show that no significant changes take place as a consequence of the stress applied by the flow. Note that the total duration of the flow cycles is <5 min. For much longer durations, modifications of the actin cytoskeleton are likely to occur.

Figure 3.

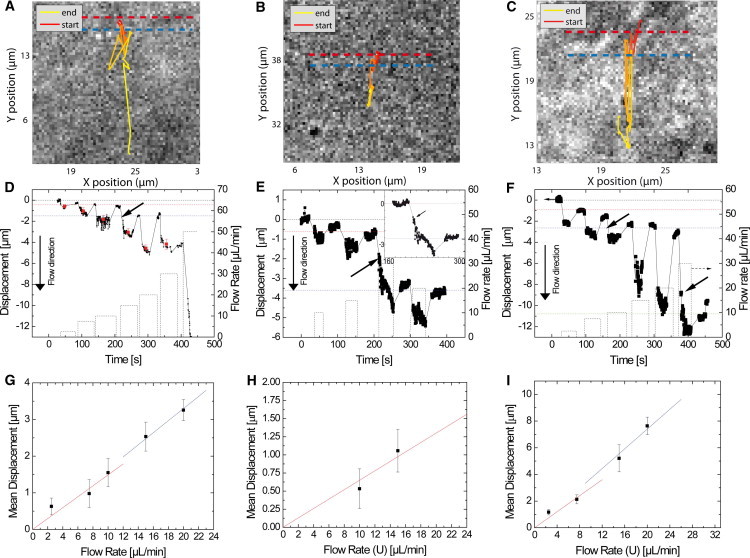
Pulling the same receptor at different flow rates to investigate the relationship between drag force and displacement. (A–C) Receptor trajectories during multiple flow cycles along with the encountered barriers (dashed colored lines). Fig. S4 illustrates how the barrier positions were determined. (Red) Beginning of a trajectory. Color gradually changes (to yellow) toward the end of the trajectory. (D–F) Corresponding displacements over time for a series of different flow rates acting on the same receptors. (Dashed line) Flow rate. (Arrows) Points where the receptor passes over a barrier. These points have been determined by careful examination of the trajectory and the recorded positions (see text). For the highest flow rate in panel D at t = 400 s, a departure of the nanoparticle is observed most probably due to dissociation of the toxin from its receptor. (Horizontal dotted red, blue, and green lines) Barrier positions. (Black horizontal dotted line) Initial receptor position. The receptor displacements are calculated from the difference in mean positions before and during flow after an equilibrium position is reached (red points in D) and are plotted versus the flow rates in panels G–I.

The average displacement of the GM1 clusters is 0.2 ± 0.1 μm (N = 21 measurements on eight cells). Individual measurements are given in the histogram in Fig. S4 C. Further experiments using sphingomyelin-BODIPY to stain the lipid rafts showed that rafts subjected to the maximum flow used in the experiments (30 μL/min) display a negligible displacement of 0.3 ± 0.03 μm (N = 20 on 6 cells; see Fig. S7).

Overall, the actin, microtubule, and raft displacements are small with respect to the displacements of the receptors in the same flow conditions, which are typically larger than 1 μm.

Receptors are displaced along with a confining raft

When no flow is present, the receptors undergo confined motion in small domains of average size of 700 nm (37). Under flow, we can distinguish two populations of tracked receptors. The first is displaced under flow (N = 50), whereas the second population remains at its initial position (N = 45) and tends to be located at the border between cells, where MDCK cells form tight junctions.

We determined the characteristics of the receptor motion before, during, and after a flow cycle exerts a drag force on it. The size of the confinement domain remains similar before application of a flow, after equilibrium under flow is reached, and after the flow is stopped. The root-mean squared (RMS) displacement of the receptor in the direction perpendicular to the flow is 0.09 ± 0.02 μm (N = 11), 0.14 ± 0.03 μm (N = 11), and 0.08 ± 0.02 μm (N = 11) before, during (after equilibrium is reached), and after application of a flow, respectively. We did not analyze the RMS displacement in the direction of the flow because, even after the equilibrium position has been reached, occasional back and forth fluctuations are observed during the flow, possibly due to rearrangements of the actin filament network.

Furthermore, for two trajectories we have enough data points to extract both the diffusion coefficient and the confining potential felt by the receptors using the Bayesian inference scheme described in Cottin-Bizonne et al. (48). The confining potentials before and after application of a flow are shown in Fig. S8 for one of these two trajectories. We have previously shown that this confining potential is well described by a second-order potential (37,49). The corresponding spring constants are similar before and after the flow and in agreement with the values reported in Türkcan et al. (37): we find 0.51 ± 0.03 (0.44 ± 0.03) pN/μm before vs. 0.7 ± 0.2 (0.91 ± 0.06) pN/μm after the flow, respectively. The same is true for the diffusion coefficient (0.056 ± 0.002 (0.068 ± 0.002) μm²/s before vs. 0.016 ± 0.002 (0.051 ± 0.002) μm²/s after the flow) and the domain radius (defined as the radius of a circle including 95% of the trajectory points) (0.26 ± 0.03 (0.35 ± 0.03) μm before vs. 0.22 ± 0.03 (0.24 ± 0.03) μm after the flow).

We also performed experiments after cell incubation with cholesterol oxidase. The RMS displacements in the direction perpendicular to the flow were 0.62 ± 0.21 μm (N = 6), 0.65 ± 0.15 μm (N = 7), and 0.51 ± 0.08 μm (N = 6) before, during (after equilibrium is reached), and after application of a flow, respectively. The amplitude of the motion is clearly larger than without cholesterol oxidation incubation, as the cholesterol oxidase destabilizes the rafts and causes an increase of the confinement domain size (37). However, the general displacement behavior of the receptors experiencing an external force remains unchanged (see Fig. S9). The average receptor displacement before cholesterol oxidase addition is 4.13 ± 0.75 μm (N = 10), compared to 3.84 ± 1.49 μm (N = 10) after the addition of cholesterol oxidase. This is not surprising given that we have previously shown that, even after incubation with cholesterol oxidase, the receptors remain confined (37).

These data imply that the receptor does not leave the raft platform it is confined in and that it is displaced through the membrane along with the confining raft. However, we cannot exclude that receptors may hop into adjacent raft platforms, as discussed in Türkcan et al. (50), during application of the flow. We reported that hopping events are rare (50) but the presence of a drag force may increase the hopping rate.

Stiffness of the encountered barriers

Generally, moving receptors undergo elastic displacement, i.e., they return close to their initial position once the flow is stopped. However, when we perform series of flow cycles with increasing flow rates, the receptors occasionally exhibit a jump in the flow direction after a first equilibrium position is reached and reach a new equilibrium position further away (see Fig. 3, D–F, inset in Fig. 3 E, and see Movie S2). After such a jumping event, the receptor does not return back to its initial position when the flow is stopped but consistently goes back to a new position further down along the flow for the following flow cycles. For example, in Fig. 3 D, the receptor goes back to the position of ∼−0.5 μm after the first three flow cycles and then returns to the position of ∼−1.5 μm after the next two flow cycles.

We interpret this behavior as follows: The displaced receptor encounters a flexible barrier and deforms it under the effect of the hydrodynamic drag. When the flow is stopped, the barrier returns close to its initial position pulling the receptor back with it. Once the force is too large or applied long enough, the receptor may pass over the barrier and encounter another one, which will in turn be deformed and will pull the receptor back close to the initial position of this second barrier, after the flow is stopped. This means that the positions where the receptor repeatedly returns indicate the positions of the barriers and are shown with dashed color lines in Fig. 3, D–F. The barrier positions thus determined are also highlighted in Fig. 3, A–C, and the distribution of distances between barriers is presented in Fig. 4 A. This model is summarized in Fig. S10.

Figure 4.

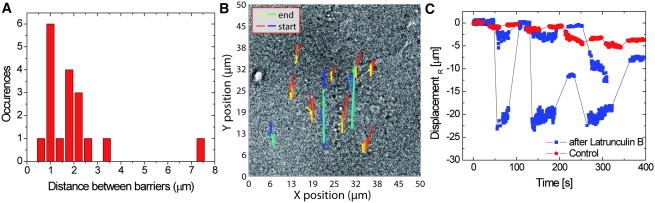
(A) Measured distance between barriers (ΔL_b, see Fig. S5) that exert a restoring force on the receptors (N = 18 measurements). (B) Receptor trajectories under a series of external forces before (red-yellow) and after (blue-green) actin depolymerization on the same cells. The beginning of a trajectory is plotted in red (blue) and the color gradually changes to yellow (green) toward the end of the trajectory for the case without (with) actin depolymerization. (C) Displacement in the flow direction for three trajectories of panel B before (red circles) and after (blue squares, two different trajectories) actin depolymerization with latrunculin B.

The elastic displacements over which the receptor returns back close to its initial position are surprisingly large. For the flow rate of 20 μL/min (flow velocity: 0.006 m/s), the receptor in Fig. 3 F returns over 7.6 ± 0.6 μm back to its initial position, after the flow is stopped. This distance is one order of magnitude larger than the average of the confining domains of 0.7 ± 0.2 μm (37). The return of the receptor close to the initial barrier position implies that the equilibrium position reached under flow corresponds to a position where the hydrodynamic drag force is equal to the restoring force that tends to bring the receptor back to its initial position.

As the flow rate increases, the hydrodynamic drag force that acts on the receptor increases linearly as: F_d = 6πηrv_flow. A higher drag force causes a larger elastic displacement of the receptor in the cell membrane by deforming the barriers. This suggests that Hooke’s law can be applied to the parts of the receptor trajectories that push against the same barrier assuming a linear relationship: kΔL. Note that this spring constant k associated with the barrier is not to be confused with the spring constant of the potential felt by the receptor inside its confinement domain in the absence of flow. For each of the barriers (colored dashed lines in Fig. 3, A–C), a linear fit of the parts of the trajectories that push against the same barrier (Fig. 3, G–I) yields an estimate of the spring constant related to the barrier. The average spring constant estimated from receptors exhibiting this elastic deformation is 2.5 ± 0.6 pN/μm (N = 17). It remains of the same order of magnitude for all the explored receptors. Note that the forces applied in our experiments (up to 8 pN) are well below those necessary to create a membrane tubule (51). In addition, the displacements observed take place in the same focal plane in contrast to what would be expected in the case of membrane tubule formation.

Barriers are actin-dependent

To determine if the boundaries are indeed part of the actin cytoskeleton, we treated the cells inside the microchannels with latrunculin B to depolymerize actin. Comparing receptor trajectories on the same cells before (red-yellow) and after actin depolymerization (blue-green) highlights the impact of the actin depolymerization (Fig. 4 B): the receptors can be displaced elastically over larger distances (Fig. 4 C), which indicates a decrease in the stiffness of the barriers. Indeed, fitting the displacement versus flow speed curves with Hooke’s law (see Fig. S11) gives an average spring constant of 0.6 ± 0.2 pN/μm (N = 5). Thus, actin depolymerization leads to a 80% decrease in spring constant, compared to the value of 2.5 ± 0.6 pN/μm (N = 17) for control cells.

In the presence of latrunculin B, the receptor is often displaced throughout the whole cell because the barriers are softer. We therefore do not have enough statistics to generate a histogram of barrier distances to compare with that of Fig. 4 A. Given the action of latrunculin B, however, an increase in the distance between barriers is probable.

Discussion

Optical-tweezer and other SMT experiments have often attributed restoring forces in the membrane to the cytoskeleton, where the spring constants were in the range of 2−10 pN/μm for directly tethered receptors (13–15). Dragging of the transferrin receptor subpopulation that is not tethered to the cytoskeleton with optical tweezers has shown that the receptor is confined by actin fences (21). When the receptor was dragged with a drag force of 0.25 pN, the fences could be deformed and stretched and the measured spring constant was 3 ± 2 pN/μm (21). This value is similar to the stiffness observed here. Moreover, we here report a decrease of the barrier-associated spring constant after partial actin depolymerization, which confirms our attribution of the restoring force to the action of actin filaments.

Furthermore, the experiments in Sako and Kusumi (21) concerned only receptors in the nonraft phase. In our case, the CPεT receptors have been shown to be confined in raft platforms (37). Our results therefore have important implications for these membrane microdomains. Indeed, the receptor motion before, during, and after application of a drag force demonstrates that the receptors are displaced inside the cell membrane along with a confining raft.

In addition, our experiments under actin depolymerization without flow have shown no modification of the confined motion parameters, indicating that the receptor is not directly tethered to the cytoskeleton (37). This absence of change upon actin depolymerization also indicates that tethering of the receptor to the actin cytoskeleton via intermediate molecules is highly unlikely, unless the interaction is very loose and does not dominate the confinement features. This fact, in combination with the small 36-kDa size of the receptor, suggests that the actin filaments do not act directly on the receptor but are probably interacting with other proteins in the same raft domain as the tracked toxin receptor. We thus deduce that the raft platform, which confines the CPεT receptors, interacts with or is tethered to the actin cytoskeleton below the cell membrane via one or more of its constituents. Thus, we interpret the data as follows: it is the raft platform containing the receptor that encounters the actin-related barriers while it is displaced through the membrane rather than the receptor itself.

Modeling the receptor displacement with the Kelvin-Voigt model

A more complete description of the receptor displacement can be obtained from the Kelvin-Voigt model of a viscoelastic material. In this model, all the reversible deformations are included in the elastic response, while all the irreversible ones are included in the viscosity of the system. Although the elastic response may include effects like elastic bending of the membrane or global shear of the cell in addition to the local elastic strain of actin filaments, we believe that the local elasticity of the actin network is the main source of the elastic response of our system, because membrane bending requires higher loads (51) and no global cell shearing is observed in white-light transmission images.

Because we are able to track the receptor during displacement, we can gather more information about the mechanics of the cell membrane and its underlying actin filament network. When we start the flow, we suddenly apply a constant stress σ = F_d/A₀, A₀ being the surface on which the drag force F_d is applied, which produces a deformation ε(t) that gradually approaches the deformation of a purely elastic material σ/E, E being Young’s elasticity modulus, with the difference decaying exponentially, as observed in Fig. 5:

$$\epsilon \left(t\right)=\frac{\Delta L}{L_0}=\frac{\sigma }{E}\left(1-e^{-\lambda /t}\right),$$

where λ = E/η is the relaxation rate, ΔL the displacement, and L₀ the initial length of the spring. Fig. 5, A and B, shows two displacement curves and their corresponding fits for a control cell and for a cell that has been incubated with latrunculin B, respectively. By fitting the deformation evolution curves as a function of time (see additional curves in Fig. S12) for various receptors and different flow values with the above equation, we extract the amplitude of the deformation curves

$$A=\frac{\sigma }{E}{L}_0=\alpha \cdot U,$$

where U is the flow rate and α captures all the physical and geometrical properties of the material and is proportional to 1/E, and the coefficient of the exponential λ. We thus obtained α = 0.35 ± 0.11 μm•min/μL (N = 6) and α = 1.04 ± 0.37 μm•min/μL (N = 5) before and after latrunculin B incubation, respectively. This implies a decrease of 70% of the Young’s modulus E and is in agreement with the decrease of 80% of the spring constant k we found above using Hooke’s law. However, the relaxation rate λ = E/η changes only from 0.54 ± 0.16 s⁻¹ (N = 6) to 0.39 ± 0.08 s⁻¹ (N = 5) which, given the decrease of E, leads to the conclusion that the viscosity η must also have decreased by 50 ± 30%. This indicates that the effective viscosity of the system η includes two components η₁ and η₂: η₁ is related to the viscoelastic properties of the actin meshwork and is reduced by F-actin depolymerization, while η₂ is the viscosity of the membrane and is unaffected by cytoskeleton destabilization, as shown by the absence of diffusion coefficient modifications in single-molecule tracking experiments (37).

Figure 5.

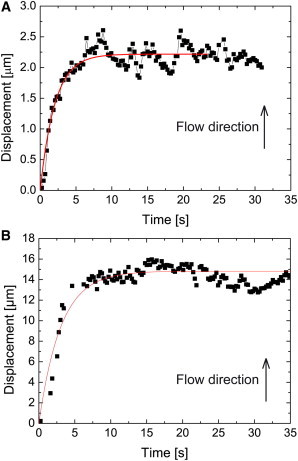
(A) Displacement of a CPεT receptor due to a flow rate of 10 μL/min (flow velocity: 0.0032 m/s), which starts at time t = 0 s. The drag force displaces the receptor until it reaches an equilibrium position where the restoring force of the actin skeleton is equal to the drag force. Note that absolute values of displacements are shown in this figure, in contrast to the data shown in Fig. 1D, Fig. 3, D–F, and Fig. 4C. (Solid line) Fit with the Kelvin-Voigt model ΔL(t) = σL₀/E(1−e^−λ/t) and gives σL₀/E = 2.22 ± 0.02 μm and λ = 0.49 ± 0.03 s⁻¹. (B) Displacement of a CPεT receptor due to a flow of 20 μL/min (flow speed: 0.0064 m/s) after latrunculin B treatment. The fit with the Kelvin-Voigt model gives σL₀/E = 7.38 ± 0.08 μm and λ = 1.2 ± 0.2 s⁻¹.

Conclusion

In this work, we introduce an intrinsically multiplexed, easy to implement, and inexpensive technique to generate drag forces on biomolecules through an enhancement of the hydrodynamic force applied by a flow via an attached nanoparticle. We applied the concept to CPεT receptors in the membrane of live MDCK cells in a microfluidic channel. We observe two types of responses: elastic deformation of barriers that hinder the displacement of the receptor and jumping events over such barriers. The restoring force of the flexible barriers brings the receptor back close to its initial condition after the flow has been stopped. Based on the fact that partial depolymerization of the actin cytoskeleton greatly increased the barrier flexibility, we attribute this restoring force to the actin cytoskeleton. We have thus been able to determine the stiffness of these actin cytoskeleton barriers and observe their softening upon partial actin depolymerization.

Moreover, our observations contribute important, apparently novel information on the motion of lipid raft platforms inside the membrane. In particular, we demonstrate that, by applying a force on the receptors, the whole lipid raft platform is dragged across the membrane. We further show that it is not the receptor itself that encounters and deforms the underlying cytoskeleton but rather one or several raft constituents that interact with the actin filament network.

The ease of implementation and inherent multiplexing of our technique render it a valuable tool for the investigation of membrane molecule interactions with the membrane and more generally of biomolecule-biomolecule interactions. Our method works for small molecules and can distinguish subpopulations, a feature inherent to single-molecule approaches. In particular, it can be used to determine k_off values that are too low to measure with standard techniques. By applying a force, the dissociation barrier can be lowered to render the dissociation rate measurable. The dissociation rate at zero force can then be determined by extrapolating the dissociation rates measured for different force values.