Nonlinear Strain Stiffening Is Not Sufficient to Explain How Far Cells Can Feel on Fibrous Protein Gels

Abstract

Recent observations suggest that cells on fibrous extracellular matrix materials sense mechanical signals over much larger distances than they do on linearly elastic synthetic materials. In this work, we systematically investigate the distance fibroblasts can sense a rigid boundary through fibrous gels by quantifying the spread areas of human lung fibroblasts and 3T3 fibroblasts cultured on sloped collagen and fibrin gels. The cell areas gradually decrease as gel thickness increases from 0 to 150 μm, with characteristic sensing distances of >65 μm below fibrin and collagen gels, and spreading affected on gels as thick as 150 μm. These results demonstrate that fibroblasts sense deeper into collagen and fibrin gels than they do into polyacrylamide gels, with the latter exhibiting characteristic sensing distances of <5 μm. We apply finite-element analysis to explore the role of strain stiffening, a characteristic mechanical property of collagen and fibrin that is not observed in polyacrylamide, in facilitating mechanosensing over long distances. Our analysis shows that the effective stiffness of both linear and nonlinear materials sharply increases once the thickness is reduced below 5 μm, with only a slight enhancement in sensitivity to depth for the nonlinear material at very low thickness and high applied traction. Multiscale simulations with a simplified geometry predict changes in fiber alignment deep into the gel and a large increase in effective stiffness with a decrease in substrate thickness that is not predicted by nonlinear elasticity. These results suggest that the observed cell-spreading response to gel thickness is not explained by the nonlinear strain-stiffening behavior of the material alone and is likely due to the fibrous nature of the proteins.

Introduction

The mechanical environment of a cell regulates its behavior and in doing so influences processes on a larger scale, such as tissue development and disease progression. These affected behaviors include differentiation, morphology, and spreading (1–3). Although important aspects of mechanosensing have been revealed, such as the role played by cell-generated tension (4–6), many details of mechanotransduction have yet to be elucidated.

Fundamental to understanding how a cell senses its environment and interacts mechanically with other cells and structures is the question of how far a cell can feel. Both computer modeling and experimental observations have demonstrated that cells are able to sense mechanical signals beyond their physical boundaries. Discher and colleagues (7) modeled the strain field between contracting cells on linear elastic substrates using finite-element analysis (FEA) and concluded that human mesenchymal stem cells (hMSCs) can sense nearby cells that are within one cell length apart (<40 μm). Experimental results of increased spreading area of hMSCs and fibroblasts on low-stiffness (1 kPa) polyacrylamide (PA) gels with decreased substrate thicknesses (8–10) are consistent with the aforementioned FEA results. Cell spread area is considered a sensitive indicator of the degree to which the cell can sense the underlying rigid substrate, as spreading is known to increase with substrate stiffness (9,11–13). Reinhart-King (14) reported a similar lateral distance of mechanical transmission (∼30 μm) for bovine aortic endothelial cells based on traction force microscopy measurements and cell-generated bead displacements 30–50 μm from the edge of cells cultured on intermediate-stiffness PA gels (2–5.5 kPa). In contrast to results for PA gels, Winer et al. (15) found that hMSCs and 3T3 fibroblasts on fibrin gels can significantly deform the gel up to five cell lengths away. Long-distance mechanosensing was also shown by Leong et al. (16), who reported a greater hMSC spread area on 130-μm-thick soft collagen gels than on 1440-μm-thick gels (8). Although it is becoming clear that cells are able to sense substantially farther both laterally and in depth on fibrin and collagen gels than on PA gels, the mechanism by which mechanical signals are propagated through protein gels is not known.

Three major differences exist between protein and synthetic gels that may explain the differences in transmission of mechanical signals. Whereas PA gels consist of polymers of small chain diameter and length relative to the scale of a cell and are linear elastic over a wide range of frequencies and strains, protein gels are viscoelastic, are fibrous in nature, and exhibit nonlinear behavior (i.e., they are strain-stiffening materials) (17). Substrate viscoelasticity, whether due to the biphasic (solid/fluid) nature of the gels or the intrinsic viscoelasticity of the fibers (18), decreases the ability of a cell to transmit mechanical signals through the matrix. Stress signals generated by cell-generated displacements relax with time, and substrate creep has been shown to reduce isometric cytoskeletal tension in mesenchymal stem cells (19). In contrast, fibers may extend stress transmission, because cell-generated traction forces may propagate preferentially along relatively stiff fibers. The strain-stiffening property of protein gels has also been hypothesized to facilitate long-distance mechanical communication between cells (15).

Our goal in this work was to characterize depth sensing of fibroblasts on protein gels and to test the hypothesis that cells can sense farther into fibrin and collagen gels than into linear materials due to the strain-stiffening material property of the protein gels. We systematically investigated fibroblast spreading on fibrin and collagen gels of variable thickness, and quantified the relationship between spread area and substrate thickness to determine the characteristic sensing distance of cells on protein gels. Because currently it is not experimentally feasible to separate strain-stiffening behavior from the fibrous nature of protein gels, we used finite-element (FE) models to numerically simulate cells by applying traction to substrates of different thicknesses and intrinsic properties, including fibrous and nonfibrous nonlinear gel models. We quantitatively analyzed the results to determine whether strain-stiffening behavior and/or fiber mechanics can explain how far cells can feel on fibrous protein gels.

Materials and Methods

Experimental studies

Gel mold design and sample preparation

Rather than creating multiple gels of different thickness, we developed a novel (to our knowledge) sloped-gel method to study cell behavior as a function of substrate thickness within the same sample. We created wedge-shaped gels by polymerizing gels between two glass slides with a spacer on one side, as shown in Fig. 1 A. To create a wedge shape, the substrate must firmly attach to the bottom glass piece, yet separate easily from the top culture surface. The lower slide to which the gel should adhere firmly was activated as described by Pelham and Wang (20). The top glass slide was left untreated because antiadhesion coatings (Rain-X, Houston, TX) and Sigmacote (Sigma-Aldrich, St. Louis, MO) were observed to affect the health of the cells. We used two No. 1 coverslips (18 × 18 mm × 150 μm; Electron Microscopy Sciences, Hatfield, PA) as spacers between the two glass slides by attaching the coverslips to the bottom slide with medical-grade silicone adhesive (Blue Star Silicones, Hoboken, NJ).

Figure 1.

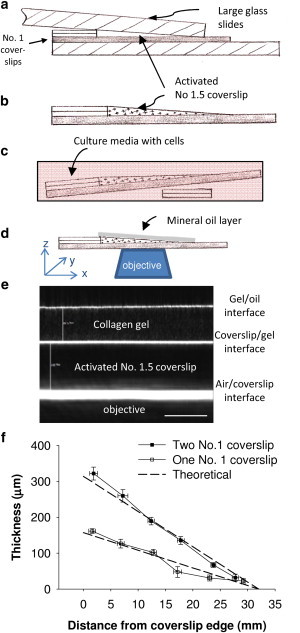
(a) Schematic of the experimental setup for creating the sloped-gel sample. The collagen or fibrin gel adheres to the activated No. 1.5 coverslip and is formed into the sloped shape by the upper large glass slide that is weighted with a 50 g object. (b) Schematic of the finished sample ready for cell seeding. (c) Samples are placed in a 100 mm petri dish and the right side is propped up with two No. 1 coverslips to ensure a level seeding surface. (d) Sample setup for imaging with mineral oil to minimize reflection at the edge of the gel. (e) Confocal reflectance image taken in cross-section mode shows the No. 1.5 coverslip between the bottom and middle white lines, and protein gel fibers with speckled pattern between the top two lines (10× dry objective; scale bar = 100 μm). The change in height (∼4 μm) cannot be readily seen over the field of view (∼400 μm) due to the gradual slope of the gel. (f) Validation of the slopes of fibrin gels created in the system using either one or two No. 1 coverslips.

We prepared fibrin gels at room temperature by polymerizing fibrinogen and thrombin (Sigma-Aldrich) with calcium as described by Balestrini et al. (21), which resulted in a cross-linked network structure. Briefly, a mixture of fibrinogen, Dulbecco’s modified Eagle’s medium (DMEM; Invitrogen, Grand Island, NY), and calcium was added to a mixture of thrombin and HBSS (20 mM HEPES in 0.9% NaCl saline solution) to bring the fibrinogen concentration to 4.5 mg/mL. After 15 min, the top glass slide was removed and the gel was allowed to polymerize for an additional 45 min in DMEM. Collagen gels were prepared with a solution of acid-extracted rat-tail tendon collagen mixed with concentrated DMEM to achieve a final collagen concentration of 4 mg/mL at 4°C to minimize polymerization during sample preparation. The gels were polymerized between the sloped glass slides after neutralization with sodium hydroxide at room temperature for ∼1 h. The schematics of a finished sample ready for use, dry, and submerged in media are shown in Fig. 1, B and C, respectively.

Cell culture

Human lung fibroblasts (HLFs, P5–P7) and 3T3-J2 fibroblasts (3T3, P7), graciously donated by Prof. George Pins (Worcester Polytechnic Institute), were cultured in DMEM with 1% streptomycin/penicillin and 10% fetal bovine serum for HLFs or 10% bovine calf serum for 3T3s, and incubated at 10% CO₂. Samples were seeded at ∼3000 cells/cm². To ensure a level substrate for the cells, the end of the sample with the thinner side of the substrate was propped up by the appropriate amount (Fig. 1 C). To make sure the cell suspension remained atop the gel, rectangular frames cut from a thin silicone sheet (0.015”; Specialty Manufacturing, Inc., Saginaw, MI) were placed on the gel immediately before cell seeding and then removed after seeding. Cells were cultured overnight (∼16 h) and then processed for imaging. HLFs and 3T3s were each cultured on collagen gels, and HLFs were also cultured on fibrin gels.

Imaging for cell area and gel thickness

Before imaging, the gels and cells were fixed with 4% paraformaldehyde for 15 min. After two 5-min rinses with PBS, the cells were stained for F-actin with phalloidin (488; Invitrogen) and incubated for 30 min at 37°C. After three 10-min rinses, the nuclei were stained with Hoechst 33342 (Invitrogen) for 3–5 min and rinsed twice with PBS.

To determine the thickness of the gel beneath the cells, an inverted confocal microscope (TCS SP5; Leica Microsystems GmbH, Wetzlar, Germany) with a 10× objective was used in reflectance mode. Rather than measuring thickness from reconstructed z-stacks in the standard imaging mode (XYZ), we utilized cross-section (XZY) imaging mode, yielding images as shown in Fig. 1 E. The bright lines are the result of differences in refractive index between the materials: the lower line is between air and glass, the next line is between the glass and collagen gel, and the top line indicates the gel/mineral-oil interface. The network of the protein gel can be seen as a speckled pattern. Due to the ratio of refractive indices of glass and air, the ratio of the true micrometer-measured distances and the image-measured distances is 1.5. This ratio was used to correct the confocal image-based gel thickness measurements. The slopes of the gels were verified by thickness measurements from confocal reflectance images taken along the length of the gel (Fig. 1 F).

We imaged FITC phalloidin-labeled cells using a Leica inverted confocal microscope with a 10× objective in fluorescence mode. We quantified the cell areas from the confocal images using the Analyze Particles tool of ImageJ (rsb.info.nih.gov/ij/) and custom MATLAB code (The MathWorks, Natick, MA). We first thresholded the images to highlight the cells, and then visually compared them with the original image to ensure that the threshold level was acceptable. Upon review of the images, areas that contained only one nucleus and were at least 50 μm away from the nearest cell were included in the quantification. In addition, the tool was set to exclude thresholded areas along the edges of the image and to include holes within closed loops.

Quantification of the relationship between cell-spread area and substrate thickness

To quantify the relationship between cell-spread area, A, and substrate thickness, h, we fit the data to a three-parameter rational equation using SigmaPlot (Systat Software, Inc., San Jose, CA):

$$A\left(h\right)=\frac{a}{1+\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$h_{50}$}\right.}+A_{\mathrm{\infty }}.$$ (1)

The parameter a is a scaling factor in units of area; larger cell types have higher a-values than those that spread more moderately. A_∞ represents the spread area of a cell on a gel of infinite thickness. The parameter h₅₀ represents the substrate thickness at which the curve reaches 50% of the maximal value over the baseline value, i.e., the spread area of cells on gels of this thickness on average is halfway between that of cells on an infinitely thick gel and cells on an infinitely thin (rigid) substrate.

Assessment of cell reorganization of fibrous structure

The extent of fiber reorganization near cells was quantified along the surface and into the depth of collagen and fibrin gels. Intensity profiles from the cells outward along 100 pixel-wide analysis regions (intensity averaged over width) were determined using ImageJ, and the distance from the edge of the cell where the intensity decayed to the background value was calculated by curve fitting in MATLAB (Fig. S1 in the Supporting Material). To quantify how deeply into the gel the fiber patterns were disturbed due to cell-mediated remodeling, we analyzed 16-bit grayscale intensity histograms of successive z-stack images spaced at 0.5 μm for the degree of normality of the data. Skewing of an intensity distribution was considered significant (nonGaussian) if the normal probability plot was linear for <80% of the data (Fig. S2; see Supporting Material for analysis details).

FE models

Linear and nonlinear elastic material models

A radially symmetric FE model of a cell exerting inward traction on the surface of a finite-thickness gel was developed based on Sen et al. (7), with cell-gel interface conditions based on Mehrotra et al. (22) and Munevar et al. (23). A constant traction along the focal adhesion area of width A (8.6 μm) was applied at a mean radius R (13.4 μm) from the axis of symmetry (Fig. S3). Six-node-modified quadratic axisymmetric triangular (CAX6M) elements were utilized, and elements ranged in number from 200 (for 0.3 μm thickness) to 8000 (for 50 μm thickness) per simulation in ABAQUS (v. 6.8; ABAQUS, Providence, RI). Elastic moduli of 0.6–40 kPa were utilized with a Poisson ratio of 0.49.

To investigate the effect of material strain stiffening on propagation of stress and strain in the substrate, we input published nonlinear mechanical properties of a 2 mg/mL fibrin gel (15) over a range of 2–100% shear strain into the FE model (see stress-strain curve in Fig. S4 A). Material models with more pronounced strain stiffening behavior were also utilized (Fig. S4, B and C). To quantify the relationship between maximum surface displacement, u_max, and substrate thickness, h, we fit the simulated data to a hyperbolic equation per Sen et al. (7):

$$u_{\mathit{max}}=\frac{u_{\mathit{inf}}\mathrm{\ast }h}{h+h_{crit}}$$ (2)

where u_inf is the saturation displacement on a semi-infinite substrate, and h_crit is a parameter indicating the substrate thickness corresponding to half-maximal displacement. Whereas u_max decreases with increasing substrate stiffness, h_crit is the same for all linear substrates in our FE model due to the linearity of the solution.

We compared the responses of substrates of different thicknesses and intrinsic properties quantitatively by calculating the effective stiffness, E_eff, adapted from Mehrotra et al. (22):

$$E_{eff}=C\frac{T}{u_{\mathit{max}}/\overline{R}}$$ (3)

where T is the radially applied traction, $\overline{R}$ is the mean radius of the focal adhesion area, and C is a scaling factor that equates E_eff to the Young’s modulus of an infinitely thick linear gel for a given set of geometric factors (R and A). For the chosen annular traction region in our FE model, C = 1.7, such that E_eff = E_gel for a 50-μm-thick linear gel. Unlike the surface displacements, E_eff is independent of the magnitude of traction applied to a linear gel.

Nonlinear fibrous model

To investigate the role of protein fibers in the propagation of stress in a fibrous substrate, we adapted a multiscale fiber-based FE model to the problem (for details, see Stylianopoulos and Barocas (24) and Sander et al. (25)). The model consists of an FE domain and a collection of microscopic fiber networks. FE domains (one element wide (4 μm), 25 elements long (75 μm), and 200, 600, or 1000 elements thick (10 μm, 30 μm, and 50 μm, respectively)) with trilinear hexahedral elements were created as simplified rectangular versions of the full radially symmetric FE model geometry described above. Two hundred unique and nominally isotropic fiber networks were created and randomly associated with an element in the model. The material properties of the fibers were selected to match the bulk material nonlinearity of a fibrin gel (15) or a collagen gel (25). Fixed boundary conditions were applied to the bottom and right faces, and symmetry boundary conditions were applied to the left, front, and back faces. The nodes on the upper surface were free, except for those in the focal adhesion area (8.6 μm long and 4 μm wide) at a mean distance of 13.4 μm from the left boundary (matching the region where traction is applied in our standard model; Fig. S3 C). The nodes associated with the focal adhesion area were displaced 2.5 μm inward (to the left), and the resulting stress field was computed. For direct comparison, a nonlinear continuum model of the same material properties, geometry, loading, and boundary conditions was created in ABAQUS as described above.

Results

Experimental results

Cell-spread area is highly dependent upon gel thickness

The cells attached and spread on the surface of the fibrin and collagen gels, with the final spread area dependent upon cell type and location along the sloped gels corresponding to thickness. We quantified cell spreading for cells cultured on sloped collagen gels, and measured the thickness below each cell using confocal reflectance cross-sectional imaging. Representative images show the difference in spread area of HLFs on thick (Fig. 2 A) and thin (Fig. 2 B) fibrin gels. The cell-spread areas span from 500 to 7000 μm², with HLFs being larger than 3T3 fibroblasts and more spread on collagen than on fibrin. Although alignment was not quantified in this study, there did not appear to be any obvious preferred alignment direction for the cells. Representative overlays of confocal fluorescence images of lung fibroblasts on confocal reflection images of underlying fibrin (Fig. 2 C) and collagen (Fig. 2 D) gels show the substantial interaction between the cells and the proteins during culture.

Figure 2.

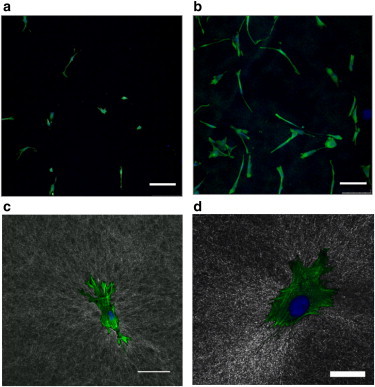
Representative fluorescent micrographs of HLFs on thick (a) and thin (b) fibrin gels used for cell area analysis (10× dry objective; scale bars = 250 μm). Actin cytoskeleton stained with phalloidin (green in color, light grey in greyscale) and nuclei stained with Hoescht (blue in color, dark grey in greyscale) after 16 h culture period. Confocal reflectance images (in standard XYZ mode) of fibrin (c) and collagen (d) gels with fluorescent stain overlays reveal local reorganization by cells, indicating stress/strain propagation through the fibrous network. (c) 20× oil objective; scale bar = 75 μm; (d) 40× oil objective; scale bar = 25 μm.

Cell areas for various positions every 5 mm along the sloped gels are shown in Fig. 3. For the thinnest gel regions that could be reliably quantified (∼20 μm), the cell-spread area was approximately the same as on the coverslip beyond the sloped gel (solid symbols at zero thickness in Fig. 3) and on the rigid control surfaces (open symbols in Fig. 3). All cell types gradually decreased in area as the gel thickness increased for both collagen and fibrin substrates. Equilibrium (minimum) area values did not appear to be reached on the thickest region that could be imaged by our equipment (150 μm), indicating that the cells can transmit mechanical signals farther than this depth in protein gels. To obtain a more robust A_∞ value, we also cultured 3T3 cells on a separate 1-mm-thick gel.

Figure 3.

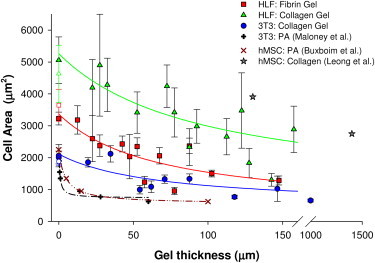
Cell spreading as a function of gel thickness for HLFs on fibrin (red squares) and collagen (green triangles) gels, and for 3T3s on fibrin gels (blue circles). Reported as mean ± SE; HLFs on collagen, mean = 9 cells per data point, n = 4 gels; HLFs on fibrin, mean = 10 cells per data point, n = 5 gels; 3T3 on collagen, mean = 20 cells per data point, n = 2 gels. Open symbols indicate control cells on tissue culture plastic. Data from the literature for 3T3 fibroblasts (+ symbols) and hMSCs (x symbols) indicate that cells on PA gels are not affected by rigid boundaries more than ∼30 μm away. On nonlinear fibrin and collagen gels, fibroblasts sense the rigid boundary on much thicker gels (>100 μm), consistent with the spread area of hMSCs on collagen gels (star symbols), and the relationship between spread area and thickness is more gradual than on PA gels.

To quantitatively assess the relationship between cell area and substrate thickness, we fit our data for the cells on protein gels and values from the literature for cells on PA gels to Eq. 1 (see Table 1 for fit parameters). The relatively large values of h₅₀ for the cells cultured on protein gels (67–94 μm) indicate a gradual spreading response to nonlinear fibrous substrates of decreasing thickness and a much larger sensing distance compared with those on PA gels, which had low h₅₀ values (0.6–4.5 μm).

Table 1.

Parameter values for rational fit of cell area versus gel thickness (A(h) = a/(1 + h/h₅₀) + A_∞)

Cell type	Substrate	a (μm2)	h50 (μm)	A∞ (μm2)	r2	Reference
HLF	4.5 mg/ml fibrin	3060	67	313	0.67
HLF	4 mg/ml collagen	4420	94	842	0.61
3T3	4 mg/ml collagen	1660	68	455	0.77
3T3	1 kPa PA	1710	0.61	737	0.97	(9)
hMSC	5.6 kPa PA	1690	4.5	556	0.99	(8)

The higher values of h₅₀ on protein gels indicate a greater sensing depth on these gels than on linear PA gels.

Cells reorganize the surrounding fibrous network

Analyses of confocal reflectance image intensity profiles indicate that the fibrous structures of the gels were substantially reorganized a minimum of 20 μm and up to 200 μm from the edge of a cell along the surface of the gels (Fig. S1). Measureable alterations of the fibrous structure were observed 7–8.5 μm into the depth of the collagen gel beneath the cell (Fig. S2). Because removal of the cells from nonfixed gels with trypsin disrupted the gel structure, we could not determine whether the dense areas emanating from the cells represent active cell-generated tension in the matrix or permanent remodeling.

FE simulations

Strain-stiffening behavior blunts stress contours and extends strain contours

The stress and strain contour plots for linear (2 kPa) and nonlinear gels of 10 μm thickness with 600 Pa of applied traction are shown in Fig. 4. The magnitudes of the stresses are similar for the linear and nonlinear materials (∼4 kPa maximum von Mises stress), yet the form of the stress field is altered in the strain-stiffening material. The extent of the stress contours is blunted compared with the linear material and there is a pinched pattern at the inner edge of the annulus where traction is applied and the stress is maximal. We confirmed that the pinched pattern was not a computational artifact by remeshing the material with both triangle and quadrilateral elements where each produced identical patterns (data not shown). The strain profiles extend further into the strain-stiffening material than into the linear material, as can be seen by the lowest contour, representing roughly 9% of the maximum strain, touching the lower boundary in the 10-μm-thick nonlinear gel (Fig. 4 D), but not in the linear gel (Fig. 4 C).

Figure 4.

(a–d) Stress (a and b; in MPa) and strain (c and d; unitless) distributions for 2 kPa linear (a and c) and nonlinear (b and d) gels of 10 μm thickness with 600 Pa traction applied. Plots for the other stiffness linear gels have different magnitude but when normalized to maximum values look identical (data not shown). The stress contours are blunted and exhibit a pinched profile in the strain-stiffening material. In contrast, the strain profiles extend farther into the strain-stiffening material compared with the linear material, as can be seen by the lowest contour, representing roughly 9% of the maximum strain, touching the lower boundary in the 10-μm-thick nonlinear gel but not in the 10-μm-thick linear gel. See Supporting Material for plots for 1, 5, and 50 μm gels.

Surface displacement values normalized to the results for the thickest gel match the displacement-thickness relationship computed by Sen et al. (7) (Fig. S5). Stress contour plots for different levels of traction are shown in Fig. S6 and peak displacements as a function of traction are given in Fig. S7. The effect of the location of application of traction on the surface is plotted in Fig. S8. Stress and strain contour plots for 1, 10, and 50 μm gel thickness with 600 Pa of applied traction are provided in Figs. S9 and S10, respectively; those for 0.3, 2.5, 5, 12, 15, and 20 μm look similar and are not shown due to space constraints. The magnitude of strain scales inversely with the material modulus, but the depth and lateral extent to which the normalized contours extend are the same for all linear materials, and thus results for only the 2 kPa gel are shown. The maximum surface displacement values for all gel thickness values and stiffness levels are provided in Table S1.

Maximum substrate displacement is lower on thinner gels

For a given level of traction, the maximum predicted displacement is lower for thin than for thick linear elastic gels due to proximity of the rigid lower boundary. The largest differences occur between 0 and 10 μm. The response saturates (negligible increase in displacement) for substrates > 50 μm thick (Fig. 5 A). The dependence of the displacement on the gel thickness is similar for the strain-stiffening material. Despite having an initial modulus of well below 1 kPa, the strain-stiffening material behaves similarly to a 2 kPa gel with a 600 Pa traction force applied (Fig. 5 A). A more nonlinear material with the same low modulus (at 10% strain) and high modulus (at 80% strain), but with stiffening occurring at higher strain values and greater curvature, was also utilized (Fig. S4 B). Similar relationships between displacement and thickness were found regardless of the degree of nonlinearity (e.g., little relative change in displacement for substrates > 10 μm; Fig. S4 C).

Figure 5.

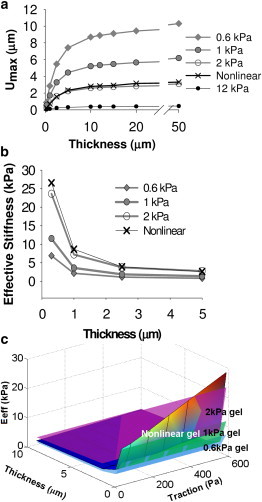
(a) For a given applied traction (600 Pa), substrate displacement decreases with decreasing thickness and increasing gel stiffness. (b) The strain-stiffening behavior causes the nonlinear material to become effectively stiffer at low thicknesses (h < 2 μm) when the applied traction is increased. (c) A surface plot of effective stiffness as a function of applied traction (100–600 Pa) and thickness (0.5–10 μm) shows that the nonlinear material (gradient colored) exhibits an effective stiffness similar to that of the 1 kPa linear material with 100 Pa applied traction, but is more stiff than the 2 kPa linear material with tractions over ∼500 Pa at low thicknesses. When viewed in greyscale, darker colors indicate lower values except immediately under the loading at the upper surface.

For a quantitative comparison of the response on the different substrates, the u_max and thickness data were fit to a hyperbolic equation (Eq. 2); parameter values are listed in Table 2. The maximum surface displacement that occurs when a cell applies a given traction may provide an indication of the stiffness that the cell feels. By inverting Eq. 3, we can calculate the thickness that yields a given displacement at an applied traction level. This analysis suggests that a cell on a 0.05-μm-thick 1 kPa gel would deflect the surface the same amount (0.1 μm) as a cell on a 13-μm-thick 40 kPa gel (see Table 2), i.e., these two substrates would have the same effective stiffness to the cell. The calculated effective stiffness values (Eq. 3) decrease rapidly from 0 to 2.5 μm thickness, and saturate to a value close to the bulk stiffness for substrates thicker than 5 μm (Fig. 5 B). The nonlinear material behaves similarly to the 2 kPa gel down to 2.5 μm thickness, and has a slightly higher effective stiffness for substrates <2.5 μm thick. The effects of both applied traction level and thickness on effective stiffness are shown as a surface plot in Fig. 5 C, where it can be observed that the nonlinear gel becomes effectively stiffer than the 2 kPa linear gel for T > 400 Pa and t < 2.5 μm.

Table 2.

Fit parameters for a hyperbolic relationship (u = u_infh/(h + h_crit)) for the FE data in Fig. 5A and calculated thickness, h(0.01 μm), corresponding to a maximum surface displacement of 0.1 μm

FE model	E (kPa)	Applied traction (Pa)	uinf (μm)	hcrit (μm)	h (0.1 μm)
Linear	1	400	4.72	2.41	0.052
	5	400	0.94	2.41	0.29
	12	400	0.39	2.41	0.82
	40	400	0.12	2.41	13.3
Nonlinear		400	2.90	3.26	0.12
		600	3.61	3.19	0.09

Effective stiffness is more sensitive to gel thickness for the fibrous model

The propagation of stress (Fig. 6 A) and strain (Fig. 6 B) through the fibrous model is qualitatively and quantitatively different from that observed for the nonlinear continuum model. The simulated fiber population, which is initially uniform, reorients toward the displaced region on the surface, and a substantial change in the degree of fiber alignment is observed through the depth of the 10 μm model (Fig. 6 C) and extends >20 μm through the gel (Fig. 6 C, inset). The predicted fiber network realignment was somewhat less extensive in the 30 and 50 μm models (Fig. S11). Despite exhibiting the same bulk tensile stress-strain behavior, the magnitudes of stress in the multiscale model are two- to fourfold lower than observed for the continuum model. Addition of an isotropic incompressible matrix supporting the fibers would likely increase the stress in the model to the level of the continuum model. For direct comparison, the results of each model are presented relative to the output for the thickest model of each type. The normalized analysis reveals that the dependence of effective stiffness on thickness is more pronounced for the fibrous models than for the continuum nonlinear model. Relative to the 50-μm-thick model, the effective stiffness of the 30-μm-thick model is 50% higher in the fibrous fibrin model but only 2% higher in the continuum model. For the 10-μm-thick model, the effective stiffness values are 125% and 29% higher than the 50-μm-thick model for the fibrous fibrin and continuum models, respectively (Fig. 6 D). The use of parameters matching those of a collagen gel had a less pronounced effect on the effective stiffness-thickness relationship than the fibrin gel model, with an 85% increase at 10 μm and a 20% increase at 30 μm relative to the 50 μm model.

Figure 6.

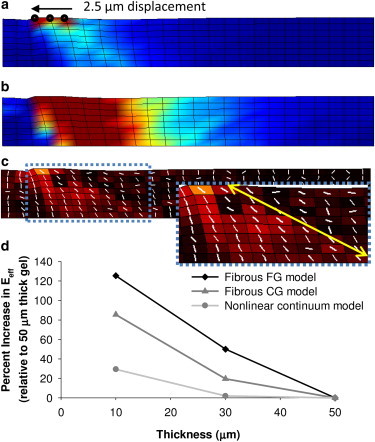
(a and b) Fibrous multiscale model results for the 10-μm-thick case indicate that stresses (a) and strains (b) propagate throughout the thickness of the substrate. (c) The change in degree of orientation from initially random to aligned is greatest at the surface and extends to areas near the lower boundary that are >20 μm away from the point of deformation at the surface (indicated by the arrow in c, inset). (d) The effective stiffness (proportional to peak stress/displacement and normalized to the 50-μm-thick case) is much greater for the 10- and 30-μm-thick fibrous models than for nonlinear models with identical loading, geometry, and nonlinear bulk mechanical properties, indicating a greater impact of the rigid boundary in the fibrous model. The simplified model is 75 μm long and one element in depth (4 μm), with 2.5 μm displacement applied over a small area on the top surface as indicated in panel a. Due to differences in geometry, results are not directly comparable with the radially symmetric model results in Fig. 4. Scale factors: (a) 0–100 Pa von Mises stress; (b) 0–0.1 engineering strain; (c) 0–1.0 change in degree of fiber alignment. When viewed in greyscale, darker color indicates lower stress in (a and c), and darker color indicates lower strain in outer areas but higher strain in the central region under the loading in (b). Fibrin gel (FG); collagen gel (CG).

Discussion

In this work, we systematically investigated the distance fibroblasts can feel through fibrous gels by quantifying the spread areas of HLFs and 3T3s as a function of collagen and fibrin gel substrate thickness. The cell areas gradually decreased as gel thickness increased, with the half-maximal spread area of cells on fibrin and collagen gels (h₅₀ > 65 μm) being much larger than published values for PA gels (h₅₀ < 5 μm). These results demonstrate that fibroblasts sense much deeper into nonlinear collagen and fibrin gels than they do into linear PA gels. These long sensing distances are consistent with previous observations of surface displacements hundreds of microns from cells cultured on thick fibrin gels (15), strain transfer up to 800 μm through a collagen gel (26), and increased spreading behavior on soft collagen gels >130 μm thick (16). Our nonlinear continuum model predicts increases in the effective stiffness that the cell feels only for very low thickness substrates (<5 μm) indicating that the spreading behavior on thick gels cannot be explained by the strain-stiffening behavior of the material alone. Results from our multiscale model demonstrate substantial changes in effective stiffness at relatively large thicknesses (e.g., 50% greater at 30 μm than at 50 μm), suggesting that the fibrous nature of the network enhances depth sensing in collagen and fibrin gels.

In addition to enhancing our understanding of how far cells can sense each other through their extracellular matrix (ECM), the use of rigid boundaries has great potential for creating experimental systems to study the effect of stiffness on cell behavior. For example, Yip and colleagues (2) observed valvular interstitial cell activation to the myofibroblast phenotype (known to be stiffness dependent) on thin collagen films but not on thick collagen gels. Utilizing this approach to modulate the effective stiffness that cells sense has advantages relative to modulating the intrinsic stiffness ECM-based gels (collagen, fibrin, Matrigel, etc.) because it avoids changes in ligand density and presentation that occur when the protein concentration and/or cross-linking are altered. However, for this approach, one must obtain reliable estimates of the effective stiffness as a function of substrate thickness.

Determining how far cells feel on biopolymer gels

To investigate how far cells can feel through compliant gels, we chose to determine how far into the depth of a gel a cell can sense rather than to analyze lateral cell-cell communication along a substrate, as done previously (27). For high-throughput and self-consistent controls, we utilized variable-thickness gels instead of attempting to control the thickness of individual gels; based on our simulations, the gradient in effective stiffness on these gels is minimal due to the low slope (see Supporting Material). Collagen and fibrin gels are used as model strain-stiffening materials with different fiber structures and degrees of nonlinearity.

In contrast to the rapid decrease in area of cells cultured on progressively thicker PA gels up to a few microns reported in the literature (8,9), our data demonstrate that the rate at which the cell area decreases with increasing thickness of the protein gels is very gradual. Quantitatively, the characteristic sensing distance, h₅₀, is >10-fold larger for protein gels than previously reported for PA gels. The relatively small cells from the immortalized 3T3 line responded almost identically to the primary HLFs, with curves overlapping when normalized to the spread area of control cells on glass (normalized graph not shown). The simple rational equation (Eq. 1) fits the published data very well (r² > 0.9) and our data relatively well (r² = 0.61–0.77) without overparameterization. We attribute the lower correlation values for biopolymer systems to the heterogeneity of fiber polymerization, rather than to the choice of regression model. Exact values of h₅₀ should be interpreted cautiously, however, because the minimum spread area is not generally reached in published data (9) or in our experimental groups due to limits on confocal working distance (∼150 μm). Despite these limitations, it is clearly evident that cells are able to sense rigid boundaries much farther into collagen and fibrin gels than into linear PA gels.

Current analytical and computational models of cells on gels (including our nonlinear continuum model) predict a decrease in surface displacement with thickness for a given surface traction (7,9,22). The most pronounced changes are predicted on substrates <5 μm thick regardless of substrate stiffness (28), which is consistent with an increase in effective stiffness and observed cell area (8–10). These models do not predict the more gradual change in cell area in the 5- to 30-μm thickness range observed on PA gels or the very gradual change in cell area in the 20-150 µm thickness range on protein gels observed in this study.

Testing the hypothesis that long sensing distances are due to strain stiffening

It is difficult to experimentally separate material nonlinearity from the fibrous nature of the protein gel network; therefore, we computationally investigated the effect of strain stiffening on cell mechanosensing. We used FE models of different material properties and thicknesses to compute the maximum surface displacement that results from a given traction field. From the many metrics for quantifying the distance into a substrate a cell can feel (see Maloney et al. (9) for a tabulated list), we chose to utilize the critical thickness h_crit, which is analogous to h₅₀ in our analysis of measured cell-spreading data. The value for linear gels of 2.41 μm is in the range of previously reported values from other linear models (h_crit ∼1.3–3.3 μm) (7). For the nonlinear gel, the characteristic sensing distance is 35% greater (h_crit ∼3.3 μm) due to greater propagation of strain, and it decreases slightly with traction applied (Table 2); however, the critical sensing distance is still far lower than observed for protein gels experimentally. Analysis of the effective stiffness from the nonlinear FE model (Fig. 5, B and C) also indicates that strain-stiffening behavior representative of a fibrin gel has little effect on the resistance to deformation that the cell senses at the surface for gels greater than a few microns thick.

The material model we utilized in our continuum model simulations was based on available shear stress-strain data from Wen and Jamney (17) for 2 mg/ml fibrin gels. Instead of simulating different polymer concentrations in our model to determine the effect of nonlinearity, we simulated different materials (e.g., collagen) by altering the degree of strain stiffening with a shift to higher transition strain (29). These simulations predict an increase in the magnitude of u_max, shifting the response from one that is similar to a 2 kPa linear gel to one that is similar to a 1 kPa linear gel, but with virtually no change in sensitively to thickness (Fig. S4 C). Higher protein concentration increases the gel stiffness, which would decrease the magnitude of u_max but would not be expected to alter the value of h_crit. The minimal change in h_crit for the model with altered nonlinearity is consistent with recent analyses by Hart and colleagues (30). Their FE models of cell interactions on strain-hardening (stiffening) substrates indicate that the propagation of stresses through the substrate is not increased when the parameters of various nonlinear material models are varied over a very large range. Taken together, these results suggest that characteristics other than nonlinearity, such as the fibrous structure, facilitate propagation of mechanical signals through protein gels and result in the observed cell-spreading behavior on relatively thick collagen and fibrin gels.

Gel fibrous structure likely facilitates long-distance sensing

Due to their high stiffness relative to synthetic PA chains (17), collagen and fibrin fibers are considered as semiflexible filaments or rigid rods with persistence length comparable to fiber length. The lengths range from a few hundred nanometers to micrometers, and are largely determined by the polymerization condition such as pH and ionic strength. Fibrous networks formed through cross-links between fibers (such as in our fibrin gels) or through noncovalent bonds and entanglements (such as in our collagen gels) enhance cell spreading. Winer et al. (15) reported that both fibroblasts and hMSCs spread to a much greater extent on compliant PA gels coated with networks of fibrin compared with gels coated with monomers or filaments of fibrin. We have also observed more pronounced spreading of fibroblasts and heart valve interstitial cells cultured on compliant PA gels when acid-extracted (telopeptide-rich) collagen was utilized as a coating rather than acidic pepsin-extracted collagen, which is less likely to form fibrous networks (A.M. Quinlan and K.L. Billiar, unpublished). Further, given sufficient time, cells cultured on and within protein matrices remodel the protein (15,31,32), which may locally stiffen the protein gel. Thus, the fibrous network at the surface likely explains the relatively large spread area on the soft, thick protein gels, but the existence of surface fibers cannot explain the dependence of cell area on gel thickness in the range of tens to hundreds of microns.

Possible explanations for the long-range propagation of forces and/or displacements include the rod-like structure of the proteins with high bending stiffness and the interconnected network structure of the fibers. Our analysis of confocal reflectance images indicates that the cells are able to reorganize the surrounding fibrous network structure of both fibrin and collagen gels up to 200 μm along the surface of the gels. These changes in local reflectance intensity suggest long-range stress and/or strain transfer through the gel, which may extend even farther than we can optically resolve. In 1959, Weiss (33) observed long-range fiber reorganization between groups of cells in fibrin gels, and Stopak and Harris (34) demonstrated centimeter-scale fiber tracts between cell explants cultured on collagen gels three decades ago. Similar local densification around cells cultured within collagen gels has been shown to lead to nonuniform compaction with profound effects on the bulk mechanics of the gels (35). In contrast, in our study, local densification was evident in z-stack images only a few microns below the cells. The lack of visual changes in fiber organization in the XY optical cross-sections may be attributed to orientation of the fibers out of the plane of the images, as predicted by the fibrous FE model (Fig. 6 C), and/or to insufficient optical resolution.

The results of the fibrous model indicate that the principal fiber directions extend from the displaced region representing the cell toward the rigid lower boundary at a diagonal (Fig. 6 C). The model also predicts substantial changes in fiber orientation >20 μm into the depth of the gel (Fig. 6 C, inset). In contrast, our linear and nonlinear models indicate that stresses decay to <10% of maximum values by <8 μm (Table S2), and previous models predict that a rigid surface under an elastic substrate several micrometers or more thick would be undetectable by adherent cells (22). The extensive fiber reorganization in the fibrous model may explain the large change in effective stiffness as gel thickness decreases below 50 μm that is not evident in the nonlinear continuum model (Fig. 6 D). The multiscale modeling approach is a powerful tool for analyzing the propagation of cell-generated mechanical signals through fiber networks. In future studies, fiber parameters such as length, stiffness, and distance between network interconnections can be investigated computationally to determine the effect on stress propagation.

In light of the differences in nonlinear behavior (29) and fibrous network structure of collagen and fibrin gels, the characteristic sensing depths are surprisingly similar for these two protein systems. Collagen and fibrin gels differ in their fiber diameter, fiber length, and architecture. At comparable protein concentrations, the collagen fibrils are found to have larger diameter and greater lengths than the fibrin fibers (32). The fibers in collagen gels are held together through physical entanglements, in contrast to the fibrin fibers, which are covalently bonded together to form a strong elastic network. To determine the key physical properties that govern the distance that cells sense in the fibrous matrix, there is a need to systematically control fiber parameters that are known to alter strain transmission, including fiber diameter, fiber length, and cross-linking density, by varying the polymerization conditions (36).

Conclusions

The data from this study demonstrate that cell-induced mechanical signals can transmit hundreds of microns within collagen and fibrin gels and feedback on cell behavior. The continuum FE analyses indicate that the strain-stiffening property of the protein gels is not sufficient to explain the observed behavior. Multiscale models with simplified geometry indicate that fiber realignment plays a large role in stress transfer through the matrix, and the development of models with fibrous elements of various geometry and properties will enable us to further investigate potential mechanisms of stress and strain transfer within protein gels and native ECM. Future experimental work is also needed to determine the effect of fiber parameters, including fiber diameter, fiber length, and cross-linking density, on distance sensing in protein gels. With this knowledge, we will be able to use thin fibrous gels as experimental test beds in which to study cell differentiation, signaling, and other stiffness-dependent biological processes in a native ECM environment. The results of this study shed light on the role of matrix mechanics in regulating cell-cell communication, which is fundamental to understanding wound healing, angiogenesis, and the organization of connective tissues in general. These topics are of critical relevance to tissue engineering and developmental biology.