Abstract
In the field of metallic materials with amorphous structures, it is vitally important to understand the glass formation and to predict glass-forming ability (GFA) in terms of constituent elements and alloy compositions. In this study, an expression has been formulated from first-principles calculations to predict the trend of GFA by hybridizing both internal energies and atomic-scale defect structures. The prediction of GFA from compositions has been verified successfully by available experimental data in the model Zr-Cu alloy system. The physical scenario revealed here has extensive implications for the design of bulk metallic glasses with superior GFA.
Bulk metallic glasses (BMGs), a new emerging class of metallic materials, have attracted extensive interest recently, due to their unique mechanical and physical properties1,2, including extremely high strength, large elastic strain limit, good corrosion resistance, and superior soft magnetic properties. In spite of these promising properties, their widespread applications are hindered primarily by their limited glass-forming ability (GFA) and high production cost for most common alloy systems, which are the major obstacles to the economic manufacture of these materials for industrial applications at present. For the past decades, considerable efforts have been devoted to exploring the GFA of BMGs and many criteria have been proposed to estimate the GFA3,4,5,6,7; however, most of them are essentially based on phenomenological and thermodynamic considerations. Furthermore, most of the criteria were developed based on the characteristic temperatures of alloys, which could be measured only with the premise that the alloy has been made into glass state already. So far, there is none that is capable of predicting the GFA only from constituent elements and alloy compositions. As a consequence, the conventional trial and error methods have been used extensively as the major approach in searching for new BMGs to date. The prediction of the trend of GFA from alloy compositions alone remains a scientific challenge in the BMG community.
From a physics point of view, glasses are metastable phases in an excited state; however, the metallic glasses with good GFA can exist at ambient temperatures for a long time without crystallization. To study the stability of the amorphous phase, the thermodynamic parameters commonly used for equilibrium states are applied. The thermodynamic stability of a system at the constant temperature and pressure is determined by its Gibbs free energy, G, defined as G = H − TS, where H is the enthalpy, T is the absolute temperature and S is the entropy. Since the contribution from entropies is much smaller as compared with that from the enthalpies of solid compounds, the entropy contribution can be neglected8. Thus, the enthalpy difference between the amorphous phase and its competing crystalline phases becomes a measurement for their relative stability of the two phases. In the late 1980s, considering the resistance of glass formation against crystallization, the formation enthalpy difference between the amorphous phase and the random solid solution counterpart had been used as a criterion to determine the glass-forming range by using data from the semi-empirical Miedema's model9,10,11. This was extended by Xia to assess the GFA in specific binary systems through γ* parameter12,13,14, where the higher γ* means the higher driving force for glass formation and the higher resistance against crystallization. In other words, a large value of γ* is in favor of GFA from a thermodynamic point of view.
The above approach does not specially concern the kinetic factors, which are believed to have a significant effect on glass formation15. A glass state can be, in principle, achievable for any alloy systems if the cooling rate is high enough to exceed their critical cooling rate, at which the nucleation and growth of crystalline phases can be suppressed. As the critical cooling rate is difficult to measure experimentally, various parameters were introduced into the study of kinetic effects on glass formation. Among them, the atomic structure features, which intrinsically affect the kinetic processes, have a pronounced influence on GFA. The relative population of some densely packed clusters, such as the Cu-centered full icosahedra with a Voronoi index of <0,0,12,0> and Zr-centered clusters <0,1,10,4>, <0,1,10,5> have been proven to influence the dynamics of Zr-Cu glass-forming liquids significantly16,17. Since the atomic configuration of MGs contains both densely packed and loosely packed structures, and excessive atomic space is expected to exist in the loosely packed structures, it is generally accepted that the overall atomic mobility in MGs is strongly related to the amount of their excessive atomic space18,19,20. Lower excessive atomic space in the supercooled liquids means more densely atomic packing and lower atomic mobility, which makes crystallization processes more difficult because of the slow diffusion of atoms. With this regard, in the present study, the total excessive atomic spaces in the system have been derived from a benchmark configuration to consider the contribution of the “defect structure” to GFA (see below for details).
In this work, by considering both of the thermodynamic and kinetic features carefully, a simplified expression has been proposed to predict the trend of GFA in the model ZrxCu1−x binary alloys system, which shows good GFA among binary alloy systems and sensitive composition-dependence of GFA. The prediction was based on first-principles (FP) density functional theory (DFT) modeling. Accurate values of the parameters in the expression were obtained from first-principles (or ab-initio) molecular dynamics (FPMD) simulations and first-principles static calculations. As compared with experimental measurements, the computer calculation is more powerful and readily to determine these parameters21,22.
Results
As higher value of γ* and lower excessive atomic space in the system both have a close correlation with the ease of glass formation, a simplified relationship can be thus expressed as follows:
where γ* represents the thermodynamic effect12, which can be calculated by 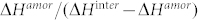 , and
, and 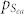 represents the kinetic effect which can be estimated in terms of ratio of the total excessive atomic spaces Sea (the exact definition of this term is given in equation (3)) by the total atom volume Vtot in the supercooled liquid near Tg. Obviously, a high value of γFP facilitates the glass formation from both thermodynamic and kinetic points of view in a given system. The ΔHamor and ΔHinter can be readily calculated by the equation:
represents the kinetic effect which can be estimated in terms of ratio of the total excessive atomic spaces Sea (the exact definition of this term is given in equation (3)) by the total atom volume Vtot in the supercooled liquid near Tg. Obviously, a high value of γFP facilitates the glass formation from both thermodynamic and kinetic points of view in a given system. The ΔHamor and ΔHinter can be readily calculated by the equation:
where E, EZr, and ECuare the internal energies per atom for the ZrxCu1−x alloy, pure hcp Zr and fcc Cu, respectively.
The excessive atomic spaces Sea in the system was estimated by an improvement of the method proposed by Liu et al.18 Firstly, an ideal polyhedron with certain coordination numbers (named as Nic) around a central atom is regarded as a benchmark configuration without any Sea. Then, those atoms with coordination numbers (CNs) exceeding Nic are expected to have no excessive atomic spaces because of their even denser packing, and those with CNs less than Nic are considered to have defected bonds with a certain degree of excessive space associated with atoms. In the previous definition, Nic was assumed to be 12 for an ideal icosahedron. In the real case of Zr-Cu alloys, however, Nic could be lower than 12 in the Cu-centered clusters when Cu concentrations are relatively low, because of the atom size difference between the Cu and Zr atoms; Similarly, Nic around Zr will vary from 14 to 15 with different Cu (Zr) concentration. To address this issue, we specified the Nic in Cu- and Zr-centered clusters respectively for each composition. Voronoi tessellation analysis23 was performed to obtain the average CNs for Cu (Zr) centered clusters in each composition, and then Nic was taken as the nearest integral number to the corresponding average CN. Since we just focus on the distribution of Sea in the system, the shape coefficient is not discussed here, and then by aggregating the Sea around every Cu (Zr) atom in the system, the value in the Cu (Zr)-centered clusters can be defined by18:
And thus,
where Rij is the actual distance from the central atom i to the coordination atom j, rijis the cutoff radius, ni is the coordination number of atom i, m is the total number of Cu (Zr) atoms in the system, and Nic is the coordination number of the benchmark configuration with Cu (Zr) atom in the center.
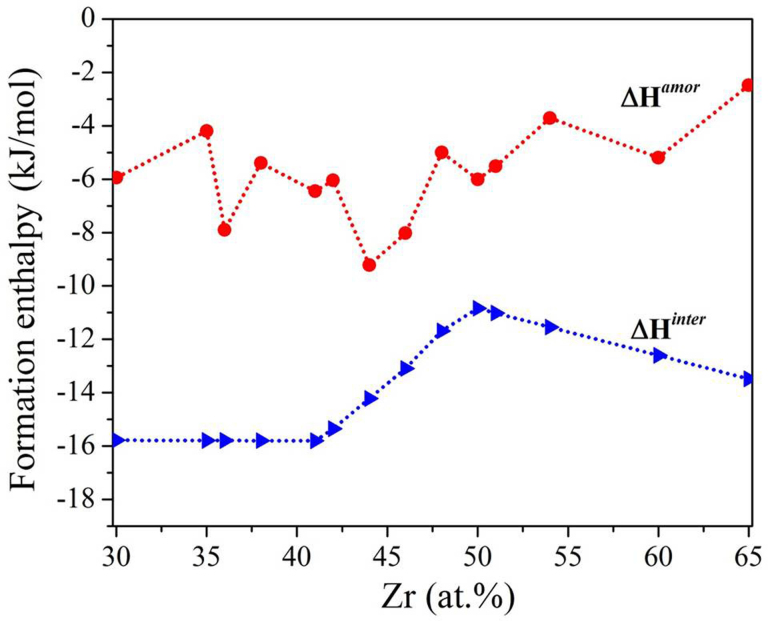
In view of the fact that the formation enthalpy of the assumed solid solution (ΔHs.s.) is much higher than that of the amorphous phase in ZrxCu1−x alloys within a wide composition range 7 < x < 90 at.%12, so it is not considered as the competing phase and not calculated here. The ground state formation enthalpies for glasses (ΔHamor, where the amorphous state was obtained by FPMD simulation) and intermetallic compounds (ΔHinter), in ZrxCu1−x alloys can be readily obtained based on the internal energies calculated by first-principles static calculations. The formation enthalpy of a composition locating between two adjacent intermetallic compounds was calculated using the lever principle. From the calculated results as shown in Fig. 1, it is noted that there are two distinct large valleys, locating at 36 and 44 at.% Zr, respectively, in the curve of ΔHamor. Moreover, there are three relatively small values, corresponding to the Zr concentration of 41, 50 and 60 at.%, respectively. The data indicate these alloys have a higher glass formation driving force than the other alloys. It should be noticed that, five BMG compostions (i.e., 35.5–36, 40, 44, 50, and 54–55 at.% Zr) were reported previously24,25,26,27,28,29, among which the Zr50Cu50 is the best one (with a critical diameter of fully amorphous rods ≥2 mm)12,28. Interestingly, our valley compositions seem close to the reported ones. However, the Zr50Cu50 alloy is not the best glass former in terms of the calculated ΔHamor, implying that the high GFA of this alloy may come from the phase competition between the amorphous phase and the intermetallic counterparts during glass formation as well as kinetic factors.
Figure 1. Formation enthalpies of amorphous and intermetallic phases as a function of Zr concentration in Zr-Cu binary alloys.
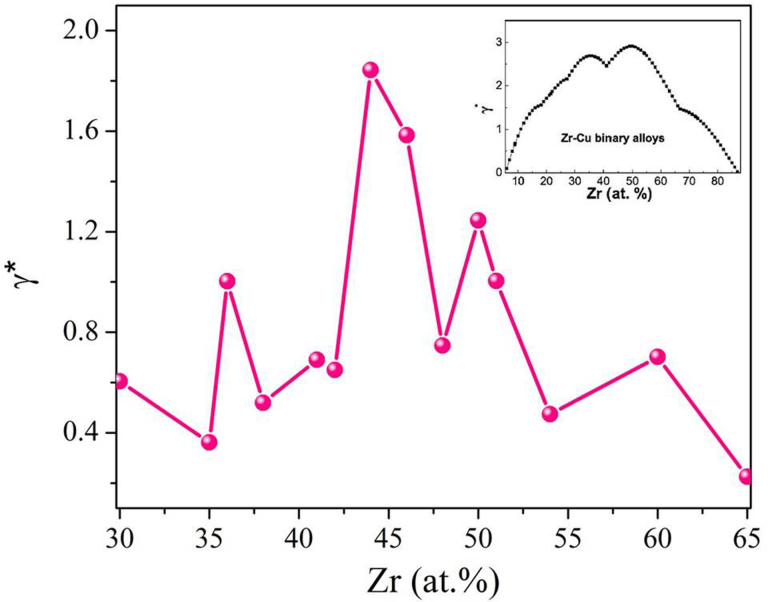
By adding the consideration of the resistance of glass formation against crystallization, the γ* parameter [ΔHamor/(ΔHinter − ΔHamor)] proposed by Xia et al.12 was calculated and shown in Fig. 2 as a function of the Zr concentration. Three distinct peaks at x = 36, 44, 50 at.%, and two small peaks at x = 41 and 60 at.% were observed respectively, which are different with the results obtained from the Miedema's model. Evidently, this comparison indicates that our FP calculations of γ* have a better agreement with the experimental data. Nevertheless, the best glass former is the Zr44Cu56 alloy rather than the Zr50Cu50 alloy if one gauges the GFA according to this calculated γ* value, which is still not consistent with experimental results. Thus, the calculation based on the thermodynamic consideration alone is insufficient to estimate GFA accurately. In the following part we will introduce the kinetic factor into the new criterion from the atomic structural perspective and show how it affects the GFA.
Figure 2. Dependence of γ* on Zr concentration in Zr-Cu binary alloys.
(The inset is γ* parameter calculated by Miedema's model (Ref. 12)).
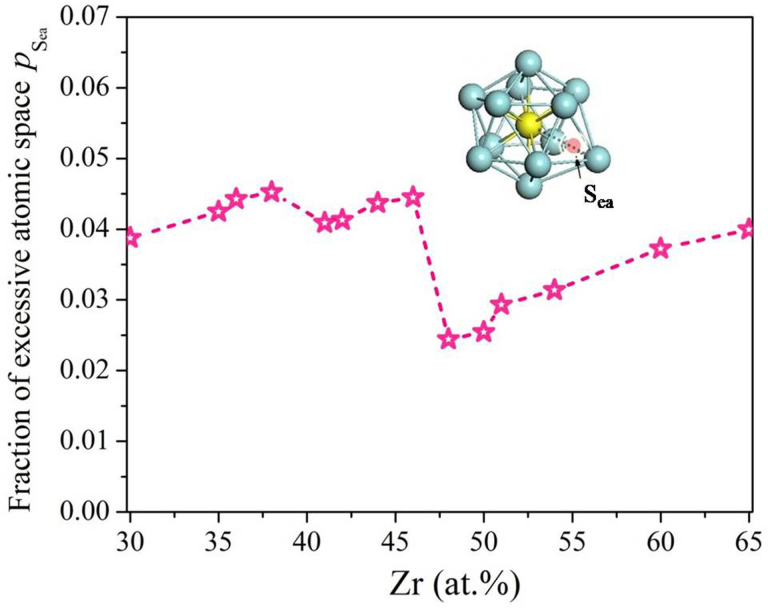
As we discussed above, lower excessive atomic space indicates more dense atomic packing and lower atomic mobility, which makes the formation of crystal phases more difficult; therefore it can be treated as a kinetic factor affecting GFA. Specifically, we calculated the proportion of the total system spaces occupied by the excessive atomic spaces 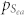 in the supercooled liquid near Tg for all of the alloys based on Eqs. (3) and (4). The results in Fig. 3 indicate two local minima of
in the supercooled liquid near Tg for all of the alloys based on Eqs. (3) and (4). The results in Fig. 3 indicate two local minima of 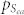 at 41 at.% Zr and 48 at.% Zr, respectively, implying these two alloys could be good BMG formers. They are very close to the Zr40Cu60 and Zr48.5Cu51.5 BMG formers in previous experiments26,30; however, the prediction of BMG formers from this sole factor can not cover all the reported BMG compositions determined from experiments. The logical thought is to incorporate the kinetic factor with the thermodynamic effect to make a synergic effect.
at 41 at.% Zr and 48 at.% Zr, respectively, implying these two alloys could be good BMG formers. They are very close to the Zr40Cu60 and Zr48.5Cu51.5 BMG formers in previous experiments26,30; however, the prediction of BMG formers from this sole factor can not cover all the reported BMG compositions determined from experiments. The logical thought is to incorporate the kinetic factor with the thermodynamic effect to make a synergic effect.
Figure 3. Dependence of excessive atomic space proportion on Zr concentration in Zr-Cu glass-forming supercooled liquids.
(The inset is the schematic picture of excessive atomic space definition when Nic = 12 (Ref. 18)).
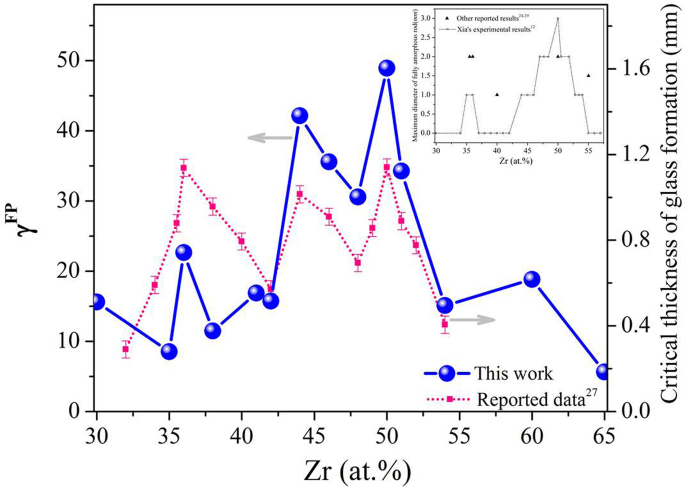
From the illustration above, the thermodynamic and kinetic considerations are capable of quantitatively predicting GFA; however, it is obviously that neither of them alone is sufficient to determine GFA. Therefore, a synergic expression 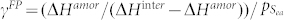 has been proposed here to predict the trend of GFA accurately. The proposed γFP is plotted as a function of Zr concentration and shown in Fig. 4 together with various experimental data reported previously. There are three sharp peaks for γFP at x = 36, 44 and 50 at.%, respectively, clearly suggesting relatively high GFAs of these alloys. The optimum compositions are similar as those from the thermodynamic consideration, but the peak value is located at Zr50Cu50 once the kinetic effect is included. The kinetic effect from the structural aspects certainly plays an important role in the predicting of GFA, even though the thermodynamic parameter is dominant. As indicated in Fig. 4, the three optimum glass formers predicted by our proposed criteria have a good agreement with the experimental observations reported recently by Li et al. and Bendert et al.27,31 Also, the calculated curve in Fig. 4 match well with other reported experimental data in the inset, showing the four distinct BMG compositions (35.5–36, 40, 44, 50 at.% Zr) with Zr50Cu50 as the best one24,25,26,27,28,29.
has been proposed here to predict the trend of GFA accurately. The proposed γFP is plotted as a function of Zr concentration and shown in Fig. 4 together with various experimental data reported previously. There are three sharp peaks for γFP at x = 36, 44 and 50 at.%, respectively, clearly suggesting relatively high GFAs of these alloys. The optimum compositions are similar as those from the thermodynamic consideration, but the peak value is located at Zr50Cu50 once the kinetic effect is included. The kinetic effect from the structural aspects certainly plays an important role in the predicting of GFA, even though the thermodynamic parameter is dominant. As indicated in Fig. 4, the three optimum glass formers predicted by our proposed criteria have a good agreement with the experimental observations reported recently by Li et al. and Bendert et al.27,31 Also, the calculated curve in Fig. 4 match well with other reported experimental data in the inset, showing the four distinct BMG compositions (35.5–36, 40, 44, 50 at.% Zr) with Zr50Cu50 as the best one24,25,26,27,28,29.
Figure 4. Dependence of the parameter γFP on Zr concentration ( ) and critical thickness of glass formation (
) and critical thickness of glass formation ( , taken from Ref. 27) in Zr-Cu binary alloys.
, taken from Ref. 27) in Zr-Cu binary alloys.
(The inset shows the maximum diameters of Zr-Cu rods with a fully amorphous structure, taken from Ref. 12 and 24,25,26,27,28,29).
Discussion
From the results illustrated, it can be seen that the proposed expression based on first-principles DFT calculations can predict the trend of GFA in the Zr-Cu system just from alloy compositions. Furthermore, our calculations have successfully predicted a sharp change of GFA between Zr35Cu65 and Zr36Cu64 alloys, which is unambiguously verified by the experimental data. The close predication and consistency with the experimental results certainly prove that the parameter γFP is effective in predicting the trend of GFA. In order to interpret the sharp change of GFA between Zr35Cu65 and Zr36Cu64 metallic glasses from the intrinsic atomic structure features, Honeycutt-Andersen bond pair analysis32 has been employed to characterize the atomic bonding behavior. It is interesting to find out that the amount of 1551-type bond pair, which represents a close-packed icosahedral ordering, increases sharply, from 23.1% in the Zr35Cu65 to 32.9% in the Zr36Cu64, due to the only 1% increase in the Zr concentration. This dramatic enhancement of the icosahedral ordering structure may be responsible for the higher GFA of Zr36Cu64.
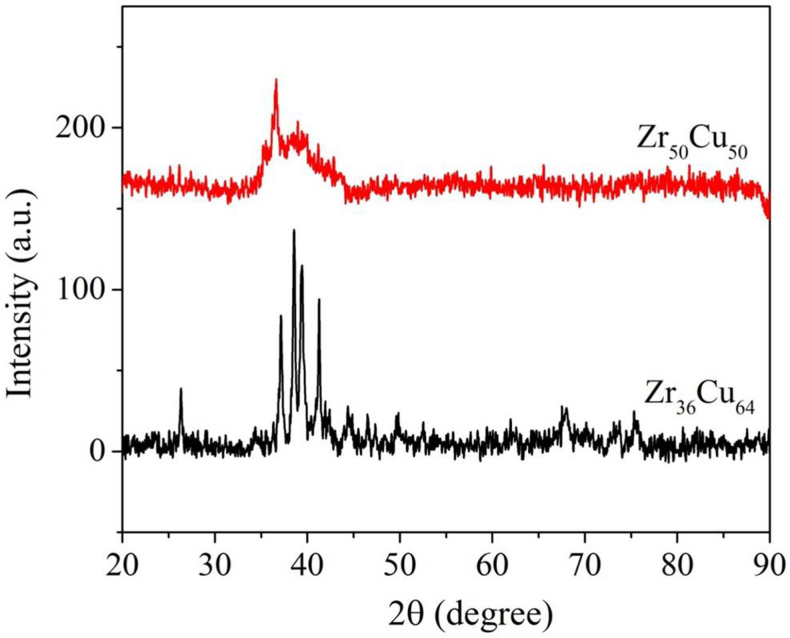
The γ* results based on the Miedema's model12, as shown in the inset of Fig. 2, and the experimental results shown in Fig. 4. from Li et al.27 indicate that both compositions of Zr36Cu64 and Zr50Cu50 have good and comparable GFAs. On the other hand, the prediction by our first-principles calculation in Fig. 4 suggests a significant difference in GFA of these two compositions. It is known that the experimentally measured GFA can vary to a certain extent due to the effects of alloy compositions, impurity levels and preparation methods. In order to verify the difference of the predictions by the first-principles and Miedema's methods, we had prepared the alloys with these two compositions, using the same method and starting materials to reduce possible experimental errors. As shown in Fig. 5, the XRD patterns of the Zr36Cu64 and Zr50Cu50 alloys clearly indicate that the structure for the as-cast Zr50Cu50 sample with a size of 2 mm in diameter is close to the amorphous state, while that of the Zr36Cu64 is almost fully crystalline. Although we did not reproduce the fully amorphous rods with 2 mm in diameter, this comparison of the diffraction patterns evidently verifies that the GFA of the Zr50Cu50 alloy is significantly better than that of the Zr36Cu64 alloy, consistent with our first-principles prediction very well. In fact, this large GFA difference between these two alloys was also observed by Xia et al. in their experiments12.
Figure 5. X-ray diffraction patterns of the as-cast Zr36Cu64 and Zr50Cu50 rod samples with a size of 2 mm in diameter.
It should be noted that the parameter proposed here may not be applied to directly compare the GFAs among different alloy systems. This is because the glass formation is a very complex process involving the thermodynamic driving force, individual atom mobility, and various crystalline-phase formations upon cooling from the molten state, and there are no simple ways to take care of all these parameters for different alloy systems during theoretical calculations. Nevertheless, the first-principles calculation scheme we developed in the present study has made major contributions to resolving the long-standing issue, i.e., predicting the promising glass forming compositions in a given alloy system without using any thermodynamic and metallurgical parameters.
In summary, an expression 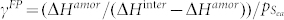 was developed to predict the trend of GFA by considering both formation enthalpies and atomic structures at atomic level in the model Zr-Cu alloy system from DFT-based first-principles static and molecular dynamics simulations. Here, we intend to correlate atomic bonding defects (e.g., proportion of excessive atomic spaces) with the kinetic factor involving atomic mobility in the supercooled liquids. The validity and the power of the proposed expression were verified substaintially by both current and previous experimental results. The physical scenario revealed from this study has extensive implications for the design of bulk metallic glasses with superior GFA for engineering applications.
was developed to predict the trend of GFA by considering both formation enthalpies and atomic structures at atomic level in the model Zr-Cu alloy system from DFT-based first-principles static and molecular dynamics simulations. Here, we intend to correlate atomic bonding defects (e.g., proportion of excessive atomic spaces) with the kinetic factor involving atomic mobility in the supercooled liquids. The validity and the power of the proposed expression were verified substaintially by both current and previous experimental results. The physical scenario revealed from this study has extensive implications for the design of bulk metallic glasses with superior GFA for engineering applications.
Methods
The simulation process contains two sections: FPMD simulation and first-principles static calculation. The FPMD simulation was employed to simulate kinetic and structural features in the glass-forming process, and to acquire the amorphous state of every alloy; while the first-principles static calculation was adopted to determine accurate internal energies for different states of the alloys, i.e., amorphous phase and intermetallic compounds. Our calculations were implemented by applying Vienna ab initio Simulation Package (VASP)33. The coulomb interaction of ion cores with the valence electrons and the electronic exchange were described by projector augmented wave (PAW) potential34,35 and the generalized gradient approximation (GGA)36, respectively.
In the FPMD simulation for every alloy, a cubic supercell containing 100 atoms was adopted; Zr and Cu atoms were distributed randomly in the cubic supercell, with initial density obtained by linear interpolation of experimental densities37. Periodic boundary conditions were always imposed on the supercell during the calculations. The simulation was performed in a canonical ensemble with a Nosé thermostat38 for temperature control. The equation of motion was solved via the velocity Verlet algorithm39 with a time step of 5 fs. For each alloy, the system was firstly equilibrated for 3000 steps at 2000 K to obtain a fully equilibrium liquid configuration out of the impact of initial configuration. Then the system was equilibrated sequentially at 1.3 Tl (Tl is the liquidus temperature in thermodynamic equilibrium phase diagram) for 3000 steps, to acquire equilibrium configurations and kinetic properties at this temperature. Finally, the system was quenched to 300 K with a cooling rate of 5 × 1013 K/s, and kept at this temperature for 1000 steps to get the ultimate amorphous configuration.
The first-principles static calculation was performed with the initial configuration of the amorphous phase obtained by the FPMD simulation, while that of the intermetallic compound was set based on the crystal lattice arrangement. Firstly, the initial configurations of the two phases for each alloy were fully relaxed to approach minimum energy of the system by using the conjugate gradient algorithm, and then RMM-DIIS (Residual minimization scheme, direct inversion in the iterative subspace) algorithm was used for calculating ultimately accurate internal energy.
In order to verify the calculation results, ingots with typical compositions of Zr-Cu binary alloys were prepared by arc melting pure metals (≥99.5wt% for Zr and 99.999 wt% for Cu) under a Ti-gettered pure argon atmosphere, and the alloy rods with 2 mm in diameter were produced by copper mold suction casting. X-ray diffraction (Cu Ka Philips APD-10) was exploited to check the structural nature of the samples.
Author Contributions
C.T.L., X.J.L. and C.Y.Y. conceived and designed the research. C.T.L. supervised the project. C.Y.Y. and X.J.L. carried out theoretical calculations and experiments. C.Y.Y., X.J.L. and C.T.L. wrote the manuscript. J.L. and G.P.Z. participated in the discussions and reviewed the manuscript. All authors analyzed the data and reviewed the manuscript.
Acknowledgments
This work was financially supported by the Hong Kong GRC grant No. 522110. X. J. L. was supported in part by the National Natural Science Foundation of China (Nos. 50901006 and 51271212), the Beijing Nova Program of China (No. 2010B017), the Program of Introducing Talents of Discipline to Universities (B07003), and the Fundamental Research Funds for the Central Universities.
References
- Inoue A. & Takeuchi A. Recent progress in bulk glassy alloys. Mater. Trans. 43, 1892–1906 (2002). [Google Scholar]
- Löffler J. F. Bulk metallic glasses. Intermetallics 11, 529–540 (2003). [Google Scholar]
- Inoue A. Bulk Amorphous Alloys -Preparation and Fundamental Characteristics-. Materials Science Foundations 4, Trans. Tech. Publications, Netherlands, 1–116 (1998). [Google Scholar]
- Inoue A., Zhang T. & Masumoto T. Glass-forming ability of alloys. J. Non-Cryst. Solids 156–158, 473–480 (1993). [Google Scholar]
- Turnbull D. Under what conditions can a glass be formed? Contemp. Phys. 10, 473–488 (1969). [Google Scholar]
- Lu Z. P. & Liu C. T. A new glass-forming ability criterion for bulk metallic glasses. Acta Mater. 50, 3501–3512 (2002). [Google Scholar]
- Guo S. & Liu C. T. New glass forming ability criterion derived from cooling consideration. Intermetallics 18, 2065–2068 (2010). [Google Scholar]
- Delamare J., Lemarchand D. & Vigier P. Structural investigation of the metastable compound A1 in an as-cast Fe-Nd eutectic alloy. J. Alloys Compd. 216, 273–280 (1994). [Google Scholar]
- Coehoorn R., Van der Kolk G. J., Van den Broek J. J., Minemura T. & Miedema A. R. Thermodynamics of the stability of amorphous alloys of two transition metals. J. Less-Common Metal 140, 307–316 (1988). [Google Scholar]
- Takeuchi A. & Inoue A. Calculations of amorphous-forming composition range for ternary alloy systems and analyses of stabilization of amorphous phase and amorphous-forming ability. Mater. Trans. 42, 1435–1444 (2001). [Google Scholar]
- Basu J., Murty B. S. & Ranganathan S. Glass forming ability: Miedema approach to (Zr, Ti, Hf)-(Cu, Ni) binary and ternary alloys. J. Alloys & Compd. 465, 163–172 (2008). [Google Scholar]
- Xia L., Fang S. S., Wang Q., Dong Y. D. & Liu C. T. Thermodynamic modeling of glass formation in metallic glasses. Appl. Phys. Lett. 88, 171905 (2006). [Google Scholar]
- Xia L., Li W. H., Fang S. S., Wei B. C. & Dong Y. D. Binary Ni–Nb bulk metallic glasses. J. Appl. Phys. 99, 026103 (2006). [Google Scholar]
- Xia L., Ding D., Shan S. T. & Dong Y. D. The glass forming ability of Cu-rich Cu-Hf binary alloys. J. Phys.: Condens. Matter. 18, 3543–3548 (2006). [Google Scholar]
- Mukherjee S., Schroers J., Johnson W. L. & Rhim W. K. Influence of kinetic and thermodynamic factors on the glass-forming ability of zirconium-based bulk amorphous alloys. Phys. Rev. Lett. 94, 245501 (2005). [Google Scholar]
- Sha Z. D., Feng Y. P. & Li Y. Statistical composition-structure-property correlation and glass-forming ability based on the full icosahedra in Cu-Zr metallic glasses. Appl. Phys. Lett. 96, 061903 (2010). [Google Scholar]
- Peng H. L., Li M. Z., Wang W. H., Wang C.-Z. & Ho K. M. Effect of local structures and atomic packing on glass forming ability in CuxZr100−x metallic glasses. Appl. Phys. Lett. 96, 021901 (2010). [Google Scholar]
- Liu X. J., Chen G. L., Hui X., Liu T. & Lu Z. P. Ordered clusters and free volume in a Zr-Ni metallic glass. Appl. Phys. Lett. 93, 011911 (2008). [Google Scholar]
- Fan C., Liaw P. K. & Liu C. T. Atomistic model of amorphous materials. Intermetallics 17, 86–87 (2009). [Google Scholar]
- Miracle D. B., Egami T., Flores K. M. & Kelton K. F. Structural aspects of metallic glasses. MRS Bulletin 32, 629–634 (2007). [Google Scholar]
- Cheng Y. Q., Ma E. & Sheng H. W. Atomic level structure in multicomponent bulk metallic glass. Phys. Rev. Lett. 102, 245501 (2009). [DOI] [PubMed] [Google Scholar]
- Hui X. D. et al. Atomic structure of Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass alloy. Acta Mater. 57, 376–391 (2009). [Google Scholar]
- Finney J. L. Random packings and the structure of simple liquids: The geometry of random close packing. Proc. R Soc. Lond. A 319, 479–493 (1970). [Google Scholar]
- Wang D. et al. Bulk metallic glass formation in the binary Cu-Zr system. Appl. Phys. Lett. 84, 4029–4031 (2004). [Google Scholar]
- Xu D. H., Lohwongwatana B., Duan G., Johnson W. L. & Garland C. Bulk metallic glass formation in binary Cu-rich alloy series -Cu100−xZrx (x = 34, 36, 38.2, 40 at.%) and mechanical properties of bulk Cu64Zr36 glass. Acta Mater. 52, 2621–2624 (2004). [Google Scholar]
- Inoue A. & Zhang W. Formation, thermal stability and mechanical properties of Cu-Zr and Cu-Hf binary glassy alloy rods. Mater. Trans. 45, 584–587 (2004). [Google Scholar]
- Li Y., Guo Q., Kalb J. A. & Thompson C. V. Matching glass-forming ability with the density of the amorphous phase. Science 322, 1816–1819 (2008). [DOI] [PubMed] [Google Scholar]
- Tang M. B., Zhao D. Q., Pan M. X. & Wang W. H. Binary Cu-Zr bulk metallic glasses. Chin. Phys. Lett. 21, 901–903 (2004). [Google Scholar]
- Duan G. et al. Molecular dynamics study of the binary Cu46Zr54 metallic glass motivated by experiments: Glass formation and atomic-level structure. Phys. Rev. B 71, 224208 (2005). [Google Scholar]
- Wu W. F. & Li Y. Bulk metallic glass formation near intermetallic composition through liquid quenching. Appl. Phys. Lett. 95, 011906 (2009). [Google Scholar]
- Bendert J. C., Gangopadhyay A. K., Mauro N. A. & Kelton K. F. Volume expansion measurements in metallic liquids and their relation to fragility and glass forming ability: an energy landscape interpretation. Phys. Rev. Lett. 109, 185901 (2012). [DOI] [PubMed] [Google Scholar]
- Honeycutt J. D. & Andersen H. C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 91, 4950–4963 (1987). [Google Scholar]
- Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
- Wang Y. & Perdew J. P. Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling. Phys. Rev. B 44, 13298–13307 (1991). [DOI] [PubMed] [Google Scholar]
- Mattern N. et al. Structural behavior of CuxZr100−x metallic glass (x = 35–70). J. Non-Cryst. Solids 354, 1054–1060 (2008). [Google Scholar]
- Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984). [Google Scholar]
- Verlet L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 159, 98–103 (1967). [Google Scholar]