Connections between survey calibration estimators and semiparametric models for incomplete data

Abstract

Survey calibration (or generalized raking) estimators are a standard approach to the use of auxiliary information in survey sampling, improving on the simple Horvitz–Thompson estimator. In this paper we relate the survey calibration estimators to the semiparametric incomplete-data estimators of Robins and coworkers, and to adjustment for baseline variables in a randomized trial. The development based on calibration estimators explains the ‘estimated weights’ paradox and provides useful heuristics for constructing practical estimators. We present some examples of using calibration to gain precision without making additional modelling assumptions in a variety of regression models.

1 Introduction

Calibration of weights (also known as G-calibration and generalized raking) and the closely-related generalized regression (GREG) estimation are a family of techniques that use population data on auxiliary variables to improve estimates in sample surveys(Deville et al., 1993; Deville and Särndal, 1992; Särndal et al., 2003; Särndal, 2007). These estimators are closely related to the augmented inverse-probability weighted (AIPW) estimators of Robins et al. (1994), but their development from regression estimators of the population total appears to be easier to understand.

Although calibration estimators are widely used in large-scale complex surveys and AIPW estimators are an important part of modern biostatistics, the connections do not appear to be widely known. For example, the ISI Web of Science database does not list any paper that cites both Robins et al. (1994) and either of Deville et al. (1993) and Deville and Särndal (1992). In this paper we aim to explain the connections between these research programmes.

In section 2 we describe survey calibration estimators, relate them to AIPW estimators, and show how they illuminate the ‘estimated weights’ paradox. We then discuss four practical examples in more detail. In section 3 we use a potential-outcomes framework to relate estimating weights by calibration to the more familiar paradigm of adjusting for baseline variables in a randomized trial. In section 4.2 we construct calibration estimators for the case-cohort design and show that the calibration approach gives new and useful insights into the modelling of auxiliary variables. In section 5 we describe calibration estimators for a measurement error problem in survival analysis, and in section 6 we use calibration to increase the efficiency for estimating a gene–environment interaction in a case–control genetic association study.

These examples all use known sampling probabilities. Calibration estimators, like AIPW estimators, are also often used for missing data with estimated sampling probabilities. In this paper we do not address issues of model choice when estimating probabilities of missingness — with missing data the precision gains we describe here are typically dwarfed by the unknown residual biases, and precise analysis is much more difficult.

2 Calibration estimators

Regression estimation of a total

The prototypical calibration estimator is the regression estimator for a population total (eg Cochran (1977)). Suppose a sample of size n is taken from a population of size N. The sampling probability π_i for each individual is known and an indicator variable R_i indicates whether individual i is sampled. It will be important to make asymptotic approximations in some of the equations that follow. We will take the simplest possible asymptotic framework, where the population of size N is an iid sample from an infinite superpopulation, with n → ∞ and N/n → C ∈ (0, ∞] (eg Isaki and Fuller (1982)). The arguments that we use can also be developed under less restrictive asymptotics, eg Krewski and Rao (1981), where a suitable law of large numbers and central limit theorem are available.

The target of estimation is the (non-random) population total of a variable y,

$$T=\sum _{i=1}^N{y}_i$$

and we observe y_i only for individuals in the sample. The Horvitz–Thompson estimator of T is

$$\widehat{T}=\sum _{i:R_i=1}\frac{1}{{\pi }_i}{y}_i=\sum _{i=1}^N\frac{R_i}{{\pi }_i}{y}_i.$$

Since E[R_i] = π_i it is immediate that this estimator is unbiased and in the absence of further information the Horvitz–Thompson estimator would be used in practice.

In addition to observing y, we may also have information on a p auxiliary variables x_i for all i = 1, …, N in the population. The regression estimator T̂_reg of T is constructed by estimating the first-order relationship between y and x from the sample data. Using the n individuals with R_i = 1 we define X as the n × (p + 1) matrix with rows (1, x_i) for i: R_i = 1, Y as the n-vector with elements y_i, and W as the n × n diagonal matrix with entries 1/π_i. We then compute the inverse-probability weighted estimate of the population least-squares coefficients as

$$\widehat{\beta }={(X^{T}WX)}^{-1}{X}^{T}WY.$$

The regression estimator T̂_reg is now defined as

$${\widehat{T}}_{\mathit{reg}}=\sum _{i:R_i=1}\frac{1}{{\pi }_i}(y_i-x_i\widehat{\beta })+\sum _{i=1}^N{x}_i\widehat{\beta }.$$ (1)

As the design matrix X contains an intercept, the first term in equation 1 is identically zero and the estimator reduces to the sum of the fitted values. The reason for retaining the first term is to make the decomposition clearer, and in particular to consider what happens when the true population regression coefficient is substituted for the estimate β̂.

Defining β₀ as the vector of coefficients for a population least-squares regression of y on x, the parameter that β̂ estimates, and ρ² as the proportion of variance explained in this population regression, we have

$$\begin{array}{l}{\widehat{T}}_{\mathit{reg}}=\sum _{i:R_i=1}\frac{1}{{\pi }_i}(y_i-x_i{\beta }_0)+\sum _{i=1}^N{x}_i{\beta }_0+\sum _{i=1}^N{x}_i\left(1-\frac{R_i}{{\pi }_i}\right)(\widehat{\beta }-{\beta }_0)\\ =\sum _{i:R_i=1}\frac{1}{{\pi }_i}(y_i-x_i{\beta }_0)+\sum _{i=1}^N{x}_i{\beta }_0+\sum _{i=1}^N{x}_i\left(1-\frac{R_i}{{\pi }_i}\right)O_p(n^{-1/2})\\ =\sum _{i:R_i=1}\frac{1}{{\pi }_i}(y_i-x_i{\beta }_0)+\sum _{i=1}^N{x}_i{\beta }_0+O_p(N/\sqrt{n})\end{array}$$ (2)

The second term in this expansion is constant, the first term has variance (1 − ρ²) var [T̂], and the third term, relating to error in β̂ is of smaller order than the first two. Ignoring the third term, the variance has been reduced by a factor of (1 − ρ²). The regression estimator T̂_reg is thus more efficient than T̂ for large enough n unless the variables x_i are uncorrelated with y_i so that ρ = 0. Although T̂ _reg is not unbiased, the sum of the first two terms is unbiased. The third term is of smaller order than the first two terms so the bias is negligible for fixed p and large n (Cochran, 1977; Särndal et al., 2003)

The lack of bias and the reduction in variance do not rely on any model assumptions linking x and y, but do rely on the regression being estimated in a probability sample of the population for which T is being estimated. When β̂ is estimated on a probability sample of the population and using the correct sampling weights, it estimates the population least squares coefficient, for which the population mean residual is zero by definition. Estimating β̂ in a separate population could lead to a regression estimator with non-negligible bias or increased variance.

Calibration of weights

The next step in linking the regression estimator to AIPW estimators is to note that the weighted least-squares estimator β̂ is a linear function of the sampled y_i, and so it must be possible to write the regression estimator as

$${\widehat{T}}_{\mathit{reg}}=\sum _{i:R_i=1}\frac{g_i}{{\pi }_i}{y}_i=\sum _{i:R_i=1}{w}_i{y}_i$$

where g_i depends on x and π but not y. An explicit form for g is

$$g_i=1+(T_x-{\widehat{T}}_x){(X^{T}WX)}^{-1}{x}_i$$ (3)

where T_x and T̂_x are the known population total for x and the Horvitz–Thompson estimator of this total respectively.

Although this computation is elementary, we found it surprising that the same 1 − ρ² reduction in variance obtained by taking residuals can also be obtained merely by adjustments to the weights, especially as these adjustments are small when n is large and T_x is close to T̂_x.

Since the g_i do not depend on y they would be the same if y_i = x_i, and in that case the regression estimator is obviously exact, so we must have

$$\sum _{i=1}^N{x}_i=\sum _{i:R_i=1}\frac{g_i}{{\pi }_i}{x}_i$$ (4)

Equation 4 can be used as an alternative definition of g. That is, given a loss function d( , ) for changes in weights, choose g_i to minimize

$$\sum _{i:R_i=1}d\left(\frac{g_i}{{\pi }_i},\frac{1}{{\pi }_i}\right)$$

subject to the constraint that equations 4 are satisified (Deville and Särndal, 1992). The regression estimator results from the loss function d(a, b) = (a − b)²/b. Other loss functions are used to give upper and lower bounds on the calibration weights g_i. For example, the loss function

$$d(a,b)=a(loga-logb)+(b-a)$$

gives non-negative weights and for discrete auxiliary variables is equivalent to the classical raking adjustment.

Estimated weights

Another way to construct adjusted weights, as recommended by Robins et al. (1994), is to fit a logistic regression model to predict R_i from x_i. Writing p_i for the fitted probability, the estimating equations for this logistic regression model can be written as

$$\sum _{i=1}^N{x}_i{p}_i=\sum _{i=1}^n{x}_i{R}_i.$$ (5)

Noting that 1/p_i plays the role of the calibrated weights g_i/π_i we can rewrite this as

$$\sum _{i=1}^N{x}_i\frac{{\pi }_i}{g_i}=\sum _{i:R_i=1}{x}_i.$$

This is similar to the calibration equations (4), but has the weights on the left-hand side rather than the right-hand side. If the model is saturated, the two sets of equations are identical and simply equate observed and expected counts in a set of strata defined by x. Even when the model is not saturated, the estimators obtained are typically very close.

Equation 5 has the advantage that the weights g_i always exist and are always non-negative. From a survey sampling viewpoint this is outweighed by the disadvantage that all the individual x_i are required, in contrast to calibration, which requires x_i only for the sample and in addition the population total ${\sum }_{i=1}^N{x}_i$.

The paradox

The connection between the regression estimator of a total and weighted sums using calibrated weights helps illuminate the ‘estimated weights’ paradox. Even though we have assumed π_i to be known, adjusting the weights from 1/π_i to g_i/π_i or 1/p_i gives an estimate of T with reduced variance. That is, using estimated weights rather than known weights reduces variance. Although there is no difficulty is showing that this result is true, using projection arguments (Henmi and Eguchi, 2004; Pierce, 1982), it has widely been regarded paradoxical. Heuristically, it seems that their should be some loss of information from estimating additional parameters, and the geometrical arguments based on projections do not seem to remove the sense of paradox for many statisticians.

We can explain the paradox in a different way by comparing the regression estimator in equation 2 to a similar decomposition of the Horvitz–Thompson estimator

$$\widehat{T}=\sum _{i:R_i=1}\frac{1}{{\pi }_i}(y_i-x_i{\beta }_0)+\sum _{i:R_i=1}\frac{1}{{\pi }_i}{x}_i{\beta }_0.$$ (6)

The first term in equations 6 and 2 is the same. The second term uses the known population total of x in equation 2 and an estimated total in equation 6. The third term in equation 2 is not present in equation 6 and represents the uncertainty due to estimation, based on β̂ − β₀.

Estimating the weights does introduce error, in the third term, but the introduced error is of smaller order than the gain in precision that comes from replacing the estimated total of x with the known total. For large enough n and N, T̂_reg will always be at least as efficient as T̂. In finite samples the estimation uncertainty need not be negligible. Judkins et al. (2007) develop a second-order approximation for the variance when x is discrete, confirming that the uncertainty from estimating β will be important if ρ² is small and the dimension of β is large. Henmi and Eguchi (2004) discuss the tradeoff in a general model-based setting, using projection arguments.

A useful analogy for biostatisticians is to adjustment for baseline variables in a randomized trial. Although the sampling distributions of all baseline variables are equal in the arms of a randomized trial, and adjustment for baseline requires additional parameters to be estimated, it is still possible to realize useful gains in precision. As section 3 shows, this analogy is exact if randomization is viewed as random sampling from a population of potential outcomes.

2.1 Two-phase studies and parameter estimates

The previous discussion focused on estimating the population total of an observed variable. To link this to the problem of semiparametric estimation with incomplete data we need two further steps.

The first step is to note that y_i can be replaced by an estimating function U_i(θ), and that under suitable regularity conditions the solution to

$$\sum _{i:R_i=1}\frac{g_i}{{\pi }_i}{U}_i(\theta )=0$$

is a consistent, asymptotically Normal estimator (Binder, 1983) of the parameter θ₀ defined by the population estimating equations

$$\sum _{i=1}^N{U}_i({\theta }_0)=0.$$

Analogous theory for calibration estimators of estimating functions is given by Rao et al. (2002). Breslow and Wellner (2007) discuss the more subtle asymptotic theory needed for the Cox model.

The regression estimator can also be rewritten

$$T=\sum _{i=1}^N\frac{R_i}{{\pi }_i}{y}_i+\left(1-\frac{R_i}{{\pi }_i}\right)x_i\widehat{\beta },$$

and when y_i is replaced by U_i(θ) we have the form of the AIPW estimator of Robins et al. (1994). In their notation

$$T=\sum _{i=1}^N\frac{R_i}{{\pi }_i}{D}_i(\theta )+\left(1-\frac{R_i}{{\pi }_i}\right){\phi }_i$$

where D_i are the estimating functions and φ_i is a p-vector of arbitrary functions of the data that are available for all N observations.

A minor difference between the AIPW formulation and the calibration formulation of these estimators is the explicit presence of β̂. The only impact of this difference is to rule out perverse choices of φ_i that are, for example, negatively correlated with the estimating functions. In practice, a tuning parameter similar to β would be included in the choice of φ in an AIPW estimator.

The second step in linking this discussion to the semiparametric missing data problem is to introduce a prior phase of sampling, so that the observations i = 1, 2, …, N are themselves a random sample from an actual population or a hypothetical superpopulation. In most biostatistical applications this first-phase sample is either a cohort or a large case–control sample in which an unweighted estimating equation

$$\sum _{i=1}^N{U}_i({\theta }_0)=0$$

is appropriate. Details of calibration in two-phase samples are discussed by Särndal et al. (2003) and when auxiliary information is available only on the first-phase sample the equations are the same as discussed in the previous section.

2.2 Regression and calibration for estimating functions

While the equivalence of regression and calibration for estimation of population totals and means has long been known in the survey statistics literature, the fact that this equivalence extends to more complex statistics when applied to estimating functions does not seem to be well-known, although the relationship between AIPW and calibration estimators has been previously noted by Robins and Rotnitkzy (1998).

Särndal’s Waksberg Lecture (Särndal, 2007) used an example from Estevao and Särndal (2004) of estimating a subpopulation total to illustrate that regression estimators of the form familiar in survey analysis were not always equivalent to calibration.

Suppose we are interested in estimating the total of Y over a subpopulation . Without auxiliary information the estimator is

$${\widehat{T}}_{\mathcal{D}}=\sum _{i\in \mathcal{D},R_i=1}\frac{1}{{\pi }_i}{Y}_i=\sum _{R_i=1}\frac{1}{{\pi }_i}{D}_i{Y}_i$$

where D is the indicator variable for membership in . If auxiliary variables X were available and the population total for XD were known, an improved regression estimator would be

$${\widehat{T}}_{\mathcal{D}}^{(\mathit{reg})}=\sum _{R_i=1}\frac{1}{{\pi }_i}{D}_i(Y_i-X_i\widehat{\beta })+\sum _{i=1}^N{D}_i{X}_i\widehat{\beta }$$

where β̂ could be estimated by a regression over the sampled members of the subpopulation or (trading bias and variance) by a regression over the whole sample. This regression estimator is exactly the same as a calibration estimator using XD as auxiliary variables.

Suppose, however, that population data is not available on membership in but is available for a closely related subpopulation 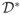(perhaps overlapping, perhaps a subset). Let $D_i^{\ast }$ be the indicator variable for membership in 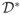and suppose that the population total is known for ${XD}_i^{\ast }$.

Estevao & Särndal argued that generalizing the regression estimator to this problem would give an estimator

$${\widehat{T}}_{\mathcal{D}}^{\ast (\mathit{reg})}=\sum _{R_i=1}\frac{1}{{\pi }_i}{D}_i^{\ast }(Y_i-X_i\widehat{\beta })+\sum _{i=1}^N{D}_i^{\ast }{X}_i\widehat{\beta }$$

where β̂ might be estimated on 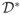∪ 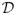or, attempting to borrow strength, on all of 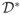. A calibration approach would use ${XD}_i^{\ast }$ as auxiliary variables to give an estimator

$${\widehat{T}}_{\mathcal{D}}^{\ast (\mathit{cal})}=\sum _{R_i=1}\frac{g_i}{{\pi }_i}{D}_i{Y}_i.$$

Estevao & Särndal show that ${\widehat{T}}_{\mathcal{D}}^{\ast (\mathit{cal})}$ and ${\widehat{T}}_{\mathcal{D}}^{\ast (\mathit{reg})}$ are not the same and that ${\widehat{T}}_{\mathcal{D}}^{\ast (\mathit{reg})}$ is more efficient. Särndal uses this example to contrast ‘regression thinking’, or modelling the mean, with ‘calibration thinking’, or standardizing the distribution of auxiliary variables.

The two approaches can be unified by thinking of the estimation problem as estimating the population total of the influence functions, which up to a scale factor are D_iY_i − E[D_iY_i]. Regression of these estimating functions on X is equivalent to regression of D_iY_i on X, which is equivalent to calibration on X. ‘Calibration thinking’ is ‘regression thinking’ combined with ‘influence function thinking’.

2.3 Efficiency

As noted above, the class of calibration estimators does not quite include the entire class of AIPW estimators. The classes would be identical if β were fixed rather than estimated, and estimating β gives asymptotically the same estimator as fixing β at its optimal value. That is, the calibration estimators include all the best AIPW estimators.

The optimal choice for a calibration variable is the conditional expectation of U_i(θ₀) given the phase-one data. This depends on the unknown θ₀, requiring an iterative procedure that alternates between estimating θ and constructing new calibration variables based on the estimate. It is often difficult both analytically and computationally to work out the optimal calibration variables, as discussed in section 2.7 of RRZ. In practice, a reasonable approximate choice may give almost the same efficiency as the optimal choice, with much less effort.

Even with the optimal choice of functions φ, the class of AIPW estimators, and thus of calibration estimators, need not include the semiparametric efficient estimator. For example, suppose the first phase is simple random sampling of N individuals to measure a binary outcome y and the second phase is case–control sampling to measure predictors z. Under the model

$$\text{logit}P[Y_i=1\mid X_i=z]=z\theta$$ (7)

logistic regression is efficient for estimating θ, and is not equivalent to any AIPW estimator.

On the other hand, if we do not assume that equation 7 holds exactly, we could still define the target parameter as the result that would be obtained by logistic regression if full data were available on all N individuals, ie, the solution to the population likelihood equations

$$\sum _{i=1}^N{z}_i\left(y_i-\frac{e^{z_i\theta }}{e^{z_i\theta }+1}\right)=0$$ (8)

In this particular example of case–control sampling, Scott and Wild (2002) give a very detailed discussion and comparison of the design-based (equation 8) and semiparametric-efficient (equation 7) estimators. Although they conclude that the semiparametric-efficient estimator is preferable, their arguments are specific to this model and design.

RRZ showed that the class of AIPW estimators contains (up to asymptotic equivalence) all regular asymptotically linear estimators consistent for this design-based target parameter. We can thus describe AIPW or calibration estimators as asymptotically efficient in the non-parametric outcome model, or as asymptotically efficent among design-based estimators.

3 Randomization, adjustment, and potential outcomes

Consider a two-group randomized trial, in which a baseline variable X is measured, N/2 participants are randomized to each of treatments A or B, and then an outcome Y is measured. The summary of interest is the average causal effect of treatment on Y. This can be estimated either as the difference in mean of Y between the treatment groups or as the coefficient of a treatment term in a regression model for Y: if treatment is coded Z = −1 for A and Z = −1 for B we have

$$E[Y\mid Z]=\mu +Z\delta$$

where δ/2 is the average causal effect of randomization to treatment. The obvious and standard estimator of δ/2 is the difference in means between treatment A and treatment B

$$\widehat{\delta }/2=\frac{1}{N/2}\sum _{Z_i=1}{Y}_i-\frac{1}{N/2}\sum _{Z_i=-1}{Y}_i.$$

Using the potential-outcomes formulation of causation (Pearl, 2000) we can consider the randomized trial as a sample from a finite population. In the finite population, each participant i has two potential outcomes: Y_(A)i if assigned treatment A and Y_(B)i if assigned treatment B. The randomization process samples one potential outcome for each participant. The use of randomization to assign treatments guarantees that the sampling probabilities are independent of the potential outcomes and of X. Under 1:1 randomization these sampling probabilities at the second phase are 1/2 for each potential outcome. The observed value of Y is the one for the assigned treatment Z_i, namely Y_i = Y_(zi)i,

The treatment effect for an individual is Y_(A)i − Y_(B)i = Σ_z Y_(z)iZ_i, so the average treatment effect is the population mean of Y Z, where the expectation is taken over the two treatments and potential outcomes for each individual. The Horvitz–Thompson estimator δ̂_HT of δ is a probability-weighted sum of Y Z over the observed outcomes and treatments. This reduces to the group difference in means

$$\begin{array}{l}{\widehat{\delta }}_{HT}/2=\frac{1}{N}\sum _{i=1}^N\frac{1}{{\pi }_i}{Y}_i{Z}_i\\ =\frac{1}{N}\sum _{i=1}^N\frac{1}{1/2}{Y}_i{Z}_i\\ =\frac{1}{N/2}\left(\sum _{Z_i=1}{Y}_i-\sum _{Z_i=-1}{Y}_i\right)\\ =\widehat{\delta }/2\end{array}$$

When additional baseline variables X are available the treatment effect can be estimated by a regression of Y on X and Z, fitting the model

$$E[Y\mid Z,X]=\mu +Z\delta +X\beta .$$ (9)

For notational simplicity we consider only univariate X, but exactly the same arguments apply for multivariate X. The baseline-adjusted estimator δ̂_reg satisfies the Normal equations

$$\begin{array}{r}\sum _{i=1}^N(Y_i-\mu -Z_i\delta -X_i\beta )=0\\ \sum _{i=1}^N{Z}_i(Y_i-\mu -Z_i\delta -X_i\beta )=0\\ \sum _{i=1}^N{X}_i(Y_i-\mu -Z_i\delta -X_i\beta )=0\end{array}$$

This estimator δ̂_reg is more efficient than the difference in means between treatment groups. If X and Y are highly correlated the efficiency gain can be large. Because Z is randomly assigned and independent of X the regression estimator is unbiased for δ regardless of whether the regression is correctly specified; a misspecified model just leads to a smaller gain in efficiency.

An alternative way to use baseline variables X is by calibrating the sampling weights. In the first-phase sample each individual appears once in each treatment group, so the sample mean of XZ is identically zero. In the observed sample there will be small imbalances in X between treatment groups, so that the Horvitz–Thompson estimator of the mean of XZ is not exactly zero.

When we calibrate on XZ to the first-phase sample the calibration constraints (4) are

$$\sum _{i=1}^N\frac{g_i}{1/2}{X}_i{Z}_i=\sum _{i:Z_i=1}2g_i{X}_i-\sum _{i:Z_i=-1}2g_i{X}_i=0,$$

ie, perfect balance in the mean of X across treatment groups. In fact, we will calibrate to S = (XZ, Z, 1), where the calibration on (1, Z) ensures that the sum of the weights stays equal to 2N and the mean of Z stays equal to zero. These additional conditions result in the calibrated estimator being algebraically equal to δ̂_reg, calibrating only on XZ gives an asymptotically equivalent estimator. We will use of the equivalence between the calibration estimator and the survey regression estimator in equation 1. We write (α₀, α₁, α₂) for the regression coefficients in equation 1. These satisfy the weighted least-squares equations

$$\begin{array}{r}\frac{1}{1/2}\sum _i(Y_i{Z}_i-{\alpha }_0-{\alpha }_1{Z}_i-{\alpha }_2{Z}_i{X}_i)1=0\\ \frac{1}{1/2}\sum _i(Y_i{Z}_i-{\alpha }_0-{\alpha }_1{Z}_i-{\alpha }_2{Z}_i{X}_i)Z_i=0\\ \frac{1}{1/2}\sum _i(Y_i{Z}_i-{\alpha }_0-{\alpha }_1{Z}_i-{\alpha }_2{Z}_i{X}_i)X_i{Z}_i=0\end{array}$$

Using the fact that Z_i = 1/Z_i and $Z_i^2=1$, we can rewrite this as

$$\begin{array}{r}\sum _i(Y_i-{\alpha }_0{Z}_i-{\alpha }_1-{\alpha }_2{X}_i)Z_i=0\\ \sum _i(Y_i-{\alpha }_0{Z}_i-{\alpha }_1-{\alpha }_2{X}_i)1=0\\ \sum _i(Y_i-{\alpha }_0{Z}_i-{\alpha }_1-{\alpha }_2{X}_i)X_i=0\end{array}$$

which are the least-squares equations for the model in equation 10, with α₀ = δ, α₁ = μ and α₂ = β, so α̂₀ = δ̂_reg.

According to equation 1, the calibration estimator for the total of Y Z is

$$N{\widehat{\delta }}_{\text{cal}}=\frac{1}{1/2}\sum _i(Y_i{Z}_i-{\widehat{\alpha }}_0-{\widehat{\alpha }}_1{Z}_i-{\widehat{\alpha }}_2{Z}_i{X}_i)+T$$

where T is the population total of the predicted values. The first term is zero, from the definition of α, an unusual special case that occurs because the sampling weights are constant. The second term T expands to

$$T=\frac{1}{1/2}\sum _i({\widehat{\alpha }}_0+{\widehat{\alpha }}_1{Z}_i+{\widehat{\alpha }}_2{Z}_i{X}_i)$$

Since the sums of Z_iX_i and Z_i are identically zero over the potential-outcome population, T simplifies to

$$T=N{\widehat{\alpha }}_0=N{\widehat{\delta }}_{\text{reg}}$$

and so δ̂_cal = δ̂_reg.

We have already seen that the calibration estimator is consistent and provides efficiency benefits whether or not the relationship between Y and X is truly linear. Similarly, when estimating the mean difference in randomized trials, adjustment for pre-randomization measurements is known to give a consistent estimator without regard to the accuracy of the model, and to give an increase in large-sample precision when the baseline variables are correlated with the trial outcome. We can see that these ‘free lunch’ improvements in precision without the need to make additional assumptions arise for exactly the same reasons.

When applied to treatment effect estimates other than the difference in means, such as the hazard ratio from a Cox model, the calibration estimators are not identical to adjusting for baseline covariates. Adjustment for baseline covariates changes the target of inference from a marginal hazard ratio to a conditional hazard ratio; calibration provides more precise estimation for the same target of inference. The increase in power for testing the null hypothesis of no treatment difference is similar for calibration and adjustment estimators.

Semiparametric estimators for randomized trials equivalent to the calibration estimators have recently been proposed (Zhang et al., 2008; Tsiatis et al., 2008). The motivation for these estimators was an increase in precision without changing the target of estimation, the same goal that motivates calibration estimators. Tsiatis et al. (2008) made the interesting observation that the optimal estimator in this class can be constructed by choosing auxiliary variables separately in each treatment group, blinded as to treatment. Separating the treatment groups in this way means that the analyst who chooses the auxiliary variables cannot be influenced by the impact that model choice has on the estimated treatment effect.

3.1 Simulation

We present a simple simulation to verify that δ̂_cal and δ̂_reg are identical in this randomized trial setting and to examine the impact of estimating weights by logistic regression instead of by calibration.

The data are 1000 observations generated as Y = 2X + Z + ε, where X, ε ~ N(0, 1) and Z alternates between 0 and 1. For each of 500 simulations we compute the simple difference estimator δ̂; the Horvitz–Thompson estimator δ̂_HT; the regression estimator adjusted for X; δ̂_reg; the calibration estimator δ̂_cal; and a weighted mean estimator with inverse-probability of treatment weights estimated by logistic regression as in equation 5, δ̂_IPTW. Table 1 summarizes the results.

Table 1.

Reweighting and baseline regression adjustment in a randomized trial

		Bias	Std Dev	Median absolute difference:
				from δ̂	from δ̂reg
Difference	δ̂	0.00	0.137	—	0.088
Regression	δ̂reg	0.00	0.067	0.088	—
Horvitz–Thompson	δ̂HT	0.00	0.137	< 2 × 10−15	0.088
Calibration	δ̂cal	0.00	0.067	0.088	< 2 × 10−15
IPTW	δ̂IPTW	0.00	0.067	0.088	8 × 10−5

As expected, the difference and Horvitz–Thompson estimators agree to within machine precision, as do the regression and calibration estimators. We would not have expected the IPTW estimator using logistic regression to agree to machine precision, but it does agree with the regression and calibration estimators to four digits, or less than 1% of a standard error. The closeness of the agreement between δ̂_cal and δ̂_IPTW in this example occurs because the fitted values in the logistic regression are close to 0.5, within the region where the logit link function is approximately linear.

4 Regression coefficients, influence functions, and calibration

4.1 Calibration in fitting linear regression models

The efficiency gain in calibration for a population total depends on the (linear) correlation between the calibration variables and the variable whose total is being estimated. For estimates more complex than a total it is useful to consider a representation using influence functions. Consider fitting a linear regression model to an independent sample of n observations (x_i, y_i) from a distribution satisfying

$$E[Y\mid X=x]=x\beta .$$

The least-squares regression estimator β̂ of β is

$$\widehat{\beta }={\left(\frac{1}{n}\sum _{i=1}^n{x}_i{x}_i^T\right)}^{-1}\frac{1}{n}\sum _{i=1}^n{x}_i{y}_i.$$

By the Law of Large Numbers the matrix inverse is approximately constant, so β̂ is approximately a population mean of independent and identically distributed terms. More precisely,

$$\widehat{\beta }=\beta +\frac{1}{n}\sum _{i=1}^{n}E{[{XX}^T]}^{-1}{x}_i(y_i-x_i\beta )+o_p(n^{-1/2}),$$

so β̂ is asymptotically equivalent to the population mean of the influence functions

$${\mathbb{I}}_{\beta }(x,y)=E{[{XX}^T]}^{-1}{x}_i(y_i-x_i\beta ).$$

Since β̂ is approximately a mean of influence functions, calibration will be most effective when the calibration variable is highly correlated with the influence functions. The same conclusion holds under complex sampling from a finite population, or two-phase sampling. Finding calibration variables highly correlated with can lead very different choices from finding calibration variables correlated with X or Y.

As an example we consider socioeconomic and academic performance data on schools in California, made available by the California Department of Education and subsequently distributed as a teaching example by UCLA Academic Technology Services. These data can be obtained from http://www.ats.ucla.edu/stat/stata/Library/svy_survey.htm or from the R survey package. We will use the apiclus1 data set, which is a cluster sample of all the schools in 15 school districts. The calibration analysis of this example is taken from Lumley (2010).

We fit a regression model where the outcome is the Academic Performance Index for the school in the year 2000 (api00). As predictors we have the percentage of students who are ‘English language learners’ (ell), the percentage of students who are new to the school that year (mobility), and the percentage of teachers with only emergency teaching qualifications (emer). That is

$$E[\text{api}00]={\beta }_0+{\beta }_{\text{ell}}\times \text{ell}+{\beta }_{\text{mobility}}\times \text{mobility}+{\beta }_{\text{emer}}\times \text{emer}$$

We assume that the three predictor variables are known for all schools in the state, and that the previous year’s Academic Performance Index (api99) is also known for all schools in the state. Individual-level calibration information of this sort is unusual in national population surveys, but is commonplace in two-phase subsampling designs. Since the correlation between the two years of Academic Performance Index is 0.975, we should have almost perfect auxiliary information for calibration. One approach is to use the variables ell, mobility, emer, and api99 as calibration variables. Another is to fit an auxiliary model

$$E[\text{api}99]={\beta }_0+{\gamma }_{\text{ell}}\times \text{ell}+{\gamma }_{\text{mobility}}\times \text{mobility}+{\gamma }_{\text{emer}}\times \text{emer}$$

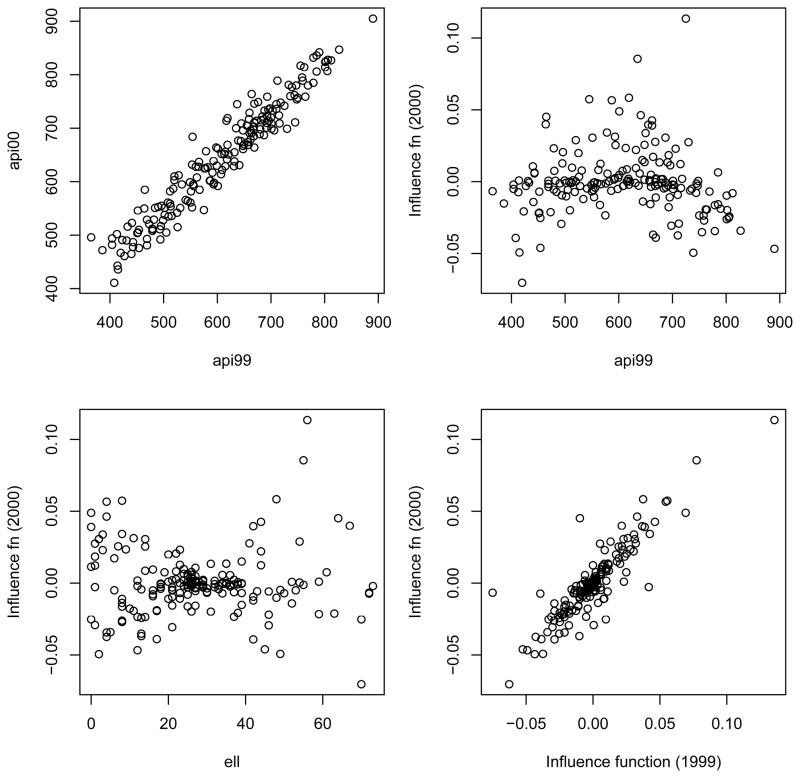
to the complete population data and use its influence functions as calibration variables. The upper left panel in Figure 1 shows the strong linear relationship between 1999 and 2000 API in this data set. If we wished to estimate the mean of 2000 API it is clear that 1999 API would be a valuable auxiliary variable. The remaining three panels have the influence function for the second element of β̂, the coefficient of ell, on the y axis. A strong linear relationship would indicate a useful auxiliary variable for estimating this regression coefficient. The upper right and lower left panels show that api99 and ell are very poor auxiliary variables for estimating the regression coefficient. The correlations are −0.09 and −0.05 respectively. The x axis in the lower right panel is the influence function for the second element of β̂ in the auxiliary regression model. The correlation in this panel is 0.88. These graphs confirm that calibration using the raw predictor or outcome variables, or proxies for them, is not an effective way to increase precision in a regression model. Instead, an effective strategy may be to construct an analogous model based on the auxiliary information and use the influence functions from that model in calibration.

Figure 1.

Auxiliary information for 2000 API and for influence functions. Upper left panel shows 2000 and 1999 API. Remaining three panels show the influence function for β̂_ell on the y-axis, with 1999 API, the predictor ell itself, and the influence function in an auxiliary model using 1999 data on the x-axes.

Table 2 shows the results. Calibration just using the variables api99, ell, mobility, and emer gives a substantial reduction in the intercept standard error, but has relatively little impact on the standard errors of the slope estimates. Calibration using the influence functions further reduces the standard error of the intercept and reduces the standard errors of all the slope parameters by a factor of 2–3. This example is taken from Lumley (2010) and the code for all the computations is available at http://faculty.washington.edu/tlumley/svybook/.

Table 2.

Coefficients and standard errors (A) using sampling weights, (B) calibrating on variables, and (C) calibrating on influence functions

	A	B	C
Coefficients
(Intercept)	780.46	785.44	790.63
ell	−3.30	−3.28	−3.26
mobility	−1.45	−1.46	−1.41
emer	−1.81	−1.67	−2.24
Standard errors
(Intercept)	30.02	13.76	5.84
ell	0.47	0.62	0.13
mobility	0.73	0.66	0.22
emer	0.42	0.37	0.22

4.2 The case–cohort design

Cox regression estimators based on unequal probability subsampling of a large cohort have a long history in the case–cohort design. In the case–cohort design the first phase of sampling is a cohort of size N. The second phase consists of a random subcohort augmented by adding all individuals who experience an event. The initial development of the design and estimation (Prentice, 1986; Self and Prentice, 1988) was based on martingale arguments and did not make use of auxiliary information. A survey-sampling approach to the Cox model was proposed by Binder (1992) and more rigorously developed by Lin (2000) and Breslow and Wellner (2007). Auxiliary information was incorporated as weights by Borgan et al. (2000), Kulich and Lin (2004), Mark and Katki (2006) and others. The semiparametric-efficient estimator has been constructed by Nan (2004), but it is difficult to compute and no implementation is currently available.

Using standard survival notation we write Z_i(t) for the possibly time-varying covariate vector for individual i and N_i(t) for the survival counting process. The hazard λ(t; z_i(t) follows the proportional hazards model

$$\lambda (t;z_i(t)={\lambda }_0(t)e^{z_i(t)\beta }$$

so that the parameters β are log hazard ratios for a one-unit difference in z. We assume that Z_i is available only for individuals in the case-cohort subsample, ie, where R_i = 1.

The Horvitz–Thompson estimator for β (Binder, 1992; Lin, 2000) solves

$$\sum _{i:R_i=1}\frac{1}{{\pi }_i}{U}_i(\beta )\equiv \sum _{i:R_i=1}\frac{1}{{\pi }_i}\int Z_i(t)-\frac{{\sum }_j{Z}_j(t)e^{\beta Z_j(t)}/{\pi }_i}{{\sum }_j{e}^{\beta Z_j(t)}/{\pi }_i}{dN}_i(t)=0$$

If, in addition to Z_i measured for i in the subsample we have auxiliary variables Z^* measured for i = 1, 2, …, N, we can improve precision with a calibration estimator. It is clear from the construction of the regression estimator in equation 1 that the ideal calibration variables would be highly correlated with U_i(β), the variable whose total is being estimated. The optimal choice is the conditional expectation of U_i given phase-one data, but this is unlikely to be tractable.

A popular choice for the related problem of estimating weights with logistic regression is the raw variables $Z_i^{\ast }$. These are unlikely to be good calibration variables as they are unlikely to be strongly correlated with U_i. Suppose that Z_i and $Z_i^{\ast }$ are one-dimensional, not time-varying, and highly correlated. If the proportional hazards model is correctly specified, E[U_i(β)|Z_i(0) = z_i] = 0, so U_i is uncorrelated with Z_i and will be at most weakly correlated with $Z_i^{\ast }$.

As in the previous example, a better candidate for a calibration variable would be an influence function for the same hazard ratios but from an auxiliary model based on $Z_i^{\ast }$ rather than Z_i. That is, where Z_i is not available, we impute it from $Z_i^{\ast }$. We then fit the Cox model

$$\lambda (t;z_i(t)={\lambda }_0(t)e^{z_i(t)\gamma }$$

to the imputed data set, and use the influence functions for this model as calibration variables. Typically there will be substantial overlap between Z_i and $Z_i^{\ast }$, with only a few variables (or even one) that are truly restricted to the case-cohort sample, so the modelling needed for imputation is not unduly burdensome. It would be possible just to use γ̂ instead of β̂, but this runs the risk that inadequacies in the imputation model could cause serious bias. By using the auxiliary model to construct calibration variables it is possible to benefit from an accurate imputation model without the risk of bias from a poor imputation model.

Breslow et al. (2009) used this approach to analyze data from the National Wilm’s Tumor Study Group, previously presented by Kulich and Lin (2004), and confirmed that calibration or estimating weights using raw phase-one variables was of little benefit and that substantial precision gains were available from calibrating to phase-one influence functions.

5 Model calibration for mismeasured covariates

Several estimation methods have been developed for Cox regression with mismeasured covariates. Perhaps the most practically successful of this is due to Prentice (1982), a method that unfortunately is also called ‘regression calibration’ and that we will refer to in this paper as Prentice’s method, to avoid ambiguity of names. This is a straightforward but approximate first-order correction that would give consistent estimation for linear regression but has some asymptotic bias for the Cox model. Consistent methods, such as the conditional score (Tsiatis and Davidian, 2001) and corrected score (Nakamura, 1992; Huang and Wang, 2000, 2006), have also been worked out.

We assume that the true Cox model for the hazard λ_i(t) of an individual is

$$log{\lambda }_i(t)=log{\lambda }_0(t)+\beta Z_i,$$

where we call Z_i the true exposure. Z_i is observed with some measurement error. Until recently, statistical methods have assumed that an observed exposure W follows the classical measurement error model

$$W_i=Z_i+{\epsilon }_i$$

where the errors ε_i are iid with zero mean and are independent of all other variables. Some methods require the additional assumption that ε has a Normal distribution.

In nutritional epidemiology, nutrient intakes are typically assessed through self-reported questionnaire data. The reporting error in these instruments is large enough to potentially obscure associations between diet and chronic disease in cohort studies (Willett, 1998; Kipnis et al., 2003; Schatzkin and Kipnis, 2004). However, it is well-established that the mean and variance of the measurement can depend on Z and on other covariates, so that classical measurement error models are not sufficient. Building on the work of several others (Prentice, 1996; Carroll et al., 1998; Jiang et al., 2001; Kipnis et al., 2001), Prentice et al. (2002) proposed a measurement error model for self-reported dietary assessment data. This model consists of both systematic and random error and allows for repeated measurements. We write

$$Q_{it}=Z_i+{\eta }_{it}$$

for the self-reported exposure and note that E[η_it] and var[η_it] will typically depend on Z_i and on other covariates.

In the presence of systematic error, it not possible to estimate dietary intake or its associated hazard ratio consistently from replicate measurements. It is also unreasonable to assume that perfect validation measurements are available. A weaker assumption is that a measure of Z with classical measurement error is available on a subset. In nutritional epidemiology such a measure might arise from recovery biomarkers (Kaaks et al., 2002) such as urinary nitrogen to estimate protein intake (Bingham and Cummings, 1985), the doubly-labelled water estimate of energy expenditure (Schoeller and van Santen, 1982), or calorimetry for resting energy expenditure. Due to expense, these measures are typically not available on the entire cohort under study. Adapting regression calibration to this setting is relatively straightforward and gives good precision, but with some bias (Shaw, 2006). Shaw (2006) also showed how the conditional score and corrected score could be adapted to non-classical measurement error giving reduced bias but substantially increased variance and some numerical instability. A semiparametric efficient estimator is not known, and does not appear easy to construct.

If the event rate in this subset is high enough, another approach to estimation is to use the non-parametric corrected score estimator (Huang and Wang, 2000) on the biomarker subset and to use the estimating functions from the Prentice (1982) first-order corrected estimator as calibration variables. The Huang and Wang (2000) estimator weakens the necessary distributional assumptions to require only that ε is mean zero and independent of the unobserved Z, which is thought to be reasonable for these biomarkers.

Our simulations compare the Prentice first-order estimator based on the whole cohort to the Huang & Wang estimator on the biomarker subset, calibrated with the estimating functions from the Prentice first-order estimator on the whole cohort. These simulations involve a Normally distributed true exposure. In the validation subset, this exposure is observed with classical measurement error as the validation biomarker. In the whole data set the exposure is also observed as three repeated measurements of a self-reported exposure. This self-reported exposure has both bias for each individual and independent measurement error around this biased value having mean and variance which depend on a binary grouping variable, following Prentice et al. (2002). R code for generating the self-reported exposure variable Q_it is in the Appendix. The validation subset is 500 observations out of a total of 5000, and censoring is at a single time point with a censoring rate of 35%.

Table 3 shows the results of simulations for three real estimators: the calibration estimator based on the corrected score, the corrected score estimated just from the validation subset, and Prentice’s estimator. These are also compared to an estimator that ignores the measurement error. There are four simulation scenarios, comparing moderate (β = log 2) and large (β = log 4) covariate effects and moderate or large exposure error. The bias, standard error, and squared error of the large-sample distributions are estimated by the median of the simulated β̂, the median absolute deviation of β̂, and the square root of the median squared error, since the estimators need not have finite moments at finite sample size and so the sample simulated moments may be misleading.

Table 3.

Bias (median [β̂ − β₀]), standard error (MAD [β̂]), and total error ( $\text{median}\sqrt{\left[{(\widehat{\beta }-{\beta }_0)}^2\right]}$) for Cox model with classical measurement error in validation sample. Based on 1000 simulations.

Error	Effect		calibrated	uncalibrated	Prentice	ignoring
Large	moderate	bias	0.00	0.00	−0.07	−0.39
		se	0.17	0.18	0.06	0.016
		total	0.11	0.12	0.074	0.39
	large	bias	−0.1	−0.1	−0.4	−0.9
		se	0.44	0.46	0.1	0.02
		total	0.33	0.34	0.37	0.90
Moderate	moderate	bias	0.00	0.00	−0.05	−0.35
		se	0.063	0.085	0.049	0.014
		total	0.046	0.057	0.059	0.35
	large	bias	−0.05	0.01	−0.32	−0.82
		se	0.15	0.19	0.08	0.017
		total	0.12	0.13	0.32	0.82

The simulations show that the calibrated corrected score estimator is competitive with the Prentice estimator in squared error, with lower bias. The calibrated corrected score is always superior to the uncalibrated corrected score, though there is only one scenario where the improvement is large. All three estimators are vastly superior to ignoring the measurement error. The gain in information from observations outside the validation subset is disappointingly small when the error is large. It is not clear how much this is a deficiency in the estimator, since an efficient estimator is not known. In contrast to Prentice’s estimator, the calibration approach does require that the event rate in the validation subset is substantial, either because the overall event rate is high or because the calibration subset is chosen to include high-risk individuals.

6 Gene–Environment interaction

Calibration is also possible when the constraints are provided by substantive knowledge about the data-generating process rather than observed population data. An example comes from studies of gene–environment interaction in genetic epidemiology and pharma-cogenomics.

As an example we consider a study by Psaty et al. (2002). The Gly460Trp mutation in the α-adducin gene has been linked to salt-sensitive hypertension in both animal and human studies. Theory, and experiments in animals, suggest that this form of hypertension might be more responsive to thiazide diuretics than to other blood pressure drugs. Psaty et al. collected data on the α-adducin genotype and medication use for treated hypertensives who had heart attack or stroke and for controls, and fitted a logistic regression model

$$\text{logit}P[Y=1]=\alpha +{\beta }_{G}G+{\beta }_{D}D+\gamma G\times D$$

where Y = 1 is an indicator for case status, G is an indicator for a carrier of the variant form of α-adducin and D is an indicator for treatment with diuretics. They found exp(γ) = 0.53, confirming the hypothesis. The data are in table 4

Table 4.

Interaction between thiazide diuretics and the α-adducin Gly460Trp polymorphism (Psaty et al, 2000)

		G
	D	0	1
Case	0	103	85
	1	94	41
Control	0	248	131
	1	208	128

It is plausible in this case that D and G are independent, since physicians do not know the α-adducin genotype of their patients. If they are independent, then a case–only analysis ((Piegorsch et al., 1994)) is also possible and is more efficient. We write n_GDY for the number of observations with G = 1, D = 1, and Y = 1; n_gdy for the number with G = 0, D = 0, and Y = 0; and so on. The interaction odds ratio e^γ can then be written as

$$exp(\gamma )=\frac{n_{\mathit{GDY}}{n}_{\mathit{Gdy}}/n_{\mathit{GDy}}{n}_{\mathit{GdY}}}{n_{\mathit{gDY}}{n}_{\mathit{gdy}}/n_{\mathit{gDy}}{n}_{\mathit{gdY}}}=\frac{n_{\mathit{GDY}}{n}_{\mathit{gdY}}/n_{\mathit{GdY}}{n}_{\mathit{gDY}}}{n_{\mathit{GDy}}{n}_{\mathit{gdy}}/n_{\mathit{Gdy}}{n}_{\mathit{gDy}}}.$$

If Y = 1 is rare in the population, as it will typically be in a case–control study, independence of G and D in the population implies independence in controls. This in turn implies the denominator in the second expression for exp(γ), the gene–drug odds ratio in controls, is unity.

Under the rare-disease and gene–drug independence assumptions, γ can be estimated by the case–only logistic regression

$$\text{logit}P[G=1]={\alpha }^{\ast }+\gamma D.$$

This estimator is always more efficient than the case–control estimator; it is as efficient as the case–control estimator with an infinitely large number of controls per case. For the data of Psaty et al, the case–control estimator was 0.53 with 95% confidence interval (0.26, 0.79) and the case–only estimator was 0.45 with 95% confidence interval (0.33, 0.84). The increase in precision is relatively small in this example as the ratio of cases to controls was about 1:3, giving an asymptotic relative efficiency of 3/4 for the case–control estimator.

This simple case–only approach is limited to situations where either D or G is binary and there are no other environmental variables in the model. More recent research has constructed semiparametric maximum likelihood estimators that have the efficiency of the case–only estimator but can be applied to arbitrary logistic regression models ((Chatterjee and Carroll, 2005)). In the rare events setting it is also straightforward to impose the gene–environment independence assumption by calibration. The resulting estimators are fully efficient in saturated models and have high efficiency in general models.

The calibration equations for the simple 2 × 2 × 2 table in the α-adducin example are

$$\sum _{i:Y_i=0}{g}_i(G_i-\overline{G})(D_i-\overline{D})=E[(G_i-\overline{G})(D_i-\overline{D})\mid Y_i=0]=0$$ (10)

where Ḡ and D̄ are the means of G and D in controls. In this simple setting the calibration weights g_i ensure that the gene–drug odds ratio in controls is estimated as exactly zero, the known population value. The resulting estimate of exp(γ) is exactly the case–only estimate and the estimated standard error also agrees with the case–only analysis.

The calibration approach extends readily to multiple drugs or doses and to more general genetic models than the dominant model used by Psaty et al. If G and D are categorical variables, we have a calibration constraint of the form in equation 10 for each combination of a category of G and a category of D. If G or D are continuous, we need to specify a finite set of basis functions such as polynomials or splines and apply the calibration constraints in equation 10 to the elements of the basis.

7 Conclusions

Survey calibration estimators give a way to construct AIPW estimators that appears to be more accessible to intuition than the constructions in Robins et al. (1994). In particular, they provide a simple explanation of the ‘estimated weights’ paradox and give insights into choosing functional forms when estimating weights.

In the first example of a case–cohort design the efficient estimator is known, although not straightforward to compute. In the second example the efficient estimator is not known and calibration provides a simple estimator with a useful precision–robustness tradeoff. In the third example of a model with finite codimension, calibration appears to be fully efficient with rare events and is very straightforward to implement.

Calibration estimators also provide a reasonably general way to combine an inefficient but design-consistent weighted estimator and a precise but possibly inconsistent model-based estimator to gain precision without losing consistency. These estimators may be useful in practice, and also provide a basis for comparison when evaluating more efficient model-based estimators, in place of the ‘straw man’ Horvitz–Thompson estimator.

Appendix: generation of exposure error from Prentice (2002) model. Z is true exposure, V is a binary covariate that affects measurement error (eg sex)

createQ<-function(nsubj,eta,k,muZeta,sigZeta,Z,V){
## Creates a nsubj by k matrix, where row i contains
## repeat observations for subject i
   d0<- 0
   d1<- 1.2
   d2<- -0.2
   d3<- -0.3
   a<- 0.5
   b<- log(2)
   ## Gamma -- random effect for person i (for Q)
   gamSig <- sqrt(a * exp(b*V))
   gam <- rnorm(n=nsubj,mean=0,sd=gamSig)
   zeta <- rnorm(n=(k*nsubj),mean=muZeta,sd=sigZeta)
   Q <- d0 + d1*rep(Z,each=k) + d2*rep(V,each=k) +
       d3*rep(Z*V,each=k) + rep(gam,each=k) + zeta
   Q <- t(matrix(Q,ncol=nsubj))
   return(Q)
}
‘Large’ error model has muZeta=2, sigZeta=1. ‘Moderate’ error model has muZeta=1,
sigZeta=0.5. Both have Z ~ N(0, 1), V ~ Bernoulli(0.5).