Effect of Retention in Elementary Grades on Transition to Middle School

Abstract

The authors investigated the effects of retention in grades 1 to 5 on students’ reading and math achievement, teacher-rated engagement, and student-reported school belonging in middle school. From a multiethnic sample (N = 784) of children who scored below the median on a test of literacy in grade 1, an average of 75 students subsequently retained in grades 1 to 5 were matched with an average of 299 continuously promoted students on the basis of propensity to be retained in the elementary grades. A total of 20 imputed datasets were analyzed, all of which showed good balance across the 67 baseline covariates used to calculate propensity scores. The hypothesis that retained students, who are “old for grade” when they make the transition to middle school, would have a more difficult transition to middle school than promoted peers was tested with 3-level, piecewise growth modeling. Piece 1 included assessments prior to the transition to middle school, and piece 2 included assessments after the transition. Retained and continuously promoted students did not differ on any of the outcome measures during the year prior to transition, nor did they differ in their post-transition trajectories. Discrepancies between these results and results of prior research are discussed in terms of demographic and generational differences as well as differences in methodological rigor.

Grade retention in schools in the United States has a long history characterized by fluctuations in the frequency and application of this educational intervention (Bali, Anagnostopoulos, & Roberts, 2005; Owings & Magliaro, 1998). In 2007, about 10% of students in kindergarten through grade 8 had ever been retained in a grade during their school career (National Center for Education Statistics, 2009). Whereas earlier reviews of the retention literature concluded that grade retention has a negative effect on achievement (for meta-analytic reviews, see Holmes, 1989 and Jimerson, 2001a, and for narrative reviews, see Jimerson, 2001b; Shepard, Smith, & Marion, 1996; and Sipple, Killeen, & Monk, 2004), recent studies that employ more rigorous controls for pre-retention differences between promoted and retained students do not report negative effects of retention on achievement (Allen, Chen, Willson, & Hughes, 2009; Lorence, 2006; Wu, West, & Hughes, 2008, 2010). Effects of retention also differ based on (a) the length of follow up, (b) the use of same-grade or same-age comparison groups, and (c) the degree to which the achievement measure is closely aligned with the curriculum (Allen et al., 2009; Hughes, Chen, Thoemmes, & Kwok, 2010; Wu et al., 2010). The present study employs propensity score matching and piecewise growth models to investigate the effect of grade retention during elementary school on students’ trajectories for scores on a nationally normed measure of reading and math for the 3 years following the transition to middle school.

Grade Retention, Middle School Adjustment, and School Completion

Students who have been retained by grade 7 are less likely to complete high school than their low-achieving but continuously promoted peers (Alexander, Entwisle, & Dauber, 2003; Jimerson, 2001b; Temple, Reynolds, & Meidel, 2000). Importantly, even when previously retained and continuously promoted students achieve at comparable levels in grades 8 and 9, retained students are less likely to leave school with a high school diploma than their matched, promoted peers (Alexander et al., 2003). Researchers have speculated that the effects of grade retention on school completion are mediated by its effects on more proximal indicators of psychological and behavioral disengagement from school during the middle school years (Alexander et al., 2003; Pagani, Tremblay, Vitaro, Boulerice, & McDuff, 2001).

Many researchers suggest that dropping out of school is best viewed as a process of disengagement from school that may begin as early as the elementary grades (Alexander, Entwisle, & Horsey, 1997; Roderick, 1994). According to this view, dropping out of school is the culminating event in a gradual process of psychological and behavioral disengagement that includes the following: (a) a lack of interest in and liking for school (Archambault, Janosz, Morizot, & Pagani, 2009; Finn, 1989;); (b) low academic participation and effort; (c) low conformity to school norms, values, and rules; and (d) absences and skipping classes (Finn & Rock, 1997; Fredericks, Blumenfeld, & Paris, 2004;). This view is supported by longitudinal studies that document a relation between disengagement in the middle school grades and noncompletion of high school (Alexander et al., 2003; Mahoney & Cairns, 1997; Ream & Rumberger, 2008).

The scant empirical literature regarding the effects of retention in the elementary grades on middle school academic and psychosocial adjustment suggests that retained students struggle academically and behaviorally after they leave elementary school (Alexander et al., 2003; Griffith, Loyd, Lane, & Tankersley, 2010; Pagani et al., 2001; Temple et al., 2000). Although these longitudinal studies have contributed a great deal to our understanding of the educational pathways of children retained in the early grades, the lack of a comparison group of promoted students who were at the same risk for grade retention, prior to any child being retained, poses challenges to reaching inferences about the causes of differences in achievement between previously retained and continuously promoted students (Campbell & Stanley, 1963; Shadish, Cook, & Campbell, 2002; West & Thoemmes, 2008). Additionally, no previous study has specifically tested the effect of retention in the elementary grades on students’ trajectories for achievement as well as psychological and behavioral engagement in middle school.

Middle School Transition and Previously Retained Students

Normative changes at transition to middle school

In the majority of school districts throughout the United States, students transition to middle school after grade 5 and make a second transition to high school at grade 8 or 9. However, other school patterns are not uncommon, including earlier transition to an intermediate school (typically grades 5 and 6), followed by a transition to junior high (typically grades 7 and 8; Snyder & Dillow, 2010). For the sake of parsimony, the term middle school will refer to the school level that follows elementary school. The move from elementary to middle school is difficult for many youth. On average, students’ grades and academic effort decrease between the last year of elementary school and the first year of middle school (Burchinal, Roberts, Zeisel, & Rowley, 2008; Chung, Elias, & Schneider, 1998; Seidman, Allen, Aber, Mitchell, & Feinman, 1994). Students also report a decline in their self-esteem and sense of school belonging and an increase in anxiety and depression as they transition to middle school (Anderman, 2003; Duchesne, Ratelle, Poitras, & Drouin, 2009; Seidman et al., 1994). Students also decline in their perceived scholastic competency at the transition, a change that persists throughout middle school (Cantin & Boivin, 2004). If these academic and psychological trajectories continue, they may lead to school failure, withdrawal, and ultimately school dropout (Finn, 1989).

Researchers have posited that changes in the context of schooling from elementary school to middle school account for some of the negative effects of the transition on student psychological and academic adjustment (Eccles & Midgley, 1989; Eccles, Wigfield, Midgley, & Reuman, 1993; Midgley, Anderman, & Hicks, 1995). For example, the social life in middle school is more complex than in elementary school as students interact with an expanded number of peers during the day. Multiple classes and teachers also increase demands on students’ organizational skills. These changes in school context occur when students are becoming more socially self-conscious and undergoing rapid psychological and physiological changes associated with adolescence. In summary, the considerable changes in educational processes, in addition to rapid, co-occurring developmental changes, mark a major transition or turning point in a young adolescent’s life, with potentially life-long implications (Elder, 1998).

Previously retained students and the transition to middle school

As discussed above, the transition from elementary school to middle school entails a change in school context that occurs at a developmentally sensitive time. Because students who have been retained in the elementary grades are typically one year older than their classmates when they transition to middle school, they are further along in the developmental changes associated with adolescence. The most significant change during early adolescence is puberty, and the physical changes during puberty are most notably the development of secondary sex characteristics. These physical changes of puberty impact not only how adolescents view themselves but also how others view their attractiveness and maturity (Alsaker, 1995). Furthermore, a major milestone in female development is menarche, or the first menstrual cycle. The mean age of menarche in the United States has been declining over the last century and is currently 12.4 years (McDowell, Brody, & Hughes, 2007). In the current study, the mean age of the promoted sample in September of grade 6 was 11 years 7 months, whereas the mean age of the retained sample was 12 years 6 months. Therefore, retained female children begin middle school at approximately the national mean age of menarche. The rapid physical and psychological changes during the middle school years may interfere with social integration for retained children.

Retained students’ advanced stage of pubertal development, relative to their younger classmates, may alter peer interactions. For example, being “old for grade” may lead to a greater preference for same-age friendships (versus same-grade friendships) that are more likely to involve out-of-school activities and a corresponding decline in attachment to school (Mahoney & Stattin, 2000). Consistent with this reasoning, previous research suggests that students who are retained in the elementary grades have more difficulty with the transition to middle school than do students who were continuously promoted during the elementary grades. In the Baltimore Schools Study (BSS; Alexander et al., 2003), children retained in grade 1 declined more in teacher-awarded grades in grade 7, relative to continuously promoted comparison students. In the Chicago Longitudinal Study (CLS), children retained in the early elementary grades performed worse on norm-referenced achievement tests in reading but not in math in grade 7, relative to a low-achieving comparison group (McCoy & Reynolds, 1999). Both the BSS and the CLS found that students retained in the early grades and continuously promoted comparison students typically did not differ in achievement at the end of the elementary grades; however, early retainees slipped in achievement after the transition to middle school, suggesting that the effects of retention may differ at different developmental periods. Consistent with “old for grade” reasoning about retention’s effects, in the CLS, students who were “old for grade” in high school, whether due to delayed school entrance or due to retention, were equally at risk for dropping out of school (Roderick, 1994).

Gender effects

Some studies suggest that girls report greater psychological stress during the transition to middle school than boys (Grills-Taquechel, Norton, & Ollendick, 2010; Nolen-Hoeksema & Girgus, 1994); however, gender effects on academic outcomes are not consistently found (Chung et al., 1998). Gender may also moderate the effects of earlier grade retention on the transition to middle school. Retained girls and boys may share experiences with adolescents who reach puberty early, in that the retained youth are more advanced in pubertal development than their classmates. Research on age of puberty finds that girls who reach puberty before their peers are more likely to be victimized and have symptoms of depression (Compian, Gowen, & Hayward, 2009), while early adolescent boys who reach puberty early are more likely to engage in deviant behavior (Williams & Dunlop, 1999).

Transition grade effects

As described above, schools differ in the grade at which students exit elementary school and the grade composition of the school to which students transition after elementary school. Although the most common pattern in the schools in the current sample involves a transition to middle school at grade 6, some students transition at grade 5. The difference in age grouping, as well as possible differences in instructional processes associated with these patterns, may affect post-elementary school transition trajectories.

Statement of Purpose

The current investigation tested the proposition that retention in the elementary grades has a negative impact on students’ academic achievement and psychological and behavioral engagement in middle school. Specifically, we examined students’ trajectories for scores on a nationally normed measure of reading and math achievement and two indices of student engagement: student perceived sense of belonging to school and teacher-reported behavioral engagement. Student reports of a sense of belonging to school, or identification with school, is positively associated with conformance to school rules and expectations, school attendance, and effort at school (Furrer & Skinner, 2003). Teacher-rated behavioral engagement in classroom learning activities consistently predicts students’ academic and behavioral adjustment as well as emotional well-being (Skinner, Furrer, Marchand, & Kindermann, 2008).

We examined the effects of retention not only on initial post-transition adjustment but also on post-transition growth. Using piecewise growth models, we investigated students’ intercept and slope estimates on measures of school engagement and achievement prior to and after the transition from elementary school to middle school. The key interest was the effect of retention in the elementary grades on post-transition level and slope of achievement and engagement (i.e., piece 2), rather than on trajectories for these outcomes prior to the transition (piece 1).

Previous publications with the same longitudinal sample used in the current study have reported on the effect of retention in grade 1 on achievement trajectories through the elementary grades (Moser, West, & Hughes, 2012). Findings revealed that by the end of grade 5, children retained in grade 1 and children promoted in grade 1 did not differ on their scores on a nationally normed measure of reading and math achievement in grade 5 (although retained students were, on average, a year older in grade 5 than their matched promoted students). Because the current investigation is based on the reasoning that being “off age” for grade may hamper the transition to middle school, participants include students retained once in any elementary school grade (not just grade 1, as in Moser et al., 2012) and students continuously promoted during the elementary school grades. Thus, pre-transition trajectories include assessment waves that precede grade retention for some students. For this reason, any differences in pre-transition trajectories between the “ever-retained” and the continuously promoted students cannot be definitively attributed to the effect of retention. We include the pre-transition trajectories for descriptive purposes only —and not for the purpose of estimating an effect of retention on pre-transition growth trajectories. Of interest is how students who are “off age” due to grade retention make the transition to middle school, relative to continuously promoted students who, at grade 1, were at comparable risk of being retained in the elementary grades.

Study Hypotheses

We hypothesized that the post-transition trajectories for reading, math, teacher-rated engagement, and student-perceived school belonging would be more negative (i.e., displaying lower intercept and slope) for students retained in the elementary grades, relative to propensity-matched continuously promoted students. We also tested whether student gender or the grade at transition to middle school (i.e., grade 5 or 6) affects post-transition trajectories or moderates the relation between retention status and post-transition trajectories. Because no prior study has investigated the moderating role of gender or grade of transition on the effect of retention on post-transition trajectories, no directional hypotheses were made.

The current study extends the existing literature on the effects of grade retention on middle school adjustment in several ways. First, the study uses modern methods for equating retained and continuously promoted students on their risk for being retained in the elementary grades, prior to any child being retained (see the following section on propensity matching). A large number of variables at the child, family, school, and district levels are associated with the treatment selection (i.e., retention versus promotion) and with the measured outcomes (Reynolds, 1992; Willson & Hughes, 2006). Due to this potential selection bias, a finding that retained children experience more negative outcomes at some future point in their academic careers, compared to all promoted children (regardless of level of risk for retention), may tell us little about the effect of retention. Second, the study employs piecewise growth models to investigate the effect of retention on the level and growth (i.e., intercept and slope) of outcomes as students transition from elementary school to middle school. The analysis of growth on outcome measures during the middle school years reflects the view that adjustment to middle school is a developmental process rather than a discrete event. Third, whereas the seminal longitudinal studies investigating the effect of retention in the elementary grades on post-elementary school performance were conducted with poor, urban, African American students who were enrolled in grade 1 in fall of 1982 (Alexander et al., 2003, using the BSS sample) or kindergarten of fall 1985 (Temple et al., 2000, using the CLS sample), the current study sample is ethnically and racially diverse and attended grade 1 in suburban or urban school districts in the Fall of 2001 or 2002. Thus, study findings may be more relevant to contemporary educational practices and a broader segment of students.

Method

Participants

Participants included a subsample of 561 students recruited in the fall of 2000 or 2001 for a larger longitudinal study when they were in grade 1 (Hughes & Kwok, 2006). Students in the larger longitudinal sample (N = 784) were enrolled in one of three school districts (one urban and two small city districts) in Texas and were selected into the study on the basis of scoring below the median on a district-administered test of literacy administered in the spring of kindergarten or the fall of grade 1. Additional inclusionary criteria for the larger study included speaking English or Spanish, not receiving special education services other than speech and language services, and not having been previously retained in grade 1. Details on recruitment of the 784 participants are reported in Hughes and Kwok (2006).

At the end of the first 5 years of participation in the study, parent consent for continued participation was received for 569 participants. Almost all nonconsent was due to nonresponse. Relative to active participants, attrited subjects were more likely to be economically disadvantaged and to have lower scores on math achievement; however, they did not differ on other variables (e.g., parent education level, literacy scores, ethnicity, and language dominance). Six students who were retained twice and two students who were retained after the transition to middle school were excluded from the current study. The remaining sample of 561 students included 384 students who were continuously promoted during grades 1 to 5 and 177 students who were retained once during grades 1 to 5. At entrance into the longitudinal study, these 561 participants (54.4% boys) were 6.6 years of age (SD = 0.38), 55.3% were economically disadvantaged, and 11.2% were enrolled in bilingual classrooms. The ethnic composition of the sample was 35.3% White, 24.2% Black, 36.4% Hispanic, and 4.1% Other. These students were enrolled in 35 schools in three school districts at Year 1 and in 77 schools in 49 school districts during their first year of middle school. Propensity scores, based on multiple imputed data sets (as described in a following section), were used to select samples (average n = 374) of students retained once in the elementary grades (average n = 75), and students continuously promoted (average n = 299) during the elementary grades who were matched at Year 1 on their propensity to be retained in the elementary grades. The propensity-matched samples were used in analyses of the effect of retention on the transition to middle school.

Design Overview

To examine the effect of grade retention on the transition from elementary school to middle school, we determined the number of years since entry into the study assessment and the grade at which students transitioned from elementary to middle school or junior high school. Retained students transitioned a year later than did continuously promoted students attending the same school. Within the original data set (n = 561), the results showed that 111 (19.8%), 301 (53.7%), and 149 (26.6%) students transitioned to middle school at Assessment Year 5, 6, and 7, respectively. Results showed that 141 (25.1%), 418 (74.5%), and 2 (0.4%) students transitioned to middle school at Grade 5, 6, and 7, respectively. Based on the average imputed data set (n = 374), results showed that 84 (22.5%), 228 (60.8%), and 62 (16.7%) students transitioned to middle school at Assessment Year 5, 6, and 7, respectively. Results showed that 98 (26.3%), 275 (73.4%), and 1 (0.3%) students transitioned to middle school at Grade 5, 6, and 7, respectively. Because students retained in the elementary grades transition to middle school a year later than do continuously promoted students attending the same schools, retained students typically have one additional wave of pre-transition data and one fewer wave of post-transition data than do continuously promoted students. In the growth curve analyses conducted, only data from the retained students’ second time in a grade was used in analyses. Thus, retained and promoted students had, on average, the same number of assessment waves pre-retention. Both retained and promoted students had the same number of assessment waves post-transition, although it took an additional calendar year to obtain the last assessment for retained students. The average age of retained students and promoted students in September of their first year of middle school was 12.3 years (SD = 0.51) and 11.3 years (SD = 0.62), respectively. Five pre-transition and three post-transition assessments were available for reading and math achievement and for teacher-rated behavioral engagement. For student-reported school belonging, three pre-transition assessments and three post-transition assessments were available. Piecewise latent growth curve analyses were employed to test the effect of retention on piece 1 (pre-transition) and piece 2 (post-transition) intercept and slope.

Assessment Overview

If children or their parents spoke any Spanish, students were individually administered the Woodcock – Muñoz Language Test (Woodcock & Muñoz-Sandoval, 1993) by bilingual (English/Spanish) examiners to determine the child’s language proficiency in English and Spanish. All measures were administered in the language in which the student demonstrated greater language proficiency. If the student demonstrated equal or greater language proficiency in English for 3 consecutive years, subsequent tests were administered in English. Children’s reading and math achievement and sense of school belonging were assessed individually at school by trained research staff, with a minimum of 8 months separating each annual assessment. Reading and math were assessed annually for 8 years; sense of school belonging was assessed annually from Year 4 to Year 8. Each year for 8 years in the spring, teachers completed questionnaires, which included questions regarding students’ behavioral engagement. Teachers received compensation for completing and returning questionnaires. In the elementary grades, the teacher with whom the child spent the most time completed the questionnaire; in middle school, the Language Arts teacher completed the questionnaire, unless that teacher indicated that another teacher knew the child better.

Measures

Reading and math achievement

The Woodcock – Johnson III Tests of Achievement (WJ III, Woodcock, McGrew, & Mather, 2001) is an individually administered measure of academic achievement for individuals 2 years of age to adulthood. The WJ III Broad Reading cluster W scores (stemming from the Letter-Word Identification, Reading Fluency, and Passage Comprehension subtests) and the WJ III Broad Math cluster W scores (stemming from the Calculation, Math Fluency, and Applied Problems subtests) were used. W scores are based on the Rasch measurement model, yielding an equal interval scale. At age 10, the mean W score in the normative sample is 507.95 (SD = 19.87). Any given distance between 2-points on the W scale has the same probability interpretation in any area measured at any level of the test, and standard deviations and standard errors of measurement have the same mathematical meaning at any level and in any area of measurement. Thus, W scores are well-suited for the analysis of longitudinal change. Across the age range of the current sample, the internal consistency reliabilities of both the Broad Reading Cluster scores and the Broad Math Cluster scores ranged from .92 to .96 (M = .94 and .95, respectively). The construct validity of scores on the WJ III and its predecessor, the Woodcock–Johnson Tests of Achievement-Revised (WJ-R; Woodcock & Johnson, 1989), are well supported by evidence (Woodcock & Johnson, 1989; Woodcock et al., 2001).

In Years 1 and 2, children tested as more proficient in Spanish than English were administered the Batería Woodcock–Muñoz: Pruebas de Aprovechamiento – Revisada (Batería – R; Woodcock & Muñoz-Sandoval, 1996), the comparable Spanish version of the WJ-R (Woodcock & Johnson, 1989). The Woodcock – Muñoz Language Survey Normative Update Scoring and Reporting Program (Woodcock & Muñoz – Sandoval, 2001) yields scores for the Batería-R that are comparable to scores on the WJ-R. In Years 3 to 9, children more proficient in Spanish than English were administered the Batería-III (Muñoz-Sandoval, Woodcock, McGrew, & Mather, 2005), which yields scores equivalent to the WJ III. The Broad Reading cluster and Broad Math cluster W scores were used in this study. Internal consistency reliabilities for children ages 6–13 range from .94 to .98 for Broad Reading Cluster scores and from .93 to .94 for Broad Math cluster scores (M = .96 and .94, respectively; Woodcock & Muñoz-Sandoval, 1996). Evidence of construct validity of scores is good (McClelland et al., 2007).

Teacher-rated behavioral engagement

Teachers rated students’ classroom engagement with an 11-item questionnaire. Items were adapted from both the teacher and the student ratings of students’ engagement (Connell & Wellborn, 1991; Skinner, Zimmer-Gemback, & Connell, 1998). Items assess effort, persistence, concentration, and interest. Example items include the following: “tries hard to do well in school, concentrates on doing work”, “tries to look busy” (reverse scored), and “participates in class discussion.” Teachers indicated the extent to which each statement was true of their student on a 1 (not true at all) to 4 (very true) scale. These 11 items demonstrated good factorial validity with the same longitudinal sample. Specifically, exploratory factor analyses with this sample supported three factors: Behavioral Engagement, Interest, and Emotional Engagement (Chen, Hughes, Liew, and Kwok, 2010). The Behavioral Engagement scale has good internal consistency. Across 8 repeated measures of longitudinal study for the current sample, the internal consistency reliability range from .88 to .95 (Median = .92). Scores on this scale predict cross-year changes in students’ reading and math achievement (Chen et al., 2010). In order to test that the 11-item questionnaire of behavioral engagement measures the same constructs across different levels of schools, we conducted factorial invariance testing using year 4 and year 8 scores, representing elementary school and middle school, respectively. We found that the measure of teacher-rated behavioral engagement met the criteria for metric invariance across different school levels.

School belonging

The Psychological Sense of School Membership Scale (Goodenow, 1993) was administered in individual interviews. Students were asked to indicate their agreement on a 5-point Likert-type scale to 18 items that assess students’ perceived acceptance, feelings of inclusion, respect, and encouragement for participation. Higher school membership scores are associated with greater school attendance, higher grades, more positive self-concept, greater time spent on homework, and better social-emotional adjustment (Goodenow, 1993; Hagborg, 1998). Across 5 repeated measures of longitudinal study for the current sample, the internal consistency reliability of school belonging scores range from .83 to .89 (median =.89). Scores on this scale are moderately correlated with students’ perceived level of teacher support and academic self-efficacy (Hughes & Chen, 2011). For the invariance testing of the school belonging measure, we used the same procedure as presented in the invariance testing for behavioral engagement measure. From factorial invariance testing using 18 items of child-rated Psychological Sense of School Membership Scale, we found that the school belonging scale measures the same construct across the elementary school and middle school levels.

Grade retention

Children were considered retained in a given grade if they were in the same grade for two consecutive years. Schools provided information on children’s grade placements each year.

The Propensity Score Matching Procedure

To overcome selection effects in comparisons between retained and promoted students, we used a sample of students matched on the basis of propensity scores. Propensity scores, defined as a student’s probability of being retained in the elementary grades, were calculated based on 67 covariates measured in grade 1, prior to any child being retained. These 67 variables were selected to be as comprehensive as possible, including variables that have been shown in prior research to be associated with grade retention or academic achievement. These variables were assessed with direct child tests and interviews (e.g., IQ, effortful control, liking for school, language proficiency, and academic achievement); teacher questionnaires (e.g., behavioral, academic, and social functioning); parent questionnaires (e.g., family demographics, home-school relationship, and educational aspirations); peer sociometric procedures (e.g., peer-rated acceptance and prosocial and aggressive behaviors); and school records (e.g., child ethnicity, age, and gender, classroom ethnic composition, and bilingual class placement). A complete list of variables is available from the second author. By mimicking an experimental design, which controls the pre-existing differences on these variables between retained and promoted children, propensity matched samples enable us to estimate the effect of grade retention.

Multiple Imputation

Not all participants had complete data on the 67 covariates or on the variables used in the growth models. From our original sample of 561 students, 8%, 8%, 26%, and 10% of the participants had incomplete data for the WJ III Broad Reading cluster, the WJ III Broad Math cluster, teacher-rated behavioral engagement, and school belonging, respectively. Multiple imputation is a statistical method that has become increasingly popular in the literature (Enders, 2011) to handle missing data. Multiple imputation fills each missing value with a set of plausible replacement scores prior to analysis. We employed the multiple imputation routine available in PROC MI in SAS (v.9.2) for creating the imputed datasets. A multiple imputation analysis can be implemented through three phases: (a) an imputation phase, (b) an analysis phase, and (c) an averaging phase. In this study, we adopted a two-step imputation procedure: (a) following the recommendation by Graham, Olchowski, and Gilreath (2007), we first generated the 20 imputed data sets with the 67 variables, which were measured in Time 1, and created the propensity matched groups within each imputed data set; and (b) we included all of the analysis variables (e.g., outcome variables, auxiliary variables, interaction terms, and linear and non-linear term variables) and further generated 20 imputed datasets for each of the propensity matched samples. A total of 400 (20 propensity matched sample data sets × 20 imputed data sets) imputed datasets were generated for the analyses. In the next section, we described the details of the imputation and propensity matching procedures.

Creating propensity-matched groups

At the first step of imputation using 67 Time 1 covariates, we generated 20 imputed data sets, each of which had unique matched groups. The propensity scores were computed utilizing logistic regression analysis. Based on the propensity scores, retained and promoted students in the elementary grades were then optimally matched. We used the one (retained child) to various number (of promoted children) matching scheme (Ming & Rosenbaum, 2001) with the PROC ASSIGN routine in SAS (v.9.2) to create the optimally matched groups. This optimal matching scheme minimizes the sampling error while simultaneously maximizing the sample size (Moser et al., 2012). We also used a caliper distance of 0.25, indicating that any pair of matched groups does not differ by 0.25 standard deviations in their propensity scores. Across the 20 imputed data sets an average of 374 children (ranging from 346 to 410) were successfully matched. The average number of retained children across the 20 data sets was 75 (ranging from 69 to 84), and the average number of promoted children across the 20 data sets was 299 (ranging from 274 to 328). Propensity scores for these cases ranged from 0.00 to 0.99 (M = 0.29, SD = 0.30).

We also checked if the matching results of 20 imputed data sets provided good balance between retained and promoted groups. In other words, for two groups to be balanced, they should not differ on the 67 variables because they were matched based on having a similar probability of being retained. Each of the 20 selected imputed data sets had good balance (i.e., none of the variables in these 20 imputed data sets produced a group difference between retained and promoted groups that was larger than the recommended 0.30 cutoff), which is based on Hedges’ effect size (Hedges, 2007).

Creation of multiple complete datasets for analyses

The second step of imputation included all of the analysis variables (e.g., outcome variables, auxiliary variables, interaction terms, and linear and nonlinear term variables) in each of the 20 propensity matched data sets, which resulted in a total of 400 complete data sets (i.e., 20 different propensity matched data sets generated in the first step of imputation × 20 imputed data sets for each). With 400 complete data sets, we performed the analyses on each complete data set and obtained 400 sets of parameter estimates and standard errors, and aggregated estimates to create a single set of final results using Rubin’s (1987) rules. We utilized SAS (v. 9.2) for all these procedures.

Data Analysis Approach

The effect of retention in elementary grades on post-transition academic achievement (reading and math), behavioral engagement, and school belonging was investigated with piecewise quadratic latent growth models. We centered the time predictor at the transition point (that is, at the grade when a child moved from elementary school to middle school). Centering the time predictor at the transition point allowed us to estimate the effect of retention on the outcome at the transition point (i.e., intercept) and the rate of change in the outcome (i.e., slope) before and after transition with the use of a piecewise (two-pieces) model. That is, piece 1 estimates the average growth trajectory before transition, whereas piece 2 estimates the average growth trajectory after the transition to middle school. As commonly found in longitudinal studies (Pianta, Belsky, Vandergrift, Houts, & Morrison, 2008), growths for reading and math follow a quadratic trajectory rather than a linear trajectory over a long period. Hence, we hypothesized a quadratic piecewise model for our data. Additionally, we examined both linear and cubic growth models and selected the best fitting model by comparing the model fit statistics over these three different growth models. To take into account the dependency among the observations, we used three level multilevel analyses (i.e., repeated measures nested within students and students further nested within propensity score matched groups) with the PROC Mixed routine in SAS (v.9.2). The Restricted Maximum Likelihood (REML) estimation method was used for estimating all the models. Below we present the equations of the multilevel piecewise model for the analysis:

Level -1 Model (repeated measures):

$${\text{Y}}_{\mathit{tip}}={\pi }_{0ip}+{\pi }_{1ip}({\text{Piece1}}_{\mathit{tip}})+{\pi }_{2ip}(\text{Piece}{2}_{\mathit{tip}})+{\pi }_{3ip}(\text{Quadratic}{1}_{\mathit{tip}})+{\pi }_{4ip}(\text{Quadratic}{2}_{\mathit{tip}})+e_{\mathit{tip}}$$ (1)

The subscripts, t, i, and p represent the t-th time measure of the i-th student from the p-th propensity score matched group. As described previously, we centered the time at the grade at which students transitioned from elementary school to middle school for testing the potential effect of grade retention at the transition year. We also created different time predictors to capture the growth rate in the level-1 outcome variable (Y _tip) before transition (i.e., Piece1, which is coded from −5 to 0, and Quadratic1, which is the squared term of Piece1) and after transition (i.e., Piece2, which is coded from 0 to 2, and Quadratic2, which is the squared term of Piece2). The random error term, e_tip, is assumed to be normally distributed with variance equal to σ², which captures the within-student variation. The term, π_0ip, represents the predicted value of the outcome variable Y for person i in matched group p at the transition year. The term, π_1ip, represents the conditional linear growth rate, while π_3ip represents the quadratic acceleration (or deceleration) for person i in matched group p in the elementary level. Similarly, π_2ip represents the conditional linear growth rate, while π_4ip represents the quadratic acceleration (or deceleration) for person i in matched group p in the middle school level.

Level- 2 Model (students):

$$\begin{array}{l}{\pi }_{0ip}={\beta }_{00p}+{\beta }_{01p}({\mathit{Retention}}_{ip})+{\beta }_{02p}({\mathit{Boys}}_{ip})+{\beta }_{03p}(\mathit{Transit}{\mathit{grade}}_{ip})+R_{0ip}\\ {\pi }_{1ip}={\beta }_{10p}+{\beta }_{11p}({\mathit{Retention}}_{ip})\\ {\pi }_{2ip}={\beta }_{20p}+{\beta }_{21p}({\mathit{Retention}}_{ip})\\ {\pi }_{3ip}={\beta }_{30p}+{\beta }_{31p}({\mathit{Retention}}_{ip})\\ {\pi }_{4ip}={\beta }_{40p}+{\beta }_{41p}({\mathit{Retention}}_{ip})\end{array}$$ (2)

Level-2 captures the between-student variation in the intercept as well as the regression coefficients of the four different time predictors. The retention status, Retention_ip, is a dummy coded variable with retained students coded as 1 and continuously promoted and never retained students coded as 0. The gender variable, Boys _ip is a dummy coded variable with male students coded as 1 and female students coded as 0. The transit grade, Transit grade_ip is a dummy coded variable with students who were transitioning at grade 6 coded as 1 and students who were transitioning at grade 5 coded as 0 from elementary school level to middle school level.

In Equation 2, β_00p is the average score at the transition year for the promoted students in the p-th propensity matched group, while β_01p is the average difference of the same score between the retained and promoted students within the p-th matched group. β_02p is the average difference of the same score between the boys and girls within the p-th matched group. β_03p is the average difference of the same score between the students who transit at grade 5 and the students who transit at grade 6 from elementary school to middle school level within the p-th matched group. β_10p is the average conditional linear growth rate on pre-transition period for the promoted kids in the p-th matched group, while β_11p captures the difference in this growth rate between the retained and promoted kids in the same matched group. Similarly, β_20p is the average conditional linear growth rate on post-transition period for the promoted kids in the p-th matched group, while β_21p captures the difference in this growth rate between the retained and promoted kids in the same matched group. β_30p is the average quadratic growth rate on pre-transition period for the promoted kids in the p-th matched group, while β_31p captures the difference in this growth rate between the retained and promoted kids in the same matched group. In the same way, β_40p is the average quadratic growth rate on post-transition period for the promoted kids in the p-th matched group, while β_41p captures the difference in this growth rate between the retained and promoted kids in the same matched group.

We originally ran models including all five random effects, but none of them converged. We then reduced the complexity of the random effects specification by removing most of the random effects and only keeping the one between-student random effect, R_0ip [with variance, V(R_0ip) = τ₀₀], (as represented in Equation 2) which captured the between-student variation in the intercept.

Level -3 Model (propensity score matched groups):

$$\begin{array}{l}{\beta }_{00p}={\gamma }_{000}+u_{00p};\\ {\beta }_{10p}={\gamma }_{100};{\beta }_{20p}={\gamma }_{200};{\beta }_{30p}={\gamma }_{300};{\beta }_{40p}={\gamma }_{400};{\beta }_{01p}={\gamma }_{010};{\beta }_{11p}={\gamma }_{110};{\beta }_{21p}={\gamma }_{210};{\beta }_{31p}={\gamma }_{310};\\ {\beta }_{41p}={\gamma }_{410};\\ {\beta }_{02p}={\gamma }_{020};{\beta }_{03p}={\gamma }_{030};\end{array}$$ (3)

Because the propensity score matched groups are the highest level clustering units in our data, which may still carry some dependency among the students within the same matched groups, we have included this level in our analysis to take into account the potential dependency within the matched groups by including a random effect (i.e., u_00p) at this level. The variance of u_00p is τ₀₀₀, which captures the variation among the propensity matched groups. In Equation 3, γ₀₀₀, γ_100, γ_200, γ₃₀₀, and γ₄₀₀ represent the average score of the outcome variable at the transition year, the conditional linear growth rate of pre-transition, the conditional linear growth rate of post-transition, the rate of acceleration/deceleration on pre-transition, and rate of acceleration/deceleration on post-transition, respectively, for the promoted group. Correspondingly, γ_010, γ_110, γ_210, γ_310, and γ₄₁₀ capture the effects of retention (i.e., the average difference between the promoted group and the retained group) at the transition year, the conditional linear growth rate of pre-transition, the conditional linear growth rate of post-transition, the rate of acceleration/deceleration on pre-transition, and the rate of acceleration/deceleration on post-transition, respectively. γ₀₂₀ and γ₀₃₀ represent the average difference between boys’ and girls’ scores and between students who transit at grade 5 and 6, respectively, of the outcome variable at the transition year.

Results

Descriptive statistics for both ever-retained and promoted groups were conducted, and the means and standard deviations based on the use of same-age comparison for the outcomes across 400 imputed data sets are presented in Table 1. We tested the three different growth models (i.e., linear, quadratic, and cubic) of elementary level grades (piece1) and middle school grades (piece2) and found that the quadratic growth model fit the data the best because the linear model was inappropriate due to the statistically significant quadratic term, and the cubic model did not converge. The results of the quadratic piecewise models for the WJ III Broad Reading cluster and Broad Math cluster are summarized in Table 2. The results of the quadratic piecewise models for teacher-rated behavioral engagement and school belonging are summarized in Table 3. The estimated parameters in Table 2 and 3 demonstrate the results after controlling for the effect of gender and transition grade using covariates in the growth model.

Table 1.

Summary of Descriptive Statistics for Outcome Measures Based on the Use of Same-Grade Comparison Across 400 Imputed Data Sets

	Ever-Retained (n = 75)		Promoted (n = 299)
Outcome measures	Mean	SD	Mean	SD
WJ III Reading
Grade 1	437.42	21.94	439.46	23.79
Grade 2	463.61	18.13	466.60	18.23
Grade 3	478.40	16.24	481.76	16.73
Grade 4	488.83	16.41	492.35	16.85
Grade 5	498.82	19.41	503.17	16.89
Grade 6	505.48	19.65	511.90	18.33
Grade 7	512.30	21.97	519.43	18.84
Grade 8			526.49	19.83
WJ III Math
Grade 1	466.21	13.71	465.79	11.96
Grade 2	463.61	10.19	478.90	9.22
Grade 3	489.69	10.55	489.81	9.38
Grade 4	498.63	9.88	499.24	8.97
Grade 5	506.20	10.85	507.40	9.23
Grade 6	509.98	11.01	513.54	9.33
Grade 7	513.71	12.02	519.91	10.32
Grade 8			521.35	10.45
School Engagement
Grade 1	3.16	1.09	3.38	0.99
Grade 2	3.23	0.87	3.51	1.05
Grade 3	3.29	0.82	3.42	0.81
Grade 4	3.18	0.80	3.39	0.80
Grade 5	3.20	0.83	3.37	0.80
Grade 6	3.21	0.85	3.35	0.79
Grade 7	3.09	0.87	3.29	0.80
Grade 8			3.29	0.84
School Belonging
Grade 1
Grade 2
Grade 3	4.00	0.62
Grade 4	3.94	0.63	3.85	0.64
Grade 5	3.89	0.70	3.90	0.63
Grade 6	3.80	0.70	3.84	0.65
Grade 7	3.80	0.72	3.85	0.64
Grade 8			3.87	0.63

Note. Because we used same-grade comparisons, ever-retained students had one fewer wave than did continuously promoted students. For ever-retained students’ in elementary grades (pre-transition), we used data only from the second time in repeated years for all outcome measures. WJ III Broad Reading cluster, WJ III Broad Math cluster, and the School Engagement measure were assessed from Year 1 to 9, whereas the School Belonging measure was assessed from Year 4 to 9.

Table 2.

Estimated Parameters for Academic Achievement Measures Across 400 Imputed Data Sets

Outcomes	WJ III Reading		WJ III Math
	Estimates	SE	Estimates	SE
Intercept
Average initial status at transition year for promoted (γ000)	502.51*	2.12	507.05*	1.05
Average difference between retained and promoted at transition year (γ010)	−0.47	2.76	−1.13	1.46
Quadratic
Average quadratic acceleration/deceleration on pre-transition for promoted (γ300)	−1.79*	0.34	−0.79*	0.26
Average quadratic acceleration/deceleration on post-transition for promoted (γ400 )	1.33*	0.67	0.79	0.50
Average difference between retained and promoted on quadratic acceleration/deceleration pre-transition (γ310 )	−0.11	0.53	−0.10	0.40
Average difference between retained and promoted on quadratic acceleration/deceleration post-transition (γ410)	1.30	2.29	1.20	1.46
Conditional Linear
Average linear slope on pre-transition for promoted (γ100)	5.51*	0.64	5.85*	0.36
Average linear slope on post-transition for promoted (γ200)	5.63*	1.20	2.96*	0.70
Average difference on linear pre-transition slope between retained and promoted (γ110)	−1.77	1.51	−1.27	0.92
Average difference on linear post-transition slope between retained and promoted (γ210)	−.23	4.58	−1.18	2.54
Covariate
Gender (γ020)	−2.62*	1.42	1.46*	0.74
Transit grade (γ030)	7.34*	1.52	4.00*	1.02
Random Effects
Residual, σ2 (etip)	131.94		42.93
Between student-level variance, τ00 (R0ip)	199.76		52.18
Between propensity-matched group variance, τ000 (u00p)	9.86		2.10

Note.

^*p < .05 (two-tailed).

Gender was coded as 1 for boys (54.4%) and 0 for girls. Transit grade was coded as 1 for Grade 6 (74.5%) and 0 for Grade 5.

Table 3.

Estimated Parameters for School Engagement Measures Across 400 Imputed Data Sets

Outcomes	Behavioral Engagement		School Belonging
	Estimates	SE	Estimates	SE
Intercept
Average initial status at transition year for promoted (γ000)	3.38*	0.08	3.38*	0.09
Average difference between retained and promoted (γ010)	0.05	0.14	0.07	0.14
Quadratic
Average quadratic acceleration/deceleration on pre-transition for promoted (γ300)	−0.01	0.08	−0.03	0.21
Average quadratic acceleration/deceleration on post-transition for promoted (γ400 )	−0.03	0.16	−0.03	0.16
Average difference between retained and promoted on quadratic acceleration/deceleration pre-transition (γ310 )	0.01	0.12	0.07	0.25
Average difference between retained and promoted on quadratic acceleration/deceleration post-transition (γ410)	0.11	0.37	0.10	0.37
Conditioned Linear
Average linear slope on pre-transition for promoted (γ100)	-0.08*	0.04	−0.09	0.11
Average linear slope on post-transition for promoted (γ200)	0.05	0.08	0.04	0.08
Average difference between retained and promoted on linear pre-transition slope (γ110)	0.06	0.11	0.18	0.19
Average difference between retained and promoted on linear post-transition slope (γ210)	−0.21	0.27	−0.23	0.26
Covariate
Gender (γ020)	−0.32	0.24	−0.29	0.24
Transit grade (γ030)	0.06	0.26	0.06	0.26
Random Effects
Residual, σ2 (etip)	0.46		0.26
Between student-level variance, τ00 (R0ip)	0.25		0.15
Between propensity-matched group variance, τ000 (u00p)	0.01		0.00

Note.

^*p < .05 (two-tailed).

Gender was coded as 1 for boys (54.4%) and 0 for girls. Transit grade was coded as 1 for Grade 6 (74.5%) and 0 for Grade 5.

Effect of Retention on Reading and Math Scores

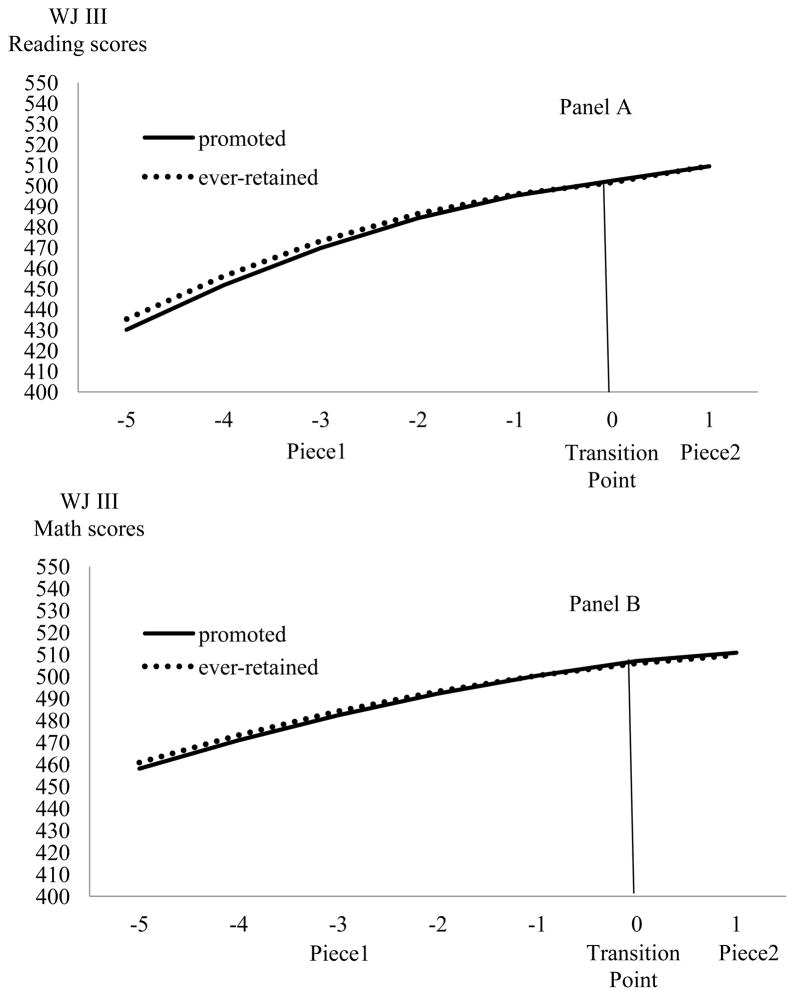
As presented in the Intercept section in Table 2, the promoted students, on average, scored 502.51 points on the WJ III Broad Reading cluster and 507.05 points on the WJ III Broad Math cluster at the transition year, which did not differ significantly from scores of the ever-retained students. Additionally, as presented in the Quadratic and Conditional Linear sections of Table 2, before transition to middle school (pre-transition), a statistically significant quadratic growth trends and the corresponding conditional linear growth rates for both WJ III Broad Reading cluster (γ _{300_quadratic_Reading} = −1.79, p <.001; γ _{100_linear_Reading} = 5.51, p <.001) and WJ III Broad Math cluster (γ _{300_quadratic_Math} = −0.79, p <.001; γ _{100_linear_Math}= 5.85, p <.001) were found for the promoted students. As shown in Figure 1, a decelerated quadratic trend (i.e., the negative sign of the quadratic growth coefficient) for both reading (Panel A) and math (Panel B) was found before transition to middle school (as marked from -5 to -1 on the x axis in each panel; Piece1). In other words, the rate of improvement on the reading and math scores was faster at the beginning of the study, and this rate of improvement reduced (or decelerated) when approaching the transition year (the shape of the curve reaching to the top at the transition year).

Figure 1.

Estimated quadratic growth trajectories of WJ III Broad Reading cluster W scores (Panel A) and WJ III Broad Math cluster W scores (Panel B) for ever retained and promoted students in elementary grades. The transition point (0 on the x axis) marks the transition from elementary school level to middle school level. Piece1 represents the developmental growth before the transition to middle school (from -5 to -1). Piece2 represents the developmental growth after the transition to middle school (from 0 to 1).

Similarly, after transition to middle school (post-transition), a statistically significant quadratic growth trend and the corresponding conditional linear growth rate of the reading scores (γ _{400_quadratic_Reading}= 1.33, p = .024; γ _{200_linear_Reading}= 5.63, p <.001) were still found, whereas only statistically significant linear growth rate of the math scores (γ _{200_linear_Math}= 2.96, p <.001) was found for the promoted students. As shown in Figure 1, these results indicate that the reading scores improved at an accelerated rate (Panel A), whereas the math scores improved at a steady rate (Panel B) for the promoted students after transition to middle school (as marked from 0 to 1 on the x axis in each panel; Piece2). There was no statistically significant difference between the promoted and ever-retained students on their level of performance on the reading and math outcome measures at the transition year or in the pre-transition and post-transition quadratic growth trends. In other words, the ever-retained students and their promoted counterparts shared very similar growth trends on both reading and math scores over the middle school years.

Effect of Retention on Behavioral engagement and School Belonging

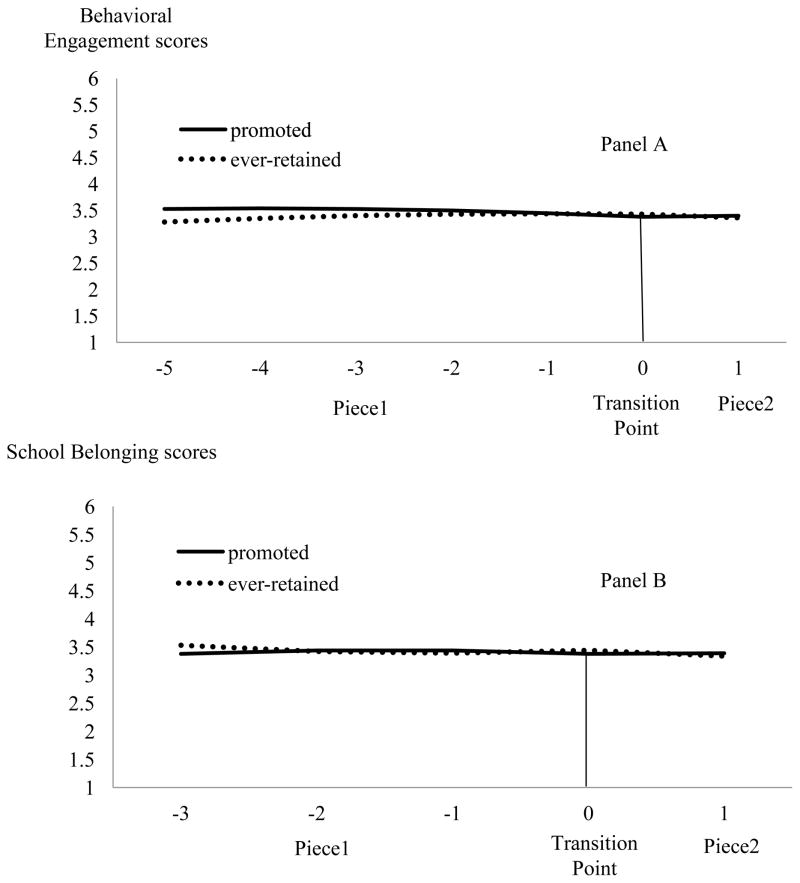
As presented in the Intercept section in Table 3, for the promoted students, the average teacher-rated behavioral engagement score was 3.38, and their average school belonging score was 3.38 at the transition year. There was no statistically significant difference between the promoted and ever-retained students on these two scores at the transition year. As presented in the Quadratic and Conditional Linear sections, a statistically significant negative linear growth rate in behavioral engagement before transition to middle school (pre-transition) was found for the promoted students, γ _{100_Engagement} = −0.08, p = .017. As shown in Figure 2, Panel A, it indicates that before transition to middle school (Piece1), their behavioral engagement was higher at the beginning (i.e., grade 1) of the study and continuously decreased when approaching the transition year. There was no change in behavioral engagement for the promoted students after transition to middle school (Piece2). Similarly, as shown in Figure 2, Panel B, the school belonging of the promoted students was very stable over the course of the study, as indicated by the statistically nonsignificant growth rate parameter estimates. There was no statistically significant difference between the ever-retained and promoted students on any of the growth parameters for these two measures (Figure 2, Panel A and Panel B, for behavioral engagement and school belonging, respectively). These nonsignificant findings between the two groups imply that both ever-retained and promoted students shared similar patterns of behavioral engagement and student-reported school belonging at the transition year as well as before and after transition to middle school.

Figure 2.

Estimated growth trajectories of teacher-rated behavioral engagement scores (Panel A) and student reported school belonging scores (Panel B) for ever-retained and promoted students in elementary grades. The transition point (0 on the x axis) marks the transition from elementary school level to middle school level.. Piece1 represents the developmental growth before the transition to middle school (from -5 to -1 and from -3 to -1 for Panel A and Panel B, respectively). Piece2 represents the developmental growth after the transition to middle school (from 0 to 1).

Supplementary Power Analyses

To further validate the statistically nonsignificant findings between the promoted and ever-retained students on all the outcome measures, we conducted additional power analyses to examine the likelihood that the nonsignificance of the findings was the result of true nondifference between the two groups or the result of insufficient power due to the sample size. The power analyses were carried out using the Monte Carlo procedure in Mplus (V.6.11; Muthén & Muthén, 2010). Based on the 400 imputed data sets, we used the average sample size, namely, 299 promoted students and 75 retained students, as the sample size for our Monte Carlo study. We adopted the parameter estimates from Table 2 to set up our model for simulation. The mean group difference between the retained and promoted students was specified based on Hedges’ effect size (Hedges, 2007). One thousand replications were generated for each achievement outcome measure separately. Given our sample size, the empirical power for detecting a small effect size (i.e., a small group difference between the promoted and ever-retained students on the post-transition growth rate based on Cohen’s [1988] guideline) were .85 for the WJ III Broad Reading cluster and .80 for the WJ III Broad Math cluster.

Effects of Covariates (Gender and Transition Grade)

We examined the main effect of gender at the transition year and only found, on average, significantly higher achievement of girls than boys on WJ III Broad Reading cluster (γ _{020_Reading}= −2.62, p = .033) and significantly higher achievement of boys than girls on WJ III Broad Math cluster (γ _{020_Math}= 1.46, p = .049).We also examined the potential gender effect on all the growth rates (i.e., gender by corresponding time predictor interaction effects) for all four outcomes. We found no significantly significant gender effect in any of the models and outcomes. Similarly, we tested the potential effect of grade of transition from elementary school to middle school at the transition year by including different grade of transition (grade 5 versus grade 6) as a covariate in the growth models. We found no significantly significant effect of transition grade on behavioral engagement or student-reported school belonging. We found significant higher achievement, on average, of the students who transitioned to grade 6 than those who transitioned to grade 5 on WJ III Broad Reading cluster (γ _{030_Reading}= 7.34, p < .001) and WJ III Broad Math cluster (γ _{030_Math}= 4.00, p < .001) at the transition year. However, student’s higher performance on reading and math test scores in grade 6 than grade 5 appears to follow the natural developmental growth of academic achievement at this age (Woodcock et al., 2001) rather than an effect of retention year.

Discussion

Using samples of students retained once in the elementary grades (excluding kindergarten) and students continuously promoted during the elementary grades who began grade 1 at equivalent likelihood of being retained during elementary school, we estimated the effect of retention on children’s pre-transition and post-transition trajectories for reading and math achievement, behavioral engagement, and student-perceived sense of school belonging. Based on previous research finding negative effects of elementary grade retention on middle school and high school academic and behavioral adjustment, and the “old for grade” hypothesis (Alexander et al., 2003), we expected that students retained in the elementary grades would perform more poorly during the transition to middle school on measures of achievement, engagement, and school belonging than propensity-matched, continuously promoted students. Using piecewise growth modeling, we tested whether retained and promoted students differed on pre-transition (piece 1) and post-transition (piece 2) growth trajectories. Because pre-retention trajectories included assessment periods that precede retention for some students, the pre-retention growth trajectories are reported primarily to provide a context for analyzing post-transition trajectories. After “shifting back” scores for retained students, such that retained students’ scores only for their second time in a grade were modeled, elementary school growth trajectories for reading achievement, behavioral engagement, and school belonging did not differ. Although retained students had lower growth in math achievement in elementary school, their math achievement levels at the end of elementary school did not differ from those of promoted students. At the year prior to transition, retained and continuously promoted students did not differ on any of the outcome measures.

Of particular interest is the effect of retention in the elementary grades on post-transition growth trajectories. Retained and promoted students did not differ in their level of performance on outcome measures during their first year in middle school or in their post-transition growth in these outcomes. It appears that retained students were not “harmed” by the experience of retention in that being a year older than their classmates did not reduce their academic achievement, behavioral engagement, or sense of belonging to school. These results are contrary to our expectations. We had reasoned that being “off age” for grade at the time of transition and being further into pubertal development than one’s classmates, on average, would hinder successful adaptation to middle school for retained students. Neither gender nor grade of transition altered the effect of grade retention on outcomes.

These results are inconsistent with those previously reported. Although our sample size was smaller than in some studies reporting retention effects on post-elementary school adjustment (Alexander et al., 2003; Temple et al., 2000; Griffith et al., 2010), power analyses suggest that the sample was sufficient to detect a small effect. Several differences between the current study and prior investigations may explain the discrepant findings. Foremost, the current study is the first to use modern propensity matching methods to control for differences between ever-retained and continuously promoted students prior to any child being retained. When a randomized experiment is not possible for ethical or practical reasons, propensity matching that achieves good balance across an extensive and carefully selected set of covariates closely approximates a randomized control design (Shadish, Luellen, & Clark, 2006). Balance checks on our samples matched on propensity scores show good balance across 67 covariates that predict children’s academic and behavioral adjustment in school. Previous longitudinal studies have employed a limited number of statistical controls to compensate for potential selection effects. For various reasons, including the violation of statistical assumptions of multiple covariates, the use of these statistical adjustment procedures is less preferable than the use of propensity matching as executed in the current investigation (Rosenbaum, 2002; Shadish et al., 2006; Thoemmes & West, 2011).

Cohort effects may also explain differences in our results and previous findings. The mid-1990s ushered in the age of standards-based reforms and high stakes testing (Heubert & Hauser, 1999). These reforms emphasized establishing competency standards for students at each grade level and holding both schools and students accountable for meeting them. The No Child Left Behind federal legislation passed in 2001 required that assessments aligned with state standards be used to measure the achievement of all children at each grade level (U.S. Department of Education, 2002). Many states, including Texas, the site of the current study, implemented policies to end social promotion, the practice of allowing students who had failed to meet standards to advance to the next grade (Texas Education Agency, 2007). The current sample entered grade 1 in Fall of 2001 or 2002, in the midst of these changes. Thus, the educational context for retention decisions likely differs in important ways for these students, relative to students who began grade 1 in the 1980s. Contemporary decisions regarding retention may be based more on performance on nationally normed tests than on other student characteristics, subjective criteria, or psychosocial functioning, relative to decisions in prior decades (Willson & Hughes, 2009). When the criteria or decision making processes involved in selecting children for the retention intervention change, it is not unexpected that retention’s effects differ.

The past 15 years have also seen substantial changes in the context of middle schools. In response to a wave of studies documenting the developmental mismatch between middle school students and the structure of middle schools (Eccles & Midgley, 1989; Eccles et al., 1993), middle schools have implemented policies to increase teacher support for students, to build smaller, more supportive groups of learners within the larger school, and to use more developmentally sensitive instructional approaches such as cooperative learning (Balfanz, Mac Iver, & Byrnes, 2006; Fogleman, McNeill, & Krajcik, 2011; Johnson & Fargo, 2010). These changes may have smoothed the transition such that it represents less of a turning point for students’ development. Indeed, in the current investigation, for the retained and promoted students together, the slope for school belonging was not statistically significantly different from zero before or after the transition to middle school. For behavioral engagement, the pre-transition slope for the combined sample was negative (slope coefficient = −.07, SE = .04 [df =58], p = .03), but the post-transition slope was not significantly different from zero. Behavioral engagement decreased slightly (by 0.07 point per school year) before reaching the transition year, and stabilized after students transitioned to middle school.

Finally, differences between the demographic characteristics of students in the current investigation and prior studies may account for differing results. Previous prospective, longitudinal studies were conducted in urban school districts serving predominantly poor African American students (Alexander et al., 2003; Temple et al., 2000). The student population in the current study was recruited during grade 1 from three ethnically diverse districts. The ethnic composition of the total student body of first graders in these schools in 2002 was 25% African American, 27% White, 43% Caucasian, and 5% Other. In summary, the current study is more representative of current retention practices and student demographics and uses modern methods to control for selection effects into retention. Thus, the results have greater relevance for contemporary retention practices.

Study Limitations

The study did not use an experimental design. It is possible that retained and promoted students differed on variables that affect middle school transition, prior to any student being retained. However, the use of propensity scores that achieved good balance across 67 covariates assessed in grade 1 that are associated with students’ future academic and behavioral trajectories, and propensity-matched groups as a level in the analyses, minimizes the risk that unmeasured variables account for our results.

Second, several factors limited our ability to test the effect of retention grade on the transition to middle school. First, of the students retained in grades 1 to 5, 56.9% were retained in grade 1. The finding that grade retention is more frequent in grade 1 than in other elementary grades is consistent with national trends for grade retention (National Center for Education Statistics, 2009). However, the few students retained at grades 2 to 5 limited our ability to test for an effect of retention grade. A more important problem in undergoing such an analysis is the difficulty of interpreting an effect, if found. Because our propensity scores were based on variables measured in grade 1, the finding of an effect of retention grade could be due to differences in post-first grade histories of children retained early versus later. Specifically, one could not rule out the possibility that retention in grades 2 to 5 is a marker of increasing academic difficulties, rather than a cause of subsequent difficulties. Our attempts to address this problem by creating propensity-matched groups of “early” versus “late” retainees, based on Year 1 covariates, were unsuccessful, probably because the early and late retainee groups were highly similar on the covariates. To date, we know of no researchers who have successfully addressed this methodological challenge.

Finally, it is likely that characteristics of the schools to which students transition, such as school climate and instructional processes (Brand, Felner, Shim, Seitsinger, & Dumas, 2003) or racial or ethnic congruence (Benner & Graham, 2009), influence students’ post-transition adaptation. Future studies are necessary to test whether these factors influence the relation between retention histories and middle school adjustment.

Implications

Students who are retained in grades 1 to 5 are performing in middle schools as well as their propensity matched, continuously promoted peers, both academically and in terms of behavioral engagement and student-reported school belonging. Whether these findings support endorsement or a condemnation of the practice of grade retention depends on one’s perspective. Retention did not appear to offer any advantage to these students, nor did it impede their performance in middle school. Importantly, retained students are one year older, on average, than their promoted peers, when they transition to middle school. Accepting the assumption that the close propensity matching mimics the results of a randomized, experimental trial (Rubin, 2007), if retained students had been promoted in grades 1 to 5, they would be performing just as well but would be one year closer to high school completion.

Additional waves of data are necessary to determine if retained students drop out of school at a higher rate than do matched continuously promoted students. Typically, previously retained students reach the age for legally dropping out of school or working as well as other developmental milestones, such as becoming a parent, when they are further away from graduation than are continuously promoted, same-age cohorts. Due to these options and constraints, retained students may perceive the costs and benefits of continuing in school until graduation differently than do their matched, promoted peers. That is, even if retention does not harm students academically or psychosocially, it may increase the risk of not completing high school.