Abstract
Biphasic contact analysis is essential to obtain a more complete understanding of soft tissue biomechanics; however, only a limited number of studies have addressed these types of problems. In this paper, a theoretically consistent biphasic finite element solution of the 2D axisymmetric human knee was developed, and an augmented Lagrangian method was used to enforce the biphasic continuity across the contact interface. The interaction between the fluid and solid matrices of the soft tissues of the knee joint, the stress and strain distributions within the meniscus, and the changes in stress and strain distributions in the articular cartilage of the femur and tibia after complete meniscectomy were investigated. It was found that (i) the fluid phase carries more than 60% of the load, which reinforces the need for the biphasic model for knee biomechanics; (ii) the inner third and outer two-thirds of the meniscus had different strain distributions; and (iii) the distributions of both maximum shear stress and maximum principal strain in articular cartilage changed after complete meniscectomy - with peak values increasing by over 350%.
1 Introduction
The menisci of the knee are C-shaped fibrocartilage discs with a cross-sectional wedge-shape. They are responsible for shock absorption, load transmission, lubrication, and stability within the knee joint [1]. Oftentimes, when the meniscus is torn, it cannot be repaired; thus the affected tissue is either partially or completely surgically removed, otherwise called a meniscectomy. Clinical and animal studies have shown that meniscectomy can lead to cartilage degeneration, bone remodeling, and ultimately the development of osteoarthritis [2]. While the exact sequence of events that leads to the development of osteoarthritis are not yet fully understood, studies have long suggested that after meniscal injury or removal, the mechanics of the joint change [3]. To understand how cells within the tissues respond to these changes requires an understanding of the stresses within the tissues. However, the stress distribution within tissues cannot be readily measured in experimental models; therefore numerical solutions are essential to provide a more complete understanding of knee mechanics.
Many finite element models have been developed to study the biomechanical contact behavior of the knee joint, and most of these models [4–7] considered cartilage and meniscus as single phase solid ignoring the fact that 60–85% of the soft tissues are fluid [1]. Biphasic theory [8], which considers soft tissue as a mixture of a porous-permeable solid phase and an interstitial fluid phase, has demonstrated that the fluid phase carries most of the load in a physiologically relevant short loading times. Therefore, to more fully represent the true physiological biomechanical behavior of the soft tissues of the knee joint, a biphasic contact analysis is required. Biphasic contact analysis is complicated because in addition to the equality conditions required for displacement and traction that a single-phase contact problem consists of, there are two additional equality conditions for relative fluid flow and fluid pressure in the biphasic contact problem [9–13]. The knee joint has femoral cartilage-tibial cartilage contact, femoral cartilage-menisci contact, and tibial cartilage-menisci contact which makes the biphasic contact analysis of the knee joint even tougher. To simplify the biphasic contact problem of the knee joint, several assumptions and simplifications have been used in previous studies [14–18]: no fluid flow takes place between contact surfaces [14–16], which is inconsistent with the equation of mass conservation across the contact interface [9]; a thin flexible membrane with a low stiffness is inserted between the articular cartilage layers and the meniscus [15, 16] – the membrane can absorb most of the applied load, which is not physiologically meaningful; and knee models exclude menisci ignoring the multi-contact feature of the soft tissues of the knee joint [17, 18]. Several studies have been done to develop theoretically consistent biphasic contact analysis of the knee joint [19–21], but these studies either only showed distributions of fluid pressure and total normal stress and therefore did not have a thorough assessment of the biphasic solution [19] or had numerical problems [20, 21]: first, the maximum contact stress was not greater than the maximum fluid pressure in the femoral cartilage, which is not physiologically correct; second, the fluid pressure in the surface layer of the cartilages did not precisely agree with the actual contact boundary due to the incapability of applying accurate zero pressure boundary condition around the contact area.
In summary, to date, there have been no successful implementations of theoretically consistent biphasic finite element contact analysis for the human knee joint, and thus the biphasic behavior of the soft tissues in the knee joint are poorly understood. The aim of this paper is to develop a theoretically consistent biphasic finite element solution of the 2D axisymmetric human knee. Using the model, the interaction between the fluid and solid phases of the soft tissues, the stress and strain distributions within the meniscus, and the changes in stress and strain distributions in the articular cartilage of the knee joint after complete meniscectomy will be investigated.
2 Methods
2.1 Biphasic Contact Modeling Method
The mixed velocity-pressure (v-p) formulation of linear biphasic theory [22] was adopted in this study. The assumption of infinitesimal deformation was used. The governing equations are
| (1) |
| (2) |
where superscripts s and f refer to the solid and fluid phases, respectively; is the solid phase velocity, which is the time derivative of the solid phase displacements ; κ is the permeability which is assumed to be a constant; p is the fluid pressure; (),i denotes the partial derivative with respect to spatial coordinates; and are the solid and fluid phase stress tensors; is the solid phase strain tensor (the superscript s is omitted); is the material property tensor of the solid phase; and δij is the Kronecker delta. In addition, there are constitutive relations for each phase
| (3) |
| (4) |
where ϕs and ϕf are the solid and fluid volume fractions, respectively, for the saturated (ϕs+ϕf = 1) mixture. Void ratio of the soft tissues was assumed to be a constant, and the strain-dependent behavior of the void ratio was not included in this study. Eqs. (3) and (4) can be used to calculate the relative load contribution of the two phases.
Kinetic continuity of contact traction and fluid pressure [9] were used as contact boundary conditions.
| (5) |
| (6) |
| (7) |
| (8) |
These equations correspond to kinematic conditions on the continuity of location of points in contact, Eq. (5); continuity of the relative flow across the contact boundary, Eq. (6); kinetic continuity conditions on the fluid pressure, Eq. (7); and the normal component of solid phase elastic stress, Eq. (8), on the contact boundary.
The augmented Lagrangian biphasic contact framework developed in our previous studies [11–13] was used. An augmentation component was introduced for the contact stress, and an additional iteration level was added where the usual displacement and fluid pressure variables were solved separately from the contact stress. The algorithm was iteratively repeated until it fulfilled a convergence criterion. The biphasic contact equations were implemented in commercial finite element software (COMSOL Multiphysics 4.2®, COMSOL, Inc., Burlington, MA). Details of the biphasic finite element formulation can be found in our previous studies [11–13]; the formulation has been verified for 2D axisymmetric and 3D problems with known solutions and applied to complex geometries, such as the shoulder.
2.2 Axisymmetric Knee Model
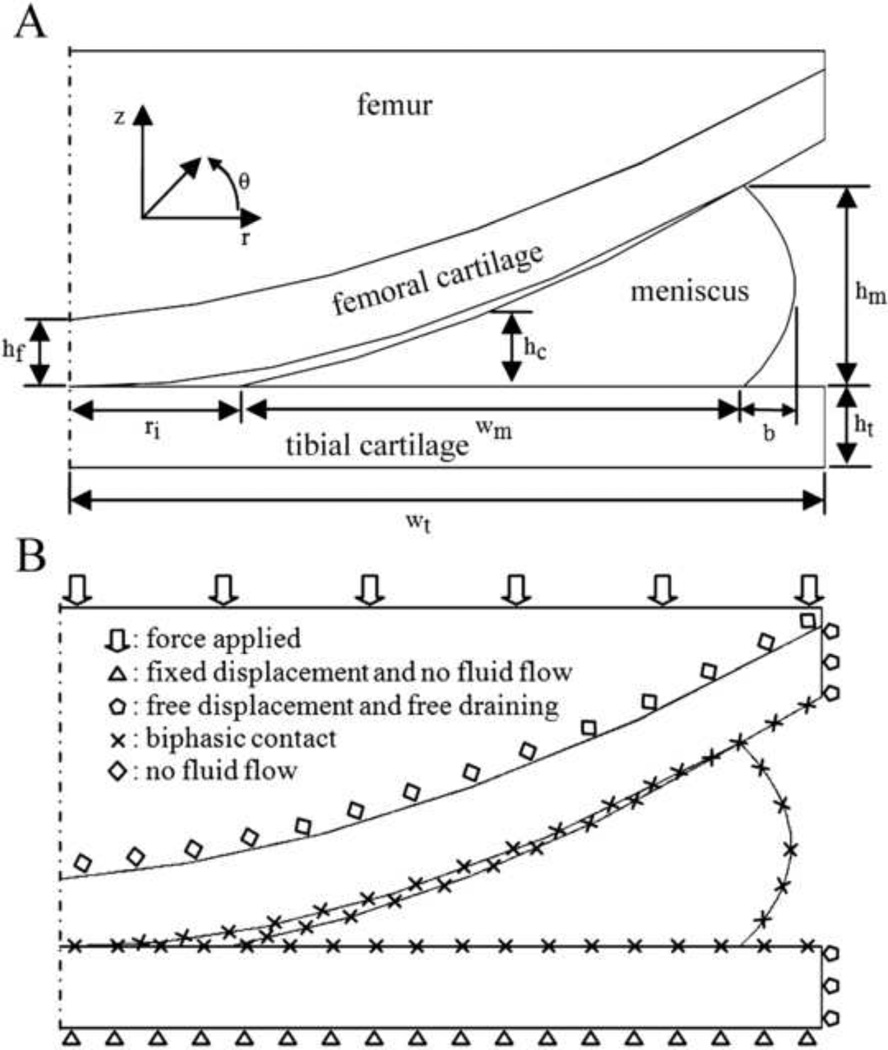
Figure 1A displays the schematic diagram for the axisymmetric tibio-femoral cartilage layers and represents one condyle of the human knee joint. The dimensions of the 2D axisymmetric model were chosen from MRI studies [23, 24] and finite element studies [15, 19, 25] of the normal healthy human knee joint (Table 1). Tibial articular cartilage was modeled as a rectangular region rigidly attached to the subchondral bone and frictionless at its top surface. The femoral cartilage was modeled by a cubic curve and tangent to the top surface of the meniscus and tibial cartilage at both contact points. The tibial surface of the meniscus was flat, while the outer surface of the meniscus was quadratic, and the femoral surface of the meniscus was cubic and tangent to tibia at contact points. Part of the femur was included in the model, and the cartilage-bone interface was assumed to be impermeable. The tibia was assumed to be rigid and impermeable, an assumption that has been used by others [15, 16, 19]. Fluid flow was allowed between contact surfaces of the soft tissues, while free drainage was used for non-contact surfaces of the soft tissues. Linear isotropic biphasic material properties were used for femoral and tibial cartilage, while transversely isotropic biphasic material properties were used for meniscus, and femoral bone was modeled as a linear isotropic solid (Table 2, [26–30]). Three contact pairs were defined to detect contact between the femoral cartilage and tibial cartilage, tibial cartilage and meniscus, and meniscus and femoral cartilage. The bottom boundary of the tibial cartilage was held fixed, and a normal force was applied on the top boundary of the femur. The boundary conditions are illustrated in Figure 1B.
Fig. 1.
A schematic diagram of the axisymmetric meniscus-femur-tibia contact (A). The values of the geometric parameters are shown in Table 1. Boundary conditions of the biphasic model of the knee joint (B).
Table 1.
| Geometric parameters | Values (mm) |
|---|---|
| Tibial cartilage width, wt | 22.4 |
| Tibial cartilage height, ht | 2.4 |
| Inner radius, ri | 5 |
| Meniscal width, wm | 15 |
| Meniscal bulge, b | 1.5 |
| Meniscal height, hm | 6 |
| Meniscal center height, hc | 2.25 |
| Femoral cartilage height, hf | 2 |
Table 2.
Material parameters for meniscus, cartilage, and bone.
| Material parameters | Meniscus [26–28] | Cartilage [29] | Bone [30] |
|---|---|---|---|
| Young's Modulus | Er=Ez=0.075 MPa | E=0.69 MPa | E=10 GPa |
| Eθ=100 MPa | |||
| Poisson's ratio | Vrθ =0.0015 | V=.018 | V=0.3 |
| Vθz=2 | |||
| Vrz=0.5 | |||
| Shear modulus | Grθ =Gθz=Grz=0.025 | N/A | N/A |
| MPa | |||
| Permeability [×10−15] | κ=1.26 m 4/Ns | κ=3 m4/Ns | N/A |
| Solid content | ϕs=0.25 | ϕs=0.25 | N/A |
In the model of two-legged stance, assuming a bodyweight of 60 kg, a total force of 147N was chosen and applied on the top surface of the femoral bone. Here, we assume that the lateral and medial sides of the knee joint share load equally in the standing posture. To help the contact algorithm go through the first several iterations, a force of 0.0147N was applied to the top surface of the femur at t=0s and kept constant until t=0.0001s, then the load linearly ramped over 0.0001 ≤ t ≤ 1s to 147N which was then held constant for 120s.
In the models to investigate the changes of stress and strain distributions after complete meniscectomy, a force of 73.5N was applied to knee models with or without meniscus. This new force is to maintain deformation of the articular cartilage in the range of small strains in the knee model without meniscus, since our preliminary study showed that applying a force of 147N to the knee model without the meniscus resulted in finite deformation of the articular cartilage surfaces. The loading criterion was similar to the model of two-legged stance.
3 Results
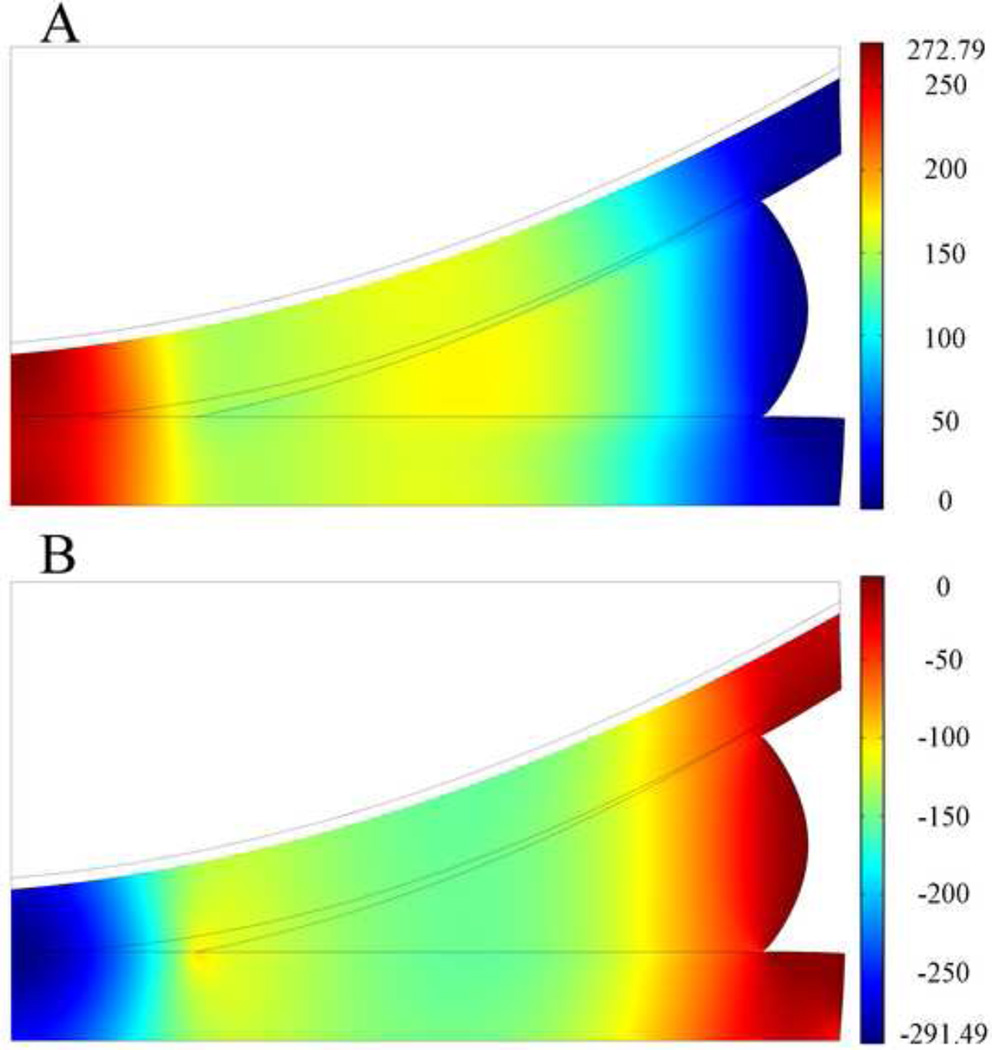
Upon the application of force, the femoral cartilage first contacted the outer part of the meniscus. The contact area increased as a function of time, as load increased. During this time, the contact algorithm correctly detected contact between the femur and tibia, tibia and meniscus, and meniscus and femur. At t=1s, all surfaces came into contact, and smooth distributions of fluid pressure p, and total normal stress , were observed (Fig. 2). The peak fluid pressure and total normal stress were found at the central contact area of tibial and femoral cartilage. There was no variation in total normal stress or fluid pressure through the depth of the cartilage or menisci. The distribution of the contact stress on the top surface of the tibial cartilage was similar to that of total normal stress and ranged from 0–295 kPa with peak contact stress occurring in the middle of the tibial surface.
Fig. 2.
Distribution of fluid pressure p (A, in kPa) and total normal stress , (B, in kPa) at t=1s on deformed geometry of the articular cartilage and meniscus in the two-legged stance model. The peak force applied in this model was 147N. Total normal stress from the femoral bone is not shown. Grey boundary lines are initial position.
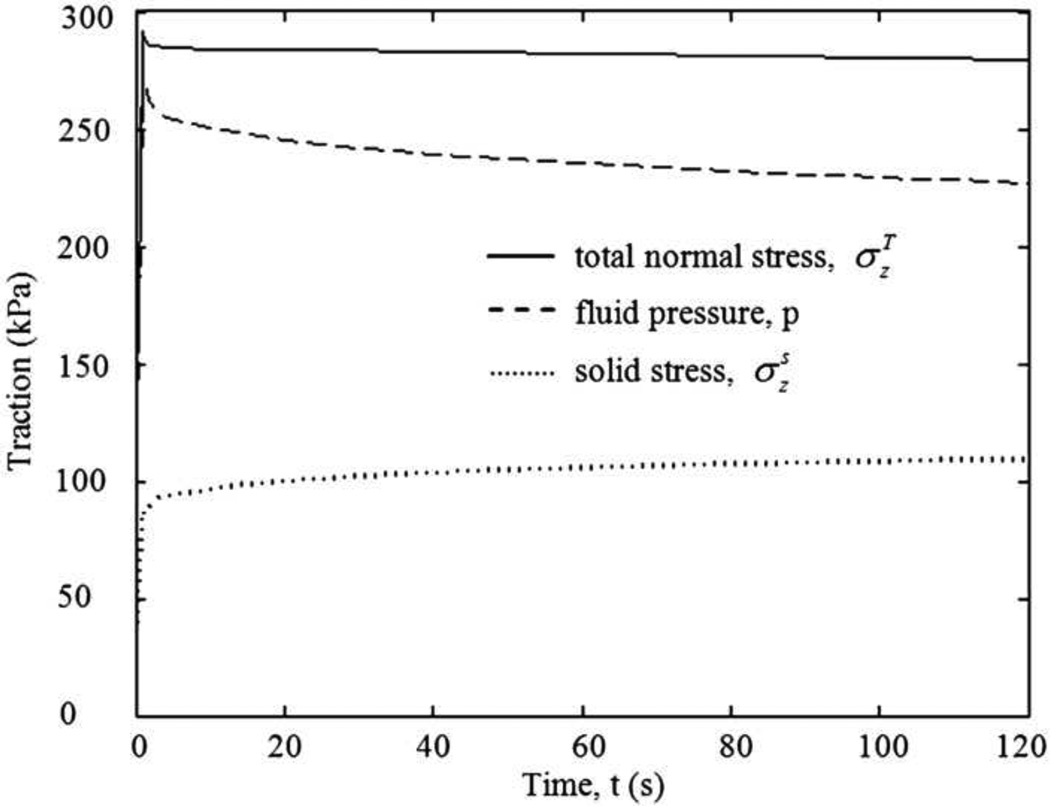
It was of interest to determine the relative contribution of the solid and fluid phases. Our analysis demonstrated that the fluid phase carried approximately 70% of the load at t=1s (Fig. 2). As the applied force was held constant, the distributions of total normal stress and fluid pressure in the soft tissues did not change over time, rather, their values decreased (Fig. 3). The decrease in total normal stress and fluid pressure was pronounced in the first 1s over time, yet the solid stress increased in the first 1s of loading, and continued to increase at the steady state suggesting that the relative contribution of the fluid phase decreased over time. At t=120s, approximately 61% of the load was taken up by the fluid phase.
Fig. 3.
Changes in the peak values of total normal stress , fluid pressure p, and solid stress , in the femoral and tibial cartilage of the two-legged stance model as a function of time. The peak force applied was 147N. The signs of total normal stress and solid stress were reversed for display purposes.
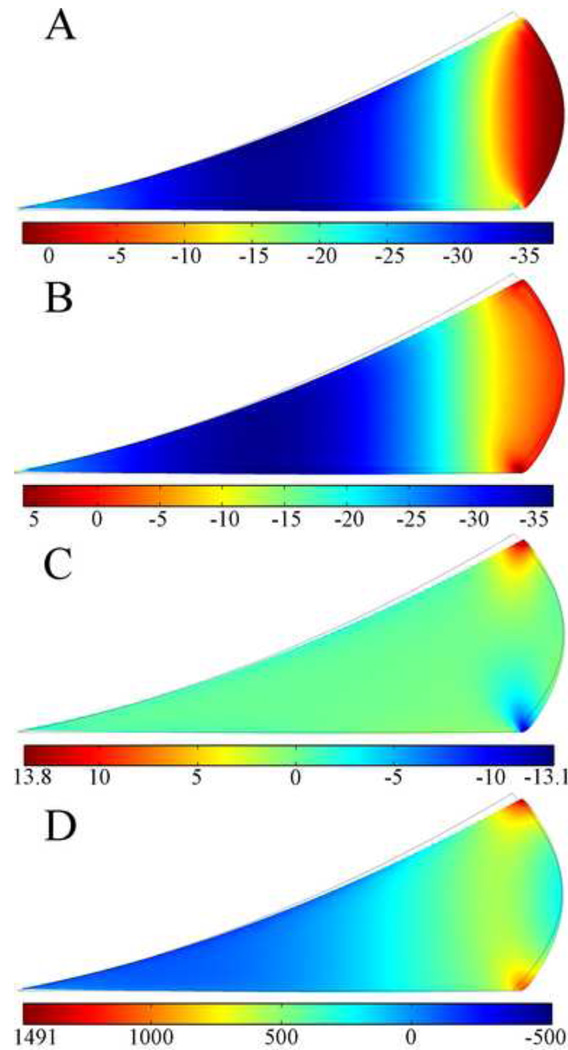
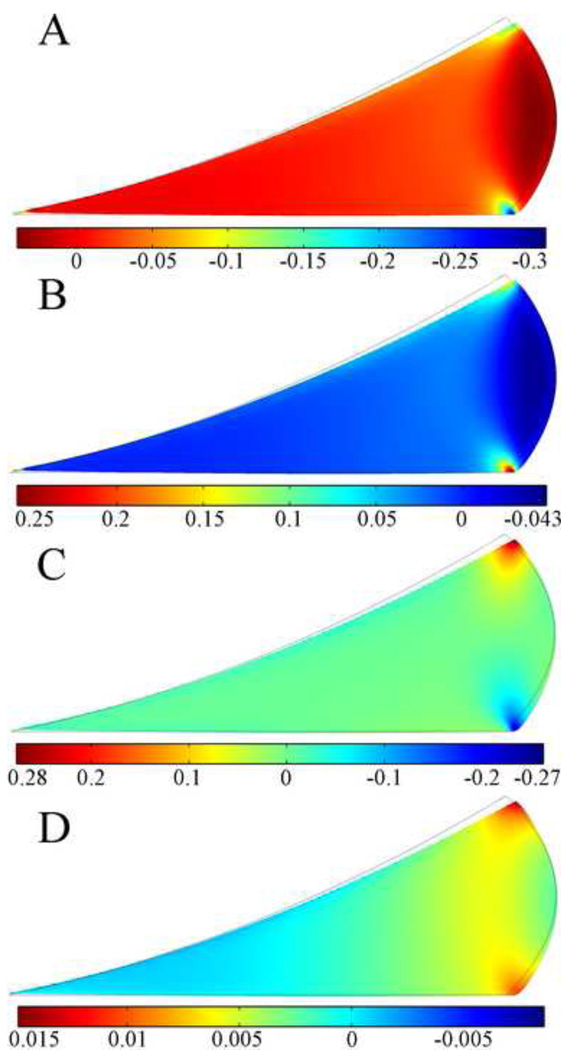
Figure 4 shows the distributions of stress components on the deformed geometry of the meniscus at the end of ramp loading stage. The axial stress σz (Fig. 4A) and radial stress σr (Fig. 4B) were compressive throughout most of the meniscus cross section, with small tensile values in the extreme peripheral region. The values ranged from about 5 kPa tension to about 37 kPa compression, and the maximum compressive values were found in the central region of the meniscus cross section. The shear stress σrz (Fig. 4C) was very small throughout most of the meniscus cross section. It was negative in the inner two-thirds of the meniscus and increasingly positive in the outer third. Peak positive shear stress was found at the apex of the femoral surface of the meniscus, and peak negative shear stress at the peripheral corner of the tibial surface of the meniscus. The circumferential stress σθ (Fig. 4D) was tensile throughout most of the meniscus cross section and ranged from −500 kPa near the inner radius to about 1500 kPa near the outer radius.
Fig. 4.
Distribution of the axial (σz, A), radial (σr, B), shear stress (σrz, C), and circumferential stress ( σθ, D) components in kPa at t=1s on deformed geometry of the meniscus in the two-legged stance model. The peak force applied was 147N. Grey boundary lines are initial position.
Distributions of strain components on the meniscus at the end of ramp loading stage are shown in Figure 5. The axial strain εz (Fig. 5A) was compressive throughout most of the outer two-thirds of the meniscus cross section; however, tensile axial strain was found throughout most of the bulged peripheral section and the inner third of the meniscus cross section. High compressive axial strain was found at the small region near the apex of the femoral surface of the meniscus and the small region near the peripheral corner of the tibial surface of the meniscus. The radial strain εr (Fig. 5B) had an opposite distribution compared to the axial strain. Similar to the shear stress σrz, the shear strain εrz (Fig. 5C) was very small throughout most of the meniscus cross section. Peak positive shear strain of 0.28 was found at the apex of the femoral surface of the meniscus, and peak negative shear stress of −0.27 at the peripheral corner of the tibial surface of the meniscus. The circumferential strain εθ (Fig. 5D) was compressive in the inner one-third of the meniscus and tensile in the outer two-thirds. High tensile circumferential strain was found at the small region near the apex of the femoral surface of the meniscus and the region near the peripheral corner of the tibial surface of the meniscus.
Fig. 5.
Distribution of the axial (εz, A), radial (εr, B), shear strain (εrz, C), and circumferential strain (εθ, D) components at t=1s on deformed geometry of the meniscus in the two-legged stance model. The peak force applied for this model was 147N. Grey boundary lines are initial position.
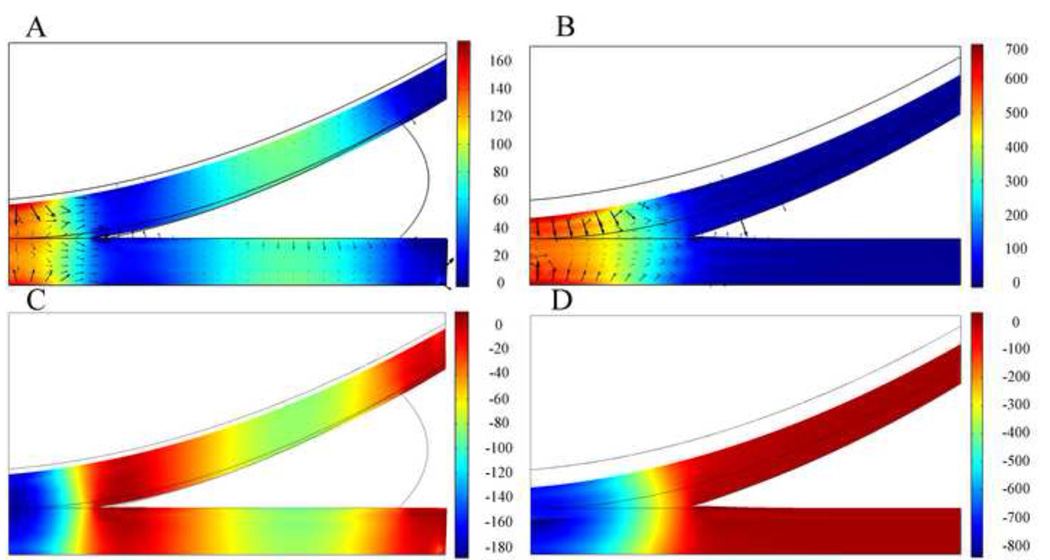
Changes in the magnitudes and distributions of the fluid pressure and total normal stress in articular cartilage before and after complete meniscectomy are shown in Figure 6. In the intact condition, at the end of the ramp loading, the femoral cartilage was not fully in contact with the inner edge of the meniscus; peak fluid pressure (approximately 170 kPa) was found at the central area of cartilage-cartilage contact; and high fluid pressure (approximately 100 kPa) was observed at the central area of cartilage-meniscus contact. In the meniscectomized knee model peak fluid pressure (approximately 700 kPa) was found at the central cartilage-cartilage contact area, and fluid pressure decreased rapidly to zero toward the edge of contact. After complete meniscectomy the peak value of the fluid pressure increased by 300%. In both intact knee model and the meniscectomized knee model, distribution of total normal stress was similar to the distribution of fluid pressure. The peak value of the total normal stress increased by 346% after complete meniscectomy. Fluid exchange was found across the cartilage-cartilage interface and cartilage-meniscus interfaces (Fig. 6A and 6B). Fluid flow was also found at the cartilage surface beside the contact area. The peak contact stress was found at the middle of the tibial surface in both the intact knee model and the meniscectomized knee model, and it is 178 kPa in intact condition and 630 kPa after meniscectomy. Therefore, after complete meniscectomy the peak contact stress increased by 254%.
Fig. 6.
Distribution of fluid pressure p, in kPa at t=1s on deformed geometry of cartilages in the knee models with meniscus (A) and without meniscus (B). Black arrows are fluid flow vectors. Distribution of total normal stress , in kPa at t=1s on deformed geometry of cartilages in the knee models with meniscus (C) and without meniscus (D). The peak force applied to these two models was 73.5N. Grey boundary lines are initial position.
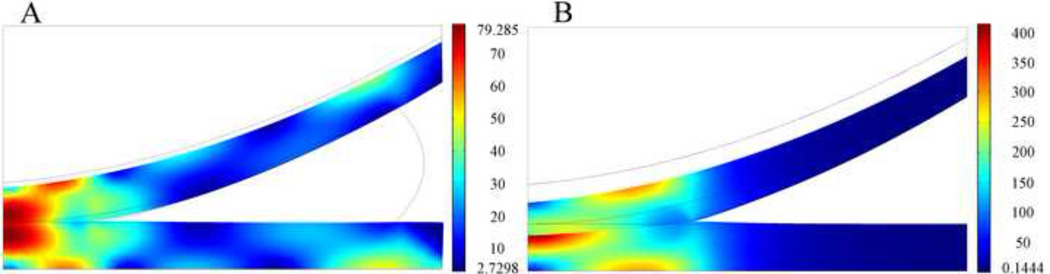
In the intact knee (Fig. 7A) peak maximum shear stress of 79 kPa was found below the surface of the femoral cartilage and the surface of the tibial articular cartilage, and in both tissues the peak shear stresses were located at the central area of cartilage-cartilage contact. High maximum shear stress (approximately 70 kPa) was also found at the tibial and femoral bony interfaces away from the central area of cartilage-cartilage contact. In the meniscectomized case (Fig. 7B) peak maximum shear stress of 415 kPa was found at the central surface of the tibial cartilage. Similar as results of the intact knee model, high shear stresses (approximately 300 kPa) were found at the cartilage-bone interface, away from the center of the contact area. After complete meniscectomy, the peak value of maximum shear stress increased by 424%.
Fig. 7.
Distribution of maximum shear stress in kPa at t=1s on deformed geometry of cartilages in the knee models with meniscus (A) and without meniscus (B). The peak force applied to these two models was 73.5N. Grey boundary lines are initial position.
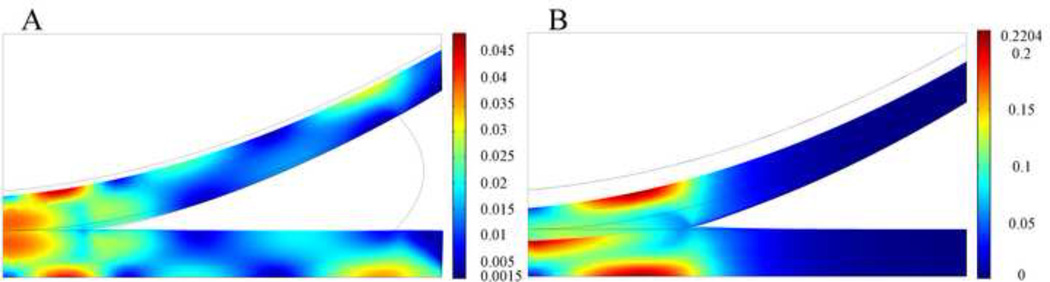
In the intact knee model (Fig. 8A) peak maximum principal strain of 0.049 was found at the cartilage-bone interface under the outer cartilage-cartilage contact area, and high maximum principal strain (approximately 0.035) was found at the central contact area and at the cartilage bone interface under the peripheral edge of the meniscus-tibial cartilage contact area. After complete meniscectomy (Fig. 8B), peak principal strain of 0.22 was found at the central surface of the tibial cartilage and at the cartilage-bone interface, away from the center of the contact area. High maximum principal strain (approximately 0.15) was found at the central surface of the femoral cartilage. After complete meniscectomy, the peak value of maximum principal strain increased by 350%.
Fig. 8.
Distribution of maximum principal strain at t=1s on deformed geometry of cartilages in knee models with meniscus (A) and without meniscus (B). The peak force applied to these two models was 73.5N. Grey boundary lines are initial position.
4 Discussion
Historically, most finite element models of the knee joint consider cartilage and the meniscus as solid; despite the fact that fluid flow plays an important role in the load-carrying ability of these soft tissues. While, several biphasic models of the knee [14–16, 19, 20] have been developed, all have limitations, and many are not theoretically consistent. To address this shortfall, the aim of this study was to develop a theoretically consistent biphasic finite element model of the 2D axisymmetric human knee joint. This biphasic contact model was designed to represent one condyle of the knee and included tibial cartilage, femoral cartilage, femur, and meniscus. It was used to study the interaction between the fluid and solid matrices of the knee soft tissues, the biomechanical behavior of the meniscus, and the changes of the stress and strain distributions in the articular cartilage of the knee joint after complete meniscectomy.
To be representative of a normal human knee joint, the width, thickness, and position of the meniscus were created based on a 3D meniscus MRIs measurement study [23]. The curvatures of the femoral surface of the meniscus, outer surface of the meniscus, and the femoral cartilages were based on previous finite element studies of the human knee joint [19, 25]. The thickness of the articular cartilage of the femur and tibia were chosen to be in the normal range of healthy human knee joint [24]. The meniscus, femoral cartilage, and tibial cartilage were modeled as 2D axisymmetric structures, thus the meniscal attachments could not be included in the present model. Nonetheless given the fact that a comprehensive theoretically consistent biphasic knee model is not available, we believe the present 2D axisymmetric biphasic knee model can provide some valuable insights of the biphasic behaviors of the human knee joint.
Among the biphasic finite element models of the knee joint, the model developed by Donzelli [19] was a 2D axisymmetric theoretically consistent biphasic model, yet only limited data (i.e., the distributions of fluid pressure and total normal stress) was presented. To develop confidence in our model, the distributions and values of fluid pressure and total normal stress were compared to those predicted by Donzelli's study [19], and good agreements were found. Specifically, peak fluid pressure and total normal stress occurred at the central contact area of the tibial cartilage and femoral cartilage, and their values decreased toward the periphery of the contact area. Agreement was also found between the interaction of the fluid and solid matrices of soft tissues in our model and other, albeit simplified, biphasic models of soft tissues [1, 19, 31]. At the end of ramp loading over 70% of the load was carried by the fluid phase. As applied force was held constant and as fluid flow diminished with time, the fluid pressure decreased and the total load was increasingly carried by the solid phase. At t=120s, about 61% of the load was taken up by the fluid phase which reinforces the need for a biphasic model to more accurately represent the role that the fluid phase plays in load bearing. Finally, good agreement was found between the distribution of stress and strain within the meniscus in our model and that found by Spilker et al. [25], in which the biphasic cartilage-meniscus contact of the knee joint was not modeled but was instead represented by a parabolically distributed load. However, by modeling the biphasic contact between the femoral cartilage-tibial cartilage and the meniscus, the present study obtained a clearer picture of the distribution of stresses and strains within the tissues of the knee joint.
The circumferential stress was dominant among the stress components, which indicate the stiffening effect of the circumferential fibers. In addition, the circumferential stress was tensile throughout most of the meniscus cross section to balance the radial component of the load transmitted from the femoral cartilage. The high compressive axial stress and radial stress in the meniscus were found in the center of the meniscus cross section indicating that load was mainly transferred through this region. The tensile axial stress and radial stress were found at the bulged peripheral surface of the meniscus. Regional variation of strains was also observed in the present model: the inner third and outer two-thirds of the meniscus have different kinds of strains (tensile or compressive). Our model predicted tensile axial strains at the inner third of the meniscus cross section and the bulged peripheral section of the meniscus. Tensile radial strains and tensile circumferential strains were found at the outer two-thirds of the meniscus cross section, except for the region near the edges of the bulged peripheral surface. A previous study [25] showed that large tensile strains, individually or in combination, can lead to meniscal tissue failure, therefore, our model predicted that the bulged peripheral surface of the meniscus and the regions near the apex of the meniscus cross section are most susceptible to tissue failure suggesting that any meniscal replacement should have reinforcement over these regions to withstand large tensile strains. Because of the stiffening effect of the circumferential fibers, the circumferential strains were the smallest of the strain components; however, these contributions may still be important since the previous experimental models [27] have demonstrated that tissue specimens taken parallel to the dominant collagen fiber direction can fail in extension at a relatively low strain levels. The regional variation in stresses and strains may further explain the regional variation in meniscal material properties, as has been previously suggested [1, 32]. Although the collagen fibers of the meniscus are arranged predominantly in the circumferential direction, large radially oriented fibers are found within human and bovine menisci. These radial fibers "tie" the circumferential fibers together, thus altering the radial tensile properties of the meniscus. From histological observations of Skaggs and coworkers [32], it was noted that the size and density of the radial tie fibers in bovine meniscus gradually increased from the inner region to the outer region of the meniscus. The regional variation in fiber distribution and material properties may help the meniscus to withstand different kinds of strains in different regions as seen in the present study.
To investigate the effect of complete meniscectomy on the biomechanical behavior of the knee joint, the peak contact stress, the distributions of fluid pressure, total normal stress, maximum shear stress, and maximum principal strain in the intact knee model and the meniscectomized knee model were compared. After complete meniscectomy, the contact area at tibial cartilage decreased by 58%; the peak value of the fluid pressure increased by 300%; and the peak value of the total normal stress increased by 346%. The peak maximum shear stress and maximum principal strain in the articular cartilage increased by 424% and 350%, respectively, after complete meniscectomy. In a similar study by Wilson et al. [15], the maximum shear stress increased by 140% after complete meniscectomy. In the present model, the peak contact stress increased by 254% after meniscectomy, which is very close to the 235% increase found in an experimental model [33], yet lower than the increase of 183% as found by Wilson et al. [15]. The smaller difference found in the Wilson study versus our study and the experimental study [33] is due to the simplifications used in the Wilson study [15]: to avoid computational issues, a low stiffness membrane was interposed between the cartilage layers and the meniscus, which could absorb most of the applied load; no fluid flow took place between contact surfaces [14–16] which is inconsistent with the equation of mass conservation across the contact interface [9], and does not capture the complexity of fluid flow as demonstrated by our model in which fluid exchange across the contact interfaces occurred. The location at which peak stresses and strains occurred within the articular cartilage also varied from the intact to the meniscectomized condition. In the intact knee, peak maximum shear stress and peak maximum principal strain occurred at the central surface of the tibial cartilage and the cartilage-bone interface, away from the center of the contact area. After complete meniscectomy the maximum shear stress and maximum principal strain increased over 350% for tibial and femoral cartilage. On the tibial cartilage, the peak maximum shear stress and peak maximum principal strain remained on the central area of the tissue, but moved closer to the articulating surface. On the femoral side, peak stress and strain were predominantly at the cartilage-bone interface. Previous studies [34–36] suggested that the early stages of osteoarthritis can manifest as either articular cartilage damage without disruption of the subchondral bone or subchondral bone damage with or without damage to the overlying cartilage. Therefore, our study suggests that the tissue failure at the cartilage-bone interface and the surface of the articular cartilage is caused by the increased maximum principal strain and maximum shear stress. Discontinuities of maximum shear stress and maximum principal strain were found at the cartilage-cartilage interface after meniscectomy. This observation is probably due to the incongruent geometry of the knee joint after meniscectomy which results in compression in the radial direction of the upper surface of the tibial cartilage. In the intact knee, negligible compression existed in the radial direction of the tibial cartilage because meniscus balanced the radial component of the load transmitted from the femoral cartilage.
This study has several limitations. Very high radial stress and circumferential stress were found at the inner corner of the meniscus, which are an artifact of the sharp geometric corner. This artifact has also been found in previous study [19]. Another limitation is the axisymmetric nature of the model. In reality menisci are C-shaped structures attached to the tibia plateau via horn attachment – in our study, the meniscus is modeled as a complete ring and the horn attachment is not included. In addition, other tissues surrounding the knee joint, for example, ligaments and muscles, may help to redistribute load across the joint, but the present 2D axisymmetric knee model cannot simulate the effect of the surrounding tissues. Moreover, because of the linear elastic biphasic theory used in this study, only small deformation behavior of the knee joint soft tissues was investigated, and finite deformation behavior was not included. To maintain deformation in the range of small strains, compressive forces of less than 200 N were used in this study, though physiological load can be up to 2400 N. We recognized the complexity of the 3D contacts in the knee, and the biphasic behavior of the 3D knee joint under physiological loadings will be investigated after we gained experiences in solving these kinds of numerical problems. Despite these limitations, we believe that our axisymmetric biphasic knee model provides some basic understanding about the load transmission role of the meniscus and the interaction between the fluid and solid matrices of the knee soft tissues.
In summary, this study describes a biphasic contact solution of the knee joint with the potential to be expanded to help understand the mechanics of the development of post-traumatic osteoarthritis. An augmented Lagrangian method was used to enforce the continuity of contact traction and fluid pressure across the contact interface. The interaction between the fluid and solid matrices of the knee soft tissues, the biomechanical behaviors of the meniscus, and the changes of stress distribution in the cartilages after complete meniscectomy were investigated. Despite the simplifications and assumptions made in constructing the computational model, we believe that our model sheds light on the changes in the distribution of stresses and strains within the articular cartilage before and after complete meniscectomy.
Acknowledgments
The authors would like to acknowledge the support of US National Institutes of Health (grant R01 AR057343).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Competing interests: None declared
Ethical approval: Not required
References
- 1.Mow VC, Gu WY, Chen FH. Structure and function of articular cartilage and meniscus. In: Mow VC, Huiskes R, editors. Basic Orthopaedic Biomechanics and Mechano-biology. Philadelphia: Lippincott Williams & Wilkins; 2005. pp. 181–258. [Google Scholar]
- 2.Freeman MA. Pathogenesis of primary osteoarthrosis, an hypothesis. Mod Trends Orthop. 1975;6:40–94. [PubMed] [Google Scholar]
- 3.Seitz AM, Lubomierski A, Friemert B, Ignatius A, Dürselen L. Effect of partial meniscectomy at the medial posterior horn on tibiofemoral contact mechanics and meniscal hoop strains in human knees. J Orthop Res. 2012;30:934–942. doi: 10.1002/jor.22010. [DOI] [PubMed] [Google Scholar]
- 4.Li G, Gil J, Kanamori A, Woo SL. A validated three-dimensional computational model of a human knee joint. J Biomech Eng. 1999;121:657–662. doi: 10.1115/1.2800871. [DOI] [PubMed] [Google Scholar]
- 5.Haut Donahue TL, Hull ML, Rashid MM, Jacobs CR. A finite element model of the human knee joint for the study of tibio-femoral contact mechanics. J Biomech Eng. 2002;124:273–280. doi: 10.1115/1.1470171. [DOI] [PubMed] [Google Scholar]
- 6.Papaioannou G, Nianios G, Mitrogiannis C, Fyhrie D, Tashman S, Yang KH. Patient- specific knee joint finite element model validation with high-accuracy kinematics from biplane dynamic Roentgen stereogrammetric analysis. J Biomech. 2008;41:2633–2638. doi: 10.1016/j.jbiomech.2008.06.027. [DOI] [PubMed] [Google Scholar]
- 7.Guess TM, Thiangarajan G, Kia M, Mishra M. A subject specific multibody model of the knee with menisci. Med Eng Phys. 2010;32:505–515. doi: 10.1016/j.medengphy.2010.02.020. [DOI] [PubMed] [Google Scholar]
- 8.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression, theory and experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 9.Hou JS, Holmes MH, Lai WM, Mow VC. Boundary conditions at the cartilage-synovial fluid interface for joint lubrication and theoretical verifications. J Biomech Eng. 1989;111:78–87. doi: 10.1115/1.3168343. [DOI] [PubMed] [Google Scholar]
- 10.Ateshian GA, Maas S, Weiss JA. Finite element algorithm for frictionless contact of porous permeable media under finite deformation and sliding. J Biomech Eng. 2010;132:061006. doi: 10.1115/1.4001034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Guo H, Spilker RL. Biphasic finite element modeling of hydrated soft tissue contact using an augmented Lagrangian Method. J Biomech Eng. 2011;133:111001. doi: 10.1115/1.4005378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guo H, Nickel JC, Iwasaki LR, Spilker RL. An augmented Lagrangian method for sliding contact of soft tissue. J Biomech Eng. 2012;134:084503. doi: 10.1115/1.4007177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guo H, Spilker RL. An augmented Lagrangian finite element formulation for 3D contact of biphasic tissues. Comput Methods Biomech Biomed Eng. 2012 doi: 10.1080/10255842.2012.739166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang H. PhD Thesis. Rochester, NY US: University of Rochester; 2000. Geometric and finite element modeling of the tibio-menisco-femoral contact under passive knee motion. [Google Scholar]
- 15.Wilson W, van Rietbergen B, van Donkelaar CC, Huiskes R. Pathways of load-induced cartilage damage causing cartilage degeneration in the knee after meniscectomy. J Biomech. 2003;36:845–851. doi: 10.1016/s0021-9290(03)00004-6. [DOI] [PubMed] [Google Scholar]
- 16.Vaziri A, Nayeb-Hashemi H, Singh A, Tafti BA. Influence of meniscectomy and meniscus replacement on the stress distribution in human knee joint. Ann Biomed Eng. 2008;36:1335–1344. doi: 10.1007/s10439-008-9515-y. [DOI] [PubMed] [Google Scholar]
- 17.Manda K, Ryd L, Eriksson A. Finite element simulations of a focal knee resurfacing implant applied to localized cartilage defects in a sheep model. J Biomech. 2011;44:794–801. doi: 10.1016/j.jbiomech.2010.12.026. [DOI] [PubMed] [Google Scholar]
- 18.Manda K, Eriksson A. Time dependent behavior of cartilage surrounding a metal implant for full thickness cartilage defects of various sizes: a finite element study. Biomech Model Mechanobiol. 2012;11:731–742. doi: 10.1007/s10237-011-0346-7. [DOI] [PubMed] [Google Scholar]
- 19.Donzelli PS. PhD Thesis. Troy, NY US: Rensselaer Polytechnic Institute; 1995. A mixed-penalty contact finite element formulation for biphasic soft tissue. [Google Scholar]
- 20.Gu KB, Li LP. A human knee joint model considering fluid pressure and fiber orientation in cartilage and menisci. Med Eng Phys. 2011;33:497–503. doi: 10.1016/j.medengphy.2010.12.001. [DOI] [PubMed] [Google Scholar]
- 21.Li LP, Kazemi M. Fluid pressurization in cartilages and menisci in the normal and repaired human knees. In: Alexandru C, editor. Modeling and Simulation in Engineering. InTech; 2012. pp. 277–298. [Google Scholar]
- 22.Almeida ES, Spilker RL. Mixed and penalty finite element models for the nonlinear behavior of biphasic soft tissues in finite deformation: Part I--alternate formulations. Comput Methods Biomech Biomed Eng. 1997;1:25–46. doi: 10.1080/01495739708936693. [DOI] [PubMed] [Google Scholar]
- 23.Bloecker K, Englund M, Wirth W, Hudelmaier M, Burgkart R, Frobell RB, Eckstein F. Size and position of the healthy meniscus, and its Correlation with sex, height, weight, and bone area- a cross-sectional study. BMC Musculoskelet Disord. 2011;12:248. doi: 10.1186/1471-2474-12-248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li G, Park SE, DeFrate LE, Schutzer ME, Ji L, Gill TJ, Rubash HE. The cartilage thickness distribution in the tibiofemoral joint and its correlation with cartilage-to-cartilage contact. Clinical Biomechanics. 2005;20:736–744. doi: 10.1016/j.clinbiomech.2005.04.001. [DOI] [PubMed] [Google Scholar]
- 25.Spilker RL, Donzelli PS, Mow VC. A transversely isotropic biphasic finite element model of the meniscus. J Biomech. 1992;25:1027–1045. doi: 10.1016/0021-9290(92)90038-3. [DOI] [PubMed] [Google Scholar]
- 26.Chern KY, Zhu WB, Kelly MA, Mow VC. Transaction of the 36th Annual Meeting of the Orthopaedic Research Society. New Orleans, LA, USA: 1990. Anisotropic shear properties of bovine meniscus; p. 246. [Google Scholar]
- 27.Proctor C, Schmidt MB, Whipple RR, Kelly MA, Mow VC. Material properties of the normal medial bovine meniscus. J Orthop Res. 1989;7:771–782. doi: 10.1002/jor.1100070602. [DOI] [PubMed] [Google Scholar]
- 28.Whipple RR, Wirth CR, Mow VC. Anisotropic and zonal variations in the tensile properties of the meniscus; Transaction of the 31st Annual Meeting of the Orthopaedic Research Society; 1985. p. 367. [Google Scholar]
- 29.Cohen B, Gardner TR, Ateshian GA. Transaction of Annual Meeting of 39th Orthopaedic Research Society. Chicago, IL, USA: 1993. The influence of transverse isotropy on cartilage indentation behavior-A study of the human humeral head; p. 185. [Google Scholar]
- 30.Reilly DT, Burstein AH. The mechanical properties of cortical bone. J Bone Joint Surg Am. 1974;56:1001–1022. [PubMed] [Google Scholar]
- 31.Ateshian GA, Lai WM, Zhu WB, Mow VC. An asymptotic solution for the contact of two biphasic cartilage layers. J Biomech. 1994;27:1347–1360. doi: 10.1016/0021-9290(94)90044-2. [DOI] [PubMed] [Google Scholar]
- 32.Skaggs DC, Warden WH, Mow VC. Radial tie fibers influence the tensile properties of the bovine medial meniscus. J Orthop Res. 1994;12:176–185. doi: 10.1002/jor.1100120205. [DOI] [PubMed] [Google Scholar]
- 33.Baratz ME, Fu FH, Mengato R. Meniscal tears: the effect of meniscectomy and of repair on intraarticular contact areas and stress in the human knee, a preliminary report. Am J Sports Med. 1986;14:270–275. doi: 10.1177/036354658601400405. [DOI] [PubMed] [Google Scholar]
- 34.Atkinson P, Haut R. Subfracture insult to the human cadaver patellofemoral joint produces occult injury. J Orthop Res. 1995;13:936–944. doi: 10.1002/jor.1100130619. [DOI] [PubMed] [Google Scholar]
- 35.Thompson RC, Oegema TR, Lewis JL, Wallace L. Osteoarthrotic changes after acute transarticular load. J Bone Joint Surg Am. 1991;73:990–1001. [PubMed] [Google Scholar]
- 36.Vener MJ, Thompson RC, Lewis JL, Oegema TR. Subchondral damage after acute transarticular loading: an in vitro model of joint injury. J Orthop Res. 1992;10:759–765. doi: 10.1002/jor.1100100603. [DOI] [PubMed] [Google Scholar]