3D object retrieval using salient views

Abstract

This paper presents a method for selecting salient 2D views to describe 3D objects for the purpose of retrieval. The views are obtained by first identifying salient points via a learning approach that uses shape characteristics of the 3D points (Atmosukarto and Shapiro in International workshop on structural, syntactic, and statistical pattern recognition, 2008; Atmosukarto and Shapiro in ACM multimedia information retrieval, 2008). The salient views are selected by choosing views with multiple salient points on the silhouette of the object. Silhouette-based similarity measures from Chen et al. (Comput Graph Forum 22(3):223–232, 2003) are then used to calculate the similarity between two 3D objects. Retrieval experiments were performed on three datasets: the Heads dataset, the SHREC2008 dataset, and the Princeton dataset. Experimental results show that the retrieval results using the salient views are comparable to the existing light field descriptor method (Chen et al. in Comput Graph Forum 22(3):223–232, 2003), and our method achieves a 15-fold speedup in the feature extraction computation time.

1 Introduction

Advancement in technology for digital acquisition and graphics hardware has led to an increase in the number of 3D objects available. Three-dimensional objects are now commonly used in a number of areas such as games, mechanical design for CAD models, architectural and cultural heritage, and medical diagnostic. The widespread integration of 3D models in all these fields motivates the need to be able to store, index, and retrieve 3D objects automatically. However, classification and retrieval techniques for text, images, and videos cannot be directly translated and applied to 3D objects, as 3D objects have different data characteristics from other data modalities.

Shape-based retrieval of 3D objects is an important area of research. The accuracy of a 3D shape-based retrieval system requires the 3D object to be represented in a way that captures the local and global shape characteristics of the objects. This is achieved by creating 3D object descriptors that encapsulate the important shape properties of the objects. This process is not a trivial task.

This paper presents our method of selecting salient 2D views to describe a 3D object. First, salient points are identified by a learning approach that uses the shape characteristics of each point. Then 2D salient views are selected as those that have multiple salient points on or close to their silhouettes. The salient views are used to describe the shape of a 3D object. The similarity between two 3D objects uses view-based similarity measure developed by Chen et al. [10] for which two 3D objects are similar if they have similar 2D views.

The remainder of this paper is organized as follows: First, existing shape descriptors and their limitations are discussed. Next, we describe the datasets acquired to develop and test our methodology. The method for finding the salient points of a 3D object is described next. Then, selection of the salient views based on the learned salient points is defined. In the experimental results section, the evaluation measures are first described, and a set of retrieval experiments is described and analyzed. Finally, a summary and suggestions for future work are provided.

2 Related literature

Three-dimensional object retrieval has received increased attention in the past few years due to the increase in the number of 3D objects available. A number of survey papers have been written on the topic [7-9,12,14,17,24,30,34,35,38]. An annual 3D shape retrieval contest was also introduced in 2006 to try to introduce an evaluation benchmark to the research area [32]. There are three broad categories of ways to represent 3D objects and create a descriptor: feature-based methods, graph-based methods, and view-based methods.

The feature-based method is the most commonly used method and is further categorized into global features, global feature distributions, spatial maps, and local features. Early work on 3D object representation and its application to retrieval and classification focused more on the global features and global feature distribution approaches. Global features computed to represent 3D objects include area, volume, and moments [13]. Some global shape distribution features computed include the angle between three random points (A3), the distance between a point and a random point (D1), the distance between two random points (D2), the area of the triangle between three random points (D3), and the volume between four random points on the surface (D4) [26,28]. Spatial map representations describe the 3D object by capturing and preserving physical locations on them [19-21,31]. Recent research is beginning to focus more on the local approach to representing 3D objects, as this approach has a stronger discriminative power when differentiating objects that are similar in overall shape [29].

While feature-based methods use only the geometric properties of the 3D model to define the shape of the object, graph-based methods use the topological information of the 3D object to describe its shape. The graph that is constructed shows how the different shape components are linked together. The graph representations include model graphs, Reeb graphs, and skeleton graphs [16,33]. These methods are known to be computationally expensive and sensitive to small topological changes.

The view-based method defines the shape of a 3D object using a set of 2D views taken from various angles around the object. The most effective view-based descriptor is the light field descriptor (LFD) developed by Chen et al. [10]. A light field around a 3D object is a 4D function that represents the radiance at a given 3D point in a given direction. Each 4D light field of a 3D object is represented as a collection of 2D images rendered from a 2D array of cameras distributed uniformly on a sphere. Their method extracts features from 100 2D silhouette image views and measures the similarity between two 3D objects by finding the best correspondence between the set of 2D views for the two objects.

The LFD was evaluated to be one of the best performing descriptors on the Princeton and SHREC benchmark databases. Ohbuchi et al. [27] used a similar view-based approach; however, their method extracted local features from each of the rendered image and used a bag-of-features approach to construct the descriptors for the 3D objects. Wang et al. [36] used a related view-based approach by projecting a number of uniformly sampled points along six directions to create six images to describe a 3D object. Liu et al. [23] also generated six view planes around the bounding cube of a 3D object. However, their method further decomposed each view planes into several resolution and applied wavelet transforms to the extracted features from the view planes. Both these methods require pose-normalization of the object; however, pose-normalization methods are known not to be accurate and objects in the same class are not always pose-normalized into the same orientation. Yamauchi et al. [37] applied a similarity measure between views to cluster similar views and used the centroid of clusters as the representative views. The views are then ranked based on a mesh saliency measure [22] to form the object’s representative views. Ansary et al. [1,2] proposed a method to optimally select 2D views from a 3D model using an adaptive clustering algorithm. Their method used a variant of K -means clustering and assumed the maximum number of characteristic views was 40. Cyr and Kimia [11] presented an aspect graph approach to 3D object recognition using 2D shape similarity metric to group similar views into aspects and to compare two objects.

We propose a method to select salient 2D silhouette views of an object and construct a descriptor for the object using only the salient views extracted. The salient views are selected based on the salient points learned for each object. Our method does not require any pose normalization or clustering of the views.

3 Datasets

We obtained three datasets to develop and test our methodology. Each dataset has different characteristics that help explore the different properties of the methodology. The Heads dataset contains head shapes of different classes of animals, including humans. The SHREC 2008 classification benchmark dataset was obtained to further test the performance of the methodology on general 3D object classification, where objects in the dataset are not very similar. Last, the Princeton dataset is a benchmark dataset that is commonly used to evaluate shape-based retrieval and analysis algorithms.

3.1 Heads dataset

The Heads database contains head shapes of different classes of animals, including humans. The digitized 3D objects were obtained by scanning hand-made clay toys using a laser scanner. Raw data from the scanner consisted of 3D point clouds that were further processed to obtain smooth and uniformly sampled triangular meshes. To increase the number of objects for training and testing our methodology, we created new objects by deforming the original scanned 3D models in a controlled fashion using 3D Studio Max software [5]. Global deformations of the models were generated using morphing operators such as tapering, twisting, bending, stretching, and squeezing. The parameters for each of the operators were randomly chosen from ranges that were determined empirically. Each deformed model was obtained by applying at least five different morphing operators in a random sequence.

Fifteen objects representing seven different classes were scanned. The seven classes are cat head, dog head, human head, rabbit head, horse head, tiger head, and bear head. A total of 250 morphed models per original object were generated. Points on the morphed model are in full correspondence with the original models from which they were constructed. Figure 1 shows examples of objects from each of the seven classes.

Fig. 1.

Example of objects in the Heads dataset

3.2 SHREC dataset

The SHREC 2008 classification benchmark database was obtained to further test the performance of our methodology. The SHREC dataset was selected from the SHREC 2008 Competition “classification of watertight models” track [15]. The models in the dataset have a high level of shape variability. The models were manually classified using three different levels of categorization. At the coarse level of classification, the objects were classified according to both their shapes and semantic criteria. At the intermediate level, the classes were subdivided according to functionality and shape. At the fine level, the classes were further partitioned based on the object shape. For example, at the coarse level some objects were classified into the furniture class. At the intermediate level, these same objects were further divided into tables, seats and beds, where the classification takes into account both functionality and shape. At the fine level, the objects were classified into chairs, armchairs, stools, sofa and benches. The intermediate level of classification was chosen for the experiments as the fine level had too few objects per class, while the coarse level had too many objects that were dissimilar in shape grouped into the same class. In this categorization, the dataset consists of 425 pre-classified objects that are pre-classified into 39 classes. Figure 2 shows examples of objects in the SHREC benchmark dataset.

Fig. 2.

Example of objects in the SHREC 2008 Classification dataset

3.3 Princeton dataset

The Princeton dataset is a benchmark database that contains 3D polygonal models collected from the Internet. The dataset is split into a training database and a test database. The training database contains 907 models and the test database contains 907 models. The base training classification contains 90 classes and the base classification contains 92 classes. Example of classes includes car, dog, chair, table, flower, trees, etc. Figure 3 shows examples of objects in the dataset. The benchmark also includes tools for evaluation and visualization of the 3D model matching scores. The dataset is usually evaluated using the commonly used retrieval statistics such as nearest neighbor, first and second tier, and discounted cumulative gain (DCG). For this paper, we only used the 907 models in the training database.

Fig. 3.

Example of objects in the Princeton dataset

4 Finding salient points

Our application was developed for single 3D object retrieval and does not handle objects in cluttered 3D scenes nor occlusion. A surface mesh, which represents a 3D object, consists of points { p_i} on the object’s surface and information regarding the connectivity of the points. The base framework of the methodology starts by rescaling the objects to fit in a fixed-size bounding box. The framework then executes two phases: low-level feature extraction and mid-level feature aggregation. The low-level feature extraction starts by applying a low-level operator to every point on the surface mesh. After the first phase, every point p_i on the surface mesh will have either a single low-level feature value or a small set of low-level feature values, depending on the operator used. The second phase performs mid-level feature aggregation and computes a vector of values for a given neighborhood of every point p_i on the surface mesh. The feature aggregation results of the base framework are then used to learn the salient points on the 3D object [3,4].

4.1 Low-level feature extraction

The base framework of our methodology starts by applying a low-level operator to every point on the surface mesh [3,4]. The low-level operators extract local properties of the surface mesh points by computing a low-level feature value v_i for every surface mesh point p_i. In this work, we use absolute values of Gaussian curvature, Besl–Jain surface curvature characterization [6] and azimuth-elevation angles of surface normal vectors as the low-level surface properties. The low-level feature values are convolved with a Gaussian filter to reduce noise.

The absolute Gaussian curvature low-level operator computes the Gaussian curvature estimation K for every point p on the surface mesh:

$$K(p)=2\pi -\sum _{f\in F(p)}\mathit{interior}\_{\mathit{angle}}_{\mathrm{f}}$$

where F is the list of all the neighboring facets of point p, and the interior angle is the angle of the facets meeting at point p. This calculation is similar to calculating the angle deficiency at point p. The contribution of each facet is weighted by the area of the facet divided by the number of points that form the facet. The operator then takes the absolute value of the Gaussian curvature as the final low-level feature value for each point.

Besl and Jain [6] suggested a surface characterization of a point p using only the sign of the mean curvature H and Gaussian curvature K. These surface characterizations result in a scalar surface feature for each point that is invariant to rotation, translation, and changes in parametrization. The eight different categories are (1) peak surface, (2) ridge surface, (3) saddle ridge surface, (4) plane surface, (5) minimal surface, (6) saddle valley, (7) valley surface, and (8) cupped surface. Table 1 lists the different surface categories with their respective curvature signs.

Table 1.

Besl–Jain surface characterization

Label	Category	H	K
1	Peak surface	H < 0	K > 0
2	Ridge surface	H < 0	K = 0
3	Saddle ridge surface	H < 0	K < 0
4	Plane surface	H = 0	K = 0
5	Minimal surface	H = 0	K < 0
6	Saddle valley	H > 0	K < 0
7	Valley surface	H > 0	K = 0
8	Cupped surface	H > 0	K > 0

Given the surface normal vector n(n_x, n_y, n_z) of a 3D point, the azimuth angle θ of n is defined as the angle between the positive xz plane and the projection of n to the x plane. The elevation angle ϕ of n is defined as the angle between the x plane and vector n.

$$\theta =\arctan \left(\frac{n_z}{n_x}\right),\varphi =\arctan \left(\frac{n_y}{\sqrt{(n_x^2+n_z^2)}}\right)$$

where θ = [−π, π] and $\varphi =\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$. The azimuth-elevation low-level operator computes the azimuth and elevation value for each point on the 3D surface.

4.2 Mid-level feature aggregation

After the first phase, every surface mesh point p_i will have a low-level feature value v_i depending on the operator used. The second phase of the base framework performs mid-level feature aggregation to compute a number of values for a given neighborhood of every surface mesh point p_i. Local histograms are used to aggregate the low-level feature values of each mesh point. The histograms are computed by taking a neighborhood around each mesh point and accumulating the low-level feature values in that neighborhood. The size of the neighborhood is the product of a constant c, 0 < c < 1, and the diagonal of the object’s bounding box; this ensures that the neighborhood size is scaled according to the object’s size. The feature aggregation results of the base framework are used to determine salient points of an object using a learning approach.

4.3 Learning salient points

Preliminary saliency detection using existing methods such as 3D SIFT and entropy-based measures [18,22] were not satisfactory. In some cases they were not consistent and repeatable for objects within the same class. As a result, to find salient points on a 3D object, a learning approach was selected. A salient point classifier is trained on a set of marked training points on the 3D objects provided by experts for a particular application. Histograms of low-level features of the training points obtained using the framework previously described are then used to train the classifier. For a particular application, the classifier will learn the characteristics of the salient points on the surfaces of the 3D objects from that domain. Our methodology identifies interesting or salient points on the 3D objects. Initially motivated by our work on medical craniofacial applications, we developed a salient point classifier that detects points that have a combination of high curvature and low entropy values.

As shown in Fig. 4, the salient point histograms have low bin counts in the bins corresponding to low curvature values and a high bin count in the last (highest) curvature bin. The non-salient point histograms have medium to high bin counts in the low curvature bins and in some cases a high bin count in the last bin. The entropy of the salient point histograms also tend to be lower than the entropy of the non-salient point histograms. To avoid the use of brittle thresholds, we used a learning approach to detect the salient points on each 3D object [4]. This approach was originally developed for craniofacial image analysis, so the training points were anatomical landmarks of the face, whose curvature and entropy properties are useful for objects in general.

Fig. 4.

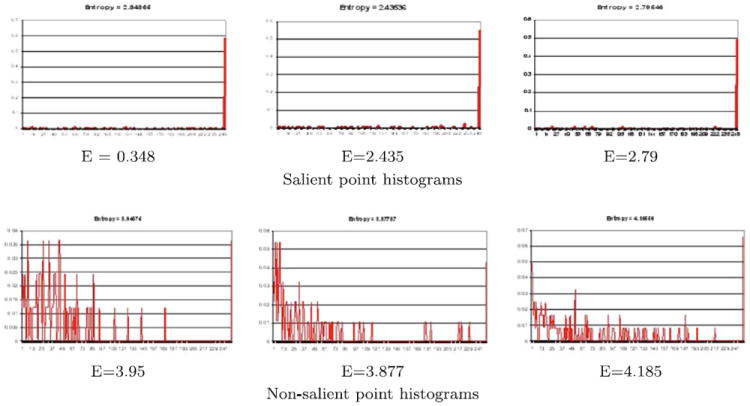
Example histograms of salient and non-salient points. The salient point histograms have a high value in the last bin illustrating a high curvature in the region, while low values in the remaining bins in the histogram. The non-salient point histograms have more varied values in the curvature histogram. In addition, the entropy E of the salient point histogram is lower than the non-salient point histogram (listed under each histogram)

The learning approach teaches a classifier the characteristics of points that are regarded as salient. Histograms of low-level feature values obtained in the base framework are used to train a support vector machine (SVM) classifier to learn the salient points on the 3D surface mesh. The training data points for the classifier’s supervised learning are obtained by manually marking a small number of salient and non-salient points on the surface of each training object. For our experiments, we trained the salient point classifier on 3D head models of the Heads database. The salient points marked included the tip of the nose, corners of the eyes, and both corners and midpoints of the lips. The classifier learns the characteristics of the salient points in terms of the histograms of their low-level feature values. After training, the classifier is able to label each of the points of any 3D object as either salient or non-salient and provides a confidence score for its decision. A threshold is applied to keep only salient points with high confidence scores (≥0.95). While the classifier was only trained on cat heads, dog heads, and human heads (Fig. 5), it does a good job of finding salient points on other classes (Fig. 6). The salient points are colored according to the assigned classifier confidence score. Non-salient points are colored in red, while salient points are colored in different shades of blue with dark blue having the highest prediction score.

Fig. 5.

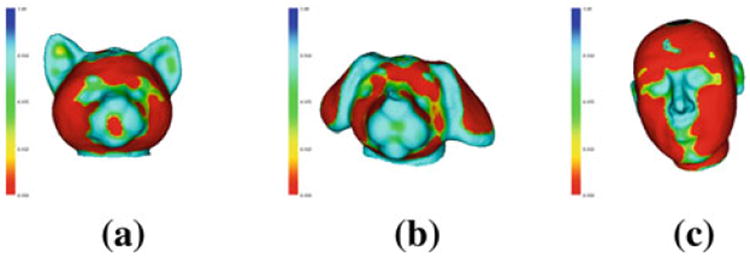
Salient point prediction for a cat head class, b dog head class, and c human head class. Non-salient points are colored in red, while salient points are colored in different shades ranging from green to blue, depending on the classifier confidence score assigned to the point. A threshold (T = 0.95) was applied to include only salient points with high confidence scores (color figure online)

Fig. 6.

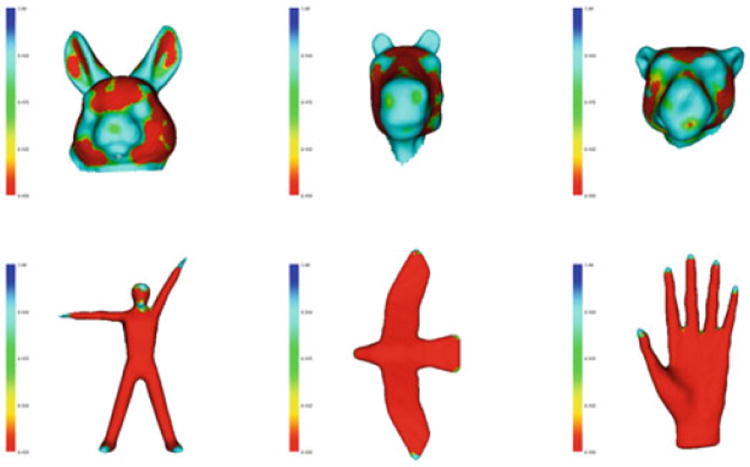
(Top row) Salient point prediction for rabbit head, horse head, and leopard head class from the Heads database. (Bottom row) Salient point prediction for human, bird, and human head class from the SHREC database. These classes were not included in the salient point training

4.4 Clustering salient points

The salient points identified by the learning approach are quite dense and form regions. A clustering algorithm was applied to reduce the number of salient points and to produce more sparse placement of the salient points. The algorithm selects high confidence salient points that are also sufficiently distant from each other. The algorithm follows a greedy approach. Salient points are sorted in decreasing order of classifier confidence scores. Starting with the salient point with the highest classifier confidence score, the clustering algorithm calculates the distance from this salient point to all existing clusters and accepts it if the distance is greater than a neighborhood radius threshold. For our experiments, the radius threshold was set at 5. Figure 7 shows the selected salient points on the cat, dog, and human head objects from Fig. 5. It can be seen that objects from the same class (heads class in the figure) are marked with salient points in similar locations, thus illustrating the repeatability of the salient point learning and clustering method.

Fig. 7.

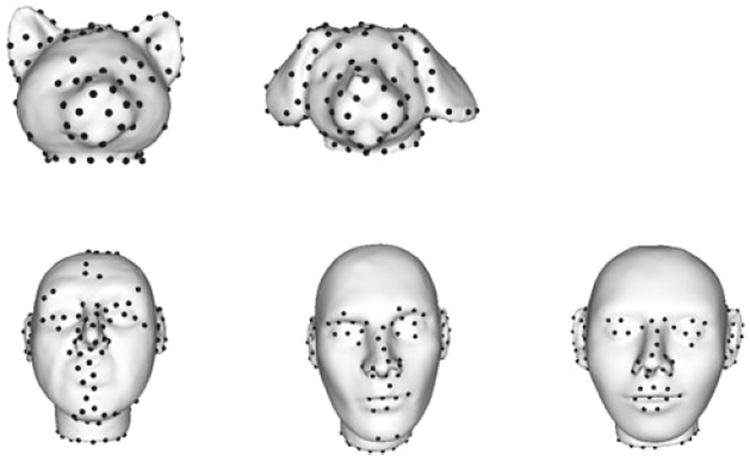
Salient points resulting from clustering

5 Selecting salient views

Our methodology is intended to improve the LFD [10] and uses their concept of similarity. Chen et al. [10] argue that if two 3D models are similar, the models will also look similar from most viewing angles. Their method extracts light fields rendered from cameras on a sphere. A light field of a 3D model is represented by a collection of 2D images. The cameras of the light fields are distributed uniformly and positioned on vertices of a regular dodecahedron. The similarity between two 3D models is then measured by summing up the similarity from all corresponding images generated from a set of light fields.

To improve efficiency, the light field cameras are positioned at 20 uniformly distributed vertices of a regular dodecahedron. Silhouette images at the different views are produced by turning off the lights in the rendered views. Ten different light fields are extracted for a 3D model. Since the silhouettes projected from two opposite vertices on the dodecahedron are identical, each light field generates ten different 2D silhouette images. The similarity between two 3D models is calculated by summing up the similarity from all corresponding silhouettes. To find the best correspondence between two silhouette images, the camera position is rotated resulting in 60 different rotations for each camera system. In total, the similarity between two 3D models is calculated by comparing 10 × 10 × 60 different silhouette image rotations between the two models. Each silhouette image is efficiently represented by extracting the Zernike moment and the Fourier coefficients from each image. The Zernike moments describe the region shape, while the Fourier coefficients describe the contour shape of the object in the image. There are 35 coefficients for the Zernike moment descriptor and 10 coefficients for the Fourier descriptor.

Like the LFD, our proposed method uses rendered silhouette 2D images as views to build the descriptor to describe the 3D object. However, unlike LFD, which extracts features from 100 2D views, our method selects only salient views. We conjecture that the salient views are the views that are discernible and most useful in describing the 3D object. Since the 2D views used to describe the 3D objects are silhouette images, some of the salient points present on the 3D object must appear on the contour of the 3D object (Fig. 8).

Fig. 8.

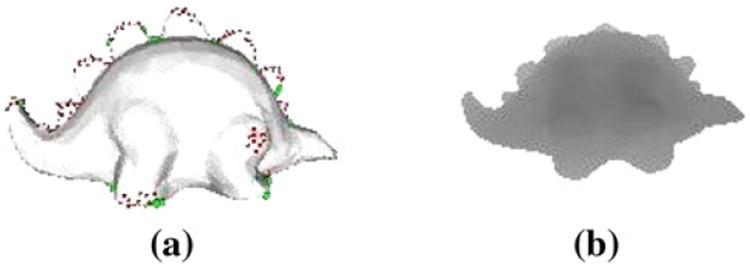
a Salient points must appear on the contour of the 3D objects for a 2D view be considered a ‘salient’ view. The contour salient points are colored in green, while the non-contour salient points are in red. b Silhouette image of the salient view in a (color figure online)

A salient point p(p_x, p_y, p_z) is defined as a contour salient point if its surface normal vector v(v_x, v_y, v_z) is perpendicular to the camera view point c(c_x, c_y, c_z). The perpendicularity is determined by calculating the dot product of the surface normal vector v and the camera view point c. A salient point p is labeled as a contour salient point if |v · c| ≤ T where T is the perpendicularity threshold. For our experiments, we used value T = 0.10. This value ensures that the angle between the surface normal vector and the camera view point is between 84° and 90°.

For each possible camera view point (total 100 view points), the algorithm accumulates the number of contour salient points that are visible for that view point. The 100 view points are then sorted based on the number of contour salient points visible in the view. The algorithm selects the final top K salient views used to construct the descriptor for a 3D model. In our experiments, we empirically tested different values of K to investigate the respective retrieval accuracy.

A more restrictive variant of the algorithm selects the top K distinct salient views. In this variant, after sorting the 100 views based on the number of contour salient points visible in the view, the algorithm uses a greedy approach to select only the distinct views. The algorithm starts by selecting the first salient view, which has the largest number of visible contour salient points. It then iteratively checks whether the next top salient view is too similar to the already selected views. The similarity is measured by calculating the dot product between the two views and discarding views whose dot product to existing distinct views is greater than a threshold P. In our experiments, we used value P = 0.98. Figure 9 (top row) shows the top five salient views, while Fig. 9 (bottom row) shows the top five distinct salient views for a human object. It can be seen in the figure that the top five distinct salient views more completely capture the shape characteristics of the object. Figure 10 shows the top five distinct salient views for different classes in the SHREC database.

Fig. 9.

Top five salient views for a human query object (top row). Top five distinct salient views for the same human query object (bottom row). The distinct salient views capture more information regarding the object’s shape

Fig. 10.

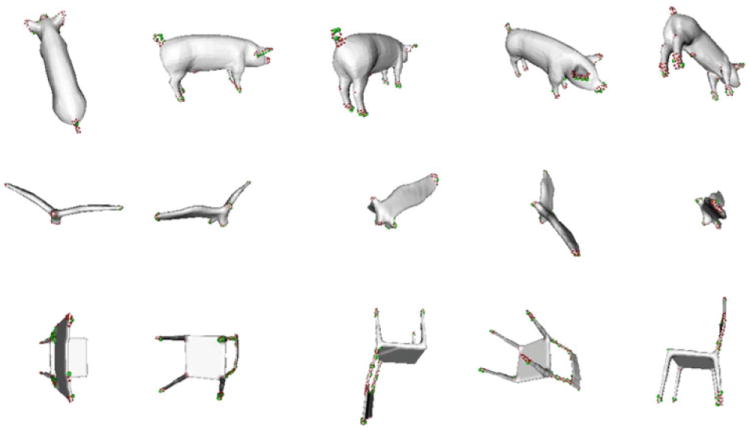
Top five distinct salient views of animal class (top row), bird class (middle row), and chair class (bottom row) from the SHREC database

6 Experimental results

We measured the retrieval performance of our methodology by calculating the average normalized rank of relevant results [25]. The evaluation score for a query object was calculated as follows:

$$\mathit{score}(q)=\frac{1}{N·N_{\mathrm{rel}}}\left(\sum _{i=1}^{N_{\mathrm{rel}}}{R}_i-\frac{N_{\mathrm{rel}}(N_{\mathrm{rel}}+1)}{2}\right)$$

where N is the number of objects in the database, N_rel the number of database objects that are relevant to the query object q (all objects in the database that have the same class label as the query object), and R_i is the rank assigned to the ith relevant object. The evaluation score ranges from 0 to 1, where 0 is the best score as it indicates that all database objects that are relevant are retrieved before all other objects in the database. A score that is ≥0 indicates that some non-relevant objects are retrieved before all relevant objects.

The retrieval performance was measured over all the objects in the dataset using each in turn as a query object. The average retrieval score for each class was calculated by averaging the retrieval score for all objects in the same class. A final retrieval score was calculated by averaging the retrieval score across all classes.

A number of experiments were performed to evaluate the performance of our proposed descriptor and its variants. The first experiment explores the retrieval accuracy of our proposed descriptor. The experiment shows the effect of varying the number of top salient views used to construct the descriptors for the 3D objects in the dataset. As shown in Fig. 11, the retrieval performance improves (retrieval score decreases) as the number of salient views used to construct the descriptor increases. Using the top 100 salient views is equivalent to the existing LFD method. For the absolute Gaussian curvature feature (blue line graph), LFD with 100 views has the best retrieval score at 0.097; however, reducing the number of views by half to the top 50 salient views only increases the retrieval score to 0.114. For the Besl–Jain curvature feature (pink line), the trend is similar with a smaller decrease in performance as the number of views is reduced.

Fig. 11.

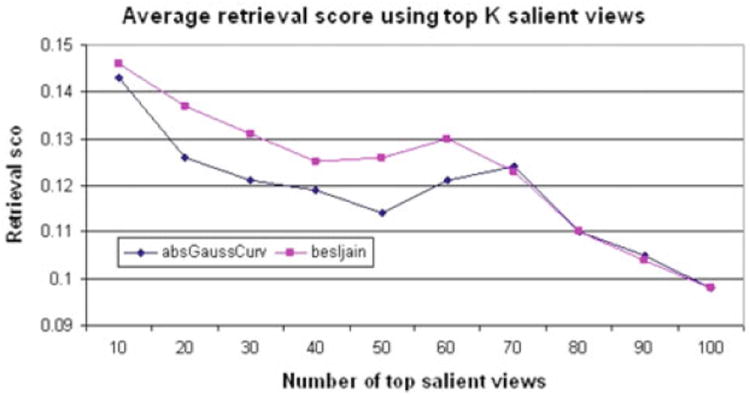
Average retrieval scores across all SHREC classes in the database as the number of top salient views used to construct the descriptor is varied. Learning of the salient points used two different low-level features: absolute Gaussian curvature and Besl–Jain curvature

In the second experiment, the algorithm selects the top salient views which are distinct. Table 2 shows the average retrieval scores across all classes in the dataset as the number of views and number of distinct views are varied. Comparing the results, it can be seen that the retrieval scores for the top K distinct views is always lower (better) than that for the top K views. For example, using the top five distinct salient views achieves an average retrieval score of 0.138 compared with using the top five salient views with retrieval score of 0.157. In fact, using the top 5 distinct salient views achieves similar retrieval score to using the top 20 salient views, and using the top 10 distinct salient views produces a similar retrieval score as to using the top 50 salient views. Each object in the dataset has its own number of distinct salient views. The average number of distinct salient views for all the objects in the dataset is 12.38 views. Executing the retrieval with the maximum number of distinct salient views for each object query achieves a similar average retrieval score to the retrieval performed using the top 70 salient views.

Table 2.

Average retrieval scores across all SHREC classes as the number of top salient views and top distinct salient views are varied

K	Score for top K views	Score for top K distinct views
1	0.207	0.207
2	0.186	0.174
3	0.172	0.163
4	0.162	0.151
5	0.157	0.138
6	0.155	0.134
7	0.152	0.131
8	0.152	0.129
9	0.146	0.127
10	0.143	0.128
11	0.137	0.127
12	0.134	0.121
20	0.126	–
30	0.121	–
40	0.119	–
50	0.114	–
60	0.121	–
70	0.124	–
80	0.110	–
90	0.105	–
100	0.098	–

Absolute Gaussian curvature was used as the low-level feature in the base framework. The averagemaximumnumber of distinct salient views is 12.38; hence there is no score available for K > 13 when using the top K distinct views

The third experiment compares the retrieval score when using the maximum number of distinct salient views to the retrieval score of the existing LFD method. Table 3 shows the average retrieval score for each class using the maximum number of distinct salient views and the LFD method. Over the entire database, the average retrieval score for the maximum number of distinct salient views was 0.121 while the average score for LFD was 0.098. To better understand the retrieval scores, a few retrieval scenarios are analyzed. Suppose that the number of relevant objects to a given query is N_rel and that the total number of objects in the database is N = 30, then the retrieval score is dependent on the rank of the N_rel relevant objects in the retrieved list. The same retrieval score can be achieved in two different scenarios. When N_rel = 10 a retrieval score of 0.2 is attained when three of the relevant objects are at the end of the retrieved list, while the same score value is obtained in the case of N_rel = 5 when only one of the relevant objects is at the end of the list. This shows that incorrect retrievals for classes with small N_rel value are more heavily penalized, since there are fewer relevant objects to retrieve. In Table 3 it can be seen that for classes with small N_rel values (N_rel < 10, the average class retrieval scores using the maximum number of distinct views are small and similar to retrieval using LFD (scores < 0.2), indicating that the relevant objects are retrieved at the beginning of the list. For classes with bigger N_rel values, the retrieval scores for most classes are <0.3 indicating that in most cases the relevant objects are retrieved before the middle of the list. The worst performing class for both methods is the spiral class with a score of 0.338 using maximum distinct salient views and 0.372 using LFD; this most probably is due to the high shape variability in the class. The retrieval score using our method is quite similar to the retrieval score of LFD with only small differences in the score values suggesting that the retrievals slightly differ in the ranks of the retrieved relevant objects, with most relevant objects retrieved before the middle of the list. Our method greatly reduces the computation time for descriptor computation.

Table 3.

Retrieval score for each SHREC class using the maximum number of distinct views versus using all 100 views (LFD)

No.	Class	# Objects	Avg # distinct salient views	Max distinct salient views score	LFD score
1	Human-diff-pose	15	12.33	0.113	0.087
2	Monster	11	12.14	0.196	0.169
3	Dinosaur	6	12.33	0.185	0.169
4	4-Legged-animal	25	12.24	0.274	0.186
5	Hourglass	2	11.50	0.005	0.001
6	Chess-pieces	7	12.14	0.085	0.085
7	Statues-1	19	12.16	0.267	0.250
8	Statues-2	1	13.00	0.000	0.000
9	Bed-post	2	12.00	0.124	0.008
10	Statues-3	1	12.00	0.000	0.000
11	Knot	13	12.00	0.006	0.003
12	Torus	18	11.77	0.194	0.161
13	Airplane	19	12.42	0.101	0.054
14	Heli	5	11.60	0.204	0.158
15	Missile	9	12.00	0.306	0.241
16	Spaceship	1	13.00	0.000	0.000
17	Square-pipe	12	12.31	0.026	0.017
18	Rounded-pipe	15	11.8	0.221	0.184
19	Spiral	13	12.46	0.338	0.372
20	Articulated-scissors	16	12.06	0.027	0.005
21	CAD-1	1	12.00	0.000	0.000
22	CAD-2	1	12.00	0.000	0.000
23	CAD-3	1	13.00	0.000	0.000
24	CAD-4	1	12.00	0.000	0.000
25	CAD-5	1	11.00	0.000	0.000
26	Glass	7	11.86	0.144	0.245
27	Bottle	17	12.12	0.093	0.081
28	Teapot	4	11.50	0.075	0.015
29	Mug	17	12.06	0.035	0.004
30	Vase	14	12.21	0.166	0.149
31	Table	4	11.50	0.099	0.153
32	Chairs	28	12.04	0.173	0.123
33	Tables	16	11.88	0.254	0.183
34	Articulated-hands	18	11.94	0.226	0.146
35	Articulated-eyeglasses	13	12.00	0.161	0.156
36	Starfish	19	12.26	0.158	0.102
37	Dolphin	23	12.35	0.071	0.053
38	Bird	17	12.12	0.239	0.211
39	Butterfly	2	12.00	0.166	0.009
Mean			12.38	0.121	0.098

The fourth experiment result shows the retrieval performance on the Princeton dataset measured using the dedicated benchmark’s statistics: (1) nearest neighbor, (2) first-tier, (3) second-tier, (4) E-measure, and (5) DCG. The first three statistics indicate the percentage of top K nearest neighbors that belong to the same class as the query. The nearest-neighbor statistics provides an indication of how well a nearest-neighbor classifier performs where K = 1. The first-tier and second-tier statistics indicate the percentage of top K matches that belong to the same class as a given object where K = C − 1 and K = 2 × (C − 1), respectively, and C is the query’s class size. For all three statistics, the higher the score the better the retrieval performance. E-measure is a composite measure of precision and recall for a fixed number of retrieved results. The DCG provides a sense of how well the overall retrieval would be viewed by a human by giving higher weights to correct objects that are retrieved near the front of the list. Table 4 shows the average retrieval results on the Princeton training dataset based on the benchmark statistics using the maximum number of distinct salient views and the LFD method. The average number of distinct salient views for all the objects in the Princeton dataset is 11 views. Table 5 shows the per-class nearest-neighbor retrieval average for both methods. Our method performs better in classes such as animal, dolphin, brain, and ship. The result shows comparable performance to the LFD even though we are only using 11 distinct salient views compared with 100 views in the LFD method.

Table 4.

Average retrieval performance on Princeton dataset

Method	Nearest neighbor	First tier	Second tier	E-measure	DCG
LFD	0.699	0.384	0.488	0.267	0.661
LFD salient 11 views	0.426	0.221	0.324	0.188	0.508

Table 5.

Per-class nearest neighbor retrieval performance on Princeton dataset

Class	LFD	Our method
Aircraft_airplane_F117	1	0
Aircraft_airplane_biplane	0.929	0.571
Aircraft_airplane_commercial	0.9	0.6
Aircraft_airplane_fighter_jet	0.92	0.84
Aircraft_airplane_multi_fuselage	0.857	0.143
Aircraft_balloonvehicle_dirigible	0.714	0.429
Aircraft_helicopter	0.412	0.176
Aircraft_spaceship_enterprise_like	1	0.818
Aircraft_spaceship_space_shuttle	1	0.833
Aircraft_spaceship_x_wing	1	0.8
Animal_arthropod_insect_bee	0.25	0.25
Animal_arthropod_spider	1	0.818
Animal_biped_human	0.86	0.66
Animal_biped_human_human_arms_out	0.952	0.381
Animal_biped_trex	0.667	0.833
Animal_flying_creature_bird_duck	0.4	0.2
Animal_quadruped_apatosaurus	0.75	0.25
Animal_quadruped_feline	1	0.5
Animal_quadruped_pig	0	0
Animal_underwater_creature_dolphin	0.8	1
Animal_underwater_creature_shark	0.714	0.571
Blade_butcher_knife	1	0.5
Blade_sword	0.8	0.467
Body_part_brain	0.714	0.857
Body_part_face	0.588	0.412
Body_part_head	0.812	0.75
Body_part_skeleton	0.8	0.4
Body_part_torso	0.75	0.75
Bridge	0.4	0.2
Building_castle	0.143	0
Building_dome_church	0.308	0
Building_lighthouse	0	0
Building_roman_building	0.333	0
Building_tent_multiple_peak_tent	0.2	0.2
Building_two_story_home	0.364	0.273
Chess_piece	0.941	0.471
Chest	0.714	0
City	0.6	0.3
Computer_laptop	0.5	0
Display_device_tv	0.167	0
Door_double_doors	0.8	0.3
Fantasy_animal_dragon	0.333	0.167
Furniture_bed	0.5	0.25
Furniture_desk_desk_with_hutch	0.857	0.429
Furniture_seat_chair_dining_chair	0.909	0.455
Furniture_seat_couch	0.733	0.267
Furniture_seat_chair_stool	0.571	0
Furniture_shelves	0.846	0.538
Furniture_table_rectangular	0.692	0.423
Furniture_table_round	0.75	0.333
Furniture_table_and_chairs	1	0.4
Gun_handgun	0.9	0.3
Gun_rifle	0.842	0.526
Hat_helmet	0.6	0.1
Ice_cream	0.667	0.417
Lamp_desk_lamp	0.857	0.429
Liquid_container_bottle	0.667	0.5
Liquid_container_mug	0.857	0
Liquid_container_tank	0	0
Liquid_container_vase	0.182	0.091
Microchip	0.857	0.571
Musical_instrument_guitar_acoustic_guitar	1	0.75
Musical_instrument_piano	0.833	0.5
Phone_handle	0.75	0.5
Plant_flower_with_stem	0.2	0.067
Plant_potted_plant	0.8	0.52
Plant_tree	0.765	0.647
Plant_tree_barren	0.455	0.182
Plant_tree_palm	0.6	0.4
Sea_vessel_sailboat	0.8	0.2
Sea_vessel_sailboat_sailboat_with_oars	0.75	0.25
Sea_vessel_ship	0.5	0.8
Shoe	0.75	0.625
Sign_street_sign	0.583	0.5
Skateboard	1	0.2
Snowman	0.5	0
Swingset	1	0.25
Tool_screwdriver	0.8	0.4
Tool_wrench	0.75	0.75
Vehicle_car_antique_car	0.4	0.2
Vehicle_car_sedan	0.6	0.4
Vehicle_car_sports_car	0.684	0.526
Vehicle_cycle_bicycle	1	0.857
Vehicle_military_tank	0.75	0.312
Vehicle_pickup_truck	0.5	0.25
Vehicle_suv	0	0
Vehicle_train	0.714	0.571
Watch	0.6	0
Wheel_tire	0.75	0.5

The last experiment investigates the run-time performance of our methodology and compares the run-time speed of our method with the existing LFD method. These experiments were performed on a PC running Windows Server 2008 with Intel Xeon dual processor at 2 GHz each and 16 GB RAM. The run-time performance of our method can be divided into three parts: (1) salient views selection, (2) feature extraction, and (3) feature matching. The salient view selection phase selects the views in which contour salient points are present. This phase on average takes about 0.2 s per object. The feature matching phase compares and calculates the distance between two 3D objects. This phase on average takes about 0.1 s per object. The feature extraction phase is the bottleneck of the complete process. The phase begins with a setup step that reads and normalizes the 3D objects. Then, the 2D silhouette views are rendered and the descriptor is constructed using the rendered views. Table 6 shows the difference in the feature extraction run time for one 3D object between our method and the existing LFD method. The results show that feature extraction using the selected salient views provides a 15-fold speedup compared with using all 100 views for the LFD method.

Table 6.

Average feature extraction run time per object

Method	Setup (s)	View rendering (s)	Descriptor construction (s)	Total time (s)
Max distinct views	0.467	0.05	0.077	0.601
LFD 100 views	0.396	4.278	4.567	9.247

7 Conclusion

We have developed a new methodology for view-based 3D object retrieval that uses the concept of salient 2D views to speed up the computation time of the LFD algorithm. Our experimental results show that the use of salient views instead of 100 equally spaced views can provide similar performance, while rendering many fewer views. Furthermore, using the top K distinct salient views performs much better than just the top K salient views. Retrieval scores using the maximum number of distinct views for each object are compared with LFD and differences in retrieval scores are explained. Finally, a timing analysis shows that our method can achieve a 15-fold speedup in feature extraction time over the LFD.

Future work includes investigating other methods to obtain the salient views. One way is to generate salient views using a plane fitting method with the objective of fitting as many salient points on the surface of the 3D object. This approach may be more computationally expensive as it may require exhaustive search in finding the best fitting plane; however, some optimization method may be used to reduce the search space.