Abstract
Prediction of cumulative incidences is often a primary goal in clinical studies with several end-points. We compare predictions among competing risks models with time-dependent covariates. For a series of landmark time points we study the predictive accuracy of a multi-state regression model, where the time-dependent covariate represents an intermediate state and two alternative landmark approaches (Cortese & Andersen, 2010). At each landmark time point, the prediction performance is measured as the t-year expected Brier score where pseudovalues are constructed in order to deal with right censored event times. We apply the methods to data from a bone marrow transplant study where graft versus host disease (GvHD) is considered a time-dependent covariate for predicting relapse and death in remission.
Keywords: Bone marrow transplant studies, Brier score, Competing risks, Prediction models, Pseudovalues, Time-dependent covariates
1. Introduction
In a competing risks setting with time-dependent covariates, the work [1] investigated alternative regression strategies for estimating the cumulative incidence of an event. In the present article we compare the predictive accuracy of such models in a case study. For a series of landmark time points we compare t-year predictions of the cumulative incidence obtained by three different approaches: a multi-state model [2], where the time-dependent covariate is modeled as an intermediate state, and two landmark models [3], one based on combination of cause-specific Cox regression models, and one based on Fine-Gray regression models. At each landmark time-point we consider the time-dependent Brier score [4] to measure the prediction performance. In order to deal with right-censored data, the possibly unknown time-dependent event status is replaced by pseudovalues [5].
We aim at comparing predictions both among the three modeling approaches and between models of a given type with or without including the time-dependent covariate. We illustrate the methods in a case study based on data from a bone marrow transplant study. Patients undergo transplant for acute leukemia in complete remission, and may later experience relapse of leukemia or death in remission. Graft versus host disease (GvHD) is a time-dependent covariate.
The paper is organized as follows. The prediction problem and how to obtain predictions from regression analysis under the three modeling approaches are described in Section 2. Section 3 introduces the bone marrow transplant example, Section 4 presents the estimator of the time-dependent Brier score based on pseudovalues, and Section 5 illustrates the results from the data and compares prediction errors.
2. Prediction models
Consider a non-homogeneous multi-state process {Z(t), t ∈ [0, τ]} with three states, 1:Remission, 2:Relapse and 3:Death without relapse. Patients in remission with and without GvHD are in state 1. Denote by X(t) a vector of internal time-dependent covariates [6] and by X̃ a vector of baseline covariates. In the following we assume that X(t) is a one dimensional binary process.
The aim is to predict the status of the process Z(t) at a future time point t, based on the survival and covariate histories up to time s (s < t). Specifically, we focus on probabilistic predictions of the following parameter:
| (1) |
Consider a set ℒ = {s1, …, sj, …, sJ} of time points (the landmarks) in the study period [0, τ]. Our objective is to predict the probabilities given in equation (1) at each s = sj in ℒ. Since the interest is in short-term predictions, we focus our attention on predicting over fix-sized intervals [sj, t], where for instance t = sj + 12 or t = sj + 24, with j = 1, …, J (time is given in months).
2.1. The multi-state approach
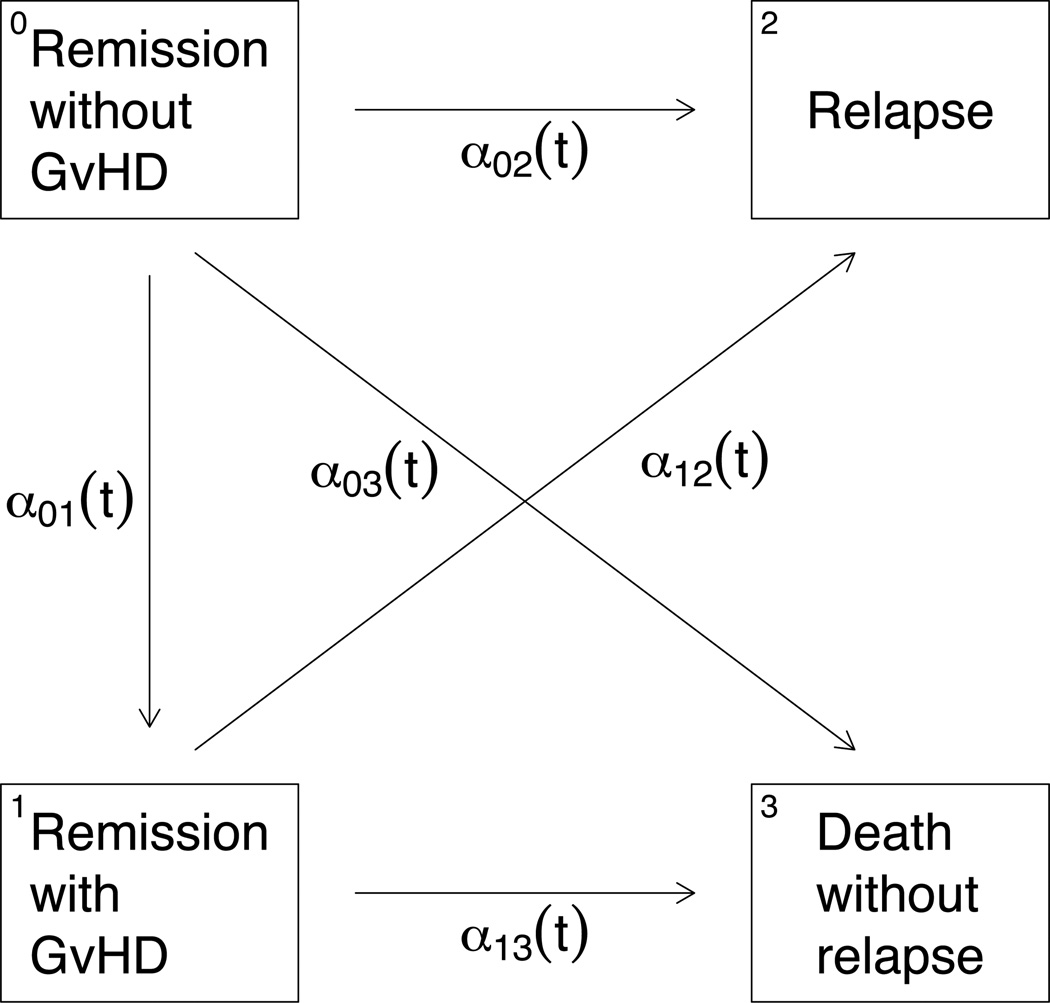
In order to describe the multi-state approach, we introduce a four state process U(t) which may take on the following states: 0:Remission without GvHD, 1:Remission with GvHD, 2:Relapse and 3:Death without relapse. The possible transitions and their associated intensities are depicted in Figure 1. The multi-state process is assumed to be irreversible, i.e. we assume that patients who develop GvHD do not recover from the condition. Note that {U(s) = 1} = {Z(s) = 1,X(s) = 1} and {U(s) = 0} = {Z(s) = 1,X(s) = 0}. In the following we assume that U is a non-homogeneous Markov process. However the Markov assumption may be relaxed by allowing transition intensities to depend on the sojourn time in the transient state 1 [1].
Figure 1.
Multi-state model showing the transitions of a GvHD patient.
Transition probabilities, for s ≤ t and h = 2, 3, have the following form:
| (2) |
| (3) |
where, for j = 0, 1, h = 1, 2, 3, j < h, αjh(t) are the transition intensities of the process U and the state occupation probabilities. Then, each of the transition intensities can be modeled by separate Cox regression models αjh(u | U(u−), X̃), for j = 0, 1, h = 1, 2, 3 and j < h. Proportional baseline hazards may also be considered between α0h(·) and α1h(·) in order to parametrize the effect of GvHD on the relapse and death rates [7]. Predictions of the parameters of interest Ph(sj, t) are then obtained by combining the results from the Cox models using the product limit method [2, Chap. VII] as demonstrated in [1]. We denote the estimates of the parameters in (1) by .
2.2. The cause-specific landmark approach
We here consider the process Z(t) corresponding to a standard three-state competing risks model. The key of the landmark approach [3] is to choose some opportune landmarks and perform a sequence of regression analysis at these time points. The choice of landmarks can be based on the distribution of the internal time-dependent covariate. Under the cause-specific approach, we assume separate Cox regression models for the cause-specific hazards:
| (4) |
For each sj, only the restricted sample of subjects still alive in remission at sj is used for the Cox regression analysis. Based on the maximum partial likelihood estimates for βj, γj and the corresponding Breslow estimates for the integrated , predictions of the future status of a patient at each landmark sj are obtained as
| (5) |
where Ŝ(·) is the Kaplan-Meier type estimator of the conditional survival probability given Z(sj) = 1.
Note that in contrast to the multi-state approach, here the prediction at sj does not directly account for the possibility of a future change of the time-dependent covariate (GvHD). The subsequent prediction at the landmark sj+1 utilizes the updated information on the covariate, X(sj+1). van Houwelingen [3] discussed the possibility of fitting simultaneous “super-models” for all landmarks, where both βj and vary smoothly with sj. This reduces the total number of parameters, however, we did not explore this option. The time since GvHD development may be accounted for by including it as a time-fixed covariate.
2.3. The Fine-Gray landmark approach
For this approach, we follow the same idea of landmarks and assume the same three-state competing risks model as above. For each type of event and at each sj ∈ ℒ, we fit a separate Fine-Gray regression model based on subjects still at risk. For a subject we predict cumulative incidences for future time-points t > sj as
| (6) |
where is the estimator of the cumulative subdistribution hazard [8] at landmark sj.
3. The bone marrow transplant data
Data on bone marrow transplant patients were collected at the Center for International Blood and Marrow Transplant Research. All recipients had a HLA-identical sibling transplant from 1995 to 2004 for acute myelogenous leukemia (AML) or acute lymphoblastic leukemia (ALL). Patients received bone morrow transplantation or peripheral stem cell transplantation in first complete remission. The infants aged less than 2 years old and subjects who received umbilical cord blood transplants were excluded. We here study the two major BMT treatment failures, relapse, that is recurrence of the primary disease, and death in complete remission. In bone marrow transplant studies, this latter outcome is generally considered the main type of treatment failure, especially in patients who developed GvHD. Thus, the effect of GvHD is of primary interest for predicting relapse and death in remission.
The data set consists of 2009 patients whose follow-up period began at time of transplant. At this time, no patients had GvHD. Moreover, patients lost to follow-up (62%) were considered as right-censored observations. For ease of presentation, we consider only age at transplant and disease type (AML or ALL) as baseline covariates in regression models. The mean age was equal to 31.9 (SD = 15.4) and AML leukemia disease was present in 1406 (70%) patients. The total number of patients observed to develop GvHD over time was 976 (49%). Relapse occurred in 259 (13%) patients, among whom 91 were previously observed to develop GvHD. Among the 505 (25%) subjects who were observed to die in remission, 307 patients had previously developed GvHD.
The assumption of covariate-independent censoring was tested by fitting a Cox model for the hazards of censoring times, and no significant dependence on covariates was observed.
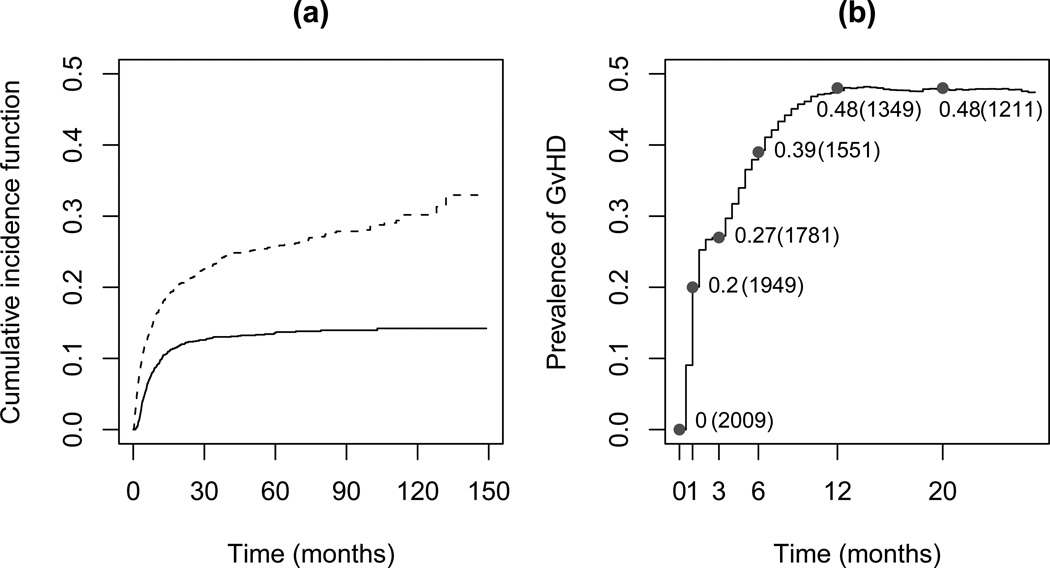
Panel (a) of Figure 2 shows that the predicted cumulative risks of relapse and death rapidly increase during the first 20 months, and that the risk of relapse stays constant at about 13% after 30 months whereas the risk of death continues to increase over time. Panel (b) of Figure 2 shows a crude estimate of the prevalence of GvHD calculated as the observed number of GvHD cases in [0, t] divided by the sample size.
Figure 2.
(a): Estimated cumulative incidence probabilities (by the Aalen-Johansen estimator) in a competing risks model for relapse (solid line) and death in remission (dashed line). (b): Prevalence of GvHD during follow-up period; values, together with the number of patients at risk (in bracket), are given at landmark times.
The set of landmark points ℒ = {0, 1, 3, 6, 12} was chosen according to the distribution of GvHD over time given in panel (b) of Figure 2. Since a substantial increase in the number of GvHD cases was observed within the first twelve months, we decided to study risk predictions at specific time points within this period.
For the multi-state approach transition intensities followed separate Cox models with disease type and age (centered with respect to its mean) as baseline covariates. For the landmark approaches we performed regression analyses at each sj including disease type, centered age and the GvHD status at sj as a time-constant covariate.
Table 1 shows estimated regression coefficients from the three approaches and from a standard competing risks model with separate Cox models for the cause-specific hazards with and without inclusion of the time-dependent covariate GvHD. From these results we note that the development of GvHD had a strong effect on the rate of dying in remission (see the standard competing risks model and the cause-specific landmark approach, where all time-varying coefficients for GvHD were found to be significant). Presence of GvHD at time sj affects strongly the cumulative risk of dying in remission. On the other hand, no significant effect of GvHD was found, neither on the rate, nor on the cumulative risk of relapse. Therefore, we expect GvHD to be an important factor only for predictions of the risk of death in remission.
Table 1.
Estimated regression coefficients and their standard errors in cause-specific hazards of a standard competing risks model with and without including the time-dependent covariate GvHD, in transition intensities of the multi-state model, in the cause-specific landmark model and and Fine-Gray landmark model.
|
Standard competing risks model | |||||
| Relapse | Death | Relapse | Death | ||
| Centered age | −0.003 (0.004) | 0.027 (0.003) | −0.003 (0.004) | 0.030 (0.003) | |
| AML disease | 0.563 (0.129) | 0.332 (0.098) | 0.550 (0.129) | 0.4 (0.097) | |
| GvHD(t) | −0.172 (0.133) | 1.048 (0.097) | – | – | |
| Multi-state model | |||||
| Alive, → Relapse | Alive, → Death | GvHD → Relapse | GvHD → Death | ||
| no GvHD | no GvHD | ||||
| Centered age | −0.006 (0.005) | 0.026 (0.005) | 0.002 (0.007) | 0.029 (0.004) | |
| AML disease | 0.564 (0.160) | 0.267 (0.159) | 0.585 (0.125) | 0.361 (0.125) | |
| Landmark, cause-specific hazards | |||||
| Cause-specific hazard for Relapse | |||||
| s = 0 | s = 1 | s = 3 | s = 6 | s = 12 | |
| Centered Age | −0.003 (0.004) | −0.003 (0.004) | −0.007 (0.005) | −0.001 (0.006) | 0.006 (0.009) |
| AML disease | 0.550 (0.129) | 0.551 (0.130) | 0.634 (0.141) | 0.844 (0.180) | 0.843 (0.256) |
| GvHD(s) | – | −0.007 (0.162) | 0.002 (0.156) | −0.017 (0.181) | 0.037 (0.250) |
| Cause-specific hazard for Death | |||||
| Centered Age | 0.030 (0.003) | 0.033 (0.003) | 0.031 (0.004) | 0.029 (0.004) | 0.034 (0.006) |
| AML disease | 0.400 (0.097) | 0.356 (0.105) | 0.207 (0.126) | 0.351 (0.142) | 0.368 (0.182) |
| GvHD(s) | – | 0.759 (0.103) | 0.899 (0.111) | 0.749 (0.129) | 0.563 (0.167) |
| Landmark, Fine-Gray model | |||||
| Subdistribution hazard for Relapse | |||||
| s = 0 | s = 1 | s = 3 | s = 6 | s = 12 | |
| Centered Age | −0.008 (0.004) | −0.010 (0.004) | −0.009 (0.005) | −0.003 (0.006) | 0.005 (0.009) |
| AML disease | 0.470 (0.131) | 0.497 (0.132) | 0.627 (0.146) | 0.820 (0.185) | 0.830 (0.266) |
| GvHD(s) | – | −0.173 (0.162) | −0.115 (0.157) | −0.096 (0.181) | 0.005 (0.249) |
| Subdistribution hazard for Death | |||||
| Centered Age | 0.030 (0.003) | 0.032 (0.003) | 0.031 (0.004) | 0.029 (0.005) | 0.033 (0.006) |
| AML disease | 0.338 (0.097) | 0.287 (0.104) | 0.122 (0.123) | 0.275 (0.138) | 0.311 (0.178) |
| GvHD(s) | – | 0.739 (0.105) | 0.885 (0.111) | 0.743 (0.128) | 0.558 (0.166) |
4. Estimation of prediction error based on pseudovalues
We aim at estimating the mean squared prediction errors of the cumulative incidences given in equation (1) over the intervals [sj, t] with sj ∈ ℒ. For this scope, we adapt the time-dependent Brier score [4] to competing risks and present an estimator based on pseudovalues. These quantities are based on squared residuals between the event status I(Z(t) = h) and the model-based prediction for patients who are at risk at time sj. For ease of presentation, in this section we consider predictions from a generic model P̂h and at a generic landmark s for a fixed prediction horizon t. We also introduce the notation Hs = (Z(s) = 1, X(s), X̃).
First, we assume that the predictions are obtained by fitting the model to a training data set 𝒟n of size n, and that there is an independent testing data set 𝒯m of size m available for estimating the prediction performance. For situations where independent data are not available, model validation and evaluation of its predictive accuracy can be performed by using cross-validation methods [9].
At landmark s the time-dependent Brier score for the prediction of Z(t) = h, for h = 2, 3 and t > s, is defined as
| (7) |
| (8) |
where W(s) = 1/P(Z(s) = 1 | 𝒟n) and the expectation is taken conditionally on 𝒟n with respect to the random variables Z(t) and Hs.
4.1. Complete data
In a complete data framework, the event status I(Z(t) = h) is always observed for all subjects still at risk at s in the testing sample 𝒯m, and a consistent estimator of the time-dependent Brier score is
| (9) |
| (10) |
where R(s) = {i ∈ 𝒯m : Zi(s) = 1} is the risk set at time s, ms is the number of subjects in R(s), and . The notation P̂h(s, t | His) indicates the prediction of the event h for individual i with His = (Xi(s), Zi(s) = 1, X̃i).
4.2. Censored data
For right censored data, the event status I(Z(t) = h) can not be observed if the patient was lost to follow-up before time t. The idea is to replace the event status with a pseudovalue. Let Q̂h(s, t) denote the marginal Aalen-Johansen estimate [10] of P(Z(t) = h|Z(s) = 1) based on the testing sample 𝒯m. Let be the same estimate based on the data where the ith patient in the risk set at s has been removed. A jackknife pseudovalue for the event status for a patient i who is at risk for event h at time s is defined by
| (11) |
Note that the pseudovalues may be higher than 1 or lower than 0, they also depend on ms and are computed only for individuals in R(s). The pseudovalue is an estimate of the event status I(Zi(t) = h) given that the subject is at risk at s. For uncensored data, the pseudovalues for individuals at risk at s are equal to the status variable . This follows immediately from the definition, since for uncensored data the Aalen-Johansen estimate is given by . For right censored data it has been shown that the pseudovalue has the same (conditional) expectation as the possibly unobserved status [11], under covariate independent censoring.
Under the assumption of covariate-independent censoring, we show in the appendix that the following formula provides a consistent estimator of the time-dependent Brier score given in equation (8):
| (12) |
where and R̃(s) = {i ∈ 𝒯m : Zi(s) = 1, Ci > s} for individual right censoring times Ci. Note that for practical purposes equation (12) can also be written as , where the weights W̃m(s) = m/m̃s account for the proportion of subjects at risk non censored at s, and the residuals are .
4.3. Cross-validation
Statistical models are expected to be used for inference on the entire population under study, and model-based predictions are expected to perform less well on a new data set than on the data set used for estimation.
Our primary interest is on evaluating the expected time-dependent Brier score, which is the mean squared error of prediction for a new subject in the population of bone marrow transplanted patients at risk at time s. This measure can be thought as the quantity (8) considered at the population level and therefore, the average over all possible samples from the population would need to be considered. The idea behind cross-validation techniques is that the available sample of observations is representative of the above-mentioned population. Thus, this sample can be used to generate a certain number K of subsamples for the estimation and prediction procedures, leading to a series of training and testing sets. When the Brier score B̂h(s, t)(k) as given in (12) is computed for each of the k = 1, …, K testing sets, the pseudovalue averaged Brier score
| (13) |
provides an estimate of the predictive ability of the model.
5. Illustration: bone marrow transplant study
The current section presents further results from the bone marrow transplant data about predictions based on the three modeling approaches described in Section 3. The first aim of this application was to compare performance of the three approaches in terms of prediction error, calculated by means of the pseudovalue-based estimator of the Brier score in Section 4. The second parallel scope of the analyses was to investigate whether and how GvHD affects the predictions for risks of death and relapse, and possibly improves prediction accuracy. In order to study the predictive ability of GvHD, beyond the other covariates, prediction errors of models without the covariate GvHD and models without any covariate (neither GvHD nor baseline covariates) were compared with prediction errors of models with GvHD. The analyses were carried out with the R software, Version 2.11.0 [12].
5.1. Individual predictions
Given the interest in short-term prediction in our example, we fixed the prediction time horizon t at 12 months from the time sj at which predictions are made, that is, we computed predictions over the intervals [sj, sj + 12], with sj ∈ ℒ = {0, 1, 3, 6, 12} (given in months). Results for t = sj + 24 were found to be very similar and are not shown here.
First, we studied individual predictions of relapse and death in remission (h = 2, 3) for all patients i included in the original data set at risk at the landmark sj. Under the multi-state model, we computed the individual predictions for subjects i without GvHD at sj, and for subjects i who had developed GvHD before sj. Under the landmark approaches, the individual predictions were calculated for M = cs, fg by equations (5) and (6). For all three regression models the estimated cumulative risks of relapse were very similar for those subjects with and without GvHD at sj, for all sj, although slightly lower for those with GvHD. On the other hand, the estimated cumulative risks of death appeared to be substantially higher for patients with GvHD. These results also agree with those in Table 1 where regression coefficients of GvHD under a Fine-Gray model indicate a significant effect on risk of death, but a non significant effect on the risk of relapse, for all chosen landmark points. Thus, we conclude that GvHD seems to affect strongly only the cumulative risk of death.
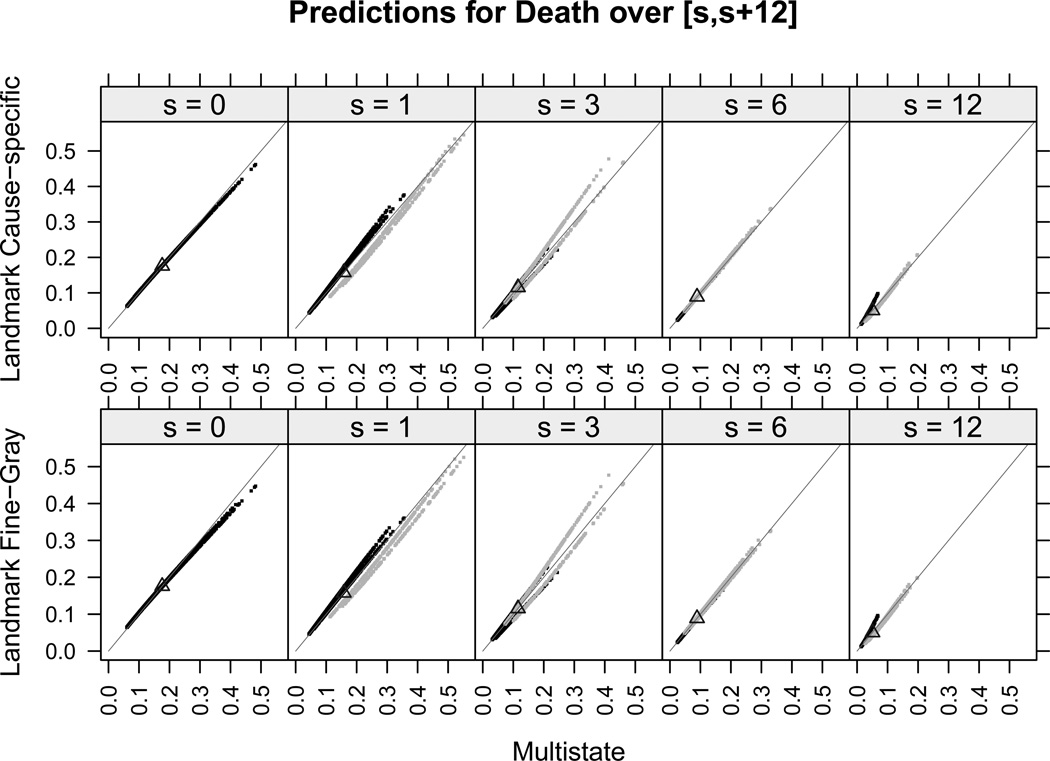
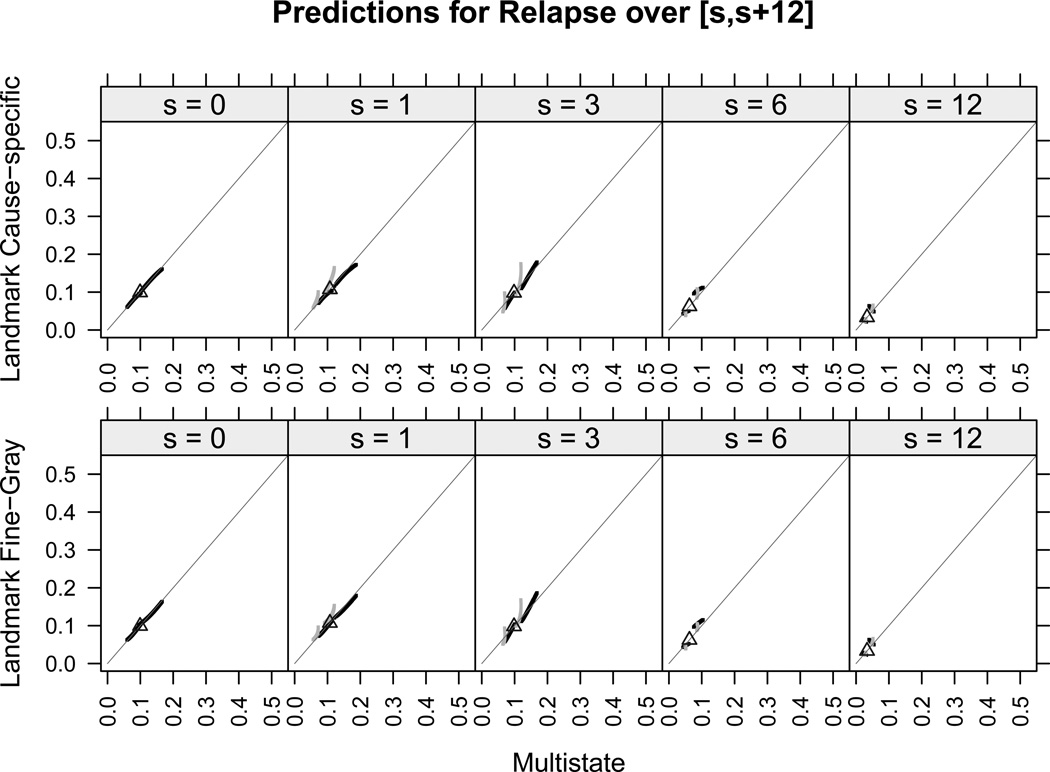
We focus now on comparing the individual predictions of all patients among the three modeling approaches. Results are shown for the risk of death in remission only, since no differences were found for the risk of relapse. Moreover, for all landmarks, the individual predicted risks of relapse were very low (below 0.2) and departed only slightly from the one-year prediction (equal to 0.1) obtained under a competing risks model with no covariates under study. Figure 3 shows, for the risk of death, the plots of predictions from the landmark approaches versus predictions from the multi-state model over the intervals [sj, sj + 12], for patients with GvHD and without GvHD at the landmarks sj (light gray and dark gray points, respectively). Under the landmark approaches, the cause-specific and the Fine-Gray methods provided virtually identical predictions for all landmarks and for both relapse and death, as seen by comparing the top panels with the bottom panels in Figures 3 and 4. Individual predictions of relapse under the multi-state model were very similar to those obtained under the landmark approaches, as seen from Figures 4, and they were slightly lower only for some patients with GvHD at times s = 1, 3, since the light gray points lie above the straight line representing equal performance between methods. Moreover, for all landmarks, all predictions of relapse were below 0.2 and thus departed only slightly from the one-year prediction obtained in case that no covariates are taken into account (thick black triangle). The comparison between the multi-state and the landmark approaches shows small differences in the individual predictions for death, mostly observed at landmarks s = 1, 3 and especially for those patients who had already developed GvHD at those times.
Figure 3.
One-year individual predictions for the risk of death in remission from time s under the multi-state, cause-specific landmark and Fine-Gray landmark approaches, together with the prediction in case of no covariates (black triangles). Black and gray points are, respectively, for patients without and with GvHD at s. Equal predictions between two methods are represented by the straight gray line.
Figure 4.
One-year individual predictions for relapse from time s under the multi-state, cause-specific landmark and Fine-Gray landmark approaches, together with prediction in case of no covariates (black triangles). Black and gray points are, respectively, for patients without and with GvHD at s. Equal predictions between two methods are represented by the straight gray line.
5.2. Prediction errors
The mean squared errors of the one-year predictions of relapse and death at the landmark points were estimated by the sequence of pseudovalue-based Brier scores B̂h(sj, sj + 12) for sj ∈ ℒ, h = 2, 3, under the three different regression approaches. We used cross-validation in order to obtain estimates of the expected Brier score and we applied the cross-validation technique based on random subsampling from the original sample as follows. We repeated the procedure K = 100 times. Thus, at each time k, the following steps were performed:
The original data set of size N was randomly partitioned into two disjoint sets: the training set of size n = (2/3)N and the testing set of size m = N − n.
The parameter estimates of the regression models were obtained from data in , for all sj ∈ ℒ.
In all time intervals [sj, sj + 12] for sj ∈ ℒ, the individual predictions and the pseudovalues were computed for all patients being at risk at time sj in the testing set . Pseudovalues were obtained by using the R package pseudo.
The sequence of Brier score estimates at the landmarks, B̂h(k)(0, 12), B̂h(k)(1, 13), B̂h(k)(3, 15), B̂h(k)(6, 18), B̂h(k)(12, 24), was computed.
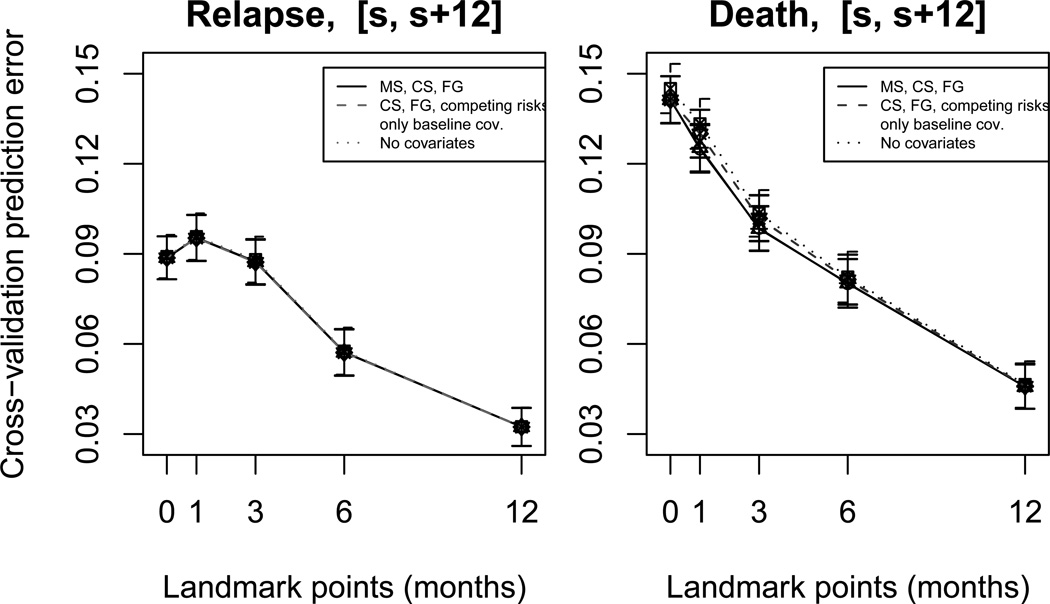
Finally, for each sj, results from the K repetitions were used to obtain an estimate of the expected Brier score (as given in equation 13) by averaging the quantities in step (4) over k = 1, …, 100. Results are shown in Figure 5.
Figure 5.
Cross-validated one-year prediction errors (and their standard deviation), evaluated by the pseudovalue estimator, at landmarks s ∈ ℒ = {0, 1, 3, 6, 12}. Prediction errors were computed under the multi-state, cause-specific and Fine-Gray landmark approaches (solid lines), under the cause-specific and Fine-Gray landmark approaches and under the standard competing risks model in case GvHD is ignored (only baseline covariates) (dashed lines), under a competing risks model with no covariates (dotted line).
Figure 6 shows the relative reduction of prediction error (or relative prediction accuracy) for the different models with covariates with respect to a model with no covariates (dotted lines at zero). Given , the Brier score for the model with no covariates, and B̂h, the Brier score for a model with covariates, this reduction is given by . This index allows proper comparisons of the gain in prediction accuracy between the different landmark points, independently of the absolute value of the errors at these points. Both Figures 5 and 6 show that the cross-validated prediction errors for both relapse and death were approximately equal under the multi-state, cause-specific and Fine-Gray landmark models with all covariates (the solid lines coincide). However, when the GvHD covariate was ignored, we observed an increase in prediction error for death at landmark points 1, 3, 6 (dashed lines). It is evident from Figure 6 that the relative prediction accuracy for death is substantially reduced at these times, as compared to models with GvHD and to the remaining landmarks. No difference in the prediction errors for relapse was found between models with and without GvHD. The systematic decrease of prediction errors for death and relapse at later landmark times is the natural consequence of number of events decreasing over time. Three possible models with only baseline covariates were considered: a standard competing risks regression, a cause-specific landmark and a Fine-Gray landmark. Finally, prediction errors for death appeared to be higher in a competing risks model with no covariates (dotted lines) than in models with covariates, while a slight difference was observed for relapse.
Figure 6.
Proportion of reduction (or increased accuracy) of the one-year cross-validated prediction errors, evaluated by the pseudovalue estimator, under the different models with covariates, as compared to prediction error of a model with no covariates (dotted lines). Error bars refer to standard errors.
In order to evaluate differences in prediction errors between models with a statistical procedure, we performed nonparametric tests of hypothesis based on the residuals , defined in Subsection 4.2, computed from the cross-validated samples, following the method proposed in [9]. We considered two-sided tests for comparisons between the three modeling approaches and one-sided tests otherwise. The nominal significance level was adjusted by using Bonferroni correction to α = 0.001, due to multiple testing of several models at the 5 landmarks. The tests confirmed that models including GvHD provided significantly better predictions for death at times s = 1, 3, compared to models with only baseline covariates and models with no covariates (p < 0.0001), whereas no relevant differences were found for relapse. Tests for pairwise comparisons between the three modeling approaches showed no significant differences in prediction errors for both relapse and death, except for s = 1. At this landmark point, the multi-state model resulted to predict better for the event of death (p < 0.0001) and worse for relapse (p < 0.001), compared to the two landmark approaches. These inverted results might be explained by the fact that death and relapse are here competing events, and the time-dependent GvHD affects only the risk of death. However, since predictions of both events are of clinical importance in our example, the inverted results at s = 1 compensate and therefore we can consider the three modeling approaches to have equal prediction accuracy.
In conclusion, our analyses indicate that predictions for relapse and death in remission have the same level of accuracy when computed under the three different regression models. Irrespective of the modeling strategy, predictions of death in remission are more accurate when the time-dependent covariate GvHD is included, especially for short-term predictions at earlier times (s = 1, 3, 6), while the prediction accuracy for relapse remains unchanged. Thus GvHD has an important predictive ability only for the event of death in bone marrow transplant patients. Moreover, accuracy diminishes, especially for death, if predictions are based on a model with no covariates.
6. Discussion
Three modeling approaches for competing risks in presence of an internal time-dependent covariate were compared, with the motivation that their performance in terms of prediction accuracy is unknown and they rely on different model assumptions. The multi-state approach assumes a certain model for the covariate process, on which inference depends, it requires estimation of coefficients in the regression models for transition intensities, but predictions rest on a single regression analysis. On the other hand, the cause-specific and Fine-Gray landmark approaches require a sequence of regression analyses performed at landmarks, whose choice, although arbitrary, is important in order to capture how the time-dependent covariate affects the cumulative risks. Regression coefficients depend on landmarks and their estimates may vary over the different time points. However, these approaches do not need to specify a model for the internal covariate, and more easily handle situations where the internal covariate is discrete or continuous.
A referee pointed out that to improve the landmark models we could have applied administrative censoring at the prediction horizon [13]. However, that would require fitting different models for each prediction horizon (here 12 or 24 months) and we did not pursue that idea.
The landmark approach for analyzing follow-up data from transplant patients presented here is related to the sequential stratification method of [14]. The latter formulates estimates of a time-dependent covariate or treatment on the hazard scale. It is, however, not clear how sequential stratification results could be translated into predictions of the cumulative incidence.
In the bone marrow transplant example, comparisons of cross-validation prediction errors suggested that the three regression modeling strategies with an internal time-dependent covariate have identical prediction accuracy. Therefore, one or the other approach may be used taking into account what is more convenient in terms of available information and underlying assumptions. Moreover, by performing analyses about prediction errors for models that ignore the time-dependent covariate, we found that GvHD had a high predictive ability and it can then be considered as an essential significant risk factor in order to predict one-year cumulative risks of death in remission.
It has to be noted that the methodology illustrated in the current paper for the three modeling approaches in order to assess whether there is a better model in terms of prediction accuracy, can be generalized to other complex competing risks models or multi-state models where internal time-dependent covariates play an important role. The present case study showed roughly identical accuracy of predictions based on the multi-state model and several landmark models. This finding may not generalize to other settings. On the other hand, given the similarity in complexity of the landmark models based on either cause-specific hazards or Fine-Gray approaches, the apparent resemblance between their predictions is likely to be found universally.
When estimating the time-dependent Brier score, the pseudovalues are computed only once, and are independent of the survival model assumed. In the inverse probability of censoring weighted estimates of the Brier score [15, 16, 4], the predictions of the model are ignored for censored observations, and those observations contribute only to the weights given to observations whose survival experience is known at the prediction time horizon. On the contrary, the pseudovalue-based estimator has the advantage that the individual predictions of censored observations are also included, since the pseudovalues for these subjects provide nonparametric estimates of their event status. However, the pseudovalue-based estimator requires the assumption of covariate-independent censoring. A useful extension of this estimator to the covariate-dependent censoring case may be possible following the lines in the work [17].
Acknowledgement
The research was supported by the Excellence program ‘Statistical methods for complex and high dimensional models’ of the University of Copenhagen, Denmark, by the National Cancer Institute [grant number R01-54706-12], and by the Danish Natural Science Research Council [grant number 272-06-0442 ”Point process modeling and statistical inference”]. We are grateful to CIBMTR for providing us with the example data.
Appendix: Consistency of the pseudovalue-based estimator
Theorem
For a prediction model P̂h with event of interest h, h = 2, 3
in probability.
Proof
We recall the notation from Section 4, Hs = (X(s), Z(s) = 1, X̃), and define the censored process as Z̃(t) = Z(t)I(C > t). By the central limit theorem and Slutsky’s lemma we have for m → ∞:
By adapting the results of [11] to the landmark setting we can show that
in probability, and hence that the remainder term satisfies
References
- 1.Cortese G, Andersen PK. Competing risks and time-dependent covariates. Biometrical Journal. 2010;52:138–158. doi: 10.1002/bimj.200900076. [DOI] [PubMed] [Google Scholar]
- 2.Andersen PK, Borgan Ø, Gill RD, Keiding N. Statistical Models Based on Counting Processes. New York: Springer-Verlag; 1993. [Google Scholar]
- 3.van Houwelingen HC. Dynamic Prediction by Landmarking in Event History Analysis. Scandinavian Journal of Statistics. 2007;34:70–85. [Google Scholar]
- 4.Schoop R, Graf E, Schumacher M. Quantifying the predictive performance of prognostic models for censored survival data with time-dependent covariates. Biometrics. 2008;64:603–610. doi: 10.1111/j.1541-0420.2007.00889.x. [DOI] [PubMed] [Google Scholar]
- 5.Andersen PK, Perme MP. Pseudo-observations in survival analysis. Statistical Methods in Medical Research. 2010;19:71–99. doi: 10.1177/0962280209105020. [DOI] [PubMed] [Google Scholar]
- 6.Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. New York: Wiley; 2002. [Google Scholar]
- 7.Klein JP, Keiding N. Plotting summary predictions in multistate survival models: probabilities of relapse and death in remission for bone marrow transplantation patients. Statistics in Medicine. 1993;12:2315–2332. doi: 10.1002/sim.4780122408. [DOI] [PubMed] [Google Scholar]
- 8.Fine JP, Gray RJ. A Proportional hazards model for the subdistribution of a competing risk. Journal of the American Statistical Association. 1999;94:496–509. [Google Scholar]
- 9.van de Wiel MA, Berkhof J, Wieringen WN. Testing the prediction error difference between 2 predictors. Biostatistics. 2009;10:550–560. doi: 10.1093/biostatistics/kxp011. [DOI] [PubMed] [Google Scholar]
- 10.Aalen O, Johansen S. An empirical transition matrix for nonhomogeneous Markov chains based on censored observations. Scandinavian Journal of Statistics. 1978;5:141–150. [Google Scholar]
- 11.Graw F, Gerds TA, Schumacher M. On pseudo-values for regression analysis in competing risks models. Lifetime Data Analysis. 2009;15:241–255. doi: 10.1007/s10985-008-9107-z. [DOI] [PubMed] [Google Scholar]
- 12.R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. 2011 ISBN 3-900051-07-0, URL. [Google Scholar]
- 13.van Houwelingen HC, Putter H. Dynamic prediction in clinical survival analysis. Chapman & Hall (CRC) 2012 [Google Scholar]
- 14.Schaubel DE, Wolfe RA, Port FK. A Sequential Stratification Method for Estimating the Effect of a Time-Dependent Experimental Treatment in Observational Studies. Biometrics. 2006;62:910–917. doi: 10.1111/j.1541-0420.2006.00527.x. [DOI] [PubMed] [Google Scholar]
- 15.Graf E, Schmoor C, Sauerbrei W, Schumacher M. Assessment and comparison of prognostic classification schemes for survival data. Statistic in Medicine. 1999;18:2529–2545. doi: 10.1002/(sici)1097-0258(19990915/30)18:17/18<2529::aid-sim274>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 16.Gerds TA, Schumacher M. Consistent estimation of the expected Brier score in general survival models with right-censored event times. Biometrical Journal. 2006;48:1029–1040. doi: 10.1002/bimj.200610301. [DOI] [PubMed] [Google Scholar]
- 17.Binder N, Gerds M, Andersen PK. Pseudo-observations of competing risks with covariate dependent censoring. To appear in Lifetime data analysis. 2013 doi: 10.1007/s10985-013-9247-7. [DOI] [PMC free article] [PubMed] [Google Scholar]