Abstract
Visuomotor adaptation is mediated by errors between intended and sensory-detected arm positions. However, it is not clear whether visual-based errors that are shown during the course of motion lead to qualitatively different or more efficient adaptation than errors shown after movement. For instance, continuous visual feedback mediates online error corrections, which may facilitate or inhibit the adaptation process. We addressed this question by manipulating the timing of visual error information and task instructions during a visuomotor adaptation task. Subjects were exposed to a visuomotor rotation, during which they received continuous visual feedback (CF) of hand position with instructions to correct or not correct online errors, or knowledge-of-results (KR), provided as a static hand-path at the end of each trial. Our results showed that all groups improved performance with practice, and that online error corrections were inconsequential to the adaptation process. However, in contrast to the CF groups, the KR group showed relatively small reductions in mean error with practice, increased inter-trial variability during rotation exposure, and more limited generalization across target distances and workspace. Further, although the KR group showed improved performance with practice, after-effects were minimal when the rotation was removed. These findings suggest that simultaneous visual and proprioceptive information is critical in altering neural representations of visuomotor maps, although delayed error information may elicit compensatory strategies to offset perturbations.
Keywords: Visuomotor adaptation, Visuomotor rotation, Feedback, Vision, Knowledge-of-results
Introduction
During goal-directed reaching, sensory information about the spatial location of the target is used to plan and initiate accurate movements (Ghilardi et al. 1995; Vindras and Viviani 1998). This requires sensory signals about target location to be transformed into an internal reference frame that can be used to specify the appropriate muscle forces required to complete the movement (Soechting and Flanders 1989; Tillery et al. 1991; Desmurget et al. 1998). For visually defined targets, this process appears to be mediated by a “visuomotor map” of the relationship between extrinsic visual coordinates and intrinsically specified motor commands (Cunningham and Welch 1994). However, when we interact with a novel tool, such as a computer mouse, or perform within a virtual reality environment, the relationship between visual information and motor commands can be unfamiliar and unpredictable. Upon initial exposure to such situations, the visual-detected movement trajectory deviates from the planned trajectory, resulting in an error between visual information about hand location and the desired target location. While this error information is utilized to correct the ongoing movement, it also serves to update the current visuomotor map (i.e., “visuomotor remapping” occurs), which allows errors to be reduced on the subsequent movements.
Visuomotor adaptation is mediated largely by visual-detected movement errors with respect to the intended movement goal (Wolpert and Miall 1996; Tseng et al. 2007). However, it is not clear how error information mediates trial-to-trial learning. For instance, visuomotor adaptation tasks are often performed with continuous visual feedback made available in each trial (Ghilardi et al. 2000; Prager and Contreras-Vidal 2003; Krakauer et al. 2005; Wang and Sainburg 2005, 2006; Schaefer et al. 2009), or with visual feedback limited to the end-phase of motion, near movement termination (Choe and Welch 1974; Bedford 1989, 1993; Ghahramani et al. 1996; Vindras and Viviani 2002). In both cases, a deviation in the displayed hand position from the predicted hand position is detected during movement. Alternatively, error information about a recent movement can be displayed after the movement has been completed, as is the case with knowledge-of-results (KR). When KR is shown as a static hand-path, it provides the same amplitude error that continuous visual feedback provides. Therefore, if the amplitude, but not the timing of error information is important for the adaptation process, then the extent of adaptation should be the same during conditions in which the hand-path is provided during the movement or delayed until after the movement is complete. In support of this notion, KR of even a single hand position (i.e., final position) has been shown to sufficiently mediate adaptation to altered visuomotor gain displays and facilitate generalization of the learned transformation to untrained target locations (Vindras and Viviani 2002). Conversely, KR is not equivalent to continuous visual feedback for adaptation to visuomotor rotations (Hinder et al. 2008, 2010). In contrast to the gain experiment, where finger location was accurately depicted during veridical movements (Vindras and Viviani 2002), subjects controlled cursor motion by applying elbow torques to a manipulandum during the rotation experiment (Hinder et al. 2008, 2010). This required visuomotor transformations of elbow torque to cursor motion for baseline conditions, potentially interfering with adaptation to the rotation when KR was provided. As a result, it is not clear whether this current discrepancy in findings reflects variations in experimental design or qualitative differences in visuomotor gain and rotation adaptation. Adaptation to gain perturbations results in remapping of scaling factors that readily generalize to untrained target directions, while adaptation to rotation perturbations results in remapping of reference axes that show limited generalization to untrained target directions (Pine et al. 1996; Krakauer et al. 2000).
One possible advantage that concurrent visual feedback may provide over KR is the ability to correct errors during the course of movement. Upon initial exposure to a visuomotor rotation, online error corrections bring the cursor successfully to the intended target. The process of correcting movements could serve to inform the visuomotor map, possibly by providing efference copy information of the distance error between the visual-detected hand position and target, or by providing proprioceptive information about hand location when the target is reached. Recent work has shown visuomotor adaptation during rapid out-and-back reaching tasks, which did not allow for online motor corrections (Krakauer et al. 2000; Tong and Flanagan 2003; Caithness et al. 2004; Miall et al. 2004; Mazzoni and Krakauer 2006), and when perturbations were introduced gradually (Kagerer et al. 1997; Klassen et al. 2005), such that movement errors were not consciously detected and online corrections were not obvious. While these results suggest that online motor corrections are not required for adaptation, they do not discount the possibility that such corrections might facilitate or inhibit adaptation relative to conditions where motor corrections are absent.
The goal of the current study was to determine whether the timing of movement error information and the occurrence of online motor corrections affect adaptation to novel visuomotor transformations. We addressed the ambiguity of previous findings by testing whether KR was sufficient to mediate adaptation to visuomotor rotations when reaching was not confounded by additional visuomotor transformations (i.e., finger and cursor positions were aligned during baseline conditions). Subjects were assigned to one of three feedback regimens and were repeatedly exposed to a visuomotor rotation. One group of subjects was shown KR, indicated by a static representation of their hand trajectory after each trial was completed. Another group received cursor feedback during the course of motion, but was instructed to refrain from correcting their initial movement plan. Finally, a third group of subjects received cursor feedback during the course of motion and was instructed to correct their movements within each trial. If the amplitude, but not the timing of the movement error is important for learning, then all groups should show similar extents of visuomotor adaptation. We also predicted that the group that was encouraged to initiate online corrections would show faster learning and/or a greater extent of learning, if motor corrections facilitate visuomotor adaptation. It is important to note that we distinguished visuomotor remapping from other strategies that might compensate the rotation (e.g., cognitive strategies or associative learning) by assessing reductions in movement errors and movement variability with practice; these are hallmarks of learning that are shown in a variety of motor learning tasks (Deutsch and Newell 2004; Mosier et al. 2005; Cohen and Sternad 2008). We further assessed the extent of adaptation in two additional sessions. The first session tested generalization of the learned rotation to different distance targets and to different areas of workspace. The third session assessed after-effects following removal of the rotation perturbation. After-effects are directional errors that are opposite to the imposed rotation and provide evidence for visuomotor remapping (Kagerer et al. 1997; Bock 2005; Mazzoni and Krakauer 2006; Hinder et al. 2008; Zarahn et al. 2008).
Methods
Subjects
Subjects were 25 neurologically intact adults (11 men, 14 women), aged from 18 to 28. Every subject completed a 35-item version of the Edinburgh handedness inventory (Oldfield 1971), and only those classified as right-handers were used for the experiment. All subjects gave informed consent prior to the start of the experiment, which was approved by the Biomedical Institutional Review Board of the Pennsylvania State University (IRB #15084).
Experimental apparatus
Subjects sat in an adjustable chair facing the experimental apparatus (Fig. 1a). The right arm of the subject was positioned just below shoulder height and was supported by a sled, connected to an air jet system, which reduced the effects of gravity and friction. Subjects were fitted with an adjustable arm brace and chest restraint to minimize movements of the wrist, trunk and scapula. The arm was covered and the lights were turned off, such that subjects could not view their arm movements. Instead, a start circle, target and cross-hair cursor, representing index fingertip position, were projected onto a horizontal back-projection screen. A mirror, located below this screen and just above the arm, reflected the visual display such that it was perceived to be in the same horizontal plane as the arm and fingertip. In order to assure that this projection was veridical, the screen was calibrated prior to the start of the experiment. Positions and orientations of the measured segments were sampled using a Flock-of-Birds (FoB; Ascension-Technology) magnetic 6 degree-of-freedom movement-recording system. One FoB sensor was fixed to the forearm support, and a second sensor was attached to the upper arm segment via an adjustable plastic cuff. Each sensor was approximately positioned at the center of each arm segment. The positions of three bony landmarks were digitized using a stylus that was rigidly fixed to a FoB sensor: index fingertip, the lateral epicondyle of the humerus and the acromion, directly posterior to the acromio-clavicular joint. These positions remained constant throughout the experimental session, relative to the sensors attached to each arm segment. As sensor data were received from the FoB sensors, our custom software computed the three-dimensional position of the index fingertip. The table surface defined our X–Y plane, and thus, we used the recorded X–Y coordinates of the fingertip position to project a cursor onto the screen. The cross-hair cursor (1.5 cm in diameter) was projected on the screen at a rate of 85 Hz. Screen redrawing occurred fast enough to maintain the cursor on the index fingertip throughout the sampled movements. Data were digitized at 100 Hz using a Macintosh computer, which controlled the sensors through separated serial ports, and stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC™ (REAL Software, Inc.), C (CodeWarrior™) and IGOR Pro™ (WaveMetrics, Inc.).
Fig. 1.
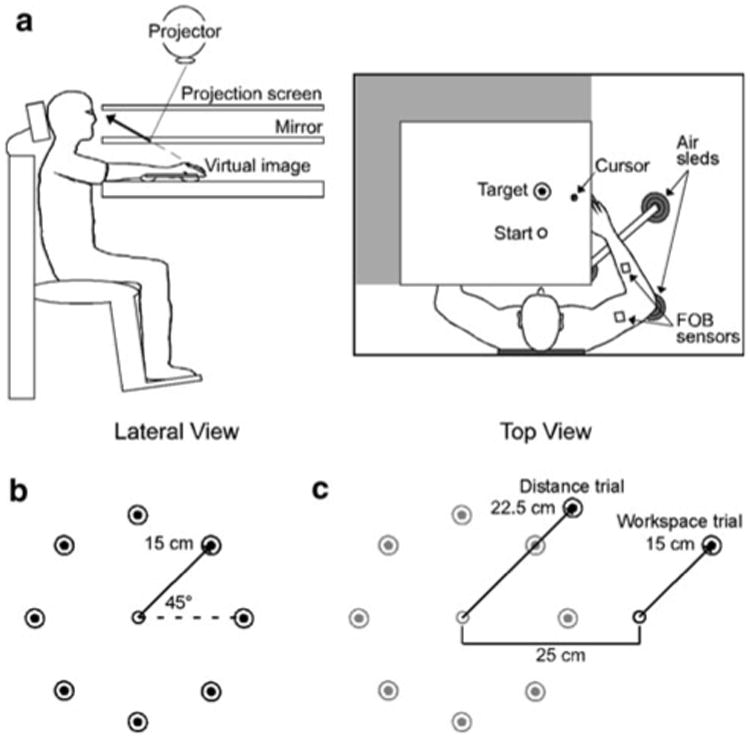
a Lateral and top view of the experimental apparatus. b Experimental task was a center-out reaching task with eight 15 cm targets oriented radially around a center start location (open circle) and separated by 45°. c For the generalization session, distance trials consisted of 22.5 cm targets oriented with respect to the baseline start location and workspace trials were oriented with respect to a new start location that was displaced 25 cm to the right of the baseline start circle
General task
As depicted in Fig. 1b, subjects completed a center-out reaching task with eight equal-spaced targets (2 cm diameter) located 15 cm from a central start location (open circle; 1.5 cm diameter). Prior to the start of each trial, one of the 8 targets was displayed on the screen in a pseudo-random sequence. Subjects were instructed to bring the cursor (i.e., fingertip) into the start circle, and following an audiovisual start signal, to move rapidly and accurately to the displayed target. At the end of each trial, the cursor disappeared and points were awarded for final position accuracy. Final position errors of <1 cm were awarded 10 points, those between 1 and 2 cm were awarded three points, and final position errors between 2 and 3 cm were awarded 1 point. Between trials, cursor feedback was restricted to within 2 cm of the start center. In order to initiate a new trial, subjects returned their finger to the start center.
Sessions and groups
Each subject performed four sequential sessions: a pre-rotation session (80 trials), a rotation session (192 trials), a generalization session (96 trials) and a post-rotation session (80 trials). Sessions were further divided into epochs (16 trials each) for the purpose of analysis.
Pre-rotation session
Baseline performance was assessed during the pre-rotation session. All subjects received the same forms of visual feedback and task instructions, so as to have comparable baseline performance measures. Continuous cursor feedback (CF) was shown during the movement, and knowledge-of-results (KR) was displayed as a static representation of the hand-path after each trial was completed. Subjects were instructed to initiate error corrections in order to reach the target.
Rotation exposure session
A visuomotor rotation was applied to all trials. This transformation rotated the screen cursor by 30° (clockwise direction), with respect to the start location. During the rotation session, subjects were assigned to one of three experimental groups, which varied the form of visual feedback and task instructions. Two groups received CF, but did not receive KR. One CF group was instructed to initiate error corrections during the course of motion (corrections; CFc group; 8 subjects), while the other CF group was instructed to refrain from initiating error corrections during the course of motion (no corrections; CFnc group; eight subjects). The third group did not receive CF, but instead received KR at the end of each movement (KR group; nine subjects). The KR group was instructed to reach their final position and to remain there until the KR was displayed. This allowed comparisons between KR and the proprioceptive position of the arm.
Generalization session
The visuomotor rotation was applied to all trials in the generalization session. Visual feedback conditions and task instructions varied by group assignment (see “Rotation exposure session”). In addition to the normal target array, catch trials to untrained target locations were randomly interspersed every 5–7 trials, in order to assess how adaptive strategies generalized outside of the immediate training space. During catch trials, either a farther distance target was shown (distance trial) or the start circle and target were displayed in a different area of the workspace (workspace trial). Task instructions did not differ from normal rotation conditions. We hypothesized that if subjects learned a remapping of movement direction, then generalization should occur for both types of catch trials. In contrast, subjects could strategically offset the linear discrepancy between finger and cursor positions (Sarlegna and Sainburg 2007). In this case, generalization should be complete for workspace trials, but incomplete for distance trials because the linear discrepancy is larger for distance trials than for the original target array. Finally, if subjects developed a local adaptive strategy (e.g., with respect to the original start location) then generalization should be incomplete for workspace trials. Figure 1c shows a sample of each type of catch trial. Distance trials consisted of a new target located 22.5 cm from the central start location. Workspace trials consisted of a new start location and target that were displaced 25 cm to the right of the original start location and target array. Similar to the original display, between-trial feedback was restricted to within 2 cm of the newly transposed start location. In total, there were eight distance trials and eight workspace trials (two each to four target directions; 45°, 135°, 225°, 315°).
Post-rotation session
The post-rotation session was identical to the pre-rotation session and was utilized to assess after-effects following adaptation. Performance was measured under baseline conditions, and all subjects received both CF and KR. Instructions were to initiate error corrections to reach the target during each movement.
Kinematic data
The 3D position of the index finger was calculated from the sensor position and orientation. All kinematic data were low-pass filtered at 8 Hertz (3rd-order, dual pass Butterworth) and differentiated to yield velocity and acceleration values. Peak velocity was calculated as the maximum in tangential velocity. The onset of movement was defined by the last minimum, which was <5% of the peak tangential finger velocity, prior to the maximum in tangential finger velocity. Similarly, movement termination was defined by the first minimum, which was <5% of the peak tangential finger velocity, following the maximum in tangential finger velocity or the peak corrective response.
We first calculated hand-path curvature, final position error, movement time and peak velocity during initial exposure to the rotation (rotation exposure session; first epoch). This was done to validate that subjects complied with instructions to correct or not correct errors during movement. To calculate hand-path curvature, the major axis of the hand-path was defined as the largest distance between any two points, and the minor axis of the hand-path as the largest distance perpendicular to the major axis. Hand-path curvature was then calculated as minor axis divided by major axis (Bagesteiro and Sainburg 2002; Sainburg 2002), such that a hand-path curvature of zero indicated a straight line. Final position error was calculated as the distance between the hand location at movement termination and the center of the target. Movement time was calculated as the total time from movement start to movement termination.
Trial-to-trial learning is generally reflected by reduced movement errors and reduced variability with practice. Thus, visuomotor adaptation was assessed by two measures of performance: initial direction error and variable initial direction error. Initial direction error was measured with respect to a reference line connecting the center of the start location and the accurate final position (i.e., the center of the target for baseline trials and the position that would bring the cursor to the center of the target for visuomotor rotation trials). Initial direction error was calculated as the angular deviation of the line connecting the starting position of the hand and the position of the hand at peak tangential velocity from the reference line. Positive values indicated hand-paths that were directed clockwise to the reference line, while negative values indicated hand-paths that were directed counterclockwise to the reference line. For variable initial direction error, we first determined the mean initial direction error for each subject, session and epoch. Variable initial direction error was calculated as the absolute value of the difference in initial direction error for each individual trial and the mean value corresponding to the same subject, session and epoch.
Finally, in order to assess generalization of learning, we calculated the angle generalized (%) for each subject. We first determined the extent to which the visuomotor rotation angle was learned for each subject (Alearn):
where Aerror is the mean initial direction error for the last eight trials in the rotation session. We then calculated the angle generalized (%gen):
where Agen is the initial direction error for a given trial in the generalization session (distance or workspace trial). Angle generalized (%) is not an absolute measure of generalization, but instead, was calculated relative to each subject's performance at the end of the rotation session.
Statistical analysis
First, in order to validate that our group manipulations resulted in significant differences in the hand-paths, reflecting the presence and absence of motor corrections, we utilized a 1-way ANOVA with group (CFc, CFnc, KR) as the between-subject factor. In order to assess adaptation between groups, we wanted to compare performance under baseline conditions to performance during the early and late trials of the rotation session, and with performance immediately following the removal of the rotation, in the post-rotation session. Therefore, we compared the transition points between the pre-rotation, rotation and postrotation sessions, hereinafter referred to as the following epochs: PRE (last epoch, pre-rotation session), EARLY (first epoch, rotation session), LATE (last epoch, rotation session) and POST (first epoch, postrotation session). We analyzed our dependent measures using two-way repeated-measures ANOVA with group (CFc, CFnc, KR) as the between-subject factor and epoch (PRE, EARLY, LATE, POST) as the within-subject factor. Finally, for the generalization session, which assessed the extent to which adaptive strategies generalized to farther distance targets and across the workspace, we utilized a two-way repeated-measures ANOVA with group as the between-subject factor and trial type (distance, workspace) as the within-subject factor. Post hoc comparisons were done using the Tukey–Kramer HSD (Honestly Significant Difference) test.
Results
Validation of task design
This study was designed to assess adaptation to visuomotor rotations under three visual feedback regimens: CFc, CFnc and KR. We first tested whether the CF groups followed task instructions to correct and not correct errors online. Typically, upon initial exposure to a visuomotor rotation, online corrections take the form of large “hooks” near the end of each hand-path, which brings the cursor to the target (Sainburg 2002). Thus, trials with motor corrections (CFc) should show greater trajectory curvatures, longer movement times and smaller final position errors relative to trials without motor corrections (CFnc and KR). The results of ANOVA showed a main effect of group (KR, CFc, CFnc) for each performance measure [absolute final position error, F2,24 = 217.3911; p < 0.0001; trajectory curvature, F2,24 = 192.8548, p<0.0001; movement time, F2,24 = 30.3792; p < 0.0001] during the first epoch of the rotation exposure session. As predicted, post hoc analysis showed that absolute final position error was significantly smaller for the CFc group (1.47 ± 0.13 cm) than the CFnc (6.20 ± 0.34 cm) and KR (8.63 ± 0.23 cm) groups (p < 0.05, in both cases). Further, trajectory curvature was significantly greater for the CFc group (0.35 ± 0.02) than the CFnc (0.11 ± 0.01) and KR (0.06 ± 0.01) groups (p < 0.05, in both cases), while movement time was significantly longer for the CFc group (902 ± 42 ms) than the CFnc (519 ± 26 ms) and KR (637 ± 35 ms) groups (p < 0.05, in both cases). Differences in movement time for the CFc and CFnc groups cannot be attributed to differences in peak velocity. Although there was a significant group effect for peak velocity [F2,24 = 11.5892; p<0.0005], the CFc group (0.85 ± 0.05 m/s) and CFnc group (1.01 ± 0.06 m/s) were comparable (p> 0.05). The peak velocity of the KR group (0.69 ± 0.04 m/s) was significantly different from the CFnc (p < 0.05), but not the CFc group (p >0.05). In summary, our task instructions and feedback manipulations produced significant differences in the performance of the CFc, and CFnc and KR groups, which reflected the presence and absence of online motor corrections, respectively.
General performance: baseline, rotation and post-rotation sessions
In order to assess adaptation to visuomotor rotations, we compared performance during a baseline session to performance following initial and repeated exposure to the rotation. Additionally, we examined performance during a post-rotation session, where participants were re-introduced to baseline conditions. Figure 2 shows hand-paths for the pre-rotation (first eight trials; left), rotation (first and last eight trials; middle) and post-rotation (last eight trials; right) sessions from representative subjects for the CFc (top), CFnc (middle) and KR (bottom) groups. Baseline performance for all three groups was very similar: hand-paths were generally straight and accurate. While only the CFc group showed online motor corrections, as indicated by the “hooks” in Fig. 2 (top, middle), both the CFc and CFnc groups exhibited adaptation to the visuomotor rotation. This was indicated by the consistent changes in the initial directions of the hand-paths from the first eight trials of the rotation session (black) to the last eight trials of the rotation session (gray). This learned rotation was also reflected in the post-adaptation session, in which substantial after-effects were evident. In contrast, the hand-paths of the KR group improved little over the course of the rotation session, and consistent after-effects were not evident during the post-rotation session.
Fig. 2.
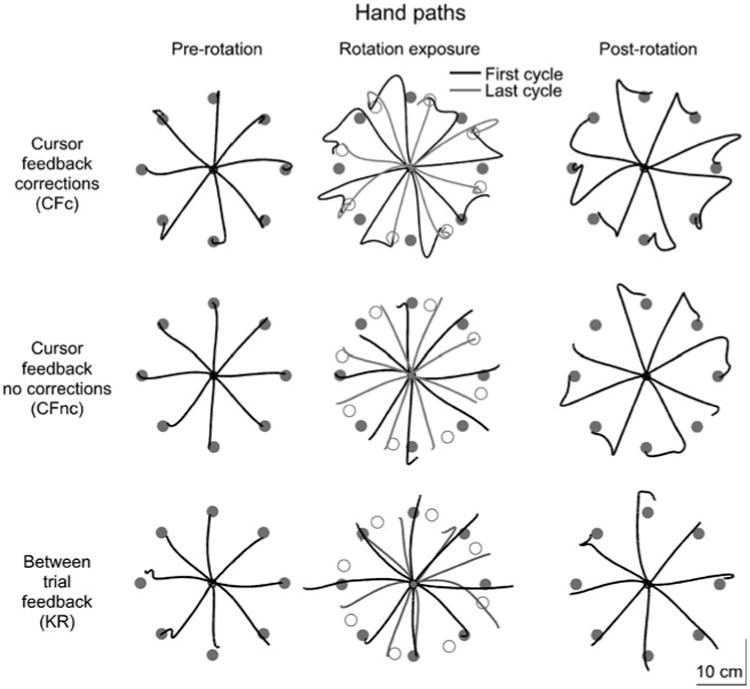
Sample hand-paths for the CFc (top), CFnc (middle) and KR (bottom) groups from the pre-rotation (left), rotation (middle) and post-rotation (right) sessions. For the rotation session, hand-paths from the first (black) and last eight trials (gray) are shown. Gray circles indicate the visually presented targets and open circles represent the locations that would bring the cursor to the targets during the rotation task
Motor learning is generally reflected by reduced movement errors and reduced variability over the course of many trials. For the current task, differences in final position error would not necessarily reflect learning-dependent changes in performance, because systematic differences in this measure were imposed by our task design (instructing participants to correct or not correct their ongoing movement). Thus, in order to quantitatively assess visuomotor adaptation, we compared initial direction error and variable initial direction error of each group during the pre-rotation, rotation and post-rotation sessions (Fig. 3a). The means and standard errors of initial direction error for each epoch demonstrated the incremental changes in performance that occurred within each group and session (Fig. 3a, left). Statistical analysis was conducted at predetermined epochs that were transition points between sessions (gray bands; Fig. 3a, left). These epochs are isolated and expanded for ease of comparison in Fig. 3a, right. The results of ANOVA revealed a highly significant interaction of group (KR, CFc, CFnc) with epoch (PRE, EARLY, LATE, POST) for both performance measures [initial direction error, F6,88 = 11.1323; p <0.0001; variable initial direction error, F6,88 = 8.9002, p< 0.0001]. Therefore, post hoc analysis (Tukey-HSD) was conducted in order to test relevant group differences within each epoch and relevant differences across epochs for each group. The means and standard errors of initial direction error and variable initial direction error are summarized in Table 1a and b.
Fig. 3.
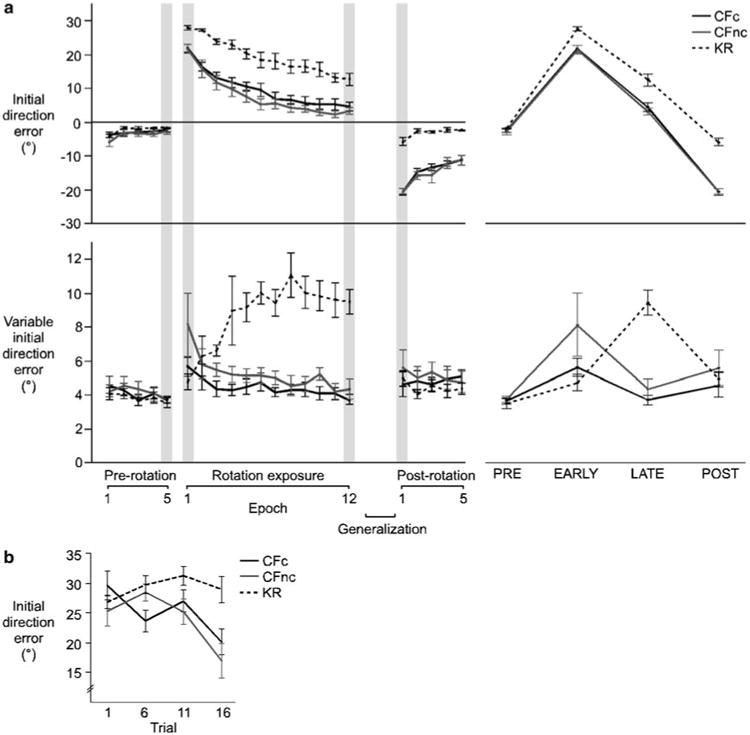
a Initial direction error (top) and variable initial direction error (bottom; means ± standard errors, across subjects) for the CFc (black line), CFnc (gray line) and KR (dotted line) groups, shown for each epoch in the pre-rotation, rotation and post-rotation sessions. While not shown, the generalization session occurred between the rotation and post-rotation sessions. Data highlighted with gray bars are expanded for ease of comparison (right). b Initial direction error (means ± standard errors, across subjects) for four trials (1, 6, 11, 16) from the first epoch of the rotation session for the CFc (black line), CFnc (gray line) and KR (dotted line) groups
Table 1. a Initial direction error and b variable initial direction error (means ± standard errors, across subjects) of the PRE, EARLY, LATE and POST epochs for the CFc, CFnc and KR groups.
| Phase | Group | ||
|---|---|---|---|
|
| |||
| CFc | CFnc | KR | |
| a | |||
| Initial direction error (°) | |||
| PRE | −2.6 ± 0.6 | −2.9 ± 0.7 | −1.9 ± 0.3 |
| EARLY | 21.7 ± 1.2 | 21.5 ± 1.3 | 27.7 ± 0.5 |
| LATE | 4.5 ± 1.4 | 3.2 ± 0.9 | 12.6 ± 1.9 |
| POST | −20.8 ± 0.9 | −20.6 ± 1.0 | −5.9 ± 1.1 |
| b | |||
| Variable initial direction error (°) | |||
| PRE | 3.6 ± 0.2 | 3.8 ± 0.2 | 3.5 ± 0.3 |
| EARLY | 5.6 ± 0.6 | 8.1 ± 1.9 | 4.7 ± 0.5 |
| LATE | 3.7 ± 0.3 | 4.3 ± 0.6 | 9.4 ± 0.7 |
| POST | 4.6 ± 0.7 | 5.6 ± 1.0 | 4.9 ± 0.4 |
CFc and CFnc groups showed similar patterns of performance
As indicated in Fig. 3a, top, and reiterated by our post hoc analysis, the initial direction errors of the CFc and CFnc groups were statistically comparable across the experiment (p > 0.05, in all cases). CFc and CFnc groups showed small initial direction errors during the baseline session (PRE epoch), large initial direction errors upon exposure to the rotation (EARLY epoch), reductions in initial direction error by the end of the rotation session (LATE epoch), and negative after-effects following removal of the rotation in the post-adaptation session (POST epoch). Within each group, these differences across epochs were statistically significant (p< 0.05, in all cases). Variable initial direction error was largest when the CFc and CFnc groups were initially exposed to the rotation and was reduced during the course of the rotation session to near-baseline performance. Following removal of the rotation, in the POST epoch, variable initial direction error showed a slight increase, which was similar to the effect of initially introducing the visuomotor rotation, although not as pronounced. Post hoc analysis revealed that the trend to reduce variable initial direction error from initial rotation exposure (EARLY epoch) to late in the adaptation session (LATE epoch) reached significant levels for the CFnc group (p< 0.05), but not the CFc group (p > 0.05).
The KR group differed in performance from CFc and CFnc groups
Performance within and across the pre-rotation, rotation and post-rotation sessions for the KR group showed marked differences from the CFc and CFnc groups (Fig. 3a). Initial direction error was near zero and comparable to both CFc groups during the baseline session (p > 0.05, in both cases). However, although there was a significant increase in initial direction error from the PRE epoch to the EARLY epoch for the KR group (p < 0.05), reflecting the imposed rotation, initial direction errors of the CFc and CFnc groups were significantly smaller than the initial direction errors of the KR group in the EARLY epoch (p<0.05, in both cases). As indicated by Fig. 3b, which shows the means and standard errors of initial direction error for select trials in the EARLY epoch, this effect reflects adaptive adjustments in initial direction error for the CF groups, but not the KR group, within the very first epoch. Still, during the course of the rotation exposure, initial direction error was significantly reduced for the KR group (EARLY, LATE; p < 0.05). However, initial direction error was significantly larger during the LATE epoch for the KR group compared to both CF groups (p< 0.05, in both cases). Interestingly, when the rotation was removed in the post-rotation session, after-effects were not evident for the KR group. Instead, initial direction error was comparable to that of baseline performance for the KR group (PRE, POST; p< 0.05) and was significantly less negative than the initial direction errors of the CF groups for the POST epoch (p < 0.05, in both cases). Another interesting finding was that while the KR group showed some improved performance during the course of the rotation session, as indicated by reductions in mean direction error from the EARLY to LATE epochs, this group showed a substantial increase in variable direction error during the rotation session. Variable initial direction error for the LATE epoch was significantly larger than any other epoch for the KR group (p <0.05, in all cases). Further, variable initial direction error was larger for the KR group than either CF group for the LATE epoch (p< 0.05, in all cases).
In summary, it appears that the extent of adaptation, as measured by initial direction error, was less complete for the KR group than both CF groups. Interestingly, variable initial direction error for the KR group increased during the rotation session relative to decreased or stable variable initial direction error for the CF groups. Furthermore, after-effects were not significant for the KR group compared to the substantial after-effects of both CF groups. Taken together, these results suggest that CF and KR lead to qualitatively different types of visuomotor adaptation and motor corrections neither facilitate nor inhibit adaptation.
Generalization
We next assessed the extent to which the adaptive strategies, adopted in the rotation session, generalized to further distance targets and across the workspace. Figure 4 shows distance (left) and workspace (right) generalization trials from representative subjects in the CFc (top), CFnc (middle) and KR groups (bottom). For the distance trials, the hand-paths of both CF groups were straight and were directed such that the rotation was offset at movement onset, bringing the cursor to the target (open circle). However, the hand-paths of the KR group were directed between the direction of the target (gray circle) and the direction that would compensate the rotation. The CFc and CFnc groups showed generalization of the learned rotation angle to the workspace trials, although this was not as complete as generalization to the distance trials; hand-paths were directed slightly closer to the target position, and the CFc group initiated corrections (small “hooks”) to bring the cursor directly to the target. The KR group showed very-little generalization to the workspace trials. The variability in the directions of the hand-paths was reduced compared to the distance trials.
Fig. 4.
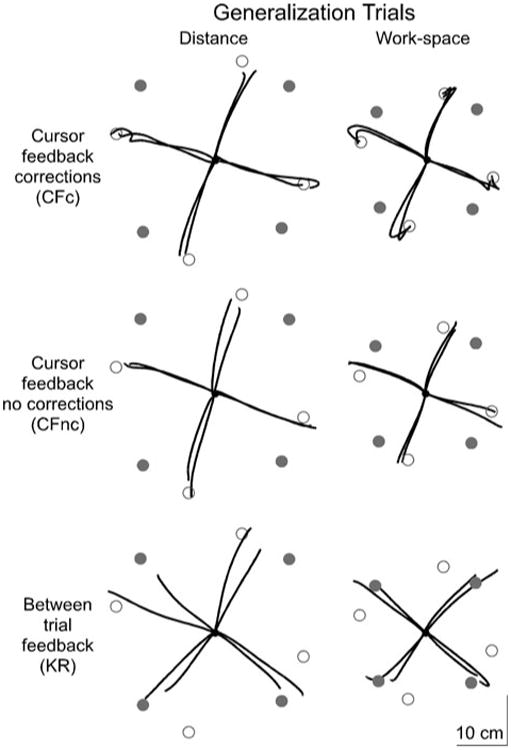
Sample hand-paths for the CFc (top), CFnc (middle) and KR (bottom) groups for the distance trials (left) and workspace trials (right) in the generalization session. Gray circles indicate the visually presented targets and open circles represent the locations that would bring the cursor to the targets during the rotation task
As previously reported, adaptation was less complete for the KR group than either CF group. This was indicated by larger initial direction errors for the KR group than the CF groups during the LATE epoch of the rotation session (Fig. 3a, top right). In order to account for these intrinsic between-group differences in adaptation, we assessed generalization as a percentage of the learned angle for each subject (see, “Methods”). Figure 5 shows the means and standard errors of the angle generalized (left), and variable initial direction error (right) for the CFc (black line), CFnc (gray line) and KR (dotted line) groups. The angle generalized was greater for the distance trials (D; 91.7 ± 3.3%) than the workspace trials (W; 72.1 ± 4.3), irrespective of feedback group. This is consistent with previous studies that have indicated that generalization tends to degrade with distance from the training space (Baraduc and Wolpert 2002). Moreover, the angle generalized was greater for the CFc (89.6 ± 3.9%) and CFnc (89.6 ± 2.9%) groups than the KR group (68.1 ± 6.1%). This was verified by ANOVA, which revealed a main effect of group [F2,44 = 6.9880; p < 0.05], a main effect of generalization trial type [F1,44 = 35.094; p< 0.0001] and no interactions of group with trial type [F2,44 = 0.2247; p = 0.81]. Post hoc analysis revealed that the differences between the KR group and each CF group were significant (p < 0.05, in both cases), as were differences between distance and workspace trials (p < 0.05). Variable initial direction error was larger for the KR group (6.5 ± 0.6) than the CF groups (CFc, 4.1 ± 0.4; CFnc, 4.4 ± 0.5), but also varied with the generalization trial type. This was also reflected by ANOVA, which indicated a main effect of feedback group [F2,44 = 7.7546; p < 0.05] and an interaction of feedback group with generalization trial type [F2,44 = 4.8175; p <0.05]. Post hoc analysis conducted within generalization trial types revealed that variable initial direction error was larger for the KR group than the CF groups for distance trials (p < 0.05, in both cases), but not workspace trials (p < 0.05, in both cases). In summary, CF leads to more complete and less variable generalization than KR, while motor corrections appear to neither facilitate nor inhibit generalization across distance and workspace trials.
Fig. 5.
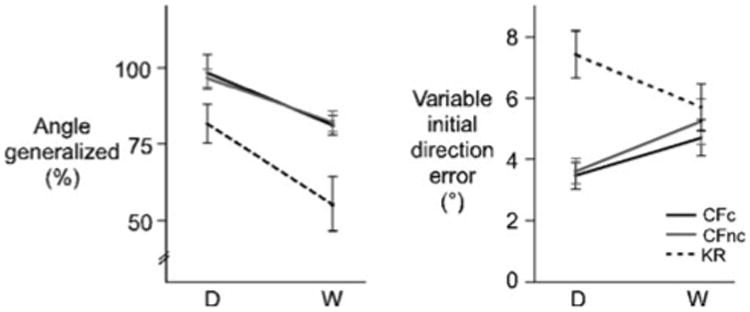
Angle generalized (left) and variable initial direction error (right; means ± standard errors, across subjects) for the distance (D) and workspace (W) trials in the generalization session, shown for the CFc (black line), CFnc (gray line) and KR (dotted line) groups
Discussion
This study was designed to determine the mechanisms that underlie sensory error assessment, as a basis for visuomotor adaptation. Specifically, we were interested in whether error information that was made available during movement might be used differently than error information presented after movement termination. We tested visuomotor adaptation for different groups of subjects who received CF or KR. CF groups were instructed to either correct (CFc) or not correct (CFnc) errors during the course of motion. Performance for the CFc and CFnc groups was similar for all aspects of the experiment. Our results indicated that all groups showed reductions in mean direction error with practice, but that direction error was reduced to a greater extent for the CF groups than for the KR group. Moreover, while improvement in performance for the CF groups was associated with a reduction in the variability of initial direction errors with practice, the KR group showed increased variability with practice. The results of the subsequent sessions showed less generalization and significantly smaller after-effects for the KR group than the CF groups. These findings indicate that qualitatively different mechanisms underlie adaptation when synchronous error information is available during the course of movement, and when asynchronous static information is available following movement termination.
Motor corrections do not facilitate visuomotor adaptation
When subjects are first introduced to a visuomotor rotation, errors arise during the course of motion, and the appropriate motor corrections are initiated to bring the cursor to the target. Further, errors that arise during each movement can also be used to modify the initial plan of subsequent movements, resulting in progressively smaller cursor errors and online corrections with practice (Roby-Brami and Burnod 1995; Wang and Sainburg 2005, 2006). The strong correlation between the extent of learning and the amplitude of online corrections raises the question as to whether motor corrections, within a given movement, somehow mediate adaptive corrections, between movements. The results of the current experiment showed that two different groups, which either corrected or did not correct errors during movement, adapted to similar extents and showed persistent after-effects when the rotation was removed. These results are consistent with previous studies, which have shown that visuomotor adaptation can occur when within-trial corrections are minimal-to-absent (Kagerer et al. 1997; Krakauer et al. 2000; Caithness et al. 2004; Miall et al. 2004; Klassen et al. 2005; Mazzoni and Krakauer 2006), and further demonstrates that online motor corrections neither facilitate nor interfere with adaptation. A recent study also showed similar adaptation to visuomotor rotations during rapid “shooting” movements that occurred without online corrections, and “pointing” movements that included online corrections (Tseng et al. 2007). Our current results extend those findings by showing that generalization of the learned rotation angle to further distance targets and different areas of the workspace is not improved by online motor corrections.
KR is not equivalent to CF for visuomotor adaptation
While the results of the current experiment suggest that motor corrections did not affect adaptation, we showed significant differences between the CF and KR groups during rotation exposure, generalization and post-rotation sessions. There is little doubt that continuous cursor feedback-mediated visuomotor remapping during the current task, as CF groups showed significant improvements in the initial directions of their hand-paths with practice, substantial generalization across distances and workspace, and after-effects following removal of the rotation in the post-rotation session. Conversely, the group that was provided KR after each trial showed less improvement with practice and less generalization than the CF groups, and no significant after-effects when the rotation was removed.
One possible explanation for the lack of after-effects for the KR group is that the inconsistency in visual feedback conditions during rotation exposure and post-rotation sessions masked the effects of visuomotor remapping. After-effects were tested in a condition that provided continuous feedback during the course of motion, while only KR was provided during the rotation exposure session. Therefore, subjects in the KR group could utilize feedback-mediated mechanisms to reach the target during post-rotation trials, possibly negating the need for adaptive processes that were elicited in response to KR. While this question cannot be addressed by the current experiment, it is well understood that after-effects are robust directional errors that occur in spite of subjects' awareness that a perturbation has been removed (Heuer and Hegele 2008). As a result, it seems unlikely that providing explicit feedback of errors during the course of motion could bias subjects toward not showing after-effects. Further, our conclusion that visuomotor adaptation differs for the CF and KR groups is not entirely based on our assessment of after-effects. Substantial performance differences between groups first emerged during the course of rotation exposure.
Another possible explanation for differences in the performance of CF and KR groups is that the KR group learned the rotation while simultaneously maintaining the standard visuomotor map. This could explain why the baseline visuomotor map was readily accessible during the post-rotation session (i.e., no after-effects were evident). Further, the added difficulty of maintaining two separate visuomotor maps could explain why performance was improved to a lesser extent for the KR group than the CF groups. We assessed learning by determining reductions in movement errors and reductions in movement variability with practice, which are hallmarks of motor learning (Deutsch and Newell 2004; Mosier et al. 2005; Cohen and Sternad 2008). The CF groups showed the predicted decrease in movement errors, as reflected by initial direction error, and variability, as reflected by variable initial direction error. However, improvements in mean performance for the KR group were associated with increased variability with practice. This suggests that the KR group did not learn a new visuomotor map, an idea that is further supported by the lack of after-effects in the post-adaptation session. Instead, the KR group may have employed an alternative strategy for reducing initial direction errors with practice.
Implicit and explicit strategies during visuomotor adaptation tasks
Implicit processes mediate visuomotor remapping, but explicit strategies can also be employed to compensate visuomotor transformations (Redding and Wallace 1996, 2002; Mazzoni and Krakauer 2006). For example, Mazzoni and Krakauer (2006) instructed subjects to adopt an explicit strategy to counter a 45° visuomotor rotation by aiming directly at the neighboring target, oriented 45° in the direction opposite to the perturbation. While this strategy initially offset the errors imposed by the rotation, subjects simultaneously adapted to the neighboring target. Eventually, the explicit aiming strategy was completely overridden by the implicit adaptation process. In the current study, the CF groups showed evidence of visuomotor remapping, while the KR group demonstrated reductions in initial direction error with practice that were associated with increased inter-trial variability, and minimal after-effects following removal of the rotation. We suggest that KR was not sufficient to mediate visuomotor remapping (i.e., the implicit adaptation process) and that this group resorted to an explicit “guessing” strategy to improve performance. The static hand-path presented after each trial informed subjects that their current movement strategy did not result in acquisition of the target. As a result, the KR group aimed to different locations in the workspace in an attempt to improve performance. This workspace sampling increased variability in initial direction error, and on occasional trials resulted in “correct” responses that reduced the mean initial direction error. Consistent with the current pattern of results, subjects in the KR group could increase workspace sampling throughout the course of the rotation exposure session, causing variable initial direction error to steadily increase with practice and mean direction error to steadily decrease with practice. We showed that the same strategy could be used to partially compensate the rotation at farther distance targets. However, for workspace trials, we showed substantially less generalization and less variability, suggesting that subjects might utilize the explicit strategy more readily in the vicinity of the training space or when the start location has not changed.
Previously, it was not clear whether the timing of visual feedback was crucial for visuomotor remapping during adaptation tasks. While KR was shown to be sufficient for remapping of movement extent in response to altered visuomotor gains (Vindras and Viviani 2002), it was shown to be insufficient for remapping of movement direction in response to rotation perturbations (Hinder et al. 2008, 2010). However, the gain experiment utilized a task in which cursor and finger positions were aligned during baseline conditions (Vindras and Viviani 2002), whereas the experimental apparatus in the rotation studies required a transformation from elbow torque to cursor motion (Hinder et al. 2008, 2010). While it was plausible that this secondary visuomotor transformation interfered with adaptation, the results of the current study, which accurately depicted finger location during baseline reaching, clearly indicated that KR was not sufficient for visuomotor remapping of movement direction. This is not entirely surprising; previous studies have demonstrated that gain and rotation adaptation are qualitatively different processes (Pine et al. 1996; Krakauer et al. 2000).
It is not known whether limiting feedback to KR will elicit explicit strategies to compensate other types of perturbations (e.g., prism and force-field perturbations). Further, provided that explicit strategies for the KR group were specific to the nature of the perturbation (i.e., changing initial direction in response to a visuomotor rotation), it is difficult to predict what affect this feedback regimen would have during perturbations not tested in the current experiment.
Simultaneous visual and proprioceptive information is critical for visuomotor remapping
Subjects that received feedback in the form of static KR were unable to learn the visuomotor rotation implicitly, and thus, resorted to alternative strategies to improve performance. This finding suggests that the simultaneous discrepancy in visual and proprioceptive information during movement may be critical for visuomotor remapping. These sensory inputs provide information about the hand and target location, and are also used in parallel to plan the arm trajectory as a vector, in extrinsic coordinates (Pine et al. 1996; Vindras and Viviani 1998; Krakauer et al. 2000), and motor commands that account for inertial interactions between the segments (Sainburg et al. 1999), in intrinsic coordinates (Soechting and Flanders 1989; Tillery et al. 1991). Recent investigations of the relative contributions of vision and proprioception to motor planning have indicated that planning of the kinematic features of movement is more dependent on visual information, while specification of dynamic control parameters, such as torque or EMG appear to depend more on proprioceptive input (Brown et al. 2003a, b; Lateiner and Sainburg 2003; Sober and Sabes 2003, 2005; Bagesteiro et al. 2006; Sarlegna and Sainburg 2007). Visuomotor adaptation, as studied here, requires changing how these two processes might map onto one another, requiring a systematic change in the relationship between required joint torques and intended cursor motion. Our current findings suggest that this remapping requires concurrent comparisons between visual and proprioceptive inputs. An important alternative explanation is that it is not the simultaneity of sensory signals that is crucial for visuomotor adaptation, but the dynamic nature of visual information received within each trial. Recent work by Saunders and Knill (2004) suggests that both static (i.e., position) and dynamic (i.e., motion) error signals are utilized during online corrections to visual perturbations. Dynamic visual cues might also mediate post-trial adjustments that occur during adaptation. In the current study, KR was displayed as a static hand-path, and thus, we cannot rule out this possibility. However, a number of previous studies have demonstrated adaptation to visuomotor transformations when visual feedback was limited to final positions or the area immediately surrounding the target (Choe and Welch 1974; Bedford 1989, 1993; Ghahramani et al. 1996), suggesting that dynamic visual information is not necessary for adaptation. Further, our current hypothesis is consistent with previous research demonstrating that learning-dependent changes in cortical representations depend largely on the timing of sensory input (Wang et al. 1995). Monkeys that were trained to differentiate tactile stimuli that were applied synchronously, but not asynchronously, to the fingers showed integrated representation of the fingers in the cortex (Wang et al. 1995). Thus, remapping neural representations of the periphery appears to critically depend on simultaneity of the involved modalities. In our current study, we suggest that concurrent sensory information, provided by visual and proprioceptive feedback, was crucial for visuomotor remapping.
Acknowledgments
We thank Marisa Alcaro for participant recruitment and scholarly discussions regarding this manuscript. This research was supported by the National Institutes of Health, National Institute of Child Health and Human Development Grant #R01HD39311.
Contributor Information
Britne A. Shabbott, Email: britneshabbott@yahoo.com, The Huck Institutes of the Life Sciences, The Pennsylvania State University, University Park, PA, USA.
Robert L. Sainburg, Email: rls45@psu.edu, The Huck Institutes of the Life Sciences, The Pennsylvania State University, University Park, PA, USA; The Department of Kinesiology, The Pennsylvania State University, 266 Recreation Building, University Park, PA 16802, USA; The Department of Neurology, Penn State Hershey Medical Center, Hershey, PA, USA.
References
- Bagesteiro LB, Sainburg RL. Handedness: dominant arm advantages in control of limb dynamics. J Neurophysiol. 2002;88:2408–2421. doi: 10.1152/jn.00901.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagesteiro LB, Sarlegna FR, Sainburg RL. Differential influence of vision and proprioception on control of movement distance. Exp Brain Res. 2006;171:358–370. doi: 10.1007/s00221-005-0272-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baraduc P, Wolpert DM. Adaptation to a visuomotor shift depends on the starting posture. J Neurophysiol. 2002;88:973–981. doi: 10.1152/jn.2002.88.2.973. [DOI] [PubMed] [Google Scholar]
- Bedford FL. Constraints on learning new mappings between perceptual dimensions. J Exp Psychol Hum Percept Perform. 1989;15:232–248. [Google Scholar]
- Bedford FL. Perceptual and cognitive spatial learning. J Exp Psychol Hum Percept Perform. 1993;19:517–530. doi: 10.1037//0096-1523.19.3.517. [DOI] [PubMed] [Google Scholar]
- Bock O. Components of sensorimotor adaptation in young and elderly subjects. Exp Brain Res. 2005;160:259–263. doi: 10.1007/s00221-004-2133-5. [DOI] [PubMed] [Google Scholar]
- Brown LE, Rosenbaum DA, Sainburg RL. Limb position drift: implications for control of posture and movement. J Neurophysiol. 2003a;90:3105–3118. doi: 10.1152/jn.00013.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown LE, Rosenbaum DA, Sainburg RL. Movement speed effects on limb position drift. Exp Brain Res. 2003b;153:266–274. doi: 10.1007/s00221-003-1601-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caithness G, Osu R, Bays P, Chase H, Klassen J, Kawato M, Wolpert DM, Flanagan JR. Failure to consolidate the consolidation theory of learning for sensorimotor adaptation tasks. J Neurosci. 2004;24:8662–8671. doi: 10.1523/JNEUROSCI.2214-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choe CS, Welch RB. Variables affecting the intermanual transfer and decay of prism adaptation. J Exp Psychol. 1974;102:1076–1084. doi: 10.1037/h0036325. [DOI] [PubMed] [Google Scholar]
- Cohen RG, Sternad D. Variability in motor learning: relocating, channeling and reducing noise. Exp Brain Res. 2008;193:69–83. doi: 10.1007/s00221-008-1596-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham HA, Welch RB. Multiple concurrent visual-motor mappings: implications for models of adaptation. J Exp Psychol Hum Percept Perform. 1994;20:987–999. doi: 10.1037//0096-1523.20.5.987. [DOI] [PubMed] [Google Scholar]
- Desmurget M, Pelisson D, Rossetti Y, Prablanc C. From eye to hand: planning goal-directed movements. Neurosci Biobehav Rev. 1998;22:761–788. doi: 10.1016/s0149-7634(98)00004-9. [DOI] [PubMed] [Google Scholar]
- Deutsch KM, Newell KM. Changes in the structure of children's isometric force variability with practice. J Exp Child Psychol. 2004;88:319–333. doi: 10.1016/j.jecp.2004.04.003. [DOI] [PubMed] [Google Scholar]
- Ghahramani Z, Wolpert DM, Jordan MI. Generalization to local remappings of the visuomotor coordinate transformation. J Neurosci. 1996;16:7085–7096. doi: 10.1523/JNEUROSCI.16-21-07085.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghilardi MF, Gordon J, Ghez C. Learning a visuomotor transformation in a local area of work space produces directional biases in other areas. J Neurophysiol. 1995;73:2535–2539. doi: 10.1152/jn.1995.73.6.2535. [DOI] [PubMed] [Google Scholar]
- Ghilardi M, Ghez C, Dhawan V, Moeller J, Mentis M, Nakamura T, Antonini A, Eidelberg D. Patterns of regional brain activation associated with different forms of motor learning. Brain Res. 2000;871:127–145. doi: 10.1016/s0006-8993(00)02365-9. [DOI] [PubMed] [Google Scholar]
- Heuer H, Hegele M. Adaptation to visuomotor rotations in younger and older adults. Psychol Aging. 2008;23:190–202. doi: 10.1037/0882-7974.23.1.190. [DOI] [PubMed] [Google Scholar]
- Hinder MR, Tresilian JR, Riek S, Carson RG. The contribution of visual feedback to visuomotor adaptation: how much and when? Brain Res. 2008;1197:123–134. doi: 10.1016/j.brainres.2007.12.067. [DOI] [PubMed] [Google Scholar]
- Hinder MR, Riek S, Tresilian JR, de Rugy A, Carson RG. Realtime error detection but not error correction drives automatic visuomotor adaptation. Exp Brain Res. 2010;201:197–207. doi: 10.1007/s00221-009-2025-9. [DOI] [PubMed] [Google Scholar]
- Kagerer FA, Contreras-Vidal JL, Stelmach GE. Adaptation to gradual as compared with sudden visuo-motor distortions. Exp Brain Res. 1997;115:557–561. doi: 10.1007/pl00005727. [DOI] [PubMed] [Google Scholar]
- Klassen J, Tong C, Flanagan JR. Learning and recall of incremental kinematic and dynamic sensorimotor transformations. Exp Brain Res. 2005;164:250–259. doi: 10.1007/s00221-005-2247-4. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Pine ZM, Ghilardi MF, Ghez C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J Neurosci. 2000;20:8916–8924. doi: 10.1523/JNEUROSCI.20-23-08916.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krakauer JW, Ghez C, Ghilardi MF. Adaptation to visuomotor transformations: consolidation, interference, and forgetting. J Neurosci. 2005;25:473–478. doi: 10.1523/JNEUROSCI.4218-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lateiner JE, Sainburg RL. Differential contributions of vision and proprioception to movement accuracy. Exp Brain Res. 2003;151:446–454. doi: 10.1007/s00221-003-1503-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci. 2006;26:3642–3645. doi: 10.1523/JNEUROSCI.5317-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miall RC, Jenkinson N, Kulkarni K. Adaptation to rotated visual feedback: a re-examination of motor interference. Exp Brain Res. 2004;154:201–210. doi: 10.1007/s00221-003-1630-2. [DOI] [PubMed] [Google Scholar]
- Mosier KM, Scheidt RA, Acosta S, Mussa-Ivaldi FA. Remapping hand movements in a novel geometrical environment. J Neurophysiol. 2005;94:4362–4372. doi: 10.1152/jn.00380.2005. [DOI] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Pine ZM, Krakauer JW, Gordon J, Ghez C. Learning of scaling factors and reference axes for reaching movements. Neuroreport. 1996;7:2357–2361. doi: 10.1097/00001756-199610020-00016. [DOI] [PubMed] [Google Scholar]
- Prager AD, Contreras-Vidal JL. Adaptation to display rotation and display gain distortions during drawing. Hum Mov Sci. 2003;22:173–187. doi: 10.1016/s0167-9457(02)00158-6. [DOI] [PubMed] [Google Scholar]
- Redding GM, Wallace B. Adaptive spatial alignment and strategic perceptual-motor control. J Exp Psychol Hum Percept Perform. 1996;22:379–394. doi: 10.1037//0096-1523.22.2.379. [DOI] [PubMed] [Google Scholar]
- Redding GM, Wallace B. Strategic calibration and spatial alignment: a model from prism adaptation. J Mot Behav. 2002;34:126–138. doi: 10.1080/00222890209601935. [DOI] [PubMed] [Google Scholar]
- Roby-Brami A, Burnod Y. Learning a new visuomotor transformation: error correction and generalization. Brain Res Cogn Brain Res. 1995;2:229–242. doi: 10.1016/0926-6410(95)90014-4. [DOI] [PubMed] [Google Scholar]
- Sainburg RL. Evidence for a dynamic-dominance hypothesis of handedness. Exp Brain Res. 2002;142:241–258. doi: 10.1007/s00221-001-0913-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Ghez C, Kalakanis D. Intersegmental dynamics are controlled by sequential anticipatory, error correction, and postural mechanisms. J Neurophysiol. 1999;81:1045–1056. doi: 10.1152/jn.1999.81.3.1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarlegna FR, Sainburg RL. The effect of target modality on visual and proprioceptive contributions to the control of movement distance. Exp Brain Res. 2007;176:267–280. doi: 10.1007/s00221-006-0613-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saunders JA, Knill DC. Visual feedback control of hand movements. J Neurosci. 2004;24:3223–3234. doi: 10.1523/JNEUROSCI.4319-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaefer SY, Haaland KY, Sainburg RL. Dissociation of initial trajectory and final position errors during visuomotor adaptation following unilateral stroke. Brain Res. 2009;1298:78–91. doi: 10.1016/j.brainres.2009.08.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sober SJ, Sabes PN. Multisensory integration during motor planning. J Neurosci. 2003;23:6982–6992. doi: 10.1523/JNEUROSCI.23-18-06982.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sober SJ, Sabes PN. Flexible strategies for sensory integration during motor planning. Nat Neurosci. 2005;8:490–497. doi: 10.1038/nn1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soechting JF, Flanders M. Sensorimotor representations for pointing to targets in three-dimensional space. J Neurophysiol. 1989;62:582–594. doi: 10.1152/jn.1989.62.2.582. [DOI] [PubMed] [Google Scholar]
- Tillery SI, Flanders M, Soechting JF. A coordinate system for the synthesis of visual and kinesthetic information. J Neurosci. 1991;11:770–778. doi: 10.1523/JNEUROSCI.11-03-00770.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong C, Flanagan JR. Task-specific internal models for kinematic transformations. J Neurophysiol. 2003;90:578–585. doi: 10.1152/jn.01087.2002. [DOI] [PubMed] [Google Scholar]
- Tseng YW, Diedrichsen J, Krakauer JW, Shadmehr R, Bastian AJ. Sensory prediction errors drive cerebellum-dependent adaptation of reaching. J Neurophysiol. 2007;98:54–62. doi: 10.1152/jn.00266.2007. [DOI] [PubMed] [Google Scholar]
- Vindras P, Viviani P. Frames of reference and control parameters in visuomanual pointing. J Exp Psychol Hum Percept Perform. 1998;24:569–591. doi: 10.1037//0096-1523.24.2.569. [DOI] [PubMed] [Google Scholar]
- Vindras P, Viviani P. Altering the visuomotor gain. Evidence that motor plans deal with vector quantities. Exp Brain Res. 2002;147:280–295. doi: 10.1007/s00221-002-1211-9. [DOI] [PubMed] [Google Scholar]
- Wang J, Sainburg RL. Adaptation to visuomotor rotations remaps movement vectors, not final positions. J Neurosci. 2005;25:4024–4030. doi: 10.1523/JNEUROSCI.5000-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Sainburg RL. Interlimb transfer of visuomotor rotations depends on handedness. Exp Brain Res. 2006;175:223–230. doi: 10.1007/s00221-006-0543-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Merzenich MM, Sameshima K, Jenkins WM. Remodelling of hand representation in adult cortex determined by timing of tactile stimulation. Nature. 1995;378:71–75. doi: 10.1038/378071a0. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Miall RC. Forward models for physiological motor control. Neural Netw. 1996;9:1265–1279. doi: 10.1016/s0893-6080(96)00035-4. [DOI] [PubMed] [Google Scholar]
- Zarahn E, Weston GD, Liang J, Mazzoni P, Krakauer JW. Explaining savings for visuomotor adaptation: linear time-invariant state-space models are not sufficient. J Neurophysiol. 2008;100:2537–2548. doi: 10.1152/jn.90529.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]


