Abstract
We report simulations of the two-dimensional electronic spectroscopy of the Qy band of the D1-D2-Cyt b559 photosystem II reaction center at 77 K. We base the simulations on an existing Hamiltonian that was derived by simultaneous fitting to a wide range of linear spectroscopic measurements and described within modified Redfield theory. The model obtains reasonable agreement with most aspects of the two-dimensional spectra, including the overall peak shapes and excited state absorption features. It does not reproduce the rapid equilibration from high energy to low energy excitonic states evident by a strong cross-peak below the diagonal. We explore modifications to the model to incorporate new structural data and improve agreement with the two-dimensional spectra. We find that strengthening the system–bath coupling and lowering the degree of disorder significantly improves agreement with the cross-peak feature, while lessening agreement with the relative diagonal/antidiagonal width of the 2D spectra. We conclude that two-dimensional electronic spectroscopy provides a sensitive test of excitonic models of the photosystem II reaction center and discuss avenues for further refinement of such models.
INTRODUCTION
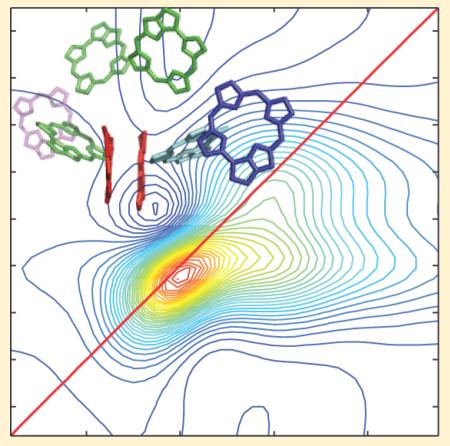
The photosystem II complex (PSII) is unique among all biological systems in its ability to harness solar energy and split water.1 A desire to understand the fundamental structure–function relationship, as well as the potential to create artificial mimics has inspired a wealth of studies aimed at understanding PSII’s unique capabilities. PSII is composed of over 25 subunits that bind >250 chlorophyll (Chl) molecules acting as light harvesting antennae to transfer energy to the PSII reaction center (RC). While similar in structure to the well-studied bacterial reaction center (BRC), our understanding of the RC is considerably poorer: its spectroscopic features are generally broad and overlapping, making it difficult to discern the roles of individual pigments in energy and charge transfer processes. In contrast to the BRC, a high-resolution crystal structure of PSII has only very recently become available.2
Because of the overlapping absorption of the pigments within PSII, preparations with fewer chlorophyll are often preferred for spectroscopic study. A purified PSII preparation capable of evolving oxygen consists of so-called BBY particles, named for the developers of the protocol.3 This preparation can be further refined to obtain the D1-D2-Cyt b559 photosystem II reaction center (PSII RC).4 This complex contains the D1 and D2 proteins as well as cytochrome b559 but lacks the antennae proteins and reducing side plastoquinone acceptors. As a consequence, these reaction centers stop short of the final charge separation, creating a short-lived radical pair PD1+PheoD1−. Despite this difference, the primary events of charge separation in this complex are thought to be representative of the intact RC5-7 in which only the D1 branch is active.7 The reasons for single-sided charge separation in both the PSII RC8 and the BRC9 is an active area of investigation. Despite the 2-fold symmetry of these structures, protein–pigment interactions tune the site energies of the pigments and the surrounding dielectric properties to promote charge separation along a single branch.8,10 In the RC, the asymmetric charge separation means that photodamage occurs mainly in the D1 protein, simplifying the necessary repair pathways.8 The major pigments of the RC and their spatial relationships are shown in Figure 1. There has been extensive effort toward understanding the structure–function relationship of the PSII RC. The energy and charge transfer processes have been studied with a wide range of experimental methods including visible pump–probe,5,11-21 visible pump–infrared probe,22,23 time-resolved fluorescence,21,24,25 photon echo,26 spectral hole-burning,27,28 Stark spectroscopy,29 and, recently, two-dimensional electronic spectroscopy (2DES).30 A number of excellent reviews summarize much of this large body of work.31-33 Despite this intense research effort, the mechanisms and time scales of the ultrafast energy and charge transfer processes are not yet fully understood.34
Figure 1.
Two different views of the PSII RC pigments (from the 3ARC structure2). Two carotenoids present in the structure are not shown.
Modeling has been crucial to the interpretation of time-resolved and steady-state spectral data for the PSII RC. One of the early efforts was the multimer model,35-37 where the transition energies of the six core pigments were assumed to be identical, and coupling between the pigments produced delocalized exciton states. Within Redfield theory, this model has been used to describe the spectral dynamics of pump–probe38 and photon echo spectroscopy experiments.26 A more complete model, taking into account many linear spectra and pump–probe experiments, was subsequently proposed by Renger and Marcus.38 They further refined their model by relaxing the restriction of equivalent site energies.39 Novoderezhkin et al. have also used an evolutionary algorithm approach to extract site energies from linear absorption, linear dichroism, circular dichrosim, and fluorescence spectra.40 They have further refined their model through fitting to pump–probe and fluorescence kinetics. More recently, they have updated their model to include fits to Stark spectroscopy.41 We use this model as a basis for 2DES simulations to compare with the PSII RC 2DES data. We explore several modifications to the model to improve the agreement with the 2DES experiments.
MODELS
The PSII RC consists of eight chromophores in the D1-D2 subunits as depicted in Figure 1: two chlorophylls belonging to the special pair (denoted PD1 and PD2), two accessory chlorophylls (ChlD1 and ChlD2), two pheophytins (PheD1 and PheD2), and two peripheral chlorophylls (ChlzD1 and ChlzD2). In this article, we begin with the model of Novoderezhkin et al.41 We then explore a modified model that uses couplings from a more recent crystal structure,2 altering some of the parameters to obtain better agreement with aspects of the 2DES data.
Novoderezhkin Model
Within this model, a single charge transfer (CT) state is included, with its assignment taken to be PD1−PD2+ based on the best simultaneous fit to fluorescence and Stark spectra.41 To obtain the one-exciton system Hamiltonian, we retrieve the atomic coordinates from the 1IZL crystal structure;42 we define the location of the chromophores to be the average location of the central nitrogen atoms. The dipoles are assumed to be oriented at a 5.5° rotation from the NB–ND direction (toward the NC atom).40 The chlorophylls have an effective Qy transition dipole strength of 4 D, and the pheophytins have an effective strength of 3 D.40,41,43 Couplings are calculated using the dipole–dipole approximation using an effective dielectric constant of 1.0. The CT state is coupled to its constituent chromophores with a strength of 35 cm−1, consistent with the range of 20–50 cm−1 reported in molecular dynamics,44 path integral,45 and Redfield theory simulations.46 The CT state has a negligible effective transition dipole; the diagonalization of the Hamiltonian lends dipole strength to the excitonic CT state. The Hamiltonian for this model is given in Table 1.
Table 1. One-Exciton Hamiltonian for the Novoderezhkin and Modified Models, Shown in the Site Basis (Transition Energies Are in cm−1 and Do Not Include Reorganization Energy Shifts)a.
| PD1 | PD2 | ChlD1 | ChlD2 | PheD1 | PheD2 | ChlzD1 | ChlzD2 | PD1−PD2+ (PD1PD2)+ChlD− | |
|---|---|---|---|---|---|---|---|---|---|
| PD1 | 15190 | ||||||||
| 15190 | |||||||||
| PD2 | 147.55 | 15180 | |||||||
| 162.2 | 15180 | ||||||||
| ChlD1 | −12.53 | −61.88 | 15000 | ||||||
| −8.66 | −56.20 | 15000 | |||||||
| ChlD2 | −53.42 | −5.25 | 12.23 | 15130 | |||||
| −59.97 | −3.13 | 11.17 | 15130 | ||||||
| PheD1 | −0.03 | 13.98 | 55.85 | −5.07 | 15050 | ||||
| −1.56 | 10.99 | 56.36 | −3.38 | 15050 | |||||
| PheD2 | 14.67 | −4.50 | −5.43 | 51.0 | 3.47 | 15060 | |||
| 9.84 | −2.31 | −3.29 | 47.84 | 1.40 | 15060 | ||||
| ChlzD1 | −3.18 | 0.76 | −0.69 | −0.85 | 0.93 | 0.53 | 15555 | ||
| −0.23 | 0.98 | 2.20 | −0.18 | −1.97 | −0.11 | 15555 | |||
| ChlzD2 | 1.25 | −3.78 | −1.14 | 0.59 | 0.66 | 1.50 | −0.08 | 15485 | |
| 0.95 | 0.51 | −0.09 | 1.88 | −0.14 | −2.12 | 0.12 | 15485 | ||
| PD1−PD2+ (PD1PD2)+ChlD1− | 35 | 35 | 0 | 0 | 0 | 0 | 0 | 0 | 15120 |
| 35 | 35 | 35 | 0 | 0 | 0 | 0 | 0 | 15120 |
In the two-exciton Hamiltonian, block pairs of singly excited molecules as well as doubly excited molecules (overtones) are included. For the overtones, the effective dipole strength of the S1–S2 state is taken to be half that of the S0–S1 transition, with the doubly excited state anharmonically blue-shifted by 150 cm−1. The S1–S2 transition of the CT state is forbidden, as are pairs of singly excited chromophores that include the CT state and any of its constituent chromophores (e.g., excitations could not simultaneously reside on PD1 and PD1−PD2+).
Inhomogeneous broadening is included by allowing the site energies of each chromophore to be drawn from a Gaussian distribution and averaging over the ensemble. The chromophoric states have a fwhm of 80 cm−1, and the CT state is taken to be broader (fwhm of 183 cm−1).
The environment is simulated using a continuous set of harmonic oscillators resulting in a smooth spectral density consisting of 48 high-frequency underdamped modes and a single overdamped Brownian oscillator (OBO) mode. The OBO component is assigned a coupling strength, λ0, of 70 cm−1 and a cutoff frequency, γ0, of 40 cm−1 for sites n = 1–8. The frequencies and couplings for the 48 high-frequency modes, obtained from fluorescence line narrowing experiments47 and adjusted to fit low temperature linear spectra, are given in detail in ref 40. For the CT state, the coupling strength to both the OBO and underdamped modes is larger by a factor of 1.6.
Modified Model
Unless otherwise specified, the updated model uses the same parameters and calculation methods as described above for the Novoderezhkin model.41 In the modified model, we use the newer 3ARC crystal structure2 to calculate dipole–dipole couplings between pigments. In the newer crystal structure, the PD1 and PD2 chromophores are more closely spaced, leading to a substantially higher coupling that strongly affects the linear spectra. To maintain good agreement with the linear spectra, we raise the dielectric constant to 1.2, effectively lowering all dipole–dipole couplings between the chromophores. Even with the increased dielectric constant, the PD1 and PD2 coupling is still larger than in the original model, although the rest of the couplings are still of the same order. We also modify the identity of the single charge transfer (CT) state to be (PD1PD2)+ChlD1−. This modification is consistent with recent work that has suggested the inclusion of the accessory chlorophyll in the initial CT state.16,48 In order to improve the agreement with our 2D peakshapes, we increase the system–bath coupling, λ0, from 70 to 100 cm−1. This has the effect of broadening the overall spectra, which we offset by decreasing the amount of disorder allowed in each state. The chromophoric states now have a fwhm of 47 cm−1, and the CT state has a fwhm of 66 cm−1. As in the original model, the CT state is more strongly coupled to the bath, but by a factor of instead of 1.6.
SIMULATION RESULTS
To simulate the linear absorption spectrum and 2D electronic spectroscopy of the PSII RC at 77 K, we employ the software package Spectron,49 using the cumulant expansion for Gaussian fluctuations and the modified Redfield theory that includes polaron effects and covers the Förster and the Marcus mechanisms of energy and charge transfer.50,51 The implementation of modified Redfield theory employs the doorway-window representation within the RWA, as summarized in the appendix and detailed in the appendices of Zhang et al.50 This theory includes polaron effects by treating the system-bath coupling nonperturbatively using the second order cumulant expansion. The simulations use all parallel polarization as was used in the experiment. The pulses are assumed to provide impulsive excitation, with the same central frequency and wavevector. Since the simulations are made in the energy basis, we must scale them by a factor of 1/λ2 to compare to experiments, which are measured in wavelength bins. Similarly, we must apply this scaling factor to the detection axis of the 2D spectra.
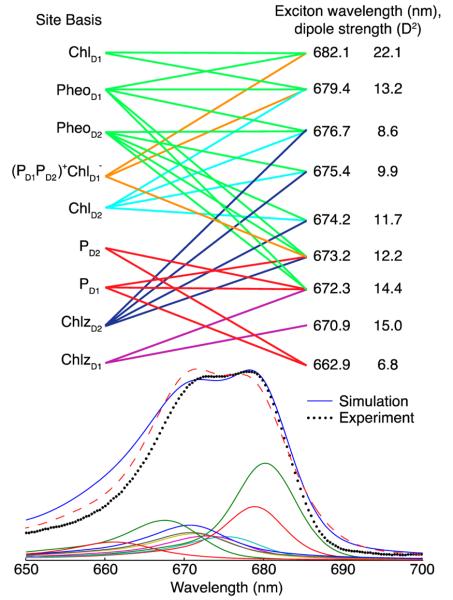
The linear absorption spectrum is averaged over 5000 realizations of the disorder. Figure 2 shows the resulting 77 K linear absorption spectrum for the original and modified Novoderezhkin models for comparison with experimental data. The contributions from the underlying exciton states in the modified model are shown beneath the overall spectrum. Note that the excitons for each realization of disorder are sorted by the exciton energy after reorganization and that this causes mixing of the identities of the states. For instance, there are localized states (from the peripheral chlorophylls); yet with disorder, these may be located anywhere from the third through the eighth exciton, giving the appearance that these localized states are coupled to other states even when they are not. The transformation from the site basis to the exciton basis is given by . The mean square of the eigenvectors, , and other indicators of the excitons are shown in Table 2, with any site contributing more than 10% indicated by boldface type. We obtain good agreement with the exciton transition wavelengths and dipole strengths reported in Figure 4 of the paper by Novoderezhkin et al.41
Figure 2.
Top, modified Novoderezhkin excitonic model of the PSII RC. Lines denote any pigments with greater than 10% probability of participating in the connecting exciton state. Also given are the dipole strengths. Bottom, the experimental (black dotted) and simulated 77 K absorption spectrum of the Qy band for the modified (blue solid) and original Novoderezhkin model (red dashed). Also shown are the underlying excitonic contributions calculated for 5000 realizations of disorder for the modified model.
Table 2. Mean Square of the Eigenvectors, Inverse Participation Ratios (IPR), (Given by ), Dipole Strengths (in D2), and the Zero Phonon Line Wavelength (λZPL), Averaged over 2500 Realizations of Disordera.
| exciton 1 | exciton 2 | exciton 3 | exciton 4 | exciton 5 | exciton 6 | exciton 7 | exciton 8 | exciton 9 | |
|---|---|---|---|---|---|---|---|---|---|
| PD1 | 0.029 | 0.041 | 0.040 | 0.058 | 0.080 | 0.106 | 0.134 | 0.050 | 0.461 |
| 0.031 | 0.025 | 0.029 | 0.051 | 0.072 | 0.108 | 0.165 | 0.030 | 0.489 | |
| PD2 | 0.040 | 0.094 | 0.051 | 0.057 | 0.067 | 0.091 | 0.123 | 0.050 | 0.427 |
| 0.093 | 0.070 | 0.066 | 0.067 | 0.063 | 0.078 | 0.103 | 0.023 | 0.437 | |
| ChlD1 | 0.088 | 0.418 | 0.144 | 0.085 | 0.078 | 0.067 | 0.063 | 0.035 | 0.021 |
| 0.406 | 0.215 | 0.055 | 0.043 | 0.058 | 0.093 | 0.096 | 0.022 | 0.012 | |
| ChlD2 | 0.031 | 0.067 | 0.201 | 0.262 | 0.197 | 0.108 | 0.070 | 0.029 | 0.036 |
| 0.023 | 0.102 | 0.325 | 0.221 | 0.112 | 0.075 | 0.085 | 0.019 | 0.037 | |
| PheD1 | 0.047 | 0.222 | 0.274 | 0.122 | 0.112 | 0.100 | 0.086 | 0.038 | 0.000 |
| 0.187 | 0.231 | 0.131 | 0.087 | 0.099 | 0.124 | 0.112 | 0.030 | 0.000 | |
| PheD2 | 0.038 | 0.099 | 0.165 | 0.196 | 0.163 | 0.146 | 0.139 | 0.053 | 0.000 |
| 0.028 | 0.063 | 0.190 | 0.213 | 0.163 | 0.146 | 0.156 | 0.040 | 0.000 | |
| ChlzD1 | 0.000 | 0.000 | 0.001 | 0.010 | 0.029 | 0.073 | 0.193 | 0.694 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.001 | 0.013 | 0.041 | 0.136 | 0.808 | 0.000 | |
| ChlzD2 | 0.000 | 0.010 | 0.085 | 0.179 | 0.241 | 0.279 | 0.167 | 0.038 | 0.001 |
| 0.000 | 0.014 | 0.107 | 0.240 | 0.338 | 0.234 | 0.062 | 0.004 | 0.000 | |
| PD2+PD2−(PD1PD2)+ChlD1− | 0.726 | 0.048 | 0.039 | 0.031 | 0.033 | 0.031 | 0.026 | 0.013 | 0.054 |
| 0.232 | 0.279 | 0.097 | 0.077 | 0.082 | 0.100 | 0.085 | 0.024 | 0.025 | |
| λZPL (nm) | 693.7 | 680.9 | 677.3 | 674.9 | 673.5 | 672.2 | 671.1 | 669.3 | 662.2 |
| 682.1 | 679.4 | 676.7 | 675.4 | 674.2 | 673.2 | 672.3 | 670.9 | 662.9 | |
| IPR | 1.45 | 2.18 | 1.87 | 1.86 | 1.85 | 1.83 | 1.88 | 1.25 | 2.41 |
| 2.27 | 2.23 | 1.84 | 1.76 | 1.73 | 2.05 | 2.5 | 1.17 | 2.30 | |
| |μ|2 | 5.3 | 28.2 | 13.4 | 13.2 | 13.1 | 13.3 | 12.1 | 13.5 | 1.9 |
| 22.1 | 13.2 | 8.6 | 9.9 | 11.7 | 12.2 | 14.4 | 15.0 | 6.8 |
In bold are the sites contributing more than 10% to a given exciton state. The parameters for the original Novoderezhkin model are italicized and listed above the corresponding parameters of the modified model.
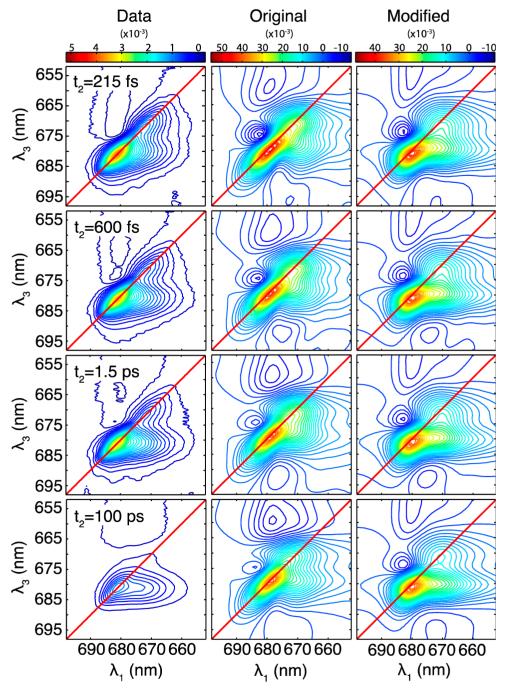
In Figure 3, we present experimental 2DES data (left column) alongside simulated 2DES spectra at different waiting times t2 for the Novoderezhkin model (center) and the modified model (right). Each column is scaled to the maximum values throughout the (λ1, t2, λ3) space, taken from the t2 = 28 fs spectrum. Both models reproduce the main qualitative features found in the data. The elongation along the diagonal reflects the large degree of inhomogeneous broadening in the system. The relative diagonal to antidiagonal width matches well with the original Novoderezhkin model and to a lesser degree with the modified model. A negative excited-state absorption feature above the diagonal is reproduced in the simulations with both models, suggesting that an anharmonic shift of 150 cm−1 is reasonable. Both simulations show the presence of a cross-peak below the diagonal at the earliest waiting time shown here (215 fs). The degree of elongation of the cross-peak along the excitation wavelength axis is better reproduced by the modified than the original Novoderezhkin model at all of the different waiting times. At the longest waiting times, the data indicates near-complete relaxation to the lowest energy state and is almost completely horizontally elongated, while the simulations maintain diagonal elongation and a significant contribution from the higher energy states. The overall decay of the spectra is more significant in the experimental data, both in the overall signal level and, specifically, for the highest energy states, which have almost entirely disappeared in the 100 ps data.
Figure 3.
Two-dimensional electronic spectra for different waiting times t2 = 215 fs, 600 fs, 1.5 ps, and 100 ps. Experimental data (left) and simulations based on the Novoderezhkin model (center) and modified model (right). Simulations are each averaged over 1500 instances of disorder. Contours are spaced every 2.5% of the maximum value of the t2 = 28 fs spectrum. Note that the absolute scale of the data cannot be compared with the absolute scale of the simulations.
DISCUSSION
The excitonic model of Novoderezhkin et al.40,41 successfully describes a wide range of spectroscopic measurements of the PSII RC. Here, we find that simulations of 2DES based on this model reproduce many aspects of the 2DES data. Notably, the degree of homogeneous/inhomogeneous broadening appears to match the data quite well. The prominent excited state absorption feature above the diagonal is also reproduced in the simulations. We note that this subtle feature was not observed in our first reported 2DES spectra,30 possibly due to a small fraction of CP47 contamination. We note that the kinetics we reported previously30 matched well with pump–probe experiments16,17,52 and that the small excited state absorption feature reported here is consistent with these reports. Other aspects of the 2DES spectra are not as well reproduced in the simulations. In particular, the main cross-peak at λ1 = 670 nm in the simulations is not reproduced: it shows up at a slightly higher energy than is seen in the experiment, and the strong horizontal elongation of this cross-peak is absent.
In modifying the Novoderezhkin model, we aimed to better reproduce the pronounced cross-peak and its strong elongation along the excitation wavelength axis. We found that this could be achieved by increasing the system–bath coupling, λ0, from 70 cm−1 in the Novoderezhkin model to 100 cm−1. This has the effect of broadening the overall spectra, which we offset by decreasing the amount of disorder allowed in each state to maintain agreement with the linear absorption spectrum; we lowered the fwhm from 80 to 47 cm−1 for chromophoric states and from 184 to 66 cm−1 for the CT state. We note that this change affects the blue side of the absorption spectrum (see Figure 2).
In modifying the Novoderezhkin model, we also take advantage of the newly available high-resolution 3ARC crystal structure2 to calculate dipole–dipole couplings between pigments. Early crystal structures pointed to a separation of the PD1 and PD2 pigments on the order of 9.6 Å,42 while the most recent structure provides a center–center distance of 8 Å, leading to a substantially higher coupling that strongly affects the linear spectra. Experimental evidence rejects strong coupling due to the lack of clear excitonic-splitting observed in the linear absorption spectrum. Therefore, we must consider the effective dielectric constant and Coulombic screening effects to regulate the PD1–PD2 coupling. Adjusting the dielectric constant is one relatively crude method for adjusting coupling strength, and widely ranging dielectric constants have been reported for different proteins in the literature.53,54 Stark spectroscopy studies of the BRC have shown substantial variations in the effective dielectric constant for the different reaction center pigments.55 Here, we used a dielectric constant of 1.2, yielding a special pair coupling of 162 cm−1. This coupling falls within the range of 140–170 cm−1 determined by Raszewski et al. based on extensive fits to linear spectra.39 It is also reasonably consistent with their calculations based on an older crystal structure56 that have gone beyond the point-dipole approximation, using the transition monopole57 and ab initio TrEsp methods.10,39,58 Finally, compared to the original model, we changed the identity of the CT state from PD1−PD2+ to (PD1PD2)+ChlD1−. This modification is consistent with recent work that has suggested the inclusion of the accessory chlorophyll in the initial CT state,16,48 following experimental work that suggested the importance of the ChlD1 in the initial charge separation step.26 Compared to the assignment of the CT state to PD1−PD2+, this modification produced slightly better agreement with the 2DES peakshapes. As in the Novoderezhkin model, we coupled the CT state more strongly to the bath, but by a factor of instead of 1.6, which provided a slight improvement.
The modified Novoderezhkin model succeeds in matching many of the qualitative features of the 2DES data. In particular, strengthening the system–bath coupling produced a strongly elongated cross-peak that perfectly matches the experimental data. However, the necessary reduction of the disorder lessened the agreement with the relative diagonal/antidiagonal widths of the diagonal peaks, indicating that the inhomogeneity of the these peaks may be too small in this modified model. Thus, while our modified model improves the agreement with the cross-peak and diagonal features in the 2D spectra, hole-burning experiments27,59,60 and Stark spectroscopy measurements41 suggest larger inhomogeneities in the system. This inconsistency may require revision of our understanding of the multimer simulation approach as described below.
Several aspects of both models limit their ability to reproduce the experimentally observed kinetics. At the very shortest time scales (up to 50 fs), the validity of the modified Redfield theory, which assumes Markovian dynamics, can be challenged. Another assumption of the model is the complete separation of classical populations from quantum density matrix coherences. A complete quantum master equation including non-Markovian and quantum transport effects may be required for propagation at very short times. The same level of sophistication may be achieved using the hierarchical equations of motion for the system density matrix. At long times, the level of theory used in our simulations may be sufficient; however, the model neglects several important effects. The simulations include only stimulated transitions (i.e., spontaneous emission is excluded), meaning that excited state populations will not decay to the ground state at long t2, and signals will persist. The radiative and nonradiative decay of excitons, charge recombination effects as well as probable protein deformation due to the CT state population should be included in a more complete model.
Another path for improving the match between simulated and experimentally observed kinetics is to compartmentalize the chromophores, allowing for different theories of energy transfer to be used for different parts of the complex. For instance, the peripheral chlorophylls in the reaction center are quite localized compared to the central six chromophores. In this case, generalized Förster theory is likely more appropriate than modified Redfield to describe the transfer of energy from the periphery to the center of the complex. Compartmentalization has been introduced within the context of the Renger model.10,39 In an earlier paper by Novoderezhkin et al.,40 the authors test multiple models of site energies, and while each matched the linear spectra, only one (Model B) was able to adequately describe transient absorption dynamics in the 0–500 fs range. Their updated model,41 used here as the basis of our 2DES simulations, incorporated fits to additional linear spectra but was not tested against transient absorption data. More recently, Novoderezhkin et al. have proposed an alternative to their 2007 model that includes 6 exciton states coupled to 4 CT states to obtain agreement with transient absorption kinetics.48 They include some degree of compartmentalization, where transfer to certain states is modeled with Förster theory instead of modified Redfield theory.
A key challenge that remains is to treat charge transfer states in an intuitive and effective manner. To date, the models for the PSII reaction center have included a variety of different charge transfer states in a phenomenological way as required to match the particular set of spectroscopic data being examined. Abramavicius and Mukamel recently developed a general framework for modeling charge transfer using a two-band tight-binding approach.61 The theory combines the two-band tight-binding model62 with the modified Redfield theory.42 In this model, a molecular excitation involves promoting an electron from the HOMO level to the LUMO level of the molecule, leaving a hole in the HOMO. The electron or hole can then “hop” to nearby molecules creating a charge transfer state.
CONCLUSIONS
In summary, we have simulated 2D electronic spectra for the Qy band of the PSII RC at 77 K and have compared the resulting simulated spectra to our experimental data. These simulations included the model of Novoderezhkin et al.41 that takes into account a wide array of spectroscopic measurements on the PSII RC. We find that this model reproduces many aspects of the 2DES data but gives poor agreement with the substantial cross-peak present in the data at early times. We also performed simulations based on a modified model that incorporates new structural data and uses the 2DES experimental data as a guide to adjust model parameters to improve agreement between simulation and experiment. The modified model succeeds in reproducing the main features of the 2DES spectra, notably the pronounced cross-peak below the diagonal. However, it gives poorer agreement with the relative diagonal/antidiagonal width of the 2DES data, indicating an underestimation of disorder, consistent with hole-burning experiments. Further work is needed to improve the agreement with this aspect of the data, as well as with the kinetics at shortest time scales and in the asymptotic long-time regime, highlighting the fact that 2DES provides a rich data set for testing excitonic models. Future work will target the model for the inhomogeneity, will employ the recently developed tight-binding model,10 and explore the use of compartmentalization to achieve the appropriate description of energy transfer between different parts of the PSII RC.
ACKNOWLEDGMENTS
We would like to thank the Department of Theoretical Physics at Vilnius University and the Mukamel group at UC Irvine for their helpful conversations and suggestions. J.P.O., J.A.M., and F.D.F. gratefully acknowledge the support of the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences of the U.S. Department of Energy through grant #DE-FG02-11ER15904. K.L.M.L. acknowledges support from a National Science Foundation graduate fellowship and National Science Foundation grant #PHY-0748470. C.F.Y. gratefully acknowledges the support of the National Science Foundation (grant # MCB-0716541). S.M. gratefully acknowledges the support of DARPA BAA-10-40 QuBE, the National Science Foundation (Grant No. CHE-1058791), and the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy. D.A. acknowledges support of Research Council of Lithuania Grant No. MIP-069/2012
APPENDIX A
In the above simulations, we utilized modified Redfield theory as developed by Zhang et al.50 In the site basis, we treat the system Hamiltonian as follows:
| (A1) |
where is the excitation creation (annihilation) operator for the nth molecule treated as boson operators, Ωn is the transition energy for site n, Jm,n is the electronic coupling between the mth and nth states, and Kn is the anharmonic energy shift of double-excitations. The third term represents additional coupling of electronic states through the bath modes, while the final term is the Hamiltonian of the bath itself, which is treated as a collection of harmonic oscillators. The coupling of the states due to the bath modes can be fully described through the spectral density:
| (A2) |
As done by Novoderezhkin et al.,40 we utilize a spectral density given by
| (A3) |
where λj = Sjωj, and the Huang–Rhys factors Sj and frequencies ωj for the 48 high frequency modes are given in ref 40. The damping constant γj = 3 cm−1.
We calculate the linear spectra, averaging over instances of disorder, using the expression
| (A4) |
where is the transition dipole connecting states g and k
| (A5) |
and Rkkkk is the Modified Redfield tensor describing one-exciton population transfer, given by
| (A6) |
where
| (A7) |
and
| (A8) |
We calculate the third order response function in the doorway window approximation using an ordinary master equation under the Markovian approximation. Full detailsnecessary to compute the third order response function within the doorway-window description are given in ref 50.
Footnotes
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of this manuscript.
The authors declare no competing financial interest.
REFERENCES
- (1).Blankenship RE. Molecular Mechanisms of Photosynthesis. Blackwell Science; Oxford, U.K.: 2002. [Google Scholar]
- (2).Umena Y, Kawakami K, Shen JR, Kamiya N. Nature. 2011;473(7345):55–60. doi: 10.1038/nature09913. [DOI] [PubMed] [Google Scholar]
- (3).Berthold DA, Babcock GT, Yocum CF. FEBS Lett. 1981;134(2):231–234. [Google Scholar]
- (4).van Leeuwen PJ, Nieveen MC, van Demeent EJ, Dekker JP, van Gorkom HJ. Photosynth. Res. 1991;28(3):149–153. doi: 10.1007/BF00054128. [DOI] [PubMed] [Google Scholar]
- (5).Holzwarth AR, Muller MG, Reus M, Nowaczyk M, Sander J, Rogner M. Proc. Natl. Acad. Sci. U.S.A. 2006;103(18):6895–6900. doi: 10.1073/pnas.0505371103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Pawlowicz NP, Groot ML, van Stokkum IHM, Breton J, yGrondelle R. Biophys. J. 2007;93:2732–2742. doi: 10.1529/biophysj.107.105452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Diner BA, Rappaport F. Annu. Rev. Plant Biol. 2002;53:551–580. doi: 10.1146/annurev.arplant.53.100301.135238. [DOI] [PubMed] [Google Scholar]
- (8).Renger T, Schlodder E. J. Photochem. Photobiol., B. 2011;104(1-2):126–141. doi: 10.1016/j.jphotobiol.2011.03.016. [DOI] [PubMed] [Google Scholar]
- (9).Faries KM, Kressel LL, Wander MJ, Holten D, Laible PD, Kirmaier C, Hanson DK. J. Biol. Chem. 2012;287(11):8507–8514. doi: 10.1074/jbc.M111.326447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Raszewski G, Diner BA, Schlodder E, Renger T. Biophys. J. 2008;95(1):105–119. doi: 10.1529/biophysj.107.123935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Muller MG, Hucke M, Reus M, Holzwarth AR. J. Phys. Chem. 1996;100(22):9527–9536. [Google Scholar]
- (12).Klug DR, Rech T, Joseph DM, Barber J, Durrant JR, Porter G. Chem. Phys. 1995;194(2-3):433–442. [Google Scholar]
- (13).Rech T, Durrant JR, Joseph DM, Barber J, Porter G, Klug DR. Biochemistry. 1994;33(49):14768–14774. doi: 10.1021/bi00253a015. [DOI] [PubMed] [Google Scholar]
- (14).Hastings G, Durrant JR, Barber J, Porter G, Klug DR. Biochemistry. 1992;31(33):7638–7647. doi: 10.1021/bi00148a027. [DOI] [PubMed] [Google Scholar]
- (15).Durrant JR, Hastings G, Joseph DM, Barber J, Porter G, Klug DR. Proc. Natl. Acad. Sci. U.S.A. 1992;89(23):11632–11636. doi: 10.1073/pnas.89.23.11632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Romero E, van Stokkum IHM, Novoderezhkin VI, Dekker JP, van Grondelle R. Biochemistry. 2010;49(20):4300–4307. doi: 10.1021/bi1003926. [DOI] [PubMed] [Google Scholar]
- (17).Groot ML, van Mourik F, Eijckelhoff C, van Stokkum IHM, Dekker JP, van Grondelle R. Proc. Natl. Acad. Sci. U.S.A. 1997;94(9):4389–4394. doi: 10.1073/pnas.94.9.4389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Visser HM, Kleima FJ, van Stokkum IHM, van Grondelle R, van Amerongen H. Chem. Phys. 1996;210(1-2):297–312. [Google Scholar]
- (19).Greenfield SR, Seibert M, Wasielewski MR. J. Phys. Chem. B. 1999;103(39):8364–8374. [Google Scholar]
- (20).Greenfield SR, Seibert M, Wasielewski MR. J. Phys. Chem. B. 1997;101(13):2251–2255. [Google Scholar]
- (21).Andrizhiyevskaya EG, Frolov D, van Grondelle R, Dekker JP. Phys. Chem. Chem. Phys. 2004;6(20):4810–4819. [Google Scholar]
- (22).Groot ML, Pawlowicz NP, van Wilderen LJ, Breton J, van Stokkum IH, van Grondelle R. FEBS J. 2005;272:449–450. [Google Scholar]
- (23).Groot ML, Pawlowicz NP, van Wilderen L, Breton J, van Stokkum IHM, van Grondelle R. Proc. Natl. Acad. Sci. U.S.A. 2005;102(37):13087–13092. doi: 10.1073/pnas.0503483102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Gatzen G, Muller MG, Griebenow K, Holzwarth AR. J. Phys. Chem. 1996;100(17):7269–7278. [Google Scholar]
- (25).Donovan B, Walker LA, Kaplan D, Bouvier M, Yocum CF, Sension RJ. J. Phys. Chem. B. 1997;101(26):5232–5238. [Google Scholar]
- (26).Prokhorenko VI, Holzwarth AR. J. Phys. Chem. B. 2000;104(48):11563–11578. [Google Scholar]
- (27).Groot ML, Dekker JP, van Grondelle R, den Hartog FTH, Volker S. J. Phys. Chem. 1996;100(27):11488–11495. [Google Scholar]
- (28).Zazubovich V, Jankowiak R, Riley K, Picorel R, Seibert M, Small GJ. J. Phys. Chem. B. 2003;107(12):2862–2866. [Google Scholar]
- (29).Frese RN, Germano M, de Weerd FL, van Stokkum IHM, Shkuropatov AY, Shuvalov VA, van Gorkom HJ, van Grondelle R, Dekker JP. Biochemistry. 2003;42(30):9205–9213. doi: 10.1021/bi0273516. [DOI] [PubMed] [Google Scholar]
- (30).Myers JA, Lewis KLM, Fuller FD, Tekavec PF, Yocum CF, Ogilvie JP. J. Phys. Chem. Lett. 2010;1(19):2774–2780. [Google Scholar]
- (31).Yoder LM, Cole AG, Sension RJ. Photosynth. Res. 2002;72(2):147–158. doi: 10.1023/A:1016180616774. [DOI] [PubMed] [Google Scholar]
- (32).Greenfield SR, Wasielewski MR. Photosynth. Res. 1996;48(1-2):83–97. doi: 10.1007/BF00040999. [DOI] [PubMed] [Google Scholar]
- (33).Dekker JP, van Grondelle R. Photosynth. Res. 2000;63(3):195–208. doi: 10.1023/A:1006468024245. [DOI] [PubMed] [Google Scholar]
- (34).Renger T, Schlodder E. ChemPhysChem. 2010;11(6):1141–1153. doi: 10.1002/cphc.200900932. [DOI] [PubMed] [Google Scholar]
- (35).Durrant JR, Klug DR, Kwa SLS, van Grondelle R, Porter G, Dekker JP. Proc. Natl. Acad. Sci. U.S.A. 1995;92(11):4798–4802. doi: 10.1073/pnas.92.11.4798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Leegwater JA, Durrant JR, Klug DR. J. Phys. Chem. B. 1997;101(37):7205–7210. [Google Scholar]
- (37).Barter LMC, Durrant JR, Klug DR. Proc. Natl. Acad. Sci. U.S.A. 2003;100(3):946–951. doi: 10.1073/pnas.0136891100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Renger T, Marcus RA. J. Phys. Chem. B. 2002;106(7):1809–1819. [Google Scholar]
- (39).Raszewski G, Saenger W, Renger T. Biophys. J. 2005;88(2):986–998. doi: 10.1529/biophysj.104.050294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Novoderezhkin VI, Andrizhiyevskaya EG, Dekker JP, van Grondelle R. Biophys. J. 2005;89(3):1464–1481. doi: 10.1529/biophysj.105.060020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Novoderezhkin VI, Dekker JP, van Grondelle R. Biophys. J. 2007;93:1293–1311. doi: 10.1529/biophysj.106.096867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Kamiya N, Shen JR. Proc. Natl. Acad. Sci. U.S.A. 2003;100(1):98–103. doi: 10.1073/pnas.0135651100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Novoderezhkin VI, Palacios MA, van Amerongen H, van Grondelle R. J. Phys. Chem. B. 2005;109(20):10493–10504. doi: 10.1021/jp044082f. [DOI] [PubMed] [Google Scholar]
- (44).Warshel A, Parson WW. Q. Rev. Biophys. 2001;34(4):563–679. doi: 10.1017/s0033583501003730. [DOI] [PubMed] [Google Scholar]
- (45).Sim E, Makri N. J. Phys. Chem. B. 1997;101(27):5446–5458. [Google Scholar]
- (46).Novoderezhkin VI, Yakovlev AG, van Grondelle R, Shuvalov VA. J. Phys. Chem. B. 2004;108(22):7445–7457. [Google Scholar]
- (47).Peterman EJG, van Amerongen H, van Grondelle R, Dekker JP. Proc. Natl. Acad. Sci. U.S.A. 1998;95(11):6128–6133. doi: 10.1073/pnas.95.11.6128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Novoderezhkin VI, Romero E, Dekker JP, van Grondelle R. ChemPhysChem. 2011;12(3):681–688. doi: 10.1002/cphc.201000830. [DOI] [PubMed] [Google Scholar]
- (49).Zhuang W, Abramavicius D, Hayashi T, Mukamel S. J. Phys. Chem. B. 2006;110(7):3362–3374. doi: 10.1021/jp055813u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Zhang WM, Meier T, Chernyak V, Mukamel S. J. Chem. Phys. 1998;108(18):7763–7774. [Google Scholar]
- (51).Yang M, Fleming GR. Chem. Phys. 2002;282(1):355–372. [Google Scholar]
- (52).Visser HM, Groot ML, van Mourik F, van Stokkum IHM, Dekker JP, van Grondelle R. J. Phys. Chem. 1995;99(41):15304–15309. [Google Scholar]
- (53).Scholes GD, Fleming GR. J. Phys. Chem. B. 2000;104(8):1854–1868. [Google Scholar]
- (54).Simonson T, Brooks CL. J. Am. Chem. Soc. 1996;118(35):8452–8458. [Google Scholar]
- (55).Steffen MA, Lao KQ, Boxer SG. Science. 1994;264(5160):810–816. doi: 10.1126/science.264.5160.810. [DOI] [PubMed] [Google Scholar]
- (56).Loll B, Kern J, Saenger W, Zouni A, Biesiadka J. Nature. 2005;438(7070):1040–1044. doi: 10.1038/nature04224. [DOI] [PubMed] [Google Scholar]
- (57).Chang JC. J. Chem. Phys. 1977;67(9):3901–3909. [Google Scholar]
- (58).Madjet ME, Abdurahman A, Renger T. J. Phys. Chem. B. 2006;110(34):17268–17281. doi: 10.1021/jp0615398. [DOI] [PubMed] [Google Scholar]
- (59).Tang D, Jankowiak R, Seibert M, Yocum CF, Small GJ. J. Phys. Chem. 1990;94(17):6519–6522. [Google Scholar]
- (60).Jankowiak R, Tang D, Small GJ, Seibert M. J. Phys. Chem. 1989;93(4):1649–1654. [Google Scholar]
- (61).Abramavicius D, Mukamel S. J. Chem. Phys. 2010;133:18. doi: 10.1063/1.3493580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Chernyak V, Zhang WM, Mukamel S. J. Chem. Phys. 1998;109(21):9587–9601. [Google Scholar]