Segregation of cortical head direction cell assemblies on alternating theta cycles

Abstract

High-level cortical systems for spatial navigation, including entorhinal grid cells, critically depend on input from the head direction system. We examined spiking rhythms and modes of synchrony between neurons participating in head direction networks for evidence of internal processing, independent of direct sensory drive, which may be important for grid cell function. We demonstrate that head direction networks of rats are segregated into at least two populations of neurons firing on alternate theta cycles (theta cycle skipping) with fixed synchronous or anti-synchronous relationships. Pairs of anti-synchronous theta cycle skipping neurons exhibited larger differences in head direction tuning with a minimum difference of 40 degrees of head direction. Septal inactivation preserved the head direction signal but eliminated theta cycle skipping of head direction cells and grid cell spatial periodicity. We propose that internal mechanisms underlying cycle skipping in head direction networks may be critical for downstream spatial computation by grid cells.

Introduction

Oscillations may coordinate neural assemblies to reliably influence and interact with downstream reader-integrators [1]. In the hippocampus and entorhinal cortex, the theta rhythm (4–12 Hz) [2–4] appears to support spatial memory function [5–7] and learning of associations [8]. Reduction in theta rhythm magnitude by pharmacological inactivation of the medial septum correlates with impairment in spatial memory tasks [5, 9, 10]. Theta rhythm may coordinate hippocampal and medial entorhinal networks via theta phase spiking relationships between cell types [11] and subregions [12], and the correlation between spiking phase and animal location, known as theta phase precession, in hippocampal place cells [13, 14] and entorhinal grid cells [15]. Models use this temporal organization to simulate spatial properties of place cells and grid cells [16–19], and to support episodic memory function [20–22].

The mechanisms of grid cell generation are debated, but input from head direction cells appears essential [23–26]. The head direction signal, or ‘internal compass’, is generated subcortically [27], passed to the thalamus [28], and terminates cortically in the dorsal presubiculum (postsubiculum) [29], retrosplenial cortex [30], parasubiculum [31], and medial entorhinal cortex [36]. The latter two structures contain grid cells [31, 32]. Head direction cells are often clustered within deeper layers, and send projections to anatomically defined grid cell patches [33]. However, little is known about the temporal organization of head direction cells.

Spike-time autocorrelations of the majority of neurons in the presubiculum, parasubiculum, and medial entorhinal cortex show temporal periodicity at theta frequency [31]. Some autocorrelations reveal theta cycle skipping [34, 35], in which the first side peak of the autocorrelogram is smaller than the second side peak, indicating that spikes are occurring on alternating theta cycles, a phenomenon more common in ventral than dorsal entorhinal cortex [35] that has been attributed to lower frequencies of intrinsic oscillations of neurons in ventral entorhinal cortex [36], and lower frequency input from prefrontal cortex [37, 38]. Theta cycle skipping has not otherwise been explored in detail.

Here we make the first report that theta cycle skipping is predominantly exhibited by neurons with significant head direction tuning, and demonstrate that cycle skipping facilitates temporal segregation of neurons with overlapping but offset directional preferences. First, we demonstrate that theta cycle skipping neurons tend to have tighter tuning curves than non-theta cycle skipping neurons, and the degree to which a neuron skips cycles is positively correlated with measures of head direction tuning. Theta cycle skipping is associated with strong input near the peak of the head direction tuning curve and center of spatial fields of conjunctive grid-by-head direction cells.

Co-recorded cells revealed that the alternating cycles (odd or even) preferred by a particular cell is not random. Cross-correlation analysis revealed that many cell pairs skipped theta cycles together (labeled as synchronous pairs, identified by high correlations at lags of 0ms and ~250ms, and a low correlation at a lag of ~125ms), while other cell pairs were segregated on alternating theta cycles (labeled as anti-synchronous pairs, identified by low correlations at lags of 0ms and ~250ms, and a high correlation at ~125ms). These cycle relationships were stable throughout each recording session and across days.

Simulations of cells with random head direction and theta cycle preferences demonstrate that without additional network mechanisms, the head direction tuning differences between cells would form equal distributions for both synchronous and anti-synchronous groups. In contrast to this expectation, we observed significantly different distributions and an absence of anti-synchronous pairs with similar head direction preferences. To our knowledge this is the first demonstration that neural content (i.e., the head direction signal) can be segregated by oscillation cycles, supporting the hypothesis that oscillatory cycles can serve as periodic attractors [22, 26] that segregate discrete content [20, 22]. Analysis of a portion of our dataset [39], in which pharmacological inactivation of medial septum disrupts grid cells, reveals elimination of theta cycle skipping in all head direction cells and conjunctive grid-by-head-direction cells. Our results suggest novel network mechanisms that segregate head direction cell assemblies by alternating theta cycles and may be required for grid cell function and the temporal segregation of attractors in the hippocampus [40].

Results

Incidence of theta cycle skipping

Our dataset contained 2313 putative neurons recorded from the dorsal medial entorhinal cortex (Fig. 1a) and parasubiculum in six male rats during 66 recording sessions in an open field arena. Consistent with prior studies, we observed normal theta rhythmicity (Fig. 1b) in addition to theta cycle skipping [34, 35] in many cells, which appears as a larger second peak, p₂ (~250ms), than first peak, p₁ (~125ms) in the spike time autocorrelation (Figs. 1c, 1d, and Supplemental Fig. 1a). To quantify theta cycle skipping, we fit an equation (Eq. S3, Online Methods) to the autocorrelogram [41] and calculated the ratio of the peaks, TS, defined as (p₂ − p₁)/max(p₁, p₂). To minimize false positive detections, we designed strict criteria for identifying theta cycle skipping cells (Online Methods, Single-unit classification) which required a baseline theta power component and good fit between the model parameters and spike time autocorrelation measured by the coefficient of determination (R²). Autocorrelations for 1294 (56%) neurons were well fit by model parameters (R² >0.7), and 806 of these cells (62% of neurons with valid fits) surpassed the threshold for theta rhythmicity. These cells represent the qualifying set of neurons for which the theta cycle skipping metric is valid; and among them, 118 exceeded the threshold for theta cycle skipping (TS > 0.1) of which 13 were removed by visual inspection (due to poor fit to Eq. S3) to give 105 theta cycle skipping neurons.

Figure 1. Theta cycle skipping covaries positively with head direction tuning.

(a) Histology showing tetrode tracks in the medial entorhinal cortex. (b) Typical autocorrelation of spikes from a theta rhythmic neuron recorded in the medial entorhinal cortex. (c) Heat map of autocorrelations of all unique theta skipping neurons, ordered by Theta skipping index (TS). Note that the second peak (−4π and 4π) is larger than the first peak (−2π and 2π) above the threshold TS of 0.1. (d) Autocorrelations and head direction tuning curves for 14 theta cycle skipping neurons. The model fit used to measure theta cycle skipping is drawn in red. (e) Relative strength of head direction tuning, measured by the z-score of neuron’s mean resultant calculated from the population of all neurons versus TS. As head direction selectivity increases, theta skipping is more prominent in the autocorrelation (n = 43 cells, TS: slope=2.5×10^−2; R=0.47; p<0.01, linear regression, t-statistic). (f) Cumulative distribution function of entire neuron population (long dash) and theta-skipping population (short dash) plotted against mean resultant. Note that theta cycle skipping cells comprised neurons with high mean resultants, indicating head direction specificity of firing. (g) ROC curve analysis for differentiating theta cycle skipping neurons from non-theta cycle skipping neurons using the mean resultant measure of head direction strength (HD). By comparison, it is clear that gridness (G) and firing rate (F) are not as effective at discriminating theta-skipping neurons (HD: AUC=.802; G: AUC=.638; F: AUC=.391), though both are associated with slightly positive and negative predictors, respectively.

Theta cycle skipping in the head direction network

Of the 105 theta cycle skipping neurons in our dataset, 82 (78%) were head direction cells with mean resultant lengths greater than 0.2 (Online Methods, Gridness and Directionality) [42]. To estimate the percentage of head direction cells that exhibit theta cycle skipping we used two methods that avoid the potential bias of including the same neuron over multiple recording sessions. First, within recording sessions, on average 17% of head direction cells displayed theta cycle skipping. Second, a conservative approach ensured that all head direction neurons were unique cells. (Online Methods section, Single-unit classification, Supplemental Fig. 4). Of 435 head direction cells in the full dataset, 157 were determined to be unique. Of the 278 head direction cells not included in the analysis, 62 exhibited theta cycle skipping (22.3%). The analyses of head direction cells reported here were restricted to the 43 head direction cells that exhibited theta cycle skipping out of the 157 (27.4%) unique head direction cells.

The theta skipping metric (Fig. 1c) reveals a significant positive correlation between degree of theta cycle skipping and strength of head direction tuning, measured by the mean resultant, R_m (P < 0.01, linear regression, t-statistic; n=43 cells, degrees of freedom=41, R=0.465) (Fig. 1e). The cumulative distribution functions (CDF) of R_m of theta skipping neurons was shifted to the right more than in the entire population of recorded cells (Fig. 1f). A receiver operating characteristic (ROC) analysis confirmed the observation that head direction tuning (R_m) was a good predictor of theta skipping (HD: AUC=.802) (Fig. 1g). By comparison, gridness (G) and firing rate (F) were not as effective at discriminating cycle skipping neurons (G: AUC=.638; F: AUC=.391). Gridness may have some predictive qualities, because it is confounded with head direction in the case of conjunctive grid-by-head-direction cells, whereas firing rate has some negatively predictive properties likely due to the large number of fast spiking interneurons which are not theta cycle skipping cells.

Theta cycle skipping occurs during increased drive

For many theta cycle skipping neurons a minority of spikes fire in a theta rhythmic manner (i.e. some theta cycles are not skipped), as detected by presence of a smaller peak at ~125ms in the autocorrelation, and in spiking rasters of theta cycle skipping neurons (Fig. 2a, 2^nd and 3^rd cycle in the bottom raster). When does a theta cycle skipping neuron fail to skip a cycle, and when is theta cycle skipping most pronounced? To answer this, we evaluated the contingencies of theta cycle skipping on a number of behavioral and neural states.

Figure 2. Characteristics of theta cycle skipping.

(a) Spike rasters of theta-skipping neurons with raw LFP signal (red) and filtered (6–10Hz) LFP signal (black) shows spiking on alternating cycles (marked by gray and white backgrounds). (b) Average autocorrelation of spike trains for all neurons in three conditions: the original spike train, spikes during the preferred theta phase, and the spikes during the non-preferred theta phase (inset: example distribution of theta spiking phase). (c) Amount of theta skipping evident in autocorrelations of spiking during all phases, preferred phases, and non-preferred phases of theta. (all spikes: n=36 cells, 0.26±.02 s.e.m. TS; spikes at preferred phases: n=31 cells, 0.21±0.03 TS; spikes at non-preferred phases: n=15 cells, −0.08±0.05 TS, P < 0.001, Wilcoxon paired signed rank test) (d) Average running speed at the time of spike generation in the three groups. Theta cycle skipping occurs during elevated running speeds. (all spikes: n=40 cells, 49.0±1.4 cm/sec; preferred theta phase: n=40 cells, 50.0±1.4 cm/sec; non-preferred theta phase: n=40 cells, 42.2±1.9 cm/sec, P < 0.001, Wilcoxon paired signed rank test). (e) Increased cycle skipping during periods marked by bursting. (all spikes: n=40, 0.37±0.02; preferred theta phase: n=40, 0.38±0.02; non-preferred theta phase: n=40, 0.21±0.02, P < 0.001, Wilcoxon paired signed rank test,) (f) Average cross correlations between the theta events of varying spike counts. Theta event trains were determined by the number of spikes in a theta cycle (n = 1–6). Theta events with only 1 spike do not occur during theta cycle skipping, whereas theta events with more spikes (theta bursts) show increasing theta cycle skipping. (g) Heatmap of angular distance between average theta phase of theta events with different spike counts. This result explains why, in Fig. 2b, segregating spikes by theta phase results in differential theta cycle skipping. (h) Running speed positively correlates with the number of spikes per theta event. (i) The distance from preferred head direction (HD) negatively correlates with the number of spikes per theta event. (j) The distance from grid field center negatively correlates with the number of spikes per theta event.

First, we examined how theta cycle skipping covaries with the network theta rhythm, finding cycle skipping most prevalent for spikes at a neuron’s preferred theta phase. We separated spikes during preferred phases of theta (within +/−90 degrees of the peak) from spikes during non-preferred phases, during epochs of time where theta power was significant (Online Methods, Theta phase of spiking). The autocorrelation of spikes during the preferred half of the theta cycle exhibited robust theta cycle skipping, whereas spiking during the non-preferred half was theta rhythmic (P < 0.001, Wilcoxon paired signed rank test; all spikes: n=36 cells, 0.26±.02 TS; spikes at preferred phases: n=31 cells, 0.21±0.03 TS; spikes at non-preferred phases: n=15 cells, −0.08±0.05 TS) (Figs. 2b, 2c). Running speeds during periods of spiking within the preferred range of theta phases were significantly elevated relative to running speeds when spiking occurred during non-preferred theta phases (all: n=40 cells, 49.0±1.4 cm/sec; preferred theta phase: n=40 cells, 50.0±1.4 cm/sec; non-preferred theta phase: n=40 cells, 42.2±1.9 cm/sec) (Fig. 2d) (P < 0.001, Wilcoxon paired signed rank test). The incidence of fast interspike intervals (ISIs< 15 ms), i.e. bursting, was elevated during epochs of spiking at preferred theta phase (P < 0.001, Wilcoxon paired signed rank test, all: n=40, 0.37±0.02; preferred theta phase: n=40, 0.38±0.02; non-preferred theta phase: n=40, 0.21±0.02) (Fig. 2e), indicating that cycle skipping may occur more during bursting modes when the animal is moving at faster speeds.

We tested how theta cycle skipping covaried with firing rate. We hypothesized that an increase in firing rate would correspond to an increase in theta cycle skipping, because short, bursting ISIs were less prevalent among the theta rhythmic spikes, and theta cycle skipping was strongest during spiking within the preferred range of theta phases where most spikes occurred. We summed the number of spikes within a sliding window of width 60ms (10ms step-size) to characterize spiking/bursting activity at theta timescales. From peaks in the resulting local spike rate function (local = 60ms), we generated separate ‘event trains’ for spikes/bursts of 1 to 6 spikes. These event trains consisted of ones when bursts of n spikes occurred and zeros at all other time steps, allowing spike/burst events with different spike counts to be separately compared to coincident neural and behavioral activity. We then looked for differences in theta cycle skipping activity (Fig. 2f), theta phase (Fig. 2g), and behavioral/spatial variables such as running speed, head direction, and position in the enclosure (Figs. 2h–j), each as a function of the strength of theta bursts. As firing increased, so did intensity of theta cycle skipping. The average cross correlations of event trains for 1 to 6 spike bursts with the full spike train (bursts with more than 6 spikes were too rare to include) show that single spike events (1 spike ‘bursts’) occurred during epochs of theta rhythmic firing, and stronger burst events (with 2–6 spikes) corresponded to epochs of theta cycle skipping (Fig. 2f).

Next, we examined the absolute angular distance between the mean phase of bursts with different spike counts (Fig. 2g). This analysis captures the similarity between any two event trains in terms of spiking phase with respect to the network theta cycle. The angular distance was smallest between bursts with similar spike counts and greatest between bursts with large differences in spike count (Fig. 2g). This result is consistent with the preferred/non-preferred theta phase analysis, as it indicates that those spikes which occurred during theta cycle skipping (higher spike count bursts) were segregated in network theta phase from those that do not. Differences in spike counts within theta bursts corresponded to differences in running speed, head direction, and location within the environment (Figs. 2h–j).

We found stronger theta bursting and cycle skipping at the preferred head direction and centers of grid fields. During periods of high spiking and high theta cycle skipping, running speeds were elevated (Fig. 2h), directional headings were close to the preferred tuning direction (Fig. 2i), and positions in the enclosure were near the centers of grid fields (in conjunctive grid cells, Fig 2j). In agreement with the observation that running speeds were elevated during periods of spiking at the preferred theta phase (Fig. 2d), the theta rate function analysis provided evidence that strong theta bursts tended to occur when the animal was running faster (Fig. 2h). However, there was no difference in running speed across theta bursts of 1 to 4 spikes (Fig. 2h), whereas theta cycle skipping was greatly strengthened across this range (Fig. 2f), reflecting that running speed alone is not an effective predictor of theta cycle skipping. Low spike count theta bursts, which are associated with theta rhythmicity, occur further away from the preferred head direction, whereas high spike count theta bursts occur closer to the preferred direction (Fig. 2i). This emphasizes that cycle skipping is strongest at the preferred head direction.

A subset (n = 10) of theta cycle skipping cells were conjunctive grid-by-head direction cells [32]. Therefore, we compared the distribution of theta bursts of different strengths relative to the centers of grid fields (Fig. 2j). As expected, similar to the tuning of head direction, theta bursts with low spike counts occurred farther away from grid field centers than stronger bursts, suggesting that theta cycle skipping increases near the center of grid fields.

These data demonstrate that theta cycle skipping occurs most robustly during elevated spiking activity driven by an animal’s behavior and location. An animal’s elevated running speed, heading at the preferred direction for a given head direction cell, and proximity to grid cell firing fields are each associated with stronger theta-locked bursting and theta cycle skipping. These associations eliminate the possibility that theta cycle skipping is a byproduct of lowered synaptic drive, but rather indicate that theta cycle skipping is related to increased drive to these neurons.

Temporal segregation of head direction cell assemblies

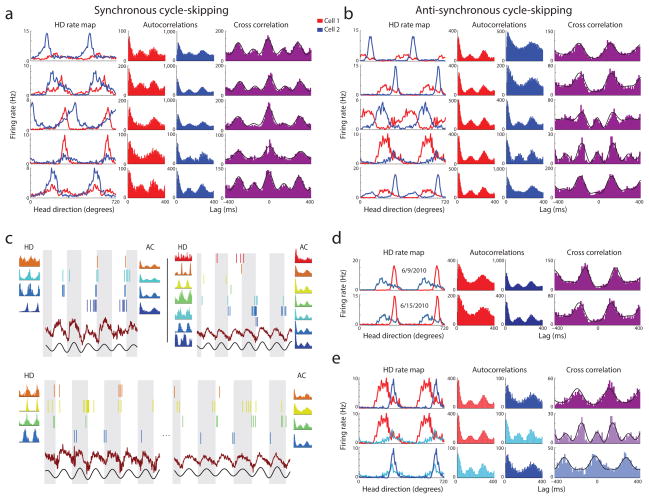
To test whether theta cycle skipping the result of cellular or network-level mechanisms we examined whether theta cycle skipping is coordinated between simultaneously recorded neurons. We calculated cross correlations between theta cycle skipping neurons with a considerable amount (N_{|latency|≤0.6 sec} > 500) of coincident spiking and analyzed whether theta cycle relationships between cells were fixed or varied over time. More than one-third of the cross-correlations between theta cycle skipping cells were clearly synchronous (Figs. 3a and Supplemental Fig. 2a) or anti-synchronous (Fig. 3b and Supplemental Fig. 2b) (34.5% of pairs had TS_xcorr>0.2, of which 59% were synchronous and 41% were anti-synchronous), revealing that these between-neuron cycle relationships were fixed. Spiking rasters of simultaneously recorded theta cycle skipping head direction cells show fixed synchronous or anti-synchronous theta cycle relationships (Fig. 3c).

Figure 3. Segregation of assemblies on alternating theta cycles.

Co-recorded theta skipping cells maintain synchronous or anti-synchronous theta cycles. (a–b) Pairs of theta skipping cells (red and blue) are shown with head direction tuning, autocorrelation (histograms), and the cross correlation (purple histogram). (a) Four examples of neuron pairs which skip theta cycles synchronously, spiking on the same alternating cycles of the theta oscillation. (b) Four examples of neuron pairs which skip theta cycles anti-synchronously, reliably spiking on opposite sets of theta cycles. (c) Spike rasters, LFP (red), theta filtered LFP (black), autocorrelations and head direction tuning curves for simultaneously recorded theta skipping neurons. Colors are reused for each panel and do not correspond to same cells in (a) and (b). In the panels on the bottom, the orange, yellow, and green cells all show a synchronous cycle relationship while the blue cell exhibits an anti-synchronous cycle relationship with all three cells. (d) Example of a theta cycle skipping pair that maintained its anti-synchronous cycle relationship across six days (6/9/2010 – 6/15/2010). (e) Three cycle skipping head direction cells recorded simultaneously on the same tetrode demonstrate both synchronous (bottom example) and anti-synchronous (top and middle example) pair combinations occur within a restricted anatomical location.

Between-neuron cycle relationships of theta cycle skipping neurons (synchronous or anti-synchronous) could not be attributed to time lags between preferred head direction fields (Supplemental fig. 5) and cycle relationships remained stable for hundreds of passes through directional fields during twenty minute recordings and in one example, remained fixed over six days (Fig. 3d). Synchronous and anti-synchronous combinations co-occur at the same recording locations, suggesting that membership to a particular set of theta cycles is not region-specific (Fig. 3e).

Directional segregation of head direction cell assemblies

Is there a difference between the directional tuning curves of cell pairs that are synchronous (assembly partners) and anti-synchronous (not assembly partners)? Strikingly, the cells of anti-synchronous pairs rarely shared similar head direction tuning preferences, whereas the head direction tuning of synchronous pairs were often very similar (Fig. 4a). Only three out of 41 anti-synchronous pairs had a tuning angle difference less than 60 degrees, and none were less than 40 degrees (Fig. 4a). Between-neuron pairs with synchronous cross correlations had significantly smaller angular distance between their preferred head direction angles (synchronous: n=58, median±m.a.d., 35.5±42.4 degrees; anti-synchronous: n=41, 103.9±27.8 degrees, P<0.001 unpaired Wilcoxon rank sum test) (Fig. 4a). These results capture an intriguing temporal organization in the head direction network: When an animal faces a direction within the shared region of overlapping tuning curves of anti-synchronous head direction cell populations, both assemblies are co-active when considered on longer timescales, but their spiking is separated at shorter timescales on alternating theta cycles (Fig. 3).

Figure 4. Characteristics of synchronous and anti-synchronous theta cycle skipping pairs.

(a) Left: Analysis of data showing the difference in preferred head direction between neurons in synchronous and anti-synchronous pairs. Synchronous pairs have a significantly smaller head direction tuning offset than do anti-synchronous pairs (synchronous: n=58, 35.5±42.4 degrees; anti-synchronous: n=41, 103.9±27.8 degrees, P<0.001 unpaired Wilcoxon rank sum test). Note that the difference is largely driven by the limited number of pairs with differences of less than 60 degrees in the anti-synchronous group. Right: Results of statistical model demonstrating that the difference of preferred directions of synchronous and anti-synchronous cell pairs are expected to have similar distributions. (b) Schematic of statistical model used to demonstrate that the expected directional tuning offsets for synchronous and anti-synchronous cell pairs are equal and evenly distributed if cycle selection is random. The model produces anti-synchronous (top right) and synchronous (bottom right) firing patterns for all neuron pairs such that the degree of directional overlap has no bearing on whether pairs are synchronous or anti-synchronous. This contrasts with our finding that anti-synchronous cycle relationships were rarely seen in neurons with similar directional preferences. (c–d) Two experimentally recorded cell pairs with overlapping tuning curves (red and blue polar plot, normalized by peak firing rate) display synchronous (c) or anti-synchronous (d) theta cycle firing during periods of coactivity, evident in the cross correlation (black histogram) and spike rasters.

We developed a statistical model to estimate the dependence of theta cycle synchronicity on the similarity of preferred head direction angles (Figs. 4a, 4b, Online Supplemental Material (OSM), Computational modeling information). In contrast to the data (Figs. 4a, 4c, 4d), the statistical model generated a broad distribution of head direction preference angle differences that was the same for synchronous and anti-synchronous pairs (Figs. 4a, 4b). These results illustrate the independence of theta cycle timing from the timing governed by head direction tuning (i.e. cells highly coactive during matching head direction are not required to be coactive during theta cycles and vice versa, although this is observed in the data.). These results demonstrate that at least two simultaneously active assemblies of head direction cells (or information streams) that are separated in time by the theta cycle. The fixed synchronous or anti-synchronous relationships between neuron pairs argues against underlying intrinsic cellular mechanisms in favor of the network-level temporal organization of the cortical head direction signal.

Theta cycle skipping is sensitive to septal inactivation

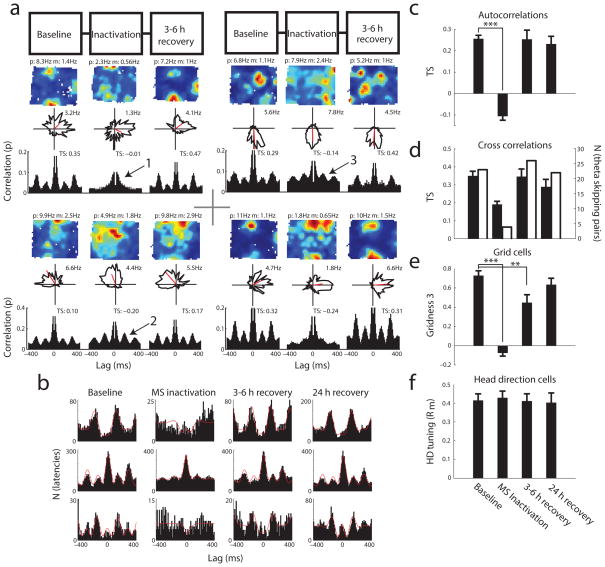
What downstream information is provided by head direction cell assemblies that are offset by at least 40 degrees of head direction and are segregated in time by alternating theta cycles? Versions of oscillatory interference and attractor network models of grid cells use theta rhythmic head direction cells as input to generate grid cells with both a rate code and phase code for position. In a prior publication, we demonstrated that grid cell spatial periodicity is eliminated by pharmacological inactivation of the medial septum [39] that reduced the power of theta oscillations and reduced the total number of theta rhythmic cells in the medial entorhinal cortex. We re-examined the subset of data for which inactivation was performed, noting that all cycle skipping in head direction cells and conjunctive grid-by-head-direction cells was eliminated (pre: n=20, 0.26±0.02 TS; infusion: n=20, −0.11±.02 TS; 3hr: n=19, 0.25±0.04 TS; 24hr: n=19, 0.23±.04 TS; P < 0.001, Wilcoxon paired signed rank test) (Figs. 5a–c). In some cases cells lost all theta rhythmicity (for example Fig. 5a, arrow 1), but in others theta rhythmicity remained intact (for example Fig. 5a, arrows 2 and 3), yet theta cycle skipping dynamics were lost. The number of theta skipping cross correlations was greatly reduced during the infusion (number of TS_xcorr > 0.2, pre: 23; infusion: 4; 3hr: 26; 24hr: 22) (Fig. 5b, 5d, white bars), and TS_xcorr dropped in theta skipping cross correlations that retained rhythmicity during the infusion (pre: n=23, 0.35±0.03; infusion: n=4, 0.19±0.02 TS_xcorr; 3hr: n=19, 0.35±.04 TS_xcorr; 24hr: n=22, .29±.04 TS_xcorr, P=0.06, Wilcoxon paired signed rank test). The gridness signal was also lost in theta skipping (and non-theta skipping) neurons during the infusion (pre: n=32, 0.73±0.05 G₃; infusion: n=32, −0.07±0.03 G₃; 3hr: n=29, 0.44±0.08 G₃; 24hr: n=23, 0.63±0.07; P < 0.001, Wilcoxon paired signed rank test) (Fig. 5e), while head direction tuning was unaffected during the infusion (pre: n=36, 0.41±0.04 R_m; infusion: n=35, 0.43±0.04 R_m; 3hr: n=29, 0.41±0.04 R_m; 24hr: n=21, 0.40±0.05 R_m, P >0.05, Wilcoxon paired signed rank test) (Fig. 5f). These data suggest the cycle skipping head direction code could be useful within various theories of the generation of spatial periodicity of grid cells. It remains to be determined why theta cycle skipping, which predominantly appears to be a feature of the head direction system, is sensitive to septal inactivation, whereas head direction tuning is not. Septal inactivation may disrupt lateral inhibition between theta cycle skipping head direction cells, as a large percentage of septal projections innervate MEC interneurons (personal communication, Menno Witter). This inhibition may normally contribute as a network mechanism for theta cycle skipping and the generation of separate anti-synchronous populations of theta cycle skipping cells.

Figure 5. Possible downstream functional implications of theta skipping head direction cells.

Medial septum inactivation eliminated theta cycle skipping and grid cell spatial periodicity in conjunctive grid-by-head-direction cells. (a) Four examples of cells which lose their theta skipping and spatial periodicity. Two examples shown remain theta rhythmic during the inactivation (arrows 2 and 3). (b) Cross correlations of synchronous or anti-synchronous pairs before, during, and after pharmacological inactivation of the medial septum. Notice that while these cells remain highly active within 400ms of each other, there is nearly complete absence of the theta cycle relationship during the inactivation. Theta cycle relationships recover 3–6 hours and 24 hours after the muscimol infusion. (c–f) Inactivation of the medial septum by infusions of muscimol simultaneously cause a reduction of theta cycle skipping in the autocorrelations (c) (pre: n=20, 0.26±0.02 s.e.m. TS; infusion: n=20, −0.11±.02 TS; 3hr: n=19, 0.25±0.04 TS; 24hr: n=19, 0.23±.04 TS; P < 0.001, Wilcoxon paired signed rank test), the number of theta cycle skipping cross correlations (d) (number of TS_xcorr > 0.2, pre: 23; infusion: 4; 3hr: 26; 24hr: 22), a reduction of grid cell spatial periodicity (e) (pre: n=32, 0.73±0.05 G₃; infusion: n=32, −0.07±0.03 G₃; 3hr: n=29, 0.44±0.08 G₃; 24hr: n=23, 0.63±0.07; P < 0.001, Wilcoxon paired signed rank test), and maintenance of the head direction cell signal (f) (pre: n=36, 0.41±0.04 R_m; infusion: n=35, 0.43±0.04 R_m; 3hr: n=29, 0.41±0.04 R_m; 24hr: n=21, 0.40±0.05 R_m, P >0.05, Wilcoxon paired signed rank test).

To further support the network mechanism hypothesis we performed in vitro whole-cell patch clamp recordings from synaptically-isolated pyramidal neurons in layer V of MEC, and demonstrate that, in contrast to in vivo conditions (Fig. 2), increased drive to an isolated neuron should reduce theta cycle skipping (Figs. 6a–c). These data motivated us to build a simple network spiking model that uses lateral feedback inhibition between a population of stellate cells or regular spiking cells and a population of inhibitory interneurons to show that increased drive to this network results in increased theta cycle skipping (Figs. 7a–c, OSM, Computational modeling information). Interactions between rhythmic signals may contribute to the spatial code, because grid cell spatial periodicity and theta cycle skipping are both eliminated by septal inactivation (while theta rhythmicity and head direction signals can persist). Theta cycle skipping may provide a significant window into the mechanisms of grid cell function and the orchestration of functional ensembles in behaving animals.

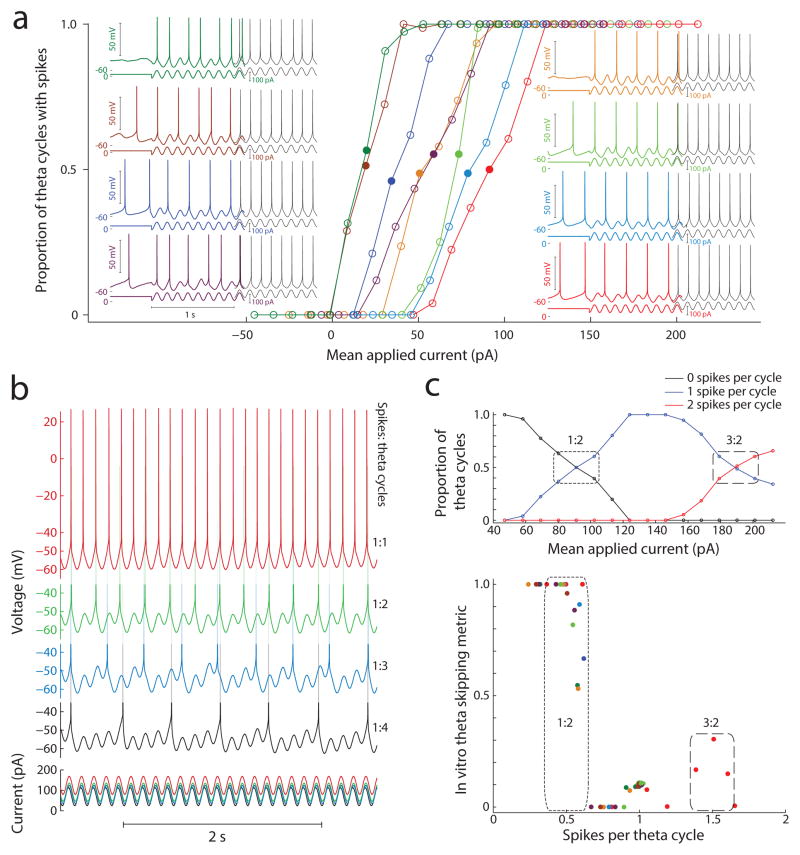
Figure 6. In vitro theta cycle skipping is reduced with stronger input.

(a) An 8 Hz sinusoidal current injection was combined with variable levels of DC current to show that the proportion of cycles with spiking increases linearly with increased DC current up to 1:1 locking to the stimulus, i.e. 1 spike per theta cycle. Insets: Spiking of eight layer V mEC neurons in response to the sinusoid stimulus (depicted below voltage traces) at DC levels driving spiking on ~ 50% of theta cycles (filled circles and color voltage traces) and 1:1 locking (black voltage traces). (b) Example of one neuron’s spiking at different DC current levels. Stable ratios of spikes (top) to theta cycles ratiometrically encode the DC component of the sinusoid stimulus (bottom). (c) Further increasing DC current drives spiking above 1:1 locking, and a second ratiometric regime appears for DC levels where the ratio of spikes per theta cycle is >1:1 (top). Theta cycle skipping in vitro is strongest for lower input levels (bottom) that drive single spikes on alternating theta cycles (0.5 spikes per theta cycle). Weaker theta cycle skipping is also evident for DC input levels that drive 3 spikes per 2 theta cycles (doublets alternating with single spikes). As expected, increased input to an isolated MEC neuron in vitro decreases the occurrence of theta cycle skipping and serve to highlight the counter intuitive finding that increased input to MEC neurons in vivo increases the probability and strength of cycle skipping. These data suggest that network mechanisms may underlie the phenomenon of theta cycle skipping.

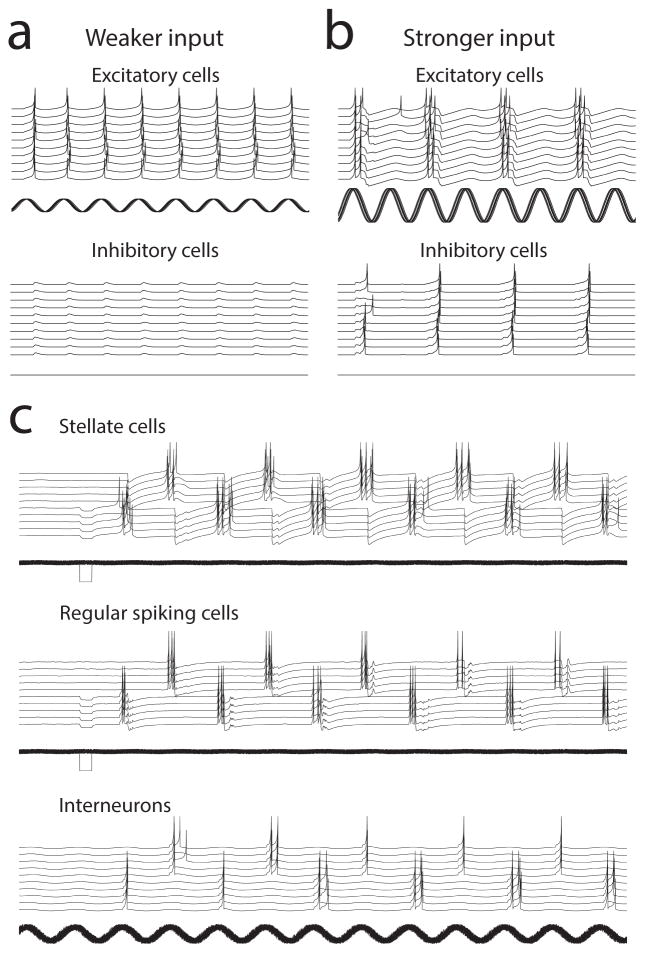
Figure 7. Stronger input can induce theta cycle skipping.

(a) With weaker theta rhythmic input, excitatory cells spike on each cycle, but there is less driving force on inhibitory cells. (b) With stronger input, the theta rhythmic input drives multiple spikes on a single theta cycle, as in the experimental data. The activation of multiple spikes causes activation of coupled inhibitory interneurons. The influence of inhibitory interneurons on slow GABA-B conductances can prevent generation of spikes on the next theta cycle, resulting in cycle skipping, in which bursts of spikes appear on alternating theta cycles. (c) A simple network with feedback inhibition and excitatory synapses between stellate cells and regular spiking cells can show anti-synchronous theta cycle skipping. A hyperpolarizing step function causes rebound spiking of 5 stellate cells. Excitatory connections between stellate and pyramidal cells cause bursts of spikes. The excitatory input activates spiking in the inhibitory neurons that hyperpolarizes the other population of stellate cells, causing rebound spiking. The interaction of feedback inhibition with properties of stellate cells causes emergence of stable anti-synchronous theta cycle skipping in simulations.

Discussion

The function of theta oscillations in the neural coding of memory is debated [4, 43, 44]. Beyond the data on phase precession in place cells [13] and grid cells [15], there has been limited evidence to indicate that theta oscillations coordinate neural representations. Here, we demonstrate that theta oscillations facilitate the segregation of information by showing that head direction cells are segregated in time by alternating theta cycles according to their directional preference.

Theta cycle skipping has been reported [38–39], but the link to the head direction system has not been emphasized previously. Theta cycle skipping was first described in the medial entorhinal cortex [34] and was more recently quantified [35]. However, these studies did not report the head direction specificity of these cells. Theta cycle skipping is readily visible in a paper that quantified theta modulation of head direction cells in the presubiculum, parasubiculum, and medial entorhinal cortex [31]. It remains unknown whether head direction cells in the retrosplenial cortex also exhibit theta cycle skipping. Interestingly, theta cycle skipping is also visible in a class of medial septal neurons that are only theta rhythmic when the animals runs in a particular direction [45]. In our data, inactivation of medial septum eliminated all theta cycle skipping in head direction cells despite leaving many cells with normal theta rhythmicity. These data suggest the medial septum may play a role in the theta cycle skipping code in cortical head direction cells.

Segregation of cell assemblies by theta cycles

We provide evidence of assembly segregation on different theta cycles by demonstrating that pairs of theta cycle skipping neurons, sensitive to head direction, have a fixed synchronous or anti-synchronous cycle relationship throughout the duration of a recording session. This temporal organization is maintained through hundreds of trials involving the rat passing its head through the cell pair’s preferred head directions (Figs. 3, 4c, 4d), and is even maintained in recordings separated by six days (Fig. 3d).

Anti-synchronous theta skipping pairs rarely contain preferred head directions within 60 degrees, whereas many synchronous pairs had preferred directions within this range (Fig. 4a). Could this reflect a mechanism that promotes the 60-degree offsets in grid cell firing field orientation? Oscillatory interference models predict a specific organization of head direction input at 60 or 120 degree intervals. This prediction has lacked experimental support as several studies have reported an even distribution of preferred direction in populations of head direction cells [29, 32], however these studies did not account for theta cycle skipping relationships between neurons. We have re-approached this topic taking advantage of theta cycle skipping rhythms to reveal orchestration of assemblies, rather than focusing on the distribution of preferred head direction across individual neurons, and we provide evidence of selective functional coupling between subpopulations of head direction cells with characteristic tuning separations. We demonstrate that some head direction cell populations are segregated by a theta cycle and by about 60 degrees or more of head direction. These results suggest a complex organization that may be consistent with models of grid cells that require organized head direction cell inputs. Future modeling can capitalize on this temporal and directional organization of the head direction network to simulate the 60-degree angles between the dominant orientations of grid cell firing fields. Separation on different cycles may facilitate distinct shifts in the dimensions separated by 60 degrees (Supplemental Fig. 6), and the combination of two wider peaks from anti-synchronous theta cycle skipping cells may allow maintenance of attractor dynamics during the inactive troughs of the theta rhythm [46].

Do synchronous populations of cycle skipping head direction cells form anatomically distinct modules? This is difficult to answer, as the probability of recording multiple head direction cells that display cycle skipping with overlapping directional preferences at the same recording location is low. However, in one case, three such neurons were isolated on a single tetrode making both synchronous and anti-synchronous pairs (Fig. 3e). These data suggest that segregated head direction cell assemblies are not anatomically distinct in a strict sense, but the possibility exists that these recordings were obtained on the border between modules.

To understand the functionality of the theta cycle skipping head direction network we focused in part on a dataset [39] in which medial septum inactivation disrupted the grid cell spatial periodicity but left head direction tuning intact. Many head direction cells and conjunctive grid-by-head-direction cells from this dataset displayed significant theta cycle skipping prior to septal inactivation (Figs. 5a, 5c). Muscimol infusion into the medial septum (1) dissociates theta cycle skipping from head direction tuning (Figs. 5a, 5c, 5d, 5f) suggesting that the head direction signal itself does not require theta cycle skipping, and (2) simultaneously disrupts the spatial signal in grid cells (Figs. 5a, 5e). These results suggest that the temporal precision of the head direction cell inputs may be important for grid cell function, though the disappearance of the two phenomena may be independent of each other. The data also point to the medial septum as a driving force of the theta cycle skipping phenomenon.

A temporal frame for downstream hippocampal content

The entorhinal cortex provides the majority of cortical information projecting to the hippocampus. What benefit could theta skipping head direction cells and conjunctive-grid-by-head-direction cells offer the hippocampus? Buzsaki and colleagues [40] report evidence that CA1 place cell assemblies are organized into 25ms windows that appear to skip theta cycles. In figure 1 of their paper these 25ms windows are clearly skipping theta cycles. These assemblies of neurons in region CA1 may be influenced by assemblies of cells in layer III of MEC. A recent study on the time course of hippocampal content noted that instantaneous transitions between spatial contexts caused spatial representations in the hippocampus to ‘flicker’, or alternate, between theta cycles [47]. In combination these data support a view that the theta cycle is a unit of hippocampal content, however the data presented here do not preclude additional mechanisms to support hippocampus content at faster time scales such as gamma cycles nested within the theta cycle [48–50].

ONLINE METHODS

Subjects and surgery

Six male Long-Evans rats (500–650g, 3–6 months old) were implanted with hyper drives aimed at the medial entorhinal cortex. Animals were housed individually in Plexiglas cages, maintained on a 24/hour light/dark cycle (testing occurred during the light cycle) and at ~85% of their ad libitum weight. Prior to surgery, animals were habituated to experimenter interaction and were trained to forage in an open field environment (100 by 115 cm or 112 by 158 cm). A white cue card on one wall provided stable landmark information. Animals were administered Atropine (0.04 ml/kg) twenty minutes prior to initiation of Isoflurane-induced anesthesia. Anesthesia was maintained with Isoflurane and a Ketamine cocktail (Ketamine 12.92mg/ml, Acepromazine 0.1mg/ml, Xylazine 1.31mg/ml). Skin and periosteum were cleared from the skull and screws were inserted along the periphery of the dorsal surface of the skull. One screw, positioned above the cerebellum, was used as a recording ground. A hyper drive was aimed at the dorsomedial entorhinal cortex (~25 degrees in the posterior direction) that housed 12–16m oveable recording tetrodes and up to four reference tetrodes (four 12.7-micron nichrome wires twisted together). Acraniotomy was performed into the left bone ridge, just anterior to the fissure between the parietal and postparietal skull bone (approximately AP −8.0mm, ML −4.6mm from bregma). Dura was removed and the hyper drive was lowered onto the cortical surface and secured in place with Kwik-Sil and dental acrylic. Tetrodes were lowered 2–3mm and were not moved during a seven day recovery period. In five of six animals, one or two guide cannulas for the microinfusions were implanted at an angle to avoid the recording drive while targeting the medial septum (AP +0.5mm, ML +/−3.0mm, angled 25 degrees medially and lowered 6mm from the dorsal surface). All surgical procedures followed National Institute of Health guidelines and the protocol approved by the Boston University Institutional Animal Care and Use Committee.

In vivo neural recordings

Animals were recorded from daily in the open field to search for conjunctive grid-by-head-direction cells [1, 2]and head direction cells [1–4]. Once theta oscillations and theta rhythmic neurons were prevalent, tetrodes were turned a maximum of ~32 microns per day, and experiments never took place on days in which any tetrode was moved. Data collected during inactivation of the medial septum were presented previously [5], but the current data set includes a much larger number of isolated cells from non-inactivation recordings (N=2313). Neural signals were preamplified by unity-gain operational amplifiers on the head stage (Neuralynx, Tucson, AZ) and were then amplified (5,000–20,000X) and band-pass filtered (0.3–6kHz; Neuralynx). When a signal crossed threshold all four channels of the tetrode were digitized at 32kHz and recorded. Local field potentials obtained from the MEC were referenced to the animal ground or to a cortical tetrode. Aceiling-mounted video camera (30 Hz sampling rate) tracked the position of two LEDs, one red and one green, mounted on the recording head stage. Position of the animals was defined as the centroid of the two LEDs, and head direction was defined as the angle formed between the LEDs and a reference defined by camera orientation. Up to five lost samples due to occlusion of tracking LEDs, or reflections in the environment were replaced by a linear interpolation for both position and directional data. Running velocity was calculated from the derivative of the Kalman-filtered position. Methods for cluster cutting and histological analysis were described previously [5]. While it was difficult to reconstruct the exact the location of each recording, as many tetrodes passed through layer I and out of the cortex, we note that all tetrodes passed through the medial entorhinal cortex or parasubiculum. Previous work on the location of head direction cells in these structures suggests that the cells analyzed here were recorded in layers III and V[1, 2, 4].

Septal inactivation

Muscimol, a GABA_A agonist, was diluted in phosphate-buffered saline. Prior to an infusion, the dummy cannula was removed and replaced with a primed injector cannula (33-gauge), that extended 1 mm past the guide cannula into the medial septum.. A microinfusion pump (Harvard Apparatus, Inc) infused 0.50 microliters of diluted muscimol at 0.125ul/minute. The injector cannula remained connected for two minutes after the infusion to allow for the drug to perfuse through the neural tissue. The experimenter was not blind to whether an infusion of muscimol had occurred. Theta oscillations, gridness, and theta cycle skipping were reduced by all of the septal muscimol infusions. Twenty minute pre-infusion baseline recordings were conducted prior to each infusion. Post-infusion recordings lasting up to 60 minutes were started fifteen minutes after the completion of the infusion. Recovery recordings were conducted three to six hours after the infusion to test whether theta oscillations and grid cells had returned and 24 hour post-infusion recordings were also attempted when neurons were held across days. Waveform profiles across the four electrodes were compared across recordings sessions to confirm stability of each neuron across recording sessions.

In vivo data analysis methods

Single-unit classification

We categorized some neurons as theta cycle skipping, head direction, or conjunctive grid-by-head direction cells. Only neurons with more than 100 spikes in a given session were included in the study. Theta cycle skipping neurons were those cells with a satisfactory fit to model equation (Eq. 3), and where TS > 0.1 (TS described in Theta cycle skipping index). A satisfactory fit was described as those where the correlation coefficient, r², was greater than 0.7. The autocorrelation theta power, defined as the time-averaged square amplitude of the oscillatory, first term of the equation divided by the time-averaged squared amplitude of the autocorrelation signal itself, was required to be greater than 0.01 to ensure an oscillatory component. Head direction cells, were defined as those neurons with a R_m>0.2 (R_m described in Directionality) [6]. Neurons with a grid score greater than zero were considered grid cells and those grid cells that were also classified as head direction cells are labeled conjunctive grid-by-head-direction cells [5].

We took a conservative approach to ensure that all reported head direction cells were unique across sessions and days (Supplemental Fig. 4). Specifically, we ensured that no two head direction cells recorded from the same tetrode had similar angles of preferred head direction. To accomplish this, we clustered (“linkage” in MATLAB R2010b) head direction cells on any given tetrode by the angular distance between their preferred directional heading. A dendrogram represents the output of the clustering algorithm for one tetrode in one animal, over many recording sessions (Supplemental Fig. 4). Clusters were cut at 30 degrees angular distance. Clusters labeled C1–C6 show head direction neurons that were flagged as potential repeat cells (Supplemental Fig. 4). From each cluster one neuron was automatically selected by maximizing Watson’s U² test statistic, which rewards high numbers of spikes and clear head direction tuning (shown in top left of each box)(Supplemental Fig. 4). The other units in the cluster were not used to take the strictest approach to ensure that no cell was included twice. Of 435 head direction cells, 157 unique cells were identified, and 278 cells representing their repeated recordings were not included in the analysis. Of the 278 cells not included in the analysis, 62 were theta cycle skipping neurons.

Gridness and directionality

Firing rate maps were constructed by calculating the occupancy normalized spike count for 3cm × 3cm bins of position data. Data were smoothed by a two-dimensional convolution with a pseudo-Gaussian kernel with a standard deviation of one pixel (3 cm). We measured the “gridness” of neurons using an analysis that accounts for elliptical distortions in assumed hexagonal firing pattern of grid cells [5]. Occupancy normalized polar plots of firing rate by head direction were generated using 6 degree directional bins. To quantify the degree of head direction selectivity, we calculated the mean resultant, R_m, of the directional firing rate map:

$$R_m=\frac{cos(\overline{\theta }){\displaystyle \sum _{i=1}^n}{F}_{i}cos({\theta }_i)+sin(\overline{\theta }){\displaystyle \sum _{i=1}^n}{F}_{i}sin({\theta }_i)}{{\displaystyle \sum _{i=1}^n}{F}_i},$$ (1)

where θ̄ represents the preferred firing direction of the cell, and is calculated by

$$\overline{\theta }=arctan\left(\frac{{\displaystyle \sum _{i=1}^n}{F}_{i}sin({\theta }_i)}{{\displaystyle \sum _{i=1}^n}{F}_{i}cos({\theta }_i)}\right),$$ (2)

and F_i and θ_i are the firing rate and heading direction for bin i.

Theta cycle skipping index

To measure theta cycle skipping in spike trains, we used the spike time autocorrelogram. The spike time autocorrelogram was estimated by collecting all non-zero lags between spikes within 400 milliseconds of one another, and generating a histogram of the lags with bins 10ms wide. The resulting autocorrelation signals were divided by the number of spikes in the train to yield probability of synchronous firing at a given lag. Each autocorrelation was fit (“fit” MATLAB r2010b) with the following equation adapted from [7], to include a second interfering oscillation:

$$y(x)=[a_1(cos(\omega x)+1)+a_2(cos(.5\omega x)+1)+b]\times exp(-\mid x\mid /{\tau }_1)+c·exp(-x^2/{\tau }_2^2),$$ (3)

where x is the autocorrelation lag, and a₁ = [0, m], a₂ = [0, m], b =[0, m], c = [−m, m], ω = [10π, 18π], τ₁ = ([0, 5]) and τ₂ = ([0, 0.05]) are the fit parameters and m is the maximum value of the autocorrelation. A subset of the parameters was used to calculate the theta cycle skipping index, specifically defined as the difference between the first and second peaks in the autocorrelation, normalized by the larger of the two:

$$TS=\frac{p_2-p_1}{max(p_1,p_2)},$$ (4)

where p₁ and p₂ are the model values at one and two full cycles (x=2π/ω and x=4π/ω) to the right of the center peak. TS is bound between −1 and 1, and higher values indicate more theta cycle skipping.

A similar equation (5) was used to model cross correlations, which did not make all of the same assumptions as the autocorrelation case. Namely, we did not assume that the center peak is the peak of the beat oscillation or that the signal is symmetric about zero lag, nor did we expect the same sharp center peak that is common in the autocorrelation.

$$y(x)=[a_1(cos(\omega x+\phi )+1)+a_2(cos(.5(\omega x+\phi ))+1)+b]\times exp(-|x+\phi {\omega }^{-1}|/{\tau }_1),$$ (5)

To address these issues, we introduced a phase offset parameter, φ, allowed a₂ to drop below zero, and eliminated the sharp center peak term (set c=0). The intervals for the parameters in (3) were: a₁ = [0, m], a₂ = [−m, m], b =[0, m], ω = [10π, 18π], φ= ([−pi, pi])and τ₁ = ([0, 5]). The average phase offset was 24.9 degrees of the theta frequency, corresponding to an offset of about 8 ms.

Theta skipping in cross correlations was defined using the fit equation and parameters from (5) as:

$${TS}_{\mathit{xcorr}}=\frac{p_{0,2}-p_1}{max(p_1,p_{0,2})},$$ (6)

where p_0,2 is the mean of the model values for x=0 and x=4π/ω corresponding to the center and second side peak, and p₁ is the model values at x=2π/ω, corresponding to the first side peak. TS is bound between −1 and 1, with negative values indicating anti-synchrony, positive values indicating synchrony, and increasing magnitude indicating more theta cycle skipping.

Theta phase of spiking

LFP channels were selected to maximize the ratio of power of the theta filtered (6–10 Hz) LFP signal to the power of the delta filtered (2–4 Hz) LFP signal to ensure accurate theta phase values. Spike phase was determined as the instantaneous phase of the theta band-pass filtered LFP signal was estimated by the phase angle of the Hilbert transform.

Control for behavior in theta skipping cross correlations

A control analysis was designed to include only spikes during right or left turns to test the null hypothesis that peaks in the cross correlation were the result of repeated turns between the preferred head directions of the pair of neurons. This would be verified if the corresponding cross correlations lost their symmetry as a result of repeated and asymmetric activation of head direction cells. However, the symmetry evident in the raw cross correlations for all spikes was maintained in the controls (Supplemental Fig. 5a, black histograms), as summarized by the cumulative distribution function of Pearson’s correlation coefficient between the negative lags cross correlation signal and the positive lag values (Supplemental Fig. 5b). For both synchronous and anti-synchronous pairs, symmetry in the cross correlations was maintained when controlling for behavior, indicating that it does not result from sequential movements of the head through different preferred angles of head direction cells (all: 0.42 ± .02 Pearson’s R; control-right: 0.37 ± .02 Pearson’s R; control-left: 0.35 ± .02 Pearson’s R).

In vitro experiments

Male and female, 17–24 days old Long Evans rats (Charles River Laboratories, Wilmington, MA) were deeply anesthetized with Isoflurane (Abbott Laboratories, North Chicago, IL) and decapitated. Brains were rapidly removed under ice-cold artificial cerebrospinal fluid (ACSF) containing (in mM) 124 NaCl, 3 KCl, 1.8 MgSO4, 10 dextrose, 26 NaHCO3, 1.09 NaH2PO4 1.6 CaCl2. Saturation of ACSF with 95% O₂/5% CO₂ was maintained throughout each experimental session. Brain slices (400 μm) were prepared in ice-cold ACSF with a Leica VT 1000S vibratome (Leica Microsystems Inc., Buffalo Grove, IL) and incubated for 25 minutes at 31°C and at room temperature for 35 minutes.

Layer V medial entorhinal neurons were visualized with an Olympus BX51WI upright microscope with a 40X water immersion objective (Olympus America, Center Valley, PA). Experiments were performed at physiological temperature of 37 °C with continuous gravity-driven exchange of ACSF containing 2 mM kynurenic acid and 100 μM picrotoxin (Sigma Aldrich, St Louis, MO) to block spontaneous fast glutamatergic and GABAergic synaptic transmission. Patch recording pipettes (3.5–7 MΩ) were pulled from borosilicate glass capillary tubes with a Sutter Instruments model P-87 micropipette puller (Sutter Instruments, Novato, CA) and filled with intracellular fluid containing (in mM) 120 mM K-gluconate, 10 HEPES, 0.2 EGTA, 20 KCl, 2 MgCl, 7 diTrisPhCr, 4 Na2ATP, 0.3 TrisGTP (pH adjusted to 7.3 with KOH) and 0.1% biocytin for staining and morphological identification of cells. Pipette-cell membrane seals of >1 GΩ were established with slight, initial negative pressure while holding the membrane at −70 mV. Access resistance during recordings was maintained below 20 MΩ. Voltage was amplified with a Multiclamp 700B (Molecular Devices, Sunnyvale, CA); capacitance neutralization and bridge balancing were applied; and data were digitized with a Digidata 1320 (10kHz) and recorded with pClamp 10 software (Axon Instruments). Cell health was deemed suitable for data collection if the resting membrane potential was <−60 mV, input resistance was >125 MΩ, spike height was >60mV, and spike peaks were >15 mV. After recording, slices were placed in 4% paraformaldehyde solution until amplification of the biotin signal with avidin-biotinylated peroxidase complex (ABC) and staining with diaminobenzidine (DAB) (Vector Laboratories, Burlingame, CA).

Stimuli delivered in current clamp mode were 8 Hz sinewaves (80pA peak-to-peak, with 0–250 pA DC current). Spiking probability was calculated as the proportion of stimulus cycles with spikes and plotted as a function of DC stimulus level. The in vitro theta cycle skipping metric was calculated as using the area under the autocorrelation of spiking during stimulus delivery as follows: The difference between the area within 50 ms windows centered on 125 ms and 250 ms lags was normalized by the area under the autocorrelation at 250 ms, giving a maximum measure of 1 for perfect theta cycle skipping. This conservative measure of theta skipping is a necessary modification of our in vivo metric, because spike timing in vitro in response to sinewave current injections is far more precise than observed in vivo.