Design study of a high-resolution breast-dedicated PET system built from cadmium zinc telluride detectors

Abstract

We studied the performance of a dual-panel positron emission tomography (PET) camera dedicated to breast cancer imaging using Monte Carlo simulation. The proposed system consists of two 4 cm thick 12 × 15 cm² area cadmium zinc telluride (CZT) panels with adjustable separation, which can be put in close proximity to the breast and/or axillary nodes. Unique characteristics distinguishing the proposed system from previous efforts in breast-dedicated PET instrumentation are the deployment of CZT detectors with superior spatial and energy resolution, using a cross-strip electrode readout scheme to enable 3D positioning of individual photon interaction coordinates in the CZT, which includes directly measured photon depth-of-interaction (DOI), and arranging the detector slabs edge-on with respect to incoming 511 keV photons for high photon sensitivity. The simulation results show that the proposed CZT dual-panel PET system is able to achieve superior performance in terms of photon sensitivity, noise equivalent count rate, spatial resolution and lesion visualization. The proposed system is expected to achieve ~32% photon sensitivity for a point source at the center and a 4 cm panel separation. For a simplified breast phantom adjacent to heart and torso compartments, the peak noise equivalent count (NEC) rate is predicted to be ~94.2 kcts s⁻¹ (breast volume: 720 cm³ and activity concentration: 3.7 kBq cm⁻³) for a ~10% energy window around 511 keV and ~8 ns coincidence time window. The system achieves 1 mm intrinsic spatial resolution anywhere between the two panels with a 4 cm panel separation if the detectors have DOI resolution less than 2 mm. For a 3 mm DOI resolution, the system exhibits excellent sphere resolution uniformity (σ_rms/mean) ≤ 10%) across a 4 cm width FOV. Simulation results indicate that the system exhibits superior hot sphere visualization and is expected to visualize 2 mm diameter spheres with a 5:1 activity concentration ratio within roughly 7 min imaging time. Furthermore, we observe that the degree of spatial resolution degradation along the direction orthogonal to the two panels that is typical of a limited angle tomography configuration is mitigated by having high-resolution DOI capabilities that enable more accurate positioning of oblique response lines.

1. Introduction

Currently there are several difficulties associated with the detection, diagnosis and staging of breast cancer. X-ray mammography is accepted as the best means to screen for non-palpable breast cancer. However, there are a few challenges mammography faces in breast cancer management. Approximately 30% of screened cases are inconclusive due to confounding factors such as radio-dense breast tissue (Rosenberg et al 1998, Mandelson et al 2000, Foxcroft et al 2000). Also, the non-specific nature of the structural signatures of breast cancer, such as micro-calcifications and masses determined by mammography, result in a very high false positive rate (~70–80%) and a significant number of unnecessary biopsies (Baines et al 1986). Any scarring produced by biopsy can cause difficulties in the interpretation of future mammograms. Furthermore, staging breast cancer through axillary dissection causes significant trauma and often yields negative results. Finally, there is no practical and accurate imaging technique to guide or monitor therapy and treatments.

To assist with the above limitations, other imaging modalities have been introduced to breast imaging in the last few decades, including x-ray computed tomography (CT) (Chen and Ning 2002, Boone et al 2006), ultrasound (US) (Piron et al 2003), magnetic resonance imaging (MRI) (Weatherall et al 2001, Kriege et al 2004, Komatsu et al 2005, Kneeshaw et al 2006) and positron emission tomography (PET) (Thompson et al 1994, Raylman et al 2000, Raylman et al 2008, Conti et al 1996, Wahl 2001, Weinberg et al 2005). PET is a noninvasive, in vivo, molecular and cellular imaging technology. PET has shown promise for more specific identification of cancer due to its unique ability to sense and visualize increased biochemical and molecular changes in malignant compared to healthy tissue. This additional information is useful since cellular changes associated with cancer can occur well before structural changes such as calcifications appear. Many studies have reported that PET is able to exhibit both higher sensitivity and higher specificity than other imaging modalities in breast cancer imaging (Conti et al 1996, Rieber et al 2002, Goerres et al 2003, Levine et al 2003, Tafra 2005).

However, PET has not been incorporated into standard practice for breast cancer patient evaluation mainly because most PET systems are whole body imaging systems and not appropriate for breast imaging due to several reasons: imaging geometry that results in poor counting efficiency, inadequate spatial and contrast resolutions for detecting small lesions, relatively high cost and long scan times. A number of other breast-dedicated PET instruments aiming to overcome these limitations have been intensively investigated with system specifications summarized in table 1.

Table 1.

Summary of some of the previously studied breast-dedicated PET system instrumentation. (PMT: photomultiplier tube, PD: photodiode, APD: avalanche photodiode, PSAPD: position-sensitive APD; DOI: depth of interaction)

	System geometry	Scintillation materials	Detectors	Crystal element size (mm)	DOI capability
PEM-I (Murthy et al 2000)	Dual panel	BGO	PMT	Continuous crystal	No
MDAPET (Baghaei et al 2000)	Partial ring	BGO	PMT	2.7 × 2.8 × 19	No
MaxPET (Doshi et al 2000)	Dual panel	LSO	PSPMT	3 × 3 × 20	No
BPET (Freifelder et al 2001)	Two curve plates	NaI (Tl)	PSPMT	Continuous crystal (~4.5)	No
Moses and Qi 2004	Box	LSO	PD/PMT	3 × 3 × 30	10 mm
Clear-PEM (Santos et al 2004)	Dual panel	LSO	APD	2 × 2 × 20	2 mm
CYBPET (Karimian et al 2005)	Ring	BGO	APD	3 × 5 × 20	No
Weinberg et al 2005	Dual panel	LYSO	PSPMT	2 × 2 × 10	No
Zhang et al 2007a	Dual panel	LSO	PSAPD	1 × 1 × 3	3 mm

The first improvement of these breast-dedicated PET systems is the system geometry. Many previously developed cameras used a planar geometry rather than the ring geometry commonly deployed in whole body PET scanners. Two panels can be put in close proximity to the breast and/or axillary nodes, resulting in high photon sensitivity while minimizing background effects from potential uptake of tracer in the nearby heart. Moreover, two panels may be positioned to include the chest wall, where breast lesions sometimes appear. However, with two panels only limited angle tomography can be obtained unless the system incorporates a means for mechanical rotation. With standard PET detector designs, limited angle tomography implies non-isotropic resolution, with the worst resolution being along the direction orthogonal to the panels. One important result from this work is that detectors with good photon DOI resolution help to mitigate the problem of non-isotropic spatial resolution in a non-rotating dual-panel PET system.

The second improvement is an optimized detector design. A common trend of these system developments is smaller crystals and finer crystal pitch, in conjunction with high-resolution position-sensitive photodetectors, either small-area position-sensitive photomultiplier tubes (PSPMTs) (Doshi et al 2000, Freifelder et al 2001) or position-sensitive avalanche photodiodes (PSAPDs) (Zhang et al 2007a). Meanwhile, new scintillation materials exhibiting good energy resolution and coincidence time resolution such as lutetium oxyorthosilicate (LSO) have been used to replace other crystals such as bismuth germanate (BGO) and NaI (Tl). The motivation for this replacement is mainly because in PET breast imaging, when using a tracer with non-specific uptake such as fluoro-deoxy-glucose (FDG), there will likely be background activity generated from the nearby heart, liver and surrounding tissue. Good energy and coincidence time resolution will help to reduce the resulting high background scatter and random coincidence rates, and therefore improve lesion contrast resolution.

The third improvement is the incorporation of photon DOI resolution. In most PET systems, the spatial resolution degrades as a function of the position from the center, also known as parallax error (Cherry et al 2003). Such degradation is proportional to the thickness of crystals. Simply reducing the thickness to address this problem is not feasible since the crystals have to maintain a certain thickness to ensure good 511 keV photon sensitivity. Most existing breast-dedicated PET systems have not incorporated DOI resolution. Until very recently, several studies (Moses and Qi 2004, Santos et al 2004, Zhang et al 2007a) have developed novel detectors with three-dimensional positioning ability and thus improved DOI capability. Such a design will facilitate a dual-panel system that achieves uniform spatial resolution, as well as high contrast-to-noise ratio (CNR) throughout the full field-of-view (FOV) for breast imaging.

In this study, we propose a CZT-based PET system dedicated for breast imaging that is similar to previous efforts with respect to the dual-panel geometry while differing significantly in several aspects. First, CZT detectors are employed, not scintillation crystals. The linear attenuation coefficient of CZT material at 511 keV is 0.53 cm⁻¹ (Berger et al 1999) and the detection efficiency of a 4 cm edge-on CZT detector for 511 keV photons is about ~88%. In such semiconductor detectors, the electron–hole pairs are directly involved in the electronic signal formation, instead of the relatively inefficient process of creation, propagation and collection of light in scintillation-based detector technology (Knoll 2000, Levin 2008). As a result, CZT detectors exhibit much better energy resolution for 511 keV photons, compared to scintillator-based PET detectors. On the other hand, the time resolution of CZT detectors is worse due to the fluctuation of charge carrier drifting times, unlike fast light signal propagation in scintillation materials (Levin et al 2004, Levin 2008). To what extent these characteristics will impact the overall system performance such as the count rate performance and the CNR needs to be addressed, particularly with the presence of high uptake background from the heart and torso in breast PET as mentioned above.

Second, the cross-strip readout scheme implements detector pixilation electronically instead of cutting scintillation crystal material into small pixels (Levin 2008, Levin et al 2004). In scintillator-based detector design, the intrinsic spatial resolution is determined by the pitch of crystal elements. In the proposed CZT detector, the intrinsic spatial resolution is determined by the pitch of electrode strips, which can be as fine as desired (e.g. <1 mm). Less than 1 mm intrinsic resolution cannot easily be achieved in high-resolution scintillation detectors due to complexity of cutting tiny crystals, assembling them into arrays as well as incomplete and non-uniform light collection (Levin 2002). Furthermore, due to the cross-strip readout scheme, the detector has the potential to incorporate the three-dimensional positioning ability with great flexibility, and our results indicate that this would result in significantly improved DOI capability for more isotropic and uniform resolution.

In this paper, we present results of Monte Carlo simulation studies for the proposed CZT breast-dedicated PET system. This simulation study aims to address the following performance parameters: (1) photon sensitivity for the dual-panel geometry, (2) count rate performance using a phantom that mimics the breast imaging environment, (3) the degree of spatial resolution uniformity and isotropy across the FOV, (4) the dependence of spatial resolution on the system DOI capability and (5) the hot sphere visualization capabilities in terms of the signal-to-noise ratio (SNR) and CNR.

2. Methods

2.1. Description of the proposed CZT system and detector unit

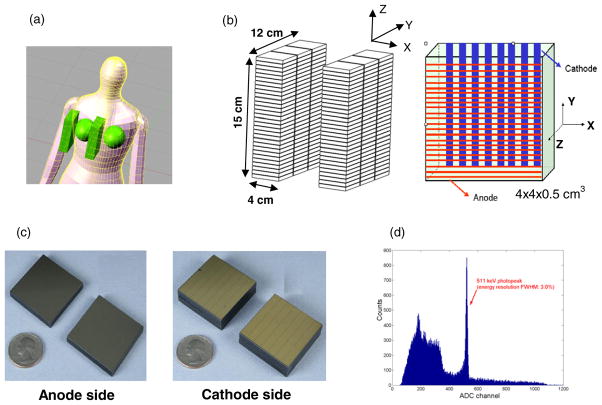
The proposed system is configured in a planar, dual-panel geometry as shown in figure 1 and each panel has 12 × 15 mm² area. These dimensions were chosen in order to cover a substantial portion of an average breast. The separation between two panels is adjustable from 4 cm to 8 cm, depending on the breast size and the degree of compression required. The panels are built from CZT detector modules, each with dimensions of 4 × 4 × 0.5 cm³. Each module is oriented in a manner so that a 511 keV photon enters the module in an edge-on fashion, which means that each photon sees a minimum path length of 4 cm of CZT detector material. CZT slabs can be tightly packed with a separation of only ~25–50 μm, resulting in > 99% packing fraction. The system consists of 180 modules in total (90 per panel).

Figure 1.

(a) Illustration of the proposed dual-panel CZT-based PET system for breast cancer imaging. (b) Each panel has dimensions of 4 × 12 × 15 cm³, consisting of 180 modules in total. Each detector module has dimensions of 4 × 4 × 0.5 cm³ with 25 μm inter-module spacing, giving a packing ratio of over 99%. Incoming photons encounter a minimum 4 cm thick CZT material. Cross-strip electrodes with sets of parallel anode (1 mm pitch) and cathode (5 mm pitch) strips deposited on either side of the CZT slab are employed to reduce the number of electronic readout channels. In the arrangement shown, DOI resolution is defined by the cathode strip pitch. (c) The pictures of anode and cathode electrodes. (d) An energy spectrum of the proposed CZT detector for 511 keV photons.

A key concept is that a cross-strip readout design is deployed as shown in figures 1(b) and (c). The anode and cathode planes are configured as orthogonal set of strips, providing positioning signals in their respective directions. This configuration reduces the number of electronic readout channels required for the same detector area compared to a fully pixilated anode. On one side, the anodes (~50 μm width with 1 mm pitch) collect the charge for pulse height analysis and provide intrinsic spatial resolution of approximately 1 mm along the Y direction. On the other side, the cathodes provide the timing signal and provide the spatial information along the X direction (the DOI direction), both of which depend on the size and spacing of cathodes. The performance of an individual CZT detector prototype used in the simulation has been studied experimentally (Levin et al 2004). The third coordinate, the Z direction is determined by either the ratio of or timing between the cathode and anode signals (Levin 2008, Levin et al 2004).

2.2. Point source coincidence photon sensitivity

GATE (Geant4 Application in Tomographic Emission) (Jan et al 2004) was used to study photon sensitivity. For an incoming 511 keV event, the history of single 511 keV photon interactions with detectors was recorded in list mode. The output information included the event number (ID), the energy information, the time information and the spatial coordinates of each photon interaction. A point source was translated from the center of the FOV to the edge of the X, Y and Z directions. The coordinate axes are indicated in figure 1. The detector energy resolution was 3% full-width at half maximum (FWHM) at 511 keV and the coincidence time resolution was 8 ns FWHM based on experimental measurements (Levin et al 2004), which were used for all simulation studies. The raw outputs of energy and time were Gaussian blurred based on these two resolutions, respectively. The energy window and time window settings were chosen to be twice the respective resolution values, which are reasonable settings for the photon sensitivity study which uses a single point source. The number of collected coincident 511 keV photons for this photon sensitivity study was approximately 1 million. In addition, a commercial whole body PET system (based on the specification of a Siemens Biograph64 TruePoint scanner, 21.6 cm axial FOV, 84.2 cm diameter bore, Townsend et al 2007) and a breast-dedicated PET system (Zhang et al 2007a) were selected for the comparison regarding photon detection sensitivity.

2.3. Coincidence count rate studies

The noise equivalent count (NEC) rate, which is an indicator of the signal-to-noise ratio for PET system benchmarking (Strother et al 1990), was studied using GATE. The NEC is directly dependent on the subject imaged. A simplified model was introduced to mimic the geometry for PET breast imaging, as shown in figure 2. The hot heart and warm torso compartment were put adjacent to the breast tissue compartments. The breast compartment completely filled the volume between two CZT panels. The sizes for all compartments, as well as the activity concentration ratio used in our simulation are provided in figure 2. On five faces of each panel (excluding the face where photons emitted from the breast enter the panel), the lead shield of 2 cm thickness was placed in the simulation in order to effectively stop those photons emitting from the torso and heart (linear attenuation coefficient of lead at 511 keV is 1.70 cm⁻¹, Berger et al 1999). The physiological complexity and inherent tracer uptake variations between subjects make it challenging to select the perfect ratio among different compartments, which is highly patient dependent. However, based on the literature on fluoro-deoxy-glucose (FDG) tracer uptake in breast cancer studies (Wahl et al 1991, Murthy et al 2000, Avril et al 2001, Vranjesevic et al 2002, Karimina et al 2005), the activity concentration in the breast phantom was set to be 3.7 kBq cm⁻³, and a ratio of 1:10:1 for the breast-heart-torso activity distribution was chosen in our simulation. The NEC (Strother et al 1990) is calculated as

Figure 2.

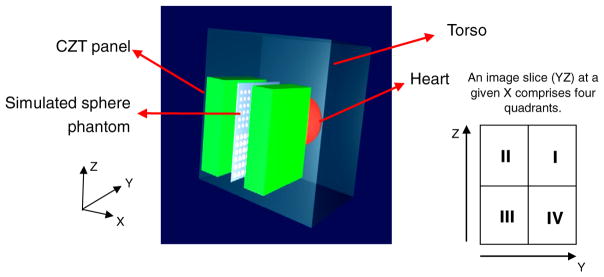
The simulated model for system NEC and resolution studies. A hot spherical heart with a 10 cm diameter and a warm torso of dimensions of 30 × 20 × 30 cm³ are adjacent to breast phantom. The breast phantom fills in the space between two panels and is not shown. The center of the heart phantom and the center of the breast phantom have the same Z value but are separated by 13 cm along the Y direction. This implies that the hot heart extends to within 2 cm of the edge of the panels. The center of the torso phantom and the center of the breast phantom have the same Z value but are separated by 7.5 cm along the X direction. For the NEC studies, the panel separation was 4 cm and the activity concentration ratio assumed for breast–heart–torso was 1:10:1.

$$\text{NEC}=\frac{T^2}{T+S+R}$$ (1)

where T, S and R are the rates of true, scatter and calculated random coincidence events. For the raw GATE outputs, the following data processing was applied. After the energy blurring and time blurring, two hits occurring within a selectable energy window and time window was considered a coincidence event. If there were more than two hits within a given time window, they were considered multiples and were rejected. For each coincidence event, if two hits had the same event ID and did not scatter within the phantom prior to its interacting within detectors, they were assigned to a true coincidence event (T). If they had the same event ID but either one or both of them scattered within the phantom, they were assigned to a scatter coincidence event (S). On the other hand, if two hits had two different event IDs, they were assigned to a random coincidence event (R). Since the random rate is directly determined from the Monte Carlo simulation data in this study, there was not a factor of 2 in front of R as would be the case from error propagation considerations using the delayed coincidence window method for estimating R (Strother et al 1990).

The dependences of the NEC on various energy window and time window settings were studied. Determining the optimum operating window settings was necessary to complete other studies in this work. For each set of NEC simulations, the number of coincidence 511 keV photons detected was approximately 6 million. With the same method used, the NEC performance was studied for the whole body (Siemens Biograph64) and the breast-dedicated PET system described in section 2.2. For these two LSO-based systems, the energy resolution FWHM for 511 keV photons and the time resolution were assumed to be 12% and 2 ns, respectively.

2.4. System sphere resolution study

For the system resolution study, the following assumptions were made based on the experimental results for the proposed CZT detectors (Levin et al 2004). The 1 mm spacing of anodes provides 1 mm intrinsic spatial resolution along the Y direction (see figure 1 for definitions of the axes); by utilizing the time difference between the signals from the anode and cathode, or, alternately the ratio of peak cathode to anode signals (Zhong 2001, Levin 2008, Levin et al 2004), the system is able to achieve 1 mm resolution along the Z direction, which is better than the thickness of the detector along that direction (5 mm). For instance, if a photon interacts within the detector at a location closer to the anode, a shorter time is required for the electrons to drift to the anode, and accordingly a longer cathode to anode time difference or a smaller cathode to anode peak signal ratio would be measured. As a result, a 1 mm spatial resolution along both Z and Y directions was assumed and fixed in the whole simulation. However, the spatial resolution along the X direction, also referred to as the intrinsic DOI resolution, would be determined by the cathode spacing and was optimized in the study.

GRAY, a new photon transport simulation package we have developed, was used for the system resolution and contrast study due to its reduced simulation time. Its performance has been validated against GATE under the same simulation conditions. GRAY is able to produce statistically equivalent results to GATE for single events detected, coincident events detected, energy and spatial distribution of events in all three dimensions while significantly reducing the simulation time (Olcott et al 2006). For a given GRAY coincidence event, its coordinate outputs (x, y, z) were rebinned to the center of the nearest 3D detector voxel element. The size of bin reflected the intrinsic spatial resolutions along three dimensions (e.g. 1 × 1 × 5 mm³ for 5 mm pitch cathodes strips). For an event involving more than one interaction inside the detectors, a weighted mean positioning scheme (energy-weighted) was applied to get the overall position for that event. The optimum energy window and time window settings for the coincidence processing were based on the results from section 2.3. List-mode 3D ordered-subset expectation maximization (OSEM) (Hudson and Larkin 1994) image reconstruction algorithm was used. Compared to filtered back projection (FBP) and focal plane tomography (Zhang et al 2007a), OSEM is expected to exhibit better performance for a limited angle tomography configuration. The pixel size in the image reconstruction was 0.5 mm in each of the three dimensions. The activity concentration in phantoms was set to be 3.7 kBq cm⁻³ as described in section 2.3 and only cold background (water) was present for the resolution studies. The total coincidence count for each image slice in the resolution study was approximately 3.5 million. The list mode 3D OSEM algorithm was implemented with 5 subsets and 6 iterations, which is believed to provide sufficient iterations for the simulated phantom. In our study, it was found that a larger number of iterations did not affect the image quality significantly in terms of CNR. The direct normalization method was deployed using a simulated slab phantom completely filling the space between the plates with uniform radioactivity concentration throughout the entire FOV of the system determined by the plate separation. Photon attenuation correction was not applied for any of the image reconstruction tasks in this study.

All the resolution studies in this section focus on the question of whether the system is able to resolve two adjacent spheres of a certain diameter. As shown in figure 2, different sphere diameters located in the YZ plane were imaged. Two components of the system spatial resolution are frequently used in this paper. The first one is the ‘in-plane’ resolution, which corresponds to the resolution measured along the Y direction in the YZ plane (parallel to the panels). The resolution along the Z direction was assumed to be the same as the in-plane resolution defined above in all four quadrants due to the approximate symmetry of the panel (15 × 12 cm²). The second resolution component is the ‘orthogonal-plane resolution’, which corresponds to the resolution measured along the X direction in an XY plane (orthogonal to the detector panels).

The resolution study reported here consists of three parts. The first part is to investigate whether the system can resolve 1 mm size spheres with different DOI resolutions. This first sphere size was chosen since it matches the intrinsic detector resolution and should be visualized in air/water provided that there are adequate counts. Spherical sources of 1.0 mm and 1.5 mm diameters were oriented in the YZ plane (at X = 0, refer to figures 1 and 2) all the way out to the edge of the FOV. Sources of two different sizes were located in two different quadrants (I and III, see figure 2) of the plane. For each quadrant, the distance between the centers of two spherical sources was twice their diameter. Detector DOI resolution values ranging from 1 mm to 5 mm were simulated. Cold water was placed in the background. Only a 4 cm panel separation was studied in this first part.

The second resolution study quantitatively assesses both the in-plane resolution and orthogonal-plane resolution as a function of the DOI resolution using spheres of larger sizes. Since the pixel size used in the image reconstruction is 0.5 mm, the intensity profile crossing a small sphere (e.g. 1.0 mm and 1.5 mm spheres) consists of only two or three data points and no good fitting results could be obtained. As a result, the spherical sources studied had 2.5, 3.0, 3.5 and 4.0 mm diameters, respectively, in the presence of air background. They were located in four different quadrants of the YZ plane (see figure 2). Compared to the 1 and 1.5 mm diameter sphere study, the spheres in each quadrant are arranged in a 6 × 6 array near the center instead of placing them all the way out to the edge of the FOV. We define a ‘row index’ to increase from 1 to 6 for rows of spheres placed from near center (row 1) outward (up to row 6) along both the positive and negative Z directions toward the edge (see figure 6). Only the profile of the first row (nearest to the center) in each quadrant was analyzed for this study. Detector DOI resolution values (cathode spacing) ranging from 0 mm to 9 mm were simulated. The DOI of 0 mm corresponds to perfect resolution along the X direction. The reason that it was included in the study is to help us isolate the resolution degradation caused by the DOI resolution from other resolution degrading factors such as the effect of limited angle tomography for a dual-panel geometry. For completeness, an 8 cm panel separation configuration was also studied for this step and a separate normalization for an 8 cm separation was implemented.

Figure 6.

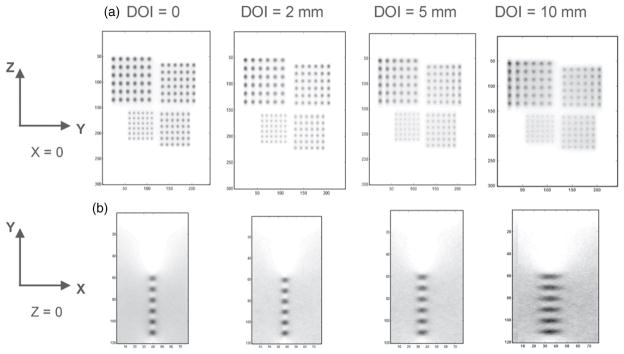
Reconstructed image slices through warm spheres in air with different DOI resolutions (0, 2, 5 and 10 mm). Pixel size: 0.5 mm. The simulated tumor diameters are 2.5 mm, 3.0 mm, 3.5 mm and 4.0 mm with twice that separation between centers placed on the YZ plane (X = 0) between the two panels separated by 4 cm. (a) In-plane (parallel to panels) (YZ plane) images (15 × 12 cm²). (b) One quadrant (6 × 4 cm²) of the orthogonal-plane (perpendicular to panels) (XY plane) images going through the 2.5 mm diameter spheres. (See figure 2 for definition of the axes.) The latter is zoomed for ease of visualization.

The third part of the resolution study is to investigate how uniform and isotropic the spatial resolution is across the FOV. Within a given YZ plane, the resolutions of different row indices were compared. Furthermore, the spatial resolution as a function of the off-center distance along the orthogonal direction (X value) was studied. This study was only performed for a panel separation of 4 cm.

2.5. Hot sphere visualization study

The sphere SNR and CNR of the proposed system was studied only for the case of a 4 cm panel separation. The configuration of the breast, heart and torso was the same as in section 2.3. However, a different phantom in the central YZ plane (X = 0) was used. Each quadrant contains three spheres of the same diameter, where the spheres nearest to the center of the plane in each quadrant were chosen for the quantitative analyses. The other spheres were only present for the visual detection study. The diameter of the spheres in four quadrants was 1 mm, 2 mm, 3 mm and 4 mm, respectively. Clinical studies show that the activity concentration ratio between lesions and normal breast tissue depends on lesion malignancy and tracer specificity. Therefore, based on the literature (Wahl et al 1991, Murthy et al 2000, Avril et al 2001), three activity concentration ratios (10:1, 5:1 and 3:1) between the spheres and the breast background were tested. The energy window and the time window settings were based on the results from section 2.3. Due to the limitations of simulation time and data storage, the total effective imaging time for each concentration ratio was 7 min and the total detected coincidences per minute were approximately 20 million. The list mode 3D OSEM algorithm was implemented with 5 subsets and 15 iterations. No significant change in image quality in terms of CNR was observed for more iterations.

The main goal for this hot sphere visualization section is to answer the question: for the proposed system to be able to detect a lesion of a given size with a given activity contrast ratio to background, how long of an imaging time is required? The image quality, in terms of the SNR and CNR, was studied as a function of the image acquisition time. The central slice of the reconstructed image volume (YZ plane, X = 0) was used to measure these figures of merit. The contrast for a given hot sphere is defined by (Kinahan and Karp 1994, Freifelder and Karp 1997)

$$\text{contrast}=\frac{C_{\text{sphere}}-C_{\text{background}}}{C_{\text{sphere}}}$$ (2)

where C_sphere is the average count density of the hot spheres in the phantom and C_background is the average count density of the background. The SNR is defined as (Freifelder and Karp 1997)

$$\text{SNR}=\text{contrast}·\frac{C_{\text{background}}}{{\sigma }_{\text{background}}}$$ (3)

where σ_background is the standard deviation of the count density of the background. For the above analysis, a circular region-of-interest (ROI) that has the same diameter as the sphere and centered on it was chosen. For the background, a circular region that has the diameter twice that of the sphere that was sufficiently away from the spheres was chosen. Note that due to the fact that the sphere in the simulated phantom has circular shape but the reconstructed image consists of pixels of square shape (pixel size: 0.5 mm), there might be some biases in estimating C_sphere for spheres of smaller sizes such as 1 mm and 2 mm.

Following the SNR analysis above, we validated the hot sphere visualization studies against the Rose criterion for consistency. The Rose criterion has been widely used in radiology and is defined as (Rose 1973)

$$\text{CNR}=\mid C_{\text{input}}\mid ·\sqrt{n_{\text{pixels}}}·\text{SNR}\ge 4n_{\text{pixels}}={(D/\mathrm{\Delta }r)}^2$$ (4)

where C_input corresponds to the input activity concentration ratio for a hot sphere and is 10:1, 5:1 or 3:1 in our study. n_pixels is the number of pixels in the reconstructed FOV for a given sphere size (D: diameter, Δr: pixel size). The SNR is based on results from formula (3). Such a comparison is not intended to replace the receiver operation characteristic (ROC) analysis, but will be used to help us evaluate the capabilities of the system and design the future protocol once the system is built.

3. Results

3.1. Coincidence photon sensitivity

The photon sensitivity as a function of the distance from the center is shown in figure 3 for a point source. For a 4 cm panel separation, at the center of the FOV, the system sensitivity is roughly 32.5%. The coincidence photon sensitivity decreases as the point source moves away from the center due to decreased solid angle coverage. However, the system is able to achieve >15% photon sensitivity within 4 cm of the center of the FOV for all three directions. For an 8 cm separation, the system photon sensitivity at the center of the FOV is about 16.8%, again much higher than that of standard clinical PET systems, and decreases as the source moves towards the edge of the FOV, but the rate of decrease is slightly slower than that of a 4 cm panel separation. The peak sensitivity that occurs at the center of the FOV is ~6.8% and ~18.0% for the whole body and the LSO-based dual-panel PET configurations, respectively, when an energy window of 449–572 keV and a time window of 4 ns are applied.

Figure 3.

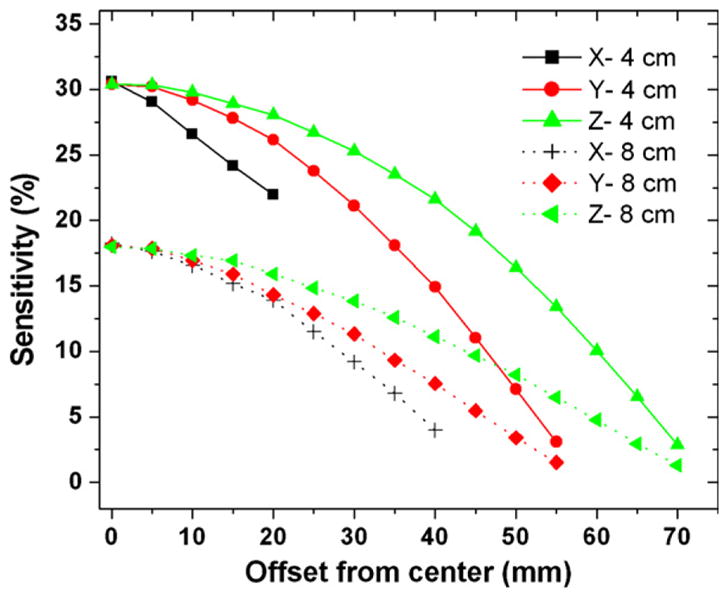
System photon sensitivity with a point source at the system center as a function of the distance (mm) from the center along the X, Y, Z directions for 4 cm (top curves) and 8 cm (bottom curves) panel separation. For these studies the energy window is 6% (496–526 keV) centered on 511 keV and the coincidence time window is 16 ns. For 8 cm panel separation, the FOV is larger so that it has more data points along the X direction. See figure 1 for definition of the axes.

3.2. Coincidence count rate studies

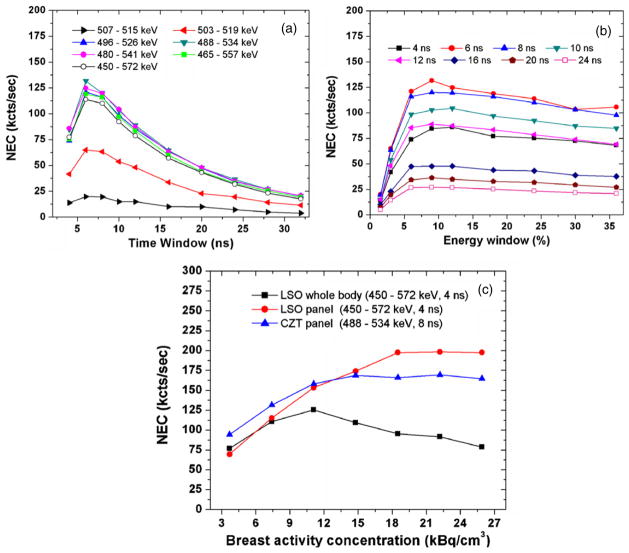
Figures 4(a) and (b) show the system NEC as a function of both coincidence time window and energy window for a 4 cm panel separation (breast compartment has a volume of 720 cm³ and an activity concentration of 7.4 kBq cm⁻³). For such an activity configuration, the NEC reaches a maximum value (~131 kcts s⁻¹) around 6–8 ns coincidence time window and around 484–536 keV (~10%) energy window centered on 511 keV. As shown in figure 4(a), for all energy windows, the NEC initially increases to a peak but then decreases. This is attributed to the higher occurrences of more than two photon coincidences, known as multiples, and random events due to the heart and torso background. As shown in figure 4(b), the NEC reaches a plateau at around 10% energy windows for all time windows. Further increasing energy window has no significant effect on NEC performance. Based on these results, the energy window of 10% at 511 keV and the time window of 8 ns were used in the following studies.

Figure 4.

(a), (b) System NEC as a function of different time window and energy window centered at 511 keV for a 4 cm panel separation (the breast activity concentration of 7.4 kBq cm⁻³). The peak NEC rate reaches a plateau at ~131 kcts s⁻¹ around a coincidence time window of ~6–8 ns and an energy window of 10% at 511 keV. (c) Comparison of NEC performance among three system configurations.

In figure 4(c), the peak NEC was studied for three system configurations, as a function of the breast activity concentration. Besides the CZT system, the other two systems are LSO based and both exhibit peak NEC at an energy window of 449–572 keV (24%) and a time window of 4 ns for all concentrations studied. The whole body scanner exhibits an initial increase up to the breast activity concentration of around 11.1 kBq cm⁻³ followed by a decrease. The peak NEC rate is 125.2 kcts s⁻¹ which is consistent with the clinical study using the same scanner (Townsend et al 2007). Besides, the results are quite comparable between the LSO and CZT panels mainly because both systems have comparable geometry and dimensions. At low activity concentrations (below 14.8 kBq s⁻¹), the NEC performance the CZT panel is slightly superior to that of the LSO panel. However, as the activity concentration further increases, the NEC exhibits a continuing increase for the LSO panel while it gradually saturates for the CZT panel.

3.3. Reconstructed sphere resolution study

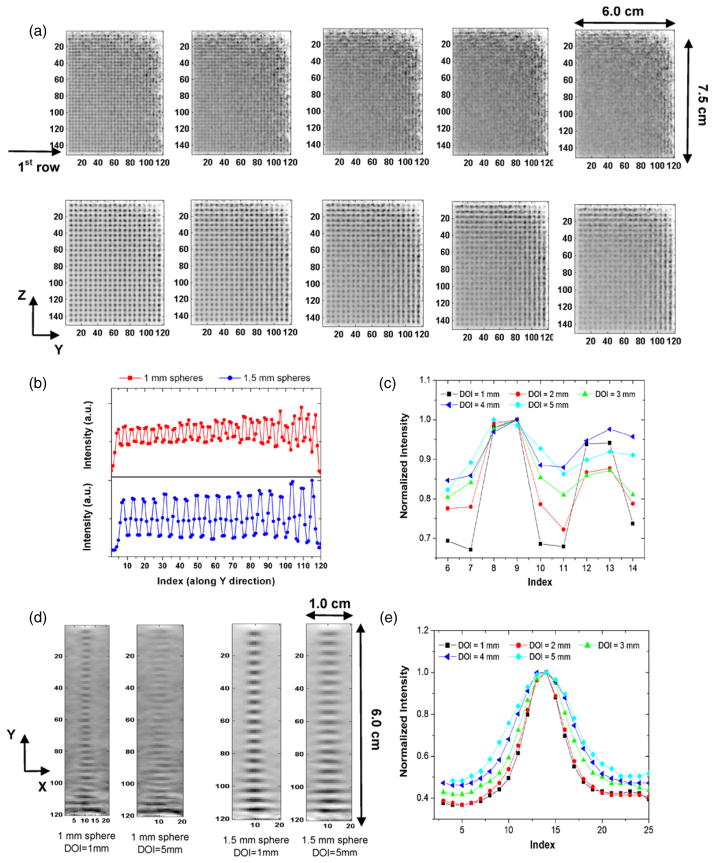
Figure 5 shows in-plane reconstructed image slices through the spherical sources (1.0 mm and 1.5 mm diameters) with different DOI resolutions for an acquisition time of 8 min. For the quadrant containing 1.0 mm diameter spheres, the spheres can be well resolved for DOI resolution better than 2 mm, implying that the system is capable of achieving a 1 mm in-plane resolution (parallel to the panels). This is in agreement with our expectation as the system has a 1 mm intrinsic resolution along both Y and Z directions. However, for the >3 mm DOI resolution data, the spheres appear to overlap more with adjacent ones (see the top row in figure 5(a)) corresponding to in-plane spatial resolution degradation. For the quadrant containing 1.5 mm diameter spheres, the spheres can be resolved for all DOI resolution values, though it becomes more difficult as DOI resolution degrades from 1 mm to 5 mm (the bottom row in figure 5(a)). For a 1 mm DOI resolution, a 1D profile of the first row (nearest to the system’s center along the Z direction) was derived for both 1 mm and 1.5 mm diameter spheres respectively, shown in figure 5(b). The index of image pixels increased from 1 to 128 for sphere positions from the center toward the edge along the Y direction. For the 1 mm diameter sphere, the 1D profile crossing the second and third spheres (located at the far left end of the profile in figure 5(b)) is shown in figure 5(c), as a function of the various DOI resolution values. The peak-to-valley ratio is 1.47, 1.38, 1.23, 1.13 and 1.16 corresponding to DOI resolution values of 1, 2, 3, 4 and 5 mm. For a 1 mm DOI resolution, the PVR is 3.52 for the 1.5 mm diameter spheres. The results indicate that for 1 mm spheres, the resolution improvement benefits could still be expected as DOI resolution varies from 5 to 1 mm, though there is no quantitative relation between PVR values and absolute spatial resolution values.

Figure 5.

(a) In-plane (parallel to panels) reconstructed image slices through warm spheres in cold background with varying DOI resolution for 1.0 mm (top) and 1.5 mm (bottom) diameter spheres. Pixel size: 0.5 mm. The simulated spheres were placed on a plane midway between the two panels which were separated by 4 cm. From the left to the right, the DOI resolution is varied from 1 mm to 5 mm in 1 mm increments. (b) 1D profile for the first row in each quadrant in YZ plane, which corresponds to the in-plane sphere resolution. (c) The 1D profile crossing the second and third sphere along the 1D profile in (b) and the peak-to-valley ratio (PVR) is calculated for two peaks, as a function of the five DOI resolution values. (d) Orthogonal-plane (perpendicular to panels, XY plane) images for the first row in each quadrant with a DOI resolution of 1 mm and 5 mm. (e) the 1D profile of the topmost sphere in (d) for 1.5 mm diameter spheres, which corresponds to the orthogonal-plane sphere resolution.

The reconstructed 1.0 mm and 1.5 mm spheres (first row in each quadrant) in the XY plane (slice orthogonal to the panels) is shown in figure 5(d) and illustrates how we characterize the orthogonal-plane reconstructed sphere diameter (see figure 6 for more details). The image is more blurred as DOI resolution varies from 1 mm to 5 mm. Only a single 1.5 mm sphere (the topmost sphere in figure 5(d)) was chosen to illustrate the dependence of the orthogonal-plane sphere resolution on the DOI resolution. 1 mm spheres were not chosen as their sizes are relatively small compared to the pixel size (0.5 mm) in the reconstructed images and no accurate quantitative results could be obtained. As shown in figure 5(e), as the DOI resolution degrades, the orthogonal-plane sphere resolution (FWHM) increases from 1.98 ± 0.10 mm (for a 1 mm DOI resolution) to 2.86 ± 0.11 mm (for a 5 mm DOI resolution). However, no significant difference is observed between 1 mm and 2 mm DOI resolution values in figure 5(e). In summary, an impact of DOI resolution on both the system in-plane sphere and orthogonal-plane sphere resolution is observed from this task.

Figure 6 shows the reconstructed in-plane images (slice parallel to the panels) of spherical sources of larger sizes (2.5 mm, 3.0 mm, 3.5 mm and 4.0 mm) for four different DOI resolutions (0 mm, 2 mm, 5 mm and 10 mm), respectively. The reconstructed image of spheres in the YZ plane is more blurred as DOI resolution degrades (figure 6(a)), similar to the results for the 1.0 and 1.5 mm diameter spheres shown in figure 5. The reconstructed image of six 2.5 mm diameter spheres (first row) in the XY plane (slice orthogonal to the panels) is shown in figure 6(b). Similar to figure 5(d), the image is more blurred as DOI resolution degrades and the effect occurs much more rapidly than that for the in-plane sphere resolution (figure 6(a)). In addition, the elliptical shape of spheres with the elongation occurring in the X direction was seen for all DOI resolutions, a limited-angle tomography effect that will be addressed in section 4.

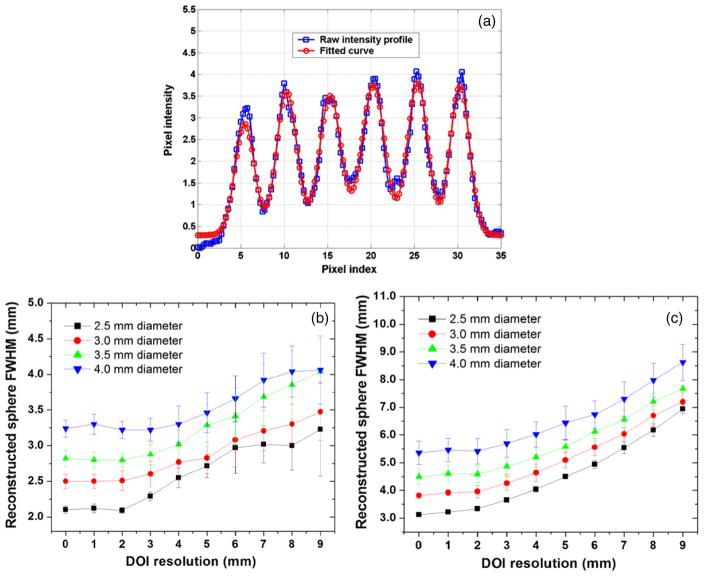
The dependence of the system reconstructed sphere size on the DOI resolution is plotted in figure 7, based on the first row of spheres in each quadrant. For the in-plane sphere resolution, the 1D profile of the six spheres was fitted by six Gaussian distributions on the top of a linear background as shown in figure 7(a). For the orthogonal-plane sphere resolution, the 1D profile of each sphere was analyzed by a single Gaussian distribution on the top of a linear background. For a given sphere diameter, the average FWHM of the six spheres was referred to as the ‘reconstructed sphere FWHM’ for both in-plane and orthogonal-plane sphere resolutions. The goodness of all fits varies from 0.90 to 1.10.

Figure 7.

Results from analysis of spatial resolution studies. (a) In each quadrant of the in-plane (parallel to panels) slice through the reconstructed six spheres (see figure 6(a)), the 1D profile of the first row (row index = 1) was fitted with six Gaussian distributions on top of a linear background. (b) The reconstructed in-plane sphere FWHM as a function of the DOI resolution. (c) The reconstructed orthogonal-plane (perpendicular to panels) sphere FWHM as a function of the DOI resolution. The analysis was not performed for the 1.0 mm and 1.5 mm spheres (figure 5) since the reconstructed pixel size of 0.5 mm limited the number of samples available for fitting.

As shown in figure 7, both in-plane and orthogonal-plane sphere resolutions degrade along with the increase of DOI resolution and such a trend is much more significant for the orthogonal-plane sphere resolution. The results clearly show that better DOI resolution can greatly help the system to achieve better sphere resolution, for both the in-plane and orthogonal-plane directions. Moreover, the in-plane sphere resolution does not show significant improvement when DOI resolution is better than 2 mm. This is consistent with results shown in figure 5(a) (DOI resolution = 1 mm and 2 mm), where 1 mm diameter spheres can be resolved and no obvious differences between the two DOI resolution values are observed. Similarly, for the orthogonal-plane sphere resolution, the results for spheres of various diameters do not show significant improvement when DOI resolution is smaller than 2 mm. This is also consistent with results shown in figure 5(e) where no obvious differences are noted between 1 mm and 2 mm DOI resolution values, for 1.5 mm diameter spheres. Here the error bars reflect the standard deviation fluctuations over six spheres which have the same row index (defined in section 2.4). We chose the 4 mm spheres to characterize the sphere resolution uniformity as they cover the largest portion of the FOV. The sphere resolution uniformity is characterized by (σ_rms/mean), the ratio between the standard deviation (error bar) and the average value (data point). For both in-plane and orthogonal-plane sphere resolutions, the (σ_rms/mean) is found to be less than 10% for all DOI resolution values within a single row. Similar results are observed for spheres of 2.5 mm, 3.0 mm and 3.5 mm diameters.

The uniformity of the in-plane and orthogonal-plane sphere resolutions across the FOV for the different row indices is shown in figure 8, assuming a DOI resolution of 2 mm. For both X = 0 and X = 1.5 cm, the in-plane sphere resolution shows no significant dependence on the row index (figure 8(a)). However, the dependence of the in-plane sphere resolution on the X value is observed in figure 8(a), as the results at X = 1.5 cm are worse than those at X = 0. This difference is more significant for smaller spheres, such as 2.5 mm and 3.0 mm. For instance, for the first row, the in-plane sphere resolution is 2.28 ± 0.14 mm (X = 1.5 cm) but 2.09 ± 0.04 mm (X = 0 cm), nearly 9.1% degradation. On the other hand, the orthogonal-plane sphere resolution maintains good uniformity for all row indices and shows no significant difference between X = 0 and X = 1.5 cm, with only a fluctuation comparable to the error bars (figure 8(b)). Within a single YZ plane, the system exhibits uniform sphere resolution ((σ_rms/mean) less than 10%) among six rows for both X = 0 and X = 1.5 cm.

Figure 8.

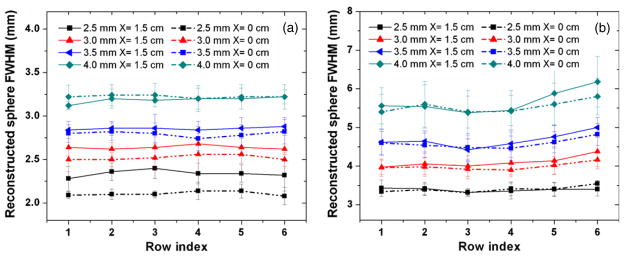
Resolution uniformity study for both central plane (X = 0) and off-center plane (X = 1.5 cm) is shown for (a) in-plane (parallel to panels) and (b) orthogonal-plane (perpendicular to panels) reconstructed image slices. DOI resolution is set to be 2 mm and the panel separation is 4 cm. Within inherent error, the system achieves very uniform in-plane and orthogonal-plane resolutions. However, a dependence of in-plane resolution on the off-center distance (X value) is observed. In the in-plane slices this dependence is most noticeable for the smaller sphere sizes. The definition of row index is shown in figure 6.

The dependence of sphere resolution in different planes parallel to the panels as a function of the DOI resolution is shown in figure 9. For simplicity, only 2.5 mm and 4.0 mm diameter spheres are chosen. For both of them, the reconstructed sphere resolution exhibits similar response to DOI resolution as described below and only the results of 2.5 mm spheres are described. When the DOI resolution is worse than 3 mm, the in-plane sphere resolution at the center (X = 0) is worse than that of the off-center planes (X = 1.0 and 1.5 cm), as shown in figure 9(a). For instance, with a 9 mm DOI resolution, the in-plane sphere resolution is 3.23 ± 0.60 mm (X = 0 cm) but 2.66 ± 0.22 mm (X = 1.5 cm), corresponding to ~17.6% reduction. However, when the DOI resolution is better than 3 mm, the in-plane sphere resolution at the center (X = 0 cm) is slightly better than that of the off-center planes (X = 1.0 and 1.5 cm) for 2.5 mm diameter spheres (also observed in figure 8(a) for the 2 mm DOI resolution, 2.09 ± 0.04 mm (X = 0 cm) against 2.28 ± 0.14 mm (X = 1.5 cm)). In contrast, for the orthogonal-plane sphere resolution, no such dependence is observed and different planes exhibit similar response to DOI resolution (figure 9(b)). The imaging plane at X = 1.0 cm achieves comparable orthogonal-plane sphere resolution to that of the central plane at X = 0. For instance, for the 2 mm DOI resolution, the orthogonal-plane sphere resolution is 3.34 ± 0.10 mm (X = 0 cm) and 3.38 ± 0.20 mm (X = 1.0 cm). In summary, if the sphere resolution components were merely determined by DOI resolution, we would not expect to observe the complicated responses seen in figure 9(a).

Figure 9.

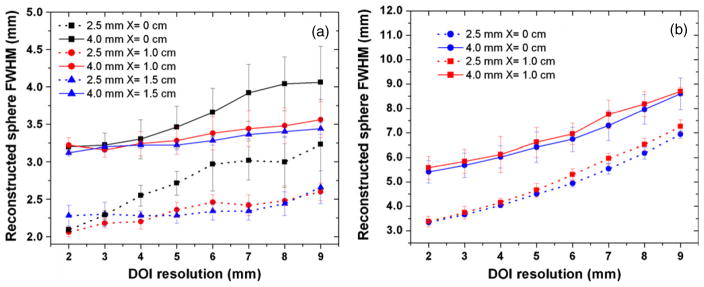
The reconstructed sphere resolution dependence on the off-center location of spheres (X value) for 2.5 mm diameter (bottom curves) and 4.0 mm diameter (top curves) spheres. The panel separation is 4 cm. (a) For the in-plane resolution, X = 0, 1.0 and 1.5 cm were studied. (b) For the orthogonal-plane resolution, only X = 0 and 1.0 cm were studied (b) (the tails of the 4.0 spheres sphere overlap the panel for X = 1.5 cm along the X direction).

The sphere resolution dependence on the panel separation is shown in figure 10 for a reconstructed slice through X = 0 using the same phantom configuration as that simulated in figure 6. The only difference is that the panel separation was enlarged to 8 mm. The comparison is only performed for the 2.5 mm diameter spheres and the DOI resolution ranges from 2 mm to 7 mm. Compared to a 4 cm panel separation with the same DOI resolution (5 mm), the 8 cm panel separation shows no significant difference in the in-pane sphere resolution (e.g. 2.55 ± 0.16 mm for an 8 cm separation and 2.71 ± 0.15 mm for a 4 cm separation), while the degradation of the orthogonal-plane sphere resolution is more significant (e.g. 4.87 ± 0.22 mm for an 8 cm separation and 4.50 ± 0.15 mm for a 4 cm separation).

Figure 10.

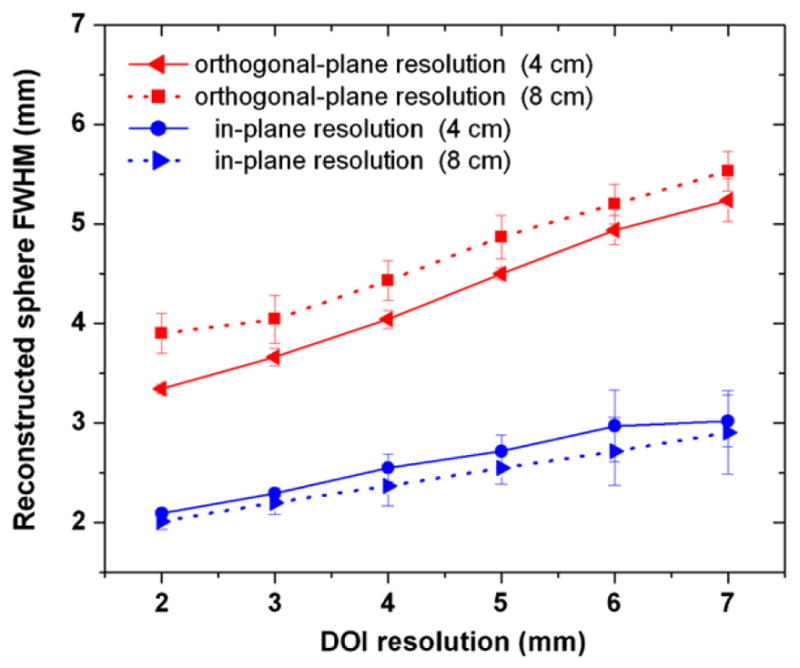
In-plane (parallel to panels) and orthogonal-plane (perpendicular to panels) reconstructed sphere resolutions versus DOI resolution for the 4 cm and 8 cm panel separation. The spheres of 2.5 mm size were chosen for the comparison. The same phantom as that simulated in figure 6 was used. DOI resolutions from 2 mm to 7 mm were studied. The larger panel separation has no statistically significant impact on the in-plane reconstructed sphere resolution but slightly degrades the orthogonal-plane reconstructed sphere resolution.

From the sphere resolution results shown in figures 7–10, several important characteristics are highlighted here prior to more detailed discussion later. First, very uniform sphere resolution across the FOV can be achieved within a given YZ plane (parallel to the panels), for both in-plane and orthogonal-plane directions (figure 8). Second, both components of the system sphere resolution (parallel to and orthogonal to panels) show dependence on DOI resolution, off-center location and panel separation (figures 7, 9 and 10). The in-plane sphere resolution behaves in a more complicated manner than the orthogonal-plane sphere resolution. Third, even at an ideal DOI resolution, the orthogonal-plane sphere resolution is always worse than the in-plane resolution, and thus the reconstructed spheres have a non-isotropic, ellipsoid shape instead of a spherical shape.

3.4. Hot sphere visualization study

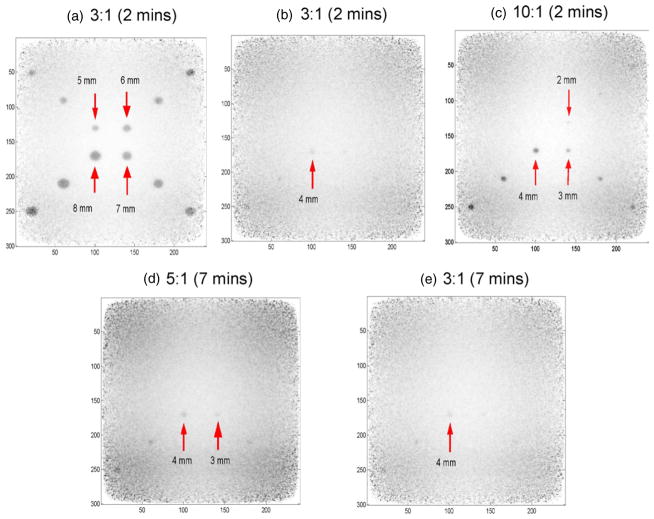
The reconstructed images of spheres of various sizes in warm background are shown in figure 11. DOI resolution was chosen to be 3 mm for this data. As stated in section 2.5, we used both the direct observation and the Ross criteria to cross-validate whether a hot sphere is visualized in this study. For large spheres with a sphere to background activity concentration ratio of 3:1, satisfactory sphere visualization is achieved within a 2 min acquisition time (figure 11(a)). However, for a 2 min imaging time and the same concentration ratio of 3:1, the 4 mm diameter sphere is the smallest visualized (CNR = 4.76) (figure 11(b)). If the concentration ratio is increased to 10:1, 2 mm, 3 mm and 4 mm diameter spheres are all visible in 2 min (CNR equals to 3.66, 7.83 and 11.8, respectively) (figure 11(c)). While for a lower contrast ratio (5:1), an imaging time around 7 min is required in order to visualize a 2 mm sphere (CNR = 3.92) (figure 11(d)), though the visualization is relatively poor than that for the case of an activity concentration ratio of 10:1 and spheres at the FOV corner are still not visible due to lower sensitivity. Furthermore, for the lowest sphere to background concentration ratio (3:1), the spheres of 3 mm and 4 mm diameter can be visualized (CNR = 4.42 and 6.93, respectively) at 7 min acquisition time (figure 11(e)), while the 2 mm diameter sphere is still not visible. In the whole study, since the simulated scan durations were relatively short (≤7 min), the visualization for spheres less than 1 mm is not achieved.

Figure 11.

In-plane reconstructed spheres of various sizes and activity concentration ratios in warm background for signal to noise and contrast to noise ratio studies (DOI resolution = 3 mm). The panel separation is 4 cm. The sphere sizes were 1–8 mm in diameter. The activity concentration ratios studied were 10:1, 5:1 and 3:1. The time inside the bracket indicates the imaging time. Spheres larger than 5 mm even with the low activity concentration ratio of 3 to 1 can be clearly resolved in 2 min. When the simulation is stopped at 7 min, the 2 mm sphere with a concentration ratio of 10:1 can be visualized. The visualization for spheres less than 1 mm diameter requires more statistics and is under investigation.

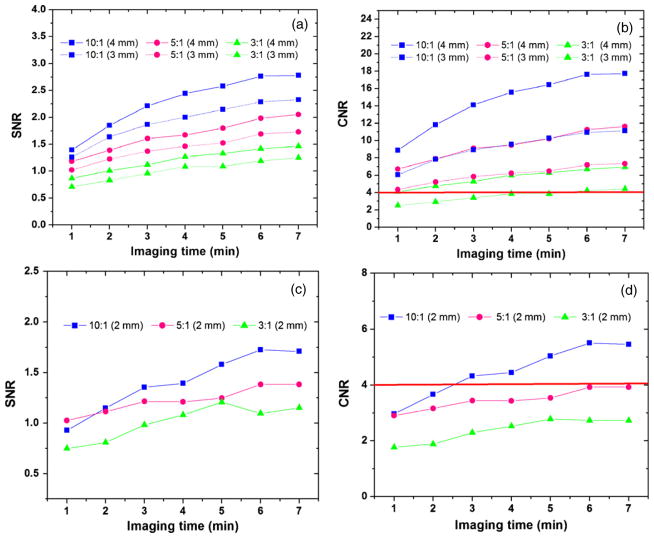
The CNR and SNR for different sphere diameters and contrasts are shown in figure 12, as a function of the imaging time. Intervals of 30 s are chosen for this analysis. For all cases, larger sphere diameter and higher concentration ratio result in higher SNR and CNR. For the same sphere size and the same concentration ratio, both CNR and SNR continuously increase as the total imaging time increases, due to the improved counting statistics. The cross-validation between the simulation results and Rose criterion is made here. The Rose criterion states that a CNR above 3–4 is required for good sphere detection (Rose 1973). As shown in figure 12(b), the CNR for a 3 mm sphere with a concentration ratio of 3:1 for a 2 min acquisition duration is roughly 3.0, but that sphere is not easily distinguished from background (figure 11(b)). On the other hand, the 4 mm sphere with the same contrast has the CNR slightly above 4 and it can be visualized above background (CNR = 4.76) (figure 11(b)). For both 3 mm and 4 mm spheres, once the imaging time is longer than 4 min, the CNR remains larger than 4 and this implies that good sphere visualization would be achieved.

Figure 12.

Reconstructed in-plane CNR and SNR for spheres of various sizes, activity concentration ratio and imaging time. The solid horizontal line in (b) and (d) marks the CNR being equal to 4, which is the requirement specified by the Rose criterion for good lesion detection. No interpretable results for 1 mm diameter spheres were obtained in this study.

For the 2 mm sphere and a 10:1 contrast ratio, the CNR for the imaging time of 2 min is 3.6 (figure 12(d)) and it is also visible (figure 11(c)). However, for a sphere to background concentration ratio of 5:1, the CNR increases slowly up to 3.9 as the imaging time is increased to 7 min. This is also in good agreement with the visualization study as shown in figure 11(d). In other words, there was not good visualization of the 2 mm sphere for a simulated acquisition time of less than 7 min. Furthermore, for the 2 mm diameter sphere, the CNR for a concentration ratio of 3:1 is about 2.8 at 7 min and thus a much longer time is required for the system to achieve good visualization. Combining the CNR requirement with the SNR results, the conclusion is that SNR exceeding ~1.25–1.5 can provide satisfactory sphere detection in our simulation.

Overall, the visualization study and the quantitative analysis results correlate well with each other and we are able to predict that for a 3 mm DOI resolution, the system is able to detect spheres larger than 4 mm within 2 min imaging time for a sphere to background activity concentration ratio as low as 3:1; the 3 mm sphere with a concentration ratio of 3:1 can be detected in 4 min and the 2 mm sphere with a concentration ratio of 5:1 can be detected in 7 min.

4. Discussion

We propose to develop a high-performance, low-cost, portable PET camera dedicated to detection, diagnosis, staging and monitoring of breast cancer. There are two unique characteristics that distinguish the proposed system from the previous efforts in breast cancer PET instrumentation. First, CZT detectors are used rather than scintillation detectors which increase the energy conversion efficiency of 511 keV photons to an electronic signal and results in an order of magnitude better energy resolution—a factor important for improved scatter and random rejection and thus contrast recovery and quantification. Second, the commercially available cross-strip CZT detectors can precisely measure the 3D interaction coordinates of 511 keV photons, including their interaction depth in the panels, enabling highly uniform spatial resolution throughout the FOV for a very close panel separation (e.g. 4–8 cm) required for enhanced photon collection efficiency. We performed a comprehensive simulation study of the performance of the proposed system, with respect to photon sensitivity, count rate capability, spatial resolution and lesion visualization.

4.1. Photon sensitivity

The proposed system is expected to achieve an ~32% sensitivity for a point source at the center for a 4 cm panel separation (figure 3). This is over an order of magnitude higher than the standard whole body clinical system (~1–2% at the isocenter) (Alessio et al 2004, Habte et al 2007). Simulation results also predict that it exhibits higher sensitivity than a state-of-the-art whole body PET (~6.8% peak sensitivity) and an LSO dual-panel PET system (~18.0% peak sensitivity) (see section 2.2 for system configurations). The increased photon sensitivity of the CZT system is attributed to the dual-panel configuration, close proximity to the breast, the minimum of 4 cm detector thickness seen by incoming photons and high packing fraction of the CZT detectors. The high photon sensitivity helps to enhance the sphere visualization capabilities of the camera by facilitating a good SNR for high-resolution image reconstructions. Alternatively, it can help to reduce the imaging time/dose.

4.2. Count rate performance

The results in figure 4(c) indicate that a CZT dual-panel system is able to achieve comparable NEC obtained with an LSO-based dual-panel system, if the breast activity concentration is relatively low (<14.8 kBq s⁻¹). Compared to CZT detectors, the LSO-APD detector module has ~12–14% FWHM energy resolution (Zhang et al 2007a) and ~2–4 ns time resolution (Zhang et al 2007b). The superior NEC performance of the CZT-based system is attributed to its higher photon sensitivity as mentioned above and its superior energy resolution, even though it has poor coincidence time resolution (~8 ns FWHM). Good energy resolution, for a narrower energy window, can improve the rejection of scatter coincidences. Furthermore, good energy resolution is also beneficial for rejecting single photons that have scattered, which results in the effective rejection of multiples and random coincidences as well.

The presence of heart and torso is a great challenge for PET breast imaging, as they will result in significant background counts which consist of scatter and random coincidence photon events. These events will greatly compromise the contrast recovery ability of the system. The random coincidence rate depends upon both single photon rates and the width of time window (Sorenson and Phelps 1986). The time window is normally set to be twice the time resolution of the system. Therefore, if a system has superior energy resolution, a very narrow energy window may be used to reject single photons that scatter, effectively reducing the single photon count rate (Levin et al 2006), and hence reducing both the S and R rates in equation (1). The contribution from the single rate is more significant than the time window as the random rate is proportional to the square of the single rate but is only linearly dependent on the time window or time resolution. This is likely to be an advantage of deploying CZT detectors over LSO- or BGO-based scintillation detectors for breast imaging. Such advantages will help to improve the SNR and CNR of the proposed system.

Furthermore, the simulation results in figure 4(c) indicate that the NEC of the whole body PET scanner is quite comparable to that of the LSO-based dual-panel system (e.g. at the breast activity concentration of 7.4 kBq s⁻¹). This brings up an interesting question that why a dedicated system does not necessarily achieve better NEC performance. We believe that this is due to two reasons. On one hand, the dedicated dual-panel system does achieve higher photon detection sensitivity due to the improved solid angle coverage, which would consequently increase the NEC. On the other hand, putting two panels closer to the breast would increase the random coincidences more significantly than the true coincidences. For instance, for a cylindrical PET system of radius r, the true coincidence is proportional to 1/r, while the random coincidence is proportional to 1/r² (Sorenson and Phelps 1986). As a result, a dedicated system sees more random events than that seen by a whole body system of large diameter, which implies that the NEC is to be reduced (equation (1)). This hypothesis is to be validated using other methods for random estimation such as using a delayed window (Brasse et al 2005, Bowen et al 2009). Furthermore, when the delayed window method is used to estimate random coincidences, we will investigate whether a factor of 2 needs to be applied (i.e. 2R instead of R in equation (1)) for a dedicated PET system, taking into account facts that a dedicated PET system has much higher photon detection sensitivity (less noisy in counting statistics) and relatively small randoms/prompts ratios (less error propagation) (Brasse et al 2005).

4.3. Sphere resolution

The simulation results show that the system is capable of achieving 1 mm in-plane (parallel to panels) sphere resolution (figure 5) with the list mode 3D OSEM image reconstruction algorithm, with a DOI resolution less than 2 mm. Moreover, for both 4 and 8 cm panel separation, the system sphere resolution shows dependence on several factors such as DOI resolution, panel separation and off-center distance (figures 7–10). A very important observation is that both of these two sphere resolution components are affected by the limited angle tomography geometry (figures 6 and 7). Although clearly the degree of DOI resolution strongly affects the reconstructed resolution isotropy, even when DOI resolution is set to be zero, the reconstructed spheres in the orthogonal plane (perpendicular to the panels) still have an elliptical shape instead of a circular shape. This implies that besides the DOI resolution, the nature of limited angle tomography of the proposed dual-panel system also introduces substantial resolution blurring in the XY plane, predominantly along the X direction. Here we discuss the relevance of simulated sphere resolution results to the practical system instrumentation, and explain why the system sphere resolution exhibits such a complicated response.

The results from our simulation will be used to guide the system design and validate the experiments once the first sub-system is built. The dependence of both in-plane sphere resolutions and orthogonal-plane sphere resolutions on the DOI resolution can be used to guide the design of cathode strip pitch (see figure 1) to meet pre-defined reconstructed sphere resolution goals, in conjunction with other system design considerations. Specifically, the simulation results indicate that in order to resolve 1 mm spheres in the in-plane image, a DOI resolution of at least 2 or 3 mm is required. However, to be able to resolve 1.5 mm spheres in the in-plane image, a DOI resolution of around 5 mm is still acceptable. This implies that the final choice of DOI resolution (determined by the cathode strip pitch) has to be selected with the intended sphere resolution requirement taken into account. Alternatively speaking, we do not have to build a system with a 2 mm DOI resolution if the sphere resolution requirement of the system is 1.5 mm. Though the finest DOI resolution would be regarded as the best choice for high-resolution 3D imaging, there are several practical issues to be considered. First, the total number of electronic channels would increase with the number of strips per detector. Second, if the DOI resolution is too small, which means that the size of a cathode pitch is too close to that of an anode pitch, we might not be able to benefit from the ‘small pixel effect’ (Barrett et al 1995) and therefore will compromise both energy resolution and potentially coincident time resolution of the proposed system (Levin et al 2004). Third, it might be likely that there are different requirements for the in-plane and orthogonal-plane sphere resolutions. The latter degrades more rapidly with reduced DOI resolution and limited angle tomography geometry, while the former is relatively insensitive to that design parameter.

Considering the fact that most dedicated PET systems do not have DOI resolution at all, it may not be necessary to require a high DOI resolution in order to reduce complexity. Furthermore, we would not be able to detect 1 mm detector spheres with the limitations in the specificity (i.e. target to background ratio) of the available cancer imaging radiotracer and in a reasonable time under the constraints of breast imaging, as shown in figure 11, where the 1 mm sphere with 10:1 activity concentration ratio could not obtain sufficient CNR for visualization within 7 min imaging time. As a result, setting the sphere resolution requirement too low is not realistic. This is also why we chose a 3 mm DOI resolution for the sphere visualization study, which we believe is a good tradeoff between sphere resolution and other practical considerations.

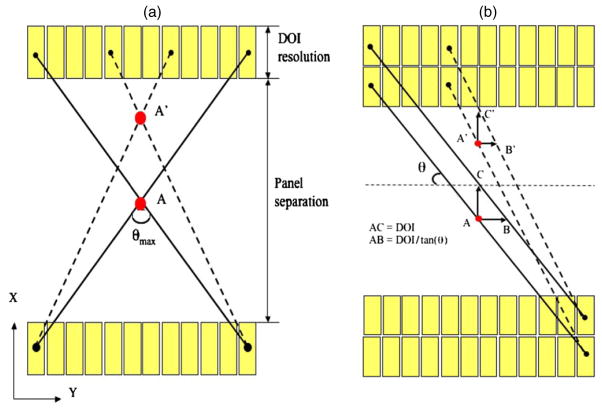
The reason why DOI resolution has different impact on the in-plane and orthogonal-plane sphere resolutions (see figure 7) can be explained by considering the effects of incomplete angular sampling for the limited-angle geometry of two panels and the DOI blurring effect (also known as parallax error) along the X direction. To help in the explanation, we first briefly provide a comparison between a standard x-ray planar radiograph and our proposed system. Similar to the planar radiograph (assume the projection to be placed in the YZ plane), the dual-panel system has complete sampling along both Y direction and Z directions. Therefore, no artifact occurs in the final 2D image. However, a limitation for the standard planar radiograph is that no spatial information is available along the X direction. Such limitation is addressed in our proposed system as it incorporates photon interaction positioning ability (DOI resolution) along the X direction. The impact of introducing DOI resolution for a dual-panel PET system configuration can be explained as follows. Let us consider an XY plane at a given Z value, with one layer of detectors (i.e. no DOI resolution) within each panel (figure 13(a)). Assume that the events are positioned at the center of each crystal. Such a configuration only covers a certain limited range of projection angles θ_max less than 180°. Such an incomplete angular sampling would cause resolution degradation or artifacts along the X direction (orthogonal to panels), as supported by the results shown in figure 6. The more limited the projection angle range, the worse the artifact will be, which is well understood for PET image reconstruction (Cherry et al 2003). By either moving a plane away from X = 0 or increasing the panel separation for a plane at a given X would degrade the in-plane sphere resolution, due to the decrease of θ_max. This explains why even with DOI resolution being zero, the orthogonal-plane image of spheres exhibits an elliptical shape (figure 6).

Figure 13.

(a) Illustration of the limited angle tomography effect. The dual-panel geometry only covers a certain limited range of projection angles (θ_max less than 180°) and the incomplete angular sampling would cause resolution degradation or artifacts along the X direction (orthogonal to panels). (b) Illustration of the DOI blurring effect (also known as parallax error) and how it affects both the in-plane and orthogonal-plane resolutions. Only two layers of detectors are shown. For an adjacent parallel LOR pair, the effective blurring (i.e. parallax error) is AB (A′B′) along the Y direction (which affects the in-plane resolution) and AC (A′C′) along the X direction (which affects the orthogonal-plane resolution).

On the other hand, the effect of incorporating DOI resolution along the X direction is illustrated in figure 13(b). We only choose two layers of detectors for explanation but the concept can also be generalized to any number of DOI resolution elements. For an adjacent parallel LOR pair, the effective blurring (i.e. parallax error) is AB (A′B′) along the Y direction (which affects the in-plane resolution) and AC (A′C′) along the X direction (which affects the orthogonal-plane resolution). Effectively, DOI resolution enables more precise LOR assignment in both directions. Thus, we observe that the degree of spatial resolution degradation along the direction orthogonal to the two panels that is typically of a limited angle tomography configuration is mitigated by having high-resolution DOI capabilities that enable more accurate positioning of oblique LORs.

Note that the distances AB and A′B′ are dependent on θ, while the distances AC and A′C′ are not. As the source moves from the center to the edge along the X direction, the length of AC (A′C′) will remain equal to the DOI blurring effect but the length of A′B′ will be smaller than the length of AB due to the increase of θ. This explains why we see the dependence on the DOI resolution for both in-plane and orthogonal plane sphere resolutions (figure 7).

Combining the effects of limited angle tomography and the DOI burring effect, we are able to explain the complicated responses of sphere resolution. First, for the orthogonal-plane sphere resolution, it is mainly determined by DOI resolution and also slightly by the limited projection angle range. As a result, the orthogonal-plane sphere resolution is very sensitive to the DOI resolution (figure 7). For a fixed DOI resolution better than 3 mm, as the image plane shifts from the center (X = 0) toward the edge (X = 1.0 cm) (figure 9(b)), or alternatively as the panel separation increases from 4 cm to 8 cm (figure 10), the orthogonal-plane sphere resolution either shows no significant variation (figure 9(b)) or degrades only slightly (figure 10). In both of these situations, the angular sampling coverage decreases, causing more sphere resolution blurring, while the blurring from the DOI resolution remains the same.

On the other hand, the in-plane sphere resolution depends on several factors. First, it is mainly determined by the detector’s intrinsic spatial resolution along the Y or Z direction (1 mm in this study). Second, sphere resolution blurring along the X direction is introduced when there is limited DOI resolution. Such a blurring factor goes as DOI/tan(θ), where DOI = DOI resolution (figure 13). Third, minor sphere resolution blurring is introduced by the limited range of projection angles, which is similar to the problem introduced in the orthogonal plane, but the extent of blurring in the Y or Z direction is less and is represented by the semi-minor (rather than semi-major) axis of the elliptical shape of the reconstructed spheres. The second and third factors together determine the overall blurring of the in-plane sphere resolution.

From the results of reconstructed 2.5 mm spheres in figure 9(a), when the DOI resolution is 2 mm, the in-plane sphere resolution for X = 0 is about 9.1% less than that of X = 1.5 cm since the spheres at X = 0 see a larger range of projection angles (figure 13(a)). However, as DOI resolution degrades above 3 mm, the opposite pattern is noted: the in-plane sphere resolution for X = 0 is 17.6% more than that of X = 1.5 cm when DOI resolution is 9 mm (figure 9(a)). This can be attributed to the fact that the blurring component DOI/tan(θ) plays a more significant role than the blurring caused by limited angle tomography geometry, and DOI/tan(θ) blurring component decreases due to the decrease of θ for those off-center planes (figure 13(b)). The implications of this competition between DOI blurring effect and the limited projection angle range are two fold: first, for a system with dual-panel geometry and DOI resolution worse than 4 mm, the in-plane sphere resolution will be non-uniform across the FOV and the extent of that variation will increase as the DOI resolution degrades. Second, the DOI resolution of about 3 mm might be an optimum configuration for the proposed system and will enable uniform sphere resolution throughout the sensitive FOV.

4.4. Hot sphere visualization

The sphere visualization studies (figures 11 and 12) show that for a panel separation of 4 cm and DOI resolution of 3 mm, using a relatively short acquisition time of 2 min one is able to the detect the 2 mm diameter sphere with a 10:1 sphere to background activity concentration ratio while 7 min are necessary to detect the 2 mm diameter sphere with a 5:1 activity concentration ratio. For larger spheres or higher activity concentration ratios, the imaging time can be further reduced. To be able to detect the smallest sphere of 1 mm diameter, we predict that even with a 10:1 activity concentration ratio, the imaging time would have to be longer than 1 h, which might not be feasible for clinical breast imaging with PET. However, we feel that being able to resolve 2 mm diameter lesions in a few minutes of acquisition time will be very useful in characterizing early signs of breast cancer or its recurrence. The proposed system exhibits superior sphere visualization within a much shorter imaging time than a standard whole body PET scanner (30–60 min for detection of 5–10 mm diameter spheres) (Alessio et al 2004). This is likely due to the improved photon sensitivity, spatial resolution and NEC performance of the proposed system. A short acquisition time could potentially help to increase PET’s role in breast cancer management by simply making it more practical to perform PET studies in the setting of a breast imaging clinic. Longer acquisition time affects patient comfort, especially if the breast is compressed, and decreases patient throughput. These are factors that currently make PET not as practical for the breast clinic. We envision that the proposed compact device will actually sit in the breast imaging clinic, so scan time, throughput, as well as footprint are critical issues.

4.5. Clinical relevance of breast-dedicated PET

The clinical relevance of such a high performance breast PET system requires investigation, but we hypothesize that it can be expected to be useful in several applications. First, it may improve the prognosis of breast cancer as, if successful, it will allow earlier detection of malignant lesions (when the lesions are smaller) and therefore help to resolve current challenges with detection, diagnosis, staging and monitoring of breast cancer. Second, such a camera may help to guide or reduce the invasiveness of biopsy in diagnosis procedures by improving accuracy of sampling malignant tissue, as it can visualize smaller aggregates of biologically active malignant cells. Third the camera can also guide a breast cancer surgeon to remove the primary tumor, including visualizing smaller clusters of malignant cells at the resection margins, which could possibly help to reduce the rate of recurrence and repeat excisions. Finally, early visualization of miniscule focal accumulation of tracer could help improve the accuracy of identifying local recurrence post-treatment.

5. Conclusions

We are developing a dual-panel CZT PET system dedicated to breast cancer imaging. A Monte Carlo simulation tool was used to investigate the system performance. The proposed system is expected to achieve ~32% sensitivity for a point source at the center for a 4 cm panel separation. For the simplified breast phantom surrounded by heart and torso compartments, the simulated peak NEC rate was ~94.2 kcts s⁻¹ (breast volume: 720 cm³ and activity concentration: 3.7 kBq cm⁻³) for a ~10% energy window around 511 keV and ~8 ns coincidence time window. The system is able to achieve 1 mm intrinsic spatial resolution for DOI resolution less than 2 mm. For a 3 mm DOI resolution, the system exhibits uniform sphere resolution uniformity (σ_rms/mean) ≤ 10%) across the FOV. The 3D positioning ability can be achieved using a cross-strip readout design, and the dependence of the sphere resolution on the system factors including the DOI resolution, off-center distance and panel separation was studied. With a 4 cm panel separation and a 3 mm DOI resolution, the system is expected to be able to detect 2 mm spheres with low activity concentration ratio of 5:1 within about 7 min. An important conclusion from this work is that the DOI resolution promotes both uniform as well as isotropic resolution throughout the FOV even for the limited-angle geometry of the dual-panel system.