Mortality by education level at late-adult ages in Turin: a survival analysis using frailty models with period and cohort approaches

Abstract

Objectives

Neglecting the presence of unobserved heterogeneity in survival analysis models has been showed to potentially lead to underestimating the effect of the covariates included in the analysis. This study aimed to investigate the role of unobserved heterogeneity of frailty on the estimation of mortality differentials from age 50 on by education level.

Design

Longitudinal mortality follow-up of the census-based Turin population linked with the city registry office.

Setting

Italian North-Western city of Turin, observation window 1971–2007.

Population

391 170 men and 456 216 women followed from age 50.

Primary outcome measures

Mortality rate ratios obtained from survival analysis regression. Models were estimated with and without the component of unobserved heterogeneity of frailty and controlling for mortality improvement over time from both cohort and period perspectives.

Results

In the majority of cases, the models without frailty estimated a smaller educational gradient than the models with frailty.

Conclusions

The results draw the attention of the potential underestimation of the mortality inequalities by socioeconomic levels in survival analysis models when not controlling for unobserved heterogeneity of frailty.

Article summary.

Article focus

• Neglecting the presence of unobserved heterogeneity in survival analysis models has been shown to potentially lead to underestimating the effect of the covariates included in the analysis.

• Although frailty models have been widely developed to account for unobserved heterogeneity, in differential mortality analyses this source of variation is seldom controlled for. This study has applied these models to a longitudinal mortality analysis by education level.

Key messages

• Mortality differentials by education (or by any other variable used as a proxy of socioeconomic status) could be larger than those estimated with standard survival analysis approaches that do not control for unobserved heterogeneity.

Strengths and limitations of this study

• The strength of this study lies in the population-based longitudinal data. The long observational time (36 years) for more than 847 000 individuals gives a solid base for statistical power and detection of trends.

• The limitation consists in the lack of individual information on lifestyle factors and health events, which could certainly help to better model the concept of unobserved individual frailty by uncovering a part of it.

Introduction

An extensive body of literature shows significant differential mortality by socioeconomic condition.^1–3 The elderly show decreasing relative social inequalities in general mortality with increasing age.^4–8 The age-as-leveller hypothesis attributes this to factors that contribute to the levelling-off of differences at old ages: governmental support to the elderly,^9–11 disengagement from systems of social stratification¹² and general vulnerability.^{13 14} However, this phenomenon could also be an artefact of selection due to the unobserved characteristics of the individuals: selective effects of earlier higher mortality, experienced by the disadvantaged group, would leave more robust individuals at old ages, causing the convergence with the risk of the lower mortality group that is subject to weaker selection.^15–18 Neglecting these hidden differences in survival chances (called unobserved frailty) has been shown to lead to biased estimates of the mortality hazard and of the effect of the covariates on the survival probability.^19–25

In longitudinal analyses on differential mortality, it is important to control for hidden frailty because not controlling for it, in models of survival analysis, could lead to biased estimates of the effect of social position on mortality risk. The statistical literature shows that the bias is towards zero.^24–26 This would lead to an underestimation of the relative differences in mortality risks by socioeconomic group. Frailty models have been developed to control for unobserved frailty and to evaluate its impact on the observed mortality dynamics.²⁷ For more detailed explanations of the frailty models and how they relate to differential mortality analyses, please see online supplementary appendix A.

This study investigated the presence of selection processes in the mortality patterns of the Turin population (North-West Italy) from age 50 on. Adopting a longitudinal perspective, this study aimed to investigate if the estimates of the mortality differentials are affected by the introduction of the unobserved heterogeneity component into the models.

Data and methods

We used high quality census-linked data from the Turin Longitudinal Study (TLS), which includes 1971, 1981, 1991 and 2001 census data for the Turin population. TLS records the individual census sociodemographic information and, through record linkage with the local population registry and other local-health information systems, collects information on vital status, cause of death and other health indicators.^{28 29}

For this study, the individuals registered in Turin during at least one of the four censuses were selected. Data on their migration and vital status were followed up until the end of July 2007. The result is an observation window of 36 years (from 24 October 1971, official date of the census, to the end of July 2007, end of the linkage) during which the individuals were followed up until death, emigration from the city or end of the observation period. The follow-up started at age 50. The study population contains 391 170 men and 456 216 women.

Study information includes an individual’s date of birth, date of exit from the study, cause of exit (death or emigration), sex, macroregion of birth and education level.

Consistent with the literature^30–33 education level was used as an indicator of social position.

The study also controlled for the individual macro region of birth, as Turin is characterised by a history of immigration from other regions of the country.³⁴

To facilitate comparison over a long follow-up and different cohorts, we created three broad educational groups: high (high school diploma or higher), medium (junior high school) and low (primary school or lower).

We estimated parametric survival models stratified by gender and as a function of macroregion of birth and education level, with and without a parameter for the unobserved heterogeneity component. The choice of using parametric models, rather than semi parametric or non parametric ones, is justified by the wide demographic literature showing that human adult mortality can be accurately described by a Gompertz function³⁵ or by some Gompertz-like variants, like Makeham. To identify the best functional form for the baseline, we compared the models with Akaike Information Criterion (AIC).³⁶

The data are both right censored (due to emigration or end of follow-up) and left truncated (due to the different age at entry in the study of individuals).

The study includes many cohorts, each passing through 36 years of observation at different ages. However, from 1971 to 2007, a significant mortality improvement occurred and younger cohorts experienced lower age-specific mortality than older cohorts.

Time is a complex variable including three dimensions: age, period and cohort. Controlling adequately for the effect of time would require simultaneous assessment of the three components, but such models have been not identifiable for a long time because of the linear dependence between the three dimensions.^37–39 Recently, it has been shown that, through the introduction of the generalised linear mixed models framework, new estimation methods and model specifications can be used to tackle the identification problem.⁴⁰ However, this goes beyond the scope of our study.

We adopted two approaches for the control of time, corresponding to an age-cohort approach and an age-period approach, being aware that they represent two different dimensions of time.

First, we regarded the improvement as a cohort phenomenon, including a covariate for the cohort to which the individuals belong. In this setting, controlling for unobserved heterogeneity was implemented with univariate frailty models, which estimate the baseline parameters, the coefficients of the covariates and the variance of frailty (assumed to follow a γ distribution with mean 1 and variance σ² to be estimated).

We then considered the improvement as a period phenomenon and split the time into several calendar period covariates, as well as the survival spell of the individuals, according to which period they were passing through. This implied organising the data into clusters, where each cluster represents one individual's survival spells. In this setting, to control for unobserved heterogeneity shared frailty models are needed, where the spells in each cluster pertain to the same individual and share the same hidden frailty. For computational reasons, the estimation of these highly complex models required the use of random subsampling.^41–43 We repeated the estimation 250 times on a 1% sample of the dataset, randomly drawn without replacement and stratified by the major variables in analysis. The aim was to approximate the parameters’ estimates based on the empirical distribution of the repeated estimates.

In the model without frailty, it was possible to include a finer calendar period division, 12-period variables of 3 years each (1971–1973, 1974–1976…), while in the model with frailty, for computational reasons, the number of variables was reduced to two broader periods: 1971–1990 and 1991–2007.

Computations were realised with the software R.⁴⁴ Formal details are in online supplementary appendix A.

Results

Figure 1 shows that the log-death rates by education level and gender, for the cohort aged 50–59 in 1971, converge at old ages. Other cohorts showed very similar patterns.

Figure 1.

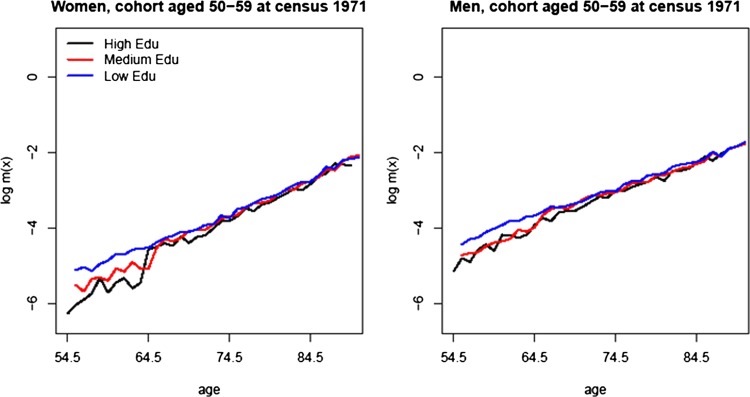
Death rates on logarithmic scale for the birth cohort aged 50–59 at the beginning of the follow-up (1971) by three education levels: high, medium and low.

A preliminary analysis found that the reduction of the gradient over age is statistically significant and more pronounced among women (results are reported in online supplementary appendix B, table B1).

Frailty modelling

Table 1 shows AIC of the survival models, fitted to the all population mortality, with Gompertz and Makeham baselines. It also shows the results of the fit when unobserved frailty was controlled for. The comparison reveals that the Gompertz baseline was a better fit for male data, while the Makeham baseline was better for female data. In both cases, the models controlling for unobserved heterogeneity performed a better fit (table 1).

Table 1.

Model selection for the baseline hazard and comparison of the model with best baseline hazard and unobserved heterogeneity of frailty component

	Model with different baseline hazards		Model with best baseline hazard and frailty
	Gompertz	Makeham	Gamma-Gompertz	Gamma-Makeham
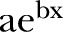
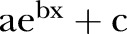
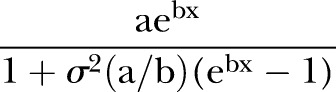
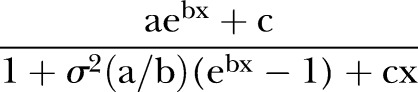
AIC women	1 327 474	1 326 878	–	1 326 695
AIC men	1 303 693	1 303 695	1 303 655	–

Comparison is based on AIC.

We then estimated the mortality differentials, using a cohort and a period approach, to control for mortality improvement over time. We included in the analysis the variables for education level (high, medium and low) and region of birth (North-West, North-East, Center, South and Abroad).

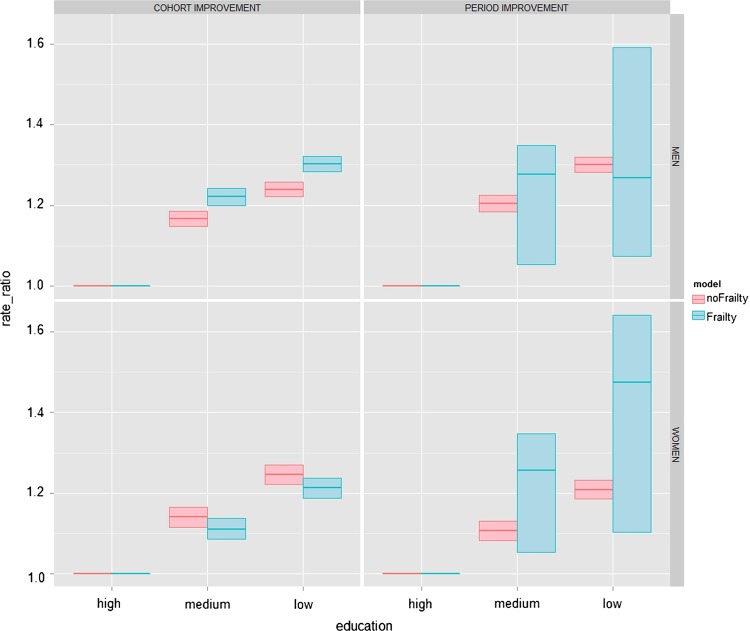
Tables 2 and 3 report the results of the models estimated with and without the unobserved heterogeneity component: the parameters of the baseline hazard (a and b of the Gompertz function for men and a, b and c of the Makeham function for women), the variance of frailty in the population and the rate ratios of the mortality differentials by education level and region of birth. Figure 2 compares the results for the educational gradient obtained by the models with and without frailty.

Table 2.

Results of the regression models with cohort covariates

	Men				Women
	Model without frailty		Model with frailty		Model without frailty		Model with frailty
	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI
a	5.241×10–5	5.237×10–5 to 5.245×10–5	4.495×10–5	4.488×10–5 to 4.501×10–5	3.767×10–6	3.755×10–6 to 3.779×10–6	1.605×10–6	1.588×10–6 to 1.623×10–6
b	0.081	0.080 to 0.082	0.083	0.082 to 0.084	0.106	0.105 to 0.107	0.117	0.115 to 0.119
c	–	–	–	–	0.001	0.001 to 0.001	0.001	0.001 to 0.001
σ2	–	–	0.035	0.027 to 0.045	–	–	0.096	0.082 to 0.111
Cohort	0.016	0.015 to 0.016	0.016	0.015 to 0.016	0.016	0.015 to 0.016	0.017	0.016 to 0.017
Education level
High	1	–	1	–	1	–	1	–
Medium	1.166	1.147 to 1.186	1.221	1.200 to 1.243	1.141	1.116 to 1.166	1.111	1.086 to 1.137
Low	1.239	1.221 to 1.257	1.302	1.283 to 1.322	1.246	1.222 to 1.270	1.213	1.188 to 1.238
Region of birth
North-West	1	–	1	–	1	–	1	–
North-East	1.053	1.036 to 1.070	1.060	1.042 to 1.077	0.989	0.973 to 1.004	0.974	0.958 to 0.991
Centre	1.011	0.984 to 1.038	0.996	0.969 to 1.024	0.939	0.913 to 0.966	0.968	0.939 to 0.998
South	1.000	0.988 to 1.012	0.950	0.938 to 0.962	0.932	0.919 to 0.945	0.987	0.973 to 1.002
Abroad	1.031	1.006 to 1.057	0.998	0.974 to 1.024	1.071	1.047 to 1.096	0.993	0.968 to 1.018
logLk	−651 219		−651 082		−663 238		−663 098
AIC	1 302 456		1 302 184		1 326 496		1 326 218

Baseline parameters (Gompertz for men and Makeham for women) and rate ratios of the differentials by education and region of birth.

Table 3.

Results of the regression models with period covariates

	Men				Women
	Model without frailty		Model with frailty*		Model without frailty		Model with frailty*
	Estimate	95% CI	Mean	0.025–0.0975	Estimate	95% CI	Mean	0.025–0.0975
a	4.159×10–5	3.196×10–5 to 5.410×10–5	0.004	0.000–0.010	8.031×10–6	6.028×10–6 to 1.070×10–5	0.008	0.000–0.016
b	0.096	0.095 to 0.096	0.069	0.061–0.163	0.121	0.120 to 0.122	0.084	0.073–0.106
c	–	–	–	–	0.001	0.001 to 0.002	2.852×10–6	8.610×10–7–2.997×10–5
σ2	–	–	0.269	0.026–0.367	–	–	0.292	0.174–0.367
Calendar period
1971–1973	1	–	1	–	1	–	1	–
1974–1976	0.999	0.972 to 1.027			0.978	0.950 to 1.007
1977–1979	0.947	0.921 to 0.973			0.919	0.893 to 0.946
1980–1982	0.928	0.903 to 0.953			0.896	0.871 to 0.922
1983–1985	0.943	0.918 to 0.969			0.967	0.941 to 0.994
1986–1988	0.870	0.847 to 0.894			0.848	0.824 to 0.872
1989–1991	0.820	0.798 to 0.843	0.728	0.613–0.985	0.796	0.774 to 0.818	0.888	0.671–1.035
1992–1994	0.796	0.774 to 0.817			0.757	0.736 to 0.778
1995–1997	0.741	0.721 to 0.762			0.704	0.684 to 0.724
1998–2000	0.701	0.682 to 0.721			0.682	0.663 to 0.701
2001–2003	0.670	0.652 to 0.689			0.657	0.639 to 0.676
2004–2007	0.631	0.615 to 0.648			0.625	0.608 to 0.642
High	1	–	1	–	1	–	1	–
Medium	1.204	1.184 to 1.225	1.277	1.054–1.349	1.107	1.083 to 1.131	1.256	1.053–1.347
Low	1.301	1.282 to 1.320	1.268	1.074–1.591	1.209	1.186 to 1.232	1.475	1.103–1.641
North-West	1	–	1	–	1	–	1	–
North-East	1.040	1.024 to 1.057	1.075	0.855–1.220	0.963	0.948 to 0.978	1.122	0.888–1.217
Centre	0.943	0.917 to 0.969	1.081	0.854–1.212	0.964	0.938 to 0.992	1.102	0.864–1.218
South	0.900	0.889 to 0.911	1.037	0.854–1.216	0.962	0.949 to 0.975	1.130	0.904–1.220
Abroad	0.965	0.941 to 0.989	1.082	0.864–1.218	0.985	0.962 to 1.009	1.082	0.847–1.215
logLk	−650 997		Na		−663 081		Na
AIC	1 302 034		Na		1 326 204		Na

Baseline parameters (Gompertz for men and Makeham for women) and rate ratios of the mortality differentials by education and region of birth.

*The model with frailty does not report conventional point estimates and CI, but the mean value and the 0.025 to 0.975 quantiles of the empirical distribution of the parameters obtained from the repeated estimates via random subsampling.

Figure 2.

Mortality rate ratios by education level in the models with cohort and period improvement, without and with frailty.

Educational gradient

In the model with the age-cohort improvement approach, the introduction of the frailty term made the male differences widen significantly, consistent with the statistical literature. The rate ratios with respect to high education changed from 1.16 (95% CI 1.15 to 1.19) to 1.22 (1.20 to 1.24) for medium education and from 1.24 (1.22 to 1.26) to 1.30 (1.28 to 1.32) for low education (left upper panel of figure 2). Among women, on the contrary, there was a slight reduction, but the confidence regions of the estimates in the two cases overlap: for medium education, the rate ratio went from 1.14 (1.12 to 1.17) to 1.11 (1.08 to 1.14), and for low education from 1.25 (1.22 to 1.27) to 1.22 (1.19 to 1.24; lower left panel of figure 2). AIC indicates that the models with frailty fit the data significantly better than the models without.

In the model adopting the age-period improvement approach, the AIC comparison of the models with and without frailty was not possible, because the utilisation of random subsampling for the estimation of the frailty model^41–43 did not allow for obtaining a likelihood value comparable with the values of the models without frailty. Moreover, it is necessary to consider that we are comparing conventional point estimates and CIs with values obtained via bootstrapping methods, whose confidence regions are usually wider than conventional CI. Nevertheless, a comparison is still possible.

The introduction of frailty affected the mortality gradient by education. Although the uncertainty around the estimates does not allow for assessing a precise effect, the rate ratios of medium and low education in respect to high education in the models with frailty lie in a higher confidence region than in the models without: among women with a medium education level, it lies between 1.05 and 1.34 compared with 1.08 and 1.13 of the model without frailty and for the low-education group, between 1.1 and 1.6, compared with 1.18 and 1.23. The same pattern can be observed among men.

The male difference between the medium-education and low-education group, on the contrary, was not as clear as that among women.

Other results and the impact of the macroregion of birth on mortality

As expected, the variance of frailty in the cohort models was smaller than in the period models, since periods are more heterogeneous than cohorts.

Women were more heterogeneous than men: 0.09 (0.08 to 0.11) vs 0.04 (0.03 to 0.05) in the age-cohort models and 0.29 (0.17 to 0.37) vs 0.27 (0.00 to 0.36) in the age-period models.

This is consistent with the more pronounced convergence of the hazards by education at old age found among women compared with men. According to the framework of the frailty models, converging hazards are the result of the effect of selection on the population hazards, due to how much variance of unobserved frailty is present in the population at the initial age of observation. The bigger the variance, the stronger the convergence is. For more information about frailty models, the process of selection and how they relate to narrowing mortality differentials at old ages, see online supplementary appendix A.

In the age-cohort models the introduction of unobserved frailty affected the coefficient for the macroregion of birth significantly. Among men, holding education equal, those born in the South show a significant survival advantage over the natives of the North-West, while in the model without frailty there was no such advantage. Among women, the model without frailty showed a significant survival advantage for those born in the South but when frailty was controlled for, this became not significant.

The pattern also resembles the regional mortality macrodynamics that have characterised Italy for most of the 20th century (although the two patterns refer to different phenomena, the first one refers to mortality by region of birth), when male mortality in the South was lower than in the North.^45–48 Cohort-based analyses have highlighted that, in recent cohorts (those born after WWII), there is a reversing trend.^{48 49}

The models with an age-period perspective did not identify any significant geographical differences. This could be due to the utilisation of random subsampling of a 1% sample. Although 250 repetitions are considered by the literature to be a sufficient number for very complex models,^50–52 it is possible that the number was inadequate to identify a clear pattern from the small sample. For more detailed results, see tables 1 and 2.

Discussion

Interest in the role of unobserved heterogeneity in a life-course approach to socioeconomic mortality differences has recently increased. Most of the studies focus on health outcomes,^53–58 while fewer studies also analyse mortality.^59–61 Their findings are not consistent and fuel a still controversial debate.

In this study, we investigated the role of unobserved individual heterogeneity on the estimation of mortality differentials at adult-old ages by education level in a longitudinal perspective. This study investigated if the estimates of the mortality differentials are affected by the introduction of the unobserved heterogeneity component into the models.

We fitted survival analysis models with and without controlling for the unobserved heterogeneity and we found that when this component was included, the models gave a significantly better fit.

We also found that in the majority of cases, the educational gradient estimated by the models with frailty was higher than the one estimated by the models without frailty. When big uncertainty around the estimates did not allow for assessing a precise value, the confidence regions in the models with frailty spanned over higher values than those in the models without frailty. It must be pointed out that, in the age-period approach, the peculiar statistical procedure used to estimate the frailty models did not allow for obtaining a likelihood value comparable with the one of the model without frailty. Thus, the statistical comparison of the models via AIC was not possible, making this evidence weaker. Nevertheless, the results seem to point to a direction that is consistent with the statistical literature about unobserved heterogeneity.^19–26

Among men, such a pattern was found in both the age-cohort and age-period approaches. Among women, on the contrary, this pattern was less clear: in the age-cohort model, controlling for hidden frailty resulted in a slight reduction of the mortality gradient. Social determinants also act on mortality through risk factors that are known to affect more men than women. Moreover, owing to a lag in the smoking and fertility transitions, highly educated women in Turin are more exposed to risk factors like cigarette smoking and a smaller number of children. Therefore, controlling for hidden frailty in the case of women might reduce the educational gradient.

In the models with age-cohort perspective, controlling for the hidden frailty also affected the estimates of the differentials by macroregion of birth, showing a survival advantage of the men born in the South, but not of the women, for whom an advantage was instead detected by the model that did not control for frailty.

The healthy migrant effect^62–67 could cause this pattern. Among the cohorts involved in the migration, women were likely to be more passive actors than men in the migratory decision,^68–70 which might have been responsible for their being selected less than men. Frailty is a general concept embedding all the hidden factors that affect the individual survival chances: innate and acquired frailty, exposure to risk factors, lifestyle factors and so on. Therefore, when controlling for frailty, the survival advantage of women was reduced, as they might have been less health selected than men by the migration. On the contrary, the advantage of men was uncovered. However, another recent study on the impact of migration on all-cause mortality in Turin did not find particularly strong gender differences in the so-called healthy migrant effect,⁶⁶ and this point deserves to be investigated further in future.

The study spanned over a long observation window of 36 years. Therefore, it was important to control for the general mortality improvement that took place during this time. We did so by adopting both an age-period and an age-cohort approach.

The age-period models, as expected, estimated higher heterogeneity than the age-cohort models. Periods aggregate different generations and are expected to be more heterogeneous than the cohorts themselves. In both the period and cohort models, the variance of frailty was higher among women than among men, indicating that men are more homogeneous than women. This could be attributed to a stronger selection process due to mortality that is usually observed to be higher among men than among women.

On the other hand, it is also possible that the industrialisation process and the internal migration experienced by Italy after WWII³⁴ played a role. The vast majority of less educated individuals in Turin came from the South, seeking a job in the car factories of the city. As less educated men were mainly employed in heavier and riskier jobs and were exposed to higher mortality, it is possible that during their life they were selected at a faster pace than other educational groups and women. This might have reduced the differences in susceptibility to death among men, contributing to determining a lower level of heterogeneity than among women.

Conclusion

This study found that neglecting selection effects due to unobserved heterogeneity in longitudinal analyses could lead to an underestimation of mortality differentials by social class. In the majority of cases, the models that controlled for unobserved heterogeneity estimated higher educational differences in mortality than the models that did not control for it.

Moreover, when compared with the AIC, the models that controlled for unobserved heterogeneity gave a statistically significantly better fit than the models that did not control for it. Although the best AIC just shows that the more complex model approximates the data better, it does not represent an unequivocal proof of the selection hypothesis; however, the results point to the possibility that the data could be better described by this hypothesis.