Nearest Hyperplane Distance Neighbor Clustering algorithm Applied to Gene Co-Expression Analysis in Alzheimer’s Disease

Abstract

Microarray analysis can contribute considerably to the understanding of biologically significant cellular mechanisms that yield novel information regarding co-regulated sets of gene patterns. Clustering is one of the most popular tools for analyzing DNA microarray data. In this paper, we present an unsupervised clustering algorithm based on the K-local hyperplane distance nearest-neighbor classifier (HKNN). We adapted the well-known nearest neighbor clustering algorithm for use with hyperplane distance. The result is a simple and computationally inexpensive unsupervised clustering algorithm that can be applied to high-dimensional data. It has been reported that the NFkB1 gene is progressively over-expressed in moderate-to-severe Alzheimer’s disease (AD) cases, and that the NF-kB complex plays a key role in neuroinflammatory responses in AD pathogenesis. In this study, we apply the proposed clustering algorithm to identify co-expression patterns with the NFkB1 in gene expression data from hippocampal tissue samples. Finally, we validate our experiments with biomedical literature search.

I. Introduction

Microarray analysis is a powerful technique that allows researchers to search for relationships among gene patterns and their behaviors in normal conditions and in the presence of a certain diseases. MiRNAs are a class of single stranded, small, non-coding RNAs. Roughly 834 human miRNAs have been identified. Of these identified miRNAs, only a specific subset are highly expressed in the brain, and these highly expressed miRNAs appear to be critical to the regulation of normal brain cell function [1]. For example, miRNA-146a (an NF-kappa-B-sensitive gene) is found in increased amounts in stressed human brain cells and in Alzheimer’s disease (AD), in which it plays a crucial role in regulating inflammation and innate immune response [2-4]. The NF-kB transcription factor is further involved in pro-inflammatory signaling and pathogenic gene expression, and has been reported to be progressively over-expressed in moderate-to-severe AD cases [2,5].

A common challenge in analyzing DNA microarray data is the large ratio between the number of genes and the number of samples. In addition, the biological interactions in a gene network are highly complex. This complexity, along with the remarkable presence of noise, makes it difficult to analyze the data. Clustering techniques, such as hierarchical clustering, k-means, and self-organizing maps, have been applied to DNA microarray data to address these problems and find sets of genes that are co-expressed. A review of clustering algorithms applied to gene expression data is reviewed by Jiang et al.[6].

The K-local hyperplane distance nearest neighbor algorithm (HKNN) [7] was introduced to overcome the generalization problems of the well-known K-nearest neighbor algorithm (KNN). The poor performance of KNN with respect to other supervised classifiers, such as support vector machine, is due to artifacts in the decision surface [7]. That is, given a finite number of training points, the space that is not covered by these points deforms the decision boundary surface leading to a lack of maximization of the local margin for new unseen points [7]. Therefore, one way to improve the generalization ability of the KNN algorithm is to implicitly “fill” the space between training points by constructing a locally approximated hyperplane [7]. This approach is presented by Vincent et al. [7]. In this approach, instead of comparing each new testing point with the k-nearest neighbors, each testing point is compared against a hyperplane (or more correctly an affine subspace) which is defined by the k-nearest neighbors of each class. Then, the class for which the hyperplane is closest to the testing point is assigned to this point. As a result, better generalization is obtained and, consequently, the algorithm performance improves.

This algorithm has been applied to address some bioinformatics classification problems. Nanni and Lumini applied HKNN to predict protein-protein interactions [8]. HKNN was applied to the protein fold recognition problem by Okun [9]. Ni et al. [10] presented an extension of HKNN to create the hyperplane in a feature nonlinear space. The authors mapped the input space, using a kernel function, and then applied HKNN in the feature space. This new method, called kernel k-local hyperplanes, was applied to protein-protein interactions.

Given the reported good performance of HKNN for supervised classification, we propose to extend HKNN to the unsupervised clustering problem. Therefore, we present a simple and computationally inexpensive unsupervised clustering algorithm that can be derived from the concept of the hyperplane nearest distance. Following the same concept presented by Vincent et al., we take the well-known nearest neighbor clustering algorithm, and we adapt it to be used with hyperplane distance. We name this method the Nearest Hyperplane Distance Neighbor Clustering algorithm (NHNC). To find the optimum parameters of the NHNC algorithm, a cluster validity index presented by Lam et al. [11] is implemented. Further details are presented in the following sections.

In this study, we apply NHNC to real-world DNA microarray data from normal and AD patients. The DNA data set is partitioned to cluster together genes that are co-expressed. Moreover, we target the cluster that contains the NFkB1, as it is of interest to this work. Finally, a literature research is performed to enhance our biological understanding of the genes obtained by this methodology. The methodology is implemented using Matlab (MathWorks).

The rest of this paper is organized as follows. In Section II the HNNC algorithm is detailed. The application of NHNC to DNA microarray data is described in Section III. The results and discussions are presented in Section IV. Finally, conclusions and future work are listed at the end of this paper in Section V.

II. The Nearest Hyperplane Distance Neighbor Clustering Algorithm

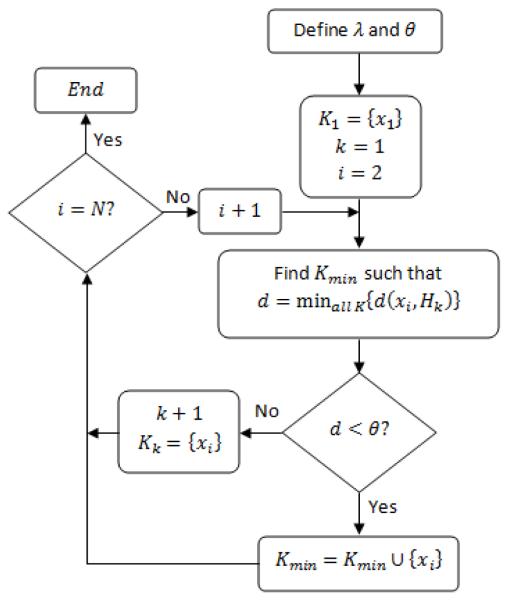
Given a set of points $\mathcal{L}=\{x_1,x_2,\dots ,x_N\}$, $x_i\in {\mathbb{R}}^D$ and a distance metric (in this study we use the Euclidean metric), the NHNC algorithm generates a set of clusters K = {K₁,K₂, …, K_k} with k not previously specified. Fig. 1 shows the flow chart of the algorithm. The algorithm is similar to the nearest neighbor clustering algorithm, but, instead of computing the distance between points, it computes the distance between the new point and a hyperplane formed by the points already clustered.

Fig.1.

Flow chart of the NHNC algorithm.

The points are drawn one-by-one from the set $\mathcal{L}$. The first point x₁ conforms the first cluster K₁.A second point is drawn, and the distance between this new point and the hyperplanes defined by the points clustered together is computed. We start with one point and one cluster. The minimum distance for all the clusters is computed and compared against a threshold θ. If the distance overcomes this threshold, a new cluster is created with the new point. If the distance is less than the threshold, the new point is added to the cluster to which the minimum distance was found. This process is repeated for all the N points of $\mathcal{L}$.

The Kth (M-1)-dimensional hyperplane is defined as in [7]:

$$H_K^M=\{p\mid p=\stackrel{\rightharpoonup }{N}+{\Sigma }_{m=1}^M{\alpha }_m{V}_m,{\alpha }_m\in \mathfrak{R}\},$$ (1)

where $\stackrel{\rightharpoonup }{N}$ is the centroid of the cluster defined as $\stackrel{\rightharpoonup }{N}=\left({\Sigma }_{m=1}^M{N}_m\right)∕M$, N_m are the points that belong to the Kth cluster and $V_m=N_m-\stackrel{\rightharpoonup }{N}$.

The minimum distance of the point x_i to all the hyperplanes H_k is defined as:

$$\begin{array}{cc}\hfill d={\min }_{allK}& \left\{d\right(x_i,H_k\left)\right\}={\min }_{allK}\mid \mid x-p\mid \mid .\hfill \\ \hfill =& {\min }_{{\alpha }_m\in \mathfrak{R}}\mid \mid x-\stackrel{\rightharpoonup }{N}-{\Sigma }_{m=1}^M{\alpha }_m{V}_m\mid \mid \hfill \end{array}$$ (2)

Vincent et al. [7] suggested including a penalty term λ to Eq. (2) to penalize large values of α, then:

$$d^2={\min }_{{\alpha }_m\in \mathfrak{R}}\{{\mid \mid x-\stackrel{\rightharpoonup }{N}-{\Sigma }_{m=1}^M{\alpha }_m{V}_m\mid \mid }^2+\lambda m=1M\alpha m2.$$ (3)

If we define α = (α₁,…,α_M)^T, I as the M × M identity matrix, and V as a D × M matrix in which columns are the V_m vectors, we can compute each α_m by solving the following linear system:

$$({\mathit{V}}^{\mathit{T}}\mathit{V}+\lambda \mathit{I})\alpha ={\mathit{V}}^{\mathit{T}}(x-\stackrel{\rightharpoonup }{N}).$$ (4)

III. Application to DNA Microarray Data Analysis

A. Data Set and Preprocessing

The DNA microarray gene expression data set used in this study is from the hippocampal tissue of postmortem normal and AD subjects [12]. The data set is accessible from NCBI’s Gene Expression Omnibus database [13], accession GSE1297. We only considered the severe cases of AD, forming a group of seven samples from which we conducted our experiments. For the control group (normal patients), nine samples were used. From this data set, only the genes that are statistically different (P value less than 0.05) were used. We further excluded the genes which had an “A” tag associated with them. This reduced the set to 1368 genes. The data set was z-score normalized to have all the points falling in the same range.

B. Clustering using NHNC

There are two parameters to be defined before applying the NHNC algorithm: the penalty term λ and the threshold value θ. To find the optimum values for these two parameters, we use a cluster geometrical validity index based on the ratio of the within-cluster density and the between-cluster separation, which was presented by Lam et al. [11]. The validity geometrical index (GI) is defined as:

$$GI\left(K\right)=ma{x}_{1\le k\le K}\left\{\frac{{\left(2{\Sigma }_{j=1}^D\sqrt{{\lambda }_{jk}}\right)}^2}{mi{n}_{1\le q\le K}(\mid \mid \stackrel{\rightharpoonup }{N_k}-\stackrel{\rightharpoonup }{N_q}\mid \mid )}\right\},$$ (5)

where K is the number of clusters, D is the dimension of the data, the denominator is the Euclidean distance of the two closest cluster centroids, and λ_jk are the eigenvalues of the sample covariance matrix, which elements are defined as:

$$q_{ij}=\frac{1}{N_M-1}{\Sigma }_{k=1}^M(x_{ik}-{\stackrel{‒}{x}}_i)(x_{jk}-{\stackrel{‒}{x}}_j),$$ (6)

where N_M is the number of genes in the Kth cluster, and ${\stackrel{‒}{x}}_i$ and ${\stackrel{‒}{x}}_j$ are the sample mean of ith and jth genes, respectively. The smaller the GI is, the better the quality of the clustering will be. The sum of the square roots of the eigenvalues gives a geometrical measure of the within-cluster scatter (see [11]). The denominator of Eq. (5) is a measure of the intra-cluster separation.

If any of the eigenvalues is negative, the square root will be a complex number. Then, the index is slightly modified by taking the absolute value of the eigenvalues. This calculation does not affect the computation of the index since the sign of the eigenvalues only determine whether the vector is shifted 180 degrees or not, and we are only interested in the length of the axis.

We used this index to find the optimum combination of λ and θ (thus K) by computing GI for each of the 176 runs of the NHNC algorithm on the control and AD groups. This corresponds to 11 values of λ (from 0.15 to 0.95) and to 16 values of θ (from 0.1 to 1.5). Note that if a cluster contains only one point the covariance matrix cannot be computed and this cluster cannot be incorporated into the calculation of GI. Therefore, to ensure that most of the clusters contain more than one data point, we select only those for which this condition is met for more than 50% of the clusters. The set of parameters which gives the minimum GI (average GI of the control and the AD group) is the one selected.

IV. Results and Discussion

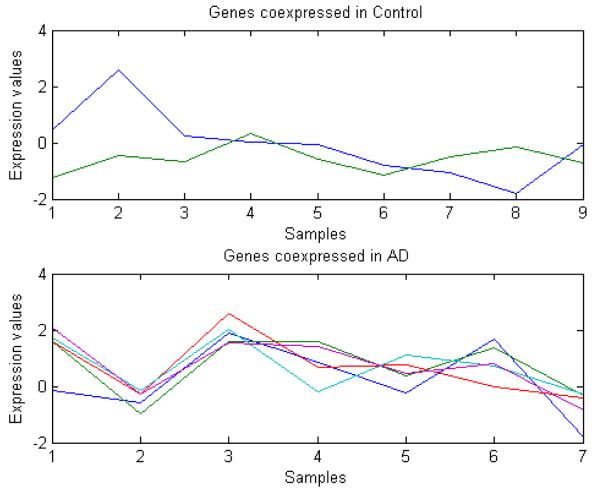
The optimum parameters found with the abovementioned methodology are λ = 0.15 and θ = 0.4. With these parameters, 300 clusters for the control group and 290 for the AD group were obtained. The clustering process took 36.53 seconds for the control group and 33.19 seconds for the AD group (implemented in a standard PC, quad I7 2.8 GHz, 6 GB RAM). Table I shows the genes found to be co-expressed with NFkB1 in the data set. A total of five genes were clustered together with the NFkB1 gene, four in the AD group and one in the control group. Fig. 2 shows the profiles of the genes found to be co-expressed with NFkB1.

TABLE I.

Genes Co-Expressed with NFKBIA Gene

Group	Gene Name	Summary
AD	KCTD14	Subunit of the mitochondrial membrane respiratory chain NADH dehydrogenase (Complex I), Complex I functions in the transfer of electrons from NADH to the respiratory chain [14, 15].
AD	NUCKS1	Encodes a nuclear protein that is highly conserved in vertebrates. The conserved regions of the protein contain several consensus phosphorylation sites for casein kinase II and cyclin-dependent kinases, two putative nuclear localization signals, and a basic DNA-binding domain [16].
AD	RREB1	Transcription factor that binds specifically to the RAS-responsive elements (RRE) of gene promoters, may be involved in Ras/Raf-mediated cell differentiation by enhancing calcitonin expression, represses the angiotensinogen gene, negatively regulates the transcriptional activity of AR, potentiates the transcriptional activity of NEUROD1 [14, 15].
AD	CDNA	No information available.
Contr.	YTHDF3	A protein of the YTH family has been shown to selectively remove transcripts of meiosis-specific genes expressed in mitotic cells. It has been speculated that in higher eukaryotic YTH-family members may be involved in similar mechanisms to suppress gene regulation during gametogenesis or general silencing [17].

Fig.2.

Profile of the genes found to be co-expressed with the NFkB1 gene.

After a literature search, we found four of the resulting genes to be related with AD (and potentially with the NFkB1 gene). The KCTD14 is a subunit of the mitochondrial membrane respiratory chain NADH dehydrogenase (Complex I) [18], which was found to be in the AD pathway [14, 15]. Mutations produced in Complex I lead to neurodegenerative diseases [18, 19]. Moreover, Complex I can damage mtDNA by producing reactive oxygen species and may cause aging [18]. In addition, since mitochondria plays a central role in neurodegenerative disease [20], its dysfunction due to damage of mtDNA might link KCTD14 to AD. NUCKS1 was proposed as one of the most likely candidates to be related in AD pathogenesis for two reasons [21]. First, this gene is strongly associated with Parkinson’s disease [22] and Parkinson’s disease has been linked to AD [23]. Second, as it is indicated by Agustin et al. [21], NUCKS1 may play a role in cell proliferation [24]. Proliferation of neural progenitor cells is reduced in mouse AD model due to the mutated form of the amyloid precursor protein [21]. The third gene clustered in the AD group was the RREB1 gene. It was found that this gene potentiates the transcriptional activity of NEUROD1/beta 2 [25]. Moreover, it was reported that beta 2-adrenoreceptors were increased in AD [26]. Finally, using the DAVID tool [14, 15], we found that there is a protein-protein interaction between the NFKB and the YTH domain family protein 3 (YTHDF3).

V. Conclusions and Future Work

In this paper, we presented the NHNC, a simple unsupervised clustering algorithm based on the HKNN classifier. The nearest-neighbor clustering algorithm was modified to use the hyperplane distance. Although the proposed algorithm needs to adjust two parameters to find the best model for a given dataset (in SOM or k-means only one parameter needs to be selected), it takes a short time to run it, which makes feasible to test the algorithm for several combinations of these two parameters. The low computational cost is an advantage over others clustering techniques. We have applied the proposed algorithm to the analysis of DNA microarray data to search for genes co-expressed with the NFkB1 gene and the results were validated with biomedical literature.

Future work involves (a) the extension of the proposed algorithm by using the kernel trick to apply NHNC in a nonlinear feature space instead of the input space (similar to the extension of HKNN presented by Ni et al. [10]), and (b) the analysis of other array-based gene expression data. Certain human brain tissue parameters, such as post-mortem interval, appear to be a major factor in both messenger RNA (mRNA) and micro RNA (miRNA) quality and stability and, hence, in the acquisition of reliable brain gene expression data [27, 28]. Together these additions should lead to an improvement of the clustering performance, as nonlinear relationships might be captured with the help of a nonlinear transformation.