Aerodynamic Factors Responsible for the Deaggregation of Carrier-Free Drug Powders to form Micrometer and Submicrometer Aerosols

Abstract

Purpose

The objective of this study was to employ in vitro experiments combined with computational fluid dynamics (CFD) analysis to determine which aerodynamic factors were most responsible for deaggregating carrier-free powders to form micrometer and submicrometer aerosols from a capsule-based platform.

Methods

Eight airflow passages were evaluated for deaggregation of the aerosol including a standard constricted tube, impaction surface, 2D mesh, inward radial jets, and newly proposed 3D grids and rod arrays. CFD simulations were implemented to evaluate existing and new aerodynamic factors for deaggregation and in vitro experiments were used to evaluate performance of each inhaler.

Results

For the carrier-free formulation considered, turbulence was determined to be the primary deaggregation mechanism. A strong quantitative correlation was established between the mass median diameter (MMD) and newly proposed non-dimensional specific dissipation (NDSD) factor, which accounts for turbulent energy, inverse of the turbulent length scale, and exposure time. A 3D rod array design with unidirectional elements maximized NDSD and produced the best deaggregation with MMD<1μm.

Conclusions

The new NDSD parameter can be used to develop highly effective dry powder inhalers like the 3D rod array that can efficiently produce submicrometer aerosols for next-generation respiratory drug delivery applications.

INTRODUCTION

Dry powder inhalers (DPIs) are currently a popular platform for respiratory drug delivery (1–3). Advantages compared with other inhalation devices include ease of use, coordination between patient inhalation and dose delivery, and stable formulations. However, performance of these devices is often poor in terms of high mouth-throat (MT) deposition, which results in increased side effects, wasted medication, increased inter-subject variability, and low lung delivery of the drug (4–6). A primary issue in developing effective DPIs, for both drug/carrier and drug only formulations, is achieving adequate deaggregation of the powder to form an aerosol with a high fine particle fraction (FPF) that can avoid MT deposition and reach the lungs for local action or systemic absorption. Current testing and development of DPIs typically focuses on producing high FPFs defined as the drug mass contained in aerosolized particles with aerodynamic diameters less than approximately 5 μm. Mass median aerodynamic diameters in the range of 2–5 μm are also considered necessary for effective performance. Typical FPFs of emitted dose for conventional and state-of-the-art DPIs are in the range of 20–70% with lung depositions of approximately 5–30% (2, 3, 7). As an example, the Flovent Diskus^® DPI (GlaxoSmithKline, Raleigh, NC), which is one of the most frequently prescribed inhalers, has a FPF of 20% based on emitted dose and approximately 70% MT deposition for a fluticasone propionate formulation with a lactose carrier during correct usage by adults (8).

Efforts to improve DPI performance have focused on modifications to both the device and powder formulation (3, 9–12). Device modifications are typically based on aerodynamic properties that first fluidize the powder and then deaggregate the aerosol into fine particles. Previous studies have reviewed both aerodynamic and formulation factors that can influence DPI aerosol performance (3, 9–13). Considering the device, correlations are needed between aerodynamic factors and aerosol formation that can be used to understand, evaluate, and improve performance. Using a combination of in vitro testing and computational fluid dynamics (CFD) or analytical predictions of aerodynamic factors, associations have previously been developed for the aerosolization and delivery performance of both spray inhalers (14) and DPIs (15–18). Considering DPIs, improved powder deaggregation and higher FPFs are typically associated with elevated device resistance, pressure drop, and power input (19, 20). However, factors most responsible for aerosol formation and deaggregation in DPIs are likely to change with different formulation types and for different devices.

DPI formulation types can be carrier-based (drug attached to larger excipient particles), carrier-free (or drug only), and agglomerates (composed of large aggregates of smaller primary particles). For carrier-based systems, deaggregation measured as a function of FPF was associated with turbulence (13), turbulent shear stress (11, 21, 22), and wall impactions of particles (18). Considering a carrier-free formulation of mannitol as a model drug and the Aerolizer^® DPI, a capsule-based device, Coates et al. demonstrated direct associations between a measure of turbulence (the integral scale strain rate) as well as inlet flow with FPF (15, 16, 23). Optimization of the Aerolizer device based on the analysis of Coates et al. and modified mouthpiece geometries produced a FPF of 63% with deposition in a MT replica of approximately 30% (24). For agglomerate formulations, Wong et al. indicated no correlation between flow-based parameters and FPF (25); however, impaction in the device appeared to be a primary deagglomeration mechanism (17, 25, 26). Using agglomerate impaction on inclined surfaces with optimized angles, Adi et al. (27) achieved maximum FPF (% loaded dose) values of approximately 30%.

In general, it appears that the deaggregation of carrier-based and large agglomerate formulations is most influenced by turbulence and impaction (11–13, 17, 18, 21, 22, 25, 26). It is expected that impaction breaks apart large aggregates and knocks smaller drug particles off of larger carriers. Turbulence plays a role in both increasing wall impactions by particle dispersion and breaking apart smaller particle structures. However, carrier-based formulations often do not require wall impactions for deaggregation. For example, studies of Xu et al. (11, 21, 22) in particular demonstrate excellent associations between turbulent shear stress and powder deaggregation in standardized entrainment tubes for carrier-based systems with conventional sized powders. For carrier-free formulations, deaggregating is strongly associated with turbulence (15, 16, 23). All of these associations are very useful for understanding aerosol formation and optimizing device performance. However, the only existing quantitative correlations established between aerodynamic factors and DPI performance are for turbulent shear stress vs. FPF in standardized entrainment tubes (11, 21, 22) and air flow rate (Q) vs. capsule emptying in the Aerolizer DPI (23). Quantitative correlations may be very useful in the device optimization process and for determining which aerodynamic factors are most influential in aerosol formation. Furthermore, these previous studies of DPI performance have focused almost exclusively on FPFs defined as drug mass in particles with aerodynamic diameters of 5 μm and below. Considering mass median aerodynamic diameters (MMADs) or mass median diameters (MMDs) of even smaller aerosols may be useful for developing next-generation DPIs and respiratory drug delivery strategies.

Generating approximately micrometer (MMD ≈ 1 μm) and submicrometer (MMD < 1 μm) aerosols from DPIs may be beneficial in a number of new respiratory drug delivery approaches. For example, nanoparticle or submicrometer formulations of poorly soluble drugs have been shown to improve dissolution and uptake characteristics in the lungs or in test dissolution systems (28–30). For improved lung delivery, the excipient enhanced growth (EEG) concept begins with approximately micrometer or submicrometer aerosols (MMD ≤ 1 μm) to minimize deposition in the extrathoracic airways. Previous studies indicate that EEG delivery provides negligible MT deposition (~ 1%), significant aerosol size increase within the airways due to the inclusion of hygroscopic excipients, full lung retention of the aerosol, and high delivery efficiency to the lower tracheobronchial and alveolar airways (31–34). A primary challenge in creating submicrometer aerosols from a DPI is overcoming inter-particle forces that are known to increase relative to aerodynamic aerosolization forces as primary particle size is reduced (9, 11). As a result, producing an effective submicrometer DPI requires a thorough understanding of aerosol deaggregation and the development of new formulations and devices that are more effective at creating high fractions of submicrometer aerosols (35, 36). However, very little is known about aerosol deaggregation down to the submicrometer scale with few previous studies considering FPFs less than approximately 5 μm.

In a series of studies, Son et al. (35–37) demonstrated the combination of particle engineering and DPI device selection and modification to effectively produce micrometer and submicrometer EEG aerosols. The model optimized formulation consisted of albuterol sulfate (AS), mannitol (MN), L-leucine, and poloxamer 188 in a ratio of 30/48/20/2% w/w, respectively. Mannitol was included as a model hygroscopic excipient to form EEG combination particles that increase in size after inhalation (34). Leucine has been employed as a dispersion enhancing agent (30, 38). In the commercial Aerolizer DPI, the emitted FPF_5μm and FPF_1μm were greater than 80% and 28%, respectively. The submicrometer combination particles had negligible (<5%) deposition in a MT model (37). By modifying a commercial DPI with a 3D rod array design, the emitted FPF_1μm was increased to 38.8% (FPF_5μm > 97%) and a submicrometer aerosol was formed with MMD < 1 μm (35). However, mechanisms responsible for particle deaggregation of the carrier-free formulation implemented and tested by Son et al. (35) to form submicrometer aerosols remains unclear. A better understanding of the aerodynamic factors that create micrometer and submicrometer aerosols will allow further optimization of DPI devices and improved FPFs at lower pressure drops.

The objective of this study was to employ in vitro experiments combined with CFD analysis to determine which aerodynamic factors were most responsible for deaggregating carrier-free powders to form micrometer and submicrometer aerosols from a capsule-based platform. The previously developed carrier-free formulation of Son et al. (37) for an EEG aerosol was implemented that consists of submicrometer primarily particles. A capsule-based platform was selected as a uniform mechanism to initially fluidize the powder and a single capsule chamber was considered. Performances of different airflow pathways downstream of the capsule chamber were then evaluated in terms of aerosol deaggregation. The airflow pathways consisted of standard inhaler configurations for powder deaggregation such as a constriction tube, impaction surface, mesh, and inward jets, as well as newly proposed 3D grids and unidirectional rod arrays. CFD simulations were implemented to evaluate previously reported aerodynamic factors associated with deaggregation along with newly proposed parameters. In vitro experiments were conducted to evaluate the performance of each inhaler system in terms of FPFs (< 5 μm and < 1 μm) as well as MMD. A single parameter was then sought that can best predict DPI performance across a range of inhalers at multiple flow rates with a carrier-free formulation for the production of micrometer and submicrometer aerosols. The best performing inhaler was then identified for future use in submicrometer aerosol delivery with the EEG approach.

MATERIALS AND METHODS

Inhalers and Flow Conditions

Multiple DPI designs were considered to evaluate different aerodynamic factors potentially affecting aerosol deaggregation for a carrier-free formulation of EEG combination particles delivering AS as the drug. The model EEG formulation was previously established by Son et al. (37) and was formed using a spray drying process. The spray dried powder was loaded into capsules in quantities of 2 mg and the capsules were pierced with a needle prior to aerosolization producing 2 holes 0.5 mm in diameter. For initial fluidization of the aerosol, the capsules for all inhaler designs were placed in the capsule chamber of the HandiHaler^® (Boehringer Ingelheim Inc., Ridgefield, CT) device. Different airflow passages downstream of the capsule chamber were then considered to form different inhaler designs and evaluate the potential for effective deaggregation of the particles into micrometer and submicrometer aerosols. By selecting a single capsule chamber design and different downstream flow passages, this study focuses on how factors in the flow passage can deaggregate the aerosol after initial fluidization.

Aerosol deaggregating airflow passages were designed to focus on both turbulence and impaction as potential breakup mechanisms. The airflow passages are illustrated in Figure 1 and summarized in Table 1. The most basic design consisted of a constricted tube to increase turbulence (Inhaler 1), which represents the flow passage of the commercial HandiHaler device. To increase both particle-wall impactions and flow turbulence, Inhalers 2 and 3 incorporate a baffle style impaction surface (Inhaler 2), as exists in some air jet nebulizers, and a 2D mesh (Inhaler 3), which is very common for increasing powder deaggregation. Inhaler 4 implements inward radial jets to generate elevated turbulence, consistent with the study of Voss and Finlay (13). It is currently not clear which existing turbulence generation mechanism is most efficient at deaggregating a powder for similar input flow rates or similar pressure drops.

Figure 1.

Flow passages of the inhalers implementing different designs for aerosol deaggregation. The inhaler numbers (Table 1) and descriptions are: (a) Inhaler 1 - constricted tube, (b) Inhaler 2 - internal impaction surface, (c) Inhaler 3 - 2D mesh of 0.5 mm wires, (d) Inhaler 4 - inward facing 0.5 mm jets, (e) Inhaler 5 - 3D grid of 0.5 mm rods, (f) Inhaler 6 - 3D array of 0.5 mm rods.

Table 1.

Inhalers considered and key dimensions.

Num.	Name	Deagglomeration mechanism	Critical dimensions of flow passages	Flow rates (LPM)
1	Constricted tube (commercial HandiHaler design)	Increases turbulence and/or wall impactions	Inlet diameter:a 10 mm Minimum diameter: 5.2 mm MP outlet: 19×7 mm	45
2	Impaction surface	Baffle surface located in center of constriction to increase impactions and promote turbulence	Minimum flow passage distance: 2 mm Baffle diameter: 3mm MP outlet: 19×7 mm	45
3	2D grid	Increases turbulence and impaction using a 2D grid structure	Midsection containing mesh: 5.7×8.6 mm Mesh diameter: 0.5 mm Outlet MP: 19×14 mm	45
4	Inward jets	Inward radial jets centralize the aerosol and create an area of high turbulence	Number of inward jets: 8 Diameter of jets: 0.5 mm Minimum diameter of flow passage: 5.7 mm Outlet MP: 19×7 mm	60 and 75
5	3D grid	3D grid structure to amplify and extend the turbulent region	Midsection containing mesh: 5.7×8.6 mm Rod diameter: 0.5 mm Outlet MP: 19×14 mm	45
6	3D array	Array of unidirectional rods to maximize turbulence over a larger area	Midsection containing rod array: 5.7×5.7 mm Rod diameter: 0.5 mm Outlet MP: 19×7 mm	45 and 60
7	Expanded 3D array	Array of unidirectional rods with a larger cross-section in the turbulence generation region	Midsection containing rod array: 5.7×8.6 mm Rod diameter: 0.5 mm Outlet MP: 19×14 mm	45
8	3D array with smaller rods	Array of unidirectional rods to maximize turbulence with reduced rod size to decrease pressure drop	Midsection containing rod array: 5.7×5.7 mm Rod diameter: 0.375 mm Outlet MP: 19×7 mm	45

^aThe inlet configuration of a 10 mm circle is the same for all inhalers.

A goal of an effective DPI is to maximize powder deaggregation while minimizing pressure drop. Therefore, airflow passages are sought that can maximize turbulence levels and particle exposure times to turbulence for a consistent or lower drop in pressure across the inhaler. Inhalers 5 and 6 seek to maximize the exposure of particles to turbulence by expanding the turbulence generation space using a 3D grid and array, respectively. The 3D grid consists of rows of 0.5 mm rods with each successive row rotated by 90°. For the 3D grid considered in this study, the rods are separated by a gap distance of 0.5 mm on each row and the rows are separated by gap distances of 0.75 mm in the direction of flow. The 3D array is characterized by rows of 0.5 mm unidirectional rods with gap distances identical to the 3D grid and staggered such that increased velocity between 2 rods impacts on the center of the rod in next row. Using these designs, it is expected that flow constriction in terms of reduced cross-sectional area and pressure drop are minimized compared with a 2D design, while turbulence generation and aerosol exposure time to elevated turbulence are maximized. To better understand aerodynamic factors within the rod array, the cross-sectional area of the array is increased with Inhaler 7 and smaller 0.375 mm rods are used in Inhaler 8. Key dimensions of all inhalers considered are reported in Table 1.

Flow rates through the eight devices were selected to be within the range of normal DPI usage for adults. As a baseline, a flow rate of 45 LPM was established for a 4 kPa total pressure drop through Inhaler 1. For consistency, all inhalers (except Inhaler 4) were tested at this flow rate and found to produce total pressure drops in the range of 4 kPa and well below the adult maximum of 7.8 kPa (39). For the low resistance Inhaler 4 device, a flow rate of 75 LPM was determined to produce 15 LPM total flow through the 8 inward jets with 60 LPM through the device and an approximate total device pressure drop of 4 kPa. Other flow rates were also tested in some devices to better understand the aerodynamic factors involved with deaggregation, such as 60 LPM in Inhaler 6. Calculated pressure drop through the airflow passages is reported in the Results section as an aerodynamic factor potentially correlating to FPF and was established to be in the range of 0.7 to 2 kPa. The Results section also includes a CFD comparison of all flow passages evaluated at a consistent pressure drop of 2 kPa.

In Vitro Experiments

The airflow passages characterizing each of the eight tested inhalers were constructed using a rapid prototyping process. An in-house Viper SLA machine (3D Systems, Valencia, CA) was used to build the geometries out of clear plastic resin (Accura 60; 3D Systems) using a build layer thickness of 0.10 mm and a laser spot diameter of 0.25 mm. Each airflow passage was connected to the capsule dispersion unit of the HandiHaler, and a wire mesh consistent with the commercial device prevented ingress of the capsule into the flow passage. Using this standard capsule dispersion unit (or chamber) at a constant set of flow rates allowed a consistent aerosol to be initially fluidized in each experiment. Subsequent deaggregation was then assessed as an effect of aerodynamic factors present in the different downstream airflow passages.

The process for obtaining the spray dried EEG powder was described by Son et al. (37) and consisted of conditions and formulation variables from Experiment 6 of that study. Briefly, the spray dried combination particles consisted of AS, MN, L-leucine, and poloxamer 188 in a ratio of 30/48/20/2% w/w, respectively. They were produced by spray drying (Buchi Nano spray dryer B-90) at an inlet temperature of 70 °C from a water:ethanol 80:20% v/v solution containing 0.5% solids. Scanning electron microscopy showed that the spray dried particles were submicrometer sized with geometric diameters between 0.2 – 1.0 μm (37). In the current study, a Next Generation Impactor (NGI; MSP Co., Shoreview, MN) was used to determine aerodynamic particle size characteristics of the drug in the combination particle formulations. A sample of each powder formulation (2 mg) was filled into size 3 HPMC capsules and placed into the HandiHaler capsule dispersion unit prior to testing. Each of the engineered airflow passages was connected to the capsule dispersion unit to form Inhalers 1–8. The DPIs were fired into a NGI through a pre-separator operating at an airflow rate of 45–75 LPM. The inhalation time was varied to draw 4L of air through each inhaler at ambient conditions (25 °C / 45–55% RH). In order to assess the particle size distribution of the total dose of formulation, the USP induction port was omitted. For each of the impactor experiments, the impactor collection stages and pre-separator were coated with Molykore®316 silicone spray to minimize particle re-entrainment and bounce. Albuterol sulfate remaining in the DPIs (including the capsule), deposited on the pre-separator, and on each of the impactor collection stages was determined by washing each item with 10 mL of deionized water to extract the drug for quantitative analysis. Collected samples were analyzed using a validated HPLC method.

Drug emitted dose (ED) exiting the DPI was determined by subtracting the amount of AS remaining in the DPI from the initial mass of AS loaded. The initial mass loaded in the DPI was calculated from weight of combination formulation and the measured %AS content for each formulation. The drug fine particle fraction (FPF_5μm/ED) and submicrometer particle fraction (FPF_1μm/ED), defined as the total emitted dose of AS with aerodynamic diameters smaller than 5 μm and 1 μm, respectively, were calculated via interpolation from the cumulative mass versus the cutoff diameter of the respective stages of the NGI, corrected for inlet flow rate. Each measurement was repeated three times. The MMAD was determined at the 50^th percentile on the % cumulative undersize (probability scale) versus logarithmic aerodynamic diameter plot and converted to MMD values based on a measured skeletal density of 1.325 g/cm³ of the combination particles.

The HPLC method for AS quantification employed a Waters 2690 separations module with a 2996 PDA detector (Waters Co., Milford, MA). Chromatography was performed using a Restek Allure PFP 15 × 3.2 mm column (Bellefonte, PA). The mobile phase, consisting of methanol and ammonium formate buffer (20 mM, pH 3.4) in a ratio of 70:30, respectively, was eluted at a flow rate of 0.75 mL/min and the UV detector was set to a wavelength 276 nm. The column temperature was maintained at 25 °C, and the volume of each sample injected was 50 μL.

CFD Simulations

Computational fluid dynamics simulations were conducted for the eight inhaler flow passages and multiple flow rates described in Table 1. Blunt inlet profiles were assumed to enter the flow passages with 1% turbulence intensity and a turbulence length scale equal to the mesh opening. Isothermal and steady state solutions were sought where possible. However, transient simulations were required to resolve flow oscillations occurring in some of the inhalers. Transient simulations were conducted with a time step of 0.001 s and at least 0.5 s of flow was resolved to ensure that startup effects were not present in the solution. Incompressible constant-property flow was also assumed in all cases. The inlet Reynolds number for the flow rates considered (Table 1) ranged from 6,010 to 10,000, indicating the occurrence of turbulent flow, which was amplified in the presence of constrictions, internal bodies, and meshes.

The flow fields in each inhaler were solved using Fluent 12 (Ansys Inc., Canonsburg, PA) with a steady or transient solution and the low Reynolds number (LRN) k-ω two-equation turbulence model. This turbulence model was selected based on its accuracy combined with high efficiency compared with more complex methods, such as large eddy simulation (LES). The LRN k-ω model was previously demonstrated to accurately predict pressure drop, velocity profiles, and shear stress for transitional and turbulent flows (40, 41). The conservation of mass and momentum equations used with the LRN k-ω model are available from Wilcox (41) and were previously reported by Longest and Xi (42). Similarly, the equations governing turbulent kinetic energy (k) and specific dissipation rate (ω) were also reported by Longest and Xi (42). Considering aerosol transport, the LRN k-ω model was previously demonstrated to accurately predict particle transport and deposition for both monodisperse and polydisperse distributions in airway models on a regional and highly localized basis (43–46).

Particle trajectories were considered in each of the eight inhalers to evaluate impaction and as a method to sample the time course of aerosol exposure to turbulence. As a characteristic size of the spray dried formulation, an aerosol of monodisperse 1 μm particles was considered. To accurately predict individual particle trajectories and record the time history of turbulence exposure on the discrete phase, a Lagrangian particle tracking algorithm was employed. The Lagrangian transport equations can be expressed

$$\frac{{dv}_i}{dt}=\frac{f}{{\tau }_p}(u_i-v_i)+g_i(1-\alpha )+f_{i,\mathit{Brownian}}\text{and}\frac{{dx}_i}{dt}=v_i(t)$$ (1)

Here v_i and u_i are the components of the particle and local fluid velocity, g_i denotes gravity, and α is the ratio of mixture to particle density ρ/ρ_p. The characteristic time required for a particle to respond to changes in fluid motion, or the particle relaxation time, is expressed as τ_p = C_cρ_pd_p²/18μ, where C_c is the Cunningham correction factor for submicrometer aerosols based on the expression of Allen and Raabe (47), d_p is the particle diameter, and μ is the absolute viscosity. The pressure gradient or acceleration term for aerosols was neglected due to small values of the density ratio (48). The drag factor f, which represents the ratio of the drag coefficient to Stokes drag, was based on the expression of Morsi and Alexander (49). The effect of Brownian motion on the trajectories of submicrometer particles was included as a separate force per unit mass term at each time-step (50). To model the effects of turbulent fluctuations on droplet trajectories, a random walk method was employed (51–53). A near-wall anisotropic correction to turbulent particle dispersion was also included (54, 55).

Computational grids of the airflow passages were constructed based on previously established best practices. Hexahedral elements were used wherever possible, based on the findings of previous studies (56, 57). Tetrahedral and wedge elements were required to resolve flow around the inlet jets and rod elements of the 2D mesh, 3D grid, and 3D arrays. For the hexahedral mesh, near wall mesh size was typically smaller than 0.075 mm. For the tetrahedral grids in the vicinity of the rods, near-wall mesh size was set at a constant 0.03 mm. The resulting 8 meshes had cell numbers ranging from 225,000 to 1,100,000. Grid convergence of these meshes was established by comparing with meshes containing at least 30% more cells in each case. These comparisons indicated that there were minimal differences (< 5% relative error) in the maximum velocity and particle deposition values. As a result, the coarser meshes were considered sufficient and used in all subsequent simulations.

The CFD package Fluent 12 was used to solve the flow field and particle trajectory equations in each of the inhalers. User-supplied Fortran and C programs were used for the calculation of initial flow and particle profiles, near-wall anisotropic turbulence approximations, near-wall particle interpolation, and Brownian motion (50). All transport equations were discretized to be at least second order accurate in space. For the convective terms, a second order upwind scheme was used to interpolate values from cell centers to nodes. The diffusion terms were discretized using central differences. The particle trajectory solution was calculated using 4th-order Runge Kutta with an error control routine (48). Both wall impactions and discrete sampling of the turbulence field were conducted using 6,000 representative monodisperse 1 μm particles with a density of 1.325 g/cm³. Simulating additional particles had a negligible effect on impaction results in terms of deposition fraction. Effects of particle number on turbulence sampling are described in the Discussion.

Deaggregation Factors

Possible deaggregation factors were categorized as flow-based, turbulence-based, and particle-based. Some overlap among the factors in each category is apparent. Equations, justifications, and previous sample references for each factor are provided in Table 2. Additional descriptions of some factors are also discussed below along with a description of volume-averaging within the inhalers.

Table 2.

Factors expected to influence dispersion of the aerosol.

Factor name and symbol	Equation	Units	Justification	Reference
Flow-based
Flow rate (Q)	$Q=\overline{V}A$	m3/s	Flow rate increases turbulence, capsule motion, and impaction velocity of particles.	(23)
Pressure difference (ΔP)	$\mathrm{\Delta }\text{P}={\text{P}}_{\text{outlet}}-{\text{P}}_{\text{inlet}}$	Pa (or N/m2)	Proportional to energy applied to the inhaler and powder during inhalation.	(19)
Power	$\mathit{Power}=\mathrm{\Delta }P·Q$	Watts (W)	Rate of energy applied to the inhaler and powder during inhalation.	(20)
Shear stress (τs)	${\tau }_s=\mu {\left(\frac{\epsilon }{\nu }\right)}^{1/2}$	N/m2	Shear stress in the flow field is capable of applying different forces on an aggregate to break it apart. Turbulent shear stress definition based on Xu et al. (11). Variables are absolute viscosity (μ), kinematic viscosity (ν), and eddy dissipation rate (ε).	(11)
Turbulence-based
Turbulent kinetic energy (k)	$k=\frac{1}{2}\left(\overline{{u^{\prime }}^2}+\overline{{v^{\prime }}^2}+\overline{{w^{\prime }}^2}\right)$	m2/s2	Turbulent fluctuations are capable of breaking apart aggregates through shear and acceleration. Over-bars in k equation represent time averaging. Primes indicate fluctuating turbulent properties.	(41)
Turbulent intensity (TI)	$TI=\sqrt{\frac{2}{3}\frac{k}{U^2}}\ast 100$	Non-dimensional (%)	Represents the ratio of fluctuating velocity (k) to time-averaged mean velocity (U) at a location. High TI indicates elevated k along with increased residence time (1/U).	(41)
Specific dissipation rate (ω)	$\omega =\frac{k^{1/2}}{C_{\mu }^{1/4}\ell }$ where Cμ= 0.09	1/s	Proportional to integral shear strain rate (γ̇) proposed by Finlay (59). Current interpretation (16, 59) is a measure of the velocity gradient across the integral scale eddies.	Similar to Finlay (59) and Coates et al. (16)
Non-dimensional specific dissipation rate (NDSD)	$\begin{array}{l}\mathit{NDSD}=\overline{\omega }·t_{exp}\\ t_{exp}=\frac{V}{Q}\end{array}$	Non-dimensional	Both ω and exposure time to turbulence directly influence deagglomeration. The ω̄ is the volume-averaged specific dissipation rate. Exposure time (texp) is based on approximate volume (V ≈ 1 cm3) and flow rate (Q).	New parameter
Particle-based
Wall impactions without restitution (Impe=0)	Percentage of particles contacting the wall vs. number injected	Non-dimensional (%)	The number of wall hits may describe the potential for deagglomeration based on impaction with device surfaces. The restitution coefficient (e) is set to zero to simulate no bounce.	(14, 16)
Wall impactions with perfect restitution (Impe=1)	Percentage of particles contacting the wall vs. number injected	Non-dimensional (%)	Large particles may hit the wall multiple times causing continued deaggregation. The restitution coefficient (e) is set to 1 to simulate full bounce.	(16, 18)
Average trajectory integral of k · dt (Ikavg)	$\overline{{\int }_{\mathit{trajectory}}k·dt}$	N·m (or J)	Represents the product of k and dt a particle experiences over its trajectory through the system. Both k and exposure time to k are expected to be directly proportional to deaggregation. Units represent work (J) performed by turbulence on particle.	New parameter
Average trajectory integral of ω dt (Iωavg)	$\overline{{\int }_{\mathit{trajectory}}\omega ·dt}$	Non-dimensional	Represents the product of ω and dt a particle experiences over its trajectory through the system. Both ω and exposure time to ω are expected to be directly proportional to deaggregation.	New parameter

Considering flow-based parameters, the pressure drop reported in this study is calculated over the airflow passageways (Figure 1). This approach for reporting ΔP was implemented to focus on the pressure drop associated with deaggregation in the flow passage. However, it is understood that additional pressure is required to actuate the capsule dispersion portion of the device. The shear stress (τ_s) definition is based on the previous study of Xu et al. (11) and is apparently an approximation of the turbulent shear stress (which dominates laminar shear stress) in the flow field. To approximate this equation (Table 2) with the CFD model, a volume-average of the eddy dissipation rate (ε) is calculated within the airflow passage, as described below.

Considering turbulent quantities, Table 2 describes local values of turbulent kinetic energy (k), turbulence intensity (TI), and specific dissipation rate (ω) that exist throughout the 3D flow field. For example, the local TI represents the turbulent kinetic energy at a point that acts to break apart aggregates normalized by the time-averaged velocity (Table 2). This normalization for TI is justified because slower local mean velocity will increase exposure time to k and hypothetically increase the deaggregation. In turbulence, the specific dissipation rate is typically defined as (41)

$$\omega =\frac{k^{1/2}}{C_{\mu }^{1/4}\ell }[s^{-1}]$$ (2)

where k has units of m²/s², C_μ is a constant equal to 0.09, and ℓ is the characteristic eddy length scale [m]. The ω parameter captures both kinetic energy available for breakup along with eddy length scale, with smaller eddies hypothetically being more effective at breaking up small aggregates and increasing FPF. Differences between this view and that of previous studies are described in the Discussion.

For the inhalers, volume-averaged values are calculated to provide a single number for quantification and correlation development. Considering ω as an example, the volume-averaged specific dissipation is calculated as

$$\overline{\omega }=\frac{1}{V}\underset{V}{\int }{\omega }_{CV}dV[1/\text{s}]$$ (3)

where V is the volume of the airflow passage and ω_CV is the local ω value in individual voxels, or control volumes (CVs), composing the geometry. It is also reasonable that exposure time to ω increases the amount of agglomerate breakup, and is calculated as

$$t_{\text{exposure}}=\frac{V}{Q}[\text{s}]$$ (4)

where Q is flow rate through the airflow passage and V is an approximate passage volume (taken to be 1 cm³ in Eq. 4). The non-dimensional specific dissipation is then developed as

$$\mathit{NDSD}=\overline{\omega }{t}_{\text{exposure}}$$ (5)

This parameter captures both the strength of the turbulence most responsible for aerosol breakup (ω̄) as well as the exposure time to ω̄. In reporting volume-averaged values in the Results, the over-bar convention is dropped for convenience. In this study, parameters are only considered in the flow passage downstream of the capsule dispersion chamber. This is justified by using the same capsule chamber in all inhalers considered.

Particle-based parameters in this study seek to capture both particle-wall interactions as well as trajectory path integrated turbulence quantities. Wall impactions with the assumption of no bounce (zero restitution; e = 0) are symbolized as Imp_e=0. However, particle-wall contact and rebound are considered effective deaggregation mechanisms in carrier-based and agglomerate DPI systems (17, 18). To simulate this condition, a limiting case was considered in which all particles hitting the wall rebound from the surface without energy loss (i.e., with a restitution coefficient of e=1), symbolized by Imp_e=1. Both Imp_e=0 and Imp_e=1 are calculated as the number of wall hits divided by the number of inlet particles (6,000) and multiplied by 100 to form a percentage.

Integrals of k and ω were also taken along trajectories of particles and averaged over all 6,000 injections. For an individual trajectory and turbulent kinetic energy, the trajectory integral is

$${\int }_{\mathit{trajectory}}k·dt$$ (6)

which represents both kinetic energy and exposure time. The units of k·dt are Joules, which represents work performed on the aerosol by turbulent fluctuations. The over-bar on this term in Table 2 denotes an average value of k taken over all 6,000 injections, which is symbolized as

$${Ik}_{\mathit{avg}}=\overline{{\int }_{\mathit{trajectory}}k·dt}$$ (7)

Similarly for ω, the integration of ωdt represents both the value of ω and exposure period, and forms a non-dimensional number (Iω_avg). Both of these trajectory integral parameters along with NDSD are newly proposed for potentially correlating with aerosol deaggregation and will be evaluated for the first time in this study.

RESULTS

Flow-Based Factors

Velocity contours along the midplane and at cross-sectional locations for each inhaler are provided in Figure 2 as a representation of the flow field and flow-based parameters. Symmetric flow in the deaggregation passage is observed for Inhalers 1 and 2. However, asymmetrical boundary layer separation and recirculation within the flow pathway is observed in Inhalers 3, 4, and 6. This recirculation reduces the effective diameter of the passage, as described by Longest and Hindle (14). While reduced effective diameters were found to impede the performance of spray inhalers, the associated increase in turbulence may improve the performance of DPI aerosols in terms of particle deaggregation and FPFs. The observed recirculation regions are a transient feature which oscillate periodically from one side of the flow passage to the other. The 3D grid geometry (Inhaler 5) appears to unify the exiting flow field, much like a flow straightener in turbulence control. The uniformity of the flow through the downstream passage of Inhaler 5 may be the result of increased small scale turbulence. For Inhaler 6, the 3D array is observed to operate as designed with elevated flow between rods impacting on the staggered rods in the next row. Moreover, the elevated velocities in the 2nd row are greater than the elevated velocities in the first row indicating the potential for turbulence amplification in the 3D array.

Figure 2.

Contours of velocity magnitude at the midplane and cross-sectional locations for (a) Inhaler 1 at 45 LPM, (b) Inhaler 2 at 45 LPM, (c) Inhaler 3 at 45 LPM, (d) Inhaler 4 at 75 LPM, (e) Inhaler 5 at 45 LPM, and (f) Inhaler 6 at 45 LPM.

Values of the flow-based factors are presented for the eight inhalers, some at multiple flow rates, in Table 3 based on the definitions provided in Table 2. Table 3 also provides the experimentally determined MMD values, as well as FPFs, for each inhaler and flow rate combination. Based on the experimental results, Inhaler 6 at 45 and 60 LPM provides the best performance in terms of the lowest MMD with values of 0.98 μm and 1.03 μm, respectively. The largest aerosols in terms of MMD are created by Inhalers 1 (MMD = 1.35 μm) and Inhaler 3 (MMD = 1.36 μm), which are the constricted tube and 2D mesh designs, respectively. Both the constricted tube and 2D mesh are common features in current inhalers as a means to increase turbulence and FPF (3, 58).

Table 3.

Key flow-based factors expected to influence deagglomeration.

Inhaler number and flow ratea	Q (m3/s)	ΔPb (Pa)	Power (W)	τs (N/m2)	MMDc (μm)	FPF1μm/ED (%)d	FPF5μm/ED (%)e
1 at 45 LPM	7.5×10−4	921.8	0.691	0.707	1.35 (0.02)f	18.8 (0.5)f	89.5 (3.2)f
2 at 45 LPM	7.5×10−4	667.7	0.501	1.10	1.21 (0.1)	26.8 (3.8)	95.8 (0.05)
3 at 45 LPM	7.5×10−4	1421.6	1.07	1.23	1.36 (0.07)	19.2 (4.7)	94.5 (2.6)
4 at 60 LPM	1.0×10−3	934.0	0.934	5.16	1.27 (0.07)	23.6 (3.4)	91.2 (2.1)
4 at 75 LPM	1.25×10−3	2004.5	2.51	11.0	1.27 (0.14)	26.9 (6.0)	95.9 (0.7)
5 at 45 LPM	7.5×10−4	758.6	0.569	1.16	1.31 (0.03)	20.4 (2.7)	95.5 (1.1)
6 at 45 LPM	7.5×10−4	1902.0	1.43	2.17	0.98 (0.04)	38.8 (6.3)	97.3 (0.3)
6 at 60 LPM	1.0×10−3	3063.9	3.06	2.85	1.03 (0.05)	35.2 (1.3)	97.3 (0.4)
7 at 45 LPM	7.5×10−4	950.4	0.713	1.21	1.28 (0.03)	23.0 (1.7)	97.4 (0.3)
8 at 45 LPM	7.5×10−4	775.5	0.582	1.23	1.18 (0.06)	28.1 (2.6)	94.6 (0.8)

^aDenotes inhaler number and flow rate (LPM)

^bPressure drop over the internal flow passage starting at the exit of the capsule chamber

^cEstimated based on measured MMAD and the skeletal density of the primary particles (ρ_p = 1.325 g/cm³)

^dFine particle fraction (% < 1 μm) of the emitted dose (ED)

^eFine particle fraction (% < 5 μm) of the emitted dose (ED)

^fStandard deviations (SD) of experimental results based on n ≥ 3 trials

Quantitative correlations between the experimentally determined MMD and CFD predicted flow-based parameters are presented in Figure 3. As expected from the similar MMD results at two flow rates with Inhaler 6, no correlation is observed between Q and MMD when all eight inhalers are considered. A weak association is observed between MMD and pressure drop in the flow passage with a coefficient of determination R² = 0.38. However, the correlation fails to capture formation of the smallest aerosol in the series. Similarly, a weak association is observed between input power and MMD that also misses the best performing case. Interestingly, this result indicates that effective breakup of the aerosol requires more than just increased power supplied to the inhaler. Therefore, an effectively designed inhaler can produce a reduced MMD compared with an inefficient design at the same or reduced power input and pressure drop. Surprisingly, no association was observed between MMD and turbulent shear stress, as defined in Table 2, for a carrier-free powder. Overall, quantitative correlations between flow-based parameters and performance considered over the set of eight inhalers appear relatively weak and strongest for ΔP and power.

Figure 3.

Quantitative comparison of CFD predicted flow-based parameters with experimentally determined MMD of the aerosol. Flow-based parameters include (a) flow rate (Q), (b) pressure drop (ΔP), (c) Power, and (d) shear stress (τ_s). Error bars denote +/− one standard deviation in the experiments.

Experimentally determined values of FPF_1μm/ED and FPF_5μm/ED are presented in Table 3 and rank similarly compared with the respective MMD values. Figure 4 presents quantitative comparisons between the MMD and FPF values for all inhalers considered. Most likely because of the relatively small aerosol size, FPF_1μm/ED is found to correlate most closely with MMD (R² = 0.97). A much weaker correlation is observed between FPF_5μm/ED and MMD (R² = 0.32). The strong correlation between FPF_1μm/ED and MMD with a weaker correlation between MMD and FPF verifies the expected trend for this relatively small aerosol. The primary focus of this study is to generate aerosols in the range of 1 μm and below for next-generation DPI applications. Therefore, correlation development in this study is focused primarily on MMD and FPF_1μm/ED. However, it is observed that the FPF_5μm/ED values (89.5–97.4%) are exceptionally high compared with existing devices (3, 58).

Figure 4.

Quantitative comparison of MMD with (a) fine particle fraction less than 1 μm of the emitted dose (FPF_1μm/ED) and (b) fine particle fraction less than 5 μm of the emitted dose (FPF_5μm/ED) based on experimental data. Error bars denote +/− one standard deviation in the experiments.

Turbulence-Based Factors

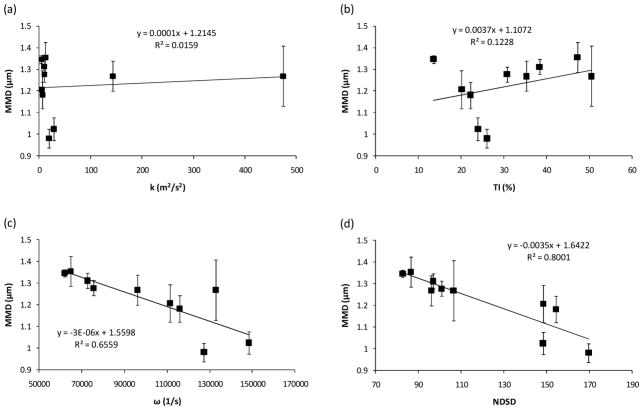
The newly proposed NDSD factor is presented as a representative turbulence-based parameter for the eight inhalers at characteristic flow rates in Figure 5. Qualitatively, increased NDSD values are observed in the center of the flow field for Inhalers 3–6. Compared with the 2D mesh, the 3D grid appears to extend the region of elevated NDSD values further into the downstream flow field. The 3D array provides an even larger region of elevated NDSD values. In contrast, both Inhalers 1 and 2 maintain elevated NDSD values only near the walls where interactions with particles is less likely. While turbulence may be highest in Inhaler 4 in terms of k and TI (Table 4), the reduced residence time associated with the higher flow rates produces a much lower value of NDSD, which is consistent with the mid-level value of MMD = 1.27 μm for this inhaler. The NDSD is maximum for Inhaler 6 at 45 LPM, which correlates well with the minimum MMD value of 0.98 μm (Table 4).

Figure 5.

Contours of non-dimensional specific dissipation (NDSD) at the midplane and cross-sectional locations for (a) Inhaler 1 at 45 LPM, (b) Inhaler 2 at 45 LPM, (c) Inhaler 3 at 45 LPM, (d) Inhaler 4 at 75 LPM, (e) Inhaler 5 at 45 LPM, and (f) Inhaler 6 at 45 LPM.

Table 4.

Key turbulence-based factors expected to influence deagglomeration.

Inhaler number and flow ratea	kb (m2/s2)	TIb (%)	ωb (1/s)	NDSDb (dimensionless)	MMDc (μm)
1 at 45 LPM	4.2	13.5	61,949	82.6	1.35 (0.02)d
2 at 45 LPM	5.6	20.1	111,303	148.4	1.21 (0.1)
3 at 45 LPM	12.1	47.2	64,846	86.5	1.36 (0.07)
4 at 60 LPM	143.0	35.3	96,020	96.0	1.27 (0.07)
4 at 75 LPM	474.2	50.5	132,866	106.3	1.27 (0.14)
5 at 45 LPM	9.5	38.3	72,673	96.9	1.31 (0.03)
6 at 45 LPM	19.1	26.03	127,277	169.7	0.98 (0.04)
6 at 60 LPM	28.3	23.9	148,323	148.3	1.03 (0.05)
7 at 45 LPM	10.0	30.7	75,565	100.8	1.28 (0.03)
8 at 45 LPM	6.7	22.2	115,799	154.4	1.18 (0.06)

^aDenotes inhaler number and flow rate (LPM)

^bVolume-averaged quantities within the flow passage of each inhaler

^cEstimated based on measured MMAD and the skeletal density of the primary particles (ρ_p = 1.325 g/cm³)

^dStandard deviations (SD) of experimental results based on n ≥ 3 trials

Considering quantitative correlations for turbulence-based parameters (Figure 6), only a weak and inconsistent relationship is observed between k and MMD. A much stronger correlation with k may be obtained if Inhaler 4 is removed. However the goal is to establish an aerodynamic factor that is predictive of performance across a range of inhalers and deaggregation devices. Similarly for TI, a relatively weak correlation is obtained overall. However in the case of TI, removing Inhalers 3, 4, 5, and 7 would significantly strengthen the relationship. The specific dissipation rate ω is observed to quantitatively predict MMD to a high degree with an R² = 0.66 for all inhalers. However, this correlation is again inaccurate for the case of minimum MMD. The correlation with ω is further strengthened by incorporating the residence time to form the NDSD parameter, which has an R² = 0.8 across all eight inhalers and captures both the maximum and minimum MMD values observed in the experiments.

Figure 6.

Quantitative comparison of CFD predicted turbulence-based parameters with experimentally determined MMD of the aerosol. Turbulence-based parameters include (a) turbulent kinetic energy (k), (b) turbulent intensity (TI), (c) specific dissipation rate (ω), and (d) non-dimensional specific dissipation (NDSD). Error bars denote +/− one standard deviation in the experiments.

Based on the strength of the correlation between NDSD and MMD, Figure 7 presents correlations between NDSD and FPF values (reported in Table 4). As expected, the NDSD parameter is observed to be highly predictive of FPF_1μm/ED with an R² value of 0.79 (Figure 7a). The NDSD factor also captures the trend of the FPF_5μm/ED data (Figure 7b); however, the coefficient of determination is R² = 0.31. This weak quantitative relationship is expected considering that MMD did not strongly correlate with FPF_5μm/ED. As with MMD, correlations between ω and FPFs were strong but had R² values below the NDSD parameter (not shown) for all eight inhalers considered.

Figure 7.

Quantitative comparison of CFD predicted NDSD with experimentally determined (a) FPF_1μm/ED and (b) FPF_5μm/ED. Error bars denote +/− one standard deviation in the experiments.

Particle-Based Factors

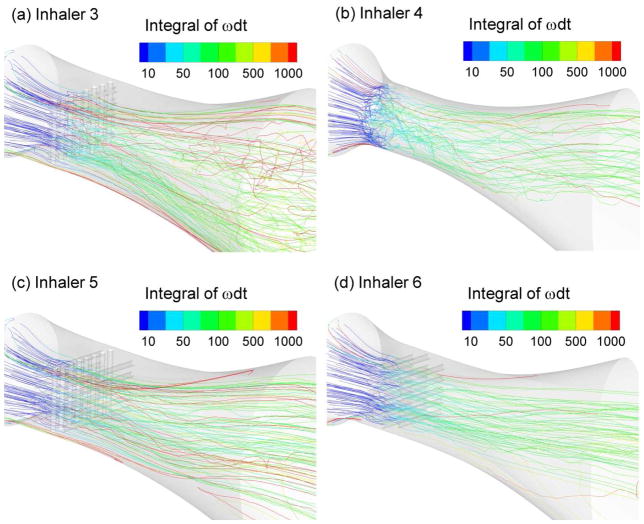
Trajectories colored according to the path integral of ωdt are presented in Figure 8 for Inhalers 3–6. As expected, trajectory integral values are observed to increase significantly in the region of the 2D mesh, inward jets, 3D grid, and 3D array. Subsequent slower increases in values are then observed downstream. Trajectories are observed to experience some turbulent dispersion in the high turbulence regions. For all inhalers, significantly elevated values of the ωdt parameter are observed near the wall.

Figure 8.

Trajectories of 1 μm particles colored according to the path integral of ω·dt for (a) Inhaler 3 at 45 LPM, (b) Inhaler 4 at 75 LPM, (c) Inhaler 5 at 45 LPM, and (d) Inhaler 6 at 45 LPM.

Considering quantitative correlations for particle-based parameters (Figure 9), weak to negligible associations were observed between the particle parameters and MMD. Due to no apparent correlation, not all cases were considered for the impaction studies. The strongest association was observed between the Iω_avg parameter and MMD with an R² of 0.24. However, this relationship did not capture the best performing case of Inhaler 6 and demonstrates an inconsistent trend.

Figure 9.

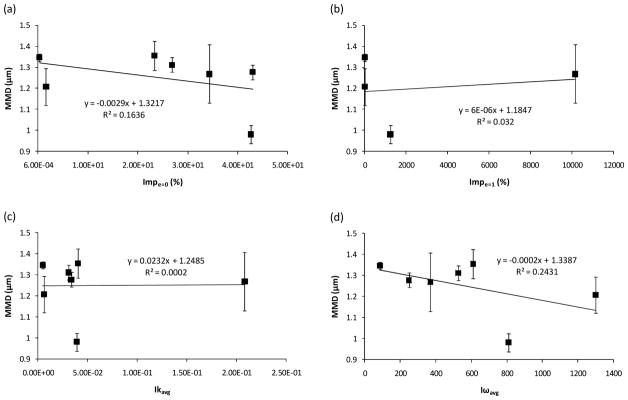
Quantitative comparison of CFD predicted particle-based parameters with experimentally determined MMD of the aerosol. Particle-based parameters include (a) wall impactions with zero restitution (Imp_e=0), (b) wall impactions with perfect restitution (Imp_e=1), (c) average trajectory integral of k·dt (Ik_avg), and (d) average trajectory integral of ωdt (Iω_avg). Error bars denote +/− one standard deviation in the experiments.

Analysis at Constant Pressure Difference

Results for a constant pressure difference of 2 kPa across the flow passages are illustrated in Figure 10. Figure 10a presents a comparison of the MMD correlation based on NDSD (solid line from Figure 6 (d) along with new experimental data for Inhaler 3 considered at 2 kPa. As observed from the figure, the correlation agrees with the new experimental data point within the relative bounds of expected difference associated with an of R² = 0.8. The MMD for Inhaler 6 at 2 kPa is also presented, based on CFD simulations. New experiments are not required for Inhaler 6 at 2 kPa because this pressure drop is bracketed by values for 45 and 60 LPM (Table 3), which did not change the MMD significantly in the experiments and agrees with the correlation value. This comparison shows that even at the same pressure drop, the 3D rod array (Inhaler 6) produces a lower MMD compared with the 2D grid (Inhaler 3).

Figure 10.

Quantitative comparison of MMD vs. NDSD at a consistent ΔP of 2 kPa through the flow passage. (a) The NDSD correlation (solid line) is in reasonable agreement with the experimentally determined performance of Inhaler 3 and indicates that the 3D array produces a smaller aerosol than the 2D mesh at the same pressure drop. (b) Evaluation of all inhalers based on the NDSD correlation (solid line) indicating that Inhaler 6 provides the lowest MMD for a ΔP of 2 kPa.

A comparison of all eight inhalers at a simulated airflow passage pressure drop of 2 kPa is presented in Figure 10b. The solid line is the MMD vs. NDSD correlation from Figure 6d. Data points indicate CFD predicted values of NDSD for each inhaler at a 2 kPa pressure drop with MMD values provided from the correlation. Again, Inhaler 6 provides the minimum MMD and Inhaler 1 produces the maximum MMD. For the 3D array, reducing the rod diameters (Inhaler 8) and increasing the cross-sectional area of the array region (Inhaler 7) both increase MMD of the aerosol. The 3D grid (Inhaler 5) produces a similar MMD compared with the 2D mesh (Inhaler 3) and a larger MMD than the 3D array (Inhaler 6) at the same pressure drop. As a result of this analysis, the 3D array design appears to provide superior performance compared with both existing deaggregation designs and other new 3D options evaluated at the same pressure drop.

DISCUSSION

A primary outcome of this study is that not all aerodynamic factors associated with deaggregation quantitatively correlate with MMD and FPF for a carrier-free formulation. Previous studies of carrier-free DPIs, and some carrier-based systems, have associated turbulence with the deaggregation of aerosols (13, 15, 23, 24). As described by Finlay (59) and Coates et al. (16), both the turbulent energy and length scale are important for deaggregation. Considering only k or TI ignores the length scale of turbulence and, therefore, does not correlate well with deaggregation across a series of multiple inhalers. It is observed that an advantage of the current study compared with previous studies is the large number of inhalers considered. Selection of 3 or 4 of the designs would have resulted in very strong correlations between deaggregation and k or TI. Similarly, shear stress was not found to correlate with deaggregation, based on a definition that included CFD volume averaging of the eddy dissipation rate (Table 2). In one of the only other existing quantitative correlations for deaggregation, Xu et al. (11, 21, 22) established very strong relationships between τ_s and FPF for carrier-based formulations within well defined sets of entrainment tubes. Reasons that τ_s does not work well in the current study include a different formulation type, i.e., carrier-free, consideration of multiple inhalers, and potentially calculation of τ_s based on CFD estimates of ε instead of analytical estimates. This study provides further evidence that deaggregation of carrier-free powders occurs by a different mechanism than with carrier-based and large agglomerate formulations. As described in the Introduction, deaggregation of carrier-based formulations was previously associated with turbulence (13), turbulent shear stress (11, 21, 22), and wall impactions of particles (18) while deaggregation of large agglomerates was associated primarily with wall impactions (17). Interestingly, ΔP and power showed weak but reasonable correlations with MMD. However, these relations failed to characterize the performance of the best inhalers considered in this study. This inconsistency indicates quantitatively that effective deaggregation cannot be achieved by simply maximizing the power delivered to the inhaler. An efficient inhaler can be developed that produces higher FPFs and lower MMDs for the same formulation at lower ΔP and power inputs compared with an inefficient design (Figure 3). An aerodynamic factor that can predict performance is then needed for device optimization that can be used to maximize deaggregation for a set pressure drop or minimum power input.

For the carrier-free leucine containing combination particle formulation considered in this study, turbulence interaction with the aerosol appears to be the primary particle breakup mechanism. Particle impactions and flow rate (which affects particle impaction velocity) showed no association with the MMD across the inhalers. Of the turbulence-based factors considered, the newly proposed NDSD parameter performed best with a coefficient of determination of approximately R² = 0.8 for both MMD and FPF_1μm/ED. This parameter is designed to account for three aspects of the interaction between the particles and turbulence. These aspects are (i) strength of the turbulence represented by turbulent kinetic energy, (ii) inverse characteristic length scale of the turbulence represented by 1/ ℓ, and (iii) time available for particle-turbulence interactions. Clearly, stronger turbulence will be more effective at breaking apart aggregates resulting in a direct association with k. The 1/ ℓ term indicates that smaller energetic eddies are more efficient at producing small particles compared with large eddies. That is, the most effective turbulence for creating small particles has high energy in the small eddies. Finally, it is reasonable that increasing the exposure time to k / ℓ will increase the amount of deaggregation that occurs. The composite NDSD term incorporates these three aspects of turbulent-particle interaction into a convenient non-dimensional form that demonstrates the strongest correlation with deaggregation observed in this study.

The NDSD factor is based on ω, which is proportional to the γ̇ or integral scale strain rate (ISSR) [1/s] term described by Finlay (59) and Coates et al. (15, 16, 23). However, there are two important differences between the NDSD factor and these previous studies. First, the NDSD parameter incorporates a residence time term that was very important in explaining the reduced inhaler performance occurring in some cases when the flow rate and ω parameters increased. This residence time theory may also be useful in interpreting previous results where increases in flow rate did not improve aerosol performance (23). Second, the current study interprets ω the term, and therefore the type of turbulence that leads to effective deaggregation, different from other studies. Finlay (59) and Coates et al. (16) emphasize that the integral scale eddies have maximum energy, are the largest of the flow field, and are most responsible for breakup of the aerosol. In contrast, the current study interprets the definition of ω (Eq. (2)) to imply that ℓ should be minimized for effective deaggregation. Hence, the most effective production of small particles occurs when high turbulent energy (k) is contained in small eddies. Efficient inhalers should then seek to maximize k but also minimize the length scale of the turbulence in order to produce the highest possible FPFs.

The particle-based integrations of turbulent quantities were not strongly associated with deaggregation. The trajectory integral of k incorporates the residence time but ignores the turbulence length scale. The trajectory integral of ω showed some agreement with MMD, but was not as strongly correlated as the volume averages of ω and NDSD. It was found that the trajectory integral average values were influenced by near-wall particles that had very large values of both ω and dt. These large values tended to dominate the final average value in a manner that was not representative of what most particles experienced in the central portion of the flow. A limit to the integral value along individual pathways may solve this problem. However, determining the physically relevant maximum value of ω·dt along a trajectory would be difficult. Large values of near-wall integrals also made it very difficult to obtain particle number independent results with high relative errors observed through 50,000 trajectories. Considering these limitations and the strength of the volume-averaged correlations, the latter approach is recommended for future design studies with carrier-free formulations.

In order to analyze the complex phenomenon of deaggregation, multiple approaches can be implemented. If the focus of a study is the deaggregation of different powder formulations, then it is critical to base the analysis on a single geometry or set of controlled geometries as described by Xu et al. (11, 21, 22). To analyze the effects of different aerodynamic mechanisms on deaggregation, a single formulation is needed along with either devices to isolate individual factors or more complex inhaler flow passages combined with CFD analysis. Voss and Finlay (13) employed the approach of designing a test apparatus to isolate individual deaggregation mechanisms. While scientifically elegant, it is very difficult to isolate individual mechanisms affecting deaggregation due to factor dependence and complex flow interrelations. For example, increasing turbulence will also increase wall impactions due to the turbulent dispersion of particles. Meshes to increase impaction will also modify the turbulence length scale, which was found to be important for aggregate breakup. In the current study, realistic flow passages were considered to form eight different inhalers, some considered at multiple flow rates, along with CFD analysis. In each inhaler, multiple deaggregation mechanisms are likely occurring. Given the complexity of these systems and the deaggregation process, it is not surprising that few successful quantitative correlations were found when considering individual variables. Interestingly, the NDSD parameter emerged as providing the strongest quantitative correlation with the MMD and FPF_1μm/ED, which were the markers for deaggregation. Other factors are likely occurring in each inhaler and contributing to deaggregation, such as wall impactions in Inhaler 6, but these parameters are either somewhat proportional to the turbulence and NDSD (as with particle impactions and turbulent shear stress) or provide a secondary breakup mechanism. While these multiple deaggregation mechanisms may be occurring, the NDSD was found to be the primary quantifiable factor correlating with deaggregation across multiple platforms, which can now be used in future flow passage and design optimization studies of inhalers delivering carrier-free formulations.

In a previous study, Son et al. (35) demonstrated that the 3D rod array design exhibited superior performance to a 2D mesh and the base HandiHaler DPI at a consistent flow rate. However, it was not obvious from Son et al. (35) why the 3D array performed better than the other designs and if this improved performance would be maintained at an identical pressure drop. The current analysis estimates the NDSD as the primary factor for carrier-free deaggregation and indicates that the 3D rod array design is effective because it maximizes NDSD. Specifically, the velocity field plots (Figure 2) indicate that the rod array amplifies velocity and turbulence, or k, as velocities were highest between the 2nd and potentially 3rd rows of rods. The spacing between the rods serves to control the turbulence length scale, with each successive row of rods further reducing ℓ as eddies are formed and then broken into smaller components through rod and eddy interactions. Finally, the 3D configuration increases the length of the high turbulence zone thereby maximizing exposure time of the particles. This rod array may also be effective at breaking apart larger aggregates, but the mechanism of action will likely shift to a combination of impaction and turbulent interaction. Furthermore, the 3D rod array is not likely to clog when presented with larger powder or agglomerate doses. Considered at a constant pressure drop of 2 kPa over the flow passage, the 3D array was again determined to maximize the NDSD value, which correlates with maximum FPF and minimum MMD.

One potential limitation of this study is the CFD analysis of only the flow passage and not the upstream capsule dispersion chamber. Previous studies have demonstrated that significant turbulence and other flow features are generated in the capsule chamber and propagated into the downstream flow passage (18, 60). Longest and Hindle (14) previously showed that by changing the air inlet size of an inhaler, turbulence levels throughout the device were significantly modified, which had an impact on mouthpiece drug retention. In the current study, the same capsule chamber was used for all 8 inhalers considered in the experiments. The CFD simulations implemented the same inlet boundary conditions to the flow passages. The results of this study then provide the relative differences in the aerodynamic factors based entirely on flow passage design. Considering that relative comparisons are made with the same inlet conditions, it is not necessary to include the upstream capsule chamber in the CFD simulations. However, exact values of the aerodynamic factors may change if the capsule dispersion chamber is included in the simulations. Therefore, the correlations developed are intended to demonstrate strengths of association and provide guidance for designing effective flow passages for deaggregation, as with the 3D rod array. Clearly, performance of the different inhalers considered will change if different capsule dispersion chambers are employed.

CONCLUSIONS

In conclusion, this study has evaluated associations between aerodynamic parameters and DPI performance for a carrier-free formulation with the goal of forming micrometer and submicrometer aerosols for EEG and other next-generation respiratory drug delivery approaches. The number of inhalers and number of aerodynamic parameters were both significantly greater than have been considered in any previous study of this type. For the carrier-free formulation considered, turbulence was identified as the primary deaggregation mechanisms of the particles. Of the 12 aerodynamic factors considered, the newly proposed NDSD showed the strongest correlation with both MMD and FPF. Factors that were determined to be important for turbulent deaggregation of the aerosol and quantified by the NDSD parameter were high turbulent kinetic energy and exposure time and small characteristic eddy length scales. The newly proposed 3D rod array design was found to have the highest NDSD values based on CFD simulations and the lowest MMD based on in vitro experiments evaluated at both consistent flow rates and pressure drops. The 3D rod array was capable of creating an aerosol with a MMD < 1 μm, and with FPF_1μm/ED and FPF_5μm/ED values of 38.8 and 97.3%, respectively. Existing DPI analyses typically ignore FPF_1μm/ED and report FPF_5μm/ED in the range of 40%. These results indicated that forming submicrometer aerosols with passive DPIs is practical for EEG and other next-generation respiratory drug delivery strategies. Furthermore, the 3D rod array design is highly configurable and can be adjusted to maximize NDSD for optimized performance. Future studies are needed to evaluate the NDSD parameter with different initial aerosolization mechanisms and with different formulations, and to apply this newly developed parameter to improve the performance of existing DPIs and newly proposed submicrometer inhalers.

ABBREVIATIONS

2D

two-dimensional

3D

three-dimensional

AS

albuterol sulfate

CFD

computational fluid dynamics

DPI

dry powder inhaler

ED

emitted dose

EEG

excipient enhanced growth

FPF

fine particle fraction

HPLC

high-performance liquid chromatography

HPMC

hydroxypropyl methylcellulose

LES

large eddy simulation

LRN

low Reynolds Number

LPM

liters per minute

MMAD

mass median aerodynamic diameters

MMD

mass median diameter

MN

mannitol

MP

mouthpiece

MT

mouth-throat

NDSD

non-dimensional specific dissipation

NGI

Next Generation Impactor

PDA

photo diode array

R²

coefficient of determination

RH

relative humidity

SD

standard deviation

TB

tracheobronchial

UV

ultraviolet