Molecular Dynamics Simulations of DPPC Bilayers Using “LIME,” a New Coarse-grained Model

Abstract

A new intermediate resolution model for phospholipids, LIME, designed for use with discontinuous molecular dynamics (DMD) simulations is presented. The implicit-solvent model was developed using a multi-scale modeling approach in which the geometric and energetic parameters are obtained by collecting data from atomistic simulations of a system composed of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) molecules and explicit water. In the model, 14 coarse-grained sites that are classified as 1 of 6 types represent DPPC. DMD simulations performed on a random solution of DPPC resulted in the formation of a defect free bilayer in less than 4 hours. The bilayer formed quantitatively reproduces the main structural properties (e.g. area per lipid, bilayer thickness, bond order parameters) that are observed experimentally. In addition, the bilayer transitions from a liquid-crystalline phase to a tilted gel phase when the temperature is reduced. Transbilayer movement of a lipid from the bottom leaflet to the top leaflet is observed when the temperature is increased.

Introduction

The lipid bilayer, the primary constituent of cellular and intracellular membranes in all living organisms, plays a central role in many biological processes including cell signaling and protein function.[(1),(2),(3)] In addition to its physiological significance, lipid bilayers are now being used to create devices for targeted delivery of proteins, nucleic acids and drugs in the treatment of a wide variety of diseases.[(4),(5),(6)] Significant progress has been made by scientists working to use these structures to develop therapeutic agents.[(7),(8),(9),(10),(11),(12)] A tool that would allow researchers to visualize the structure and function of the lipid bilayer on a molecular level could help enhance the rate of advancement in these areas. For example, we are now using the model discussed in this manuscript to study the release of drug molecules from liposomes composed of lipid mixtures as a result of a change in pH. [(13),(14),(15)]

In this paper we take a multiscale modeling approach to develop a new implicit-solvent intermediate-resolution lipid model, “LIME” for Lipid Intermediate Resolution Model, that enables molecular dynamics simulation of the self-assembly of a lipid bilayer. The model system chosen for study is the lipid 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) in water. We show that discontinuous molecular dynamics (DMD) simulations using the LIME forcefield accurately reproduce the structural properties of a DPPC bilayer, including the area per lipid, bilayer thickness, bond order and mass density profiles. This model is the culmination of a systematic program of research aimed at developing simulation tools based on coarse-grained lipid models that are fast enough to simulate self assembly of large structures yet have accuracy that is comparable to that found in atomistic simulations. By using multiscale modeling, which translates the atomistic details from well established force fields, GROMOS96 53a6 in this case, into coarse grained simulations, we avoid the pitfalls associated with fitting many molecular parameters to the limited data on lipid systems.

Molecular dynamics studies of phospholipid bilayers can be divided roughly into two categories: high-resolution models and low-resolution models. High-resolution or atomistic models are based on a realistic representation of membrane geometry and energetics and typically account for the motion of every atom on the membrane and every solvent atom. Atomistic simulations of lipid bilayers have been performed to study the permeation of small molecules through a lipid bilayer [(16)], the interaction between lipid bilayers and substrates [(17)], the behavior of charged and neutral bilayers [(18)], and a large variety of additional bilayer properties and behaviors.[(19),(20),(21)] In a recent united-atom study, Kukol demonstrated that the GROMOS96 53a6 forcefield [(22)] and the Kukol DPPC3 topology could be used with GROMACS [(23),(24)] to reproduce the experimental area per lipid of a preformed DPPC bilayer for a united-atom system composed of 128 lipids and 3655 water molecules with 3% accuracy without assuming constant surface area or including surface pressure.[(25)] However, one drawback associated with atomistic models is that the detail that makes these high resolution models so realistic and appealing also makes them extremely computationally intensive and prevents them from examining large conformational changes or long time scales. For example, the 90 ns atomistic simulation of 1017 DPPC lipids and 106,563 water molecules by de Vries et al. in 2004, which shows the spontaneous formation of a DPPC vesicle, was run on four or eight processors at a rate of only 1 ps per processor CPU hour (1.7 GHz Intel Pentium IV processors).[(26)]

Coarse-grained models of lipids have been developed in order to reduce simulation time so as to access longer time scales than are achievable in atomistic simulations. In these models clusters of atoms are grouped together into single sites to reduce the number of events that require calculation.[(27)] A popular explicit-solvent coarse-grained model for lipids is MARTINI which was developed by Marrink et. al. and has been used to simulate the spontaneous aggregation of a DPPC bilayer.[(28)] In this model, an average of four atoms are represented by a single interaction site, 10 different types of interaction sites are defined, and the interaction strengths between any two sites are assigned one of five values.[(28)] The Marrink predictions of the DPPC area per head group, bending modulus, area compressibility, lipid lateral diffusion coefficient and water permeation rate closely matched the experimentally measured quantities.[(28)] Marrink et al improved the MARTINI force field (creating version 2.0) by increasing the number of types of possible interaction sites from 10 to 18 and increasing the number of interaction strength levels from 5 to 10.[(29)] MARTINI (version 2.0) was applied to model molecular raft formation in model membranes.[(29),(30)] Although we have looked, we have been unable to locate any information about the computational speed of the MARTINI model for lipid systems. Orsi and coworkers developed a coarse-grained explicit solvent model for DMPC lipids which represents the 118 atoms of DMPC by 10 coarse-grained sites; the predicted structure, elasticity, electrostatics and dynamics of a DMPC bilayer quantitatively matched experimental data.[(27)] In this model, the spherical units representing the headgroup choline and phosphate groups interact via the Lennard Jones potential and the glycerol and hydrocarbon groups of the lipids are modeled as soft uniaxial ellipsoids through the Gay-Berne potential.[(27)] The Orsi model was extended to dioleylphosphatidylcholine (DOPC) by adopting a 12 site coarse-grained representation.[(31)] Their simulations in 2010 of the formation by 128 DOPC lipids of a defect-free bilayer required approximately 2.5 days; those of the formation by 128 DMPC lipids of a defect-free bilayer with an embedded water pore required approximately 25 days (Intel 2.8 GHz processors in serial).[(31)] Subsequently, Orsi and Essex developed the electrostatics-based “ELBA” 1.0 force field for coarse-grained models of lipid membranes which explicitly represents charges and dipoles.[(32)] In this new model the Gay-Berne components are replaced with Lennard Jones potentials. DOPC, DOPE and DSPC are each represented by 15 spherical CG sites and water is treated explicitly. The ELBA 1.0 force-field was found to accurately reproduce several of the experimentally observed physical properties of single-species lipid bilayers composed of DOPC, DOPE or DSPC in the liquid crystal phase and DSPC in the gel phase. ELBA 1.0 was later refined to become ELBA 1.1 to correctly reproduce the hexagonal inverse phase for DOPE-water systems.[(33)] ELBA 1.1 was also used to simulate mixed DOPC-DOPE bilayers at various compositions and to calculate the first reported values for the lateral pressure and electrical potential profiles for mixed DOPC-DOPE bilayers.[(33)] In a recent study, DeNicola and co-workers developed an explicit-solvent coarse-grained model for phospholipids for use with hybrid particle field molecular dynamics simulations.[(34)] In this work, the MARTINI coarse-grained mapping scheme is used to represent DPPC and the model parameters are optimized so that the coarse-grained model reproduces the structural properties of the reference particle-particle simulations.[(34)]

Some coarse-grained models ignore the motion of solvent atoms to further enhance the computational efficiency associated with coarse-graining. Instead, the effect of solvent atoms is included implicitly through the use of effective potentials, or potentials of mean force. Recently, Wang and Deserno presented an implicit solvent, coarse-grained model for POPC bilayers derived using a multiscale modeling approach based on structure-matching methodology.[(35)] In this model the 134 atoms in each POPC lipid molecule are represented by 16 coarse-grained sites of 8 different types. The coarse-grained potentials were optimized iteratively to reproduce radial distribution functions and the area per lipid of the bilayer obtained from all-atom simulations performed with the molecular dynamics program NAMD [(36)] and the fully atomistic CHARM27 [(37)] parameters. In order to promote lipid aggregation in this model, it was necessary to introduce additional cohesive interaction potentials between the alkyl tails and between the interfacial head group sites. The strength of the cohesive interaction potentials were chosen to promote bilayer stability, to match RDFs for the coarse-grained and atomistic simulations, and to optimize the lateral stress profile; without it, the bilayer falls apart. This model was used to simulate the self-assembly of 288 POPC lipids into a bilayer from a random lipid dispersion that quantitatively matched experimental bilayer properties. A defect-free bilayer formed in approximately 32 CPU hours (Xeon E5430 2.66 GHz chips in parallel with infiniband connection).[(35)] A similar approach was taken by Lyubartsev who constructed a coarse-grained, implicit-solvent lipid model containing 10 coarse grained sites to represent the 118 atoms of DMPC; the parameters were optimized to reproduce the radial distribution functions from all-atom molecular dynamics simulations performed with the MDynaMix [(38)] package and the all-atomic CHARMM27 [(20),(37)] force field.[(39)] Simulations of DMPC lipids using this model show the formation of bicelles and vesicles starting from a disordered system of lipids.[(39)] Izvekov et. al. used a multiscale coarse-graining approach to develop a model in which 11 different coarse-grained types are used to represent DMPC and cholesterol molecules.[(40)] The Izvekov model accurately reproduced the structural and elastic properties of a DMPC lipid bilayer and was used to simulate pre-formed DMPC/cholesterol liposomes. However, simulations of a DMPC/cholesterol system starting from a random dispersion did not form a bilayer. Instead, this system assembled into aggregates composed of DMPC and cholesterol and aggregates composed primarily of cholesterol.[(40)]

In this paper, we describe the development of an implicit-solvent, coarse-grained model, LIME, derived using a multi-scale modeling approach that enables simulations of large numbers of phospholipids in aqueous solution. The number of coarse-grained sites per lipid, 14, is very similar to the coarse-grained phospholipid representation of DPPC in other models,[(28),(31),(35),(39)] but the interactions are not. Instead the interactions between coarsegrained sites are represented by hard sphere and square well potentials as opposed to Lennard Jones potentials, thereby allowing us to use discontinuous molecular dynamics, a fast alternative to traditional molecular dynamics. The multiscale modeling procedure used to determine the model parameters involves the following steps. The trajectory data from a 20 ns GROMACS simulation using the GROMOS96 53a6 united-atom forcefield for a fully hydrated DPPC bilayer is coarse-grained into 14 sites. United-atom simulations are essentially the same as atomistic simulations with the exception that hydrogen atoms bonded to carbon atoms are represented as a single site. Radial distribution functions (RDF) between all bonded and non-bonded pairs of coarse-grained sites are calculated and used to determine LIME geometrical and energetic parameters. The hard sphere diameter between non-bonded coarse-grained sites is estimated to be the smallest distance at which the RDF takes a non-zero value. composed primarily of cholesterol.[(40)] estimate the square well width, and the minimum and maximum bond lengths between bonded pairs. The relative stiffness of each lipid is maintained by imposing pseudobonds, which limit the bond length fluctuations to the values observed in the GROMACS simulations. Interaction energies between non-bonded coarse-grained sites are determined by calculating the potential of mean force using a one-step Boltzmann inversion scheme.[(41),(42)] In the model each coarsegrained site has its own realistic mass.

Highlights of our results include the following; The model successfully simulates the spontaneous assembly of a DPPC bilayer composed of 256 lipids in less than 4 CPU hours starting from a random initial configuration, which is approximately an order of magnitude faster than the fastest reported coarse-grained implicit solvent model. The area per lipid of our bilayer is within 2% of the value calculated from our GROMACS simulation data and the literature value. The thickness of our bilayer is within 5–7% of the literature value and within 4–8% of the thickness of the bilayer in our GROMACS simulations. The orientational order parameter of the alkyl tail bonds in LIME are in excellent agreement with those calculated from the GROMACS model. The mass density profiles of the LIME and GROMACS models closely match each other. Finally, LIME is able to simulate transbilayer flip-flop in which a lipid flips from the bottom leaflet of a membrane to the top leaflet.

Theoretical Methods

In LIME six different coarse-grained types (I – VI) are used to represent the 130 atoms that make up a DPPC molecule. DPPC is composed of a polar head group that includes a choline, phosphate and two ester linkages, and two nonpolar hydrophobic acyl tails. Figure 1 illustrates the coarse-graining of a DPPC molecule from 50 united-atom (Figure 1a) s to the 14 coarsegrained sites in the LIME representation. This figure and all other figures depicting lipid molecules throughout the paper were generated with Visual Molecular Dynamics (VMD).[(43)] Each coarse-grained site that represents a unique set of atoms and is assigned a different coarsegrained type. Each coarse-grained type is represented by a different color in Figure 1b. Table 1 lists the atoms included in each coarse-grained site, the “type” assigned to each coarse-grained site and the mass of each coarse-grained site. Types I and II represent the choline entity and the phosphate group, respectively. Ester coarse-grained sites 3 and 9 are assigned types III and IV, respectively. The coarse-grained sites in the hydrocarbon tails (excluding the terminal sites) are assigned type V. Finally, the terminal tail coarse-grained sites are classified as type VI. We considered treating the terminal tail beads (sites 8 & 14) as the same type as the nonterminal tail beads (sites 4–7 & 10–13) because type V differs from type VI only by a single hydrogen atom. However, we found that the epsilons for type V&V pairs (ε = −0.050 eV) are significantly different than the parameters for type VI&VI pairs (ε = −0.070 eV). This is probably because of the differences in connectivity between the two types. Therefore, we felt that it was important that the different groups have their own unique types.

Figure 1.

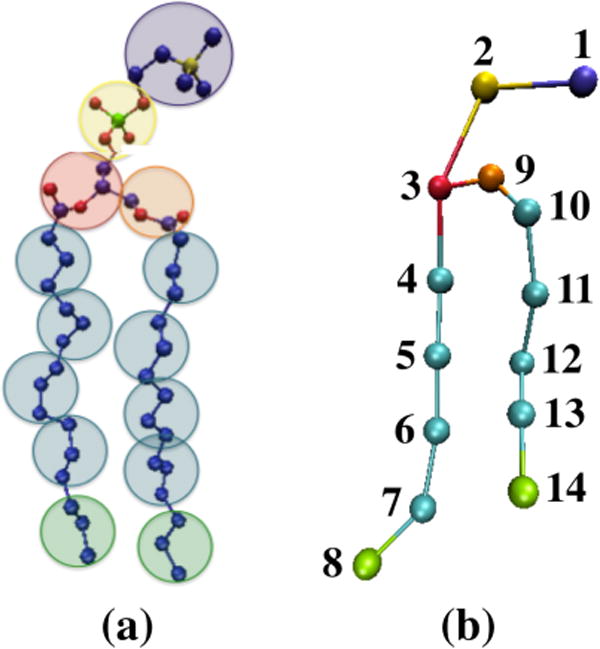
(a) United atom and (b) coarse-grained representation of DPPC. The color scheme is; purple (choline entity – type I for site 1); yellow (phosphate group – type II for site 2); red (ester group – type III for site 3); orange (ester group – type IV for site 9); cyan (alkyl tail groups – type V for sites 4–7 & 10–13); green (terminal tail groups – type VI for sites 8&14). The coarsegrained site size does not represent the actual size of each site.

Table 1.

The type, number of atoms, and mass for all of the coarse-grained sites in the LIME representation.

CG Site	CG Type	Atoms per CG Type	Mass of CG Type (amu)
1	I	C5H13N	87.2
2	II	PO4	95.0
3	III	C3HO2	71.1
9	IV	C2H2O2	58.0
4–7, 10–13	V	C3H6	42.1
8, 14	VI	C3H7	43.1

In addition to coarse-graining and treating solvent implicitly, we employ discontinuous molecular dynamics (DMD) simulation to further increase the speed of our code. DMD [(44)] is a very fast alternative to traditional molecular dynamics simulation that is applicable to systems of molecules interacting via discontinuous potentials, e.g., hard-sphere and square-well potentials. For this reason, all of the inter- and intra- molecular interactions in our lipid model are represented by a combination of hard-sphere and square well potentials, as opposed to the Lennard Jones, Coulombic and harmonic potentials found in traditional molecular dynamics simulations. Unlike continuous potentials, such as the Lennard-Jones potential, discontinuous potentials exert forces only when particles collide. This enables the exact (as opposed to the numerical) solution of the collision dynamics. This imparts great speed to the algorithm and allows sampling of much wider regions of conformational space, longer time scales and larger systems than in traditional molecular dynamics. Molecules are given an initial random configuration that satisfies both excluded volume and angular constraints. Initial velocities are chosen randomly from a Maxwell-Boltzmann distribution about the desired temperature. Particle trajectories are followed by calculating the time between each collision and advancing the simulation to the next event. Types of events include a collision between two spheres, a bond event when the distance between two bonded spheres reaches a minimum or maximum limit, and a square well event when two spheres enter (capture), unsuccessfully attempt to escape (bounce) or successfully leave (dissociation) a square-well attraction.[(44),(45),(46),(47)] The simulations are performed with the number of particles, the temperature and the volume held constant. The temperature is maintained constant using the Andersen thermostat, which uses ghost collisions with randomly selected particles in the system to maintain the Maxwell-Boltzmann velocity distribution about the desired temperature.[(48)] The simulations were run at constant volume as this is the most straightforward ensemble for use in DMD. In the Conclusion section we discuss the possibility of simulating lipids in the NPT ensemble using a combination of a hybrid Monte Carlo/DMD approach.

Data used to calculate the coarse-grained model parameters was obtained by running explicit-solvent NPT ensemble united-atom simulations on a system containing 30 DPPC phospholipids and 8655 water molecules. The GROMACS simulation package [(23),(24)], version 4.5.4, was used with the GROMOS96 53a6 forcefield [(22)] and the Kukol DPPC3 topology, which has been shown previously to accurately reproduce the experimental area per lipid, lateral self diffusion constant and deuterium order parameters for the acyl chains in DPPC bilayers in solution.[(25)] The initial configuration of this system was random in a box with equal sides of length 100.0 Å. The Berendsen thermostat [(49)] was used to keep the temperature constant at 325K throughout the simulation with a time constant of 0.1ps. The simulation was run for 20 ns with a time step of 0.002 ps for approximately 48 CPU hours. Periodic boundary conditions were applied and the pressure was maintained at 1.0 bar. Throughout the GROMACS simulation the coordinates of each atom were written to an output trajectory file every 1 ps. These output files were used to calculate the centers of mass for each of the 14 coarse-grained sites on the 30 phospholipids.

We chose to run atomistic simulations of a small system to gather data for use in calculating coarse-grained parameters because we did not want to restrict the movement of the lipids during the atomistic simulation. It is not uncommon to gather data for a coarse-grained model from a small system. For example, Lyubartsev performed atomistic simulations of only 16 DMPC lipids to obtain data for use in calculating coarse-grained parameters.[(39)] To ensure that our atomistic simulation of 30 DPPC lipids was not too small or at too low a density, we compared the radial distributions we calculated from this simulation with those calculated from a GROMACS simulation of 128 DPPC lipids in a box with dimensions of 64Å × 64Å × 90Å. The sigma and lamda values calculated from each GROMACS simulation were nearly identical. Furthermore, the epsilon values calculated from each simulation differed by minimal amounts.

Results and Discussion

The LIME interaction energies were determined using a one-step Boltzmann inversion procedure inspired by the iterative Boltzmann inversion scheme, which is a popular strategy used to systematically compute potentials for coarse-grained simulations.[(35),(41),(42)] We begin by reminding the reader of the iterative Boltzmann inversion scheme, an approach based on the idea that the effective potential, or potential of mean force, U(r), between two molecules in a sea of molecules can be obtained from the radial distribution g(r) using:

$$\text{U}(\text{r})=-k_{\text{B}}\text{T}\ln [\text{g}(\text{r})]$$ Equation 1

where k_B is the Boltzmann constant and T is the temperature of the system. The iterative Boltzmann inversion scheme involves the following steps: (1) Data from an atomistic simulation is used to calculate the intermolecular radial distribution function g(r) between coarse-grained sites. (2) An initial guess for the potential of mean force, U(r), between the coarse-grained sites is determined using Equation 1. (3) A coarse-grained simulation using the initial guess for the potential of mean force is run and a new g(r) between coarse-grained sites is calculated. (4) The difference between the coarse-grained and the atomistic potentials of mean force is used to generate a correction to the coarse-grained potential of mean force. (5) This process is repeated iteratively until the coarse-grained and atomistic potentials of mean force match each other within a prescribed tolerance.[(41),(42)]

Instead of using the iterative Boltzmann inversion procedure described above, we use a simplified, one-step Boltzmann inversion to obtain the LIME interaction energies. Figure 2 outlines this approach, the procedure is the following: (1) the average radial distribution function between two intermolecular coarse-grained sites is determined, (2) the potential of mean force is calculated using Equation 1, and (3) the minimum value of the potential of mean force between the coarse-grained sites, ε, is chosen to be the depth of the square well potential. Mathematically this can be expressed as:

$$\text{ε}=-k_{\text{B}}\text{T}\ast \ln [\text{g}{(\text{r})}_{\text{MAX}}]$$ Equation 2

where g(r)_MAX is the maximum value of g(r) in the radial distribution function and T is the temperature of the system. If the ε between two coarse-grained sites is greater than −0.005 eV, the sites are assumed to have a hard-sphere interaction (ε = 0.0 eV).

Figure 2.

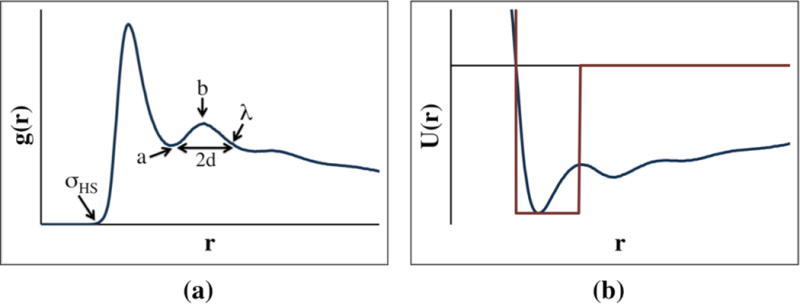
A schematic of the approach used to calculate the LIME interaction energies for two coarse-grained types: (a) the radial distribution function is calculated (b) the one-step Boltzmann inversion scheme is used to calculate the potential of mean force by inverting the RDF; ε is chosen as the minimum U(r) value (blue line); the depth of the square well potential or the interaction energy is assigned the ε value (red line)

The iterative Boltzmann inversion approach was not used to obtain the LIME parameters because the shape of the radial distribution function for a discontinuous potential obtained by coarse-graining the GROMACS simulation is dramatically different from the shape of the radial distribution function associated with a square-well potential. See for example the radial distribution function for sites 1 & 1 obtained during a LIME simulation shown in Figure 3. As is expected for square-well systems, there are no oscillations and there are discontinuities in g(r) at distances that correspond to the discontinuity in the potential. Thus it does not make sense to use an iterative procedure to try to match the GROMACS and coarse-grained potentials. By using the one-step Boltzmann inversion scheme we are able to develop a model that very accurately matches experimental observations for a lipid bilayer. Since we were able to obtain very good agreement between the physical properties of our LIME bilayer with experimental values we did not attempt to go beyond a one-step scheme.

Figure 3.

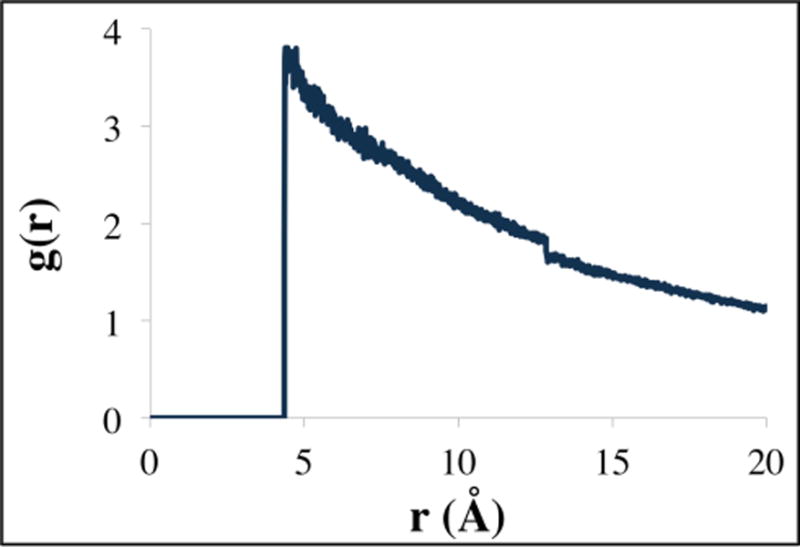
A radial distribution function for sites 1 & 1 obtained during a LIME simulation. The first non-zero value is located at the hard sphere diameter (4.75 Å) and the small discontinuity is located at the square-well width (12.55 Å). The shape of the radial distribution function differs significantly from the shape of a distribution function associated with a more traditional Lennard Jones potential.

The LIME hard sphere (σ_HS) diameters and square-well (λ) widths were determined from the radial distribution functions between pairs of non-bonded coarse-grained sites in the GROMACS simulations which were run on 30 DPPC and 8655 water molecules. As shown in Figure 2a the hard sphere diameter (σ_HS) for each pair of interaction sites was determined by locating the smallest non-zero separation between the two sites. The square well sphere diameter (λ) for each pair of interaction sites was determined by examining the radial distribution function between those sites. First, the local maximum (labeled b in Figure 2a) located at the largest distance less than 15 Å was identified. Next, the local minimum (labeled a in Figure 2a) preceding this local max was identified. Finaly, λ was calculated using:

$$\text{λ}=\text{a}+2\text{d}$$ Equation 3

where d = (b − a). If a λ value greater than 15 Å was calculated, the procedure for calculating λ was repeated using a local maximum closer to the origin. Sample radial distributions for intermolecular coarse-grained types 1&1, 1&2 and 5&5 are provided in Figure 4. The hard sphere diameters (σ_HS) determined for coarse-grained types 1&1, 1&2 and 5&5 are 4.35 Å, 3.85 Å and 3.75 Å, respectively. The values of λ for coarse-grained types 1&1, 1&2 and 5&5 were found to be 12.65 Å, 9.85 Å and 11.56 Å, respectively. A complete list of all hard sphere diameters, square well widths and interaction energies is provided in Table 2.

Figure 4.

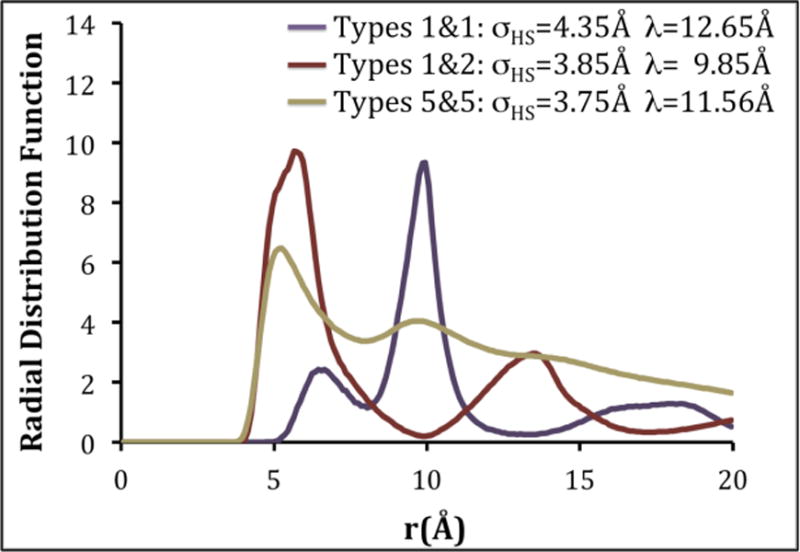
(a) The intermolecular radial distribution functions, hard-sphere diameters (σ_HS) and square-well diameters (λ) for coarse-grained types 1 & 1, 1 & 2, and 5 & 5.

Table 2.

The hard sphere diameters, square well widths and interaction energy for each pair of coarse-grained type.

Coarse-grained Type i	Coarse-grained Type j	σHS ij (Å)	Λij (Å)	εij (eV)
1	1	4.35	12.65	−0.065
1	2	3.85	9.85	−0.070
1	3	3.85	9.95	−0.050
1	4	3.75	10.25	−0.047
1	5	4.15	8.00	0.000
1	6	4.15	8.00	0.000
2	2	4.05	12.15	−0.080
2	3	3.45	13.05	−0.048
2	4	3.35	12.35	−0.030
2	5	3.75	8.15	0.000
2	6	3.65	6.40	0.000
3	3	3.65	10.45	−0.037
3	4	3.25	9.95	−0.036
3	5	3.65	10.53	−0.022
3	6	3.55	7.70	−0.015
4	4	3.15	11.65	−0.035
4	5	3.45	11.43	−0.026
4	6	3.45	10.85	−0.023
5	5	3.75	11.56	−0.050
5	6	3.75	11.66	−0.054
6	6	3.65	11.02	−0.070

The minimum and maximum bond lengths were determined by plotting the radial distribution functions for bonded coarse-grained sites. The minimum bond length (σ_MIN) was chosen as the smallest possible distance between two bonded coarse-grained sites. The maximum bond length (σ_MAX) was chosen as the largest distance for which a non-zero g(r) was observed. Sample distributions for intramolecular coarse-grained types 1&2, 3&5, and 5&6 used to determine σ_MIN and σ_MAX for bonds and the resulting values of σ_MIN and σ_MAX are provided in Figure 5.

Figure 5.

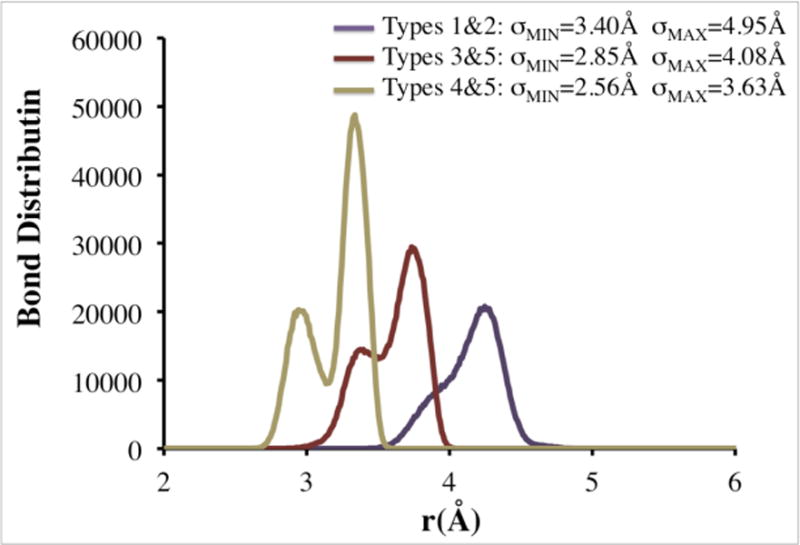
The intramolecular bond distribution functions, minimum bond lengths (σ_MIN) and maximum bond lengths (σ_MAX) for coarse-grained types 1 & 2, 3 & 5, and 5 & 6

The relative stiffness of the lipid molecule is maintained by imposing pseudobonds, which limit the fluctuation of coarse-grained sites to the angles and torsional angles observed during the GROMACS simulations. Bond angles were maintained by imposing pseudobonds between all next nearest neighboring sites along the chain. Torsional angles were maintained with pseudobonds between next next nearest neighboring sites along the chain. Bond distributions for intramolecular sites calculated from the GROMACS simulations were used to determine the minimum and maximum values for the pseudobond lengths in LIME. The minimum pseudobond length was determined by finding the smallest distance at which the intramolecular bond distribution function exceeds 30% of its maximum value. The maximum pseudobond length was determined by finding the smallest distance, larger than the distance at which the bond distribution function maximum occurs, where the intramolecular bond distribution function falls below 30% of its maximum value. Pseudobonds were also added between intramolecular coarse-grained sites 5&11, 6&12, 7&13 and 8&14 on the same chain to restrict the separation between the tails to the distances observed during the GROMACS simulations. This was done to prevent the tails from adopting conformations that were not frequently observed during the GROMACS simulations. The minimum pseudobond lengths between intramolecular sites 5&11, 6&12, 7&13, and 8&14 were determined by locating the smallest distance at which the intramolecular bond distribution function exceeds 30% of its maximum value. The maximum pseudobond lengths between intramolecular sites 5&11, 6&12, 7&13 and 8&14 were determined by finding the smallest distance, larger than the distance at which the intramolecular bond distribution function maximum occurs, where the bond distribution function falls below 30% of its maximum value.

In all the simulations run using the LIME force field, periodic boundary conditions were implemented to eliminate any artifacts that might be caused by the box walls. In addition, all simulations were carried out in the canonical ensemble where the number of particles, the temperature and the volume are held constant. Simulation temperature in LIME is expressed in terms of the reduced temperature, T*:

$$T\ast =k_{\text{B}}T/\text{ε}\ast$$ Equation 4

where k_B is Boltzmann’s constant, T is the temperature, and ε* is the reference interaction strength.[(50)] The reference interaction strength, ε*, was calculated using:

$$\epsilon \ast =\frac{{\displaystyle \sum _{ij}{n}_{ij}{\epsilon }_{ij}}}{{\displaystyle \sum _{ij}{n}_{ij}}}$$ Equation 5

where n_ij is the number of coarse-grained sites with a type i and type j interaction and ε_ij is the interaction energy between coarse-grained types i and j. The ε_ij values were obtained from the GROMACS simulations at T = 325K. The resulting value for ε* calculated from Equation 4 is 0.0363. Thus when T* = k_BT/ε* = (8.6173 × 10⁻⁵eV/K)*(325K)/(0.363eV) = 0.77 in our DMD/LIME simulations, the lipid molecules will behave as they would at a real temperature of 325K. The Andersen thermostat is used to hold the temperature constant. In this method randomly selected particles collide infrequently with ghost particles, effectively reassigning the particle’s velocity randomly so as to maintain a Maxwell-Boltzmann distribution centered at the simulation temperature.[(48)] All LIME/DMD simulations were run with a DMD software program developed in the Hall research lab called EMBLEM. This program is written in C++. The Intel compiler was used to compile this code and all other codes used in the development and analysis of LIME. All simulations were run in serial. DMD can be run in parallel and in the future it is likely that we will parallelize our code.[(51)]

Five independent DMD simulations starting from different random configurations were run using the LIME force field to determine whether or not a bilayer could be formed starting from a random configuration of 256 DPPC phospholipids at a T* = 0.77. The lengths of the sides of the simulation cell were set to 90 Å. A bilayer was formed in all five simulations. Simulations of the 256-lipid system were run with several different box sizes to ascertain which box size should be used to evaluate bilayer properties. First, we simulated a system of 256 lipids in a box with dimensions of 100Å × 100Å × 100Å. This system formed a bilayer with a large hole in it as shown in Figure 6a. The area per lipid of this bilayer, counting only portions external to the hole, was 63.3 Ų ± 0.1 Ų. (If it had spanned the box, the area per lipid would have been 78.1 Ų). Although at first glance the hole in our bilayer may appear to be a hole of vacuum, this is not the case. In the implicit-solvent approach that we are using all of the empty space is meant to represent a structureless solvent. This is a consequence of using the McMillan-Mayer solution approach in which a two-component system is mapped onto to a one-component system by integrating out the degrees of freedom of solvent and hence increasing the speed of our simulations.[(52)] Since our lipid parameters are calculated using a method that accounts for the effect of water, they are expected to behave as they would in an aqueous solution, not a vacuum. See the Conclusions section for more discussion of this issue. Next, we ran a simulation of 256 DPPC lipids in a box with dimensions of 80Å × 80Å × 80Å. The bilayer formed in this simulation did not span the box; instead portions of the bilayer crawled upwards along the sides of the simulation box. Thus there were obviously too few lipids in the first box size (100ų) and too many lipids in the second box size (80 ų). Since the bilayer formed in the first simulation adjusted its size naturally, unencumbered by the constraints imposed by periodic boundary conditions, we surmised that its area per lipid (63.3 Ų) was likely to be characteristic of an equilibrium structure. Hence we decided to perform all of our 256-lipid production simulations in boxes of size of 90Å × 90Å × 90Å, since this gave the best chance of having an area per lipid of 63.3 Ų. Figure 6b shows an aerial image of a bilayer formed during one of those simulations.

Figure 6.

Snapshots of the areal view of a DPPC bilayer formed from 256 lipids in a box with dimensions of 100Å × 100Å × 100Å (a) and in a box with dimensions of 90Å × 90Å × 90Å (b)

Snapshots of one system at different time points throughout the simulation are provided in Figure 7. Each lipid is represented according to the following color scheme: purple (choline entity – type I); orange (phosphate group – type II); red (ester groups – type III and type IV); cyan (alkyl tail groups – type V and type VI). The initial random configuration of the system is shown in Figure 7(a). The lipids begin aggregating at around 15 million collisions (Figure 7(b)) and form a single disordered aggregate (Figure 7(c)) at 50 million collisions. The snapshots in Figures 7(d – f) show the aggregate as it rearranges to form a defect free bilayer. The 150 million collisions required to form the defect free bilayer shown in Figure 7f took approximately 3.8 CPU hours. The time scale for aggregate formation, 50 million collisions, is rather quick compared to the time it takes, 150 million collisions, to organize into a defect free bilayer.

Figure 7.

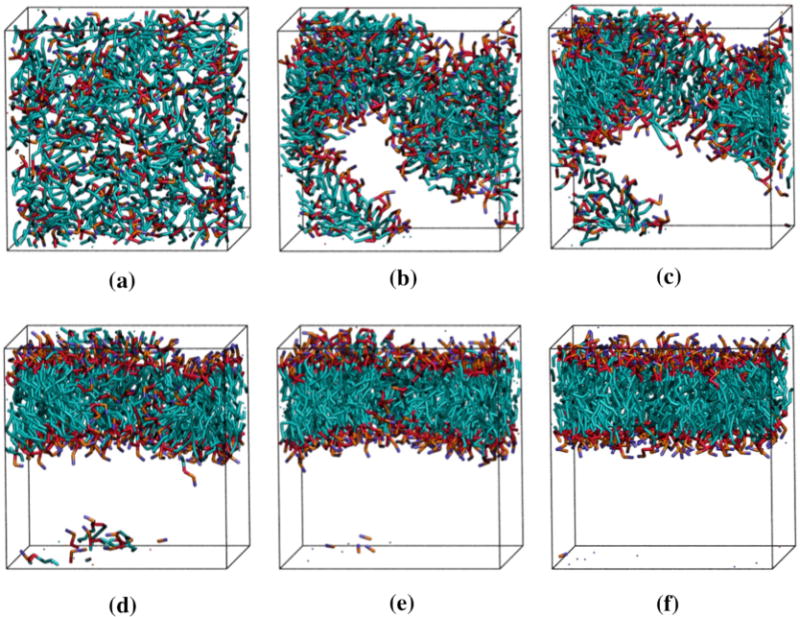
Snapshots from a simulation of DPPC spontaneous bilayer formation. The figures were created with VMD.[] The color scheme is: purple (choline entity – type I); orange (phosphate group – type II); red (ester groups – type III and type IV); cyan (alkyl tail groups – type V and type VI). (a) – (f) = 0, 15, 50, 100, 125 and 150 million collisions, respectively. The system is started from a random configuration (a) and aggregates in only 50 million collisions (d). An additional 100 million collisions are required for the aggregate to adopt the conformation of a defect-free bilayer (h).

It is of interest to compare the structural properties of the DPPC bilayer formed using LIME/DMD simulations with the structural properties obtained from a GROMACS simulation. Accordingly, a GROMACS simulation of a pre-formed defect-free DPPC bilayer composed of 128 DPPC lipids was performed using the GROMOS96 53a6 forcefield in the NPT ensemble. The initial coordinates for the bilayer were obtained from the supporting information provided by Kukol.[(25)] The Berendsen thermostat was employed to maintain the temperature at 325K; the pressure was held constant at 1.0 bar.[(49)] The simulation was run for 20 ns with a time step of 0.002 ps. The bilayer remained stable throughout the simulation.

The bilayer thickness and the area per lipid of the bilayers formed during the LIME simulations closely match both experimental values and the values calculated from the GROMACS simulation described above. The LIME values for the bilayer thickness and the area per lipid were calculated by averaging the data from the five independent DMD simulations, which were all started from different initial configurations. After a bilayer formed, the simulation was continued for an additional billion collisions. Data from the billion collisions following the formation of a defect free bilayer was used to calculate the physical properties of that bilayer, including the bilayer thickness, area per lipid and bond order parameters. The bilayer thickness is defined as the distance along the direction perpendicular to the bilayer normal between the average location of phosphate groups in the top and bottom leaflets of the bilayer. The LIME/DMD value for the thickness of the DPPC bilayer is 35.7 Å ± 0.3 Å at a reduced temperature of 0.77. The experimental value for the DPPC bilayer thickness, which is measured as the distance between phosphate groups in the upper and lower leaflets of the bilayer in the electron density profile is approximately 38.0 Å at 50oC.[(53),(54)] The bilayer thickness measured between two type 2 coarse-grained (phosphate) groups during the GROMACS simulations was 38.0 Å ± 0.6 Å at 52°C. Thus, the LIME bilayer thickness is within 5–7% the experimental value and 4–8% the GROMACS bilayer thickness. The area per lipid in our LIME/DMD and GROMACS simulations was calculated by multiplying the length and width of the bilayer and dividing by half of the number of the lipids in the system (to approximate the number of lipids in each leaflet). The area per lipid for the bilayer formed by DPPC in our DMD/LIME simulations is 63.3 Å ², which is very close to the experimental area of 63.0 ± 1.0 Å2 at T = 323K reported by Kucerka et al.[(54)] The area per lipid calculated for the DPPC bilayer in our GROMACS simulations at a T = 325K is 64.6 ± 0.1 Ų.

To further evaluate the structural properties of our coarse-grained model the orientational order parameter, s_bond, for different bonds along the chain was calculated; it is defined to be:

$$S_{\mathrm{bond}}=\frac{1}{2}\langle 3{\cos }^2\theta -1\rangle$$ Equation 2

where θ is the angle between the vector along a coarse-grained bond and the bilayer normal.[(28),(35)] S_bond values of 1, −1/2 and 0 correlate to bonds with a parallel, an alignment perpendicular to the bilayer normal and completely random alignment with the bilayer normal.[(28),(35)] To obtain the orientational bond order parameters from the GROMACS simulation of the DPPC bilayer, the data was coarse-grained and the bond order parameters for different site types along the chain were calculated. The GROMACS simulation was run at a temperature of 325K and the LIME/DMD simulation was run at the equivalent reduced temperature of 0.77. Figure 8 shows the values of the orientational bond order parameters obtained for the LIME coarse-grained model (green line) and for the GROMACS simulation (blue line) versus the bond numbers, which are defined in the figure insert. The orientational bond order parameters from the DMD model and the GROMACS simulations are in very close agreement. The bond order parameters range from approximately 0.26 to 0.52 in Figure 8, indicating that the bonds in both the GROMACS and the DMD simulations are not very well ordered and have between a parallel and a completely-random alignment with the bilayer normal. These bond order parameters are very similar to those calculated by Marrink and co-workers for a DPPC bilayer at a temperature of 323K; their values ranged from approximately 0.3 to 0.5.[(28)] A direct comparison cannot be made between the LIME forcefield and the model developed by Marrink and co-workers because in LIME each alkyl tail of DPPC is represented by 5 coarse-grained sites and in the Marrink model each alkyl tail of DPPC is represented by 4 coarse-grained sites.

Figure 8.

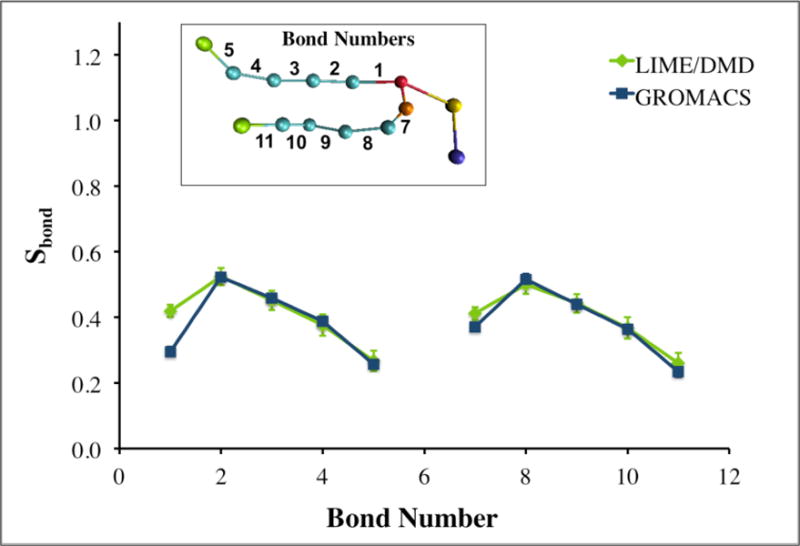
Comparison of the orientational bond order parameter S_BOND for intra-molecular bonds in LIME/DMD (green line) and GROMACS simulations (blue line) versus the bond number: the latter is defined in the inset.

As the temperature is cooled in our DMD system, the bilayer undergoes a phase transition from a liquid-crystalline phase to a tilted gel phase. Experimentally, as a DPPC bilayer is cooled it also undergoes a phase transition from a liquid-crystalline phase to a tilted gel phase in which the lipid tails are tilted with respect to the bilayer normal.[(55),(56)] The tilted gel phase generally has a smaller area per lipid than in the liquid-crystalline phase and the lipid tails are straighter.[(56)] The temperature at which a DPPC bilayer transitions from the liquid-crystalline phase to the gel phase is reported experimentally as 314.4K.[(57)] Three LIME/DMD simulations, each starting from a different configuration of a preformed DPPC bilayer composed of 128 lipids at T* = 0.77 and at constant volume in a box with dimensions of 64Å × 64Å × 90Å were run. During each simulation the following cooling procedure was implemented: T* was decreased from 0.77 to 0.30 at a rate of 0.01 T*/million collisions and then maintained at 0.30 for 550 million collisions. All properties were calculated using the last 100 million collisions that a bilayer was at T* = 0.30. Figure 9 provides snapshots of a DPPC bilayer in a DMD/LIME simulation at (a) a reduced temperature of 0.77 where a liquid crystalline phase is observed and (b) a reduced temperature of 0.30 where a tilted gel phase is observed. Figure 9c shows a cross-tilted gel phase, which we observe in some of our simulations but not in others. We are currently investigating the conditions that lead to the tilted gel phase and the cross-tilted gel phase. We believe that the cooling rate may determine whether the tilted or cross-tilted gel phase is formed. As the temperature of the DPPC bilayer is decreased the tails become more straight and rigid causing the bilayer thickness to increase from 35.7 Å ± 0.3 Å at T* = 0.77 to 40.9 Å ± 1.0 Å at T* = 0.30. Consistent with our predictions, experimental observations also show that the bilayer thickness increases with decreasing temperature. For example, the experimental bilayer thicknesses at T = 323K and T = 293K are reported as 38.3 Å and 44.2 Å, respectively.[(58)] We find that as the DPPC bilayer transitions to the gel phase, the area per lipid decreases; e.g. the area per lipid at T* = 0.77 and T* = 0.30 was 63.3 Ų and 49.6 Ų ± 1.4 Ų, respectively. The decrease in area per lipid with decrease in temperature agrees with experimental observations. The experimental value of the area per lipid at T = 323K and T = 293K are 64.0 Ų and 47.9 Ų, respectively.[(58)] These simulations were run at constant volume with box dimensions of 64Å × 64Å × 90Å. At a T* = 0.77 the bilayer spans the entire x-y plane. As the bilayer is cooled it stops spanning the entire x-y plane because its area per lipid decreases. A view of the bilayer from the top of the box shows that the bilayer is present in only a small portion of the x-y plane. The volume of the simulation box was constant with dimensions of 64Å × 64Å × 90Å as the bilayer was cooled to T* = 0.30. In our constant volume production run simulations, we adjusted the box volume so that our bilayer would span the entire x-y plane throughout the simulation. We did not adjust the box volume during the cooling simulations for the bilayer in the interest of computational efficiency because this would have required us to constantly change the box volume. In the future we plan to adjust the box volume during cooling simulations. The tilted gel phase, which we observe in our LIME/DMD simulations is not usually observed in coarse-grained simulations. For example, coarse-grained simulations performed by Marrink and co-workers and by Wang and Deserno also show the formation of untilted gel phase lipid bilayers.[(56),(59)] However, atomistic simulations performed by Leekumjorn and Sum did show the formation of a tilted gel phase of DPPC.[(60)] The question naturally arises as to why we had to go to such low reduced temperatures to observe the gel phase when it is typically reached experimentally at 314.4K [(57)] when the liquid crystalline phase is simulated at a temperature of 325K. Our explanation is that the LIME epsilon values were only calculated at a temperature of 325K, which is equivalent to a LIME/DMD reduced temperature of 0.77 and that they were then assumed to be independent of temperature. In the future, a multiscale modeling procedure may be used to determine the temperature dependence of the epsilons. This would require data from atomistic simulations at various temperatures. We speculate that once the temperature dependence of the epsilon values is incorporated into our DMD/LIME simulations, it will be unnecessary to reduce T* so dramatically to observe the gel phase.

Figure 9.

Snapshots of a lipid bilayer in DMD/LIME as the system temperature is cooled from (a) a liquid-crystalline phase at T* = 0.77, (b) a tilted gel phase at T* = 0.30 and (c) a cross-tilted gel phase which is only observed in some simulations. The snapshots were generated in VMD.[]

The transbilayer movement of phospholipids from one leaflet to another, known as “translocation” or “flip-flop,” was measured during the DMD/LIME simulations. Translocation is thought to play an important role in numerous cellular processes including cell apoptosis and drug function.[(61)] Unless protein-mediated, this lipid migration is thought to occur very slowly, with half-lives on the order of hours.[(61),(62),(63)] We did not observe any flip flops in any of our simulations of lipid systems at T* = 0.77. However, when we performed a simulation of DPPC bilayer composed of 128 lipids at a slightly higher temperature, T* = 0.85, we did see one flip flop. Figure 10 shows snapshots of a lipid (in yellow) that flips from the bottom leaflet of the membrane to the top leaflet of the membrane during one of these simulations. Over the course of 1 billion collisions only one lipid successfully flipped from one leaflet to another. It required approximately 19 million collisions for the lipid to complete the flip-flop.

Figure 10.

Snapshots of a lipid (spherical representation) as it flips from the bottom leaflet of a bilayer to the top leaflet. The tail beads of the lipid that flips are highlighted in yellow and the head beads are highlighted in lime. The images were created with VMD. (a) – (c) = 866, 883, 885 million collisions, respectively.

A comparison of the mass density profile of different coarse-grained types along the bilayer normal between the LIME and GROMACS simulations is presented in Figure 11. The mass density profile is the mass per unit volume at a distance (z) from the bilayer normal. Since the GROMACS simulation from which the mass density profile was obtained used a bilayer consisting of 128 DPPC molecules, we ran a DMD/LIME simulation on a bilayer consisting of 128 lipids. The LIME/DMD simulation was started from a random initial configuration of 128 lipids and formed a defect free bilayer in 1.1 CPU hours. The mass density distributions from the DMD/LIME simulation were taken from conformations once the lipids had formed a defect free bilayer (after 41 million collisions). The density profiles for the GROMACS simulations, were obtained by coarse-graining the GROMACS simulation result. The mass density profiles of the GROMACS and LIME simulations closely align with each other in that peaks of the mass density distributions for corresponding coarse-grained types are within 2 Å of each other.

Figure 11.

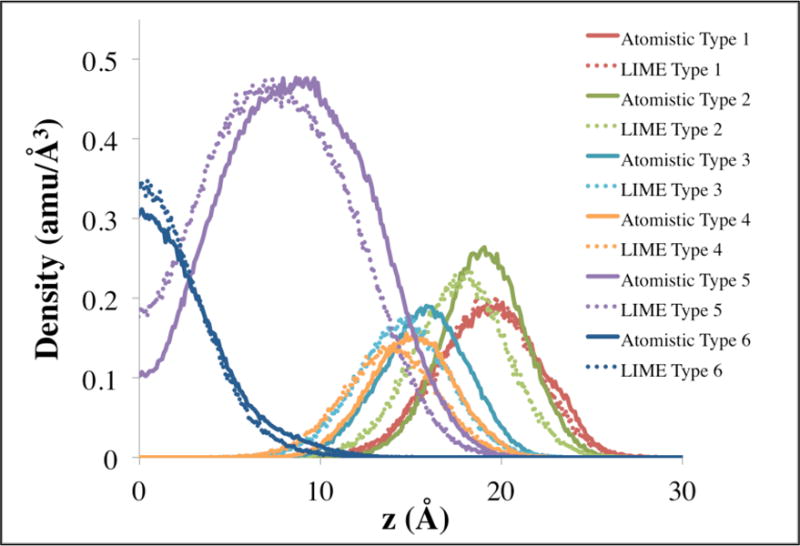
Mass density distribution of coarse-grained sites in DMD/LIME simulations (dotted lines) and GROMACS simulations (solid lines) versus the distance from the bilayer center (z = 0 Å).

It is useful to compare LIME with other coarse-grained lipid models that have recently been described in the literature. Most of the previously reported coarse-grained lipid models use continuous potentials, which are usually derived from atomistic or united-atom simulations to describe the forces between interacting sites. For example, Wang and Deserno report the development of a POPC lipid model that is similar to LIME in that it coarse-grains molecules and treats solvent implicitly.[(35)] In the Wang and Deserno model, each POPC molecule is represented by 16 coarse-grained sites that have one of 8 different types. In contrast to LIME however, this model uses continuous potentials and an additional cohesive interaction potential between alkyl tails and interfacial head groups to drive lipid aggregation and to prevent the bilayer from falling apart.[(35)] Another recently developed coarse-grained model for lipids is that of Orsi and co-workers.[(32)] This model was parameterized for DOPC, DOPE and DSPC lipids and represents all three lipids with 15 coarse-grained sites.[(32)] Unlike LIME however, the Orsi model accounts for water explicitly and system electrostatics which allows the membrane dipole potential to be studied.[(32)] The popular MARTINI force field, developed by Marrink and co-workers uses Lennard Jones potentials to describe the interactions between coarse-grained lipid sites.[(28),(29)] In the MARTINI model, water is treated explicitly and DPPC is represented by 12 coarse-grained sites and each site is assigned one of 4 types. This model was parameterized by systematically reproducing partitioning free energies between polar and apolar phases of a large number of chemical compounds.[(29)] In addition, the MARTINI force field allows charged groups to interact via an electrostatic Coulombic potential.[(28),(29)] In comparison, the current version of LIME does not include any additional forces for charged particles. LIME accounts for strong and weak attraction between sites by adjusting the depth of the square-well potential appropriately. Similar to other models LIME is parameterized from simulations and reproduces the spontaneous formation of a lipid bilayer and the formation of a gel phase with a decrease in temperature. In addition, the bilayer thickness, area per lipid and orientational bond order parameters closely agree with experimental values.

Conclusion

We described the development of LIME, an intermediate-resolution, implicit-solvent, coarsegrained model for phospholipid molecules designed for use with discontinuous molecular dynamics. In LIME, each of the 14 coarse-grained sites that make up a DPPC molecule are assigned one of 6 different types: the choline entity, the phosphate group, each ester group, each alkyl tail group and each terminal tail group. The “LIME” parameters were obtained using a multiscale modeling approach in which the geometric and energetic parameters were calculated from data collected from GROMACS simulations of a system composed of 30 DPPC molecules. A one-step Boltzmann inversion approach, which is a simplified version of the iterative Boltzmann inversion scheme, was used to calculate the depth of square well interactions in the model.

The physical properties of a DPPC bilayer, which formed spontaneously in each of 5 LIME/DMD simulations that started from a different random configuration, accurately match experimental values. The area per lipid of the bilayer is within 2% of the experimentally reported value. The bilayer thickness is within 4–8% of the range of error of the value calculated from the GROMACS simulation data and within approximately 5–7% of the experimental value. The bond order parameter values calculated from the LIME/DMD simulations and the GROMACS simulation are in very good agreement. LIME also reproduces the transbilayer movement of lipids. This phenomenon, which is, found to occur infrequently experimentally was observed only once in a total of 2 billion collisions. The phase transition of a DPPC bilayer from a liquid-crystalline phase to a tilted gel phase was also simulated. As the DPPC bilayer was cooled from a liquid-crystalline phase to a gel phase the area per lipid decreased and the bilayer thickness increased which is the trend that is observed experimentally.

LIME has one distinctive characteristic compared to the other implicit solvent coarse-grained lipid models: its speed. One of the main advantages of combining coarse-graining with discontinuous molecular dynamics is the reduction in the computational time required to simulate systems of lipid molecules. The use of discontinuous molecular dynamics greatly enhances the speed of the simulations because calculations are required only when particles experience an event, as opposed to the calculations in traditional molecular dynamics that are required to determine the net force of every particle in a system at each time step. Therefore, our LIME model paired with discontinuous molecular dynamics enhances our ability to look at long time scale phenomena without sacrificing the ability to observe many of the essential features observed at the atomistic scale (e.g. bilayer formation, phase transition, lipid translocation). In LIME the spontaneous formation of a bilayer composed of 256 lipids requires less than 4 CPU hours (Intel Xeon E5520 2.27GHz).

While the LIME/DMD approach has many advantages for simulating lipid self assembly it does have the following limitations: (1) treating solvent implicitly prevents diffusion and hydrodynamics from being taken into account, (2) approximating interactions with hard and square-well spheres forces the particles to interact sequentially rather than simultaneously as they do when the net force on each particle is calculated in traditional molecular dynamics, (3) a direct correlation can only be made between the temperature at which LIME was parameterized and its corresponding reduced temperature. Although we cannot correlate reduced temperatures other than T* = 0.77 with a real temperature, we do reproduce the experimentally observed phase transition of a bilayer by decreasing the reduced temperature in our simulations. In addition to these limitations, LIME also lacks an explicit representation of electrostatics. This means we do not account for the very long-range portion of the electrostatic interactions, although we do account for its short range effects. Long range effects are known to play an important role in biomolecular systems.[(64)] We do however, account for electrostatic interactions implicitly during the parameterization process. Another limitation of LIME is that it does not measure real time during a simulation. Therefore, we cannot determine exactly how long in real time units it took for the DPPC bilayer to form, or for the lipid flip flop to occur. However, if the amount of time that it takes for a certain event to occur is known, the time scale of the DMD/LIME simulation could be approximated. Finally, we will address the use of constant volume in our DMD/LIME simulations. The use of constant volume conditions in this work means that we do not allow the system to adjust its volume to the condition most favorable to the formation of bilayers. This leads to phenomena such as the large hole in the bilayer that we see in Figure 6a. We have gotten around this problem by performing test runs at a number of different volumes to see which volume sustains a defect-free bilayer. A more rigorous approach would be to perform the simulations at constant pressure, adjusting the volume as part of the simulation to find the state with the minimum free energy. To do this we would need to perform hybrid Monte Carlo—DMD simulation in which the volume change moves are made with Monte Carlo and particle displacement moves are made with DMD, as we have done in earlier work on chainlike systems.[(65),(66)] This would however slow down the code. We are considering this for future work.

ABBREVIATIONS

DPPC

1,2-dipalmitoyl-sn-glycero3-phosphocholine

DMD

discontinuous molecular dynamics

LIME

Lipid Intermediate Resolution Model

VMD

visual molecular dynamics

CG

coarsegrained