Abstract
We know much about the glucose regulatory system, yet the application of this knowledge is limited because simultaneous measurements of insulin and glucose are difficult to obtain. We present a data assimilation framework for combining sparse measurements of the glucose regulatory system, available in the intensive care unit setting, with a nonlinear computational model to estimate unmeasured variables and unknown parameters. We also demonstrate a method for choosing the best variables for measurement. We anticipate that this framework will improve glucose maintenance therapies and shed light on the underlying biophysical process.
I. INTRODUCTION
Blood glucose concentrations are tightly regulated via a closed-loop system involving the pancreas and liver. Disruption of these dynamics can have profound effects on the acute and long-term health of the individual. The ability to estimate, predict, and control glucose dynamics would be beneficial in the Intensive Care Unit (ICU) so that targeted therapies can be quickly implemented. Several mathematical models of glucose homeostasis have been developed. Because simultaneous measurement of all model variables is not possible, the use of these models has been somewhat limited. Therefore, data assimilation methods are necessary. These methods utilize both the mathematical models as well as real-time measurements to produce the best estimate of all variables and unknown parameters.
Estimates of unmeasurable values, such as interstitial insulin, and unknown model parameters can provide crucial insight into the health of the individual. They can also aid in improving exogenous insulin delivery therapies. In addition, access to the full current dynamics allows for short-term prediction of future dynamics.
In previous work [1] we applied data assimilation methods based on the unscented Kalman filter (UKF) to a high-dimensional model of the sleep-wake regulatory system and developed methods for optimizing the framework parameters, dynamically fitting and tracking model parameters, and gauging relative partial observability of model variables. As a first step in bringing these tools to clinical ICU care for insulin control, we apply these methods to the glucose homeostasis system. We then demonstrate this framework using simulation studies. Finally, we outline the potential use of these techniques in the ICU setting.
II. METHODS
A. Glucose-Insulin Physiology
Blood glucose concentrations are regulated through the body’s internal closed-loop feedback control mechanism. High glucose levels serve as a signal for the pancreas to release insulin, which speeds up glucose metabolism and leads to glucose being stored faster than it is released. Conversely, low glucose levels signal the pancreas to release glucagon, which slows down metabolic reactions and leads to faster release of glucose from the liver.
Several models of the glucose regulatory system have been published. We use the model presented in Sturis et al. [2], modified to include a variety of external driving, or exogenous glucose delivery, cycles realistic to the ICU, hospital, and daily life [3]. The model describes the homeostasis between plasma insulin Ip, remote interstitial insulin Ii, and glucose G:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where the state variables h1, h2, and h3 form a three-stage linear filter. Some of the major parameters include: E, a rate constant for exchange of insulin between the plasma and remote compartments; IG, the exogenous glucose delivery rate; tp, the time constant for plasma insulin degradation; ti, the time constant for the remote insulin degradation and td, the delay time between plasma insulin and glucose production. For a full list of all parameters, see [2], [4].
B. UKF for State and Parameter Estimation
The Kalman filter estimates the state (all model variables) of a system from a noisy, sparsely measured, subset of variables. The details of the UKF algorithm can be found in many standard textbooks and are not duplicated here. We refer the reader to [5] as well as [6] for detailed equations.
Using the ‘augmented state’ approach, model parameters can also be estimated using the UKF. In this algorithm, parameters are considered as constant system variables, and the state space is augmented with an additional variable for each parameter to be estimated. For details, see [7].
III. RESULTS
A. Data Assimilation
We can reconstruct unmeasured variables of the glucose homeostasis model using the UKF framework. To demonstrate this, we generate data from this model including the exogenous glucose delivery dynamics. We then apply a noisy observation function which produces a noisy subset of the variables to be used as measurements in the UKF framework. We then reconstruct the unobserved variables and validate these estimates by comparing to the original data.
In the ICU setting, we would likely have measurements of plasma insulin and glucose at sampling rates between several times per minute and once every few minutes. In addition, we may access an estimate of the exogenous glucose delivery rate by monitoring food intake. To mimic these experimental conditions, we therefore observe these three variables and use them to reconstruct the rest of the dynamics.
It should be noted that IG, the exogenous glucose delivery rate appears as a constant in (3) because it is an observed input into the system and has no differential equation governing its dynamics. In incorporating this model into the UKF framework we treat this parameter as the 7th state variable and define its rate of change to be zero. This allows us to use this variable as an observable and to reconstruct its dynamics when it cannot be directly measured.
An example of data assimilation with the UKF is shown in Fig. 1A 9 day time-series of glucose dynamics was generated form the model. The feeding regiment producing IG consisted of random meals followed by exponential decay of glucose delivery. Noisy versions of Ip, G, and IG, sampled at 4 minute intervals, served as the measured variables. The model integration time was 1 minute. To produce noisy observations we added random Gaussian zero-mean noise, with variance 9% of the variance of the variable, to the generated data. The parameters used to generate the data were also used for the UKF model. A default value of 10−2 times the variance of each variable was used for the UKF additive covariance inflater CI. To improve reconstruction, a factor of 10 was added to CIIG.
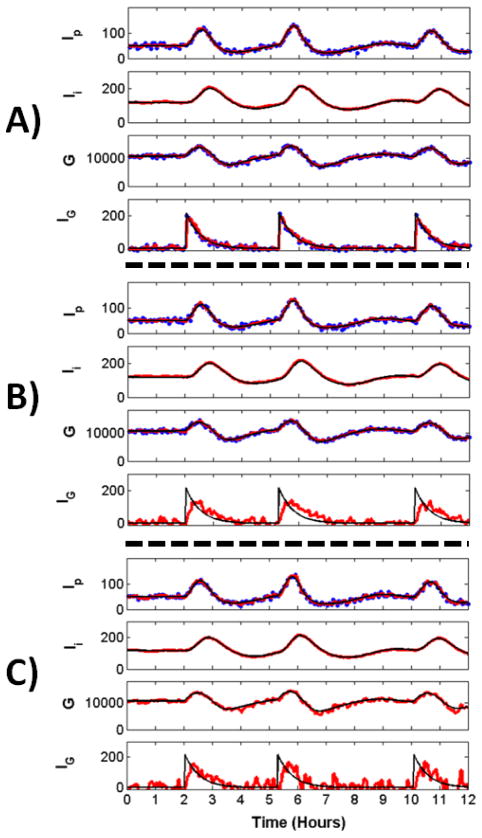
Fig. 1. Reconstruction of Glucose Model Dynamics.
Noisy measurements (blue) were recorded at 4 minute intervals and passed to the UKF framework to reconstruct all variables. Shown are the reconstructed (red) and true (black) dynamics for Ip, plasma insulin; Ii, remote insulin; G, glucose; and IG, the exogenous glucose delivery rate a.k.a the food intake. A) Reconstruction through the observation of Ip, G, IG. After a transient period (not shown), reconstructed dynamics remain close to true dynamics, even for the unobserved variable Ii. B) Reconstruction through the observation of Ip and G. Reconstruction is reasonably good for all hidden variables, notably for IG which receives no inputs from other variables. The estimate for IG is noisy compared to the estimate when this variable is observed. These perturbations do not affect the reconstruction fidelity of the rest of the system. C) Reconstruction through the observation of Ip alone. Reconstructed estimates are close to true dynamics. The estimate for IG is noisy, though the peaks representing food intake are clearly seen.
Shown in Fig. 1A is a 12 hour period from reconstruction of the 9 day time-series. The true (black), measured (blue) and reconstructed (red) values are shown for Ip, Ii, G, and IG. All variables, including the unobserved remote insulin Ii are reconstructed well despite the relatively low sampling rate of the measurements. The reconstructed dynamics of the three filtering variables (h1, h2, h3) are not shown to preserve space. We show in Fig. 3 that these variables are also reconstructed well.
Fig. 3. Parameter Estimation with UKF.
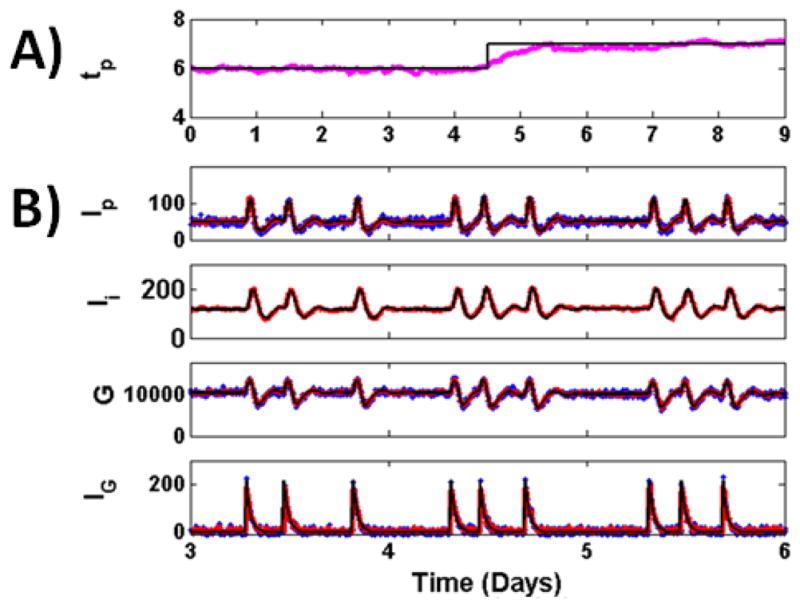
for reconstruction of glucose model from measurements of Ip, G, and IG, sample at 4 minute intervals, with unknown value for parameter tp. Parameter tp used to generate the data (black) abruptly shifts at day 4.5 from a value of 6 to a value of 7, which might reflect a sudden change in kidney function. A) Parameter estimate (magenta) is shown overlapped with the true parameter value used to generate the data (black). The estimated parameter is close to the true value during periods where the parameter has a low value, a high value, and when the parameter undergoes a sudden shift. B) True (black), measured (blue) and reconstructed (red) dynamics for some model variables shown in the 3–6 day period.
From these results, we hypothesized that measurements of all three variables may not be necessary to ensure adequate reconstruction. To test this hypothesis we reconstructed glucose dynamics from observations of Ip and G, shown in Fig. 1B, and from the observation of Ip alone, shown in Fig. 1C. Aside from the observed variables, all other settings are the same across panels.
It can be seen in Fig. 1B that measurement of Ip and G alone can be used to reconstruct the remaining dynamics reasonably well. The reconstruction of Ii is very good and similar to that in Fig. 1A when three variables were observed. Notably, IG is reconstructed well, despite the fact that it receives no inputs from other model variables. The perturbations in the reconstruction of this variable result from sparse sampling and would be reduced with higher sampling rates. These perturbations do not overtly affect the rest of the system.
Observation of the single variable Ip can also be used to reconstruct the state with reasonable accuracy, as shown in Fig. 1C. The estimate for IG is noisier, though major peaks corresponding to food-intake can be clearly seen.
B. Empirical Observability Coefficient
Visual inspection of the similarity between the reconstructed and true dynamics is only a qualitative result. We therefore use the mean squared difference between the reconstructed and true values for each variable to quantify the accuracy of state reconstruction. We normalize this error by the variance of each variable’s dynamics to form , a normalized mean square error for the ith variable:
| (7) |
For perfect reconstruction, . Its maximum depends on the ratio of the range of the variable to the square root of its variance. For regularization purposes, we use the inverse of , which is bounded between [0, 1] with improved reconstruction at higher values. We refer to this metric as the Empirical Observability Coefficient (EOC):
| (8) |
where is the normalized reconstruction error for variable i given measurement j.
We assert that the EOC is a useful empirical metric for gauging the partial observability of the state space from a measured variable within the UKF framework. Observability is a structural property of a model defined as the ability to recover the model state through the observation of one or more of its outputs. In nonlinear systems, many variables may not be observable. Nonetheless, information regarding the partial observability of each variable can be used to choose the optimal variable for measurement.
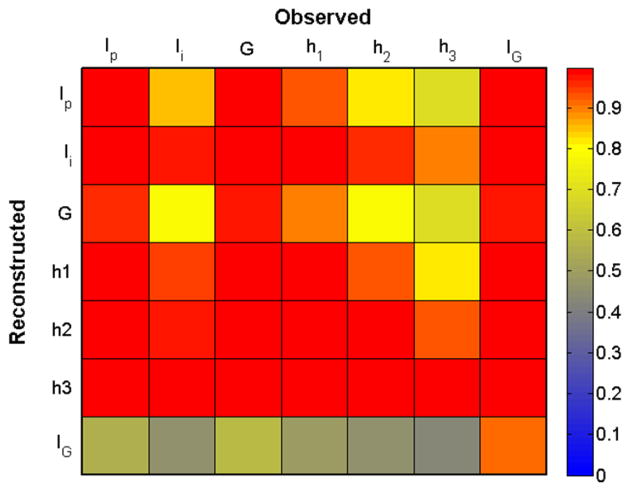
In Fig. 2, we show the EOC coefficient for each reconstructed variable (down the columns) as a function of observation variable (across rows) in a matrix format. We have used constant default values for the UKF additive covariance inflation parameter and relative observation noise R. Based on the mean EOC across columns, we conclude that the best observables for reconstruction are either Ip, G, or IG.
Fig. 2. Empirical Observability Coefficient (.
EOC) Matrix for the glucose model. EOCi,j is an empirical measure of how well variable i is reconstructed from measurement of variable j. Here EOC was computed using 9 days of data. From the EOC matrix, we observe that all variables can observe the system reasonably well, although Ip, G, and IG would serve as the best measurements.
The relative reconstruction accuracy of a variable from other variables can be gauged by colors across its row. Here we see that IG has lower EOC values for reconstruction from any variable but itself. However, the results shown in Fig. 1 indicate that this variable is reconstructed reasonably well at least from Ip and G. We note that the dynamics of IG are different than the dynamics of all other variables. Specifically the dynamics of IG are spike-like and not Gaussian and, as a result, the variance of this variable is much smaller than its range. The EOC for each variable is proportional to the ratio of the variance to the square of the range and comparison of EOC across variables assumes a similar variance:range ratio. Therefore, the reconstruction fidelity of variables with a low variance:range ratio, such as IG, is better than the EOC indicates.
We have shown elsewhere [1] that the EOC matrix, and the information it implies about partial observability, can be used to tune the UKF covariance inflation parameter-which can greatly improve reconstruction fidelity.
C. Parameter Estimation
As applied here, the UKF framework requires both a model for the dynamics as well as the model’s parameters. In the ICU setting, we will not know the correct parameter values for each patient and will need to estimate them. This can likely be done in an off-line phase to arrive at a first-guess estimate. This value can then be used as the initial parameter value in the on-line data assimilation phase.
We estimate parameters, simultaneously with variables, using the UKF augmented state approach [7]. We chose to estimate the parameter tp, the time constant of plasma insulin degradation and an indication of kidney function, for illustrative purposes. Except for tp, the value of all other parameters in the UKF are fixed and equal to the value used to generate the original data set.
The results are shown in Fig. 3. State and parameter values were estimated with the UKF through the observation of Ip, G, and IG, sampled at 4 minute intervals, for the 9 day data set. The value for tp used to generate the data (black) abruptly shifts at day 4.5 from a value of 6 to a value of 7, which may reflect a sudden change in kidney function. It would be beneficial in the ICU setting if we could detect the underlying parameter as well as any abrupt changes in its value. The parameter estimate (magenta) stays close to the true parameter value during periods of stability, before day 4 and after 5. During the abrupt change, there is a transient period where the estimated parameter value is smaller than the true value. The rate of this convergence is proportional to the sampling rate of the measurements, with higher sampling rates resulting in shorter convergence times.
The reconstructed states between the days 3–6 are shown in the bottom panels of Fig. 3. These values are estimated in the same UKF step used to calculate parameter estimates. In this scheme, the UKF model was incomplete since it contained an unknown parameter value. Despite this deficit, the UKF framework accurately estimated system dynamics.
IV. DISCUSSION
Previously, we have implemented a data assimilation framework to study sleep-wake dynamics [1]. During this process we developed novel tools to assess the partial observability of a non-linear system using the UKF framework, developed a method to use this observability analysis to optimize the UKF, and developed a robust parameter estimation method. We now apply our toolbox to the study of the glucose regulatory system. We are aware of another group who has used data assimilation to study glucose homeostasis [8], however they used a different model of glucose dynamics and did not address framework issues such as parameter estimation and the choice of observable.
Simultaneous measurements of glucose, interstitial insulin, and plasma insulin would aid in maintaining appropriate glucose concentrations in the ICU. We have demonstrated with simulation studies that data assimilation methods can be used to simultaneously estimate all variables of the glucose homeostasis system. These reconstructed values enable short-term predictions of future glucose dynamics-which may drastically improve closed-loop glucose control. For instance, these predictions may help to settle the question of whether glucose should be regulated with a tight or wide margin.
We have demonstrated an intuitive method, using the EOC matrix, to determine the observables that result in the best state reconstruction. We found that the optimal observed variables for the glucose system, Ip, G, and IG coincide with measurements available in the ICU. Therefore, data assimilation methods are suited quite well for the ICU setting. We also show that we can reconstruct the system reasonably well without access to all three variables, which is important if sampling frequency is too low or measurements are too noisy.
ICU glucose maintenance systems typically rely on population-based data and do not have the ability to account for individual variability [9]. Our framework allows for estimation of parameters for each individual, even if the initial guess for the parameter is far from its true value or if there is a sudden change in the parameter dynamics. This may have important implications for identifying the individual underlying pathophysiology.
Acknowledgments
Support: NIH NINDS FNS070545A (MSS), NIH NLM RO1LM06910 (DJA), NIH NINDS R01NS065096 (BJG).
Contributor Information
Madineh Sedigh-Sarvestani, Email: mus236@psu.edu, Department of Engineering Science and Mechanics. The Pennsylvania State University, University Park PA 16802 USA.
David J. Albers, Email: david.albers@dbmi.columbia.edu, Department of Biomedical Informatics, Columbia University, 622 West 168th Street VC-5, New York, NY 10032 USA.
Bruce J. Gluckman, Email: BruceGluckman@psu.edu, Penn State Center for Neural Engineering and Associate Professor with the Department of Engineering Science and Mechanics, the Department of Bioengineering, The Pennsylvania State University, University Park, PA 16802 USA, and with the Department of Neurosurgery at the Hershey Medical Center, Hershey, PA 17033 USA.
References
- 1.Sedigh-Sarvestani M, Schiff SJ, Gluckman BJ. Reconstructing mammalian sleep dynamics with data assimilation. 2012. Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sturis J, Polonsky KS, Mosekilde E, Cauter EV. Computer model for mechanisms underlying ultradian oscillations of insulin and glucose. Am J Physiol Endoerinol Metab. 1991;260:E801–E809. doi: 10.1152/ajpendo.1991.260.5.E801. [DOI] [PubMed] [Google Scholar]
- 3.Albers DJ, Hripcsak G, Schmidt M. Population physiology: leveraging population scale (EHR) data to understand human endocrine dynamics. 2011. Submitted. arXiv:1110.3317v1[q-bio,QM] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kneer J, Sneyd J. Mathematical physiology II: Systems physiology. 2. New York, NY: Springer; 2008. The Endocrine System. [Google Scholar]
- 5.Schiff SJ. Neural Control Engineering. Cambrige, MA: MIT Press; 2012. [Google Scholar]
- 6.Simon D. Optimal State Estimation: Kalman, H [infinity] and Nonlinear Approaches. Hoboken, NJ: Wiley Interscience; 2006. [Google Scholar]
- 7.Voss HU, Timmer J. Nonlinear dynamical system identification from uncertain and indirect measurements. International Journal of Bifurcation and Chaos. 2004;14:1905–1933. [Google Scholar]
- 8.Eberle C, Ament C. The unscented Kalman filter estimates the plasma insulin from glucose measurement. Biosystems. 2011;103:67–72. doi: 10.1016/j.biosystems.2010.09.012. [DOI] [PubMed] [Google Scholar]
- 9.Zhang Y, Szolovits P. Patient-specific learning in real time for adaptive monitoring in critical care. J Biomed Inform. 2008;41(3):452–60. doi: 10.1016/j.jbi.2008.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]