Mode Specific Elastic Constants for the Gel, Liquid-Ordered, and Liquid-Disordered Phases of DPPC/DOPC/Cholesterol Model Lipid Bi-layers

Abstract

Using a microscopic molecular theory, we determine the bending and saddle-splay constants of three-component lipid bilayers. The membrane contains cholesterol, dipalmitoyl-phophatidylcholine (DPPC), and dioleoylphosphatidylcholine (DOPC) and the predictions of the theory have been shown to qualitatively reproduce phase diagrams of giant unilamellar vesicles (GUVs) of the same three components. The bending and saddle-splay constants were calculated for gel, liquid-ordered (lo), and liquid-disordered (ld) phases. By proper expansion of the free energy, the molecular theory enables us to determine the effects of the mode of membrane bending deformation on the value of the elastic constants for different phases. In particular, we refer to the ability of the molecules to arrange the composition between the two monolayers upon deformation. The bending and saddle-splay constants obtained from the free energy expansion can be expressed in terms of moments of the local lateral pressures and their derivatives all evaluated for a symmetric planar bilayer. The effect of blocked vs free exchange of lipids across the two monolayers on the values of the bending constant is as high as 50 k_BT in the ld phase to as high as 200 k_BT in the lo phase. These results show that one must strongly consider the mode of deformation in determining the mechanical properties of lipid bilayers. We discuss how the different contributions to the lateral pressures affect the values of the elastic constants including the effects of cholesterol concentration and temperature on the membrane elastic constants. We also calculate the equilibrium binding concentrations of lipid tail anchors as a function of membrane curvature by explicitly determining the chemical potential difference of species across a curved bilayer. Our results are in excellent agreement with recent experimental results.

1 Introduction

The elastic properties of lipid bilayers are a key component to the understanding of many cellular processes ¹. Several examples include endocytosis, cell division, and pathogen infection as well as many others ². The bending modulus can be experimentally obtained by several techniques ^1,3–9, and the findings of these experimental studies show that for phospholipid membranes the bending constant is typically on the order of ~ 10k_BT. Simulation work on determining the bending modulus by both studying undulations ^10–13 and measuring tensile forces in tethers ^14,15 are in agreement with experimental results. Recently, there has been simulation work on determining the Gaussian curvature modulus of lipid bilayers showing that the order of magnitude is also ~ −10k_BT 16. On the theoretical level, most studies on the elastic properties of surfactant mixtures have used phenomenological models ^17–19. In this work we use a molecular mean-field theory that explicitly accounts for the physical conformational degrees of freedom of the hydrophobic tails of the lipids ²⁰. Previous work with this molecular theory was used to determine the equilibrium elastic properties of lipid bilayers by expanding the free energy of a symmetric planar bilayer in curvature ^21,22. This method has several powerful advantages over other theoretical methods in that the molecular level detail of the lipids is properly accounted for, and the elastic moduli can be calculated for different conditions of deformation without the need to perform explicit calculations for each particular mode of deformation ²¹. Examples of using this method of expanding the molecular theory free energy for determining the elastic properties of surfactants are determining the stability of lipid bilayers grafted with poly(ethylene oxide)^23,24, as well as determining the elastic properties of diblock copolymer films at liquid-liquid interfaces ²⁵ and cylindrical micelles ²⁶.

An extension of the molecular theory to account for the attractive energy between lipid tails has been shown to qualitatively reproduce phase diagrams of giant unilamellar vesicles (GUVs) of dipalmitoyl-phophatidylcholine (DPPC), dioleoylphosphatidylcholine (DOPC), and Cholesterol ^27–30 will be used in this work. As mentioned above, one of the major advantages to using the curvature expansions of the free energy to calculate the elastic properties of the lipid bi-layer is that it is relatively easy to compare different conditions of deformation. We calculate the area per molecule of the planar bilayer by minimizing the free energy with respect to area ²⁷. This area per molecule, a(0), is taken to be the area of the ”surface of inextension” or ”neutral surface” and this is the only surface of the film that does not change its area upon deformation ²¹. In bilayer systems, the molecules have the possibility of partitioning between the two monolayers (leaflets) in order to minimize their free energy at different curvatures. We will consider several modes of deformation in regard to the exchange of lipids between the two leaflets. The first is call ”blocked exchange” and this corresponds to the case that the molecules are not allowed to rearrange. Another mode of deformation is called ”free exchange”, and that is the case where the molecules are allowed to flip between the two leaflets to allow the free energy for a given curvature to reach a minimum ²¹. There are several other modes that are determined by constraining either one or two of the lipid species to not be able to rearrange upon curvature deformation. Under blocked exchange the chemical potentials of the lipid species are not equal in the two leaflets due to the constraint of the lipids not being able to rearrange between the two monolayers. Blocked exchange sets up a chemical potential gradient that would be the driving force for lipids to flip when this constraint is removed. Under free exchange of lipids, the chemical potentials of each species are equal in the two leaflets, however the value of these chemical potentials are a function of curvature and do not have the same value as the chemical potentials for the symmetric planar bilayer.

Throughout this work we are deforming the bilayer under a constant total number of molecules. The chemical potential of the lipid species in both leaflets upon a curvature deformation under free exchange is not necessarily the same as the chemical potential in the planar bilayer. These considerations become very important when comparing our theoretical results with experimental data. For example, we will show that if cholesterol is allowed to flip-flop in the DPPC/DOPC/Cholesterol system and the other lipid species are blocked, then the bending elastic constant is 20–40 k_BT larger then the case where all of the lipid species are allowed to be exchanged from leaflet to leaflet. The very large role of the mode of deformation on the quantitative determination of the elastic constants presents an important caveat on the value that should be attributed to bending constants when using phenomenological approaches, particularly in systems where the time scale of the deformation is shorter than the ability of lipids to flip-flop.

In the next section we provide a review of the molecular theory, and we show how the free energy for the planar bilayer can be expanded in terms of curvature deformations to determine the elastic properties of the system. In section 3 we present the results for the saddle-splay and bending elastic constants for both a pure component DPPC bilayer at the main-chain transition temperature of 315K and the results for the three component DPPC/DOPC/Cholesterol system at a lo-ld tie-line at 300K and 290K. We also include a brief discussion of work on the binding of lipid chain anchors as a function of the curvature of a pure component DPPC bilayer, and we directly compare these results with experimental data. We conclude in section 4 by summarizing our findings.

2 Molecular Theory and Elastic Constants from Lateral Pressures

In this section we will give some details of the molecular theory used throughout this work as well as a brief derivation of the elastic constants from their phenomenological definitions. A greater detailed description of the molecular theory used in this work can be found in Uline et al. ²⁹.

2.1 The Model

We consider a fluid lipid bilayer of thickness 2l, that is composed of a ternary system of cholesterol, a lipid with two saturated hydrocarbon chains of 16 carbons, such as dipalmitoylphosphatidylcholine (DPPC), and a lipid with two mono-unsaturated hydrocarbon chains of 18 carbons, such as dioleoylphosphatidyl-choline (DOPC). The chains are described by Flory’s Rotational Isomeric States Model ³¹ in which each CH₂ group is in one of three configurations: the lowest energy trans, or gauche-plus or gauche-minus both of which are of a energy, 500 cal/mol, greater than that of the trans configuration. There are N molecules of which a fraction, x_c, is cholesterol, x_s, is saturated lipid, and x_u, is unsaturated lipid. Let us denote the number of molecules of species i attached to the external interface of the bilayer as N_i,E, and correspondingly the number of molecules of species i attached to the internal interface as N_i,I. We will denote the fraction of these molecules by x_i,E = N_i,E/(N_i,E + N_i,I). For a symmetric planar bilayer x_i,E = x_i,I = 0.5, but rearrangement of the molecules upon bending could lead to deviation of the fraction in each leaflet from one-half ²¹. We define the z axis to be perpendicular to the interfaces with its origin at the midplane of the bilayer. The total area at distance z, parallel to the midplane of the bilayer, is given by ²¹

$$A(z)=A(0)\left[1+(C_1+C_2)z+C_1{C}_2{z}^2\right],$$ (1)

where C₁ and C₂ are the principal curvatures defined as C_i = 1/R_i, where R_i is the radii of curvature of the midplane of the bilayer. We use a(z) to denote the average area available per molecule at a distance z from the midplane of the bilayer, a(z) = A(z)/N. a(0) is the molar area of the midplane of the bilayer, the total volume of the bilayer divided by its thickness 2l:

$$a(0)=\frac{2x_s{\nu }_s(n_s+1)+2x_u((n_u-1){\nu }_s+2{\nu }_{CH})+x_c{n}_c{\nu }_c}{2l}.$$

Here ν_s, ν_CH, and ν_c are the volumes of a CH₂ unit, of half a –CH=CH– unit, and of each carbon unit in cholesterol. The volume of the monomer unit CH₂ is taken to be ν_s = 27ų, and that of a CH₃ group is 54 ų. Each half of the –CH=CH– segment of the cis-unsaturated bond is assigned a volume of ν_CH = 0.8 ν_s. The number of carbons in each saturated chain is n_s = 16, while the number of carbons in each unsaturated chain is n_u = 18. The number of carbons in cholesterol is n_c = 27, and the volume of the carbons is ν_c = 21.0ų.

We solve the molecular theory under the constraint that the total density of the hydrophobic region is a constant (i.e. that it be incompressible) ^27–30. The constant density constraint implies that the average area occupied by the molecules in any layer within the hydrophobic core must be equal to the average available area. That is,

$$a(z)=\sum _{i,\delta }{x}_i{x}_{i,\delta }{n}_i^{\mathit{tails}}\langle {\nu }_{i,\delta }(z)\rangle$$ (2)

for −l < z < l, where δ = I,E and < v_{i, δ} (z) > is the ensemble-averaged contribution to the volume of the hydrophobic core at z from the molecules of species i in the leaf δ. $n_i^{\mathit{tails}}$ is the number of tails of species $n_s^{\mathit{tails}}=n_u^{\mathit{tails}}=2,n_c^{\mathit{tails}}=1$. The constraint is imposed by means of a local Lagrange multiplier, p(z;c⃗), where the explicit dependence on curvature c⃗ = [C₁, C₂] is explicitly included.

The molecular theory works by explicitly writing each of the contributions to the free energy and then minimizing the free energy with respect to the free variables (for more details please see previous work with this model ²⁹. Through minimization we obtain the probability of finding the chain of molecular species j in leaf δ in a particular conformation specified by the index α_j,δ, one with a total internal energy ε (α_j,δ). The internal energy arises from the gauche bonds whose energies exceed that of the trans configuration. The probability distribution functions have the same form for all of the components:

$$P({\alpha }_{j,\delta },\overrightarrow{c})=\frac{1}{q_{j,\delta }(\overrightarrow{c})}exp\left[-\beta \epsilon ({\alpha }_{j,\delta })-\int \beta \pi (z,\overrightarrow{c})v_j({\alpha }_{j,\delta },z)dz-\int \beta b_j(z,\overrightarrow{c}){\xi }_j({\alpha }_{j,\delta },z)dz\right],$$ (3)

where β = 1/k_BT and q _{j, δ} (c⃗) is the conformational part of the partition function of a single chain of component j

$$q_{j,\delta }(\overrightarrow{c})=\sum _{{\alpha }_{j,\delta }}exp\left[-\beta \epsilon ({\alpha }_{j,\delta })-\int \beta \pi (z,\overrightarrow{c})v_i({\alpha }_{j,\delta },z)dz-\int \beta b_j(z,\overrightarrow{c}){\xi }_j({\alpha }_{j,\delta },z)dz\right].$$ (4)

The mean-fields βb_i(z,c⃗) act upon the orientation of a molecule of species i at the coordinate z and result from the average orientational interactions arising from the other molecules. They are determined by the equations

$$\beta b_i(z,\overrightarrow{c})dz=-\sum _j\sum _{\delta }{n}_j^{\mathit{tails}}\frac{\beta J_{ij}{x}_j{x}_{j,\delta }}{a(0)v_s}\langle {\xi }_{j,\delta }(z)\rangle dz,$$ (5)

where j runs over the three components. The fields acting on saturated or unsaturated lipids are identical, βb_s(z)dz = βb_u(z)dz ≡ βb_l (z)dz. < ξ_i,δ(z) > is the ensemble average of the local density of bonds weighted by their relative orientation to the bilayer normal ^27–30. We take the strengths of the local interactions between bonds in lipid tails to be the same irrespective of whether the bonds are in a saturated or unsaturated chain: J_ss = J_uu = J_su = J_ll, Thus the difference in free energy between saturated and unsaturated lipids arises solely from the fact that the configurations of these lipids differ due to the presence of the double bond, and not to any explicit difference in interaction energies.

The strength of the interaction between lipid chain segments, J_ll, is set such that the calculated main-chain transition temperature of a lipid with two saturated tails of 16 carbons, C16:0, is equal to that of dipalmitoylphosphatidylcholine, (DPPC), T = 315K. The main-chain transition temperature is the point where the gel phase is in equilibrium with the liquid-disordered (ld) phase. The conditions for phase equilibrium are that the temperature, surface tension, and the chemical potential of each of the molecular species be the same in both phases. Note that the surface tension of the equilibrium symmetric planer bilayer system is zero ^27–29. This determines that J_ll = 3.1 × 10⁻³k_BT*(T* = 315K) for our calculations. The three-component bilayer system has two additional free parameters that need to be set, J_lc and J_cc. To obtain the best qualitative fit of our phase diagram to those of experiment, we have chosen J_lc = 0.85J_ll and J_cc = 0.80J_ll. For a sample three component phase diagram and more information on the phase equilibrium calculation please see Uline et al. ²⁹. We will provide the explicit details of the tie-lines used in the calculations when the results are presented below.

The three equations (2), (3), and (5) comprise the set of self-consistent equations whose solution yields the equilibrium values of the fields p(z, c⃗) and b_i(z, c⃗) from which all densities and the free energy follow. The minimized free energy of our system is

$$\begin{array}{l}\frac{\beta W}{N}=\frac{\beta {\gamma }_0}{4}\left[a(l)\left(1+{\left(\frac{(1-x_c)a_0}{a(l)}\right)}^2\right)+a(-l)\left(1+{\left(\frac{(1+x_c)a_0}{a(-l)}\right)}^2\right)\right]\\ +\sum _i\sum _{\delta }{x}_i{x}_{i,\delta }ln\left(\frac{x_i{x}_{i,\delta }{\lambda }_i^2}{a(0)e}\right)-{\int }_{-l}^l\beta \pi (z,\overrightarrow{c})a(z)dz\\ -\sum _i\sum _{\delta }{x}_i{x}_{i,\delta }{n}_i^{\mathit{tails}}ln{q}_{i,\delta }(\overrightarrow{c})\\ -\sum _i\sum _j\sum _{{\delta }_1}\sum _{{\delta }_2}\beta J_{ij}{x}_i{x}_j{x}_{i,{\delta }_1}{x}_{j,{\delta }_2}\frac{n_i^{\mathit{tails}}{n}_j^{\mathit{tails}}}{2v_{s}a(0)}{\int }_{-l}^l\langle {\xi }_{i,{\delta }_1}(z)\rangle \langle {\xi }_{j,{\delta }_2}(z)\rangle dz\\ -\sum _i\sum _{\delta }{x}_i{x}_{i,\delta }{n}_i^{\mathit{tails}}{\int }_{-l}^l\beta b_i(z,\overrightarrow{c})\langle {\xi }_{i,\delta }(z)\rangle dz.\end{array}$$ (6)

The thermal wavelength of the i’th component is denoted λ_i. The first term on the right-hand side of equation 6 is the contribution of the polar head groups of the lipids interacting with the surrounding water both at z = l and z = −l. We use the opposing force model of Tanford ³², in which there are attractive interactions arising from the hydrocarbon-water surface tension and repulsive terms that account, in an approximate way, for the steric interactions between the head groups. This contribution to equation 6 is different from previous work using this model by the inclusion of the additional repulsive interaction accounting for the excluded volume of the phosphocholine head groups of DPPC and DOPC ²⁴. We take the parameter a₀ to be equal to 30Ų/molecule, and the fact that cholesterol does not share the same phosphocholine head group as the two other lipids is the reason for the (1 − x_c) term in this expression. γ₀ is the bare water-oil interfacial tension taken to be 0.12k_BT/Ų. The second term in equation 6 is the contribution to the total free energy from the translation of the lipids, and the remaining terms are the collective contributions of the hydrophobic tails of the lipids which are described in detail in previous work ^27–30. It is important to note that the x_i,δ terms and any term that is an ensemble average, 〈…〉, in equation 6 are also explicit functions of the the curvature, c⃗.

2.2 Phenomenological Definition of the Elastic Constants

In this section we expand the free energy in terms of the principal curvatures in order to get an expression of how the free energy changes upon elastic deformations. For a symmetric layer, the surface of inextension (the surface where the area does not change upon deformation) is at the midplane ²¹. The expansion is preformed at constant area per molecule, and the area is that of the surface of inextension. It is convenient to use the sum, C₊ = C₁ + C₂, and the difference, C₋ = C₁ − C₂, curvatures as the variables for the expansion 21. Expanding the free energy up to quadratic terms around C₊ = C₋ = 0 (planar configuration), we obtain

$$w(C_{+},C_{-})=w(0,0)+{\left(\frac{\partial w}{\partial C_{+}}\right)}_{0,0}{C}_{+}+{\left(\frac{\partial w}{\partial C_{-}}\right)}_{0,0}{C}_{-}+\frac{1}{2}{\left(\frac{{\partial }^{2}w}{\partial C_{+}^2}\right)}_{0,0}{C}_{+}^2+\frac{1}{2}{\left(\frac{{\partial }^{2}w}{\partial C_{-}^2}\right)}_{0,0}{C}_{-}^2+{\left(\frac{{\partial }^{2}w}{\partial C_{+}\partial C_{-}}\right)}_{0,0}{C}_{+}{C}_{-},$$ (7)

where we take w = βW/N. The terms linear in C₋ in equation 7 must vanish due to symmetry ²¹. We get the following expression for the expansion of the free energy

$$w(C_{+},C_{-})=w(0,0)+{\left(\frac{\partial w}{\partial C_{+}}\right)}_{0,0}{C}_{+}+\frac{1}{2}{\left(\frac{{\partial }^{2}w}{\partial C_{+}^2}\right)}_{0,0}{C}_{+}^2+\frac{1}{2}{\left(\frac{{\partial }^{2}w}{\partial C_{-}^2}\right)}_{0,0}{C}_{-}^2.$$ (8)

Using Helfrich’s expression for the curvature free energy per unit area ³³, one can obtain the spontaneous curvature, C₀, the bending (splay) constant, k, and the saddle-splay constant, k̄, by their relation to the curvature derivatives used in the expansion of the free energy ²¹:

$$\begin{array}{l}{kC}_{0}a(0)=-{\left(\frac{\partial w}{\partial C_{+}}\right)}_{0,0},\\ \frac{\overline{k}}{2}a(0)=-{\left(\frac{{\partial }^{2}w}{\partial C_{-}^2}\right)}_{0,0}\\ \left(k+\frac{\overline{k}}{2}\right)a(0)={\left(\frac{{\partial }^{2}w}{\partial C_{+}^2}\right)}_{0,0}.\end{array}$$ (9)

We can take the appropriate derivatives of equation 6 to obtain the elastic constants in terms of the curvature derivatives of π(z, c⃗), b_i(z, c⃗), and x_i,E. The spontaneous curvature and saddle-splay constants are

$$\begin{array}{l}\beta {kC}_0={\int }_{-l}^l\beta \pi (z,\overrightarrow{c})\mathit{zdz},\\ \beta \overline{k}=0.5\beta {\gamma }_0{l}^2\left[1+\frac{{\left((1-x_c)a_0\right)}^2}{a{(0)}^2}\right]-{\int }_{-l}^l\beta \pi (z,\overrightarrow{c})z^{2}dz.\end{array}$$ (10)

The bending constant, k, is a more complicated expression due mostly to its dependence on the derivative ∂x_i,E/∂C₊. We will call this derivative the relaxation ratio which is defined as

$${\eta }_i\equiv \frac{2}{l}{\left(\frac{\partial x_{i,E}}{\partial C_{+}}\right)}_{0,0}.$$ (11)

This definition allows us to write the bending constant in the following form ^21,22

$$\beta k=\beta k_b+\sum _i\beta k_{c,i}{\eta }_i+\sum _i\sum _j\beta k_{s,ij}{\eta }_i{\eta }_j,$$ (12)

where k_b, k_c,i, and k_{s,i j} denote the blocked exchange, coupling, and stretching constants, respectively, and are given by

$$\begin{array}{l}\beta k_b=-{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z,\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}\mathit{zdz},\\ \beta k_{c,i}=-\frac{l}{2}{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z,\overrightarrow{c})}{\partial x_{i,E}}\right)}_{0,0,x_{[i],E}}\mathit{zdz}\\ +\frac{{lx}_i{n}_i^{\mathit{tails}}}{2a(0)}{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z,\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}\left[\langle v_{i,E}(z)\rangle -\langle v_{i,I}(z)\rangle \right]dz\\ +\frac{{lx}_i{n}_i^{\mathit{tails}}}{2a(0)}{\int }_{-l}^l{\left(\frac{\partial \beta b_i(z,\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}\left[\langle {\xi }_{i,E}(z)\rangle -\langle {\xi }_{i,I}(z)\rangle \right]dz\\ \beta k_{s,ij}=\frac{l^2}{a(0)}\delta (i,j)+\frac{l^2{x}_i{n}_i^{\mathit{tails}}}{4a(0)}{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z,\overrightarrow{c})}{\partial x_{j,E}}\right)}_{0,0,x_{[i],E}}\left[\langle v_{i,E}(z)\rangle -\langle v_{i,I}(z)\rangle \right]dz\\ +\frac{l^2{x}_i{n}_i^{\mathit{tails}}}{4a(0)}{\int }_{-l}^l{\left(\frac{\partial \beta b_i(z,\overrightarrow{c})}{\partial x_{j,E}}\right)}_{0,0,x_{[i],E}}\left[\langle {\xi }_{i,E}(z)\rangle -\langle {\xi }_{i,I}(z)\rangle \right]dz.\end{array}$$ (13)

where δ (i, j) is the Kronoker delta which is set to unity if i = j and zero otherwise. The notation x_[i],E means to hold the exterior mol fractions for every species fixed except i.

Now that we have the expressions for the elastic constants in terms of the derivatives of π (z, c⃗), b_i(z, c⃗), and x_i,E with respect to curvature, we need to show how we calculate the derivatives. We take the appropriate derivatives of the packing constraints, equation 2, and the definitions of b_i(z, c⃗), equation 5. The full set of equations is

$$\begin{array}{l}za(0)=\sum _i\sum _{\delta }{x}_i\frac{n_i^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z^{\prime },\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}\left[\langle v_{i,\delta }(z)\rangle \langle v_{i,\delta }(z^{\prime })\rangle -\langle v_{i,\delta }(z)v_{i,\delta }(z^{\prime })\rangle \right]{dz}^{\prime }\\ +x_i\frac{n_i^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta b_i(z^{\prime },\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}\left[\langle v_{i,\delta }(z)\rangle \langle {\xi }_{i,\delta }(z^{\prime })\rangle -\langle v_{i,\delta }(z){\xi }_{i,\delta }(z^{\prime })\rangle \right]{dz}^{\prime },\\ {\left(\frac{\partial \beta b_i(z,\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}=\sum _j\sum _{\delta }\frac{\beta J_{ij}}{v_{s}a(0)}[x_j\frac{n_j^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z^{\prime },\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}\left[-\langle {\xi }_{j,\delta }(z)\rangle \langle v_{j,\delta }(z^{\prime })\rangle +\langle {\xi }_{j,\delta }(z)v_{j,\delta }(z^{\prime })\rangle \right]{dz}^{\prime }\\ +x_j\frac{n_j^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta b_j(z^{\prime },\overrightarrow{c})}{\partial C_{+}}\right)}_{0,0,x_{i,E}}\left[-\langle {\xi }_{j,\delta }(z)\rangle \langle {\xi }_{j,\delta }(z^{\prime })\rangle +\langle {\xi }_{j,\delta }(z){\xi }_{j,\delta }(z^{\prime })\rangle \right]{dz}^{\prime }],\\ 0=\sum _j\sum _{\delta }{x}_j\frac{n_j^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z^{\prime },\overrightarrow{c})}{\partial x_{i,E}}\right)}_{0,0,x_{[i],E}}\left[\langle v_{j,\delta }(z)\rangle \langle v_{j,\delta }(z^{\prime })\rangle -\langle v_{j,\delta }(z)v_{j,\delta }(z^{\prime })\rangle \right]{dz}^{\prime }\\ +x_j\frac{n_j^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta b_j(z^{\prime },\overrightarrow{c})}{\partial x_{i,E}}\right)}_{0,0,x_{[i],E}}\left[\langle v_{j,\delta }(z)\rangle \langle {\xi }_{j,\delta }(z^{\prime })\rangle -\langle v_{j,\delta }(z){\xi }_{j,\delta }(z^{\prime })\rangle \right]{dz}^{\prime }\\ +x_i{n}_i^{\mathit{tails}}[\langle v_{i,E}(z)\rangle -\langle v_{i,I}(z)\rangle ],\\ {\left(\frac{\partial \beta b_k(z,\overrightarrow{c})}{\partial x_{j,E}}\right)}_{0,0,x_{[j],E}}=x_j\frac{\beta J_{kj}}{v_{s}a(0)}{n}_j^{\mathit{tails}}[-\langle {\xi }_{j,E}(z)\rangle +\langle {\xi }_{j,I}(z)\rangle ]+\\ \sum _i\sum _{\delta }\frac{\beta J_{ki}}{v_{s}a(0)}[x_i\frac{n_i^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta \pi (z^{\prime },\overrightarrow{c})}{\partial x_{j,E}}\right)}_{0,0,x_{[j],E}}\left[-\langle {\xi }_{i,\delta }(z)\rangle \langle v_{i,\delta }(z^{\prime })\rangle +\langle {\xi }_{i,\delta }(z)v_{i,\delta }(z^{\prime })\rangle \right]{dz}^{\prime }\\ +x_i\frac{n_i^{\mathit{tails}}}{2}{\int }_{-l}^l{\left(\frac{\partial \beta b_i(z^{\prime },\overrightarrow{c})}{\partial x_{j,E}}\right)}_{0,0,x_{[j],E}}\left[-\langle {\xi }_{i,\delta }(z)\rangle \langle {\xi }_{i,\delta }(z^{\prime })\rangle +\langle {\xi }_{i,\delta }(z){\xi }_{i,\delta }(z^{\prime })\rangle \right]{dz}^{\prime }].\end{array}$$ (14)

3 Results and Discussion

For clarity, we have split the results and discussion section into three parts. The first is focused only on the pure DPPC bilayer at the main-chain transition temperature T = 315K. The second section is focused on the three component DPPC/DOPC/Cholesterol bilayer. For the three component system we take tie-lines at T = 300K and T = 290K where the liquid-disordered phase (ld) is in equilibrium with the liquid-ordered phase (lo). The third section describes our results on studying the effects of varying curvature on the binding of lipid chain anchors to curved liposomes.

3.1 Pure DPPC

The results for a pure component DPPC lipid bilayer at the main-chain transition temperature, T = 315K, are given in table 1. For all of the systems used in this study, the spontaneous curvature is zero due to the symmetry of the planar bilayer around which the expansion of the free energy is made. To start, we are going to first focus on the ld phase.

Table 1.

Elastic constant results for a pure component DPPC lipid bilayer at the main-chain transition temperature T = 315K.

Elastic Constants	ld Phase	Gel Phase
βkC0	0	0
βk̄	−4.99	−67.35
βkb	80.56	693.12
βkc	−256.15	−2167.50
βks	217.11	1661.23
βkmin	5.01	−13.90

The saddle splay constant for the ld phase is −4.99k_BT. So, in order for the planar bilayer to be stable, both of the second derivatives in equation 9 have to be positive. Mathematically, this is equivalent to saying that we need to have −2k < k̄ < 0 for the planar bilayer to be stable ²¹. We see then that k must be larger than 2.5k_BT for the planar layer to be the stable geometric configuration. If the DPPC molecules are not allowed to flip from the interior leaflet to the exterior leaflet, then the relaxation ratio is equal to zero and we are deforming under blocked exchange. The blocked exchange bending constant is calculated to be 80.56k_BT. Under blocked exchange there is a natural chemical potential gradient that is the driving force for molecules on the inner-leaflet to flip to the outer-leaflet. The value of k as a function of the relaxation ratio,, is given in figure 1A. The value of the bending constant has a minimum value in, and this value of η_equil determines when the system has equal inner- and outer-leaflet chemical potentials. The equilibrium relaxation ratio is η_equil = 0.59, and this corresponds to an equilibrium bending elastic constant of k_min = 5.01k_BT. This value of the bending constant is in quantitative agreement with experimental results on similar systems ³⁴.

Fig. 1.

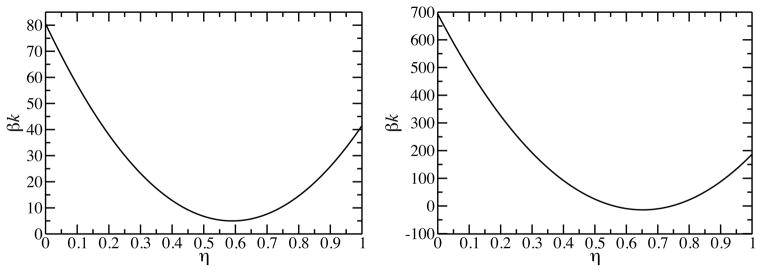
The bending elastic constant, k, as a function of the relaxation ratio, η, for a pure component DPPC lipid bilayer at T = 315K. Figure A is the result for the liquid-disordered (ld) phase. Figure B is the result for the gel phase.

Table 1 also includes the values of the elastic constants for the gel phase at T = 315K. The blocked exchanged bending constant has a value of 693.12k_BT, which is a full order of magnitude larger than the ld blocked exchange bending constant at the same temperature. The planar area per molecule of the gel phase is 48Ų/molecule, and this is considerably more dense compared to the planar area per molecule of the ld phase at 64Ų/molecule. This high density is a contributing factor to the extremely high value of the blocked exchange bending constant in the gel phase. The value of k as a function of the relaxation ratio, η, for the gel phase is given in figure 1B. The numerical value of k drops very quickly with increasing relaxation ratio. The equilibrium relaxation ratio is η _equil = 0.65, and this corresponds to an equilibrium bending elastic constant of k_min = −13.90k_BT. The negative value of the equilibrium bending constant means that the system will spontaneously curve if the molecules are allowed to freely exchange (flip) between the two leaflets.

The saddle splay constant is −67.35k_BT for the gel phase, so the planar geometry would be stable if the bending constant is required to remain greater than 34k_BT. This means that for the planar geometry to be stable for this system, the relaxation ratio must be between 0 < η < 0.48 or η > 0.82. It is intriguing to consider that the very high density of the gel phase prohibits the relaxation ratio from getting to its equilibrium value of 0.65 by keeping the relaxation ratio below 0.48. This would mean that the planar geometry is the stable one and that the bending constant has a value greater than or equal to 34k_BT. However, further work needs to be done before we can say anything conclusive.

3.2 DPPC/DOPC/Cholesterol

The three component bilayer has the added complexity of allowing all three species to have their own relaxation ratio. This way we can see how the composition changes between the two leaflets upon deformation. To our knowledge this is the first work with full molecular level detail being used to study the elastic properties of a three component lipid bilayer where the composition of all three components can independently vary between the two leaflets. We will start with a tie-line at T = 300K and then focus on a tie-line at the lower temperature of 290K. Table 2 is the elastic constant results for a three component DPPC/DOPC/Cholesterol lipid bilayer at T = 300K. The composition of the ld phase is x_s = 0.22, x_u = 0.46, and x_c = 0.32. The planar area per molecule of this ld phase is 57Ų/molecule. The composition of the lo phase is x_s = 0.26, x_u = 0.22, and x_c = 0.52. The planar area per molecule of this lo phase has a smaller value compared to the ld phase and is 47Ų/molecule. Please note that the stretching constants have an inherent symmetry: k_{s,i j} = k_{s, ji}.

Table 2.

Elastic constant results for a three component DPPC/DOPC/Cholesterol lipid bilayer at T = 300K. The composition of the ld phase is x_s = 0.22, x_u = 0.46, and x_c = 0.32. The composition of the lo phase is x_s = 0.26, x_u = 0.22, and x_c = 0.52. Note that k_{s,i j} = k_{s, ji}.

Elastic Constants	ld	lo
βkC0	0	0
βk̄	−10.78	−26.20
βkb	53.98	185.91
βkc,s	−41.42	−186.04
βkc,u	−92.71	−180.71
βkc,c	−40.17	−318.88
βks,ss	15.27	49.79
βks,su	18.22	37.36
βks,sc	7.47	57.58
βks,uu	48.78	55.12
βks,uc	17.22	60.96
βks,cc	14.18	120.51
βkmin	7.20	−38.34

The saddle splay constant for the ld phase is −10.78k_BT. This means that k must be larger than 5.4k_BT for the planar layer to be the stable geometric configuration. The blocked exchange bending constant is calculated to be 53.98k_BT. This is a lower value compared to the pure component DPPC bilayer in the ld phase at a higher temperature. We attribute the lower value in the blocked exchange bending constant to the presence of unsaturated lipid tails. Unfortunately, the high dimensionality of the parameter space makes a visual representation of the bending constant as a function of the three relaxation ratios impossible. We can, however, report that the three equilibrium relaxation ratios are η_s,equil = 0.35, η_u,equil = 0.67, and η_c,equil = 0.41 and this corresponds to an equilibrium bending elastic constant of k_min = 7.20k_BT. If cholesterol were the only species allowed to exchange between the two leaflets, then the constrained equilibrium relaxation ratio for cholesterol is ${\eta }_{c,\mathit{equil}}^{\prime }=1.42$ and this corresponds to a constrained equilibrium bending elastic constant of $k_{\mathit{min}}^{\prime }=25.52k_{B}T$.

Table 2 also includes the values of the elastic constants for the lo phase. The blocked exchanged bending constant has a value of 185.91k_BT. Again, the higher density of the ordered phase is a major contributing factor to the higher value of the blocked exchange bending constant in the lo phase. The three equilibrium relaxation ratios are η_s,equil = 0.70, η_u,equil = 0.16, and η_c,equil = 0.91 and this corresponds to an equilibrium bending elastic constant of k_min = −38.34k_BT. The values of the equilibrium relaxation ratios for the lo phase show that the composition of the two leaflets may change considerably upon deformation. If, however, cholesterol were the only species allowed to exchange between the two leaflets, then the constrained equilibrium relaxation ratio for cholesterol is ${\eta }_{c,\mathit{equil}}^{\prime }=1.32$ and this corresponds to a constrained equilibrium bending elastic constant of $k_{\mathit{min}}^{\prime }=-25.05k_{B}T$. The negative value of the equilibrium bending constant means that the system will spontaneously curve if the molecules are allowed to freely exchange (flip) between the two leaflets.

The saddle splay constant is −26.20k_BT for the lo phase, so the planar geometry would be stable if the bending constant is required to remain greater than 13.5k_BT. Similar to the gel phase described earlier, if we again consider the fact that the lo phase has a greater density in comparison to the ld phase, then it is possible that the relaxation ratios do not get to their equilibrium values and that the planar geometry may be the stable one. This means that the bending constant would have a value greater than or equal to 13.5k_BT.

In order to look at the temperature dependence on the elastic constants we now focus on the results for a tie-line at 290K. Table 3 is the elastic constant results for a three component DPPC/DOPC/Cholesterol lipid bilayer at T = 290K. The composition of the ld phase is x_s = 0.21, x_u = 0.52, and x_c = 0.27. The planar area per molecule of this ld phase is 59Ų/molecule. The composition of the lo phase is x_s = 0.30, x_u = 0.22, and x_c = 0.48. The planar area per molecule of this lo phase is 46Ų/molecule.

Table 3.

Elastic constant results for a three component DPPC/DOPC/Cholesterol lipid bilayer at T = 290K. The composition of the ld phase is x_s = 0.21, x_u = 0.52, and x_c = 0.27. The composition of the lo phase is x_s = 0.30, x_u = 0.22, and x_c = 0.48. Note that k_{s,i j} = k_{s, ji}.

Elastic Constants	ld	lo
βkC0	0	0
βk̄	−11.66	−33.13
βkb	47.15	201.94
βkc,s	−29.78	−211.93
βkc,u	−79.94	−181.41
βkc,c	−24.15	−311.82
βks,ss	11.25	52.28
βks,su	12.53	38.08
βks,sc	3.24	60.71
βks,uu	41.50	50.50
βks,uc	9.36	56.24
βks,cc	8.80	113.25
βkmin	6.32	−39.04

The saddle splay constant for the ld phase is −11.66k_BT, and the blocked exchange bending constant is calculated to be 47.158k_BT. We anticipated that a lower temperature would increase the blocked exchange elastic constant, however we see here that this ld phase has a lower blocked exchange elastic constant in comparison to the 300K ld phase. The composition is different in these two systems since we are following a tie-line, so this leads us to speculate that the composition of the bilayer has a greater effect on the elastic constants relative to the effect of temperature. A full study of these competing effects on the elastic moduli of DPPC/DOPC/Cholesterol bilayers is currently underway.

The three equilibrium relaxation ratios for this ld phase at 290K are η_s,equil = 0.35, _u,equil = 0.76, and η_c,equil = 0.43 and this corresponds to an equilibrium bending elastic constant of k_min = 6.32k_BT. If cholesterol were the only species allowed to exchange between the two leaflets, then the constrained equilibrium relaxation ratio for cholesterol is ${\eta }_{c,\mathit{equil}}^{\prime }=1.37$ and this corresponds to a constrained equilibrium bending elastic constant of $k_{\mathit{min}}^{\prime }=30.58k_{B}T$.

Table 3 also includes the values of the elastic constants for the lo phase. The blocked exchanged bending constant has a value of 201.94k_BT. Here we see that the lower temperature does give us a higher number for the blocked exchanged elastic constant. The possibility that temperature plays a greater role on the values of elastic moduli for the lo phase in comparison to the ld phase is also currently being studied. The three equilibrium relaxation ratios are η_s,equil = 1.05, η_u,equil = 0.22, and η_c,equil = 0.71 and this corresponds to an equilibrium bending elastic constant of k_min = −39.04k_BT. The values of the equilibrium relaxation ratios for the lo phase show that the composition of the two leaflets may change considerably upon deformation. If, however, cholesterol were the only species allowed to exchange between the two leaflets, then the constrained equilibrium relaxation ratio for cholesterol is ${\eta }_{c,\mathit{equil}}^{\prime }=1.38$ and this corresponds to a constrained equilibrium bending elastic constant of $k_{\mathit{min}}^{\prime }=-12.70k_{B}T$. The negative value of the equilibrium bending constant means that the system will spontaneously curve if the molecules are allowed to freely exchange (flip) between the two leaflets.

The saddle splay constant is −33.13k_BT for the lo phase, so the planar geometry would be stable if the bending constant is required to remain greater than 17k_BT. Our results of a negative bending constant for the fully free exchange mode of deformation are consistent for all of the dense phase systems (gel and lo phases) we studied. Interestingly, recent simulations by Risselada et al. ³⁵ predict that when a phase separated lipid vesicle is compressed, the lo phase preferentially segregates to the highly curved edge. The connection between these simulation results and a negative lo phase elastic constant under a free exchange deformation are not directly obvious, but the connection between this result and the simulations are nevertheless very intriguing. It has been shown both experimentally and theoretically that curvature can control the lateral sorting of membrane components ^35,36. There is also evidence that the separation into different phases, which are characterized by different partition coefficients, ^{29,30,37–39} can also be controlled by lateral tension and curvature. To couple these two effects is an ongoing effort.

3.3 Binding of Lipid Tail Anchors as a Function of Membrane Curvature

We are going to end with some work on calculating the curvature dependent binding of lipid tail anchors into lipid bilayers. We have recently published work on calculating the partition coefficients of lipid chain anchors of various degrees of unsaturation and number of tails in lo-ld phase separated lipid bilayer mixtures ²⁹. Here we use a similar methodology to determine how the binding of chain anchors to bilayers with a degree of curvature. In this work we are only going to take spherical curvature deformations, so there is only one principal radius of curvature to describe the geometry.

We already described earlier that when a lipid bilayer deforms that the chemical potential of the lipids change. The change is dependent on the amount of curvature and the mode of deformation. If the bilayer is curved under blocked exchange, then the exterior leaflet (the one exposed to the solution containing the chain anchors) experiences the greatest change in chemical potential. If the bilayer is curved under free exchange (the molecules are allowed to flip-flop between the two leaflets) then there is still a change in the chemical potential compared to the planar limit, but the change is considerably reduced. We are going to focus for this work on the blocked exchange mode of deformation.

When the bulk solution is in contact with the planar lipid bilayer we can determine the amount of adsorption by equating the two chemical potentials

$$\beta {\mu }_{\mathit{bulk}}^{\mathit{anchor}}=\beta {\mu }_E^{\mathit{anchor}}(c=0)=ln[\rho (c=0){\lambda }^2]-n^{\mathit{tails}}{\mathit{lnq}}_E^{\mathit{anchor}}(c=0),$$ (15)

where ρ(0) is the areal density of lipid anchors in the lipid bilayer. ${\mu }_E^{\mathit{anchor}}(c=0)$ is the chemical potential of the anchor in the exterior leaflet, and $q_E^{\mathit{anchor}}(c=0)$ is the single molecule partition function of the chain anchor in the exterior leaflet. Upon deformation of the lipid layer, the chemical potential of external leaflet of the lipid bilayer changes. However, the chemical potential of the bulk anchors does not change. So, the required equality of chemical potentials can now be expressed as

$$\beta {\mu }_{\mathit{bulk}}^{\mathit{anchor}}=\beta {\mu }_E^{\mathit{anchor}}(c)=ln[\rho (c){\lambda }^2]-n^{\mathit{tails}}{\mathit{lnq}}_E^{\mathit{anchor}}(c).$$ (16)

So now we can relate the density of bound lipid anchors in the curved bilayer to the density of bound lipid anchors in the planar bilayer. We will call the ratio ρ(c)/ρ (c = 0), the ”normalized maximum protein density” since we are bending the bilayer under the blocked exchange of lipids. Note that we are excluding everything except the lipid tail anchors from our calculation of protein binding, so we are assuming that the architecture of lipid anchors is the dominate factor in determining binding. There is experimental evidence to show that this is a good assumption ⁴⁰. We can write the expression for the normalized maximum protein density as

$$\frac{\rho (c)}{\rho (c=0)}={\left(\frac{q_E^{\mathit{anchor}}(c)}{q_E^{\mathit{anchor}}(c=0)}\right)}^{n^{\mathit{tails}}}.$$ (17)

All that is needed to determine the ratio of anchors as a function of curvature is the calculation of the single molecule partition function in each of the geometries. We did this using the potential distribution theory ⁴¹ as outlined in Uline et al ²⁹ for the calculation of partition coefficients of lipid anchors into lo and ld phases. Figure 2A is taken directly from Hatzakis et al. ⁴⁰ and is a plot of experimental results of lipid anchor binding in a DOPC/DOPG/DOPE mixture liposome in the LD phase. Figure 2B is a plot of our theoretical results of binding into a pure DPPC liposome at a temperature of 320K to assure the liposome is in the LD phase. The results are in excellent quantitative agreement for both a single saturated tail with 16 carbon units and a double tail anchor with two saturated 16 carbon units.

Fig. 2.

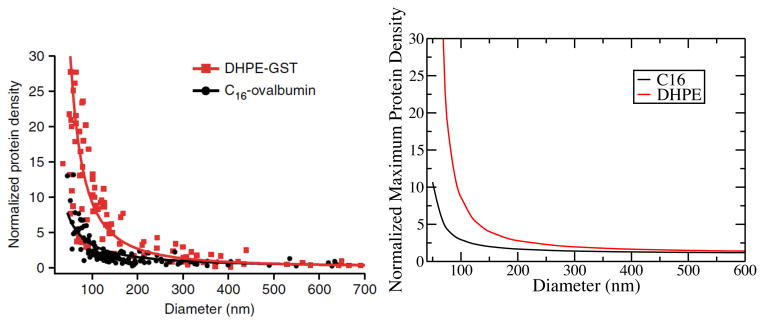
Adsorption of lipid chain anchors into liposomes of varying diameter normalized to the planar limit. C16 is a single saturated tail with 16 carbon units, and DHPE is a double tail anchor where both tails are fully saturated with 16 carbon units. Figure A is taken directly from Hatzakis et al. ⁴⁰ and is a plot of experimental results of lipid anchor binding in a DOPC/DOPG/DOPE mixture liposome in the LD phase. Figure B is a plot of theoretical results from this work of lipid anchor binding in a pure DPPC liposome at a temperature of 320K to assure the liposome is in the LD phase.

4 Conclusions

In this work we used a microscopic molecular theory to determine the bending and saddle-splay constants of both pure DPPC and three component DPPC/DOPC/Cholesterol lipid bilayers under various modes of deformation. The bending and saddle-splay constants were calculated for gel, liquid-ordered (lo), and liquid-disordered (ld) phases by expansion of the planar free energy in terms of curvature. The effect of blocked vs free exchange of lipids across the two monolayers on the values of the bending constant is as high as 50 k_bT in the ld phase to as high as 200 k_BT in the lo phase. These considerations become very important when comparing our theoretical results with experimental data. For example, we show that if cholesterol is the only species allowed to flip-flop in the DPPC/DOPC/Cholesterol system, then the bending elastic constant is 20–40 k_BT larger then the case where all of the lipid species are allowed to be exchanged from leaflet to leaflet. The very large role of the mode of deformation on the quantitative determination of the elastic constants presents an important caveat on the value that should be attributed to bending constants when using phenomenological approaches, particularly in systems where the time scale of the deformation is shorter than the ability of lipids to flip-flop.

Our results also show that the bending elastic constant is negative in the lo and gel phases under the free exchange mode of deformation. This is a surprising result that needs to be explored further. The possibility that the very high density of both the lo and gel phases make it impossible for the relaxation ratios to achieve their equilibrium values and therefore resulting in a positive bending constant also needs further study. In addition to this work, we also are undertaking efforts to incorporate the electrostatic interactions of the head groups, ^42,43 and elucidating the competition between temperature and composition on the elastic constants. We also calculated the equilibrium binding concentrations of lipid tail anchors as a function of membrane curvature by explicitly determining the chemical potential difference of species across a curved bilayer, and our results are in excellent agreement with experimental results. Future work is this area is exploring the role of temperature, composition, and phase of the curved liposome as well as accounting for the full molecular level architecture of various chain anchors.