Chemical Effects in the Separation Process of a Differential Mobility / Mass Spectrometer System

Abstract

In differential mobility spectrometry (DMS, also referred to as high field asymmetric waveform ion mobility spectrometry, FAIMS), ions are separated on the basis of the difference in their mobility under high and low electric fields. The addition of polar modifiers to the gas transporting the ions through a DMS enhances the formation of clusters in a field-dependent way and thus amplifies the high and low field mobility difference resulting in increased peak capacity and separation power. Observations of the increase in mobility field dependence are consistent with a cluster formation model, also referred to as the dynamic cluster-decluster model. The uniqueness of chemical interactions that occur between an ion and cluster-forming neutrals increases the selectivity of the separation and the depression of low-field mobility relative to high-field mobility increases the compensation voltage and peak capacity. The effect of polar modifiers on the peak capacity across a broad range of chemicals has been investigated. We discuss the theoretical underpinnings which explain the observed effects. In contrast to the result from polar modifiers, we find that using mixtures of inert gases as the transport gas improve resolution by reducing peak width but has very little effect on peak capacity or selectivity. Inert gases do not cluster and thus do not reduce low field mobility relative to high-field mobility. The observed changes in the differential mobility α parameter exhibited by different classes of compounds when the transport gas contains polar modifiers or has a significant fraction of inert gas can be explained on the basis of the physical mechanisms involved in the separation processes.

Introduction

This paper is the fifth in a series of papers presenting a body of work regarding the theory of operation and optimization of differential mobility and differential mobility mass spectrometry instrumentation (DMS/MS). The first paper describes the most recent understanding of the theory of differential mobility separations¹. In the second paper we described the control and optimization of the important physical parameters of such a system including analyzer geometry, transport gas flow control, and ion transmission efficiency.² In the third paper we described novel electronics optimized to provide the asymmetric radiofrequency fields at the high voltages required for these devices and the effects of different waveforms on resolution.³ In the fourth publication we described three important areas that need consideration in order to capitalize on the chemical processes that dominate a DMS separation.⁴ These include controlling the dynamic equilibrium of the clustering reactions with high concentrations of specific reagents, dealing with unwanted heterogeneous cluster ion populations that degrade resolution and sensitivity, and fine control of the temperature and pressure which influence the fundamental collision processes that lie at the core of the separation phenomena.

Classical ion mobility spectrometry (IMS) measures the low field mobility coefficient by allowing ions and clusters to drift under the influence of a static electric field.⁵ Under typical atmospheric conditions, the cluster state of the ion in IMS remains in a singe equilibrium state during the transit of the ion through the analyzer because the effective temperature of ion-neutral collisions remains constant. With DMS, the effective temperature of ion-neutral collisions changes continuously during separation field waveform in the analyzer. In the clusterization model, the cluster state of the ion changes continuously during the waveform synchronously with the effective temperature of ion-neutral collisions because the high collision rate at atmospheric pressure maintains equilibrium.^{6, 7, 1} To simplify the picture, the ion can be described as being in a clustered state during the low electric field period of the separation field cycle and in an unclustered or less clustered state during the high field portion of the waveform. The size of the molecule and the nature, number, and steric relationships of the functional groups all contribute to the free energy of clustering with particular gas phase molecules, thereby imparting a high degree of chemical specificity to the separation process. As of yet, available data and theoretical analysis is inadequate to create an integrated model with predictive capabilities for the degree of clustering or the collision cross-sections of the resulting species.

In this paper we expand upon our earlier studies⁴ of the chemical processes involved in a DMS/MS separation demonstrating the influence of the composition of the transport gas on DMS separations for a diverse library of compounds, and providing the theory underpinning the results. Four phenomena are explored. First, the effect of transport gas composition on peak capacity across a broad analyte ion chemical space is shown. The differences observed from the different transport gases can be understood in the framework of 2 distinct separation models, the clusterization model⁷ which appears to dominate the separation process in the presence of polar clustering modifiers, and the rigid sphere scattering model^{1, 8} which can be used in the absence of clustering. Second, resolution and separation power in relation to the transport gas composition are explored and shown to be congruent with the physical models of the separation process described. Third, some light is shed on the physical basis of the types of field strength dependent behavior that ions exhibit in different transport gas compositions, by comparing the influence of the clusterization model and the rigid sphere scattering model.

Experimental

Discussion of the data requires a clear definition of several parameters and scan modes used throughout the discussion. These will be defined in this section. Of central importance is the field dependence of the ion mobility, also known as the α function, a characteristic property of ion-neutral collisions that is directly related to conditions for DMS ion transmission. A definition of peak capacity in the context of DMS separations is also in order. Density-normalized electric fields (E/N, Townsend units), the concept of the DMS effective gap, and additional DMS-specific parameters are defined here followed by the general instrumentation conditions and experimental details.

Ion Mobility and Alpha Function

All ion mobility analyzers are based on selected properties of the ion mobility coefficient and its dependence on a variety of parameters; including field strength, drift gas composition, temperature, and pressure. The ion mobility coefficient is defined as the ratio of the ion speed to the field magnitude,

$$v_d=K(E)E$$ 1)

where v_d is the drift velocity and E is the applied field. The coefficient K is a positive scalar quantity in general field dependent. At normal densities, where binary collisions can be assumed, ion mobility coefficient is a function only of the ratio E/N. E/N is the electric field strength (E) normalized to the gas number density (N). At low electric fields the mobility K(0) is a constant independent of E/N because the field contribution to ion-neutral collision energy is small compared to the thermal energy. However, at high electric fields, where the collision energy added by the field is comparable to the thermal energy, the mobility K(E) is dependent upon the ratio of E/N, and not on the separate values of E and N, at pressures below a few atmospheres. Therefore, in this article separation fields are normalized to the gas density (E/N), and are expressed in terms of the defined unit for E/N, the Townsend, 1 Td= 10⁻¹⁷ Vcm². Under standard conditions (N₀ = 2.688 10¹⁹ cm⁻³) 1 Td = 268.8 V/cm.

It is customary to express the mobility coefficient in terms of the low-field value measured in IMS devices and field-dependent parts accessed by DMS. Field-dependent part of the ion mobility called alpha function is a basic of the DMS separation.

$$K(E)=K(0)\left(1+\alpha (E)\right)$$ 2)

In terms of ion-neutral collision parameters, the ion mobility coefficient and alpha function can be written as a function of the mean ion-neutral collision energy, which can also be interpreted as a temperature called the effective temperature, T_eff. It encapsulates the fact that ion-neutral collision energy is determined by the bulk gas temperature and electric field strength..

$$\begin{array}{c}\text{a})T_{\mathit{eff}}=T+\frac{{Mv}_d^2}{3k}\\ \text{b})K(T_{\mathit{eff}})=\frac{3q}{16N}\sqrt{\frac{2\pi }{\mu k{T}_{\mathit{eff}}}}\frac{1}{\sigma (T_{\mathit{eff}})}\\ \text{c})\alpha (T_{\mathit{edf}})=\frac{\sigma (T)}{\sigma (T_{\mathit{edf}})}\sqrt{\frac{T}{T_{\mathit{eff}}}}-1\end{array}$$ 3)

where N, gas density; σ(T), the temperature-dependent ion-neutral cross-section; T_eff, an effective temperature; k is Boltzmann’s constant; μ, ion-neutral reduced mass; M is the neutral mass. If the neutral mass much less than the ion mass, the reduced mass is approximately equal to the neutral mass. Under those conditions, since v_d = K (T_eff) E, the effective temperature giving the center of mass collision energy is approximately independent of the neutral mass, but dependent on the ion-neutral cross-section, that is, $\left(T_{\mathit{eff}}-T\right)T_{\mathit{eff}}{\mid }_{m>M}\propto \frac{E^2}{{\sigma }^2\left(T_{\mathit{eff}}\right)}$.

The DMS filter condition

Differential mobility devices filter an ion population by passing them in a transport gas stream through a region with an oscillating field applied transverse to the ion motion. The applied waveform generates net transverse ion motion that depends on the difference between averaged high and low field mobility coefficients. The filter is tuned by applying an additional transverse field to modify the ion trajectory. The largest number of ions passes successfully through the field region (without contacting walls and being neutralized) when the net transverse motion due to the total applied field is zero over one period of the field. In terms of the field-dependent ion mobility coefficient, this filter condition can be written as

$$\underset{0}{\overset{T}{\int }}{v}_{d}dt=\underset{0}{\overset{T}{\int }}K(E)\mathit{Edt}=0$$ 4)

The integral is over one period of the waveform shape, T. The field E may be expressed in any convenient units, including the density normalized Townsend unit. The applied field in DMS is written as a sum of a time-dependent separation field, Sf(t), and a quasi-static DC compensation field, C.

$$\begin{array}{l}E(t)=Sf(t)+C\\ \underset{0}{\overset{T}{\int }}f(t)dt\equiv \langle f\rangle =0\end{array}$$ 5)

The separation field is the peak magnitude of the AC waveform affected the ions inside the DMS cell confining the flowing gas and transporting the ions. S is often expressed in the density-normalized form, S/N, in Townsend units. The waveform is asymmetric³ such that the high field portion of each period is shorter in time then the low field portion, the net field averaged by period equaling zero. Ions are driven to one electrode or the other and neutralized depending on their relative mobilities in the high and low periods of each cycle.

The compensation field, C, is a DC field affected the ions inside the DMS cell to correct the trajectory for a given ion under the influence of the separation field. The C value necessary to satisfy the filter condition is a small fraction of S. In addition, the α(E) parameter is small, and is a smooth function of the field. As a result, the filter condition can be used to express the compensation field in terms of averages of the α(E) parameter over the separation field.⁹

$$\frac{C}{S}=-\frac{\langle \alpha f\rangle }{1+\langle \alpha \rangle +S\langle {\alpha }^{\prime }f\rangle }$$ 6)

S and C in application to DMS instrument are often reported as separation voltage, SV, and compensation voltage, CV, respectively, with the understanding that a fixed known gap is present in the DMS analytical region. We have not included the spatial dependence of the field present in a cylindrical FAIMS apparatus, but its inclusion would not affect the filter condition, which states that ions must traverse the analytical region without contacting the walls. Since units cancel in Eq. 5, the ratio of compensation voltage to separation voltage, CV/SV, is given by the same expression.

Peak Capacity

Peak capacity, as used here, is analogous to peak capacity in chromatography, qualitatively defined as the theoretical number of peaks that can be separated with a given resolution within a given analysis time. In chromatography, peak capacity depends on the peak width, and the total elution time. With DMS the analogous resolution parameters would be the compensation voltage peak full width at half height (W), and the CV range. The peak capacity for DMS can then be calculated using

$$PC=\frac{{CV}_{max}-{CV}_{min}}{W_{av}}$$ 7)

where PC is the peak capacity, CV_max – CV _min is the voltage range within which a set of compounds transmit through the DMS cell, and W_av is the average full width half maximum observed for the peaks during a CV scan. The DMS peak width is determined by the geometry of ion trajectories in planar DMS in a straightforward way. The net result is that the peak width can be written as

$$W~\frac{1}{\langle K\rangle }\frac{d^2}{t_{\mathit{res}}}$$ 8)

where d is the gap, t_res is the ion residence time in the analytical region, and K is ion mobility coefficient averaged over one cycle of the waveform. Because their trajectory is more sensitive to field, light molecules of high mobility appear in DMS with narrower peak widths.

Separation and Compensation Voltages

The separation voltage, SV, is high voltage, high frequency asymmetrical potential applied between the electrodes of the DMS cell to provide DMS separation. A bisunusoidal separation voltage was generated using a custom two-harmonic resonant generator.² The fundamental frequency of the generator was 3 MHz, with peak magnitude from 0 – 3333 V (0–5000 V p-p) across the 1 mm gap. The 3 MHz component and the 6 MHz component were applied to opposing electrodes, creating an asymmetric bisinusoidal field within the analyzer gap. The amplitude and phase ratio of the 2 harmonics were adjusted to provide the general waveform shape labeled as “Waveform #2” in Figure 3 of Ref ¹⁰, with the difference that we report the absolute value of the waveform amplitude. With this configuration, positive ions with positive values for alpha (i.e. K(E) > K(0)) require a negative CV to be transmitted through the DMS analyzer. However, this behavior is a simply an instrumental sign convention since reversing the polarity of the waveform would invert the sign of the required CV.

The compensation voltage, CV, is a DC offset potential applied between the DMS cell electrodes to correct the trajectory for a given ion under the influence of the separation field. A scan of this voltage sequentially transmits ions with different mobility characteristics through the DMS cell. CV was stepped in increments of 0.1 or 0.2 V for all of the data presented in this paper, and could be scanned over a range from −100 V to +100 V across the 1 mm gap, or set to a particular value within that range. All of the data presented in this paper were generated in MRM mode using a 10 ms dwell and a 20 ms pause time. Under these conditions, an entire cycle for 3 MRM transitions would require approximately 90 ms.

Other Instrument Parameters and Conditions

DMS devices require a gas flow to carry ions from the inlet through the analyzer to the outlet. This gas flow is referred to as the transport gas throughout this paper. The composition of the transport gas was varied for each of the molecular ions studied in this work, and included nitrogen, nitrogen with varying amounts of helium, and nitrogen with 1.5% 2-propanol vapor added as a clustering agent (gas modifier). The transport gas flow was fixed at an optimal value as described below and further detailed in Ref. 2.

All DMS/MS experiments were run at atmospheric pressure with the local barometric pressure recorded at the time of the experiment. The barometric pressure was monitored during these experiments to correct both the separation voltage and the compensation voltage for fluctuations in the barometric pressure using a Model 276 barometer with 0.1% accuracy (Setra, Boxborough, MA).

The gap height for the DMS electrodes used in these experiments was 1 mm, and the length and width dimensions were 30 mm and 10 mm, respectively. The DMS coupling involved sealing the analyzer cell to the inlet orifice of the mass spectrometer, as described previously in Ref. 2. The transport gas flow through the cell (≈ 3 L/min) was drawn from the mass spectrometer curtain chamber by the vacuum drag through the inlet orifice. The curtain gas flow was maintained at approximately 3.7 L/min, providing approximately 0.7 L/min of curtain gas outflow from the curtain plate, the remainder serving as the transport gas through the DMS cell and inhaled by the mass spectrometer. Modifiers and/or helium were added to the curtain gas supply line, metered in to achieve the specified gas phase concentrations. An HPLC pump with 1% flow accuracy (Shimadzu model 10A) was used to deliver the 2-propanol liquid modifier at the appropriate flow rate to achieve the gas phase concentrations cited. At a 2-propanol flow of 150 μL/min mixing with a curtain gas flow of 3.7 L/min a 1.5% gas phase concentration of modifier was produced. More details of the design of the DMS cell and the means utilized to interface to the mass spectrometer are described in Ref. 2.

The mass spectrometer used for these experiments was a modified API 5000 triple quadrupole system. Samples were infused at 10 μL/min from a syringe pump (Harvard Apparatus, Syringe Infusion 22, South Natick, MA) into the standard Turbo V^™ ion source and no additional source heat was used for these experiments. A modified curtain plate was designed in-house to enclose the DMS cell within the curtain chamber. The curtain plate included a ceramic heat exchanger (Kyocera, JP), as previously described ². An extension flange was used to adjust the position of the source relative to the extended protrusion of the curtain plate when the DMS was installed. A custom heater controller was designed in-house to heat the ceramic heater to variable temperatures up to a maximum of approximately 350° C.

The temperature of the transport gas was determined at each heater setting using a thermocouple. All experiments were conducted in multiple reaction monitoring mode (MRM) using optimized Q1/Q3 m/z values for the particular compounds. The dwell time was 10 ms and the pause between mass ranges was 20 ms.

Chemicals and Reagents

A positive ion mode test mixture that yields in electrospray 70 singly charged analytes with diverse chemical structures, and a negative ion mode test mixture that results in 25 different singly, doubly, and triply charged ions were prepared for these experiments. The list of test chemicals is provided in Table 1 and Table 2 with other relevant information. The chemical formulae are provided in Tables 1–2 for each of the compounds used in these studies.

Table 1.

Sample	Q1 m/z	Chemical Structure	SignalIPA/SignalNit	SignalHe/SignalN2 at Max SV
Histamine	112.0	C5H10N3	0.42	0
Methylhistamine	126.0	C6H12N3	1	0.02
Melamine	127.1	C3H7N6	1	0.02
Ammelide	129.1	C3H5N4O2	0.32	0
Leucine	132.1	C6H14NO2	1	0
Acetaminophen	152.2	C8H10NO2	0.32	0.02
Ephedrine	166.1	C10H16NO	1	0
Caffeine	195.1	C8H11N4O2	0.01	0.04
Nirvanol	205.3	C11H13N2O2	0.007	0.14
Minoxidil	210.1	C9H16N5O	1	0.25
Butabarbital	213.2	C10H17N2O3	1	0.16
Mephenytoin	219.1	C12H15N2O2	0	0.14
Bucetin	224.1	C12H18NO3	1	0.15
Acyclovir	226.1	C8H12N5O3	1	0.01
Naproxen	231.1	C14H15O3	0.004	0.08
Norfentanyl	233.2	C14H21N2O	1	0.23
Bentazon	241.1	C10H13N2O3S	0	0.12
Methoxymephenytoin	249.2	C13H17N2O3	0.007	0.37
Lamotrigine	256.0	C9H7Cl2N5	1	0.34
Tramadol	264.2	C16H26NO2	0.76	0.16
Tolbutamide	271.1	C12H19N2O3S	0.09	0.41
Nordiazepam	271.1	C15H12ClN2O	1	0.39
Clenbuterol	277.1	C12H18Cl2N2O	1	0.32
Venlafaxine	278.2	C17H28NO2	0.82	0.52
Imipramine	281.2	C19H25N2	0.67	0.40
Diazepam	285.1	C16H14ClN2O	1	0.42
Morphine	286.1	C17H20NO3	1	0.84
Benzoylecgonine	290.1	C16H20NO4	1	0.81
Trimipramine	295.2	C20H27N2	0.65	0.48
Dianabol	301.1	C20H29O2	0.48	0.31
Carboxytolbutamide	301.1	C12H17N2O5S	0	0.69
Cocaine	304.1	C17H22NO4	0.83	0.44
Quinoxyfen	308.0	C15H9Cl2FNO	1	0.56
Phenylbutazone	309.1	C19H21N2O2	1	0.75
Nifenazone	309.1	C17H17N4O2	0.45	0.83
Warfarin	309.1	C19H17O4	0.82	0.57
Benoxinate	309.2	C17H29N2O3	0.74	0.75
Cannabinol	311.2	C21H27O2	0.01	0.77
Safranin Orange	315.1	C20H19N4	1	0.65
Ranitidine	315.2	C13H23N4O3S	0.71	0.55
Bromazepam	316.1	C14H10BrN3O	1	0.45
Chlorprothixene	316.1	C18H19ClNS	0.90	0.62
Clonazepam	316.1	C15H11ClN3O3	1	0.68
Oxycodone	316.1	C18H22NO4	0.82	0.67
Oxfendazole	316.1	C15H14N3O3S	0.57	0.82
Fendiline	316.2	C23H26N	1	0.73
Pamaquine	316.2	C19H30N3O	0.73	0.65
Oxyphenbutazone	325.1	C19H21N2O3	1	0.6
Quinine	325.2	C20H25N2O2	0.75	0.71
Citalopram	325.2	C20H22FN2O	0.56	0.75
Midazolam	326.1	C18H14ClFN3	1	0.49
6-Acetylmorphine	328.3	C19H22NO4	1	1
Piroxicam	332.1	C15H14N3O4S	1	0.58
Buscopan	360.1	C21H30NO4	0.81	0.73
Prednisolone	361.1	C21H29O5	0.65	0.52
Hydrocortisone	363.2	C21H31O5	0.05	1.12
Tamoxifen	372.1	C26H30NO	0.88	0.82
Trazodone	372.2	C19H23ClN5O	0.70	0.98
Haloperidol	376.1	C21H23ClFNO2	0.76	0.93
Lovastatin	405.2	C24H37O5	0.25	0
Beclomethasone	409.1	C22H29ClO5	0.52	0
Verapamil	455.3	C27H39N2O4	0.92	0.75
Morphine Glucuronide	462.1	C23H28NO9	1	1.2
Testosterone Glucuronide	465.1	C25H37O8	0	1.16
Sildenafil	475.2	C22H31N6O4S	0.84	0.83
Ketoconazole	531.1	C26H28Cl2N4O4	0.68	0.89
Leucine Enkephalin	556.4	C28H38N5O7	0.92	1.15
Reserpine	609.2	C33H41N2O9	0.92	1.12
Bromocryptin	654.1	C32H40BrN5O5	0.44	1.14
Erythromycin	735.0	C37H68NO13	0.55	0.98

Table 2.

Sample	Q1 m/z	Chemical Structure	SignalHe/SignalN2 at Max SV
5-Fluorouracil	−129.1	C4H2FN2O2	0
Aspartic Acid	−132.0	C4H6NO4	0
Glutamic Acid	−146.1	C5H8NO4	0
Hexanoylglycine	−172.1	C8H14NO3	0.1
Ibuprofen	−205.1	C13H17O2	0
Naproxen	−229.0	C14H13O3	0.09
Amaranth	−268.3 (2−)	C20H13N2O10S3	0.05
Sulfamethazine	−277.1	C12H13N4O2S	0.35
Acid Black 1	−285.3 (2−)	C22H14N6O9S2	0.1
Sulfonic Acid	−301.4 (2−)	C28H14N2O10S2	0.16
Efavirenz	−314.3	C14H8ClF3NO2	0.41
Acid Orange	−327.3	C16H11N2O4S	0.73
Furosemide	−329.0	C12H10ClN2O5S	0.64
Fluoroscein	−331.1	C20H11O5	0.45
Estradiol Sulfate	−351.2	C18H23O5S	0.92
Acid Red 88	−377.3	C20H13N2O4S	0.72
Tinopal SFP	−390.0 (3−)		0.17
Acid Red 151	−431.3	C22H15N4O4S	0.90
Aztreonam	−434.0	C13H16N5O8S2	0.81
Taurocholic Acid	−514.3	C26H44NO7S	1.20
Fosinopril	−562.3	C30H45NO7P	0.76
Bromophenol	−669.1	C19H9Br4O5S	0.71
Acid Yellow 151 Dimer	−807.3	C32H32N8O10S2Fe	0.42
Digitoxin	−809.5	C41H63O13	0.75
Digoxin	−825.4	C41H63O14	0.91

Solutions of standards were diluted in solvent comprising 50/50 methanol/water with 0.1% formic acid (Fischer Scientific, Nepean, ON).

Safety Considerations

High voltages are required to generate the asymmetric waveforms necessary for DMS operation. Proper interlocks and shielded cables should be used to prevent accidental contact. Many of the chemicals used for these studies are hazardous and should only be used with the safety precautions listed in the relevant MSDS documents.

Results and Discussion

One of the important analytical parameters of the ion pre-filter is separation power. It directly relates peak capacity defined in previous section. In this section we discuss various phenomena affecting the peak capacity aiming to find conditions of the maximum DMS resolution. The consideration is based on the experimental data and confirmed by the theory.

Transport Gases and Separation Models

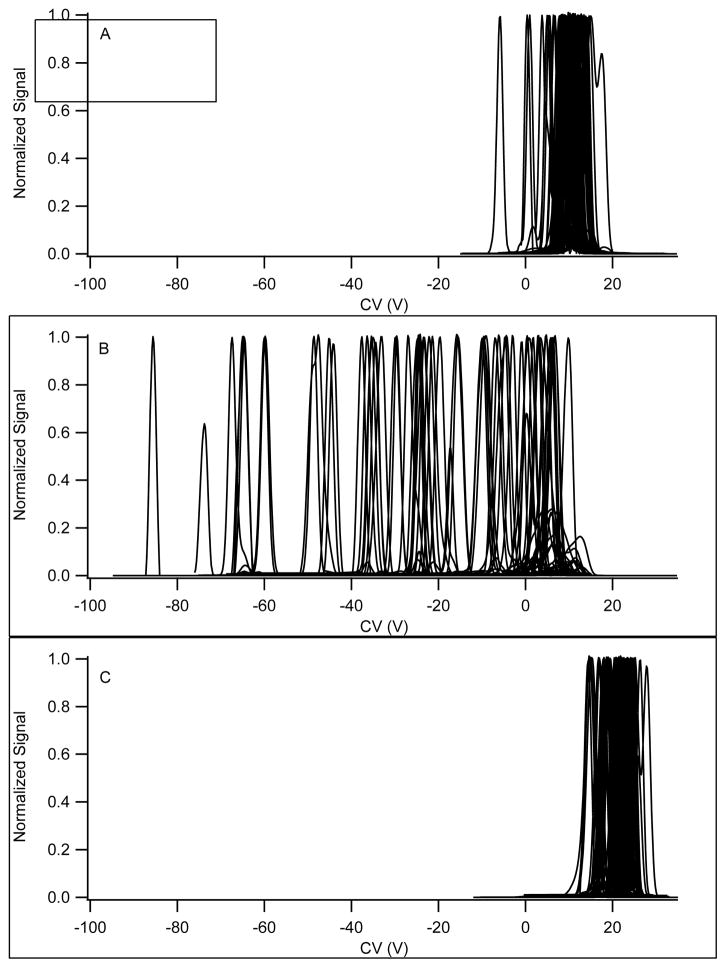
As defined in the Experimental section, peak capacity is a metric to provide some measure of the number of compounds that could potentially be separated in a single CV scan provided sufficient selectively is available. The data in Figures 1 and 2 demonstrate the dramatic effect of gas composition on peak capacity, followed by an explanation of the data in terms of the theoretical underpinnings of the separation mechanisms at play.

Figure 1.

Separation of a 70 compound mixture with various transport gas conditions. A. Nitrogen transport gas. B. Nitrogen with 1.5% 2-propanol. C. Nitrogen gas with 44% helium. The mixture contained 70 compounds generating singly charged positive ions. MRM transitions are monitored for each compound with a dwell time of 10 ms, total cycle time of 2.1 s. The separation field was 132 Td, and under these conditions the number of compounds observed was 69, 58, and 57 out of a total of 70 compounds for the data presented in 1A, 1B, and 1C, respectively. The presence of 44% helium in the transport gas eliminated all compounds with m/z below 195 for the data presented in 1C. The approximate peak capacities are 13, 45, and 11, respectively.

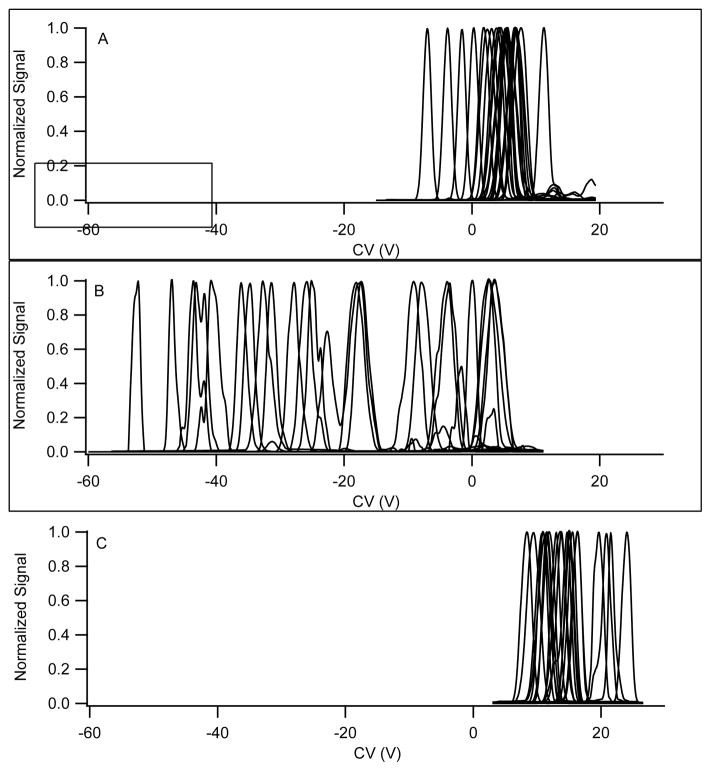
Figure 2.

Separation for a 25 compound mixture in negative ion mode. A. Nitrogen transport gas. B. Nitrogen with 1.5% propanol. C. Nitrogen with 44% helium. The separation field was 115.5 Td. MRM transitions were monitored for each compound with a dwell time of 10 ms and a pause between mass ranges of 20 ms for a total cycle time of 750 ms. The number of compounds observed was 24, 24, and 20, for the data presented in 2A, 2B, and 2C, respectively.

Figure 1 is a positive ion CV scan of a 70 compound mixture of chemical entities representing a broad range of chemical space performed under conditions of different transport gas mixtures. Table 1 lists the compounds which include examples of bases, neutrals, and quaternary amines spanning a range of 112 – 735 m/z.

Comparing the CV scans in pure nitrogen (Figure 1a) to the identical experiment with the transport gas containing a polar modifier (Figure 1b) a shift toward negative CV values is observed for all compounds, but with a great deal of chemical differentiation, leading to a dramatically higher peak capacity. The approximate peak capacities are 13, 45, and 11, for nitrogen, 1.5% 2-propanol, and 44% helium in nitrogen, respectively. The alpha parameters for the compounds, as defined earlier, have moved toward positive values and the peak capacity is greatly enhanced with the polar modifier in the transport gas. The difference between the low and high field mobility constants for the compounds has been amplified for most compounds. Nitrogen and helium (Figures 1a & c) show similar peak capacity but differ in absolute values for the CV, with helium CV values more positive than in nitrogen, and all of positive sign, corresponding to alpha parameters decreasing with field for each compound. The shift towards a more negative α parameter in helium is consistent with hard sphere scattering as described further below. Figure 2 is the same experiment conducted in negative ion mode with a different set of 25 compounds composed primarily of strong and weak acids demonstrating the general nature of these phenomena across a broad chemical space.

The behavior described above indicates that different separation mechanisms are being emphasized in the case of inert versus polar transport gases. Other types of modifiers such as water or other alcohols show effects qualitatively similar to 2-propanol.⁴

Clusterization Model

The theory that underlies the positive shift in the alpha parameter with polar transport gases is best understood in terms of reversible cluster formation, the “clusterization” model. The asymmetric waveform used in DMS varies between high field and low field regimes at a rate in the MHz range. This variation can be modeled as a field-dependent effective temperature synchronous with the SV field because of the high collision frequency at atmospheric pressure.²¹ When ion-neutral clustering is occurring to a significant extent, the time-varying effective temperature can cause a time-varying change in ion size and, therefore, a synchronous change in ion-mobility cross-section. Ions are clustered during the low field portion of the waveform and undergoing declustering due to heating during the high field portion of the waveform. The extent of clustering and the relative change in mobility due to clustering dictates the magnitude of CV shift toward negative values, and the structural and chemical differences between compounds leads to a spread in peak positions in the presence of clustering modifiers. This reversible cluster formation provides a method for the amplification of differential mobility effects in DMS. Because the change in cluster number occurs between the low and high field regimes during the SV waveform in DMS, with the low field mobility reduced more than the high field mobility, the differential mobility is greatly enhanced. Thus hard clusterization corresponds to α(E) positive and increasing.

Hard Sphere Scattering Model

The hard sphere scattering model has been a reference point throughout the history of ion mobility studies. It was the basis of some of the earliest work by Wannier¹¹, has been the subject of several theoretical papers during the last decade, and, furthermore, has formed the basis of ion mobility computational software packages such as Mobcal (for more background, see Ref. 12 and references therein). Hard sphere scattering is computationally tractable and provides reasonable agreement with experiment, especially for low field mobility coefficients under ideal conditions. In one recent example, the mobilities of 50 aromatic cations were studied and compared to hard sphere calculations, with good results that aided in the assignment of conformers.¹³ It is rather more difficult to predict the field dependence of ion mobility because of the importance of long-range (chemical) forces in determining the change of mobility with field. When long range attractive interactions are strong, (for example, ion-dipole interactions of an ion interacting with a polar gas), ion mobility will increase with field, while, for systems dominated by pure hard sphere interactions, ion mobility will decrease with field. Intermediate interactions, such as ion-polarizability and Leonard-Johnson 12-4 potentials with an added repulsive hard sphere core can cause intermediate behaviors, with mobility increasing, and then decreasing.

At field strengths where the hard sphere behavior is expected to dominate, the differential ion mobility coefficient is expected to decrease with field. This essentially universal result is a consequence of Eq. 3b, c for the alpha function, taking cross-section σ to be a constant. Then alpha decreases with field magnitude, E, slowly at low fields, then more rapidly, as in the standard type C behavior.

$${\alpha }_{\mathit{HSS}}(T_{\mathit{eff}})=\frac{K}{K_0}-1\to \sqrt{\frac{T}{T_{\mathit{eff}}}}-1=\sqrt{\frac{3kT}{(3kT+{MK}^2{E}^2)}}-1$$ 9)

Thus hard sphere scattering corresponds to α(E) negative and decreasing. Physically, the random-walk nature of hard-sphere collisions prevents the ion velocity from increasing purely linearly with the field, causing the ion-mobility coefficient to fall off with field strength.

As a result of these general considerations, the hard sphere model is expected to work well for ions in helium, both for low field mobility and for the field dependence, and will usually predict mobility coefficients falling with field / effective temperature. Mobility in helium is so much higher than in polarizable gases or in polar gases, that, when helium behavior is being tested, small admixtures of polar molecules can dominate the ion-helium interaction. Mobility in mixtures is predicted by Blanc’s law, and shows that small amounts of polar gases can prevent the expected hard sphere mobility coefficients from being observed. For instance, the comprehensive drift gas IMS results from the Hill group¹⁴ scale for each ion as expected with reduced mass for several drift gases, but not to the full extent predicted for helium, while low pressure, fully-declustered experiments by Bierbaum and Leone¹⁵ do scale as expected, showing the very high mobility in helium of 11.8 cm²/V·s for C₆H₆⁺. This polar-nonpolar mixing effect has also been examined for t-C₄H₉⁺ in Ref¹⁶. As another example of the applicability of the hard-sphere model under highly-controlled conditions, calculations of the mobility of cluster ions drifting in helium and in nitrogen were made using hard-sphere and polarizability interactions in Ref¹⁷. For nitrogen, which has a large permanent quadrupole moment and significant polarizability, deviations from hard-sphere predictions are seen to occur when compared to helium.

Regardless of the details of the experimental conditions, the hard sphere model should be qualitatively relevant to admixtures of helium to the N₂ drift gas, according to Blanc’s law. Because of the absence of long-range interactions, this model predicts mobility decreasing with field, corresponding to CV values becoming more positive in our sign convention.

In summary, the two ion-drift gas interaction mechanisms are highly orthogonal. The clusterization mechanism is dominated by gas phase ion-neutral chemical effects that decrease low field mobility coefficients more than the high field one, making CV dramatically more negative and sensitive to chemical interactions. The rigid scattering model is dominated by the short-range scattering effects during ion/neutral collisions. Because of the lack of long range terms and of chemical interactions, CV values become more positive without any increase in chemical specificity.

Transport Gas and Effective Gap

If the current values of SV and compensation voltage are incorrect for a particular ion, the continuous net transverse displacement due to the separation field waveform will result in the ion being neutralized on the electrode surface before exiting the DMS region. In addition, if an ion transits too great a distance during each period of the waveform it will touch the SV electrode and be lost regardless of the application of a compensation voltage. The physical gap is effectively reduced in aperture by the oscillation amplitude that neutralizes ions near the side. The effective gap is defined as the physical gap reduced by the oscillation amplitude.

$$g=d-\frac{\mathit{SKT}}{2}\langle \mid f\mid \rangle$$ 10)

Instrument design minimizes this loss to the electrodes by choosing the optimal combination of SV frequencies, voltage amplitudes, and distance between the electrodes. The transport gas composition can also have an influence on these losses by altering the ion mobility, figuratively altering the gap between electrodes, described above as the effective gap. Peak capacity will be reduced under some conditions if mobility is increased so much that low mass ions are lost. Low mass non-polar transport gases such as helium increase the transit distance of an ion during a single SV period because the ion mobility for a particular ion is predicted to scale approximately as (reduced mass)^−1/2 (note that reduced mass is dominated by the lightest species for differing masses). Since the effective gap is reduced by the ion transit distance, ions with a mobility that is already high because of small size or compact geometry may see the effective gap drop to zero at high SV settings.

Of the 70 positive ion compounds analyzed in the experiment of Figure 1, 13 were lost due to this effect when a transport gas containing 44% helium was used compared to pure nitrogen (Figure 1A&C). Of the 25 negative ion compounds analyzed in the experiment of Figure 2, 5 of 25 were lost (Figure 2A&C) in the presence of 44% helium. The signal reduction with the addition of 44% helium to the transport gas is illustrated in column 5 of tables 1 and 2. In this case, an entry value of 0 means that the compound was completely eliminated from the spectra in the presence of 44% helium. As shown in the tables, the losses correlate strongly with ion mobility, as evidenced by dramatic losses for low m/z ions and almost no losses with high m/z ions.

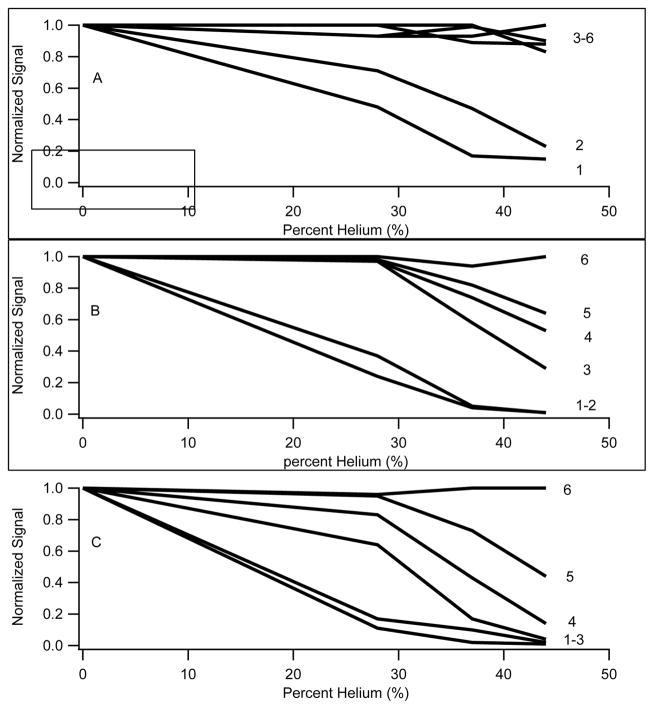
A more detailed study of this phenomenon was conducted to determine the effects of separation voltage magnitude and nitrogen/helium ratio for the 70 compound mixture. A subset of the results is presented in Figure 3 for 6 ions ranging from m/z ≈112 to m/z 556. Figures 3A–C demonstrates data collected for the 6 compounds with separation fields of 99.0 Td, 115.5 Td, and 132 Td, respectively.

Figure 3.

Relative intensity plots for 6 ions from the 70 compound mixture with increasing helium content in the transport gas. The separation field was 99.0 Td, 115.5 Td, and 132 Td, for the data present in panes A, B, and C, respectively. The ions were 1) Histamine (m/z 111.6), 2) Leucine (m/z 132), 3) Caffeine (m/z 195), 4) Mephenytoin (m/z 219), 5) Cocaine (m/z 304), and 6) Leucine enkephalin (m/z 556). Increased losses are observed for the majority of ions with increasing helium content in the transport gas. The losses are most dramatic for low m/z ions at high separation voltages. There was a low m/z cut-off when running at the higher 2 separation voltage settings.

In all cases, the data are normalized to the intensity observed in pure nitrogen transport gas to clearly show the effects of increasing the fraction of helium. As shown in 3A, all of the 6 compounds are transported through the DMS analyzer when the separation field is maintained at 99 Td, however, there is substantial reduction in the intensity for the 2 lowest m/z ions as the fraction of helium increases. There was no significant attenuation of the intensity for ions of m/z 195 or greater.

Figure 3B shows the same experiment conducted with the separation field increased to 115.5 Td. Under these conditions, ion losses were more significant with increasing helium fraction in the transport gas. With 44% helium, the signals for all ions of m/z lower than 132 were completely eliminated from the spectra. Ions over the range of m/z 195–304 were also affected, but to a diminishing extent with mass. There was no reduction in signal for m/z 556. Increasing the SV further to 132 Td, there was a complete elimination of all ions with m/z less than 195, and further reductions in intensity for ions of m/z ranging from 195–500. At the highest helium fractions, a low m/z cut-off exists with the DMS operating at various SV values.

Transport Gas, & Ionization Efficiency

The concept of peak capacity attempts to quantify the range of chemical species separable under a given set of conditions. We have discussed the importance of using transport gas modifiers and minimizing effective gap losses by avoiding the use of very light transport gases. In principle physical phenomena other than those directly related to the separation process can restrict the chemical space accessible under a given set of separation conditions. The loss of ions due to competing ion-molecule reaction channels is one of them, particularly when one considers the use of polar modifiers in the transport gas.

The principles of gas phase ion chemistry apply. When the modifier added to the transport gas has gas phase basicity greater than the analyte ion, the analyte ion current will be depleted in positive ion mode. When the modifier has gas phase acidity greater than the analyte ion, the analyte ion current will be depleted in negative ion mode. With the compound set and experimental conditions shown in Figure 1, 12 out of 70 compounds and in Figure 2, 1 of the 25 were lost when using 2-propanol modifier. In each polarity, the loss of one compound could not be explained on the basis of gas phase ion-molecule reactivity.

Because the gas phase reactivity of ions relative to neutral modifiers can be reasonably estimated from chemical structures and data base values, in practice this restriction of peak capacity can be managed and the enhancement in peak capacity afforded by the use of modifiers can be leveraged without compromise. Flexibility in the use of modifiers with different gas phase reactivity is one way to manage this situation. Under conditions where the compounds, and likewise their gas phase chemical reactivity, are unknown then the possible loss of ions from ion-molecules reactions must be taken into account. Proton affinities are available for most volatile liquids considered for use as a modifier as well as for many chemical species from NIST. This phenomenon can be used to advantage to further reduce the chemical noise for high proton affinity analytes by choosing a modifier with lower proton affinity than the analyte, but higher than at least a portion of the chemical noise. In this case, the background reduction would be due to a combination of DMS filtering and transfer of charge from background ions to the modifier.

From the entire compound set, two compounds were lost using the conditions of Figures 1 & 2 by means that could not be explained by either effective gap or ionization losses: in positive ion mode, bentazon, and in negative mode, naproxen. Both compounds have structures that favor fragmentation and produce product ions at low collision energies in a tandem MS experiment. When the SV was reduced by 500 volts, the signal for both compounds returned, the difference in intensities between low and high voltage being approximately 2 orders of magnitude. In all likelihood these two compounds were fragmenting during the DMS separation at atmospheric pressure from heating caused by the strong separation field.¹⁸ Fragmentation is a third means by which peak capacity can be reduced with DMS, but is relatively rare in our large test set.

Separation Power, Resolution, and Transport Gases

Separation power is a qualitative description of the ability to separate two chemically similar compounds. Increased peak capacity does not necessarily result in increased separation power. Peak capacity describes the potential bandwidth to separate a large number of compounds but does not measure improvements to selectivity for a particular separation. It is difficult to develop a generalized equation for separation power because it depends entirely upon the chemical species considered, otherwise to note that the upper limit on separation power would likely be represented by the separation of chemically identical compounds such as enantiomers.¹⁹ Separation power and resolution are often equated in mass spectrometry, particularly when using the full width half maximum (FWHM) definition. With mobility they are unrelated. Using the classical definition of resolution (peak position divided by FWHM), the peak width in CV volts gives no tangible indication of the separation power.

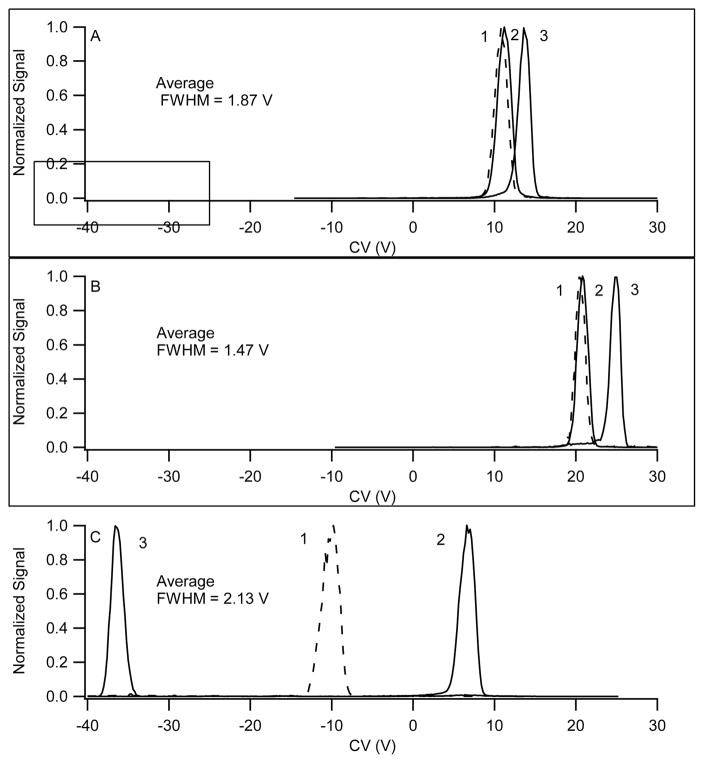
A case in point is the data shown in Figure 4. The narrowest peaks were obtained with the greatest amount of helium in the transport gas, intermediate with nitrogen, and the widest peaks with nitrogen modified with 2-propanol. This behavior is very much in accordance with our discussion of mobility coefficient (Eq. 2) and of peak capacity (Eq. 6 and 7) given above. In agreement with Eq. 6, width is smallest in the He mixture because of the higher mobility in He, and largest in 1.5% 2-propanol because of the reduced mobility with strong ion-neutral interactions. Mobility is increased in helium because the reduced mass for the ion-helium system is low (Eq. 2), and because the polarizabilty of He is lower than that of N₂ (0.2 and 1.7 ų, respectively)²⁰ in addition to the reduced mass factor. Peaks further increase in width (mobility decreases) in the presence of polar modifiers because of additional long-range interactions that increase the cross-section, σ, and clustering that also increases the cross-section. These observations are left at a qualitative level because of the heterogeneous nature of electrospray conditions.

Figure 4.

Comparison of the separation of 3 selected ions from the 70 compound mixture, demonstrating the differences in peak position and peak FWHM observed when operating with (A) nitrogen transport gas, FWMH ~ 1.87 V, (B) nitrogen with 44% helium transport gas, FWMH ~ 1.47 V, and (C) nitrogen with 1.5% 2-Propanol, FWMH ~ 2.13 V. The ions are 1) dianabol, 2) benoxinate, and 3) clenbuterol, and the separation fields was 132 Td. FWHM is smallest in the He mixture because of the higher mobility in He, and greater in 1.5% 2-propanol because of the reduced mobility of clusters.

In Figure 4, of the 3 compounds subjected to a compensation voltage scan, two failed to separate with inert transport gas mixtures. The separation power, as indicated by the separation of all three compounds, was improved with the use of the polar modifier taking advantage of chemical specificity inherent in the gas phase ion molecule chemistry involved in the formation of clusters of different sizes, shapes, and internal bond strengths. Improvements in selectivity with the use of modifiers were seen in almost all cases for the compounds shown in Figures 1 and 2. However, there were a few cases where compounds that did not overlap using nitrogen transport gas did overlap with 2-propanol modifier. Examples were acetaminophen and melamine as well as quinine and piroxicam. This highlights the orthogonal nature of the separation mechanisms occurring under these different experimental conditions, where the dominating physical mechanisms are dissimilar. Finally, there was also at least one example where 2 compounds were not separated with either approach, including the prednisolone and morphine glucuronide combination.

Classifying the Field Dependence of α

As far back as 1992 three distinguishable types of ion mobility behavior were observed and classified in DMS, each exhibiting different trends in the mobility coefficient and alpha parameter as the SV is increased.^{3,1,21,22,23,24} The mobility has been observed to increase strongly with field, or to increase and then decrease with field, or to decrease with field as shown in Figure 5. Because ion-neutral interactions have a hard repulsive core that becomes important at high energies, mobility and alpha must eventually decrease with field, although that field may be difficult to apply experimentally, and fragmentation or charge loss may dominate at very high energies, preventing the eventual decrease from being observed. Different nomenclature has been assigned to each behavior by different authors. The three behaviors (strongly increasing, increasing then decreasing, and decreasing) are labeled by Purves et. al.¹³ as (A, B, C), by Krylov et. al.¹ as (1,3,2), and by Shvartsburg ²⁴ in his section (2.2.2), as (1,1,2). The later description combining types A and B acknowledges the theoretical understanding that mobility should decrease a high field even if the ions cannot survive those conditions. The first two descriptions are more applicable to experimental results. The (A, B, C) notation has been used more frequently in the literature, and is also used here. There is an evident connection between mobility type and the ion-neutral interaction mechanism dominant at a particular field amplitude, with type C behavior observed when hard-collisions dominate (at low field for non-polar systems, and at very high field for most systems), and types A/B when clustering and long-range forces are important.

Figure 5.

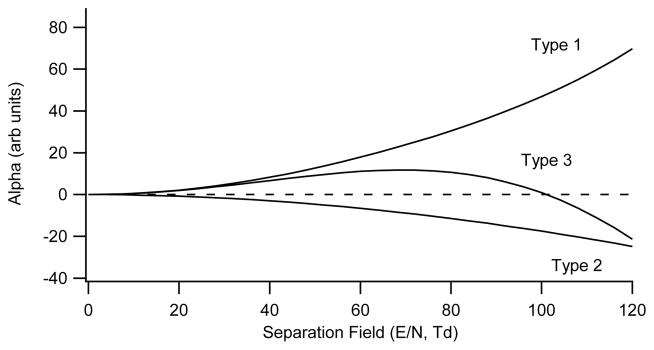
Three types of alpha behaviour. The general trends are alpha monotonically increasing (Type A), alpha monotonically decreasing (Type C), and intermediate behaviour with alpha increasing at low separation fields and decreasing at high separation fields (Type B).

Our data demonstrates that there is a close relationship between this mobility classification and the interaction mechanisms at play between ions and the transport gas environment. For molecular systems, we find that these interactions are in turn predominantly controlled by the degree to which an ion is clustered or adducted to neutral polar or nonpolar molecules. Because of the complexity of interactions between ions and mixtures of polar and non-polar neutrals at atmospheric pressure, this relationship has been largely neglected in previous work in favor of analysis of simpler, computationally accessible, models. Because of the startling enhancement to resolving power of these chemical effects in planar DMS instrumentation, we are exploring them in detail in this paper, building on a previous publication⁴. We find that types A and C represent limits (extremes) where one mechanism dominates, and type B is observed under conditions such that a mixture of mechanisms is apparent.

Type A – strongly increasing mobility

Figure 6A shows CV scan data at different separation fields for the molecule norfentanyl, MW = 233 Da, which exhibits type A behavior under transport gas conditions that favor clustering. As described for Figures 1 & 2, this shift toward negative CV values is seen in all the compounds tested with a high concentration of modifier added to the transport gas. The alpha function becomes increasingly positive indicating that the mobility under low field conditions is reduced by clustering relative to its value at high field. The low-field ion is more highly clustered than the high field ion that is declustered by separation field heating. This mechanism dominates the separation process and the selectivity achieved is highly influenced by the chemical characteristics of the ion in relation to the neutral clustering species.

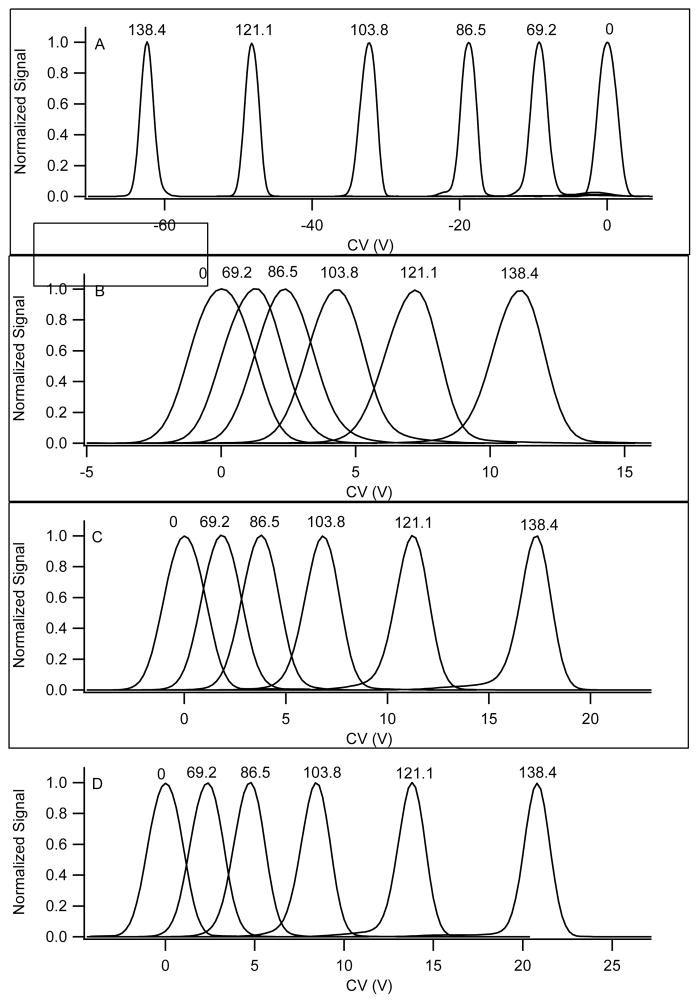
Figure 6.

Comparative data for norfentanyl under 4 different transport gas conditions. The transport gas composition was A) nitrogen with 1.5% 2-propanol, B) nitrogen, C) nitrogen with 28% helium, and D) nitrogen with 37% helium. The data are normalized to illustrate peak position more clearly. The measured signal was approximately equivalent under each of these conditions, with a full spread ranging from 600,000 to 1,400,000 cps across all transport gas compositions and separation voltage settings. The separation field corresponding to each peak is displayed (Td units) in each pane.

From the data in 6A, a plot is constructed of the alpha function versus separation field in Townsend units as shown in Figure 7 plot (i). The alpha function rapidly climbs with increasing SV. Higher fields reduce clustering accentuating the difference in the state of the ion, and thus mobility, under the two field conditions. The slope of this curve reflects the peak capacity which is much greater for chemically dominated separations (Type A) than for physically dominated separations (Type C).

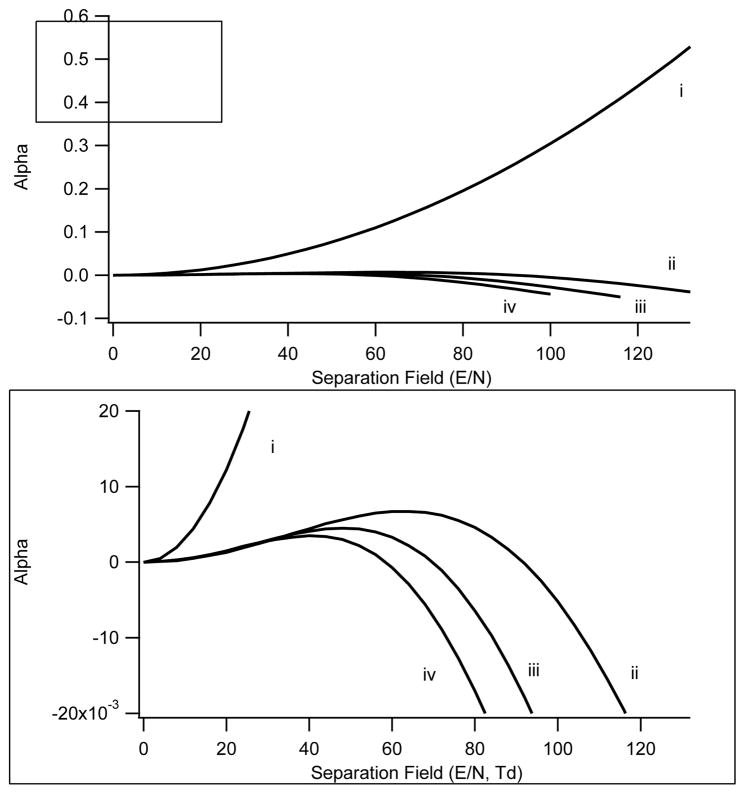
Figure 7.

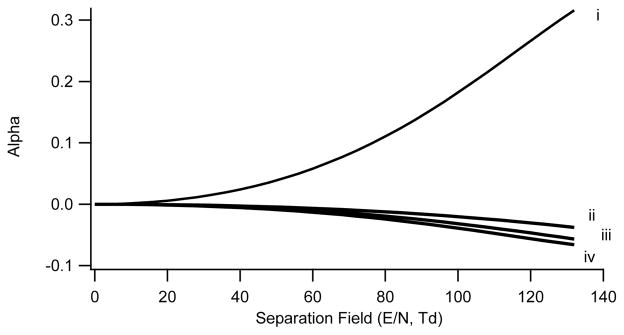
Alpha curve plot for norfentanyl. Alpha Plot for norfentanyl under 4 different transport gas conditions. i) nitrogen with 1.5% 2-propanol, ii) nitrogen, iii) nitrogen with 28% helium, and iv) nitrogen with 37% helium.

Type C – decreasing mobility

Under transport gas conditions where clustering and adduct ion formation are minimized or nonexistent the behavior of the norfentanyl ion shifts to a Type C classification. From the data in Figure 6B–D the alpha functions are calculated and plotted versus field strength in Figure 7, plots (ii–iv). With nitrogen as the transport gas, the CV for norfentanyl shifts positive with increasing field strength and the alpha function becomes increasingly negative. Under high field conditions the mobility is decreasing relative to the low field value. In high fields and in the absence of clusters, the rigid sphere scattering mechanism becomes dominant, as we have discussed above. At high interaction energies the short-range repulsive potential becomes important resulting in a decreasing mobility (Eq.9). With increasing concentrations of helium the alpha function continues to become more negative (Eq.9, Figure 7, plots iii–iv), again consistent with the rigid sphere mechanism. In contrast to the situation with modifiers present, the separation process and the selectivity achieved is less under these conditions, since it is controlled solely by geometric cross-sections with no influence from chemical effects.

Type B – increasing, then decreasing, mobility

An identical experiment to that shown in Figures 6 and 7 is shown in Figures 8 and 9 for methyl histamine, mw=125. The trend toward a more negative CV (Figure 8A) with concomitant positive shift in the alpha function (Figure 9(i)) under conditions of polar transport gases is consistent with observations on all the other compounds shown earlier. With inert gases and under relatively low SV amplitudes the CV shifts negative indicating a positive trend in alpha (Figure 8B–D and 9(ii–iv). Under inert transport gas conditions the separation mechanism exhibits declustering behavior at low SV amplitudes. Compounds that exhibit this behavior are present as adducts or clusters even under dry transport gas conditions. As the field strengths increase, the CVs reverse direction and shift toward positive values exhibiting a negative trend in alpha. This bimodal behavior, most evident in the alpha plots (Figure 9), is typical of Type B behavior. The negative alpha trend is stronger in helium than in nitrogen once again consistent with the hard sphere mechanism dominating under high SV amplitudes, and we have discussed in terms of the random-walk nature of hard-sphere collisions. It should be noted that methylhistamine is one of the low m/z ions that was neutralized on the DMS electrodes when operating at high separation fields with helium present in the transport gas. As shown in Figure 9, the negative shift in alpha for this compound was limited by complete loss of the ion signal with greater than ≈ 20% helium present in the transport gas.

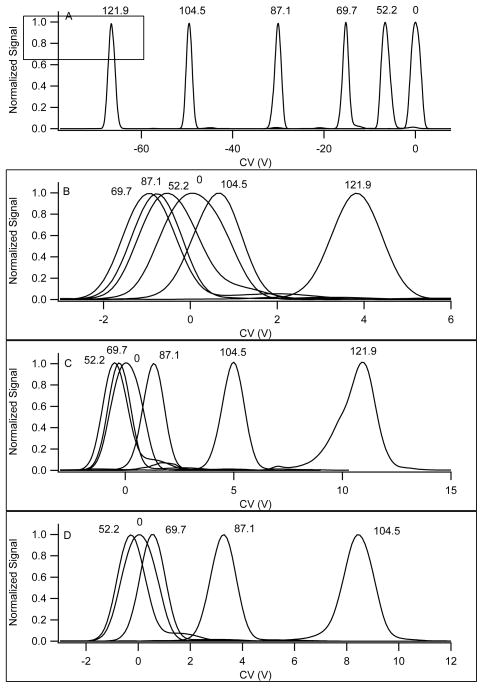
Figure 8.

Methylhistamine data under 4 different transport gas conditions. The conditions are A) nitrogen with 1.5% 2-propanol, B) nitrogen, C) nitrogen with 28% helium, and D) nitrogen with 37% helium. Note that different scales are used for each figure. The separation field (Td units) corresponding to each peak is displayed in each pane. The data are normalized to more clearly illustrate peak positions. With increasing helium fraction in the transport gas there was a significant reduction in signal at the highest separation voltages, with complete elimination of the peak demonstrated in pane D when the SV was 3500 V.

Figure 9.

Alpha curve plots for methyl histamine under 4 different transport gas conditions. i) Nitrogen with 1.5% 2-propanol, ii) nitrogen, iii) nitrogen with 28% helium, and iv) nitrogen with 37% helium. The bottom pane shows an expansion along the Y axis to more clearly demonstrate the Type B behavior in the absence of modifiers.

Predicting type A, B, C behavior from structures and conditions

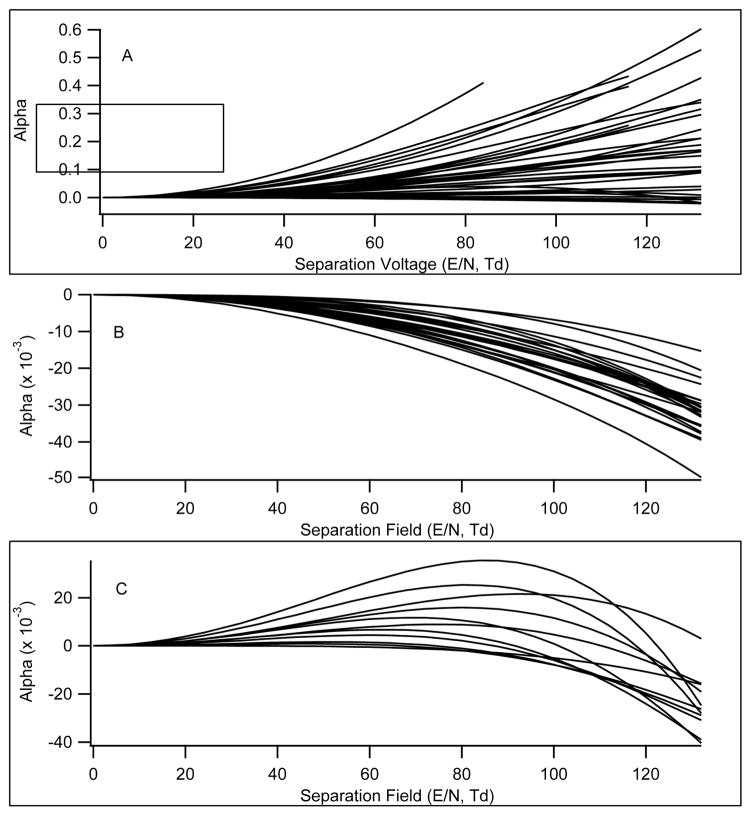
Type A behavior is observed in separations occurring under conditions of reversible clustering that causes the mean cluster size to change during the SV waveform. Increases in alpha are also caused by the presence of weaker long-range interactions that do not result in cluster formation, but the effect on CV is less (Type B behavior can result). The addition of suitable clustering modifiers favors Type A and B behavior. Figure 10A shows a clear trend towards increasingly positive alpha parameters for compounds as the field strength increased with high modifier concentrations. The slopes of these curves are different for the various compounds indicating that the tendency to cluster is compound-specific in the gas phase. There is a strong mass dependence in the data as indicated in Table 1 where lower molecular weight species show larger alpha parameters indicating that the relative mobility differences between the clustered and declustered states are larger than for bigger ions. As the mass increases, the alpha parameters may be negative, seen here in the mass range 669–825, but the trend toward positive values with the addition of clustering agents remains consistent. The change in mobility for clustering of 2-propanol with larger molecules is smaller than for lighter molecules so the enhancement in CV is reduced. A different modifier selection might modify the optimum mass range. Levin et. al.²⁵ tested a series of alcohols as modifiers, but no extensive survey has yet been done.

Figure 10.

Plots of alpha versus separation field for a subset of 36 compounds under different transport gas conditions. A) Data for all 36 compounds with nitrogen transport gas modified with 1.5% 2-propanol. B) Data for 25 compounds demonstrating Type C behavior with nitrogen transport gas. C) Data for 11 compounds demonstrating Type B behavior with nitrogen transport gas.

Under conditions that emphasize the introduction and transport of dry ions some compounds exhibit Type C and others Type B behavior with norfentanyl and methyl histamine in inert transport gases being examples from each category. Compounds that exist primarily as unclustered ions in the gas phase show a monotonic negative trend in alpha with field strength indicating the hard sphere mechanism is largely at play. The compounds that are dominated by this mechanism are plotted in Figure 10B. Compounds that exhibit bimodal behavior may in fact be weakly clustered even under relatively dry ion production conditions and completely lose the neutral adducts as the field strength increases, reverting to the hard sphere mechanism. The compounds that are dominated by this mixed mechanism are plotted in Figure 10C. The tendency of a specific ion to separate according to the clusterization versus the rigid sphere mechanism lies on a continuum between the two extremes as is clear in the plots from Figures 10A–C. This is entirely expected as it is subtle differences in the gas phase ion-molecule chemistry that drive an ion toward one mechanism or the other. There is a strong correlation with m/z from this data set transitioning toward the rigid sphere mechanism at above 180 m/z and the declustering mechanism below this mass. There also may be a potential correlation between solution based physical chemical parameters and the alpha trends that is worthy of investigation.

The clusters that lie at the heart of these mechanisms are in the form of weakly bound neutrals that span a large molecular weight range from a small number of adducts, typical of type B behavior, to higher cluster numbers typical of Type A behavior. For the bimodal behavior the number of these adducts is likely very low. It is difficult to quantify the number of these adduct molecules or for that matter the size of the large more robust clusters formed when modifiers are added. This is because all of these entities have bond energies substantially less than 1eV and they do not survive the free jet expansion from the atmospheric source to the vacuum conditions of the mass spectrometer. Their existence is however confirmed by the mobility separation at atmospheric pressure. The selectivity of the separations reflects the subtle nature of these interactions which appear to conserve chemical specificity of individual molecules by virtue of the number of adducts they form and their bond strengths.

The transition from Type C to Type B also qualitatively correlates with observations regarding the electrospray ionization of low molecular weight, high polarity compounds in general. Under high ESI liquid flow rates (hundreds of μL/min), where ion production is desolvation limited, the compounds that exhibited Type B behavior in this study are observed to exist in the form of highly heterogeneous cluster ion populations. The effect is much more dramatic with compounds low in mass (<180 Da) than high in mass (>180 Da). DMS/MS CV scans under high flow conditions show this effect as poorly resolved peaks spread out over a large portion of the CV scan range.³ As solution based ions become more similar to the solvent in terms of size and polarity it is more likely they will desorb to the gas phase in weak association with one or a few solvent molecules. The CV spectra produced in this study used experimental conditions geared toward the production of dry ions and show well defined high resolution peaks for all ions as shown in all the data figures. This to be expected if only a small number of adducts are involved resulting in a highly homogeneous adduct ion population. But those small number of adducts are enough to force the separation mechanism to be dominated by the declusterization process particularly under low SV field strengths. The possibility is presented that the field dependant trends of the alpha parameter could be a predictor of useful physical chemical properties of molecules for a variety of purposes such as the rapid determination of ADME properties of drug candidates, however, it remains to be proven.

Conclusions

Planar DMS has been recognized as having resolution advantages over other configuration²⁶, and has been the subject of recent papers from other groups²⁷. However, the results presented here indicate that DMS resolution can be increased dramatically beyond results that have been presented previously. Peak capacity and separation power with ESI/DMS/MS are highly influenced by the composition of the transport gas. Differential mobility of compounds in the presence of polar modifiers versus inert gas mixtures show enhanced peak capacity and selectivity. Factors such as the increased amplitude of ion oscillations in helium transport gases, ion chemistry effects with modifiers, and fragmentation can serve to reduce peak capacity particularly for situations where the compounds are unknowns and their behavior under these conditions cannot be compensated.

The theory underlying the separation mechanisms at play with DMS explains the amplification in peak capacity and separation power observed in the presence of polar modified transport gases versus inert gases. The consistency of the correlation of the theoretical explanation of the mechanisms, described here and elsewhere as the “clusterization model” and the “rigid sphere model”, and the experimental data across a broad chemical space demonstrates the generalization.

In the past the mobility behavior that various compounds exhibited with respect to the field dependence of the alpha parameter had been classified into three general types of behavior. It is shown here that these classifications reflect the dominant separation mechanism at play whether it is clusterization, rigid sphere, or a gradual switch between the two at different field strengths. The electric field dependence on mobility is influenced by the degree to which the ion exists as a naked molecular ion or whether it is clustered in the gas phase which has correlation to the molecular weight and other physical chemical properties of a molecule. The energy involved in the formation and dissociation of the clusters is highly specific to the chemical interactions between a particular ion and neutral gas phase molecules and appears to be preserved in the mild conditions of the atmospheric pressure separation but are lost during the free jet expansion into vacuum.

The state of the ion generated by electrospray and transported through the DMS cell, and thus its mobility behavior, is determined by several factors in addition to the composition of the transport gas such as the mode of ionization, the liquid flow rate under which ionization is performed, and any other accommodations to enhance or minimize the clusterization process such as heat or dry counter current gas flows. The conditions under which the data in this paper were taken are narrow, well defined, and reproducible. Mechanistic generalizations from the results presented here are broadly applicable but specific values for alpha functions for individual compounds will be affected by the experimental conditions. These values are stable and reproducible when separation conditions are kept consistent.