Measuring how much work the chaperone GroEL can do

Significance

Noncovalently “stacked” tetramethylrhodamine dimers are used to report and perturb the allosteric equilibrium in GroEL. The spectroscopic differences between the TMR monomers and dimers allow for quantitative measurements of the population of allosteric states. The noncovalent intersubunit stacking interaction within a dimer mimics the cross-linking constraint that SP places on the structure of GroEL. This feature allows TMR dimers to be used as SP surrogates to quantitate the impact of SP on the chaperonin cycle of GroEL. GroEL overcomes a load of 7.8 kJ/mol, demonstrating its ability to perform work on SP.

Abstract

Noncovalently “stacked” tetramethylrhodamine (TMR) dimers have been used to both report and perturb the allosteric equilibrium in GroEL. A GroEL mutant (K242C) has been labeled with TMR, close to the peptide-binding site in the apical domain, such that TMR molecules on adjacent subunits are able to form dimers in the T allosteric state. Addition of ATP induces the transition to the R state and the separation of the peptide-binding sites, with concomitant unstacking of the TMR dimers. A statistical analysis of the spectra allowed us to compute the number and orientation of TMR dimers per ring as a function of the average number of TMR molecules per ring. The TMR dimers thus serve as quantitative reporter of the allosteric state of the system. The TMR dimers also serve as a surrogate for substrate protein, substituting in a more homogeneous, quantifiable manner for the heterogeneous intersubunit, intraring, noncovalent cross-links provided by the substrate protein. The characteristic stimulation of the ATPase activity by substrate protein is also mimicked by the TMR dimers. Using an expanded version of the nested cooperativity model, we determine values for the free energy of the TT to TR and TR to RR allosteric equilibria to be 27 ± 11 and 46 ± 2 kJ/mol, respectively. The free energy of unstacking of the TMR dimers was estimated at 2.6 ± 1.0 kJ/mol dimer. These results demonstrate that GroEL can perform work during the T to R transition, supporting the iterative annealing model of chaperonin function.

The GroEL/GroES nano-machine facilitates the folding of a large number of diverse substrate proteins (SPs), converting them from one of many misfolded states to unique native states, which are no longer recognized by GroEL. This machine is ultimately powered by the binding and hydrolysis of ATP, driving GroEL through a series of allosteric states. Two views of GroEL function have emerged: one as a passive antiaggregation chamber and the other as an active folding device, performing work on SP (1, 2). Our experiments support the latter view, demonstrating that GroEL has the ability to perform work on its SPs via domain movements that accompany the allosteric transitions.

Allostery.

The chaperonin protein GroEL consists of 14 57-kDa subunits, arranged in two back-to-back heptameric rings (3). A GroEL subunit contains three distinct domains: apical, intermediate, and equatorial domains. The equatorial domain houses the nucleotide-binding pocket, whereas the site for SP and GroES binding is found between helices H and I in the apical domain (4). The SP binding sites, primarily composed of hydrophobic residues, line the inner wall of the heptameric ring’s central cavity and bind the exposed hydrophobic regions of the misfolded SP. The “mobile loops” of GroES displace the SP from this site (5, 6). In the chaperonin cycle, SP first binds to, and then becomes encapsulated inside, GroEL’s barrel-like structure. After a short time (a few seconds at 37 °C), the SP is released, whether folded or not.

The chaperonin cycle involves a series of allosteric transitions within a heptameric ring (7). In the absence of ATP, the ring adopts the T state, which has a high affinity for SP, low affinity for nucleotide, and cannot bind GroES. The binding of ATP triggers a transition to the R state, which is accompanied by a rotation of the apical domains, the expansion of the central cavity, and the separation of the peptide binding sites (8). The R state has a high affinity for nucleotide, low affinity for SP, and is the acceptor state for GroES. ATP binding is positively cooperative between subunits within a ring and negatively cooperative between rings within a 14mer. In the absence of GroES, GroEL can adopt three distinct allosteric states: TT, TR, and RR.

In the presence of Mg²⁺ and K⁺, GroEL hydrolyzes ATP to ADP and inorganic phosphate (9). In the absence of SP, the release of ADP is the rate-limiting step in the catalytic cycle (10). The addition of SP increases the rate of ATP consumption by GroEL by accelerating ADP/ATP exchange. A single SP binds to the apical domains of two or more GroEL subunits introducing a load on the ring in the form of noncovalent intersubunit cross-links that stabilize the T state. This constraint shifts the allosteric equilibrium in favor of the T state, whose weak affinity for nucleotide leads to the dissociation of the product, ADP, effectively increasing the rate of ATP consumption (11).

SP Binding Problem.

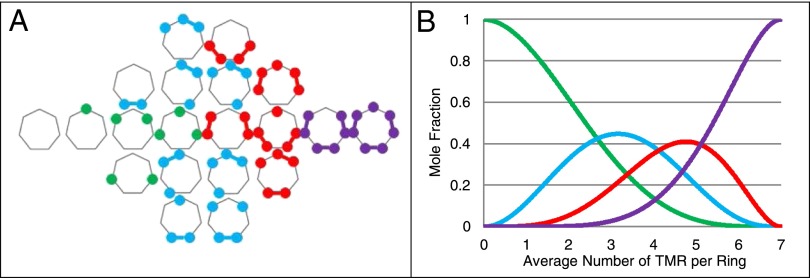
Many GroEL SPs contain multiple GroES-like motifs of the generic sequence P-HHH-P-H, where P and H represent polar and hydrophobic residues, respectively (12–14). The association of these motifs with GroEL is difficult to quantitatively analyze due to three levels of heterogeneity (Fig. 1). First, for every one native SP, there exist multiple misfolded states that form an ensemble of structures, all of which have the potential to interact with GroEL differently. The second level of heterogeneity is topological. Any one of the misfolded states has several GroEL binding motifs, which can be arranged in multiple ways between the seven SP binding sites of a ring. The third level occurs within the binding pocket itself. Although the seven SP binding pockets of GroEL are all identical, they bind the general sequence P-HHH-P-H, which, being degenerate, covers a wide range of structural sequences. Thus, within a single SP–GroEL complex, the various SP binding site contacts differ from one another. This heterogeneity makes it difficult to use GroEL’s natural SPs to quantitatively characterize their impact on the chaperonin cycle.

Fig. 1.

The substrate protein binding problem: a schematic illustration of the heterogeneous nature of SP binding. Level 0: SP’s native confirmation. Level I: every SP has multiple misfolded states. Level II: each misfolded state can bind to GroEL with different topological arrangements. Level III: each SP binding contact will differ because GroEL binds the general sequence P-HHH-P-H.

We sought to address the SP binding problem by using an SP surrogate with greatly reduced heterogeneity. The stimulatory effects of SP on the chaperonin cycle are rooted in the structural load that bound SP places on the movement of the apical domains within a heptameric ring. Because a typical SP forms multiple (at least two) noncovalent cross-links between the apical domains of GroEL, an effective surrogate should impose similar noncovalent, intersubunit cross-links. It should also be a single species that interacts with each GroEL subunit in an identical fashion. Because there are seven GroEL subunits, there are numerous topological arrangements for such a probe, and therefore the number and distribution of the surrogates across the subunits within a ring should be predictable. Finally, the surrogate should create an intersubunit load that is of uniform energetic value; i.e., the stabilization energy of each intersubunit cross-link should be identical. These qualities can be found by using noncovalently stacked tetramethylrhodamine (TMR) dimers as an SP surrogate.

Tetramethylrhodamine.

TMR is commonly used in biochemical studies due to its high absorbance and fluorescence in the visible region. It is often covalently attached using a thiol- or amine-reactive linker group. As in previous studies (15–17), we took advantage of the dimer formation or stacking propensity of TMR. Dimer formation is accompanied by a change in the absorbance and fluorescence properties of the dye, a deviation that can be explained by Kasha’s exciton coupling model (18). Fluorescence is forbidden from this state, and large decreases in fluorescence are consistently observed under conditions that favor dimer formation. A blue shift in the peak absorbance indicates that the xanthene planes housing the electronic transition are oriented parallel to one another. Various studies have demonstrated that the xanthenes of the two TMR molecules are stacked in the dimer (16, 19, 20).

TMR has been used as a spectroscopic probe in other biomolecular experiments due to the spectroscopic difference between the dimeric and monomeric dye species. Here we exploit TMR as both an allosteric probe and an SP surrogate. The fluorophore can be covalently attached to the protein at a cysteine residue using maleimide chemistry. The self-association of TMR is distance dependent, and dimers only form when two labeled residues are in close proximity. To use TMR dimers as an allosteric probe, the residues to which TMR is attached were chosen such that in the T state they are close enough to allow dimer formation and in the R state they are distant enough to prevent dimer formation.

Results and Discussion

TMR₂-DTT as a Model System for Stacked TMR Dimers.

The equilibrium of TMR dimer formation (stacking) can be shifted in favor of dimers by lowering the entropic barrier to self-association. To accomplish this, TMR-maleimide was reacted with dithiothreitol (DTT) (21) to yield TMR₂-DTT to allow for the concentration-independent formation of dimers. The stacking event is largely driven by favorable van der Waals contacts and the entropy gain associated with the expulsion of water.

The TMR dimer and monomer have distinct absorption and fluorescence spectra (Fig. 2). TMR alone has an absorbance spectrum that peaks at 551 nm with an extinction coefficient of ∼75,000 cm⁻¹⋅M⁻¹. A purified sample of TMR₂-DTT has a comparatively strong peak absorbance at 518 nm and a shoulder peak around 551 nm. The dimer sample is also only weakly fluorescent; an equal concentration of monomer is 8–13 times more fluorescent.

Fig. 2.

Comparison of TMR dimers and monomers. The model monomer sample is free TMR-5-maleimide (red), and the model dimer sample is a purified sample of TMR₂-DTT (blue). All measurements are taken at room temperature in 50 mM Tris-HCl, pH 7.5. In A and B, the displayed values are relative to the total amount of dye. (A) Relative molar absorptivity. (B) Relative steady-state fluorescence emission; excitation at 540 nm. (C) Normalized steady-state excitation spectra of the monomer and dimer samples. The dimer is likely non- or weakly fluorescent.

Although the dominant population in a sample of TMR₂-DTT is the stacked form, it consists of molecules in equilibrium between their stacked and nonstacked conformations. Thus, the fluorescence observed from the TMR₂-DTT sample may either be due to the intrinsic fluorescence of the stacked form or to the residual population of nonstacked molecules. Evidence suggesting that the stacked form is nonfluorescent can be found by comparing the monomer and dimer fluorescence excitation spectra. The fluorescence excitation spectrum of purified TMR₂-DTT is identical to the excitation spectrum of the monomer (Fig. 2C), i.e., the absorbance of the peak at 518 nm makes no contribution to the fluorescence of the dimer. The fluorescence of TMR₂-DTT thus reflects the residual population of nonstacked molecules. Because the total concentration of dye molecules in a sample of TMR₂-DTT is known from its absorbance in the presence of SDS, and the size of the nonstacked population is known from the fluorescence, the size of the population in the stacked form, and thus the equilibrium constant for stacking, can be calculated. The equilibrium constant allows us to calculate the free energy of formation of the dimer ΔG_dim. The average free energy of stacking is calculated to be −2.8 ± 0.3 kJ/mol dimer (±SEM). Although the calculated free energy is unique to the TMR₂-DTT system, it can be used as a reference for the formation of TMR dimers in the EL242C-TMR system.

Criteria for Positioning the TMR Probe.

If an enzyme is labeled with TMR such that in one allosteric state, labeled residues are close enough to form dimers and in another state, too far to associate, the dye can be used as a probe to report the allosteric state of the enzyme. Using simple ball and stick structures of TMR, the maximal C_α–C_α distance between residues that allows for the formation of dimers is ∼25 Å. In selecting a suitable residue for the placement of TMR, we used the crystal structure of apo GroEL (PDB 1OEL) (22) and the cryo-EM structure of the ATP bound GroEL (PDB 2C7E) (8). These structures were used to find a residue that (i) met the distance criteria for an allosteric probe, (ii) was near the peptide-binding site defined by the cleft between helices H and I, (iii) was solvent accessible and hence amenable to chemical modification, and (iv) whose mutation would not result in enzyme inactivation. Residue K242, which is located at the N-terminal end of helix H on the apical domain and is solvent accessible, was selected for mutation and labeling with TMR (Fig. 3). In the T state, the C_α–C_α distance between K242 residues in adjacent subunits is 24.5 Å. On ATP binding, this distance increases to 25.4 Å. Mutagenesis was used to create the K242C mutation in the WT GroEL sequence (23). EL242C can be purified using the same protocol as WT GroEL. The location of residue 242 near the SP binding pocket allowed formation of stacked TMR dimers between adjacent subunits in the T allosteric state and their disruption on addition of ATP. Moreover, as homogeneous noncovalent, intersubunit cross-links, the TMR dimers serve as SP surrogates.

Fig. 3.

Image of GroEL heptameric ring in the T (A) and R (B) state. Helices H and I are highlighted in cyan. Residue 242 is highlighted in pink. T state image from PDB 1OEL and R state image from PDB 2C7E.

TMR as an Allosteric Probe.

TMR has been used to report the allosteric state of GroEL. Fig. 4 shows the absorption and fluorescence spectra of a sample of EL242C-TMR with an average of 4.3 dyes per ring. In the absence of ATP, GroEL adopts the T state, and the presence of a strong absorption peak at 518 nm indicates the presence of a population of TMR dimers. In the presence of ATP, the allosteric equilibrium is shifted in favor of the R state. As supported by both absorbance and fluorescence measurements, the allosteric transition increases the C_α–C_α distance between 242C residues in adjacent subunits, leading to the dissociation of the TMR dimers into monomers. In the presence of ATP, the 518-nm dimer peak drops and the 551-nm monomer peak rises. Likewise, addition of ATP is marked by a significant increase in fluorescence. Thus, qualitatively, TMR dimers are a suitable allosteric reporter.

Fig. 4.

TMR dimers as allosteric probes. The absorbance (A) and steady-state fluorescence emission (B) of a sample of EL242C-TMR with 4.3 TMR per ring is examined in the absence (green) and presence (orange) of 500 µM ATP. In the absence of ATP, the enzyme is in the T state, indicated by the population of dimers. On transition to the R state, the dimers dissociate into monomers, causing a change in the peak absorbance and increase in the fluorescence.

To use TMR dimers as quantifiable allosteric probes, we determined the size of the population of the individual dye species in a given sample. To accomplish this, we first demonstrated that, in a sample of EL242C-TMR, there exists only two spectrally distinct species. The two species model implies that, in every sample, the entire population of dye molecules can be classified as either dimers or monomers. Mathematically, this can be stated as the sum of the mole fraction of monomer and dimer, and , respectively, is equal to unity

A previous study has indicated that, in solution, concentration-dependent self-association events proceed beyond dimer formation and higher-order aggregates are formed (24). The presence of higher-order aggregates in the EL242C-TMR system would preclude a simple two-species model.

The validity of the two-species model was tested by analyzing a series of relative absorption spectra (Fig. 5A). If the two-species model is correct, then relative changes in the population of one species will be compensated by an equal and opposite change in the other species. Plotting the relative absorbance of each sample at 518 vs. 551 nm demonstrates a linear relationship (Fig. 5 B and C). Principal component analysis using singular value decomposition was also used to validate the two-species model (SI Materials and Methods). Thus, we conclude the total population of dye molecules on EL-242C can be classified as either monomers or dimers and there are no higher-order aggregates.

Fig. 5.

Two species model and extent of labeling. TMR bound to GroEL can be classified into two spectrally distinct species. The following experiment lends support to the idea that bound dye molecules can only exist as either monomers or dimers; no higher-order aggregates exist. (A) Relative absorbance of various samples of EL242C-TMR, ranging from 0.57 TMR per ring (dark red) to 5.9 TMR per ring (purple). (B) A plot of the absorbance at 551 vs. 518 nm for each curve. (C) The residuals calculated from a linear fit. The straight line indicates that the change in the size of the population of one species is equally and oppositely accounted for by a change in the size of the other population.

It is also important to ensure that the spectral properties of the population of monomers in the T state are equivalent to the population of dissociated dimers in the R state. The addition of ATP to a sample of EL242C-TMR shifts the allosteric equilibrium in favor of the R state, causing the dissociation of dimers and increasing the population of monomers. As time elapses, the ATP is hydrolyzed to ADP, which slowly shifts the allosteric equilibrium in favor of the T state, increasing the population of dimers. Fig. S1 shows the results of this experiment, and the validity of the two-species model. A plot of the absorbance at 551 vs. 518 nm shows a strong linear relationship (R² = 0.9998). For the purposes of subsequent analysis, we will assume the spectral properties of the monomer in the T and R states are equivalent. Principal component analysis using singular value decomposition also lends credibility to the simple two-species model (SI Materials and Methods; see also Fig. S2). Thus, in the T state, dye molecules bound in close proximity spontaneously associate, forming weakly fluorescent dimers, which absorb maximally at 518 nm. The addition of ATP triggers the T to R allosteric transition, causing dissociation of the dimers into monomers, marked by a fluorescence increase and exchange between the 518- and 551-nm absorbance peaks.

Stochastic Binding Model.

Each EL242C heptameric ring contains seven possible TMR binding sites, such that a substochiometric addition of TMR creates an ensemble of different structures. In fact, there are 20 possible distinct orientations of dye molecules on a ring (Fig. 6A). There is evidence that only cysteines at 242 are labeled (SI Materials and Methods; see also Fig. S3). We assume that the labeling process is stochastic: that all binding events are independent and occur with equal probability. This assumption permits the development of the stochastic binding model (Fig. 6B) that describes the distribution of labeling states in any sample from the measured average number of dye molecules per ring, ρ. The distribution of states is described by a binomial distribution (Eqs. 2 and 3). Given the average number of dye molecules per ring, the stochastic binding model gives the fraction of the population containing k dye molecules per ring, where k = 0–7 in integer values. Each of the labeled states corresponding to k dye molecules per ring are equally likely

Fig. 6.

The stochastic binding model. The stochastic binding model allows us to quantify the distribution of labeled states. (A) An illustration of the 20 distinct labeled states in the system. (B) The probability of selecting any one labeled state from the total population is governed by a binomial distribution (Eqs. 2 and 3). Each column of labeled states in A corresponds to one of the eight curves in the binomial distribution. States within a column are all equally likely.

Exclusive Nearest Neighbor Assumption.

The stochastic binding model allows us to convert a single measured value, the average number of dye molecules per ring, to the fraction of the population in each of the 20 distinct labeled states. We further assume that only adjacent subunits are able to form dimers and that, at any given moment, a single TMR can only be associated with one other TMR: the exclusive nearest neighbor assumption. This assumption is justified considering the geometric constraints imposed by the relatively rigid GroEL structure, and the distance constraint of dimer formation. The exclusivity in the assumption is supported by the observation that no higher order aggregates exist in the sample. The nearest neighbor assumption allows us to attach the fractional contribution to the monomer and dimer populations to each of the 20 distinct labeled states (Fig. 7A).

Fig. 7.

Combining the stochastic binding model and the exclusive nearest neighbor assumption. (A) Each of the 20 distinct labeled states can be assigned a fractional contribution to the population of monomers (red) and dimers (blue). These weights are collected into the matrix . (B) The matrix product yields two equations, the mole fraction of monomers (red) and the mole fraction of dimers (blue), as a function of TMR per ring, .

Mathematically, the fractional contribution of the two species is accounted for in the matrix . The first and second rows in 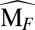correspond to the fractional contribution to the monomer and dimer population, respectively. Taking the two assumptions together, one can predict the mole fraction of the population in the dimer, , and monomer form, , given an average number of dye molecules per ring, (Eq. 4; Fig. 7B)

The proposed model predicts the change in the mole fraction of monomers and dimers with the extent of labeling (Eq. 4). To test this model, we exploited the linear relationship between the mole fraction of dimer and the relative absorbance of the sample, found by combining the two species model (Eq. 1) with Beer’s law for two species (Eq. 5) to yield Eq. 6

The plot of the calculated mole fraction of dimer against the observed absorbance at 518 and 551 nm was linear (Fig. 8A). However, the nonrandom nature of the residuals points to a small source of error of unknown origin (Fig. 8B). This error can be explained by invoking positive cooperativity in the labeling process; i.e., a dye molecule has a slight preference to react with a vacant subunit that is adjacent to an already labeled subunit as opposed to reacting in a strictly stochastic manner.

Fig. 8.

Testing the stochastic binding model and the exclusive nearest neighbor assumption in the EL242C-TMR system. (A) Testing the model by exploiting the linear relationship (Eq. 6) between the predicted mole fraction of dimer, , and the relative absorbance (Fig. 5) of a samples of EL242C-TMR at 518 (blue) and 551 nm (red). (B) The fit is relatively good, R² > 0.98, but the residuals are not randomly distributed.

TMR as an SP Surrogate.

SP binds to the T state of GroEL and stimulates its ATPase by placing a load on the apical domains of the ring. The bound SP serves as a noncovalent tether between two adjacent subunits. This stabilizes the T state, which has weak affinity for nucleotide, accelerating the rate of product release, and increasing the rate of ATP consumption (10, 11). Likewise, the apical domains of the EL242C-TMR are tethered by the noncovalent stacking of the dye molecules. Similarly, an increase in the steady-state turnover rate is observed with increasing number of dimers per ring (Fig. 9A). This results supports the assertion that TMR dimers behave as surrogates for SP in the chaperonin cycle. The stimulation is due to the cross-linking effect of TMR dimers and not merely to the presence of a hydrophobic fluorophore close the SP binding site. To address this, EL242C was labeled with fluoresceine-5-maleimide (F5M), a compound structurally similar to TMR. However, it neither forms dimers nor stimulates ATPase activity (Fig. 9B). The TMR dimers are thus behaving as molecular latches, perturbing the allosteric equilibrium to favor the T state.

Fig. 9.

ATPase activity of dye-labeled EL242C in 1 mM ATP. (A) Turnovers per minute plotted against TMR per ring at 10 mM K⁺ (blue) and 100 mM K⁺ (red). The ATPase activity of GroEL increases as the mole fraction of dimers increases. (B) Turnovers per minute plotted against dyes per ring for EL242C labeled with TMR (pink) and F5M (yellow) in the presence of 100 mM K⁺. The increase in the turnover rate is not due to the mere presence of fluorophore, as indicated by the lack of ATPase stimulation observed in samples of EL242C-F5M.

In addition to being an allosteric probe, TMR dimers act as an SP surrogate because they serve as noncovalent cross-links, between subunits within a ring, that place a load on the apical domains in the same way as SP. TMR serves as an ideal SP surrogate because it circumvents the problems of heterogeneity inherent in the SP binding problem (Fig. 1). As opposed to SP, TMR is a small molecule that covalently binds to a single position near the SP binding site. In demonstrating the use of TMR as an allosteric probe, we showed that the topological arrangement is readily predictable using the stochastic binding model. The proportion of the bound TMR that is in the dimeric state can be computed with the exclusive nearest neighbor assumption. Finally, each noncovalent dimeric stacking bond is of identical strength. Because the T to R transition is concerted among the subunits within a ring, the energetic contribution to the stabilization of the T state is a simple sum of the number of dimers per ring. A ring can contain from zero to three dimers, and thus by increasing the number of dimers per ring, we can vary the cross-linking stabilization energy that shifts the allosteric equilibrium.

Expanded Nested Cooperativity Model of GroEL.

The negative and positive cooperativity displayed by GroEL during nucleotide binding requires a hybrid MWC/KNF type allosteric model known as the nested cooperativity model (NCM). As originally formulated (25, 26), the NCM contained a simplifying assumption that ATP bound exclusively to the R state. Subsequent work, however, showed that the T state could also bind and hydrolyze ATP (10, 26). An expanded version of the NCM, without the exclusive binding assumption was developed by Gresham (27) and was used to quantitatively analyze the turnover rate of GroEL (Eq. 7). The original formulation can be recovered from the expanded form by setting c equal to zero. It contains seven independent parameters that are to be fit for a given set of conditions. At its core, the NCM is an allosteric partition function of GroEL that accounts for the positive intraring cooperativity and negative interring cooperativity. The equation gives the fraction of the population with ATP bound, in each of the three allosteric states, as a function of ATP concentration. In its expanded form, this fraction is multiplied by the allosteric state’s V_max, and the sum of these three terms gives the steady-state turnover rate. Two other parameters include the dissociation constants, k_T and k_R, of ATP from a T ring and an R ring, respectively. The two terms appear in the NCM as and . Last, the NCM contains two allosteric equilibrium terms, L₁ for the TT to TR transition and L₂ for the TR to RR transition

In our analysis, the NCM (Eq. 7) is modified to predict the distribution of allosteric states as a function of ATP concentration. Doing so decreases the number of independent parameters, replacing the three V_max terms in the expanded derivation, with a single proportionality constant, A. This constant converts the instrument’s arbitrary fluorescence readout value to the fluorescence increase observed from the dissociation of a dimer, on transition of a ring to the R state. Given a single GroEL 14mer with m TMR dimers on one ring and n TMR dimers on the other, there will be a fluorescence increase proportional to m on the TT to TR and an increase proportional to n on the TR to RR transition. The modified NCM (Eq. 8) predicts the observed fluorescence increase in a labeled species with m dimers on the first ring and n on the second

As pointed out above, each sample consists of an ensemble of labeled states. The stochastic binding model and the exclusive nearest neighbor assumption were used to calculate the size of each labeled state, in a given sample, as a function of the average number of dye molecules per ring. Each state can be binned corresponding to the number of dimers it contains (Fig. 10A). Mathematically, this function is performed by the matrix . The matrix product of and (Eq. 3) produces four functions, , where m is an integer between 0 and 3 (Fig. 10B; Eq. 9). These functions give the size of the population of the four cross-linked states (m = 0–3 per ring) as a function of the average number of dye molecules per ring

It is known that SP places a load on the apical domains of a ring and that the presence of SP leads to a stimulation in ATPase activity. To arrive at a quantitative impact of SP on the chaperonin cycle, we view the load that SP places on the ring to result in the stabilization of the T state and thus an increase in the free energy of the T to R allosteric transition (Fig. 11A). Likewise, the cross-linking effect of the stacking interaction in TMR dimers stabilizes the T state of GroEL. The advantage of the TMR dimer is that it is of uniform energetic value and likely to be of a comparable magnitude to the TMR₂-DTT stacking free energy: −2.7 ± 0.3 kJ/mol dimer. Furthermore, a ring can have from zero to three TMR dimers. Because of the concerted nature of the allosteric transitions exhibited by GroEL, the energetic contribution of the stacked dye molecules to the stabilization of the T state can be assumed to be additive across a ring. The stabilization of an allosteric state quantitatively enters into the NCM as a modification to the allosteric equilibrium terms L₁ and L₂ (Fig. 11B). The end result is a modified form of the NCM that predicts the biphasic fluorescence increase observed for a given labeled state, taking into account the perturbation placed on the allosteric equilibrium by the presence of the dimers (Eq. 10)

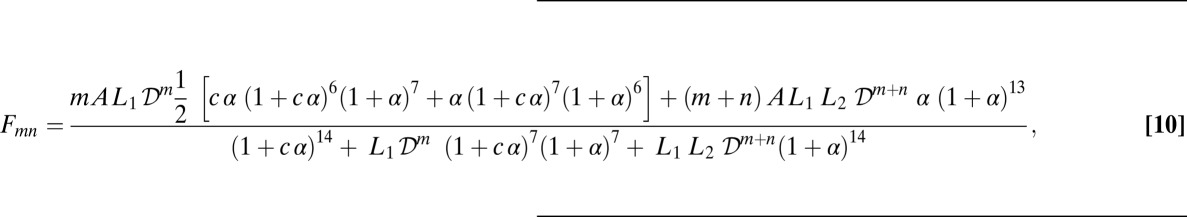Combining the modified NCM in Eq. 10 with the statistical distribution of cross-linked states (Eq. 9) yields an equation that predicts the fluorescence increase associated with the allosteric transitions in a sample with a known average number of dye molecules per ring, as a function of ATP concentration (Eq. 11). The solution to Eq. 11 depends on the value of the various independent parameters in the equation: A, c, k_R, L₁, L₂, and, D. The large number of parameters gives the equation a great deal of flexibility when being fit to a particular data set. However, we have collected data sets for multiple samples, with varying numbers of average dye molecules per ring. These data sets were fit globally with Eq. 11 (Fig. 12). Varying any one parameter will change the fit for all data sets, allowing for increased confidence in the fitted values.

Fig. 10.

Distribution of cross-linked states. (A) Illustration of how the 20 distinct labeled states can be assigned to one of the four cross-linked states: 0 dimers per ring (green), 1 dimer per ring (blue), 2 dimers per ring (red), and 3 dimers per ring (purple). These weights are collected in the matrix . (B) The matrix product yields four equations, where m is an integer between 0 and 3 that corresponds to the size of the population of heptameric rings with m dimers.

Fig. 11.

Quantifying the effect of SP on the allosteric equilibrium. (A) A free energy diagram of GroEL’s first allosteric transition: TT to TR. The diagram indicates how the presence of a TMR dimer on a ring stabilizes the T state and increases the free energy gap between the TT and TR states. Because the allosteric transition is concerted, the effect of multiple dimers is additive. (B) Mathematically, this interpretation leads us to quantitatively account for the presence of TMR as a perturbation to the allosteric equilibrium.

Fig. 12.

Fluorescence increase vs. [ATP]. The fluorescence increase observed in the presence of various concentrations of ATP is plotted for samples of EL242C-TMR with an average of 1.8 (red), 2.8 (orange), 3.8 (green), 4.7 (blue), and 5.6 (purple) TMR per ring. (A) [ATP] range from 0 to 100 µM. (B) [ATP] range from 0 to 1 mM. Two of the data sets, 1.8 and 5.6 TMR per ring, were collected over an [ATP] range of 0–100 µM and the remaining three sets over an [ATP] range of 0–1 mM. Solid lines are the results of the global fit of the data sets to the expanded NCM (Eq. 11).

The results of the global fit to Eq. 11 are summarized in Tables 1 and 2. The indicated range of each parameter falls within the 95% CI of the fit. The free energy of the TT to TR and TR to RR transitions were found to be 27 ± 11 and 46 ± 2 kJ/mol, respectively. TMR dimers acting as an SP surrogate increase this free energy gap by 2.6 ± 1.0 kJ/mol dimer, a value that is similar to that for the dissociation of TMR₂-DTT. These experiments demonstrate that the GroEL nano-machine is able to perform work and overcome a load of at least 7.8 kJ/mol ring. This result supports the idea of GroEL function that relies on forced unfolding of bound substrate protein to free it from a kinetic folding trap, affording it another opportunity to reach its native state.

Table 1.

Results of the global fit of the expanded NCM (Eq. 11) to the fluorescence vs. [ATP] data

Parameter	Value
A	0.98 ± 0.10
kR (μM)	0.9 ± 0.3
c	0.042 ± 0.008
ΔGL1 (kJ/mol)	26 ± 11
ΔGL2 (kJ/mol)	46 ± 2
ΔGD (kJ/mol)	2.6 ± 1.0

See text for explanation of fitted parameters. The range of each parameter that falls within the 95% CI of the global fit is given.

Table 2.

R² value of each curve in the global fit of fluorescence vs. [ATP] data to the expanded NCM (Eq. 11)

TMR/ring	R2 value
1.79	0.9115
2.78	0.9776
3.78	0.9909
4.68	0.9828
5.49	0.9966

Concluding Remarks

TMR as an Allosteric Probe for GroEL.

TMR, covalently bound near the SP binding site of GroEL’s subunits, forms populations of monomers and dimers depending on nearest neighbor occupancy. Combining the stochastic binding model and the exclusive nearest neighbor assumptions allows us to predict the distribution of labeled states from the average number of TMR molecules per ring. Introducing ATP induces an allosteric conformational change that causes dimers to dissociate into monomers. Because the monomers and dimers have different spectroscopic signatures, the transition can be monitored using either absorbance or fluorescence spectroscopy. The change in the observed fluorescence or absorbance, on the addition of ATP, can be directly correlated with a change in the population of the T and R allosteric states, providing a quantitative measure of the allosteric activity.

TMR Dimers as Surrogates for SP.

In the T state, TMR-labeled 242C residues are close enough to self-associate into dimers. These dimers act as noncovalent intraring, intersubunit cross-links that place a load on the apical domain, mimicking the effects of the cross-linking force provided by SP. Consequently, SP and the TMR dimers stimulate the ATPase activity of GroEL by stabilizing the T state with this cross-linking force. However, TMR dimers avoid the problems associated with the heterogeneous nature of SP binding to GroEL. The predictable distribution of dimers and the uniformity of the cross-linking force make TMR dimers a suitable surrogate for quantifying the role of SP in the catalytic cycle of GroEL.

The cross-linking force of the dimer increases the free energy gap in the T to R allosteric transition by an amount equal to the free energy of dimer formation. The effect of this stabilization can be factored into the NCM as a modification to the allosteric equilibrium terms L₁ and L₂. The NCM can also be modified for use as an allosteric partition function to predict fluorescence increases that correlate with allosteric population changes instead of turnover rates. When the modified NCM is paired with the predicted distribution of labeled states, the parameters in the equation can be globally fit to a series of data sets allowing for increased confidence in the fitted parameters.

The proposed model highlights the importance of the SP cross-linking energy within the allosteric cycling of GroEL. The load placed on the apical domain stabilizes the T state, increasing the free energy gap and shifting the allosteric equilibrium in favor of the T state. Because of negative cooperativity, this effect is more significant for the TR to RR transition than the TT to TR transition. The model also supports the iterative annealing model of GroEL function. GroEL performed work on the TMR dimers, overcoming the free energy of dimer formation while transitioning from the T to R state. Likewise, the iterative annealing model suggests that GroEL can perform work on SPs by forcibly unfolding the bound SP on its release into the central cavity, rescuing it from its kinetic folding trap and affording it another opportunity to reach its native state.

Materials and Methods

Additional information on instrumentation, synthesis and purification of TMR₂-DTT, labeling GroEL K242C, and fluorescence vs. [ATP] is provided in SI Materials and Methods.

Construction of GroEL K242C.

The mutant K242C was prepared as described in ref. 23 and in SI Materials and Methods. We inserted the K242C mutation into a WT background rather than into a cysteine-free background because cysteine-free GroEL is much less stable than the WT.

Purification of GroEL.

WT GroEL and the mutant GroEL K242C, free of tryptophan-containing contaminants, were purified as previously described (11). Typically, GroEL preparations contained <0.2 mol of contaminating SP/GroEL14; i.e., <10% of the rings may be contaminated with an ensemble of SPs. The concentration of purified EL242C was calculated by measuring the absorbance at 280 nm and using the extinction coefficient of 9,600 cm^-1⋅M⁻¹.

Steady-State ATP Hydrolysis.

The steady-state hydrolysis of ATP was measured at 37 °C as previously described (10).

Data Analysis.

Data from all instruments was saved in ASCII format and imported into Microsoft Excel 2010. All data analysis, except singular value decomposition (SI Materials and Methods) was performed in Excel. Globally fitting the fluorescence vs. [ATP] experimental data to Eq. 11 was performed by nonlinear least-squares analysis. The least-squares value for each curve was summed and minimized using Excel solver. The 95% CI of the fit was taken to be ±1.65 SDs from the mean of the residuals. Error in fitted parameters was calculated as the largest deviation from the fitted least-squares value that falls within the 95% CI. R² values for each curve were calculated as detailed in DeVore (28). Singular value decomposition, performed in MATLAB, was used in a principle component analysis of the spectra of EL242C-TMR in support of the two-species model. More than 98% of the variance was accounted by this model (29).