Retinal layer segmentation of macular OCT images using boundary classification

Abstract

Optical coherence tomography (OCT) has proven to be an essential imaging modality for ophthalmology and is proving to be very important in neurology. OCT enables high resolution imaging of the retina, both at the optic nerve head and the macula. Macular retinal layer thicknesses provide useful diagnostic information and have been shown to correlate well with measures of disease severity in several diseases. Since manual segmentation of these layers is time consuming and prone to bias, automatic segmentation methods are critical for full utilization of this technology. In this work, we build a random forest classifier to segment eight retinal layers in macular cube images acquired by OCT. The random forest classifier learns the boundary pixels between layers, producing an accurate probability map for each boundary, which is then processed to finalize the boundaries. Using this algorithm, we can accurately segment the entire retina contained in the macular cube to an accuracy of at least 4.3 microns for any of the nine boundaries. Experiments were carried out on both healthy and multiple sclerosis subjects, with no difference in the accuracy of our algorithm found between the groups.

1. Introduction

Optical coherence tomography (OCT) captures three-dimensional (3D) images at micrometer (μm) resolutions based on the optical scattering properties of near infrared light in biological tissues. The high resolution capability together with other properties such as ease of use, lack of ionizing radiation, patient comfort, and low cost have made OCT extremely popular for imaging retinal cell layers in the macular cube in both ophthalmology [1] and neurology [2]. For example, patients have quantitative abnormalities of different retinal layers in multiple sclerosis (MS) [3–5], type 1 diabetes [6], Alzheimer’s disease [7], Parkinson’s disease [8], and glaucoma [9]. To better understand the effects of these and other diseases on specific types of cells within the retina, it is necessary to accurately segment the different tissue layers that appear in retinal OCT images. Since large numbers of these images can be acquired in a single patient (especially if collected over time) and also within clinical and normal populations, it is necessary that such segmentation be automated.

Automated segmentation of the cellular boundaries in OCT images has been explored extensively [10–19]. The focus of most automated approaches has been the approximation of nine boundaries, partitioning an OCT image into ten regions. Traversing from within the eye outwards, these regions are: 1) vitreous humor, 2) retinal nerve fiber layer (RNFL), 3) ganglion cell layer and inner plexiform layer (GCL+IPL), 4) inner nuclear layer (INL), 5) outer plexiform layer (OPL), 6) outer nuclear layer (ONL), 7) inner segment (IS), 8) outer segment (OS), 9) retinal pigment epithelium (RPE) complex, and 10) choroid areas. We note that within some boundaries exist extracellular membranes. Specifically, boundaries associated with the vitreous humor to RNFL, the ONL to IS, and the RPE to choroid contain the inner limiting membrane (ILM), the external limiting membrane (ELM), and Bruch’s membrane (BrM), respectively. Figure 1 shows a zoomed portion of a typical OCT image, with indications to denote the various layers. As the boundary between the GCL and IPL is often indistinguishable in typical OCT images, in this study we group these layers together as one layer (GCIP). We also note that our segmentation of the RPE represents what might be better thought of as the RPE complex as it goes into the OS through the Verhoeff membrane. We have chosen this definition, although there is some debate about the distinguishing line between these regions [20].

Fig. 1.

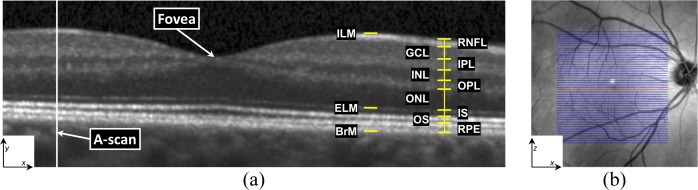
(a) A typical retinal OCT image (B-scan) enlarged with the layers labeled on the right-hand side. Every B-scan consists of a set of vertical scan lines (A-scans). The fovea is characterized by a depression in the surface of the retina where the top five (inner) layers are absent. (b) A fundus image with lines overlaid representing the locations of every B-scan within a volume. The red line corresponds to the B-scan in (a).

Previous work on retinal layer segmentation has used a variety of methods in exploring retinal OCT data including analysis of intensity variation and adaptive thresholding [11], intensity-based Markov boundary models [10], and texture and shape analysis [21]. The more recent works have had at their core more complex imaging segmentation tools. In particular, graph theoretic based approaches have been increasingly used with the work of Chiu et al. [15] using a dynamic programming version of the classic shortest path algorithm, with similarities to Yang et al. [14]. The simultaneous multi-surface segmentation by the graph cuts approach of Garvin et al. [13, 22], with its extensions incorporating texture based features [18] and soft constraints [19], are more examples of the many graph-based segmentation methods reported in the literature. Others have used active contour segmentation models [12, 16]. Concurrent to these works has been the development of machine learning approaches, including support vector machines (SVM) [17] with features based on image intensities and gradients.

We propose an algorithm for retinal segmentation that uses a pair of state-of-the-art segmentation tools. In the first step, we estimate the positions of retinal layer boundaries using a random forest (RF) classifier [23]. Using such a classifier has many advantages, including the ability of a single classifier to estimate all of the boundaries, as opposed to using a single classifier per boundary that is seen in other work [17]. A more subtle advantage of this approach is its ability to generate probability maps for the boundaries, providing a “soft” classification of their positions. The second step of our algorithm uses these probability maps as input to a boundary identification algorithm, which finds contours that separate the retinal layers in each OCT image. Two approaches are explored for generating the final boundaries from the RF outputs: a simple boundary tracking approach and a more complex graph based approach.

The paper is organized as follows. Section 2 explains our method thoroughly including preprocessing steps. Section 3 describes the experiments and results including a comparison to a human rater on 35 data sets, and Section 4 has a discussion of the results, including their relation to other work and potential future impact. We note that part of this work originally appeared in conference form in Lang et al. [24]. The present paper is a major improvement over that work including many technical improvements and a more complete validation.

2. Methods

To introduce the problem of retinal segmentation, we first review some key terminology. In 3D, OCT volumes comprise multiple cross-sectional images, or B-scans (see Fig. 1). Every B-scan consists of a series of scan-lines, or A-scans, which are in the direction of the light propagation into the tissue of interest. The inter-B-scan distance is often greater than the in-plane resolution, but this can vary by manufacturer and scanner settings. A coordinate system consisting of x, y, and z axes is created from the lateral, axial, and through-plane directions.

Our algorithm is depicted in Fig. 2 and can be described in three steps. The first step (Section 2.1) consists of preprocessing the data using intensity and spatial normalization. In the second step (Section 2.2), a set of 27 features are calculated on the preprocessed data and input into a trained RF classifier to produce boundary probabilities at every pixel. The classifier is trained from ground truth labels created by a human rater. In the last step (Section 2.3), the final retina segmentations are generated from the boundary probabilities using a boundary refinement algorithm. We explore the use of two such algorithms, a simple boundary tracking method and a multi-surface graph based method.

Fig. 2.

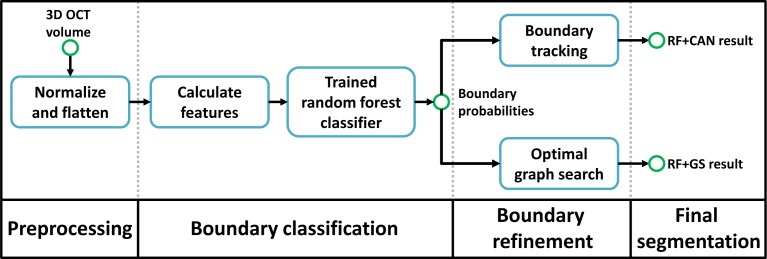
Flowchart of our algorithm. The RF+CAN result refers to the segmentation using the random forest (RF) boundary classification output with a Canny-inspired boundary tracking algorithm, while RF+GS refers to the result of using the RF output with an optimal graph search (GS) algorithm.

2.1. Preprocessing

As with many segmentation algorithms, several preprocessing steps are used to transform the data into a common space; this involves intensity normalization and a simple spatial alignment of the data called retinal boundary flattening.

2.1.1. Intensity normalization

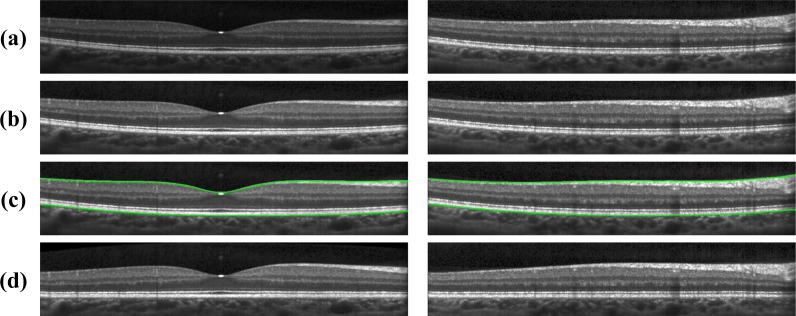
For any segmentation algorithm, it is important that the intensity ranges of the data are consistent. That is, the intensity values observed in a particular tissue type should be approximately the same within an image and across populations of images. Such consistency allows for better training in machine learning paradigms on features such as intensity and gradient profiles for each layer and boundary. The data used in our experiments showed considerable inconsistency, with two B-scans in the same volume often having very different intensity ranges, as exemplified in Fig. 3(a) where the left and right images are different B-scans from the same volume. Two possible causes of these differences are (1) automatic intensity rescaling performed by the scanner being adversely affected by high intensity reflection artifacts and (2) the automatic real-time averaging performed by the scanner, meaning one B-scan could undergo more averaging, causing differences in its dynamic range. These issues are scanner dependent and may not affect other scanners in the same way as in our experiments.

Fig. 3.

Row-wise: Shows two B-scans from within the same volume (a) with the original intensities, (b) after intensity normalization, (c) with the detected retinal boundary, and (d) after flattening.

To address the intensity inconsistency issue, we carry out a contrast rescaling on each B-scan. Specifically, intensity values in the range [0, I_m] are linearly rescaled to [0, 1] while intensities larger than I_m are set to unity. The value I_m is interpreted as a robust maximum of the data, which is found by first median filtering each individual A-scan within the same B-scan using a kernel size of 15 pixels (58 μm). Then, I_m is set to the value that is 5% larger than the maximum intensity of the entire median-filtered image. This rescaling removes hyperintense reflections found at the surface of the retina while maintaining the overall intensity values in the B-scan. A result of this normalization step is shown in Fig 3(b).

2.1.2. Retinal boundary detection and flattening

The second step in preprocessing is to estimate the retinal boundaries and flatten the image to the bottom boundary of the retina. This serves to give more meaning to the spatial coordinates of pixels for use in our random forest classifier, to help to constrain the search area for the final segmentation, and to reduce the algorithm sensitivity to retinal curvature and orientation. The top and bottom boundaries of the retina are defined as the ILM and the BrM, respectively. Flattening is a common preprocessing step performed by many retina segmentation algorithms [13, 15, 25] and refers to translating all of the A-scans in each B-scan such that a chosen boundary in the image is flat. We choose to flatten the retina to the BrM boundary. We note that these initial boundary estimates are improved in our segmentation algorithm, but flattening is only carried out at the beginning using these initial estimates.

To find the top and bottom boundaries of the retina, our algorithm starts by applying a Gaussian smoothing filter (σ = 3 pixels isotropic or σ_(x,y) = (17, 12) μm) on each B-scan separately. Then it computes an image derivative of each A-scan (i.e., the vertical gradient) using a Sobel kernel [26]. Looking along each A-scan, we find an initial estimate of either the ILM or the ISOS boundary from the two pixels with the largest positive gradient values more than 25 pixels (97 μm) apart, since both of these boundaries have a similar gradient profile. To find an estimate of the BrM, we take the pixel with the largest negative gradient below that of the IS-OS, but no more than 30 pixels (116 μm) from it. These two collections of largest positive and negative gradients are taken to be the ILM and BrM, respectively. Of course, using only the maximum gradient values leads to spurious points along each surface. Correction of these errors is accomplished by comparing the estimated boundaries to the boundary given by median filtering the two collections. The algorithm replaces outlying points using an interpolation scheme [27], with outlying points defined as those more than 15 pixels (58 μm) from the median filtered surfaces. The final retina boundary surfaces are then found after applying Gaussian smoothing to the position values of each surface (σ_(x,z) = (10, 0.75) pixels or (56, 91) μm for the ILM and σ_(x,z) = (20, 2) pixels or (111, 244) μm for the BrM). This final smoothing step acts to smooth out smaller outlying boundary points, often caused by variations in the choroid intensity. Examples of the detected boundaries and the finally flattened image are shown in Figs. 3(c) and 3(d), respectively.

2.2. Boundary classification

We find the retinal layers in an OCT B-mode image using a supervised classifier that is trained from manual delineations to find the boundaries between layers. Focusing on identifying the one pixel wide boundaries between layers rather than directly finding the layers themselves is different than previous work [17]. Since pixels found in between boundaries are more difficult to classify due to a weaker feature response, we believe that our approach takes better advantage of the distinctive features that exist on and near boundaries and also permits better control of layer ordering. Also note, we will be converting these boundaries to layer segmentations by assigning each boundary pixel to the layer above it. Therefore, the boundaries are not truely one pixel wide, but only exist at the boundary between layers.

There are many algorithms that might be used for supervised classification [28], including SVMs [29], RFs [23], and boosting [30]. We have chosen to use a RF classifier because it has a small number of parameters to tune, it can accurately learn complex nonlinear relationships, its performance is comparable or better than other state-of-the-art classifiers, it can handle multi-label problems, it is computationally efficient, and it generates a probability for each label. This last benefit acts to provide a soft classification, which is particularly helpful since hard classification of a one pixel wide boundary suffers dramatically from both false positives and false negatives. In summary, the RF works by constructing multiple decision (or classification) trees, with each tree providing a separate classification for an input feature vector. Each tree can potentially provide a different classification since the training process is randomized between trees. The output across all trees can then be aggregated to provide a probability of belonging to each class.

We train the RF classifier using 27 features (defined below) calculated at each pixel. During training, the classifier uses ground truth labels—created by a human rater—to learn the relationship between the high-dimensional feature space and the boundary labels. Once trained, the classifier will be applied to unlabeled data sets by computing these features and inputting them into the classifier to retrieve a set of boundary probabilities at each pixel (see Fig. 2).

2.2.1. Features

We used 27 features as inputs to our RF classifier. The first three features give spatial awareness, while the remaining are local, context-aware features. The first spatial feature is the relative distance of each pixel (along the A-scan) between the retinal boundaries computed in Section 2.1.2 (see Fig. 4(a)). The second and third features are the signed distance to the center of the fovea in the x and z directions, respectively, with the center of the fovea being taken as the thinnest position between the retinal boundaries near the center of the volume. Together, these three features help to localize retinal pixels within a generic retina using a coordinate system that is defined by the geometry of the subject-specific retina.

Fig. 4.

Example images of the different types of features used by the classifier: (a) the relative distance between the bottom and top boundary with contour lines overlaid, (b) the average gradient in a neighborhood below each pixel, and anisotropic Gaussian (c) first and (d) second derivatives oriented at −10 (top), 0 (center), and 10 (bottom) degrees from the horizontal.

The first set of context-aware features we use are the intensity values of the nine pixels in a 3 × 3 neighborhood around each pixel. Together, these nine values allow the classifier to learn local relationships between neighboring points without explicitly calculating any new features. It has previously been shown to be an effective feature when compared to other sets of filter banks [31].

Although the 3 × 3 neighborhood pixels are useful local features, larger neighborhoods can also provide helpful information. Therefore, we supplement these features with an added filter bank of vertical first and second derivatives taken after oriented anisotropic Gaussian smoothing at different orientations and scales [32] (see Figs. 4(c) and 4(d)). A similar type of filter bank has been used in the texture classification literature [33]. Twelve features per pixel are generated by using the signed value of the first and magnitude of the second derivatives on six images corresponding to two scales and three orientations. The two scales for Gaussian smoothing are σ_(x,y) = (5, 1) pixels ((30, 4)μm) and σ_(x,y) = (10, 2) pixels ((61, 8)μm) at an orientation of 0 degrees. These kernels are then rotated by −10 and 10 degrees from the horizontal (−6.4 and 6.4 degrees when scaled to μm) for oriented filtering [32]. Since the data were previously flattened, these three orientations are sufficient for learning the central foveal shape. The final context-aware features are the average vertical gradients in an 11 × 11 neighborhood located at 15, 25, and 35 pixels (58, 97, and 136 μm) below the current pixel, calculated using a Sobel kernel on the unsmoothed data (see Fig. 4(b)). These features help to determine whether or not other boundaries exist in the areas below the current pixel. For example, the OPL-ONL and IPL-INL boundaries can be differentiated since the IPL-INL has the positive gradient of the INL-OPL below it, while the OPL-ONL boundary does not have a similar response below it.

2.2.2. Random forest classifier and training

The RF classifier works by building an ensemble of N_t decision trees, {h_i(x), i = 1,...,N_t} [23]. Here, x is a X-dimensional feature vector, where X = 27 in our case. Each of the decision trees are grown until no additional splits can be made, and at each node the decision for how to split the data is based on only N_n randomly selected features. Given a data vector x, every tree provides a label estimate, ŷ_i = h_i(x) ∈ Y, where Y is the set of all possible labels. By looking at the predicted label for each tree, a posterior probability for each class can be calculated as $p\left(y=k|\mathbf{x}\right)=\frac{1}{N_t}{\sum }_{i=1}^{N_t}{\mathbf{I}}_k\left({\widehat{y}}_i\right)$, where I_k(·) is an indicator function for class k[34]. In many classification approaches, a final label estimate is taken as the label voted by the relative majority of the trees, ŷ = argmax_y p(y|x). Selecting retinal boundaries in this manner will not produce very good estimates, however, since both false positives and false negatives will ruin the desired property that the boundaries are just one pixel thick. Therefore, the posterior probabilities are further processed to generate a final segmentation, as described in Section 2.3.

It is important to carefully choose the data that are used to train a RF classifier. Our full data set comprises 3D OCT volumes and manual delineations from 35 subjects. Each volume contains 49 B-scans, and 3–8 of these are foveal B-scans, meaning that they include part of the foveal depression. Training the classifier with all of these data would take too much time, but because there is significant similarity across the volumes, it should be sufficient to use a subset of these data for training. We explore this experimentally below (Section 3.2) by optimizing over two training parameters: N_s, which is the number of subjects to use for training, and N_b, which is the number of B-scans to include per subject. To balance the training process, we use an equal number (N_b/2) of foveal and non-foveal B-scans, all randomly selected from within each respective collection. For a given B-scan, we use all of the segmented boundary points for training—1024 points for each of the nine boundaries (since there are 1024 A-scans per B-scan in our data). Since the number of background pixels greatly outnumbers the boundary points, we balanced these training data by randomly choosing 1024 background pixels for training from each of the layers between boundaries and from the regions above and below the retina.

2.3. Boundary refinement

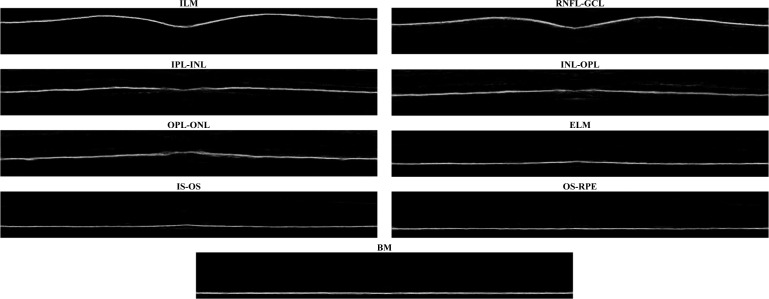
The output of the RF classifier is a set of boundary probabilities, as shown in Fig. 5. Although the boundaries are quite well-defined visually, the automatic identification of a set of one-pixel thick, properly-ordered boundaries is still challenging due to boundaries that have dropouts or are spread out vertically. We implemented and evaluated two methods to generate boundary curves from the boundary probabilities to compare the necessary complexity required to compute the final boundaries. The first, more simple method follows the spirit of the Canny edge detector [35] and is referred to as RF+CAN. The second, current state-of-the-art method uses an optimal graph-based search algorithm [36] and is referred to as RF+GS. The RF+CAN method can be classified as a 2D algorithm, operating on each B-scan independently, while RF+GS operates on the entire 3D volume. We note that the graph search optimization approach has been used previously in OCT [13, 18, 19, 22] though not with the costs we define. Also, we only use the basic algorithm in [36] and do not incorporate the spatially-varying smoothness, regional costs, and soft constraints that are used in more recent works. Our two approaches are described next.

Fig. 5.

An example of the probabilities for each boundary generated as the output of the random forest classifier. The probabilities are shown for each boundary, starting from the top of the retina to the bottom, going across each row.

RF+CAN approach

The RF+CAN approach uses the non-maximal suppression and hysteresis thresholding steps that are found in Canny’s seminal work on edge detection [35]. While Canny’s work found edges by looking for image gradient peaks, our algorithm finds boundaries by looking for peaks in the probability images. Given a boundary probability map, we apply the following steps to find the final boundary:

1. Two-dimensional Gaussian smoothing with σ = 2 pixels isotropic σ_(x,y) = (12, 8)μm

2. One-dimensional non-maximal suppression on each A-scan;

3. Hysteresis thresholding; and

4. Boundary tracking from left to right.

Gaussian filtering smooths out abrupt jumps within the data, thereby helping to reduce spurious results in the following steps. Non-maximal suppression [26] examines all three-pixel windows on each A-scan and zeros out the probabilities at the center pixel that are not maximal in the window. Remaining points are considered to be strong boundary points if their probabilities exceed 0.5 and weak boundary points if their probabilities are between 0.1 and 0.5. All other points are removed from consideration. Hysteresis thresholding [26] is applied next in order to remove all weak boundary points that are not connected to strong boundary points. All remaining points are considered to be highly likely to belong to the the final boundary.

Given the collection of putative boundary points determined in the first three steps, the fourth step defines the RF+CAN boundary by connecting boundary points across the entire B-scan image. First, the boundary point having the largest probability in the leftmost A-scan (which is by definition the one that is farthest away from the optic nerve, assuming a right eye) is identified. The boundary continues its path to the right by following the maximum point within three pixels above and below in the next A-scan. If there exists a second largest non-zero intensity pixel within the A-scan search window (taking note that the majority of the values are zero due to the non-maximal supression step), we also keep track of potential paths following from this point. In this way, if the main (primary) path has no points to move to, we check to see if any alternative (secondary) paths continue beyond where the primary path stops. If these secondary paths do continue beyond the primary path, it is now considered the primary path for tracking the boundary and we continue to track it accordingly. If there are no better secondary paths, we continue the boundary straight across. Therefore, in the absence of boundary evidence, this strategy favors flat boundaries, which is consistent with our initial flattening step.

This four-step process is repeated for each boundary, starting by finding the ILM and RNFLGCL interfaces in a top to bottom order, and then finding the BrM through IPL-INL boundaries in a bottom-to-top order. To resolve any discrepancies in layer ordering, during the boundary tracking step we simply move any conflicting points one pixel away from the previously estimated boundary points. The direction of movement is down for the RNFL-GCL boundary and up for all other layers. (We find that there is never a discrepancy between the RNFL-GCL and IPL-INL boundaries where the two boundary detection processes meet.)

RF+GS approach

The RF+GS approach defines a cost based on the estimated boundary probabilities in all B-scan images and finds the collection of boundary surfaces having the correct ordering and minimum cost over the whole 3D volume. A graph-theoretic algorithm to find an optimal collection of layered structures was presented in [36], and we follow this approach here. Accordingly, the RF+GS algorithm constructs graphs for each retinal surface boundary and then connects the graphs together such that inter-surface relationships are preserved. Multiple constraints are used to limit both the intra-surface distances between adjacent pixels in each direction (Δ_x and Δ_z, for the x and z directions, respectively) and the inter-surface distances (δ^l and δ^u, representing the minimum and maximum distance between surfaces). Further details regarding graph construction can be found in [36]. In our work, we use the values Δ_x = 1, Δ_z = 10, δ^l = 1, and δ^u = 100 pixels (with respective values of 4, 39, 4, and 388 μm). Also note that since a minimum nonnegative cost solution is calculated in this algorithm, the cost is specified as 1 minus the boundary probabilities. Once the graph is constructed, the maxflow/min-cut algorithm is used to solve for the optimal collection of surfaces [37]. Note that solving for the optimal cut simultaneously for all nine boundaries requires an enormous amount of memory. To alleviate this problem, we separately estimate the final surfaces in three groups. These three groups are the ILM surface, the 2nd to 4th surfaces, and the 5th to 9th surfaces, with the boundary numbering going from top to bottom of the retina. Following this process, we did not find any problems with ordering between the groups. Similar schemes were used to solve for the different boundaries in [13] and [19].

3. Experiments and results

3.1. Data

Data from the right eyes of 35 subjects were obtained using a Spectralis OCT system (Heidelberg Engineering, Heidelberg, Germany). The research protocol was approved by the local Institutional Review Board, and written informed consent was obtained from all participants. Of the 35 subjects, 21 were diagnosed with MS while the remaining 14 were healthy controls. All scans were screened and found to be free of microcystic macular edema (a pathology sometimes found in MS subjects). The subjects ranged in age from 20 to 56 years old with an average age of 39.

All scans were acquired using the Spectralis scanner’s automatic real-time function in order to improve image quality by averaging at least 12 images of the same location. The resulting scans had signal-to-noise ratios of at least 20 dB. Macular raster scans (20° × 20°) were acquired with 49 B-scans, each B-scan having 1024 A-scans with 496 pixels per A-scan. The B-scan resolution varied slightly between subjects and averaged 5.8 μm laterally and 3.9 μm axially. The through-plane distance (slice separation) averaged 123.6 μm between images, resulting in an imaging area of approximately 6 × 6 mm. The volume data was exported from the scanner using the vol file format. For all processing steps in our algorithm except for Section 2.1.1, we used the intensity data after transforming the original values by taking the fourth root.

The nine layer boundaries were manually delineated on all B-scans for all subjects by a single rater using an internally developed protocol and software tool. The manual delineations were performed by clicking on approximately 20–50 points along each layer border followed by interpolation between the points using a cubic B-spline. Visual feedback was used to move each point to ensure a curve that correctly identifies the boundary.

3.2. Parameter selection

The general properties of our RF classifier are specified by the number of trees N_t and the number of features N_n that are used at each node of each tree. The quality of training is dependent on the number of subjects N_s and number of B-scans N_b per subject. In selecting values for these parameters, we are interested in finding the set which provide a good segmentation accuracy without adding significant computational cost (as would be the case with more trees, more training data, etc.). We are not necessarily interested in finding the optimal set. To find suitable values for these parameters, we evaluated the performance of our RF classifier (using the RF+CAN algorithm) in a series of four experiments applied to 10 out of the 35 subjects. We did not use the entire dataset to carry out parameter selection because of the computational burden.

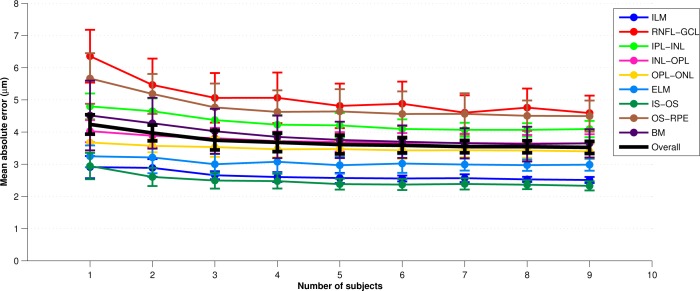
In each experiment, we swept through the values of one of the four parameters while keeping the other three fixed to a reasonable value (thus generating a new set of parameters). For example, to find appropriate values for each of N_t, N_n, and N_b, we used three training subjects (N_s = 3). To reduce the possibility of bias from training on particular subjects, a cross-validation strategy was used whereby a set of 10 classifiers were trained for every parameter set, each trained with N_s different randomly chosen subjects (from the pool of 10 subjects). For each trained classifier, we generated segmentations for the 10 − N_s test subjects not used in training. The overall error for each parameter set was calculated by averaging the absolute error between the segmentation and the manual segmentation across all test subjects evaluated with each of the 10 classifiers. Figure 6 provides an example error plot for each layer as the parameter N_s is varied from one to nine. The error bars represent the standard deviation of the error across the 10 trials. Similar experiments were performed for the other 3 parameters. Finally, we note that for the N_s experiments, a separate test set of 10 subjects was used to maintain a consistant number of test subjects as N_s was varied (it would not be fair to compare N_s = 1 with N_s = 8 by evaluating on 10 − N_s = 9 and 2 test subjects, respectively).

Fig. 6.

A plot of the mean absolute error across all boundary points vs. the number of subjects, N_s, used in training the classifier. For each value of N_s, the experiment was repeated with a random set of subjects ten times. Averages are across these ten trials and error bars represent one standard deviation.

Each of the parameters exhibited good stability and accuracy over a range of values. As a balance between performance and efficiency, we chose the final set of parameters (FSP) to be {N_t = 60, N_n = 10, N_s = 7, N_b = 8}. Using values larger than these show only a small performance improvement at a much larger computational burden. With N_s = 7 and N_b = 8, a total of 56 manual B-scan segmentations are needed for training. In an effort to reduce the amount of training data that are needed and to reduce the loading time, computation time, and memory requirements of the classifier, we also evaluated the algorithm using a minimal set of parameters (MSP), chosen to be {N_t = 20, N_n = 5, N_s = 2, N_b = 4}. In this case, with N_s = 2 and N_b = 4, only 8 manual B-segmentations are needed for training. We denote this set of parameters as minimal since we feel that using this set requires the minimum amount of training data necessary for the algorithm to perform acceptably well, in addition to being more efficient in the time required to compute the final segmentation (see Section 3.4). The memory footprint of the classifier is also significantly smaller, from 4 GB down to about 200 MB (a factor of 20), making it possible to run the algorithm on a wider variety of computational platforms.

3.3. Results

We evaluated our two segmentation methods, RF+CAN and RF+GS, on all 35 subjects using both the MSP and FSP. Since a cross-validation strategy was used in Section 3.2, there were 10 previously trained classifiers constructed using the FSP. We used these classifiers for the final evaluation of each algorithm. With the FSP, N_s = 7 randomly chosen subjects (out of the pool of 10 subjects) were used to train each of the 10 classifiers. Each classifier was evaluated by computing a segmentation on the 35 − 7 = 28 remaining test subjects. To be clear, we are simply extending the results of Section 3.2 using the FSP to the entire set of subjects. Since the MSP was chosen in a more ad-hoc manner, this parameter set did not have a corresponding experiment from Section 3.2. Therefore, we trained 10 classifiers using the MSP with a random set of N_s = 2 subjects chosen from the same pool of 10 subjects used in Section 3.2. In our first set of results, we compare RF+CAN and RF+GS using both parameter sets. We then show additional results using only the best algorithm and parameter set, which is RF+GS with the final parameter set.

To compare the results of our algorithm against the manual delineations, we calculated the absolute and signed boundary errors for every point on every surface. These errors were then averaged over all boundaries, subjects, and cross-validation runs. Table 1 shows the results for the two different algorithms with both parameter sets. The standard deviations were calculated assuming that every error value is separate (i.e. errors were not averaged for each subject before calculation). For both algorithms, we observe significantly better performance using the FSP over the MSP (p < 0.001). Significance was not found when comparing RF+CAN with RF+GS using the FSP, but was found using the MSP (p < 0.01). Significance was calculated on the average signed error over the whole volume across subjects using a one-sided paired Wilcoxon signed rank test. The MSP still performs well, however, having mean absolute errors about0.60 μm larger than the FSP. For the same parameter set, the main difference between RF+CAN and RF+GS is that RF+GS has a lower standard deviation of error.

Table 1.

A Comparison of the Two Boundary Refinement Algorithms^*

Algorithm	Minimal Parameter Set		Final Parameter Set
	Absolute Error	Signed Error	Absolute Error	Signed Error
RF+CAN	4.09 (6.41)	−0.60 (7.58)	3.40 (4.82)	−0.12 (5.90)
RF+GS	4.01 (5.70)	−0.56 (6.95)	3.38 (4.10)	−0.11 (5.31)

^*Both mean signed and absolute errors with the minimal and final parameter sets are included. Units are in μm and standard deviations are in parentheses.

It is informative to learn how each algorithm performs in certain regions of the macular cube. To do this, we assume that the acquired macular volumes are in alignment across the population. Therefore, the means and standard deviations of boundary error on each A-mode scan can be displayed as a fundus image, as shown in Fig. 7. Only the FSP was used here. Each image is oriented with the superior and nasal directions to the top and right, in agreement with the fundus image in Fig. 1(b). Although the subjects are not spatially aligned before averaging, this figure provides a meaningful illustration as the volumes are all similarly orientated with the foveae at their center.

Fig. 7.

(a,b) Images of the mean absolute error (μm) of each boundary at each pixel for the RF+CAN and RF+GS algorithms, respectively, with (c,d) the corresponding standard deviation of the errors. Averages are taken over all subjects and all cross-validation runs (280 values).

Figures 7(a) and 7(b) show that the mean errors in RF+CAN and RF+GS are almost identical. In fact, the errors show some structural bias, indicating that particular areas of the retina are equally difficult to accurately segment for each algorithm. The central fovea area is a consistent source of larger error; an expected result as this region is where several layers converge. Since the layers are converging, the localization of individual boundaries becomes more difficult not only for the algorithm, but also for a manual rater. We also see areas of larger errors in the nasal (right) side of the RNFL-GCL boundary as well as in the outer area of the OS-RPE boundary. The errors in the RNFL-GCL boundary are most likely due to the presence and large size of blood vessels running through this region. We can attribute the errors in the OS-RPE boundary to the fact that this boundary is more difficult to see in these areas as there is a transition from mostly cones near the fovea to mostly rods in the outer macula. Looking at the images in Figs. 7(c) and 7(d), the patterns of standard deviation between the two algorithms are visually similar. RF+CAN shows larger overall standard deviations, particularly in the RNFLGCL boundary and occasional very large outliers. Since the RF+GS algorithm shows more overall stability, all further experimental results are shown only for the RF+GS algorithm using the FSP.

Boundary specific errors for RF+GS are given in Table 2, with an additional breakdown by population—all subjects, controls, and MS patients. The best performing boundaries, the ILM and IS-OS, are the boundaries with the largest gradient response, thereby making them readily identifiable. The BrM benefited from the accuracy of the boundary detection in Section 2.1.2. The average errors are quite consistent across all boundaries, with errors of less than 1 pixel in all but the the RNFL-GCL and OS-RPE boundaries. Interestingly, we see very few differences with boundary errors between control and MS subjects. The average boundary errors between the two groups all have differences of less than 1 micron, with no statistically significant differences between them.

Table 2.

Mean Absolute and Signed Errors (and Standard Deviations) in μm for the RF+GS Refinement Algorithm on All Segmented Boundaries for All the Subjects and Broken-Down by Controls and MS Patients

Boundary	Absolute Errors (μm)			Signed Errors (μm)
	All	Control	MS	All	Control	MS
ILM	2.60 (3.33)	2.62 (3.89)	2.59 (2.89)	−0.22 (4.22)	−0.04 (4.69)	−0.34 (3.86)
RNFL-GCL	4.03 (6.34)	4.00 (6.11)	4.04 (6.48)	−0.88 (7.45)	−0.78 (7.26)	−0.95 (7.58)
IPL-INL	3.87 (4.54)	3.78 (4.41)	3.94 (4.62)	−1.93 (5.65)	−1.66 (5.57)	−2.11 (5.69)
INL-OPL	3.57 (3.75)	3.44 (3.61)	3.66 (3.84)	0.79 (5.12)	0.36 (4.97)	1.08 (5.19)
OPL-ONL	3.27 (4.06)	3.40 (4.24)	3.19 (3.93)	0.23 (5.21)	0.37 (5.42)	0.14 (5.06)
ELM	2.96 (2.84)	2.79 (2.68)	3.07 (2.93)	−0.65 (4.05)	−1.04 (3.73)	−0.39 (4.23)
IS-OS	2.34 (2.56)	2.38 (2.49)	2.30 (2.61)	0.13 (3.47)	0.33 (3.43)	0.00 (3.48)
OS-RPE	4.32 (4.23)	4.16 (4.13)	4.43 (4.30)	0.79 (6.00)	1.51 (5.67)	0.31 (6.17)
BrM	3.50 (3.56)	3.87 (3.69)	3.24 (3.44)	0.74 (4.93)	1.63 (5.10)	0.14 (4.72)
Overall	3.38 (4.10)	3.38 (4.09)	3.39 (4.10)	−0.11 (5.31)	0.08 (5.31)	−0.23 (5.31)

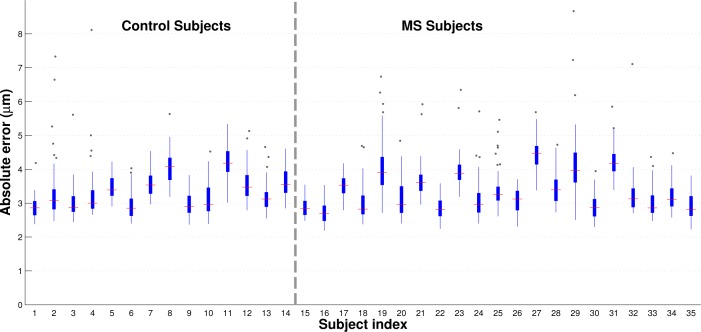
Figure 8 shows standard box plots of the boundary errors across all of the subjects. A total of 49 points were included for each subject, where each point represents the absolute error averaged across all boundaries and cross-validation repetitions of a single B-scan. Subjects are divided by disease diagnosis and ordered by age within each diagnostic group. This figure again shows that our algorithm yields similar results in both MS and control subjects, with no age-dependent error trends in either population. Outliers are few relative to the numbers of trials carried out and still mostly fall below 2 pixels in error. A detailed examination of these outliers shows the presence of blood vessel artifacts in these scans.

Fig. 8.

Box and whisker plots of the mean absolute errors for every subject used in this study. Subjects are ordered by diagnosis and then age (increasing from left to right within each diagnostic group). A total of 49 data points were used to generate each subject’s plot, with each data point representing the error of a particular B-scan averaged across all cross-validation runs. For each subject, the red line represents the median absolute error and the edges of the box correspond to the 25th and 75th percentile of the error. All points lying outside of the whiskers are greater than 1.5 times the interquartile range.

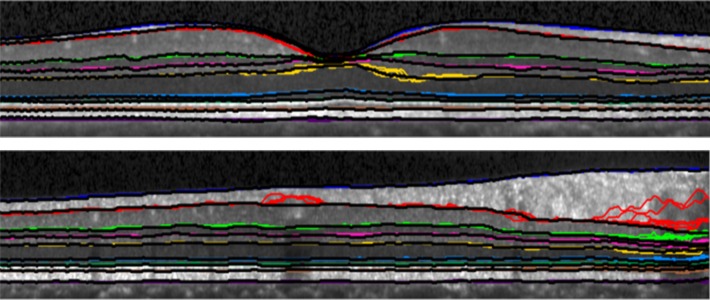
Figure 9 shows estimated boundaries from two B-scans taken from two different subjects. Boundaries for each of 10 cross-validation trials are plotted on the same B-scan, using a different color for each boundary. The manually traced boundary is plotted using a black curve after all other boundaries are drawn. When only the black curve is apparent, this indicates that all estimated curves agree with the truth. In areas where colors are visible near the black curves, this is indicative of some or many boundary estimates disagreeing with the truth. We observe that larger errors tend to be located within the shadows of blood vessels.

Fig. 9.

Two B-scan images from two different subjects are shown with the resulting boundaries from each of the 10 cross-validation runs overlaid. Each boundary is represented by a different color with the manual delineation shown atop the other boundaries in black. Therefore, if the color is not visible at a particular point, the automatic and manual segmentation are in agreement.

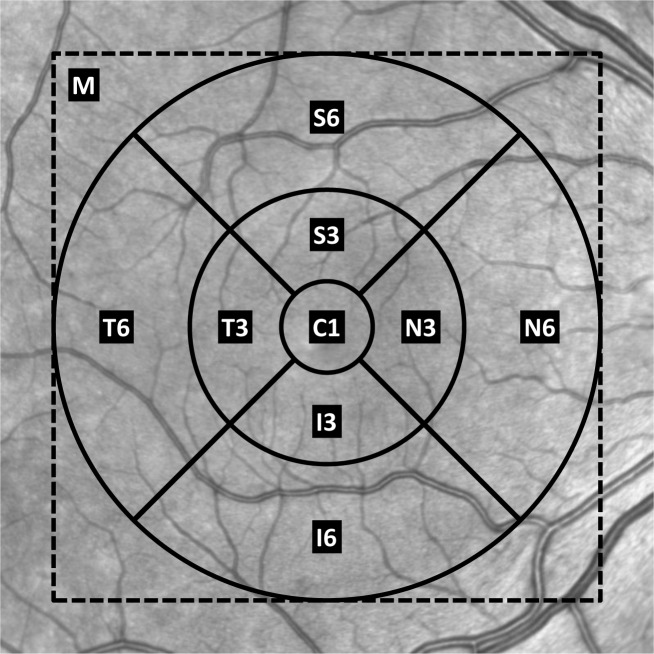
So far, our focus has been on accurate boundary estimation; however, the clinically important measure is generally considered to be the layer thicknesses. These thicknesses are often reported as average values within different sectors of the macula surrounding the fovea [4, 38]. A standardized template is centered over the fovea and used to divide the macula into these sectors [39]. Figure 10 shows this template over a retinal fundus image. The sectors are labeled with C1 representing the central 1 mm diameter area, S3, I3, N3, and T3 representing the superior, inferior, nasal, and temporal areas of the inner 3 mm diameter ring, and S6, I6, N6, and T6 representing the same areas in the outer 6 mm diameter ring. We also use M for the macular region within the dashed box (the imaged area). Table 3 lists the absolute errors of the average thickness for each layer within the nine sectors and the whole macula. To be clear, the average thickness error for layer l in sector r is calculated as,

$${\text{e}}_{r,l}=\frac{1}{\left|S\right|}\sum _{i\in S}\left|{\overline{w}}_{\text{auto},i}^{r,l}-{\overline{w}}_{\text{true},i}^{r,l}\right|,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\begin{array}{l}r\in \left\{\text{C}1,\text{S}3,\dots ,\text{M}\right\}\hfill \\ l\in \left\{\text{RNFL},\dots ,\text{RPE}\right\}\hfill \end{array},$$ (1)

where ${\overline{w}}_{\text{auto},i}^{r,l}$ and ${\overline{w}}_{\text{true},i}^{r,l}$ are the average thickness of layer l over all pixels in sector r of subject i for the automatic and true boundary segmentations, respectively. S is the set of all subjects over each cross-validation test set—|S| = 10·28 = 280 in our experiments. The template was aligned to the center of each subject’s volume, again assuming that all of the data is already in rough alignment with the fovea at the center. The OPL and ONL show the largest errors, especially in the central area where the layers converge. Many of the other sectors have errors around 4 μm with standard deviations less than 2 μm. Table 3 gives a clinically relevant thickness interpretation of the boundary errors, visualized in Fig. 7.

Fig. 10.

The template for the sectors of the macula overlaid on a fundus image. The dashed square surrounding the template represents the imaged area. The concentric circles are centered on the geometric center of the OCT volume and have diameters of 1 mm, 3 mm, and 6 mm.

Table 3.

Retinal Layer Thickness Absolute Errors (in μm, with Standard Deviation) Calculated for Different Sectors of the Macula (See Fig. 10 for Sector Positions)*

Layer	C1	S3	I3	N3	T3
RNFL	2.88 (1.78)	1.73 (1.28)	0.97 (0.83)	1.50 (0.97)	1.75 (1.19)
GCIP	2.62 (1.84)	2.14 (1.26)	1.76 (1.23)	1.54 (1.21)	2.14 (1.14)
INL	2.62 (1.84)	3.35 (1.86)	2.73 (1.86)	3.86 (1.90)	2.88 (1.54)
OPL	3.46 (3.35)	3.16 (2.94)	2.71 (4.20)	2.86 (2.80)	2.10 (2.50)
ONL	4.35 (3.26)	3.02 (2.08)	3.36 (3.85)	2.83 (2.26)	2.51 (2.13)
IS	2.54 (1.98)	2.58 (1.94)	2.60 (1.90)	2.75 (1.80)	2.39 (1.77)
OS	2.48 (1.79)	2.31 (1.93)	1.97 (1.55)	2.33 (1.70)	2.04 (1.68)
RPE	2.08 (1.57)	2.80 (2.05)	2.81 (1.97)	2.55 (1.92)	2.65 (2.13)
Overall	2.88 (2.37)	2.64 (2.05)	2.37 (2.55)	2.53 (2.03)	2.31 (1.85)

Layer	S6	I6	N6	T6	Macula
RNFL	1.87 (2.00)	1.61 (1.44)	2.19 (2.39)	1.36 (1.03)	1.33 (1.29)
GCIP	1.51 (1.10)	1.49 (0.93)	1.69 (1.16)	2.03 (0.96)	1.24 (0.76)
INL	2.90 (1.74)	2.76 (1.74)	3.37 (1.98)	2.48 (1.60)	2.90 (1.56)
OPL	1.53 (1.27)	1.61 (1.12)	1.94 (1.56)	1.44 (1.08)	1.54 (1.21)
ONL	2.05 (1.40)	2.18 (1.44)	2.13 (1.48)	1.83 (1.24)	1.96 (1.26)
IS	2.72 (2.00)	2.65 (1.95)	2.87 (2.07)	2.40 (1.70)	2.48 (1.86)
OS	3.44 (3.07)	2.96 (2.97)	3.06 (2.73)	2.71 (2.23)	2.52 (2.35)
RPE	4.06 (3.16)	3.67 (3.24)	3.51 (2.70)	3.54 (2.60)	3.14 (2.36)
Overall	2.51 (2.27)	2.37 (2.14)	2.60 (2.18)	2.22 (1.78)	2.14 (1.80)

^*The ‘Macula’ column represents the absolute error of the average thickness of the entire imaged area. Errors are between the results of RF+GS in comparison to the manual rater.

3.4. Computational performance

The algorithm was coded in MATLAB R2012b (The Mathworks, Inc., Natick, MA, USA) using external, openly available packages for the RF classification [40], the graph-search algorithm [37], and calculation of anisotropic Gaussian features [32]. All other code used built-in MATLAB functions. Experiments were performed on a computer running the Fedora Linux operating system with a 3.07 GHz quad-core Intel Core i7 processor.

To assess the algorithms’ computational behavior we calculated the average time taken to perform each step of the algorithm. The preprocessing stages (normalization and flattening) took an average of 17 seconds per volume and calculation of image features took an average of 33 seconds. The random forest classification averaged 114 seconds per volume using the FSP and 24 seconds with the MSP. Boundary tracking using the Canny approach took an average of 19 seconds per volume. Therefore, the RF+CAN algorithm took an average of 183 seconds per volume for the FSP and an average of 93 seconds per volume for the MSP. Boundary tracking using the graph segmentation approach took an average of 54 seconds per volume. Therefore, the RF+GS algorithm took an average of 218 seconds per volume for the FSP and 128 seconds for the MSP. Thus, the best performing algorithm (RF+GS using the FSP) takes less than four minutes to process a volumetric macular scan comprising 49 B-scans.

Training time is a bit more difficult to analyze, as manual delineation time is involved and is the most time consuming part of the process. Based on feedback from our manual rater, we estimate that it takes about 10 minutes to manually delineate a single B-scan. Since there are56 B-scans required to train using the FSP, this alone takes 560 minutes. Training the random forest takes only 17 minutes for these 56 delineations, which means that it takes just under 10 hours to train for the FSP. Since the minimal set requires only 8 B-scans and 25 seconds to train the classifier, the random forest can be trained—including time for manual delineation—in just one hour and 20 minutes for the MSP.

The algorithm can be sped up significantly by taking advantage of several potential optimizations, including using a faster programming language, such as C (our current implementation is in Matlab). We can also speed up the classification part of the algorithm by parallelizing the random forest across multiple computer cores or utilizing a graphics processing unit [41].

4. Discussion and conclusion

The results for both of our algorithms show excellent performance with overall average absolute errors below 3.5 μm and less than 4.5 μm for any one specific boundary. Although the overall average errors are nearly identical between the two algorithms, the standard deviation of the RF+CAN algorithm is slightly larger due to the occasional possibility that the boundary tracking algorithm fails in some areas. The spatial smoothness constraints imposed by the graph search algorithm prevent these failures in the RF+GS algorithm. Looking at the thickness values calculated using the RF+GS algorithm, we see average errors of less than 3 μm in 81% of the sectors and standard deviation values less than 3 μm in 90% of the sectors indicating a high level of confidence in these measurements. When using the minimal training set, the errors are larger but the performance is still quite good, with errors only slightly larger than the axial resolution of the system. Therefore, training the RF from a new data source—i.e., for a new system or for new parameters on an existing system—could be carried out within only a few hours in order to achieve adequate performance when using the minimal training set.

When comparing our algorithm with other retinal segmentation methods found in the literature, we see comparable performance to the best algorithms [14, 15, 19], each of which shows average errors of between 3–4 μm. This comparison is inherently difficult, however, as the methods are evaluated on data acquired with different types of scanners using different numbers of manually delineated subjects (as few as 10 subjects). Due to the time consuming nature of manual segmentation, evaluations are often performed against only a subset of the full data (5–10 B-scans per subject). In our case, evaluations were carried out against entire volumes (all 49 B-scans per subject), which includes many poor quality images. Our manual segmentations are also generated as smooth spline curves from a small set of control points, which is different from other manual delineations and thus may introduce bias. Additionally, only a few methods provide results showing that they are able to accurately segment eight layers or more [14, 16, 21]. Although it may be possible to use other algorithms to segment all of the retinal layers, it is not clear how they will perform. In terms of computational performance, our algorithm runs significantly faster than the most similar method to ours [17], which uses machine learning for classification and regularization on only one layer at a time. We still lag behind faster algorithms including [14] and [19], the latter of which does a 3D segmentation of six layers in about 15 seconds. Complete characterization of the advantages and disadvantages of these algorithms will require a direct comparison on the same data using the same error criteria.

Looking to the future, although the algorithm performance was not degraded for MS subjects, we expect that modifications will be necessary to handle other pathologies such as microcysts, drusen, and geographic atrophy (GA). Microcystic macular edema occurs in about 5 % of MS patients and is characterized by the appearance of microcysts in the INL [4, 5]. The appearance of these microcysts negatively impacts the performance of our algorithm’s ability to segment the INL due to the poor performance of the random forest classifier at these areas. Drusen appear as an extracellular buildup between the RPE and BrM and can be an indicator of age-related macular degeneration (AMD), although they also commonly appear in healthy aging populations [42]. In areas of the retina with drusen, it is important to delineate both the lower boundary of the separated RPE and the BrM. Our algorithm would do a poor job of identifying either of these boundaries due to the high curvature of the RPE or the lack of a strong feature response at the BrM. In GA, often occuring in late-stage AMD, severe morphologic changes to the outer layers of the retina occur including the disappearance of the retinal layers from the RPE up to the OPL [43]. It is not likely that our algorithm would perform well on GA cases since the spatially sensitive features used by the random forest would not be able to identify the out-of-place boundaries. These features rely on a consistent spatial organization of the layers across the retina for different subjects.

There are many possible solutions for modification of our algorithm to handle these retinal pathologies. One possible approach for handling microcysts and drusen is by a pre-classification of the pathological areas. These areas could then be incorporated into the spatial features enabling the random forest classifier to learn an alternate model in these regions. In the case of partially or completely missing layers, it may be necessary to remove the spatial features from these areas and rely on intensity features to guide the final segmentation. A pre-identification of the ILM and BrM would still prove to be invaluable to the segmentation as additional constraints on the graph algorithm can be incorporated to handle these cases [13, 19].

In the case of structurally normal eyes, there are still several potential areas of improvement—for example, allowing the RF to know if an A-scan has a blood vessel shadow could improve our results. Looking at Table 3, we have a good idea of which regions and layers are more difficult to segment allowing us to focus on finding improvements for these areas. As far as feature selection goes, little effort was put into selecting the best set of features for retinal segmentation. Other groups have used a larger set of multi-scale features, including intensities, gradients and Gabor filters [17, 18]. It is also possible that a sampling of features from a large class of generalized features within the training phase of the algorithm [44], will help improve results. With regards to the graph-based segmentation in the second part of our work, learning boundary specific constraints at each surface position would improve the segmentation and further help to eliminate outliers in the final segmentation [13, 19].