Multilayer thin-film phantoms for axial contrast transfer function measurement in optical coherence tomography

Abstract

In optical coherence tomography (OCT), axial resolution is one of the most critical parameters impacting image quality. It is commonly measured by determining the point spread function (PSF) based on a specular surface reflection. The contrast transfer function (CTF) provides more insights into an imaging system’s resolving characteristics and can be readily generated in a system-independent manner, without consideration for image pixel size. In this study, we developed a test method for determination of CTF based on multi-layer, thin-film phantoms, evaluated using spectral- and time-domain OCT platforms with different axial resolution values. Phantoms representing six spatial frequencies were fabricated and imaged. The fabrication process involved spin coating silicone films with precise thicknesses in the 8-40 μm range. Alternating layers were doped with a specified concentration of scattering particles. Validation of layer optical properties and thicknesses were achieved with spectrophotometry and stylus profilometry, respectively. OCT B-scans were used to calculate CTFs and results were compared with convetional PSF measurements based on specular reflections. Testing of these phantoms indicated that our approach can provide direct access to axial resolution characteristics highly relevant to image quality. Furthermore, tissue phantoms based on our thin-film fabrication approach may have a wide range of additional applications in optical imaging and spectroscopy.

1. Introduction

Optical coherence tomography (OCT) has made a significant impact on the clinical practice of ophthalmology and promises to improve minimally invasive diagnostics in a variety of other medical fields, including cardiology and gastroenterology [1]. Despite the rapid pace of advancement in OCT technology, there have been relatively few advances in test methods for characterization of OCT system performance. In recent years there has been increasing activity in the development of standardized performance test methods for medical imaging modalities, due in part to the recognition that such techniques can facilitate technical advancement, clinical translation and commercialization. It is likely that the most appropriate test methods for optical imaging will be largely analogous to those developed for established modalities such as ultrasound and x-ray computed tomography (CT), where phantom-based approaches represent not only good scientific practice, but, in some cases, the legal obligation of medical facilities [2]. The phantoms used for established imaging modalities often eschew biologically realistic morphologies for non-biological structures that enable quantitative assessment of key image quality characteristics such as spatial resolution, signal-to-noise ratio and uniformity. Lamouche et al and Pogue et al, respectively, have provided excellent reviews on phantoms developed specifically for OCT [3] and for optical diagnostics in general [4].

Recently, our group [5] and others [6] have developed phantoms for three-dimensional characterization of the OCT point spread function (PSF) using a sparse distribution of nanoparticles or microparticles embedded in a transparent polymer. This type of phantom permits rapid and detailed measurements of spatial resolution in both lateral and axial dimensions, and indicates how the resolution varies over the imaged volume. In addition, the mapped PSF information can be used for spatial deconvolution to improve image quality [6]. However, obtaining the most accurate data with this type of phantom requires well-known spatial sampling intervals in all three dimensions and especially fine spatial sampling during image acquisition, though Tomlins et al have presented one method to overcome spatial sampling limitations [7]. Control and/or knowledge of these system parameters may not be available, especially for the clinical end-user. In addition, since the PSF is measured under idealized (100% contrast) conditions, it reveals the OCT system axial resolution as defined primarily by the illumination source spectral/coherence properties. Other system parameters, such as signal-to-noise ratio, influence imaging resolution and may not be apparent in the PSF. It is also well-known that multiple scattering in the sample leads to blurring of the axial length of structures [8–10]. Thorough and accurate evaluation of axial resolution is of particular interest when imaging the retina, which consists of many layers of varying reflectivity and thickness on the order of 10 μm.

An alternate method to evaluate the spatial resolution of an imaging system involves a target with adjacent bright and dark objects of accurately known dimensions, e.g., a bar chart. An example of such a phantom would be the well-known USAF 1951 resolution target, which is typically realized as bars of thin metal film deposited on glass. This target can be used to determine the contrast transfer function (CTF) – a frequency domain analog to the PSF – which characterizes the system’s intensity modulation contrast versus spatial frequency. The USAF 1951 target can be used for determining spatial resolution only in lateral dimensions, but phantoms with small, controlled axial dimensions have been developed for OCT. de Bruin et al [11] have fabricated layered phantoms with controlled scattering characteristics and thickness down to 50 μm. Gu et al and Curatolo et al used soft lithography techniques to fabricate phantoms with bars [12] or other patterns [13] having dimensions of tens of microns; smaller dimensions are theoretically possible. Chang et al [14] recently developed phantoms using particle monolayers with thicknesses in the 1-5 μm range; however, their approach does not provide substantial flexibility in modifying layer thickness or optical properties. No phantoms have yet been demonstrated with highly controlled feature dimensions and optical properties suitable for axial CTF determination in OCT devices.

Therefore, our present work focuses on fabrication, characterization, and testing of multilayer thin-film phantoms specifically for determining OCT axial resolution characteristics via the CTF. This type of resolution evaluation is recommended in performance standards for medical imaging modalities like CT [15]. When using a multilayer phantom for OCT, images can be captured in the native format without oversampling, and no knowledge about the system’s spatial calibration is required. With a collection of phantoms covering a range of OCT-relevant spatial frequencies, a CTF curve can be generated, providing a more thorough analysis of system performance than previously possible.

2. Materials and methods

2.1 Phantom design and fabrication overview

Analogous to the bars of the USAF 1951 resolution chart, the layers of a phantom for OCT axial resolution characterization should alternate between bright (backscattering) and dark (transparent). For each spatial frequency, all layers should be of identical, well-known thickness and be free of optical discontinuity between layers which could introduce specular reflections and thus corrupt the underlying spatial frequency. The reflective layers should also have homogeneous scattering characteristics in order to generate uniform signal intensity across the phantom. Taking these factors into account, we developed an approach involving spin coating of thin films to generate robust, stable phantoms with appropriate micro-scale layer geometries. The general procedure involved layer-by-layer fabrication of scattering and non-scattering thin films, as illustrated in Fig. 1. Each phantom consists of five layers built up from the substrate: a transparent layer (1) between the substrate and the spatial frequency layers, three layers (2-4) representing a particular spatial frequency in a bright-dark-bright configuration, and another transparent layer (5) on top. The transparent layers at the top and bottom are ~40 μm thick serve to isolate the spatial frequency layers from the index mismatches with air and substrate, respectively. We fabricated six different phantoms intended to cover spatial frequencies higher and lower than those corresponding to nominal OCT axial resolution values of 5-10 μm (in air) reported for commercial OCT devices [16].

Fig. 1.

Phantom design. The colors of the five layers represent their appearance with OCT. Dimensions are not to scale.

2.2 Thin film material preparation

The matrix material for the phantoms was polydimethylsiloxane (PDMS; Sylgard 182, Dow Corning, Midland, MI) a transparent two-part silicone elastomer formulation. The elastomer base must be mixed with a curing agent at a ratio of 10:1 by weight and then heat cured, which results in a flexible material with high mechanical and optical stability over at least one year [3,13]. The cured polymer’s refractive index (n) is 1.41 ± 0.01 in the near infrared (800-1300 nm), determined by OCT optical pathlength measurements of samples with known physical thickness. As compared to other materials like polyurethane or epoxy resin, silicone’s refractive index is lower and uniquely close to that of tissue (n≈1.38).

For a transparent film, we mixed the base and curing agent thoroughly with a glass rod, and then placed the mixture in a degassing vacuum chamber for 20 minutes to remove air pockets within the sample prior to spin coating and curing. The process for a scattering film involved the addition of barium sulfate powder (BaSO₄, B-3758, Sigma-Aldrich St. Louis, MO) at 10% by weight to the PDMS base prior to mixing with the curing agent. The powder does not have a controlled particle size which has been characterized by the manufacturer, but the polydisperse particles are nominally micron-sized, as determined by comparison to 0.75 μm diameter polystyrene microspheres with brightfield microscopy. To maximize homogeneity, the particles were dispersed in the PDMS through 3 minutes of sonication with a probe tip and 10 minutes in a sonicator bath. Then, the sample was placed in the vacuum chamber to remove air pockets. The sonication and degassing steps were repeated 8-12 times to provide a suitable level of homogeneity, verified visually with brightfield microscopy. The stock PDMS-BaSO₄ mixture was diluted with an equal quantity of additional PDMS base (by weight) to achieve a mixture with 5% BaSO₄ concentration by weight. The diluted sample and PDMS curing agent were then mixed in a 10:1 ratio, followed by a single round of probe and bath sonication and a final degassing step in the vacuum chamber prior to spin coating and curing.

As shown in Fig. 2, the BaSO₄-doped film yields a scattering coefficient of 15 mm⁻¹ at 855 nm, measured via collimated transmittance spectrophotometry (Lambda 1050, PerkinElmer, Waltham, MA) of a 30 μm test film. Under these single-scattering measurement conditions and the assumption that the particles have negligible absorption, Beer’s law can reveal the scattering coefficient directly. This scattering coefficient is within the 12 to 22 mm⁻¹ range reported for retinal tissue [17,18] and thus can provide OCT signal levels relevant to one of the primary tissues of interest. The effective refractive index (i.e., optical thickness) of BaSO₄-doped films is only ~0.2% greater than pure PDMS, as determined from the volumetric concentration of BaSO₄ in PDMS (1.1%, based on manufacturer-provided specific gravity of 4.5 for BaSO₄ and 1.03 for PDMS) and n = 1.64-1.65 for BaSO₄ [19].

Fig. 2.

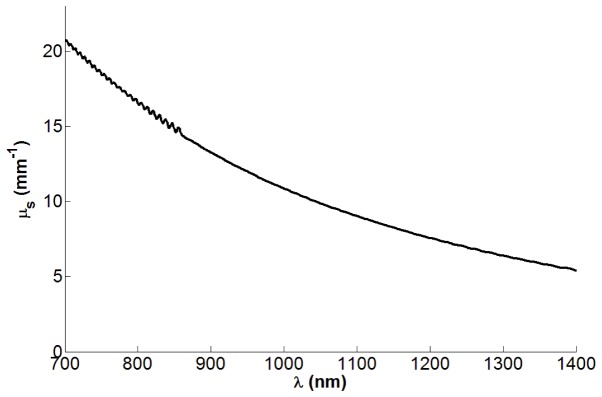
Scattering coefficient of 5% (by mass) BaSO₄ in PDMS. Ripples in spectrum are a result of interference between the front and back surfaces of the test film.

2.3 Spin coating procedure

The substrate for each phantom was a 1 mm thick glass microscope slide that was washed with deionized water, then dried with pressurized air that also removed dust particles. Evaporation of any additional moisture was achieved using a hotplate at 50°C for 30 minutes. The slide was then cooled to room temperature and affixed to the spin coater (WS-650Mz-23NPP, Laurell Technologies, North Wales, PA), and a drop of PDMS was placed on the center of the slide. The work of Koschwanez et al [20] provided a relationship of PDMS film thickness versus rotational speed and spin time. After spin coating, the slide was then placed on a hot plate for curing at 150°C for 1.5 hours. Once the film was cured, another drop of uncured PDMS could be placed on top to spin coat and cure the next layer in the five layer sequence.

2.4 Phantom thickness and spatial frequency characterization

We measured the thickness and surface profile of phantom layers with a stylus profilometer (Dektak 150, Veeco, Plainview, NY), capable of measuring step height changes over a range of 50 nm to 1 mm. We were able to determine each layer’s thickness by measuring the total height of all accumulated layers relative to the substrate surface after each film was deposited and cured. In this way, we had independent and highly accurate measurements of layer thickness, which are necessary for reliable CTF calculations. The surface profile provides important quality control information post-fabrication to locate any defective regions.

To produce a conventional CTF graph, it was necessary to determine the spatial frequency of each phantom. This value was derived by calculating the mean physical thickness of each of the three layers as determined by profilometry, then converting to optical thickness by multiplying by n = 1.41. The reciprocal of twice the optical thickness was taken to be the spatial frequency in line pairs per millimeter (lp/mm_opt).

2.5 OCT imaging and CTF analysis

All phantom samples were imaged with both spectral domain OCT (SDOCT) and time domain OCT (TDOCT) systems. The SDOCT system (Physical Sciences, Inc., Andover, MA) [21] operates at a center wavelength of 855 nm with 56 nm FWHM spectral bandwidth, yielding a theoretical coherence length of 6 μm in air. We also analyzed images after applying a Gaussian window to acquired spectra such that the FWHM bandwidth becomes 25.5 nm, approximating a source with 12.7 μm coherence length. Gu et al used this approach to reduce SDOCT axial resolution to better match the feature dimensions of their phantom [12]. The TDOCT system [22] is based on an all-fiber common-path interferometer (AIF-INST-02, Optiphase, Van Nuys, CA) and has two different illumination sources available, both operating at a center wavelength of 1310 nm: one has 83 nm FWHM bandwidth (9 μm coherence length) and the other has 54 nm FWHM bandwidth (14 μm coherence length). Three spatially separated B-scan images 500 μm wide were captured from each phantom, and the aligned A-scans from each image were averaged together, yielding three average A-scans. From each of the average A-scans, we subtracted the background as a DC offset level and then found the mean of the peak intensities from the two bright layers (I_bright) and the minimum intensity at the dark layer (I_dark). For each spatial frequency, Michelson contrast (C) [23] was derived as shown in Eq. (1).

$$C=\frac{I_{bright}-I_{dark}}{I_{bright}+I_{dark}}$$ (1)

It should be noted that the intensity values used were the raw intensities in linear units, without any logarithmic transformation or scaling for visualization purposes. This approach gives us access to the inherent, unbiased resolution capabilities of the OCT device. The contrast versus spatial frequency data were used to determine axial CTFs for the four different OCT system configurations: wideband (unfiltered spectrum) SDOCT (wS), narrowband (filtered spectrum) SDOCT (nS), wideband TDOCT (wT), and narrowband TDOCT (nT).

3. Results and discussion

3.1 Phantom thickness characterization

The measured thicknesses of the key CTF layers are presented in Table 1. The thinnest layer we achieved was 8 μm, which may be too thick to challenge ultrahigh resolution OCT systems but is near the resolution limit of many commercially-available clinical devices. The thickness precision is reasonable, with all standard deviations ~10% or less of the mean. Variations in thickness are likely due to uncontrolled steps in the fabrication process, such as the amount of uncured PDMS placed on the substrate for spin coating.

Table 1. Profilometry Results for CTF Phantoms.

Phantom ID	Thickness (μm)				Mean (SD*) of Spatial Frequency (lp/mmopt)
	Layer 2	Layer 3	Layer 4	Mean (SD*)
A	8.6	8.5	7.4	8.2 (0.7)	43.6 (3.8)
B	15.4	12.3	15.0	14.2 (1.7)	25.2 (3.2)
C	17.0	16.6	17.6	17.1 (0.5)	20.8 (0.6)
D	22.7	27.3	24.7	24.9 (2.3)	14.3 (1.3)
E	34.0	33.6	36.2	34.6 (1.4)	10.3 (0.4)
F	52.1	52.7	54.4	53.1 (1.2)	6.7 (0.1)

*SD: standard deviation

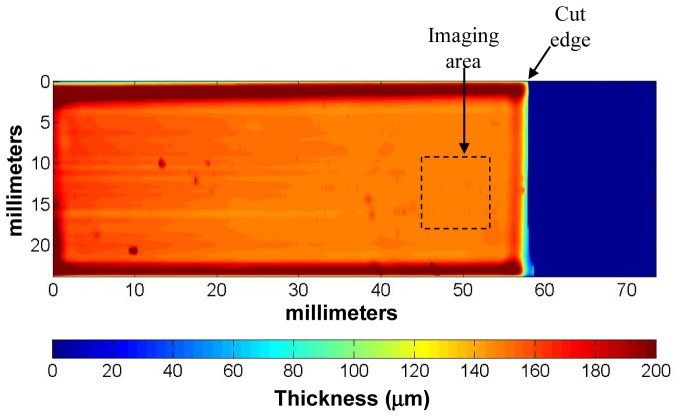
To get a more detailed understanding of the thickness variation across a phantom, we used the stylus profilometer to also obtain a high resolution 2D thickness profile over the entire phantom surface, shown in Fig. 3. The image consists of horizontal scans, with 2.1 μm sampling within each scan and 100 μm between scans. In general, the spin coating process tends to produce films which are thinner and relatively flat in the central region, with thicker beads near the substrate edges. Some point defects are noticeable, due to dust particles on the surface and local aggregation of BaSO₄ particles within the phantom. But the phantom is quite uniform within a 10 mm x 10 mm area near the cut edge, thereby defining the optimum region for OCT imaging.

Fig. 3.

Surface profile of phantom C. Blue region indicates substrate surface.

3.2 OCT imaging

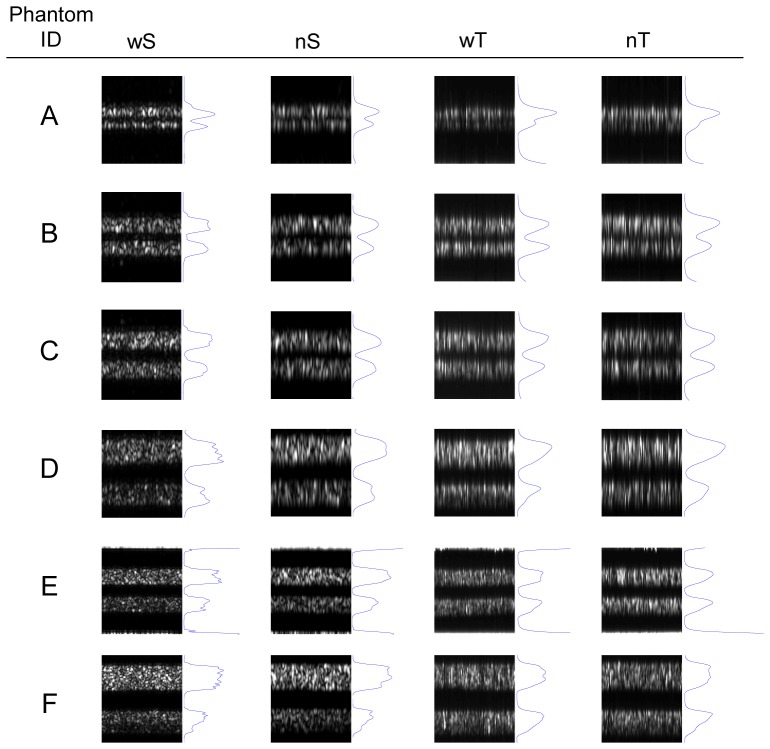
Images of the six phantoms acquired with the four OCT configurations, along with average A-scans, are presented in Fig. 4. The signals due to the specular reflections above layer 1 (air-silicone interface) and below layer 5 (silicone-glass interface) are cropped out of the images, though some evidence of the signals can be seen in the phantom E images. Those reflections are not strong enough to corrupt the images, in part because the beam focus is axially positioned within the spatial frequency layers. For wT and nT, it is relatively easy to resolve the individual layers in phantoms representing lower spatial frequencies, up to 14 or 21 lp/mm_opt. Thicker scattering layers are more likely to introduce signal attenuation, clearly noticeable in the bottom layer of phantom F. Occasionally the signal does appear to increase near the bottom of layers, as with the wS image of phantom D, but we attribute that effect to random intensity fluctuations induced by local scattering heterogeneity. Reduced contrast is apparent at higher spatial frequencies, and the two layers are difficult to distinguish in the images of phantom A. The individual layers of all phantoms can be resolved visually in the images from wS and nS, with the main difference between the two caused by the increased speckle size for nS. It is worth noting that several standards, including the aforementioned CT standard [15], also recommend visual distinction of individual layers for evaluating system resolution. While representation of resolution through a CTF graph is more rigorous and objective, visualization of the individual phantoms does provide intuitive insight into how resolution affects imaging performance in an image with tissue-relevant scattering and speckle.

Fig. 4.

OCT images of the six phantoms, with the average A-scans in blue next to the images. All images are 500 μm wide. Images for phantoms A-D are 150 μm optical depth, while those for phantoms E and F are 300 μm optical depth (wS: wideband SDOCT, nS: narrowband SDOCT, wT: wideband TDOCT, nT: narrowband TDOCT).

3.3 Quantitative CTF analysis

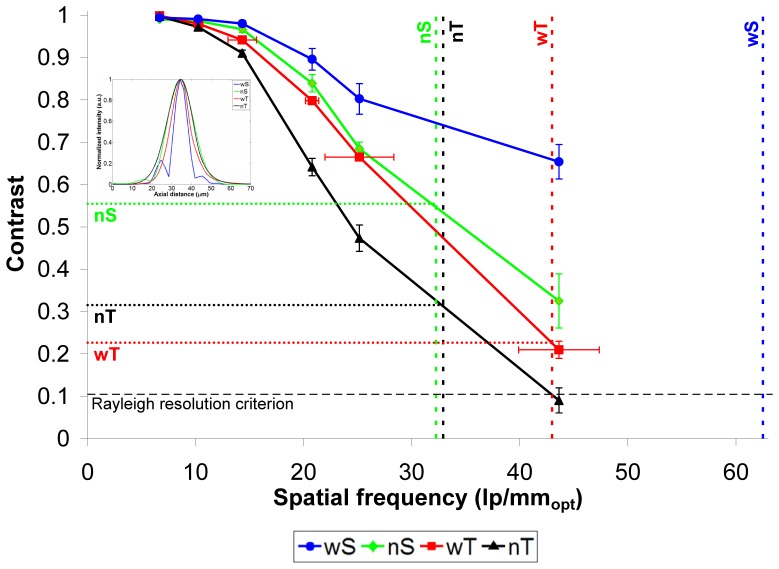
Final CTF curves – contrast values as a function of spatial frequency – for the four OCT configurations are shown in Fig. 5. In general, the CTF curves show the expected trend, with contrast levels close to 1 at low spatial frequencies and decreasing monotonically with increasing spatial frequency. A distinction among the four configurations becomes apparent at 14 lp/mm_opt, a spatial frequency which all configurations can clearly resolve. Such a distinction would be quite difficult to identify without this type of phantom. As expected, the wideband SDOCT and TDOCT configurations demonstrate markedly better contrast than their narrowband counterparts at 14 lp/mm_opt and can resolve higher spatial frequencies. wS and nS CTFs tend to diverge from each other as spatial frequency increases, whereas wT and nT maintain a more constant separation. It is interesting to note that the nS CTF is superior to both TDOCT curves even though its PSF-based resolution is poorer, especially compared to wT’s PSF. One reason for this may be the improvement in signal-to-noise with SDOCT over TDOCT, since our TDOCT instrument utilizes older analog circuitry to filter and amplify the raw interferogram captured with the photodiode. TDOCT is also operating at a longer source wavelength, which yields less scattering and therefore less available signal.

Fig. 5.

CTF curves for the four OCT configurations. Error bars represent the standard deviation of each data point. Horizontal error bars are shown only on the wT curve for clarity; they are the same for all curves. Vertical dashed lines indicate the equivalent spatial frequency to the FWHM of each configuration’s axial PSF. Inset shows axial PSFs for the four OCT configurations (wS: wideband SDOCT, nS: narrowband SDOCT, wT: wideband TDOCT, nT: narrowband TDOCT).

For comparison to the common approach for axial resolution determination, the inset of Fig. 5 shows the axial PSFs obtained via specular reflections for the four configurations. Keeping in mind that the PSF and CTF are effectively (though not directly) Fourier transforms of one another, we can see the correspondence of the shapes of the PSF and CTF curves. The nS, wT, and nT PSFs are all quite Gaussian in shape, corresponding to CTFs generally similar in shape and differing in slope. The wS PSF is distinctively non-Gaussian with its sidelobes, resulting from a non-Gaussian spectrum. Likewise, the wS CTF has a unique shape compared to the other three CTF curves, with its own “sidelobe” across the two highest spatial frequencies. The FWHM of the PSF curves yields axial resolution estimates (in air) of 8.0, 15.5, 11.6, and 15.2 μm, for wS, nS, wT, and nT, respectively., These are equivalent to spatial frequency values of 65.0, 32.3, 43.0, and 32.9 lp/mm_opt respectively, which are marked with vertical dashed lines in Fig. 5. These PSF-derived spatial frequencies correspond to CTF-derived contrast values (horizontal dotted lines in Fig. 5) around 20-30% for wT and nT and >50% for nS. The phantom layer thicknesses achieved in this study did not challenge wS to a degree that its CTF would cross its corresponding PSF spatial frequency. Lord Rayleigh’s criterion for two overlapping images being just resolved says that I_dark should be 8/π² × I_bright [24], which for Gaussian-shaped peaks corresponds to a contrast value of 10.5%. This suggests that the actual axial resolution capabilities of OCT are likely to be better than what a simple FWHM measure of the PSF reveals. The Rayleigh criterion is not necessarily relevant for examining OCT axial resolution in the presence of speckle, but it offers a resolution threshold well-known in optical imaging. In the end, having a complete CTF allows the system designer to decide what contrast level construes adequate resolution and then know what structure size can be truly resolved.

3.4 Implications and future work

As seen in Fig. 5 and in prior studies, the standard approach involving measurement of OCT PSF based on a specular surface is simple and provides useful quantitative and qualitative information on spatial resolution. While the CTF-based approach introduced here involves a more complicated process for phantom development and data analysis, it also provides direct visual access to unique details related to spatial resolution, and concomitant image quality, not apparent from the PSF. The effects of critical system and sample parameters like signal-to-noise ratio and bulk scattering are present in the recorded signal from which contrast is determined. Differences between OCT system configurations under particular imaging conditions, such as low spatial frequency content, are readily observed and quantified. When a simple test is needed, such as for quality assurance in a clinical setting, even a single spatial frequency could suffice to provide a qualitative visual assessment or “pass/fail” criterion. Such a test can also readily incorporate the effects of logarithmic intensity transformation and display scaling of the OCT device.

There are a variety of improvements in thin-film fabrication which may benefit phantom development for optical imaging. We plan to investigate enhanced fabrication techniques, such as a modified PDMS formulation [20] and coating procedure [14], to realize thinner layers (~2 μm) with suitable thickness precision and control of optical properties. Such phantoms are needed to fully challenge devices with high axial resolution. Additionally, increased consistency in executing particular steps in the fabrication process can offer improvement of thickness precision and homogeneity of scatterer distribution, both of which would reduce variability in contrast measurements. The current study utilized separate phantoms for each spatial frequency as a proof-of-principle for the fabrication and CTF analysis; however, it would be straightforward to create a single phantom with all the spatial frequencies by simply taking a small piece from each phantom and affixing them onto a single substrate, with each spatial frequency labeled for ease of use.

Thin-film fabrication approaches can also be applied to development of biologically realistic phantoms to simulate tissues with micro-scale layers of varying scattering coefficients. For example, it may be possible to replicate retinal layers which vary widely in both backscattering and thickness. Furthermore, thin-film phantoms may be useful for assessment of a range of other optical devices from confocal or two-photon microscopy systems to fluorescence and reflectance spectroscopy or microscopic photoacoustic imaging systems.

4. Conclusions

We have fabricated and characterized novel multilayer thin-film phantoms for system-independent assessment of OCT axial resolution characteristics, thus enabling the determination of the axial CTF, a fundamental figure of merit of imaging systems. The resolution capabilities of an OCT device can be readily visualized and quantitatively characterized with these phantoms. The availability of stable, well-characterized layered phantoms for axial OCT resolution evaluation can offer device developers and users an effective means to critically assess and compare one of the most important aspects of OCT device performance.