Super-resolution spectral estimation of optical micro-angiography for quantifying blood flow within microcirculatory tissue beds in vivo

Abstract

In this paper, we propose a super-resolution spectral estimation technique to quantify microvascular hemodynamics using optical microangiography (OMAG) based on optical coherence tomography (OCT). The proposed OMAG technique uses both amplitude and phase information of the OCT signals which makes it sensitive to the axial and transverse flows. The scanning protocol for the proposed method is identical to three-dimensional ultrahigh sensitive OMAG, and is applicable for in vivo measurements. In contrast to the existing capillary flow quantification methods, the proposed method is less sensitive to tissue motion and does not have aliasing problems due fast flow within large blood vessels. This method is analogous to power Doppler in ultrasonography and estimates the number of red blood cells passing through the beam as opposed to the velocity of the particles. The technique is tested both qualitatively and quantitatively by using OMAG to image microcirculation within mouse ear flap in vivo.

1. Introduction

Optical coherence tomography (OCT) is a depth-resolved cross-sectional non-invasive three-dimensional (3D) optical imaging modality for measuring and visualizing morphological features within highly scattering sample using interference of near-infrared light [1,2]. Recently, Fourier-domain OCT (FD-OCT), including spectral domain OCT (SD-OCT) [3] and swept-source OCT (SS-OCT) [4,5], has been developed, which has been widely used in research and clinical applications. Due to the relative transparent optical properties of human eye, ophthalmology is a perfect application for OCT. OCT has shown promising results in structural and functional imaging of posterior segment of the eye (retina, optic nerve head and choroid) [6–9], anterior segment of the eye (cornea, iris and lens) [10,11] as well as their mechanical properties [12,13] for diagnosis, monitoring and preventing many eye disease such as glaucoma [14], diabetic retinopathy [15] and age-related macular degeneration [16].

Similar to ultrasound imaging, OCT functional and hemodynamic information can be acquired in addition to structure information. Optical micro-angiography (OMAG) is a label-free non-invasive imaging and processing method to obtain 3-D blood perfusion map in microcirculatory tissue beds in vivo using FD-OCT [17,18]. Ultrahigh-sensitive OMAG (UHS-OMAG) is an variation of OMAG technique, capable of imaging microvasculature with capillary detail [19–21], in which data acquisition is often based on repeated B-scan (frame) acquisition at the same spatial location [21], and then separating dynamic scatters (e.g. moving red blood cells within patent vessels) from static scatters (e.g. structure tissue) by the use of phase-compensated subtraction [22] or eigendecomposition-based [23] (ED-) OMAG algorithms. By synergistically utilizing both the amplitude and phase information of complex OCT signals, the OMAG technique is sensitive to both the axial and transverse blood flows, providing blood flow map at small vessels and capillaries as well as larger vessels. UHS-OMAG has been applied to visualize blood perfusion and micro-vasculature map in various living tissues such as retina [22], brain [24], renal [25] and skin [21]. Hemodynamic quantification can be very useful in the investigation of cancer, stroke and some other disease which involve vascular components. However, UHS-OMAG is mostly known so far as a qualitative method and its quantitative capabilities have not been fully explored yet.

There are several methods reported in the literature that attempt to quantify and visualize blood flow in micro-vessels and capillaries by contrasting them from stationary and/or slowly-moving surrounding tissues (e.g. subject movement). Depending on the component of the signal used for flow velocity measurement, functional OCT hemodynamic imaging can be divided into three main categories: the methods that utilize phase component, amplitude component and complex signal (both phase and amplitude).

Some methods such as phase-resolved Doppler OCT (PRDOCT) utilize only OCT phase information [26,27]. In PRDOCT, the phase difference between A-lines acquired at the same spatial location is related to the blood flow velocity passing through probing beam. Although variance of the phase information may be sensitive to blood flow in lateral direction [28], most of the phase-resolved methods are based on the Doppler Effect, which restricts it to mainly characterize the axial component (parallel to the OCT beam) of the flow velocity. However, phase-resolved methods are difficult to detect slow flow within small blood vessels, including capillaries, in part due to phase noise arising from the surrounding static tissues [29], and in part also due to the required fast imaging speed to image faster flows to avoid aliasing. Since the phase information can be unstable in some systems, e.g. SS-OCT, and is highly influenced by tissue motion and system noise, several methods only use the amplitude value (intensity) of the OCT signals to contrast the blood flow signals. The intensity-based methods are based on the speckle effect and are capable of characterizing the transverse component (perpendicular to the OCT beam) of the flow velocity. Intensity-based Doppler variance algorithm [30], amplitude speckle [31], intensity threshold binarization-based method [32], split-spectrum amplitude-decorrelation angiography method [33], logarithmic intensity-based motion contrast methods [34] and amplitude autocorrelation (AAC) method [35] are among the intensity-based methods.

Based on OMAG approach, there are also some other methods which utilize both OCT phase and amplitude information such as single-pass volumetric bidirectional blood flow imaging [36]. Utilizing both phase and amplitude information of the OCT signal can potentially sense both axial and transverse components of the flow velocity (absolute blood flow velocity). However, most of the above methods were only sensitive to fast flow in larger vessels and blood flow at capillary level was not well characterized. Based on AAC method [35], Srinivasan et al. [37] proposed complex autocorrelation (CAC) method which utilized OCT complex signal instead of only the amplitude information of the OCT signal.

In CAC method, the widening of the bandwidth in the power spectral density (PSD) of autocorrelation function of the input data around Doppler frequency is estimated (instead of the Doppler center frequency). Such estimation gives rise to an opportunity to estimate the absolute blood flow velocity in the capillaries and vessels. The advantage of CAC method is its sensitivity to slow flow in capillaries but without capability to distinguish the flow direction. In addition, CAC method requires capturing a large data set (a long acquisition time in other words), is sensitive to tissue motion, exhibits artifacts at the vessel boundaries and has aliasing in vessels with fast flows.

All of the existing methods are not capable of dynamically estimating and separating moving tissues from stationary tissues, and usually a static high-pass filter should be designed. Dynamic estimation requires adaptively changing the filter characteristics based on the input signal while static estimation often makes some assumptions about the input signal to design a filter with fixed parameters. Also, the frequency resolution of flow estimation highly depends on the number of available discrete Fourier transform (DFT) points that itself depends on the number of A-line acquisitions per location. There is always a trade-off between frequency resolution and number of acquired data points and scanning time. Moreover, the total scanning time for three-dimensional in vivo applications is relatively long and the flow estimation is highly sensitive to respiratory and circulatory induced tissue motion.

In this paper, we propose a super-resolution spectral estimation technique which quantifies hemodynamics in micro-vessels from UHS-OMAG data. The proposed technique can dynamically estimate and separate the flow from stationary tissue using both amplitude and phase information which makes it sensitive to both axial and transverse flow. The scanning protocol and total scanning time are identical to 3-D ultrahigh sensitive optical micro-angiography and it does not have aliasing at large vessels. In contrast to traditional spectral estimation techniques, the resolution of this frequency estimator is not directly dependent on the number of sample points, which makes it a super-resolution approach. Also, the proposed method is less sensitive to tissue motion. Therefore, this method is capable of quantifying blood flow in microvasculature and capillary beds for in vivo applications.

2. Proposed method

Multiple signal classification (MUSIC) is a super-resolution spectral estimation technique in the class of noise subspace frequency estimators which is based on the principle of orthogonality [38]. The estimator relies on this property that the noise subspace eigenvectors of the autocorrelation matrix (or the data matrix) are orthogonal to the signal eigenvectors, or any linear combination of the signal eigenvectors [39]. MUSIC is advantageous over widely used, so-called maximum-likelihood method of Capon [40] and Burg’s maximum entropy method [41]. The latter methods have certain fundamental limitations in sensitivity and parameter estimation bias, because of their use of an incorrect autoregressive model rather than autoregressive and moving average. In contrast to the classical spectral estimation methods, such as periodogram and correlogram [39] that use fast Fourier transform (FFT), the frequency resolution of MUSIC is independent of the number of FFT points, which makes it a super-resolution method.

We model OCT measurement at each voxel to be superposition of tissue signal (stationary and non-moving structure information), hemodynamic signal (mostly influenced by moving red blood cells) and noise (shot noise and system noise). Assuming that these components are independent and can be decomposed into orthogonal basis functions, MUSIC has the capability to separate those components.

The interference signal of one A-scan captured in FDOCT can be expressed by

$$I(k)=S(k)E_R^2+2S(k)E_R{\displaystyle {\int }_{-\infty }^{\infty }a(z)\cos (2knz)dz}+2S(k)E_{R}a(z_1)\cos [2kn(z_1-vt)]$$ (1)

where I(k) is the light intensity detected at a wavelength with wavenumber of k at time t, E_R is the light reflected from the reference mirror, S(k) is the spectral density of the light source used at k, n is the refractive index of the tissue, z is the depth coordinate, a(z) is the amplitude of the backscattered light and z_l is the depth from which the light back scattered from, and ν is the velocity of moving blood cell in a blood vessel which is located at depth z_l.

In Eq. (1), the first term is a dc component produced by the light reflected from the reference mirror. The second term is the spatial frequency component of the static tissue sample, which provides static structural information (i.e. morphological features) of the sample. The third term is contributed from moving particles such as red blood cells in the tissue sample. The dc component can be easily subtracted from the equation by removing a common average from A-lines [42].

Assuming that the 3D OCT signal at each voxel is given by a complex value x[n], where n corresponds to the temporal sampling at that voxel location, we can decompose x[n] in terms of its exponential basis function, given by

$$x\left[n\right]= {\displaystyle \sum }_{i=1}^P{a}_i{e}^{j\left(n{\omega }_i+{\varphi }_i\right)}$$ (2)

where p is the total number of orthogonal components in the signal, ω_i is the angular frequency of each component, and a_i and φ_i are the amplitude and phase of that component, respectively. Then, the autocorrelation function of x[n] is given by

$$r_{xx}\left[k\right]=E\left\{x\left[n\right]x\left[n-k\right]\right\}={\displaystyle \sum }_{i=1}^P{A}_i{e}^{jn{\omega }_i}$$ (3)

where A_i = a_i². Based on different autocorrelation lag values for |k| = 1,…,M, the autocorrelation matrix is given by

$$R_{xx}= \left[\begin{array}{cc}\begin{array}{cc}{r}_{xx}\left[0\right]& r_{xx}\left[-1\right]\\ r_{xx}\left[1\right]& r_{xx}\left[0\right]\end{array}& \begin{array}{cc}\cdots & r_{xx}\left[-\left(M-1\right)\right]\\ \cdots & r_{xx}\left[-\left(M-2\right)\right]\end{array}\\ \begin{array}{cc}⋮& ⋮\\ r_{xx}\left[M-1\right]& r_{xx}\left[M-2\right]\end{array}& \begin{array}{cc}\cdots & ⋮\\ \cdots & r_{xx}\left[0\right]\end{array}\end{array}\right]$$ (4)

where M is the number of temporal samples.

If M>p (acquiring more samples than the number of signal components), then

$$Rank\left\{R_{xx}\right\}=\min \left\{M,P\right\}=P.$$ (5)

Let the eigenvalues of R_xx be λ₁ ≥ λ₂ ≥ λ₃ ≥ … ≥ λ_M, corresponding to the normalized eigenvectors u_1, u_{2 …,} u_M. Then, the eigendecomposition of R_xx is given by

$$R_{xx}={\displaystyle \sum }_{i=1}^M{\lambda }_i{u}_i{u}_i^H.$$ (6)

Since R_xx is of rank p, then λp + ₁ = λp + ₂ = … = λ_M = 0 and R_xx can be represented by its first p eigenvalues and eigenvectors given by

$$R_{xx}={\displaystyle \sum }_{i=1}^P{\lambda }_i{u}_i{u}_i^H.$$ (7)

The eigenvectors {u_1, u_{2 …,} u_p} are the principal eigenvectors of autocorrelation matrix R_xx that spans the signal subspace. We can write the autocorrelation matrix as

$$R_{xx}={\displaystyle \sum }_{k=1}^P{A}_k{s}_k{s}_k^H=SA{S}^H$$ (8)

Where S_MxP = [S₁ S₂ … S_p], Si = [1 e^jωi e^j2ωi … e^j(M-1)ωi]´ and A = diag([A₁ A₂ … A_p]). H is the matrix Hermitian (complex conjugate transpose) and diag([•]) is a diagonal matrix. The vector space S_MxP = [S₁ S₂ … S_p] is called the signal subspace of {x[n]}

Based on the noise subspace principles [39], a frequency estimator function can be developed that exhibits pseudo-spectrum plots with sharp peaks. Theoretically, the M-P noise subspace eigenvectors {u_{p + 1,} u_{p + 2 …,} u_M} of the autocorrelation matrix of M total eigenvectors and p principle eigenvectors {u_1, u_{2 …,} u_p}, will be orthogonal to the sinusoidal signal subspace vector (S). Therefore, a linear combination with an arbitrary weighting α_k is given by

$${\displaystyle \sum }_{k=P+1}^M{\alpha }_k{\left|S^H\left(\omega \right)u_k\right|}^2=S^H\left(\omega \right)({\displaystyle \sum }_{k=P+1}^M{\alpha }_k{u}_k{u}_k^H ) S\left(\omega \right)$$ (9)

where S(ω) = [1 e^jω e^j2ω … e^j(M-1)ω]´ is the sinusoidal vector that would be zero if evaluated at S(ω_i) = S_i, one of the input sinusoidal signal frequencies. Therefore, the MUSIC spectral estimator function

$$P\left(\text{ω}\right)=\frac{1}{{{\displaystyle \sum }}_{k=p+1}^M{\left|S^H\left(\omega \right)u_k\right|}^2}$$ (10)

will theoretically have an infinite value if evaluated at one of the sinusoidal signal frequencies (ω = ω_i). In practice, the MUSIC frequency estimation function is finite due to estimation error, but exhibits a local maximum (i.e. a peak) at the sinusoidal frequencies. Locating the peak and its corresponding value will be an indicator of the hemodynamics at the voxel of interest. Accurate estimation of the hemodynamic velocity (frequency) requires temporal sampling at Nyquist rate [43]. However, the estimated peak value P(ω_i) is less dependent on the sampling rate and its biased estimate can be acceptable, even when frequency aliasing happens. This concept is analogous to the difference between ultrasound color Doppler (CD) [44] and power Doppler (PD) [45,46] modes. In CD mode, the Nyquist sampling rate is essential for accurate estimation of directional flow velocity and the temporal sampling rate should be above the Nyquist rate to avoid aliasing. In this mode, the center of Doppler frequency shift is estimated and visualized. In PD mode, the power of the shifted Doppler signal on the spectrum is estimated rather than its center frequency. This allows estimating the number of particles passing through the beam. PD has higher sensitivity than CD and is independent of velocity and direction of flow and vessel-beam angle [45,46].

The backscattered OCT signal has relatively higher signal-to-noise ratio (SNR) at stationary and non-moving tissue boundaries because the structure pattern is repeatable. However, the backscattered signal from moving scatters such as moving red blood cells inside patent vessels is typically weaker and temporally varying. Since the tissue component is always stronger than the hemodynamic component, their corresponding MUSIC eigenvalues will be in order so that the larger eigenvalue belongs to tissue signal subspace while smaller eigenvalue belongs to the hemodynamic signal subspace. Therefore, their corresponding subspaces can be separately estimated.

In MUSIC, the number of input signal components (P) is a user-defined input variable. By defining the number of input signal components to be P = 2, the largest peak in the MSUIC pseudo-spectrum of UHS-OMAG data corresponds to the stationary tissue and the second largest peak corresponds to the hemodynamics. We can also approach this problem by first removing the stationary and non-moving tissue structural components (also known as clutter) from the input data, and then characterizing the remaining component which corresponds to the hemodynamics. This can be done using eigendecomposition-based clutter rejection filtering technique [23], which is performed on repeated A-lines at the same spatial location. The advantage of this approach is that after removing the clutter, a mask image based on the remaining flow information can be created and MUSIC is performed only on the voxels with high flow value, which would dramatically reduce the total processing time.

3. System set up and experiment preparation

3.1 System set up

In this study, we used an SD-OCT system to test and validate the proposed super-resolution spectral estimation technique. The SD-OCT system is schematically shown in Fig. 1A, in which the light source was a superluminescent diode (SLD, DenseLight, Singapore) with the center wavelength of 1310 nm and bandwidth of 65 nm. This light source gave an axial resolution of ~12 μm in the air. An optical circulator (OC) was used to couple the light from the SLD into fiber-based Michelson interferometer. In the reference arm of the interferometer, a stationary mirror was utilized after polarization controller. In the sample arm of the interferometer, a microscopy objective lens with 18-mm focal length was used to achieve ~5.8 μm lateral resolution. The backscattered light from the sample and the reflected light from the reference mirror were recombined at the 2 × 2 optical fiber coupler. Since the wavelength of the light source is invisible to the human eye, a 633-nm laser diode was used as a guiding beam to locate the imaging position. This guiding beam helps adjust the sample under the OCT system and image the desired location. The recombined light was then routed to a home-built high-speed spectrometer via the optical circulator (AC Photonics, USA). In the design of the spectrometer, a collimator with the focal length of 30 mm and a 14-bit, 1024-pixels InGaAs linescan camera (SUI, Goodrich Corp) were used. The camera speed was 47 000 lines per second. The spectral resolution of the designed spectrometer was ~0.141 nm that provided a detectable depth range of ~3.0 mm on each side of the zero-delay line. The system had a measured signal to noise ratio of ~105 dB with a light power on the sample at ~3 mW. The mouse ear pinna was used as a living sample in the experiments with the goal to visualize and quantify the blood flow with microcirculatory tissue beds.

Fig. 1.

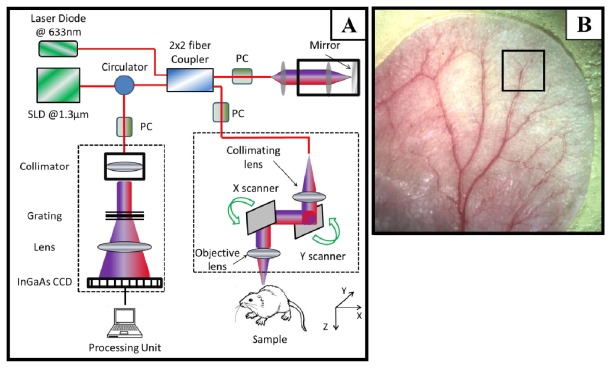
(A) Schematic diagram of the imaging system. (B) A digital image of the mouse ear pinna flat mounted. The rectangle on the ear shows a typical OCT imaging field of view which is 2.2 × 2.2 mm² in our experiment.

3.2 Animal preparation

Non-invasive in vivo images were acquired from pinna of healthy ~8 weeks old male hairless mice weighing approximately 28g. During experiments, the mouse was anesthetized using 2% isoflurance (0.2 L/min O₂, 0.8 L/min air). The ear was kept flat on a microscope glass. The animal was placed in supine position on a heating blanket (Harvard Apparatus). The animal internal body temperature was constantly monitored using an intra-rectal temperature monitoring system which was used to actively maintain the animal body temperature by the use of temperature feedback provided by the heating blanket. The experimental protocol was in compliance with the Federal guidelines for care and handling of small rodents and approved by the Institution Animal Care and Use Committee (IACUC) of the University of Washington, WA.

A photograph of a mouse ear pinna captured by a digital camera is shown in Fig. 1B, in which the rectangle shown is a typical field of view and scanning range for OCT (~2.2 × 2.2 mm²). In order to scan a larger field on the ear, we used a mechanical translating stage to move the tissue sample to the desired location and after acquisition and processing, the mosaics were stitched together to form a larger image.

3.3 Scanning protocol

The scanning protocol was based on three-dimensional UHS-OMAG technique. The x-scanner (fast B-scan) was driven with a saw tooth waveform and the y-scanner (slow C-scan) was driven with a step function waveform. The fast and slow scanners covered a rectangular area of ~2.2 × 2.2 mm² on the sample. Each B-scan consisted of 400 A-lines covering a range of ~2.2 mm on the sample. The duty cycle of the saw tooth waveform rising edge was set at ~80% per cycle, which provided a B-scan frame rate of ~94 frames per second. The C-scan consisted of 400 scan locations with B-scan repetition of 8 frames per location for flow imaging and quantification. The total size of the data set was 1.28 × 10⁶ A-lines and total acquisition time was 32 seconds. The captured data was processed off-line using MATLAB^© (MathWorks).

4. Experimental results and discussion

4.1 MUSIC-OMAG visualization

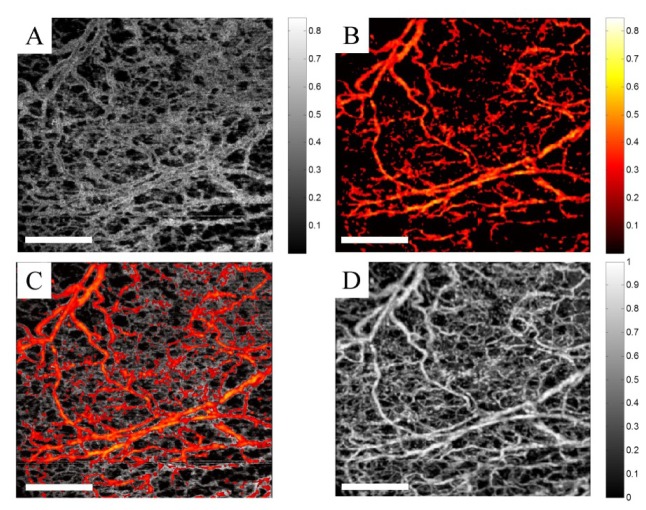
For better visualization of MUSIC-OMAG quantification, we divided the dynamic range of MUSIC power (P(ω)) into two bands: the lower-band and the upper-band power, which were separated using a threshold value. The threshold was manually set to a value such that blood flow in small vessels and capillary loops were separated from that of larger vessels. This threshold value can be variable depending on the sampling rate and the structure to be imaged and the user can arbitrarily choose it based on the characteristics to be emphasized. We should note that this threshold value is only for visualization purposes and does not have any impact on the quantification itself. The upper-band was color coded and overlaid on the gray-coded lower band. Figures 2A-2C show the lower-band power (gray), upper-band power (color-coded) and combined power, respectively. We set the threshold such that the lower-band power corresponded to the slower flow inside small vessels and capillary loops. Due to the parabolic flow profile inside vessel lumen, the lower-band power is also expected near vessel wall in larger vessels while the upper-band power is expected towards the large vessel center line. Figure 2D shows the corresponding UHS-OMAG processing of the same data set. By comparing UHS-OMAG and MUSIC-OMAG, it can be observed that they are almost identical and all of the small vessels and capillaries observed on UHS-OMAG can also be found in MUSIC-OMAG which confirms the sensitivity of MUSIC-OMAG quantification.

Fig. 2.

MUSIC-OMAG visualization. (A) Lower-band power, gray-coded. (B) Upper-band power, color-coded. (C) Combined MUSIC-OMAG power, where upper-band power is overlaid on the lower-band power. (D) UHS-OMAG of the corresponding data set processing using ED method (The scale bar = 500 μm).

The entire mouse ear pinna was divided into 2.2 × 2.2 mm² overlapping mosaics and each mosaic was scanned using UHS-OMAG scanning protocol. Then, the mosaics were processed separately using ED-OMAG and MUSIC (for quantification) and their corresponding maximum intensity projection maps were stitched together to form the entire ear pinna en-face angiogram. Figures 3A and 3B show the UHS-OMAG and MUSIC-OMAG images of the mouse pinna, respectively. It can be observed in MUSIC-OMAG image that the larger arteries and veins are dominated by upper-band power and color-coded while smaller vessels and capillary loops toward the pinna edge are mainly dominated by lower-band power and gray-coded. This quantification and visualization technique allows observing certain response in capillary loops while the change in larger vasculature is not significant. Figures 3A and 3B are resulted by using two different algorithms: ED-UHS-OMAG (for visualization of blood flow perfusion) and MUSIC-OMAG (for quantification of blood flow perfusion or flux rate). We should emphasize that these algorithms are different in nature. ED-UHS-OMAG is based on processing A-line by A-line, whereas MUSIC-OMAG is based on voxel-processing by the use of the proposed algorithm. Assuming that the signal is divided into tissue, blood and noise contributions, tissue and blood flow contributions are estimated by orthogonality principle (Eq. (9). The estimated contributions will have a center frequency (ω, i) and a corresponding spectral power [P(ω_i)] estimated using Eq. (10). For better visualization of capillaries and large vessels using different color-maps, these results are visualized using the method explained in Fig. 2. Again, we have to emphasize that the data acquisition protocol and scanning pattern is similar to the ones previously used for UHS-OMAG visualization, and we propose to quantify blood flow perfusion within capillary beds using the proposed MUSIC-OMAG algorithm.

Fig. 3.

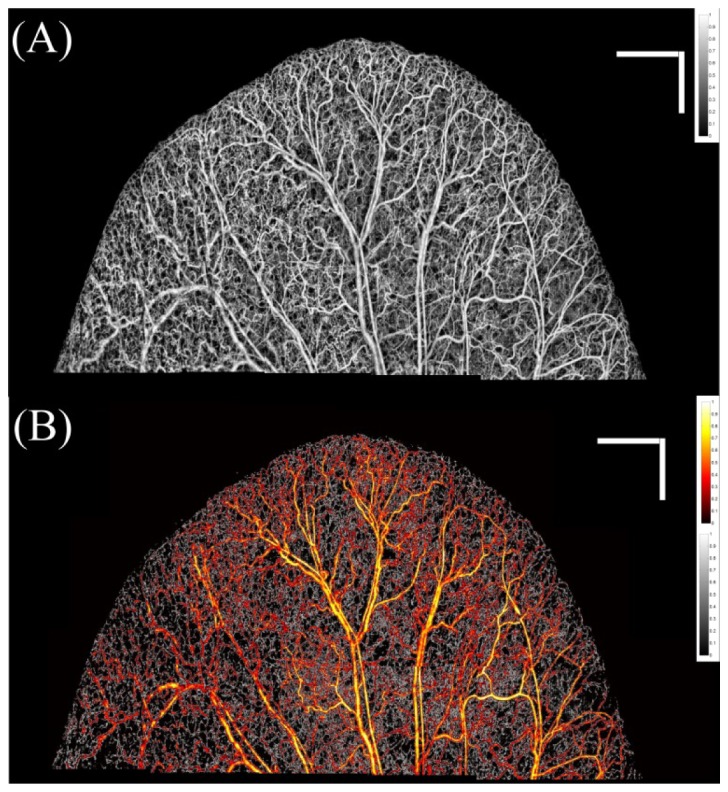
(A) UHS-OMAG image of the entire mouse ear processing using ED method, stitched together. (B) MUSIC-OMAG processing of the same data set of (A). Large vessels and faster flow are color-coded while slower flow and capillary loops are gray-coded. The bar size is 1x1 mm.

During the experiments, the animal’s body temperature was actively maintained by the feedback loop provided by the heating blanket, while the OCT system was continuously capturing the UHS-OMAG data set over the time. Over the time period of 60 minutes, due to the active control of body temperature by the feedback loop, the temperature was changed from 37 °C, gradually raised to 39.5 °C followed by a gradual drop to 32 °C, and then returned back to the 37.6 °C which was the target temperature for normal physiological condition. Accidently, this feedback control process gave us an opportunity to monitor the microcirculation response to the changes of body temperature, asserting the sensitivity of MUSIC-OMAG to capillary hemodynamic variations. On the other hand, this process also simulated the process of a thermoregulatory experiment in terms of physiological process. At the body temperature of 39.5 °C, the animal experienced hyperthermia, while a body temperature of 32 °C leaded to hypothermia for the animal. Because we continuously captured the UHS-OMAG data at the same location over the whole process, we processed the data set to obtain the response of microcirculation within the tissue beds to the changes of the body temperature. Compared to normothermia (37.6 °C), we expect that the capillary flow activity should increase (vasodilation) during hyperthermia, while it should decrease (vasoconstriction) during hypothermia. Although, transient vasodilation, vasoconstriction and blood flow response to temperature challenge is a multi-factorial phenomenon and can be very complicated in nature [47], we expect that hemodynamic should follow a hysteresis-like curve in response to thermoregulatory challenge in the current study.

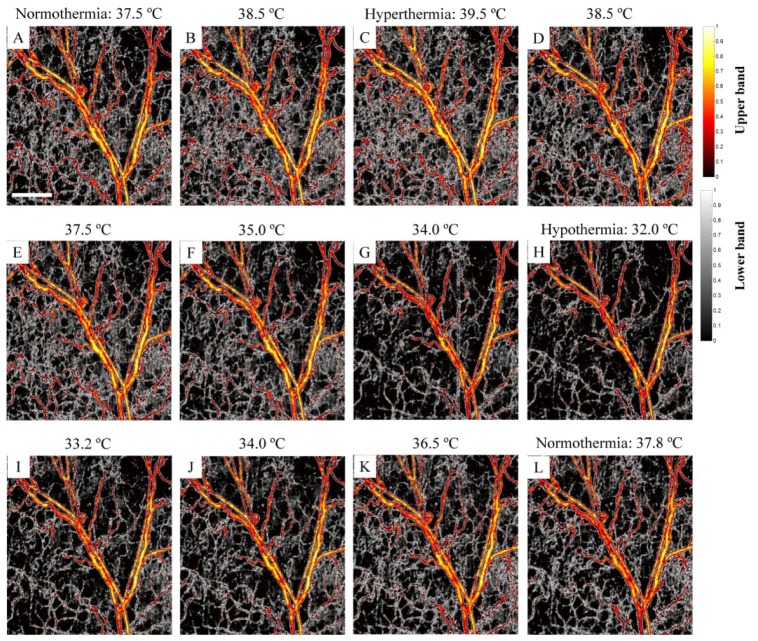
Figure 4 shows a series of the dynamic MUSIC-OMAG images captured during active feedback control of the heating blanket to the body temperature of the animal used, where the response of the capillary flow to the temperature change can be observed. The increase of the body temperature towards hyperthermia (39.5 °C) leads to the increase of the density of capillary network in the areas in between larger vessels; and in the meantime, some new capillaries appeared (e.g., green pointer in Fig. 4C), demonstrating the increase of blood flow within microcirculatory tissue beds during hyperthermia. These changes were mostly observed at capillary level where the density of gray-coded areas corresponding to small vessels and capillaries was increased. During the feedback control of the body temperature towards hypothermia (32.0 °C), it was observed that most of the small capillaries disappeared and blood flow in some larger vessels also decreased (e.g. green pointer in Fig. 4H). However, these changes were more obvious at capillary level shown by gray map which corresponds to lower-band power. By the increase of the body temperature towards normothermia (37.6 °C), the functional capillaries which were missing in hyperthermia appeared again. At this point, the appearance of the blood vessel network was very similar to the baseline image at 37.5 °C (e.g. green pointer in Fig. 4L).

Fig. 4.

MUSIC-OMAG monitoring the vasculature response to the thermoregulatory challenge. During the hyperthermia (39.5 °C), new capillaries appear while most of the small vessels and capillaries disappear during hypothermia (32.0 °C), and they go back to the baseline image when returning to normothermia (37.8 °C) (The scale bar = 500 μm).

Total blood flow rate at capillaries is related to blood flux which is the rate of red blood cells passing through a unit area cross-section. Assuming that the MUSIC power estimates blood flux, we can estimate total blood flux by integrating these values in a given region of interest. We measured mean and standard deviation of total blood flux in Figs. 4A-4L. Then, we normalized the mean value by the total blood flow in the beginning of normothermia and plot it as a function of temperature in Fig. 5A. As we expected, total blood flow increased during the hyperthermia, decreased during hypothermia and almost went back to the baseline. We also measured the normalized vessel area density [48] of the ear and plot it over the temperature values in Fig. 5B. As we already observed from the vessel map, the vessel area density increased during hypothermia which means that more capillaries appeared. During hypothermia, the vessel area density decreased which was observed in Fig. 4H that small capillaries disappeared. By increasing the temperature and moving towards normothermia, more capillaries appeared again, therefore vessel area density increased. Measuring total blood flow requires some assumptions and calibration. What we’re measuring here is a function of number of particles passing through the beam at a vessel cross-section and their velocity. In order to measure total blood flow, more parameters would be required.

Fig. 5.

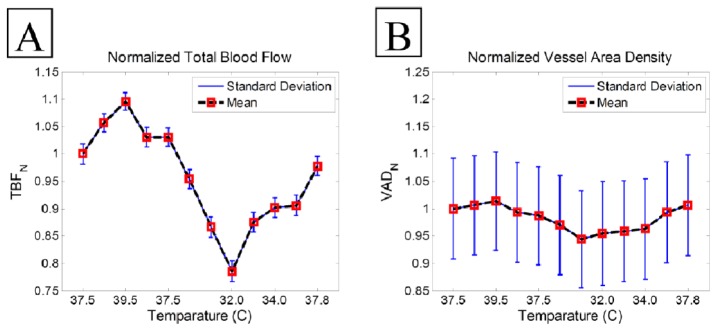
Normalized total blood flow (A) and normalized vessel area density (B) average in response to the thermoregulatory challenge.

4.2 Flow profile measurement

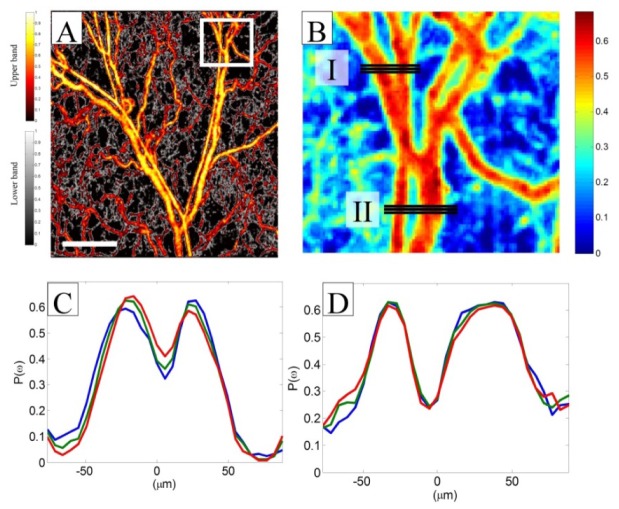
Normal blood flow inside relatively large blood vessels is not uniform at the vessel cross section and has a parabolic distribution with the maximum value at the center of the vessel and slower towards the vessel wall. Parabolic or laminar flow allows minimum loss kinetic energy and fluid pressure transfer and reduces friction by allowing the blood layers to slide smoothly over each other in concentric layers or laminae [49]. Therefore, we expect a parabolic quantity across the vessel cross-section after quantifying the flow using MUSIC-OMAG. Figure 6A shows the en-face view of maximum-intensity projection map of MUSIC-OMAG quantification of micro-vasculature in the mouse ear pinna in a 2.2x2.2 mm² area color-coded with the thresholding visualization technique. Figure 6B is the zoomed area of the designated white rectangle in Fig. 6A visualized with a different color map for simplification. Three flow profiles at two vessel locations marked by solid lines (I and II) are shown in Figs. 6C and 6D, respectively. We plotted the flow profile of each horizontal line of Fig. 6B such that X-axis is given by horizontal line in μm and Y-axis is the estimated MUSIC-OMAG power P(ω) (normalized units) and each color (red, green and blue) corresponds to one plot. Three consecutive locations were plotted to confirm their similarities along the vessels and repeatability of MUSIC-OMAG. It can be observed that the flow profile meets a typical laminar flow profile inside vessels where the flow value is largest in the middle of the vessel and decreases towards the vessel wall. Also, the flow goes to nearly zero outside vessels where no flow exists. In the areas that other capillaries are present at a different depth plane above or below the vessel of interest, the flow profile may not completely go below the noise level. This phenomenon is more obvious in Fig. 6D. Since there are two vessel branches in the Figs. 6C and 6D, two parabolic flow shapes are observed. Based on our knowledge of anatomy, the thinner vessel corresponds to an arteriole and the larger vessel is a venule. Therefore, blood flow direction in these pairs should be opposite of each other.

Fig. 6.

Flow profile characteristics of vessels using MUSIC-OMAG method. (A) MUSIC-OMAG processing. (B) Zoomed in version of (A) color-coded for better visualization. (C and D) Flow profile of the vessels marked in box (I) and (II) in (B), respectively (The scale bar = 500 μm).

4.3 Comparison

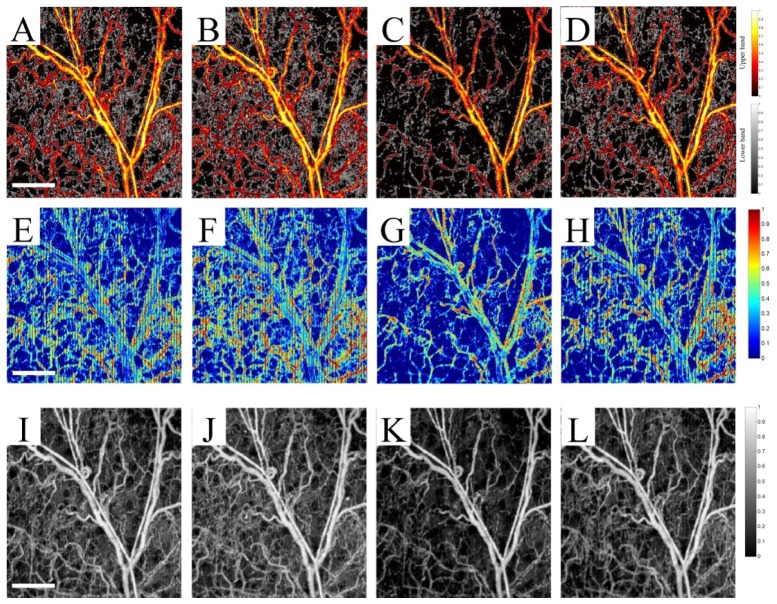
We compared MUSIC-OMAG with CAC method over four data sets from thermoregulatory experiments: normothermia (37.8 °C), hyperthermia (39.5 °C), hypothermia (32.0 °C) and return to normothermia (37.5 °C). Figures 7A-7D show the performance of MUSIC-OMAG on these data points, respectively. Similarly, Figs. 7E-7H show the performance of CAC method and Figs. 7I-7L show the corresponding UHS-OMAG processing of those data points. It can be observed that CAC was capable of picking up changes in the capillary blood flow. However, it was very sensitive to respiratory-induced motion, which showed up as vertical stripes on the image. Besides the observed artifacts on the vessel wall, the signal inside the large vessels was aliased, mainly due to the fast flow (fast relative to the Nyquist rate) and the received signal at that location was completely decorrelated. Although the background of UHS-OMAG images shown in Figs. 7I-7L was obviously lower during hypothermia, the variations between different data points were not as apparent as MUSIC-OMAG.

Fig. 7.

A comparison between MUSIC-OMAG (A-D), autocorrelation method (E-H) and UHS-OMAG (I-L) processing of the mouse ear capillary response to thermoregulatory challenge, where the first column (A, E and I) is the normothermia condition (37.5 °C), the second column (B, F and J) is hyperthermia condition (39.5 °C), the third column (C, G and K) is hypothermia (32.0 °C) and the last column (D, H and L) is return to the normothermia condition (37.8 °C) (The scale bar = 500 μm).

The performance of CAC method highly depends on the sampling rate (to avoid aliasing) and the number of data points (frequency resolution). Since the signal at each voxel decorrelates within few samples, the dynamic range of the CAC method is relatively small. Compared to UHS-OMAG and MUSIC-OMAG, the CAC method was sensitive to tissue motion which eventually caused vertical dark stripes on the image. Also, there were some artifacts on vessel walls and aliasing inside larger vessels which were not observed in MUSIC-OMAG.

While MUSIC-OMAG overcame these artifacts as well as the frequency resolution, it came with the price of computational power which was relatively longer than CAC. Processing time per frame on a 6-core processor (AMD Phenom(tm) II X6 1090T, 3.21 Ghz) desktop computer based on Matlab code implementation was 0.19, 2.78 and 12.15 seconds/frame for ED-based UHS-OMAG, CAC and MUSIC-OMAG, respectively. Another major advantage of MUSIC-OMAG over CAC is the data acquisition time and volume. Due to sensitivity of the frequency estimation technique to the frequency resolution, at least 128 samples per location were required to get a reasonably good estimate using CAC method. However, MUSIC-OMAG is performed on data acquired using UHS-OMAG scanning protocol which requires a significantly smaller data volume and time.

One way to increase the processing time is to mask the input data before MUSIC processing by UHS-OMAG. This allows processing only the voxels which are supposedly inside the vessels. We should emphasize that the characteristics of all of the quantification techniques such as CAC and MUSIC-OMAG highly depends on the received signal and the local conditions such as surface and specular reflection and absorption, which eventually may influence the repeatability of capillary flow quantification.

5. Conclusion

In this paper, we proposed a super-resolution spectral estimation technique to quantify hemodynamics in micro-vessels using optical coherence tomography. The proposed technique can dynamically estimate the flow using both amplitude and phase information which makes it sensitive to the number of particles passing through blood vessels. The total scanning time for 3-D application is identical to three-dimensional ultrahigh sensitive optical micro-angiography and it does not have aliasing at large vessels. Therefore, this method can efficiently quantify blood flow in capillary beds as well as large vessels. In order to test the sensitivity of MUSIC-OMAG to capillary hemodynamic variations, we utilized the experimental data set of UHS-OMAG, which were continuously acquired during active control of the body temperature of the animal, giving an opportunity to observe capillary flow response in the mouse ear pinna. We observed that the capillary network became denser in areas between larger vessels and some new capillaries appeared during hyperthermia, demonstrating the increase of blood flow within the microcirculatory tissue beds. During hypothermia, most of the small capillaries disappeared and blood flow in some larger vessels also decreased. When the body temperature returned to normothermia status, the capillaries appeared again. We also compared MUSIC-OMAG with CAC method over four data points during the change of the body temperature in the animal. We showed that the performance of MUSIC-OMAG was superior to CAC; and furthermore no apparent motion artifacts were observed at vessel walls and inside large vessels. Also, MUSIC-OMAG method was sensitive to small capillary response to the change of the body temperature. The flow profile at large vessels evaluated by the MUSIC-OMAG was in agreement with typical flow characteristics.