Improvement of axial resolution and contrast in temporally focused widefield two-photon microscopy with structured light illumination

Abstract

Although temporally focused wide-field two-photon microscopy (TFM) can perform depth resolved wide field imaging, it cannot avoid the image degradation due to scattering of excitation and emission photons when imaging in a turbid medium. Further, its axial resolution is inferior to standard point-scanning two-photon microscopy. We implemented a structured light illumination for TFM and have shown that it can effectively reject the out-of-focus scattered emission photons improving image contrast. Further, the depth resolution of the improved system is dictated by the spatial frequency of the structure light with the potential of attaining depth resolution better than point-scanning two-photon microscopy.

1. Introduction

Temporally focused wide-field two-photon microscopy (TFM) of ultrafast optical pulses is an imaging technique by which depth-resolved wide-field two-photon images can be acquired without the need for raster scanning of the focal spot [1,2]. Because of its simplicity and high-speed image acquisition capability, TFM has been adapted to various biological imaging applications such as 3D super-resolution imaging [3], cellular dynamics imaging [4] and the depth-resolved fluorescence and phosphorescence lifetime imaging [5]. In addition, TFM has been applied to single cell precision optogenetic control of neuronal activity [6,7] and high throughput microfabrication [8,9]. Recently, it has been also shown that TFM can maintain a uniform illumination field of view even in a highly scattering medium [10].

However, TFM suffers from a broader axial resolution when compared to the standard two-photon laser point scanning microscopy (TPLSM), which is caused by the under-utilization of the numerical aperture (NA) of the objective [11]. The FWHM axial resolution achieved to date is 1.6µm through optimizing the spectral width of the ultrafast pulse and the parameters of the intermediate optical elements which is still worse than TPLSM by a factor of two [3,8]. Further improvement in axial resolution down to 0.85µm FWHM was achieved by filling the back aperture of the objective with the spectrum of an ultrafast pulse that is dispersed in two dimensions at the expense of increasing complexity of the system [11]. More significant problem is that the axial extent of the excitation volume is progressively broadened in a turbid medium as the imaging depth increases, which further increases the background noise [12]. Recently, it has been shown that this effect can be partly avoided by using the line focused TFM which maintains axial resolution even at 2.5 scattering mean free path (MFP) [13].

Apart from a reduced axial resolution TFM uses imaging detectors such as a CCD or a CMOS. The resolution is based on the telecentric mapping of emission photons from the specimen plane to the image plane. For deep imaging, the scattering of emission photons degrades the image contrast obscuring the fine features of the specimen. In contrast, the scattered emission photons of TPLSM are integrated with a large area detector and the spatial structure and resolution of image depends only on the temporal sequence of the scanning process and the excitation point-spread function [14].

In this paper, we demonstrate that the use of structured light illumination (SLI) in TFM can effectively reject background scattered emission photons and thereby improve image contrast when imaging in a turbid medium. Equally importantly is that the axial resolution of this system is dictated by the spatial frequency of the structured light thereby allowing an axial resolution that is significantly better than TFM even in the absence of scattering. The core idea of this approach is that SLI acts as a virtual pinhole and the low frequency out-of-focus scattered photons beyond the depth of field of the objective can be removable computationally.

2. Methods of generating structured light illumination in TFM

A class of depth-resolved imaging techniques based on SLI have been proposed to select a particular imaging plane and to reject out-of-focus background for standard wide-field single-photon microscopy [15,16] and it has been shown that the axial resolution of these techniques is comparable to that of the confocal microscope [17,18]. Of these methods, one effective approach we adapted is termed ‘HiLo microscopy’ which generates an optically sectioned image by post-processing the uniformly illuminated image (UI) and the structured light illuminated image (SI) [16]. More specifically, the in-focused high frequency contents are extracted by high-pass filtering UI with a Gaussian shaped high-pass filter. The in-focus low frequency contents are extracted by low-pass filtering the absolute of UI subtracted by SI with the complementary low pass filter to the high pass filter. The cutoff frequency of the Gaussian filter is determined by the sinusoidal spatial frequency of the structured illumination. Subsequently, the optically sectioned image is obtained by combining the two with an adjusting factor so that the transition from low to high frequencies occur smoothly [19]. HiLo microscopy has been widely used in the context of background rejection for light-sheet microscopy [19,20], TFM [21,22] and depth-resolved microrheology [23].

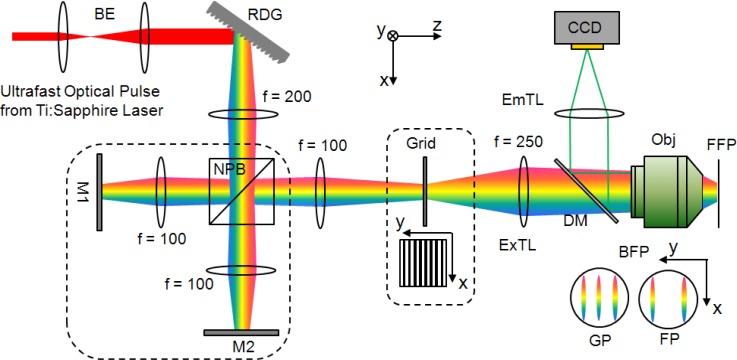
Figure 1 shows the schematic diagram of an SLI TFM based on a Michelson interferometer. Ultrafast optical pulses from Ti:Sappire laser with 100fs pulse width, 80MHz repetition rate at the center wavelength of 780nm (MaiTai, Spectra-Physics, Mountain View, CA) are diffracted off the reflective diffraction grating with the groove frequency of 600 grooves/mm (53004BK02-35IR, Richardson Grating Lab, Rochester, NY) and each spectral component of the beam is focused at the back focal plane of the objective (Zeiss C-Apochromat 40x, NA 1.2 water immersion, Zeiss MicroImaging, Thornwood, NY) that collimates each spectral components and recombine them at the focal plane of the objective to restore the original input pulse width.

Fig. 1.

Generating SLI is possible through either an interferometer or a grid. The interferometric setup shown here is much simplified for grid projection where the components in the dotted box are bypassed and the light goes directly from RDG through the f = 200mm and f = 100mm lenses before passing through the grid and onwards. BE: beam expander, RDG: reflective diffraction grating, NPB: non-polarizing beam splitter, M: mirror, ExTL: excitation tube lens, EmTL: emission tube lens, DM: dichroic mirror, Obj: objective, BFP: back focal plane, FFP: front focal plane, GP: grid projection, FP: fringe projection.

There are two possible methods of generating SLI. First, it can be generated by projecting a fringe (Fringe Projection (FP)) where the incoming beam diffracted off a grating is split by a beam splitter and travels down two separate arms. The angle of mirrors 1 and 2 are adjusted so that two parallel strips of pulse spectrum are focused at the back focal plane of the objective and they interfere at the front focal plane of the objective resulting in fringe pattern. The optical path length of the two arms is matched to maximize the contrast of SLI. The other method is projecting a grid (Grid Projection (GP)) where the grid is placed at a plane conjugate to both the grating and the front focal plane of the objective. The entire interferometric arm may be bypassed so that the incoming beam off the grating passes directly through the f = 200mm lens onto the f = 100mm lens before passing through the grid and the rest of the optical setup. In GP, there are three strips of focused spectrum at the back focal plane each corresponding to 0th and ± 1st order diffracted beam from the grid. The interference of these three orders generates the fringe pattern at the focal plane of the objective. SI and UI are obtained sequentially by manually blocking and unblocking one of the beam path in the Michelson interferometer for the case of FP. However, one could use the optical chopper to automate this process. For the case of GP, we manually move the grid in and out of the optical path at the position indicated in Fig. 1. Another way is to use two different beam paths of which one includes a grid and the other without a grid. SLI is accomplished by switching between the two beam paths with a galvanometer mirror as demonstrated by Ford et al. [24]. Finally, one may combine TFM with a spatial light modulator and generates an arbitrary excitation pattern for various applications which need patterned two photon excitation [4,7,25].

The intensity at the front focal plane of the objective for FP can be expressed as

$$I_{Fringe}=1+\cos (2k\sin {\theta }_{f}y)$$ (1)

where k is the wave number of the center wavelength and θ_f is the half angle between the two beams after the objective. Here, we ignore the complexity of the pulsed beam and take only the center wavelength and assume equal intensity for the two interfering beams. Likewise, the intensity for GP can be expressed as

$$I_{Grid}=1+4\alpha \cos (k\sin {\theta }_{g}y)\cos \left(k\left(\cos {\theta }_g-1\right)z\right)+2{\alpha }^2\left(1+\cos (2k\sin {\theta }_{g}y)\right)$$ (2)

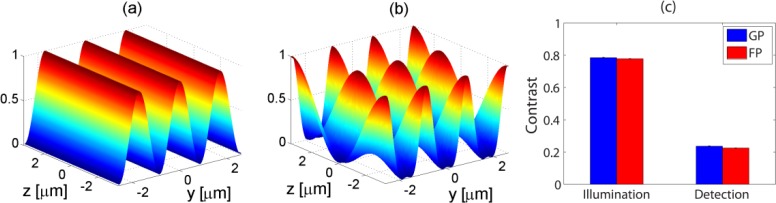
where α is the relative strength of the first order beam compared to zero order beam and θ_g is the angle between the zero order beam and the first order beam after the objective. In case of rectangular grid, α = 2/π. The 3D plots of both Eq. (1) and Eq. (2) are shown in Figs. 2(a) and 2(b) respectively. In case of GP the fringe pattern is formed not only laterally (along y-axis) but also axially (along z-axis). This property was utilized to increase the resolution both laterally and axially in a conventional wide-field microscope [26].

Fig. 2.

(a) The profile of the illumination fringe pattern of FP predicted by Eq. (1). (b) The profile of the illumination fringe pattern of GP predicted by Eq. (2). λ = 780nm, θ_f = 13.2 degree, θ_g = 27.2 degree, α = 2/π (c) The experimentally measured contrast of the coherent illumination fringe pattern and the incoherent detection fringe pattern of both FP and GP. Standard deviations are small compared to averages and not well visible in the plot.

The two methods of SLI generation are compared in terms of the fringe contrast and density. The contrast of the sinusoidal fringe pattern is defined as

$$\text{Contrast}=\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }}$$ (3)

Instead of using Eq. (3), we calculate the contrast of either case in the frequency domain from the recorded fringe patterns. This method is superior to the direct calculation of the contrast using Eq. (3) in that it is less affected by the shape of the illumination pattern and the local intensity variation due to the noise. For example, for the Gaussian illumination shape the sinusoidal fringe pattern is expressed as

$$f(y)=\frac{1}{2}(1+M\cos (ky))\cdot \exp \left(-\frac{y^2}{2{\sigma }^2}\right)$$ (4)

where M and k are the contrast and the spatial frequency of the sinusoidal fringe pattern respectively. The Fourier transform of Eq. (4) is

$$F(m)=\left[\frac{1}{2}\delta (m)+\frac{1}{4}M\delta (m-k)+\frac{1}{4}M\delta (m+k)\right]\otimes \left[\sigma \sqrt{2\pi }\exp \left(-\frac{{\sigma }^2{m}^2}{2}\right)\right]$$ (5)

where ⊗ represents convolution, δ(m) is delta function. Therefore, M can be calculated as follows.

$$M=2\frac{F(m=\pm k)}{F(m=0)}$$ (6)

The coherent illumination fringe pattern is recorded by reflecting SLI from a mirror placed at the focal plane of the objective. The emission filter in the detection path is removed to allow detection in the excitation wavelength. The incoherent detection fringe pattern is recorded by illuminating SLI on thin layer of Rhodamine solution. The thin Rhodamine solution is prepared by first dissolving Rhodamine power in alcohol and diluted to 300μM concentration. Then, a drop of Rhodamine solution is placed on the cover slip and covered with the same size cover slip and squeezed to form a meniscus around the edge of the cover slip. The volume of a drop of Rhodamine solution is determined by multiplying the area of the cover slip with the desired thickness that needs to be less than the axial resolution of TFM. The recorded image is a fluorescence image and the emission filter is placed in the detection path.

In principle, the contrast of the illumination fringe pattern for GP and FP should be close to 1 as long as the pulse spectrum is within the pass band of the coherent optical transfer function (OTF) of the excitation path as can be predicted by Eq. (1) and Eq. (2) and their plot in Figs. 2(a) and 2(b). The contrasts of the detected fringe pattern of thin Rhodamine solution are attenuated by the incoherent OTF of the detection path. The average and standard deviation of 10 independently measured contrasts for the structured illumination period of Tg = 1.71µm are summarized in Fig. 2(c), which shows 0.785 ± 0.002 and 0.778 ± 0.014 for GP and FP respectively in case of illumination and 0.236 ± 0.002 and 0.225 ± 0.001 for GP and FP respectively in case of detection. There are quite differences between the estimated contrast values shown in Fig. 3(a) and the measured contrast values. This could be attributable to the broad-band excitation and emission wavelengths. The estimated contrast of fringe pattern is based on the peak wavelength of both excitation and emission band. In case of illumination, the bandwidth of pulsed excitation laser has about 10nm FWHM (20nm full width). The sum of interference pattern by each individual wavelength components has the effect of adding a DC value and this reduces the contrast. In case of detection, this effect is much stronger since the emission band of Rhodamine has about 50nm FWHM (100nm full width). The other reason could be the out of focus background. The estimated thickness of the thin Rhodamine solution is 2um, which is thicker than the SLI resolution and the signal from out-of-focus background could reduce the contrast.

Fig. 3.

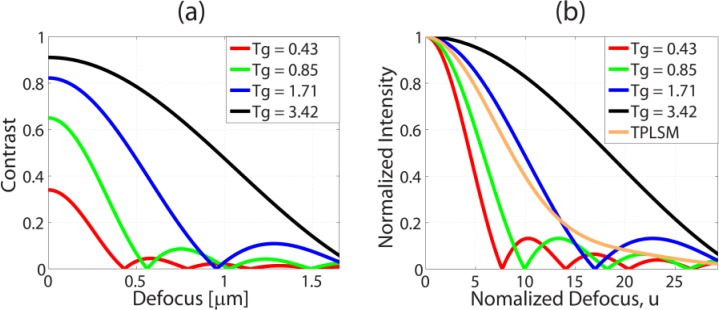
(a) Contrast decay of fringe pattern of the spatial period of Tg = 0.43, 0.85, 1.71, 3.42 µm as a function of the defocus (distance from focal plane). (b) Normalized intensity of SLI and TPLSM as a function of the normalized defocus unit.

In terms of the fringe pattern stability from the external disturbances such as mechanical vibration or air flow, GP is more stable than those obtained through FP since GP is essentially a common path geometry whereas FP is formed by the two different beam paths in Michelson interferometer. In instances when signal level is low and longer exposures are required, the contrast of FP is slightly worse than GP since the fringe pattern jitters due and the image of the fringe is smeared and therefore averaged during the exposure time. Practically, the power loss due to reflection from the grid surface is significant and this lowers the excitation efficiency.

The fringe density of the illumination pattern determines the signal to noise and the depth resolution of HiLo processed image. FP can generate higher density pattern than GP for objectives with limited aperture size such as GRIN lens. For example, in case of the fringe period of 1.71µm, θ_g is about two times larger than θ_f, which means the distance between + 1 and −1 order of the pulse spectrum of GP has to be two times larger than the distance between the two pulse spectrum of FP.

3. Depth resolution improvement using SLI in TFM

3.1 Theoretical estimation

It has been shown that the integrated two photon excitation (TPE) signal of TFM at an axial plane at position z decays proportional to z⁻¹ [27] whereas that of the TPLSM has z⁻² dependence. Also, the shape of this integrated TPE curve of TFM is similar to the square root of Lorentzian function [3], which has a long tail on both sides of the peak of the curve. Therefore, the axial confinement of the excitation volume of TFM is worse than TPLSM and the long tails of the excitation volume generate out-of-focus background. Thus, the use of SLI in TFM has the potential of removing such background signal and improving the axial resolution of TFM.

Theoretical axial resolution of SLI can be estimated using the defocused 2D OTF derived by Stokseth [28].

$$C\left(u,m\right)=f\left(m\right)\left\{\frac{2J_1\left(um\left[1-m/2\right]\right)}{um\left[1-m/2\right]}\right\}$$ (7)

where f(m) = 1 − 0.69m + 0.076m² + 0.043m³, m is the normalized fringe frequency and is related to the real fringe period T_g via m = λ/(T_g NA), NA = n sin(α) and u is the normalized defocus and is related to the actual defocus z via u = 4kznsin2(α/2), k = 2π/λ. In incoherent detection, OTF represents the contrast of the fringe detected at the image plane and is equivalent to the signal generated when a thin sheet of fluorescence is scanned through the focus [29].

Figure 3(a) shows the plot of Eq. (7) at the fringe periods of Tg = 3.42µm, 1.71µm, 0.85µm, 0.43µm which correspond to the normalized fringe frequencies of 0.13, 0.26, 0.52, 1.04, respectively. For the fringe period of 1.71 µm and higher, FWHM of the axial resolution is expected to be better than that of TFM reported in the literatures [3,8]. Furthermore, theoretically, SLI has the potential of attaining depth resolution better than TPLSM when the normalized fringe frequency is higher than 0.3 as shown in Fig. 3(b). Ideally, the best optical sectioning is achieved when the normalized fringe frequency comes close to 1 but with the tradeoff of the reduced signal to noise ratio [29]. For this comparison, the intensity of SLI is obtained by normalizing the defocused 2D OTF and the total fluorescence intensity of TPLSM generated at a given z-plane for a uniform specimen is calculated by integrating the two photon intensity in each z section [30].

3.2 Experimental verification

A thin sheet of Rhodamine 6G (Sigma-Aldrich, St. Louis, MO) solution is used to measure how much SLI improves the axial resolution in different scattering conditions. A scattering medium is simulated by using, Lipofundin-20 (B. Braun, Germany), as the immersion medium of the objective. This approach allows us to precisely vary the scattering coefficient of the specimen by controlling the concentration of Lipofundin ranging from 2% to 5% v/v. The reduced scattering coefficients (μ’s) of the Lipofundin solutions were measured with a commercial near-infrared spectrometer (OxiplexTS, ISS Inc, Champaign, IL) at 690nm, 830nm and the μ’s at 780nm is estimated by the linear interpolation, which is subsequently used to calculate the scattering MFP (l_S) and anisotropy coefficient, g was estimated to be 0.65 [31]. z represents the scattering length and z / l_S is calculated assuming z is equal to the working distance of the objective which is 280μm. The result of these measurements is summarized in Table 1. The 2% scattering property is similar to the human dermis [32] and has been used for characterizing point spread function of TPLSM in turbid medium [33] and well characterized by previous studies [31,34].

Table 1. Reduced Scattering Coefficients.

	2%	3%	4%	5%
μ’s (cm−1) at 690nm	14.6 ± 0.8	20.1 ± 0.2	27.2 ± 0.5	32.6 ± 0.6
μ’s (cm−1) at 830nm	11.3 ± 0.6	15.6 ± 0.2	21.3 ± 0.4	25.6 ± 0.4
μ’s (cm−1) at 780nm	12.5	17.2	23.4	28.1
lS (μm) at 780nm	282.4	204.8	150.6	125.4
z / lS at 780nm	1.0	1.4	1.9	2.2

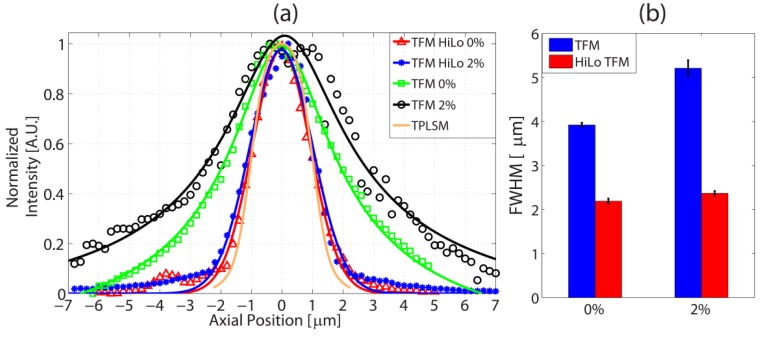
We performed the measurement under two scattering conditions. First, the experiments are performed without any scattering medium (0% Lipofundin) and then undertaken with 2% Lipofundin as an immersion medium. The measurements were repeated 10 times independently at each scattering condition. The FWHM value is estimated by fitting the raw data with a Gaussian curve. From Fig. 4, it is evident that SLI improves the axial resolution of TFM significantly. At 0% Lipofundin, TFM’s FWHM is 3.92 ± 0.05µm and TFM HiLo’s FWHM is 2.19 ± 0.06µm. At 2% Lipofundin, they are 5.21 ± 0.18 µm and 2.37 ± 0.05µm, respectively. The axial resolution of TFM measured with 0.1µm fluorescent polystyrene beads (F-8803, Invitrogen, Carlsbad, CA) is 2.01 ± 0.10µm. We may deconvolve the measured depth profile of the thin Rhodamine solution using the point spread function measured with 0.1 µm bead and estimate that the thickness of the Rhodamine solution to be about 2 µm. As a comparison the theoretical TPLSM response to the thin Rhodamine solution is also shown in Fig. 4(a) with FWHM of 2.08 µm. Considering the thickness of the Rhodamine solution is about 2 µm, the axial resolution is broadened about 1.67 times at 1 scattering MFP condition. This broadening of the axial resolution has already been reported in the literature [12]. Although the direct comparison with the previous results might not be possible since the important parameters affecting the axial resolution including the grating groove frequency, the pulse width and the objective (NA, magnification) are not the same as the setup used for this paper, we can make comparison of general trend of broadening effect. According to the Fig. 3 in [12], at 200 μm scattering depth which corresponds to about 1 scattering MFP, the FWHM of TFM is broadened about 1.6 times compared to 0μm scattering depth for both 40x, NA = 0.8 and 60x, NA = 1 imaging conditions. This result agrees well with our result shown in Fig. 4. It is interesting to note that HiLo processed data is not much affected by the scattering medium, which implies that HiLo based SLI works robustly even in highly scattering medium.

Fig. 4.

(a) Axial resolution measured with the thin Rhodamine solution. Fringe period of SLI is 1.71µm (red) TFM HiLo at 0% intralipid (blue) TFM HiLo at 2% intralipid (green) TFM at 0% intralipid (black) TFM at 2% intralipid (orange) TPLSM in Fig. 3(b) convoluted with 2 µm thick Rhodamine solution. (b) Averages and standard deviations of FWHM of 10 measurements for 0% and 2% scattering condition of both TFM and HiLo TFM.

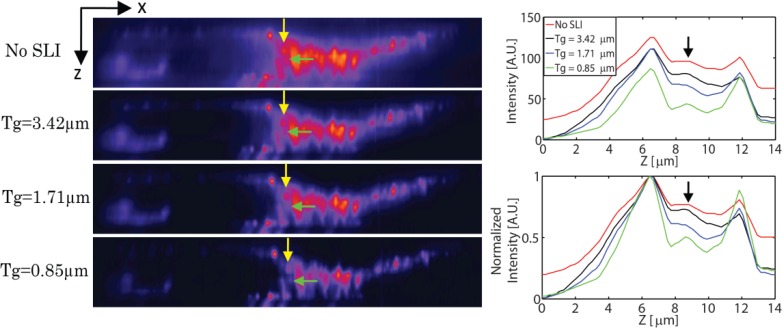
The axial resolution improvement is further demonstrated with a prepared slide of sectioned mouse kidney (F24630, Invitrogen, Carlsbad, CA). At 0% Lipofundin condition, the sample is imaged at 0.5µm step size for a total of 14µm scanning range axially. Figure 5 shows the xz section view of TFM image without SLI and HiLo processed TFM images with fringe period of 3.42µm, 1.71µm, 0.85µm respectively. As the fringe frequency increases the sectioning capability of SLI increases and finer features of the specimen becomes visible more clearly. The intensity profiles along the axial direction at the point indicated by the yellow arrows are also shown on the right side of Fig. 5. The weak intensity object in the middle of the sample indicated by green arrows, which is hidden by the two high intensity objects above and below, becomes discernible with SLI at T_g = 0.85µm. This effect is better visualized in the normalized intensity plot where the intensity is normalized with the peak intensity value. Clearly, the SLI approach improves TFM axial resolution.

Fig. 5.

xz sections of the fine glomeruli and convoluted tubules structure in a mouse kidney sample acquired with TFM without SLI, HiLo processed TFM with fringe period of 3.42µm, 1.71µm, 0.85µm, respectively. The thickness of the imaged portion is 14µm. Intensity increases from purple to red. The cross sectional intensity plot along the line indicated by the yellow arrow is also shown on the right side. Further details on the sample can be found in http://products.invitrogen.com/ivgn/product/F24630.

4. Contrast enhancement using SLI in TFM

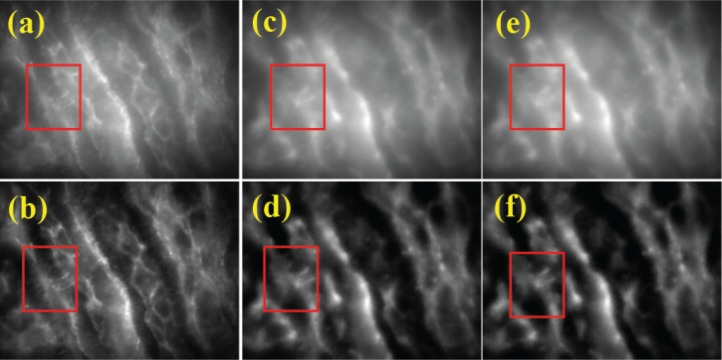
In addition to the depth resolution improvement, SLI is beneficial to rejecting the out-of-focus scattered emission photons and consequently improves the signal to background ratio or image contrast. To simulate the various scattering conditions the sample was imaged through 280µm of immersion fluid and approximately 5µm into the sample at 0% (Figs. 6(a) and 6(b)), 3% (Figs. 6(c) and 6(d)), 5% (Figs. 6(e) and 6(f)) Lipofundin concentration. The sample is identical as the one used in Fig. 5. SI was imaged with the fringe period of 1.71 µm. It is clear that the background rejection improves the contrast dramatically and fine structures are more clearly visible in HiLo processed images. However, the fine features are progressively lost as the concentration increases and this lost information cannot be recovered by the background rejection as shown in red box in Fig. 6. This can be viewed in two ways. First, the axial confinement of the excitation volume is broadened at the scattering condition as shown in Fig. 4 and this contributes to increased out-of-focus background signal. Although this background signal can be removed by the HiLo processing, the shot noise generated by the background signal still survives and the reduced signal to noise ratio ultimately limit the imaging depth in turbid medium. Second, the fine features are lost by the scattering of the emission photons in widefield imaging modes and this cannot be recovered by the HiLo processing.

Fig. 6.

Unprocessed images in scattering conditions (a) 0% v/v, (c) 3% v/v, and (e) 5%v/v Lipofundin-20. Processed images are (b), (d), and (f) for the same scattering conditions, respectively. Each image represents a 90µm x 70µm.

5. Conclusion

In conclusion, we have demonstrated the first use of a HiLo based SLI in TFM. While TFM has intrinsic optical sectioning, the presence of excitation and emission photon scattering can compromise this ability. It is therefore useful to implement SLI to counter the broadening of the axial extent of the excitation volume in a scattering medium as well as to reject the scattered background photons, which improves the axial resolution and the contrast of the image. However, the increased shot noise from the background signal in the turbid medium and the information lost due to emission photon scattering cannot be avoided with the use of SLI.

Current implementation of SLI in TFM is not optimized in terms of imaging speed, excitation efficiency and the sample exposure to the excitation light for minimizing the photobleaching and phototoxicity effect. Here, we propose methods to improve the current performance of SLI TFM. First, HiLo TFM is slower than TFM due to the fact that it requires two images per z-section. Thus, the imaging speed can be improved by automating the switching mechanism between UI and SI. For example, 10Hz imaging speed was demonstrated by using a galvano-mirror to switch between UI and SI in case of GP SLI [24] or one can split the beam into + 1 and −1 order using a diffractive optical element and modulate one of the diffracted beam using high speed laser beam shutter in case of FP SLI. This also reduces the power lost in the FP SLI where the interferometer based FP SLI wastes half of the excitation beam power. Second, the excitation efficiency of TFM is limited by the available laser power in a turbid medium. As demonstrated by Cheng et al. [35], high peak regenerative amplifier can be used to increase the excitation efficiency and thereby improving the imaging speed of the TFM. Imaging speed can be further improved by increasing the repetition rate of the pulsed laser source using the pulse multiplier. However, this works only in a regime where the two photon excitation probability is low enough so that increasing repetition rate would not induce the saturation of fluorophores. In addition to the increased signal level, the photo-bleaching effect was also shown to be reduced in this way [36].

Lastly, this technique might be useful for improving the depth resolution of TFM based endoscopy which has poor depth resolution due to limited NA of the GRIN lens.