Modeling Perceptual Similarity Measures in CT Images of Focal Liver Lesions

Abstract

Motivation: A gold standard for perceptual similarity in medical images is vital to content-based image retrieval, but inter-reader variability complicates development. Our objective was to develop a statistical model that predicts the number of readers (N) necessary to achieve acceptable levels of variability. Materials and Methods: We collected 3 radiologists’ ratings of the perceptual similarity of 171 pairs of CT images of focal liver lesions rated on a 9-point scale. We modeled the readers’ scores as bimodal distributions in additive Gaussian noise and estimated the distribution parameters from the scores using an expectation maximization algorithm. We (a) sampled 171 similarity scores to simulate a ground truth and (b) simulated readers by adding noise, with standard deviation between 0 and 5 for each reader. We computed the mean values of 2–50 readers’ scores and calculated the agreement (AGT) between these means and the simulated ground truth, and the inter-reader agreement (IRA), using Cohen’s Kappa metric. Results: IRA for the empirical data ranged from =0.41 to 0.66. For between 1.5 and 2.5, IRA between three simulated readers was comparable to agreement in the empirical data. For these values , AGT ranged from =0.81 to 0.91. As expected, AGT increased with N, ranging from =0.83 to 0.92 for N = 2 to 50, respectively, with =2. Conclusion: Our simulations demonstrated that for moderate to good IRA, excellent AGT could nonetheless be obtained. This model may be used to predict the required N to accurately evaluate similarity in arbitrary size datasets.

Introduction

Radiological diagnosis from imaging data remains today a largely unassisted process, whereby medical experts will often rely on recalling similar cases for diagnosis and may occasionally consult colleagues or textbooks for support. Liver lesion diagnosis is particularly challenging, owing to a wide range of appearances of benign and malignant lesions [1]. Studies have shown that medical decision support systems relying on content-based image retrieval (CBIR) may provide improvement in efficiency and accuracy of diagnosis [2]. While CBIR has gained much popularity in non-medical applications [3, 4], a great deal of work remains to be done in the medical field. This is particularly true because images judged to be similar using a quantitative distance metric based on described and/or computed features may not actually appear to be visually similar to observers or be considered similar from a medical implication standpoint. The need for an accurate and appropriate reference standard of perceptual similarity is thus critical to the training and validation of CBIR systems [5]. Studies have shown that presentation of perceptually similar images, as may be done in a CBIR system, improve radiological decision making in some cases [6].

Research on perceptual similarity in medical images has been conducted using mammography [7–11] and lung CT images [12]. A variety of paradigms for creating a perceptual gold standard exist, including training artificial neural networks [13], and asking readers to compare several images at a time on a computer screen. Studies indicate that the use of these gold standards in decision support may improve diagnosis [14]. However, it is challenging to create reference standards of perceptual similarity for large databases using the methods presented in these works, as most of the studies have focused on the analysis of perceptual similarity rather than ways to acquire this data in a manner scalable for large datasets.

In our approach, we seek to create scalable gold standards that contain numerical scores for similarity between every pair of images in a database. Accurate development of such a gold standard, however, is challenging for a variety of reasons. First, the amount of perceptual input needed to create a similarity reference standard is large, as the number of pairs of images scales with the square of the number of images, thus making it extremely time-consuming. Second, experiments such as these may exhibit moderate to high inter-reader variability; this requires a knowledge of the distribution of responses and the aggregation of a large number of readers’ responses [15]. Furthermore, the notion of “similarity” is complex as there are a variety of features for which the basis of similarity is assessed, necessitating development of a robust framework for describing and evaluating similarity.

Determining if a method for constructing a gold standard is accurate and scalable for large databases—with input from many readers—is difficult and costly due to the amount of expert time required. While we must ultimately do this to validate our approach, we would be better prepared for the task if we first have a rough idea of the numbers of readers required for specific database sizes. These parameters include number of objects, inter-reader variability, and number of readers needed to get a good estimate of the gold standard. To this end, we have developed a statistical model based on empirical data of perceptual similarity collected from readers’ ratings of similarity in a set of images.

Materials and Methods

Experimental Overview

We first collected image similarity ratings from expert readers viewing pairs of images on a monitor, which we will refer to as the empirical data. To build the statistical model, we calculated the distribution parameters of the empirical data and modeled the similarity scores with the functional form and parameters of this distribution. We assumed that the mean of the readers’ scores would provide a more accurate estimate of the true similarity ratings than any individual reader’s score. We modeled variation in the readers’ scores as additive noise and determined the magnitude of this additive noise that provided inter-reader agreement similar to that observed in the empirical data. Finally, we computed the means of the simulated scores and calculated agreement between these and the simulated similarity ground truth. Each of these steps is explained in more detail below.

Analysis of the Empirical Observer Data

Institutional Review Board approval was obtained for this project. We used a dataset of 19 CT images of focal liver lesions with 12 different diagnoses (Table 1), each containing a manually drawn region of interest (ROI). The patient population consisted of 9 male and 10 female patients, with ages ranging from 26–80 years (median = 64). The patients were chosen from a cohort of patients scanned with a multidetector CT scanner with slice thicknesses in the range of 2.5 to 5 mm, 140 kVp, 140–400 mAs. We asked 3 body imaging radiologists to rate perceived similarity between the liver lesions on a 9-point scale in all 171 pair-wise combinations of the 19 images, with a score of 1 given if the image pair was extremely similar.

Table 1.

List of diagnoses in the 19 CT focal liver lesions

Diagnosis	Number of lesions with diagnosis
Hepatocellular carcinoma	3
Hemangioma	2
Cholangiocarcinoma	2
Neuroendocrine neoplasm	2
Focal nodular hyperplasia	2
Metastasis	2
Gastrointestinal stromal tumor	1
Abcess	1
Lymphoma	1
Fibrosis	1
Cyst	1
Infection	1
Total	19

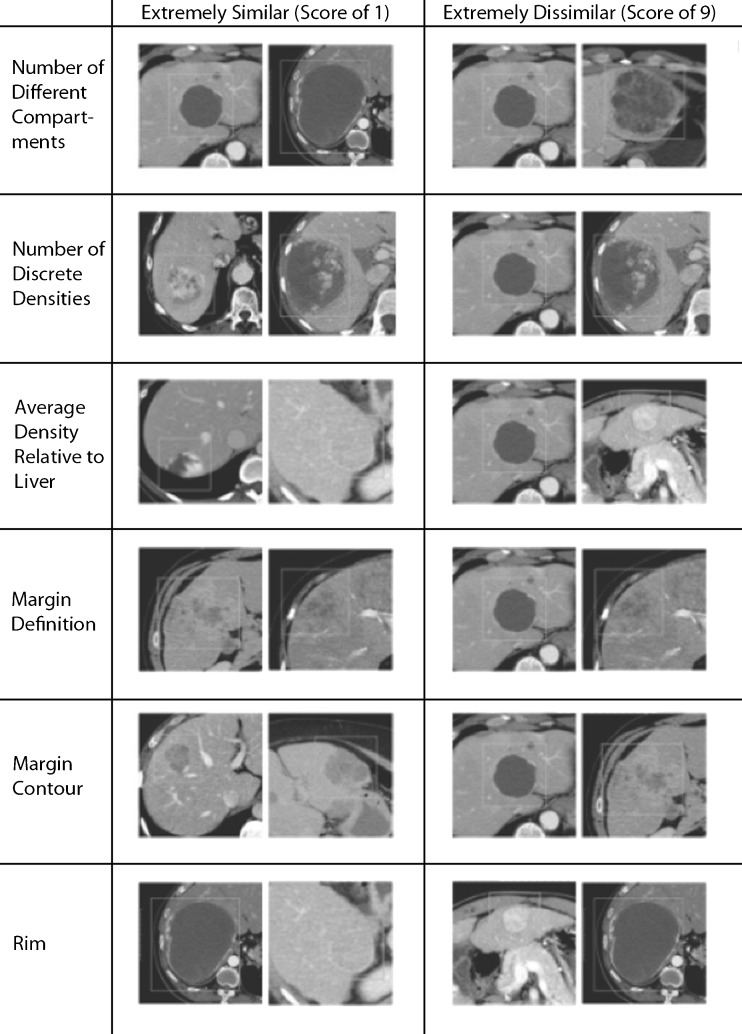
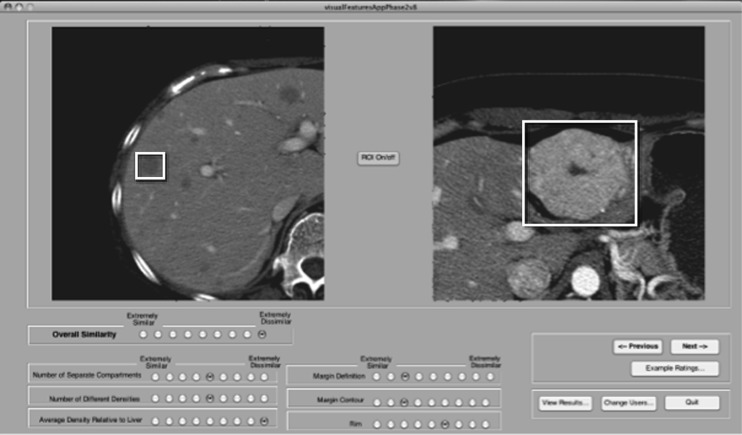
As a baseline training stage, we provided the readers with example images, both on-screen and printed, that provided them with example ratings of the spectrum of appearances expected for each image feature (Fig. 1). In collecting the empirical observer data, we presented pairs of images on a computerized interface developed in Matlab (R2011b, Natick, MA) (Fig. 2). To avoid any effects resulting from image ordering, we randomized the order of images for each reader. The readers had the option of viewing the images with or without the ROI visible. We asked the readers not to change their ratings for previously viewed pairs of images, which combined with the example images, was intended to promote independence of the ratings. The images were presented with a 400/40 HU window/level. All of the readers viewed the images on a Dell UltraSharp 2007FP screen with resolution of 1,600 by 1,200 and a monitor diagonal measurement of 20.1 in.

Fig. 1.

Rating guide provided to readers during the study

Fig. 2.

GUI used to collect data for pairs of lesions. Each image contained a rectangular region of interest that could be turned on or off. Readers were instructed to ignore lesion size and to concentrate on specific image features or overall lesion similarity, regardless of size

Using the readers’ similarity ratings, we first calculated inter-reader agreement for each of the attributes and overall similarity ratings using Cohen’s Kappa metric, which is used to compare variability between data pairs, with 0 being no agreement and 1 being perfect agreement [16–18]. We used quadratic weighting in which the agreement score is penalized as a function of the square of the point differences in scores.

Parameter Estimation

Based on the bimodally distributed appearance of the perceptual observer data (Fig. 3), we assumed each distribution to be a mixture of two Gaussian distributions and approximated a maximum-likelihood estimate of the parameters using a Matlab implementation of an expectation maximization (EM) algorithm.

Fig. 3.

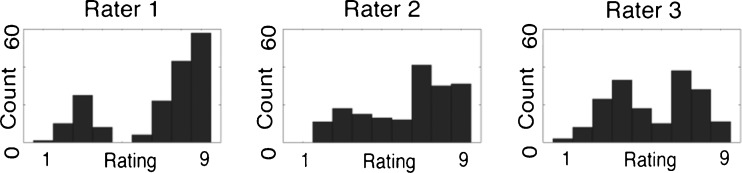
Histograms of the empirical observer data for ratings of overall similarity

Model Development and Evaluation

We used the empirical data as a basis for our statistical model. We assumed that the readers’ ratings contained additive Gaussian noise that could be reduced by averaging the value of readers’ ratings. Using the R computing language, we created a statistical model whose parameters may be varied to simulate larger datasets. We designed the model to allow arbitrary (a) numbers of readers, (b) numbers of image pairs being evaluated, and (c) additive noise amplitude. The model itself consisted of two parts: (1) a simulation of a noise-free “ground truth” and (2) additive noise in readers’ ratings. For (1), we used a bimodal mixture of Gaussians, as per the appearance of the data.

For (2), we generated zero-mean Gaussian noise, which we added to the simulated ground truth. After adding the noise, we converted the simulated scores to a 9-point categorical scale by first thresholding them to fall between 1 and 9, and then discretizing them to integer values. Since the amount of noise present in the scores was not clear from a dataset of 3 readers, we tried a variety of values (0.2 and 0.5 to 5 in 0.5-point steps) for noise standard deviation. After combining (1) and (2), we computed the inter-reader agreement resulting from the simulated values and sought to determine the value(s) of the noise standard deviation for which the inter-reader agreement was similar to that of the collected data. Next, we estimated the simulated ground truth from the noisy data, using the mean of the raters’ scores as an estimator. We computed the agreement of these mean scores with the simulated ground truth using Cohen’s Kappa metric. For each noise standard deviation, we ran 1,000 iterations of the simulation. Our final estimate of the agreement was the mean value of the Kappa metric resulting from the iterations at each noise level.

After determining a range of noise parameters that resulted in inter-reader agreement comparable to the observer data, we used these parameters to predict how many readers would be necessary to produce an inter-reader agreement score of 0.8 (excellent according to Landis and Koch [16]). We did this by running our simulation with these noise parameters while varying the number of readers, over a range of 2–50 readers. We also computed inter-reader agreement for these values; since Cohen’s Kappa can only be applied to pairs of readers, our final value for inter-reader agreement was the mean value of all of the inter-reader agreement scores between all pairs of readers. To test for significance, we used Fisher’s method [19] to combine p values from the 1,000 iterations.

Results

Analysis of the Empirical Observer Data

The similarity data appeared to follow a bimodal trend (Fig. 3). Inter-reader agreement for overall similarity in the empirical data, which we later used to compare to the simulations, ranged between 0.41 and 0.66, a range which is considered moderate to good. Linear regression resulted in R² values of 0.56 (95 % CI [0.46, 0.66]), 0.48 (95 % CI [0.37, 0.59]), and 0.42 (95 % CI [0.31, 0.53]) for readers 1, 2, and 3, respectively. When the readers’ ratings were averaged before computing the regression, linear regression yielded a correlation coefficient of 0.65 (95 % CI [0.57, 0.73]). Table 2 shows the weighting of each of the attribute ratings in the regressions; the average density attribute consistently had the highest weighting.

Table 2.

Linear regression weights for regressions performed for reader 1, reader 2, reader 3, and mean value of the readers’ ratings

Attribute	Reader 1	Reader 2	Reader 3	Mean value of readers
Number of separate compartments	0.2015	0.1186	0.1494	0.2170
Number of discrete densities	0.0899	0.1943	0.2803	0.2489
Average density relative to liver	0.4719	0.4240	0.2117	0.4060
Margin definition	0.0358	0.1557	0.2324	0.0770
Margin contour	0.0368	0.1399	0.1104	0.1067
Rim density	0.1371	0.0308	–0.0220	0.0897
Constant term	1.4276	1.4796	0.8445	0.5439

Parameter Estimation

Using a bimodal Gaussian assumption, we calculated the means and standard deviations for the two peaks in the readers’ ratings of overall similarity (Fig. 4). For the first peak, the mean values for the 3 raters were 2.9, 3.6, and 3.8; and the corresponding standard deviations were 0.5, 1.2, and 1.2, respectively, for the 9-point rating scheme. For the second peak, the mean values were at 8.2, 7.7, and 7.5, and the corresponding standard deviations were 0.7, 1.0, and 0.7, respectively, again with a 9-point rating scheme. The proportions of the scores in the first peak were 0.26, 0.34, and 0.51, respectively; the corresponding proportions in the second peak were 0.74, 0.66, and 0.49, respectively.

Fig. 4.

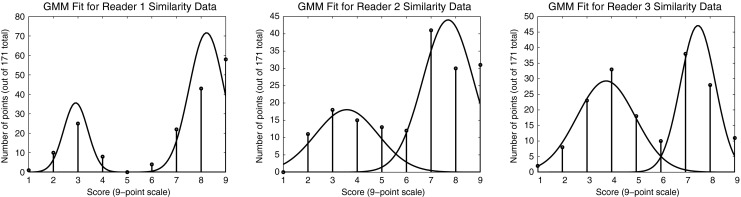
Histograms for overall perceptual similarity for the three readers with a bimodal Gaussian model fit for reader 1, reader 2, and reader 3

Model Development and Evaluation

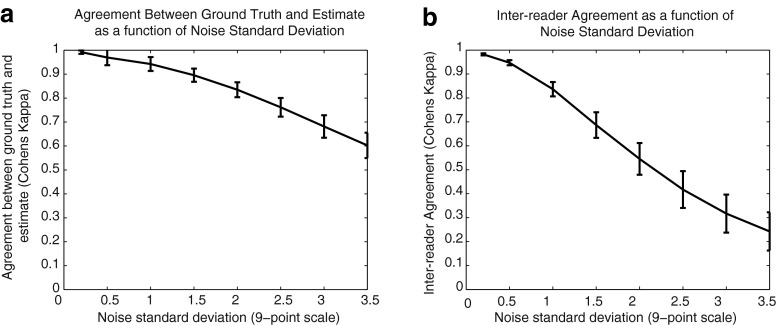
In our model, we set the first and second peaks of the Gaussians to be at 3.4 and 7.8, and standard deviations of 1 and 0.8, respectively; these parameters were chosen as the mean values of the respective parameters from the radiologists’ observer data. We implemented equal proportions of scores in the two peaks, as the wide variation in the mixing proportions of the 3 readers’ scores made it difficult to determine accurate proportions. When we varied the noise standard deviation from 0.2 to 5 to search for values of noise standard deviation that resulted in similar inter-reader agreement to what was found in the emprical data, we found similar values in the simulations when the noise standard deviation ranged from 1.5 to 2.5 (Fig. 5), when the simulated inter-reader agreement ranged from 0.44 to 0.69. The values for Cohen’s Kappa were statistically significant (p < 0.05) only when the noise standard deviation was 3.5 or less.

Fig. 5.

Agreement as a function of noise standard deviation between a ground truth and estimated scores and b inter-reader agreement

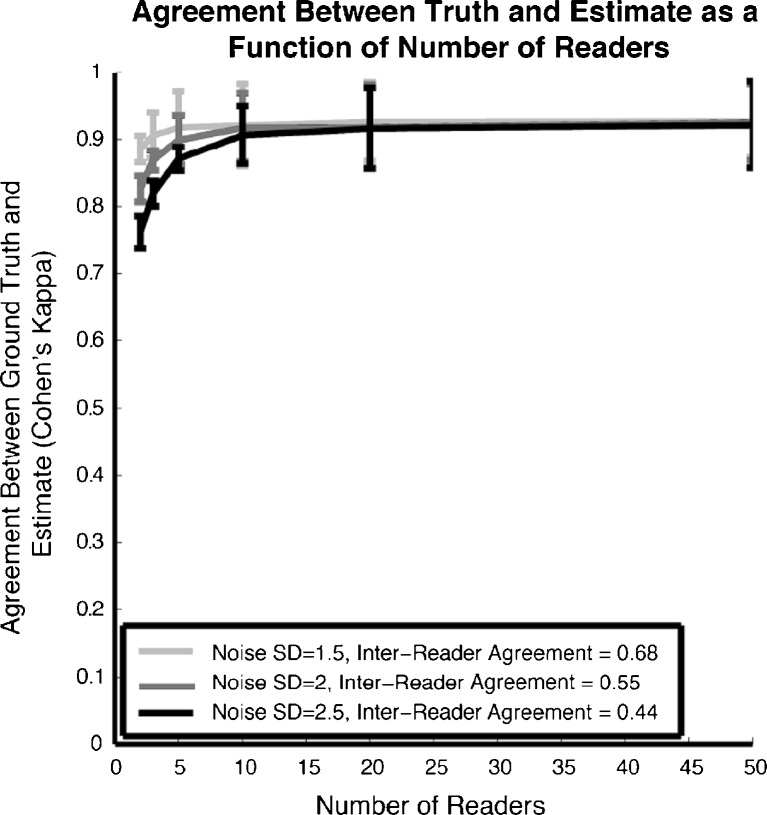
To determine how many readers were needed for sufficient agreement of the mean overall similarity scores with the simulated ground truth, we calculated agreement for a range of 1 to 50 readers for each of the noise standard deviations of 1.5, 2, and 2.5 (Fig. 6). The respective mean values of inter-reader agreement for these values of noise standard deviations were 0.68, 0.55, and 0.44; as expected, these mean values stayed constant when the number of readers were varied. Agreement with the simulated ground truth with three readers was 0.91, 0.87, and 0.81, respectively. For three or more readers, using these values of the noise standard deviations, all of the values of agreement with the simulated ground truth were above the desired level of 0.8. All of these differences were statistically significant (p < 0.05).

Fig. 6.

Predicted agreement from model of overall similarity between simulated ground truth and mean similarity scores as a function of number of readers for noise standard deviations of 1.5, 2, and 2.5

Discussion

In this study, we have collected empirical observer data for perceptual image similarity such as what we would use to train and validate a content-based image retrieval system. We have analyzed the data to establish an understanding of the amount of variability in the observer data, since low inter-observer variability is crucial for a viable reference standard. The statistical model we have developed from this analysis is essential in predicting the feasibility of creating a similarity reference standard for large databases.

Collection of the Empirical Observer Data

The main limitation in developing a statistical model is the small number of readers that participated in the study; ideally we would use several more expert readers’ ratings as a basis for a statistical model. However, this is a circular process in the sense that we need to first develop a statistical model from empirical data, use the model to design more experiments, use the empirical data to improve the model, and so forth. Thus, we hope that our model will provide a starting point for future studies in perceptual similarity of medical images that in turn can be used to validate and improve our current model. Including more readers in the future will also have other benefits such as more accurate prediction of inter-reader agreement between pairs of readers.

When collecting the observer data, we requested that readers do not change their answers to previous questions, as we had other measures for consistency such as the use of a guide showing sample images and ratings. We hoped that readers would rate according to this guide rather than any unspecified model, as this would be likely to be prone to variability. Second, given the design of the GUI, it would be unreasonable to expect readers to change large numbers of previous ratings if their model changed. Last, if we told readers that they are free to go back and change their answers, then some readers may and some may not, which may create another inconsistency. However, one limitation of this study design is that this may invite inconsistency in readers whose method of rating the images changed over the course of the study as they viewed more images.

Analysis of the Empirical Observer Data

The bimodality of the data collected from the raters indicates that most raters perceived that the image pairs were either generally similar or generally dissimilar. Thus, in addition to modeling point-wise scores for the readers, our model may also be applicable for creating a model for classification of images as either similar or dissimilar; for example, for selecting primarily “similar” pairs of images for further reader studies for CBIR.

Model Development and Evaluation

In general, the model appeared to behave as expected, with inter-reader variability and variability between the simulated ground truth and estimated scores decreasing with an increase in noise. Inter-reader agreement ranged from excellent at lower values of noise to poor at higher values of noise. The method of combining readers by taking the mean score seemed to work well in the simulations. However, it is not clear that this would work as well when combining empirically collected data, as the means and standard deviations may have higher variation.

A limitation in validation of our model is that in experiments with readers, an intrinsic ground truth of perception of similarity is not directly measurable, and it may not be the case that only one ground truth exists. Including more readers in future studies will allow us to determine if readers’ ratings fall into different groups instead of being derived from a single ground truth. Another limitation is that we cannot predict based on these studies of liver lesions that analogous modeling would apply to other types of medical images such as for lung nodules or breast masses.

Agreement between the simulated ground truth and estimated results was excellent at low values of noise. Unlike inter-reader agreement, which decreased rapidly with noise, this value remained high with increasing values of noise. In the range of noise levels that produced similar inter-reader agreement as the empirical data, the agreement between the simulated ground truth and estimate was excellent. Thus, our simulations showed that in the presence of only moderate inter-reader agreement, it is nonetheless possible to obtain an estimate that has excellent agreement with the intrinsic similarity ground truth. It is thus indicated that in the empirical data, low inter-reader agreement values may nonetheless correspond to a reasonably good estimate. Finally, we demonstrated that the inter-reader agreement values of overall similarity seemed to plateau as more readers were added to the simulated study. This indicates that after including some number of readers, adding more readers to the study may result in only marginal improvement of the estimated ground truth score.

Conclusions

We have created a model for perceptual similarity in CT liver lesions based on data collected from expert readers and have gained some insights from this model. We have determined that we can obtain an excellent estimate of a simulated ground truth similarity score with a relatively small number of readers’ ratings that exhibit moderate to good inter-reader agreement. Future work includes validating this model with more readers and correspondingly larger databases and using it to design other observer studies.