Detection of Tones and Their Modification by Noise in Nonhuman Primates

Abstract

A fundamental function of the auditory system is to detect important sounds in the presence of other competing environmental sounds. This paper describes behavioral performance in a tone detection task by nonhuman primates (Macaca mulatta) and the modification of the performance by continuous background noise and by sinusoidally amplitude modulating signals or noise. Two monkeys were trained to report detection of tones in a reaction time Go/No-Go task using the method of constant stimuli. The tones spanned a wide range of frequencies and sound levels, and were presented alone or in continuous broadband noise (40 kHz bandwidth). Signal detection theoretic analysis revealed that thresholds to tones were lowest between 8 and 16 kHz, and were higher outside this range. At each frequency, reaction times decreased with increases in tone sound pressure level. The slope of this relationship was higher at frequencies below 1 kHz and was lower for higher frequencies. In continuous broadband noise, tone thresholds increased at the rate of 1 dB/dB of noise for frequencies above 1 kHz. Noise did not change either the reaction times for a given tone sound pressure level or the slopes of the reaction time vs. tone level relationship. Amplitude modulation of tones resulted in reduced threshold for nearly all the frequencies tested. Amplitude modulation of the tone caused thresholds for detection in continuous broadband noise to be changed by smaller amounts relative to the detection of steady-state tones in noise. Amplitude modulation of background noise resulted in reduction of detection thresholds of steady-state tones by an average of 11 dB relative to thresholds in steady-state noise of equivalent mean amplitude. In all cases, the slopes of the reaction time vs. sound level relationship were not modified. These results show that macaques have hearing functions similar to those measured in humans. These studies form the basis for ongoing studies of neural mechanisms of hearing in noisy backgrounds.

Introduction

The use of nonhuman primates, especially macaques, in auditory research has been increasing during the last decade. While many studies have looked at the behavioral and neurophysiological responses to simple and complex stimuli presented in isolation (Populin 2006; O’Connor et al. 2011; Populin and Rajala 2010; Fishman and Steinschneider 2011; Tsunada et al. 2011, 2012), there have been very few studies of nonhuman primate hearing in noisy backgrounds. This study describes modification of behavioral responses by noise, as a prelude to our studies of the neurophysiological bases of hearing in natural environments.

A fundamental function of the auditory system is to detect environmental events. Detection has been studied in many species, including humans, and these studies have allowed us to determine the audiometric curves for those species (e.g., humans: Sivian and White 1933; nonhuman primates: Stebbins et al. 1966; cats: Costalupes 1983; starlings: Kuhn et al. 1982). The time to detection (the reaction time) decreases as the sound pressure level of the signal increases (Stebbins 1966). One of the features of detection is that detection is modified by competing environmental sounds or distractors, such as noise, and is modified in the presence of noise such that the signal to noise ratio at detection threshold remains unchanged over a wide range of frequencies (Hawkins and Stevens 1950). Detection thresholds in noisy backgrounds were modified if the noise was temporally modulated (Hall et al. 1984; Verhey et al. 2003). However, while effects of noise on detection thresholds have been documented for many species, such data do not exist for nonhuman primates, and macaques in particular.

To address that issue, two macaques were trained in a reaction time Go/No-Go task to report the detection of a tone presented alone or embedded in noise. Signal detection theoretic analyses were used to estimate thresholds from experiments that employed the method of constant stimuli. Temporal structure was introduced into signal (noise) by amplitude modulating the signal (noise), and the effects of the manipulation were evaluated using the same behavioral procedure. The results of this study match some of the reported results for other species, especially humans, supporting the use of macaques as an auditory model, and form the baseline for future investigations of the neuronal correlates of behavior.

Methods

Experiments were conducted on two male rhesus macaque monkeys (Macaca mulatta) that were 6 (monkey A) and 7 (monkey B) years of age that had been prepared for chronic experiments using standard techniques. All procedures were approved by the Institutional Animal Care and Use Committee at Wake Forest University and were in strict compliance with the guidelines for animal research established by the National Institutes of Health.

Briefly, a surgical procedure was required to prepare monkeys for the behavioral experiments described in this paper. The surgery was conducted while the monkey was under isofluorane anesthesia and was performed using sterile procedure. During this surgical procedure, bone cement was used to secure a Cilux head holder (Crist Instruments, Hagerstown, MD) to the skull by 8-mm-long stainless steel screws (Synthes). The head holder was used to position the monkey's head in a constant location in the chair (via a headpost) during experiments, so that sound source location was constant relative to the animal’s ears for all trials and days. Postsurgically, analgesics were administered, and the monkey was monitored carefully until complete recovery had occurred.

After the monkeys recovered from surgery, they were acclimated to head restraint. They were then trained incrementally in a lever release task with positive reinforcement. In stages, they were trained to touch the lever, then hold the lever, then press and release the lever, all for fluid reward. Then, they were trained to release the pressed lever in response to sounds and not at other times. When monkeys were sufficiently conditioned to perform this behavior, they were tested on the experimental task.

All experiments were conducted in an anechoic room (Industrial Acoustics Corp., NY) that measured 1.8 × 1.8 × 2 m. During experiments, the monkeys were seated comfortably in an acrylic primate chair that was specially designed to have no obstruction to sounds on either side of the head (audio chair, Crist Instrument Co., Hagerstown, MD). The monkeys' heads were fixed to the chair by means of the holder implanted on their head and were positioned so that the head was level with the middle of the speakers. The speakers were positioned 90.1 cm from the ears, directly in front of the monkey. The speakers could deliver sounds between 50 Hz and 40 kHz (SA1 speaker, Madisound, WI). The SA1 speaker calibrations revealed that between 1 and 40 kHz, the output of the speakers varied less than 3 dB. At 500 Hz, the output of the speakers was about 10 dB less than the output at 1 kHz for a comparable voltage. These differences as a function of frequency were compensated for in the stimulus delivery routines. All calibrations were performed with the probe microphone being placed at the location of one of the ears of the monkey with its head fixed. The same speaker was used to deliver tones and noise, so there was no spatial separation between the two stimuli.

Behavioral task

The experiments were controlled by a computer running OpenEx software (System 3, TDT Inc., Alachua, FL). All behavioral contingencies were implemented using this program and were tested before being used with monkeys. Signals were generated with a sampling rate of 97.6 kHz, which allowed us a theoretical maximum signal limit of 48.8 kHz. The analog input representing lever state was sampled at a rate of 24.4 kHz, allowing us a temporal resolution of about 40 μs on the lever release. Tones were generated using the formula 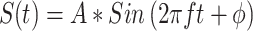, where S(t) represents the signal, A represents the amplitude, f represents the frequency, and ϕ represents the phase. Usually, the phase was set to be 0 (zero) in all of the experiments described below. Broadband noise was generated using the “Random” function, which generated flat spectrum noise, and was band-limited to 40 kHz. The amplitude of the broadband noise is always represented as the total level, in decibels. The amplitude in spectrum level may be computed by subtracting from that overall level an amount equal to 10*log(bandwidth), 46 dB.

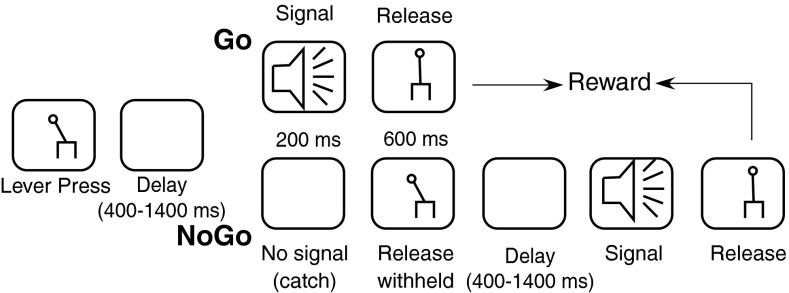
The monkeys were trained to perform a lever release task to report the detection of a short, 200-ms tone burst with 10-ms rise and fall times that reduced onset and offset transients. All training involved positive reinforcement and involved multiple steps, with each successive step representing a closer approximation to the final task, shown in Figure 1. Monkeys initiated trials by pressing down on a lever (Model 829 Single Axis Hall Effect Joystick, P3America, San Diego, CA). After a variable hold time, a signal (tone) was presented on about 80 % of trials. On hearing the tone, the monkey was required to release the lever within a response window, usually 600 ms after the offset of the tone. The response window began with the onset of the stimulus, and the monkeys were free to respond even before stimulus offset. If the lever was released correctly (hit), the monkey was rewarded with a drop of fluid. There were no penalties for not releasing the lever (miss). The monkey’s action of not releasing the lever was taken to indicate that the tone was not detected. In these experiments, the sound pressure levels of the tone were varied over a 80-dB range, going from −6 to 74 dB sound pressure level (SPL). Tone levels were presented in steps of 5 or 10 dB, and sound pressure levels were randomly interleaved.

FIG. 1.

The flow diagram for the behavioral task that was used in the study. Monkeys were trained to initiate a trial by pressing a lever. Initiating the trial could get them into a signal trial (top row) or a catch trial with no signal (bottom row). Monkeys were required to release lever in signal trials for reward and withhold lever release in catch trials. The reward used was dilute apple juice.

In 20 % of the trials, no tone was presented (catch trials). In those trials, the monkey was required to hold the lever pressed. If the monkey held the lever pressed correctly (correct reject), then a loud tone was played in the following trial, which would have a very high likelihood of being detected, and ensure a reward for the monkey. The monkey was not explicitly rewarded for a correct reject response. In the case of an incorrect release on these trials (false alarms), the monkey was penalized with a variable time-out (6–10 s) in which no tone was presented.

In tone alone conditions, the above sequence was presented with about 30 repetitions per tone level (the method of constant stimuli). In the background noise condition, continuous background noise, with uniform amplitude between 0.1 Hz and 40 kHz, was presented at all times. In these cases, the monkey was required to release the lever to indicate detection of tones in noise (Go response), and when no tone was presented (catch trials), hold the lever depressed during continuous noise presentation (No-Go response). The noise conditions were blocked, with each block representing detection performance at a particular noise sound pressure level. Noise sound pressure level was varied between the noise floor of the set up (22–24 dB total level) and a maximum of 64 dB total sound pressure level between blocks. At the beginning of each block, the monkey was adapted to that level of noise for about 10 s.

Some of the experiments related to modification in detection due to dynamic signals relative to steady-state signals. To create dynamic signals, tones were sinusoidally amplitude modulated. In other experiments, time-varying noise was tested by sinusoidally amplitude-modulating the noise. For any sound S(t) (which could be a tone or broadband noise), sinusoidal amplitude modulation was produced according to:

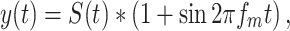where y(t) is the amplitude-modulated sound and f_m is the modulation frequency. These sounds were used in experiments to test whether detection in dynamic broadband noise provided an improvement over detection in steady-state noise, and in experiments that investigated whether sinusoidal amplitude modulated tones provided any improvement in detection relative to steady-state tones. In both of these cases, the mean sound pressure level was maintained constant, so the signal and the noise had peaks that were 6 dB higher than the mean level. In both of these experiments, modulation frequencies of 5, 10, and 20 Hz were used. Our analysis showed no significant differences between the effects of the different frequencies used, so only the data using 10 Hz modulation frequencies is shown.

Data analysis

All analyses were based on signal detection theoretic methods (Green and Swets 1966; Macmillan and Creelman 2005), and implemented using MATLAB (Mathworks, Matick, MA). Briefly, for each block, we determined the false alarm rate (F) and the hit rate (H) for each tone level. Using signal detection theory,

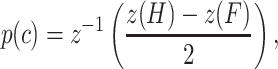where the z transform converts hit rate and false alarm rate into units of standard deviation of a standard normal distribution (z-score, norminv in MATLAB) (Macmillan and Creelman 2005). Thus, a hit rate of 0.5 would be converted to a z-score of 0, and larger hit rates to positive z-scores. The inverse z-transform (z⁻¹) then converts a unique number of standard deviations of a standard normal distribution into a probability correct (p(c), normcdf in MATLAB). Such an analysis is problematic when hit rates are perfect (1.0) and false alarm rates are zero because the z-score of those values are plus and minus ∞. Therefore, in those cases, we calculated the probability correct using non-signal detection theoretic methods, and also used a correction that was based on the number of trials at each sound pressure level (Macmillan and Creelman 2005). We found no systematic differences using those methods, so we will specify the methods used when such data are presented. The probability correct value was calculated for all tone levels.

A Weibull cumulative distribution function was fit to the probability correct vs. sound level relationship at each condition (each frequency and noise level) according to the following equation:

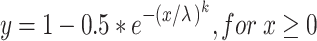after the analyses of Britten et al. (1992) and Palmer et al. (2007), where x is sound pressure level, and λ and k represent the threshold and slope parameter. However, since the monkeys’ false alarm rates influenced both the maximum performance and the estimate of chance performance at sound levels below threshold, these probabilities were allowed to be free parameters in our fitting method. The modified equation was:

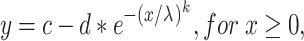where c and d represent the probability correct at higher sound levels and the estimates of chance performance at sound levels below threshold, respectively. To account for the sound pressure levels below 0 dB SPL, the data were translated by 6 dB and fit with a Weibull function, and then the thresholds were translated by −6 dB to account for the original translation. From this curve, threshold was calculated as that tone sound pressure level that would cause a probability correct value of 0.76. Similar analyses were performed at different noise levels and for the various tone frequencies.

In all cases, reaction time was also computed, based on the time of the lever release. Reaction time was computed as follows:

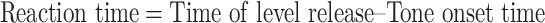Reaction time was computed on all correct Go responses. We performed statistical analyses on the reaction times to explore the variation of reaction time with signal strength and with noise level, and with modulation of noise or signal.

Statistical analysis

All statistical analyses were implemented using MATLAB and were coded by one of the authors based on theory described in Zar (1984). The analyses were verified by dummy data and real data sets using SPSS, and the appropriate functions in MATLAB.

In many cases, the variability in the data was only able to be estimated using bootstrap methods (Efron and Tibshirani 1993). Briefly, the data were resampled using random draws with replacement, while taking care to maintain the substructure of the data. For example, the variability in threshold measurements would be estimated by resampling the data in a block of behavioral data 1,000 times. The responses at each tone level (including catch trials) were drawn from the original data set at that particular tone level with replacement, making sure that the number of bootstrapped trials at that tone level matched that obtained behaviorally. This was done at all tone levels to generate one estimate of the bootstrapped behavioral data to generate one threshold. The same procedure was repeated 1,000 times to generate 1,000 estimates of threshold, so that the variability of the threshold could be determined. If the distribution of metrics such as shift rate needed to be estimated, then individual thresholds at each noise level were estimated to generate a bootstrapped estimate of threshold shift for each noise level. From these threshold shifts and noise levels, one bootstrapped estimate of shift rate could be computed. Repeating the same method 1,000 times generated the required distribution of shift rates. In all cases, the number of iterations was restricted to 1,000 because there were no changes in parameter distribution shapes between 1,000 and 10,000 iterations.

Results

Detection of tones presented alone

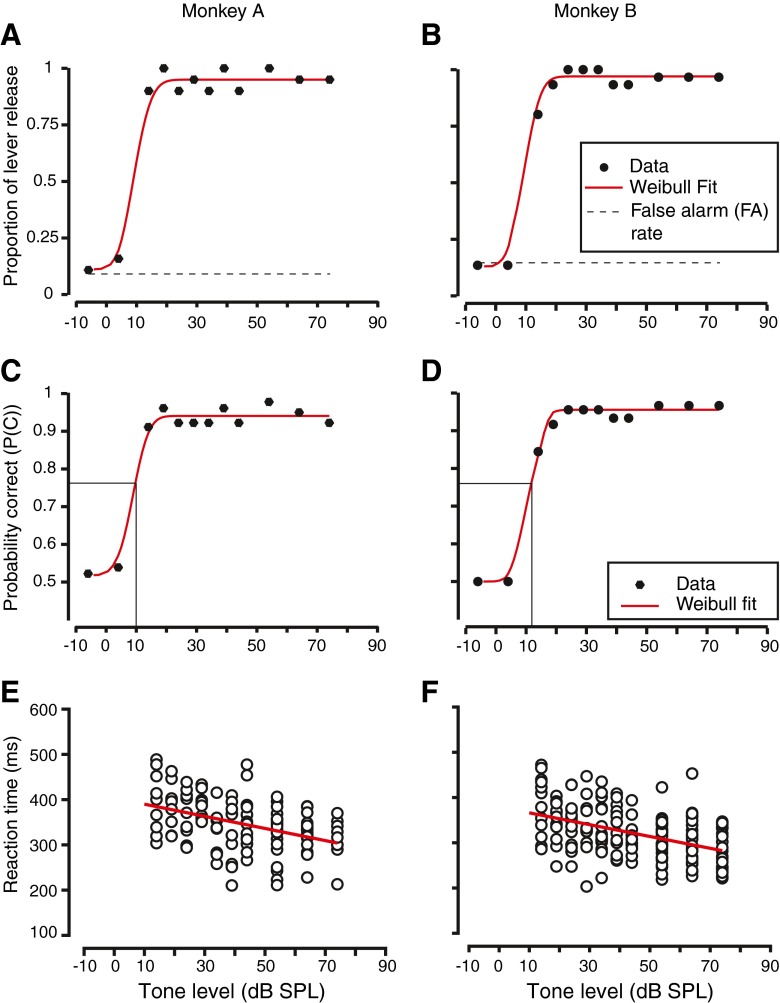
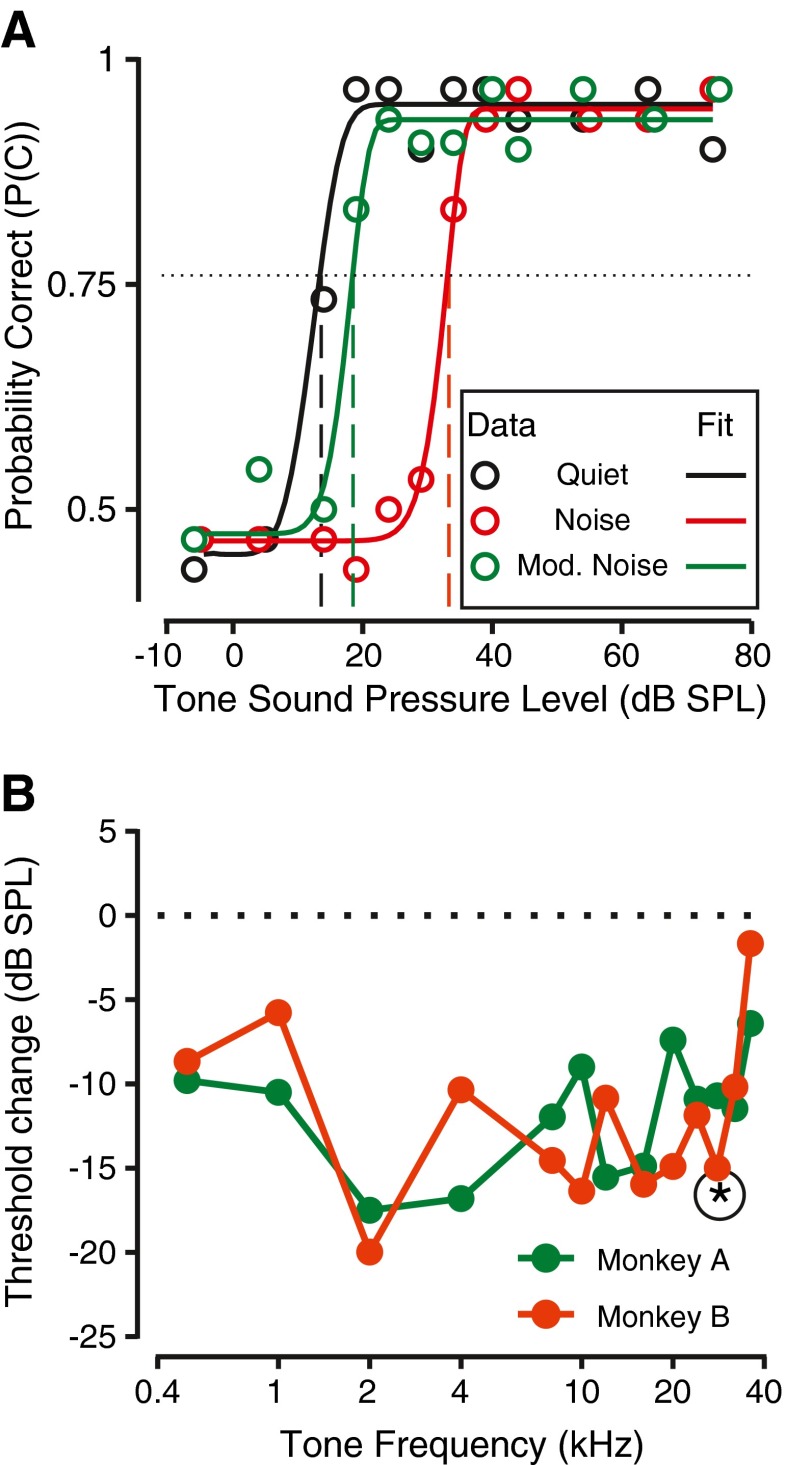
Figure 2 shows the behavioral performance of the two monkeys during detection of tones. Figure 2A and B shows the hit rate (filled circles) as a function of tone level and the false alarm rate (thin dashed lines) for two monkeys during a session in which they detected tones presented alone. The figures show detection performance for a 2-kHz tone for monkey A, and 8 kHz for monkey B. At low tone levels, the hit rates for the monkeys were comparable to the false alarm rate. As the tone sound pressure level increased, the hit rates increased to a high value close to one, indicating that the monkeys almost always released the lever when high sound pressure level tones were used as stimuli. Figure 2C and D shows psychometric functions generated by signal detection theoretic analyses that measure true behavioral sensitivity and account for the false alarm rate. The figures show probability correct (p(c)) as a function of tone sound pressure level. At low sound pressure levels, where hit rate was similar to the false alarm rate, probability correct was close to 0.5, indicating chance performance in a two alternative forced choice task (Macmillan and Creelman 2005, see “Methods” for details). At high tone levels, the monkeys’ behavioral performance had a high p(c). The psychometric function was fit by a steep sigmoidal relationship for both monkeys (red curve, Fig. 2C, D). From the psychometric functions, thresholds for detection were calculated as the sound pressure level at which the p(c) attained a value of 0.76 (shown by the solid vertical lines).

FIG. 2.

Behavioral performance of the two monkeys in the task. A Hit rate for monkey A, plotted as a function of tone sound pressure level. Circles represent proportion of trials in which the monkeys released the lever (hit rate) and the dashed line the proportion of lever releases on catch trials when no tone was presented (false alarms). The red curve through the data points is a Weibull function fit to the hit rate data. Tone frequency was 2 kHz. B Hit rate for monkey B. Plot is in the same format as A. Tone to be detected had a frequency of 8 kHz. C Behavioral sensitivity of the monkey A derived from signal detection theory taking into account the false alarm rate. Figure shows probability correct vs. tone sound pressure level. Filled circles show the p(c) values at each tone level; red curve, the Weibull fit to the data. The thin black vertical line shows the threshold, the sound level at which p(c) equals 0.76. D Behavioral sensitivity for monkey B. Figure convention is similar to C. E Plot of reaction time to lever release as a function of tone sound pressure level for monkey A. Each data point shows reaction time on an individual trial. The red line represents a linear regression through the data. F Similar to E, but for monkey B.

Figure 2E and F shows the reaction times for these monkeys to detect tones at these frequencies as a function of tone sound pressure level. Reaction times are shown only for those levels that are above threshold, so as to ensure reliable measures. Each circle represents the reaction time on each trial at each sound pressure level. Reaction times decreased as a function of tone level, suggesting that the monkeys’ task became easier as the tone level increased. A linear regression of reaction time vs. sound pressure level was calculated, and the slope of the regression was called reaction time slope. The reaction time slopes for the two exemplars shown are −1.34 ms/dB (Fig. 2E) and −1.31 ms/dB (Fig. 2F). The linear regression is shown for both cases as red lines in Figure 2E and F. Irrespective of frequency, the reaction times decreased with increases in tone level, and the reaction time slope was negative and significantly different from zero (t test, t₁₈₃ = 2.74, p < 0.01 and t₁₉₂ = 2.84, p < 0.01). Rate of change of reaction time with increasing stimulus sound pressure level may be related to "rate of growth in loudness" (Pfingst et al. 1975) and is a relevant measure for hearing impaired populations.

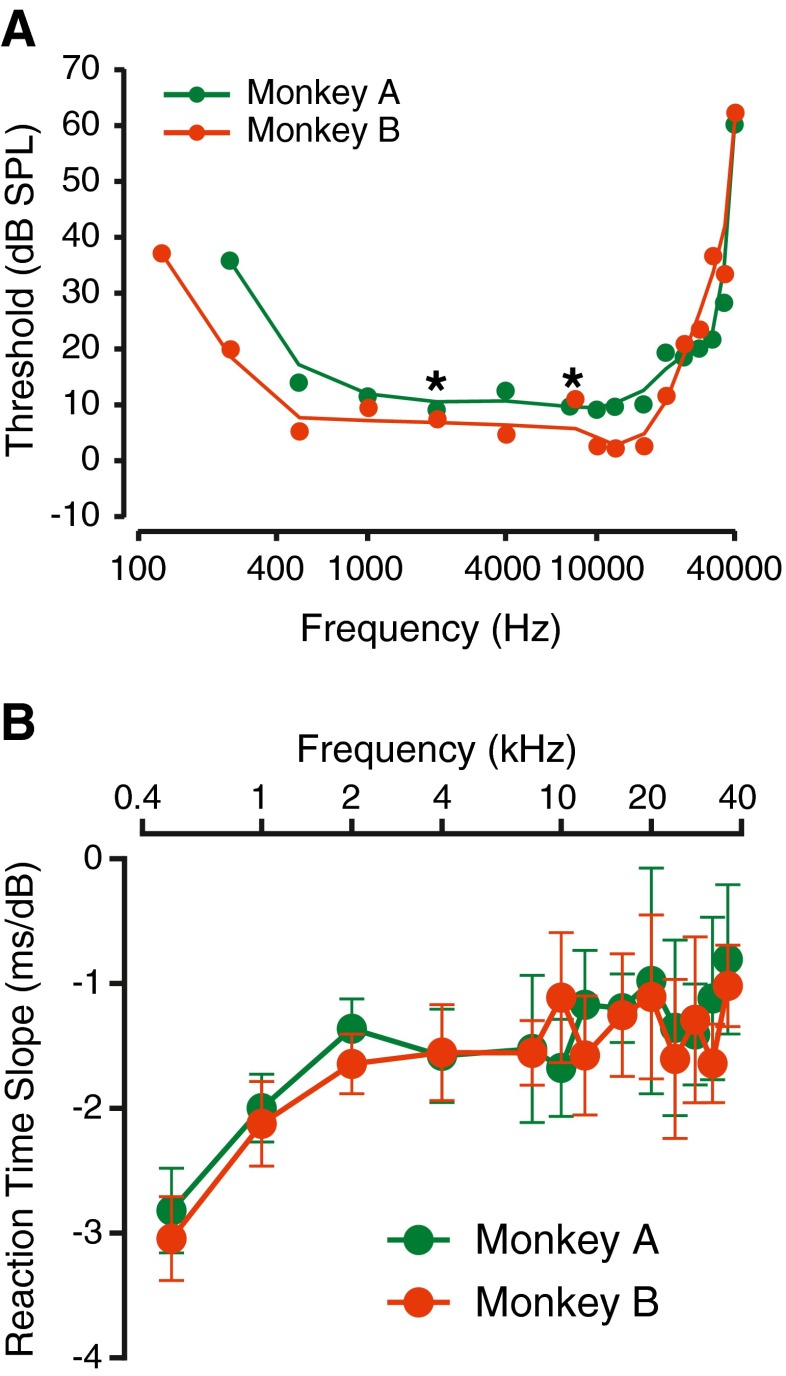
Figure 3 shows the trends in these measures of detection as a function of tone frequency. Detection was tested over a wide range of frequencies, between 250 Hz and 40 kHz, based on previous studies in monkeys (Stebbins et al. 1966; Pfingst et al. 1978; Lonsbury-Martin and Martin 1981; Heffner and Heffner 1986). Figure 3A shows detection threshold plotted as a function of tone frequency for both monkeys. The two curves show the U-shape characteristic of threshold functions that have been observed for multiple species. In this study, thresholds were lowest between 8 kHz and 16 kHz, consistent with previous results, which showed greatest sensitivity around 8 kHz (Heffner and Heffner 1986). Thresholds were higher at frequencies higher than 20 kHz, and were higher at frequencies lower than 1 kHz. The audible range of frequencies for the macaque also matches those described earlier for the species (Stebbins et al. 1966; Pfingst et al. 1978; Lonsbury-Martin and Martin 1981; Heffner and Heffner 1986).

FIG. 3.

Summary of detection metrics for tones presented alone for the two monkeys. A Threshold as a function of tone frequency. Circles show thresholds, and the lines are a cubic spline that shows a smoothed relationship between threshold and frequency. The colors represent different monkeys. B Reaction time slope as a function of frequency. Convention is similar to Figure 3A. Error bars represent 95 % confidence limits, estimated by resampling methods.

The reaction time slopes shown in Figure 2E and F were very similar. To examine if the reaction time slope was independent of frequency or individual macaque, the relationship between reaction time slope and tone frequency was plotted for both subjects. Figure 3B shows a plot of reaction time slope vs. frequency for the two monkeys. The error bars representing the 95 % confidence limits of this measure was obtained by resampling the data with replacement 1,000 times to create 1,000 reaction time vs. tone level relationships at each frequency and fitting a separate line through each of them. The standard deviation of the distribution of the slopes represents the standard error. The reaction time slope at lower frequencies were steeper (more negative) than those measured at frequencies larger than 1 kHz (F(25,999) = 3.31, p = 1 × 10⁻⁷, ANOVA, and t₉₉₉ = 2.39, p = 0.0085, after Bonferroni correction). The reaction time slopes at frequencies higher than 1 kHz were not significantly different from each other (F(21,999) = 1.48, p = 0.0755, ANOVA, and consistent with similar slopes observed in Figure 2E and F), and the reaction time slopes observed for the two monkeys were not significantly different from each other (p > 0.05). These data appear consistent with previous data reported for nonhuman primates (Stebbins 1966; Pfingst et al. 1975).

Effects of steady-state noise on detection of tones

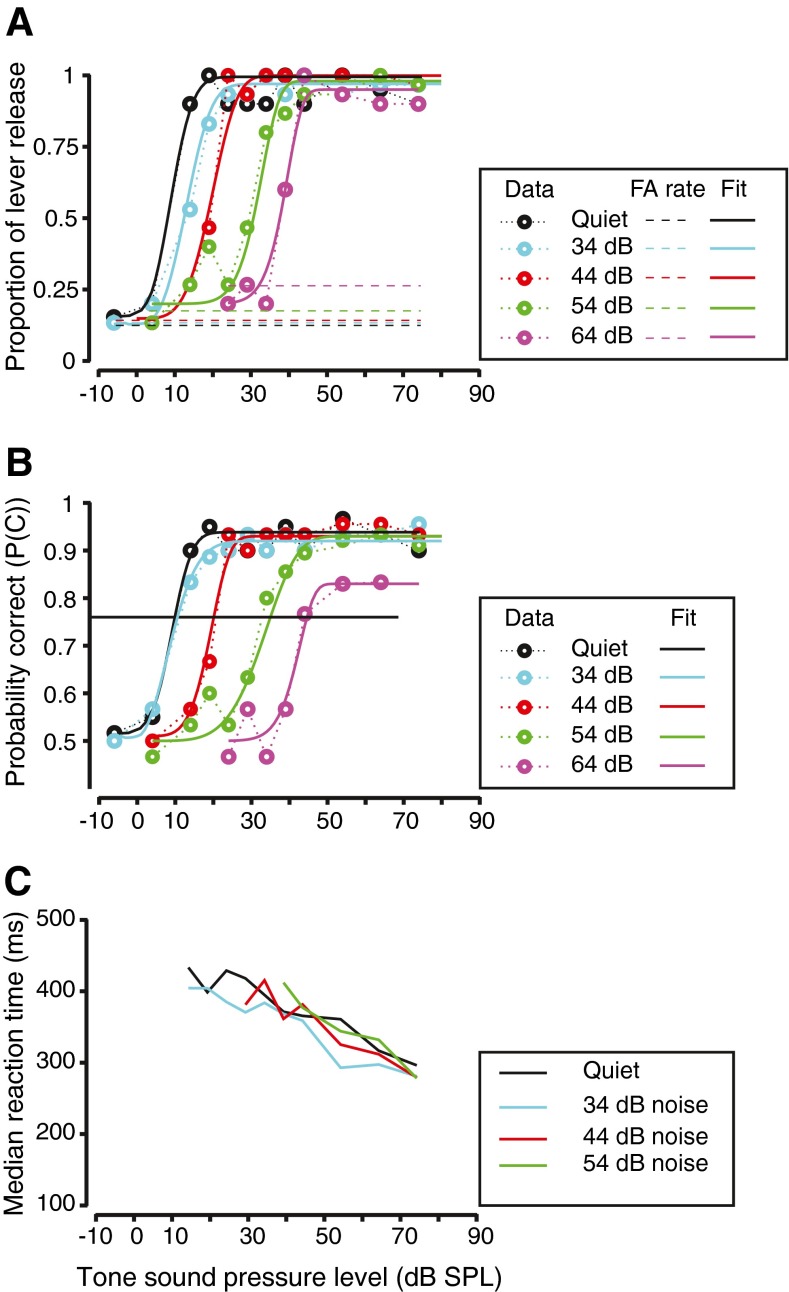
To evaluate hearing in more natural environments, hearing thresholds were measured in continuous broadband noise. Figure 4 shows the behavioral performance of monkey A, in the same format as Figure 2. Figure 4A shows the hit rate and false alarm rate for detection of tones in various levels of noise for one of the monkeys, monkey A, reporting detection of a tone at 2 kHz, the same frequency for which data were shown in Figure 2A. Note that in all cases, the hit rate vs. tone sound pressure level relationship could be fit by a smooth, sigmoidal function. Noise had two observable effects on the behavioral performance. One effect of noise was to shift the dynamic portion of the hit rate vs. tone level curve to higher levels (Fig. 4A). The other effect for the noise was to cause an increase in false alarm rate (note that the dashed lines show an increasing trend with noise level). These two trends suggest that the noise, in addition to causing a threshold shift, increased the uncertainty of low-level stimulus perception.

FIG. 4.

Effects of noise on the detection performance at one frequency. A Hit rate as a function of frequency for monkey A. Figure convention is the same as in Figure 2A. Different colors represent the different noise conditions. B Behavioral sensitivity of the monkey. Figure convention is similar to Figure 2B. Different colors represent the various noise conditions. Horizontal line represents p(c) = 0.76. C Median reaction time as a function of tone sound pressure level for different noise levels (different colors). Highest noise level (64 dB) is not shown because of limited data points.

The psychometric functions relating probability correct (p(c)) to tone level are shown in Figure 4B. The first effect of noise is clearly manifested in the rightward shift of the psychometric functions in noise relative to the psychometric function to tones alone (compare colored lines to black line). The second effect is reflected in the highest probability correct values falling short of one at higher noise levels (at which the false alarm rates were high, at about 23 %). While these effects were typical across frequency and subject, the exemplar represents the highest change in false alarms that was observed. Typically, the false alarm rate changed from about 0.1 to about 0.15–0.2. Detection threshold was calculated the same way as for the tones alone condition, as the tone level at which p(c) = 0.76 (horizontal solid line, Fig. 4B). All thresholds in noise were analyzed for whether they were significantly different from the thresholds obtained in the tone alone condition. This analysis was performed by resampling data with replacement so as to generate multiple curves of hit rate vs. tone level, and thus multiple p(c) vs. tone level curves for each noise condition. The distribution of thresholds was compared across noise levels and differences were analyzed using ANOVA, and significance was evaluated at a 0.05 level.

The effects of noise on reaction time to lever release were also examined. The results for the exemplar condition for monkey A are plotted in Figure 4C. The finding is that the reaction times in noise as a function of absolute tone level were not significantly different from those elicited in response to tones alone at the same sound pressure level (p > 0.05, Kruskal–Wallis test). This was true at all frequencies that we tested detection behavior. The reaction time slopes did not differ significantly as a function of adding noise (two-factor non-parametric ANOVA testing for the effect of noise level (factor 1, df = 4) and tone frequency (factor 2, df = 12), χ² (df = 4) = 4.1, p = 0.3926, after resampling the data). These data are consistent with data obtained in humans that show that reaction times to detect tones in noise is strongly dependent on absolute tone level and not just on signal to noise ratio (Kemp 1984).

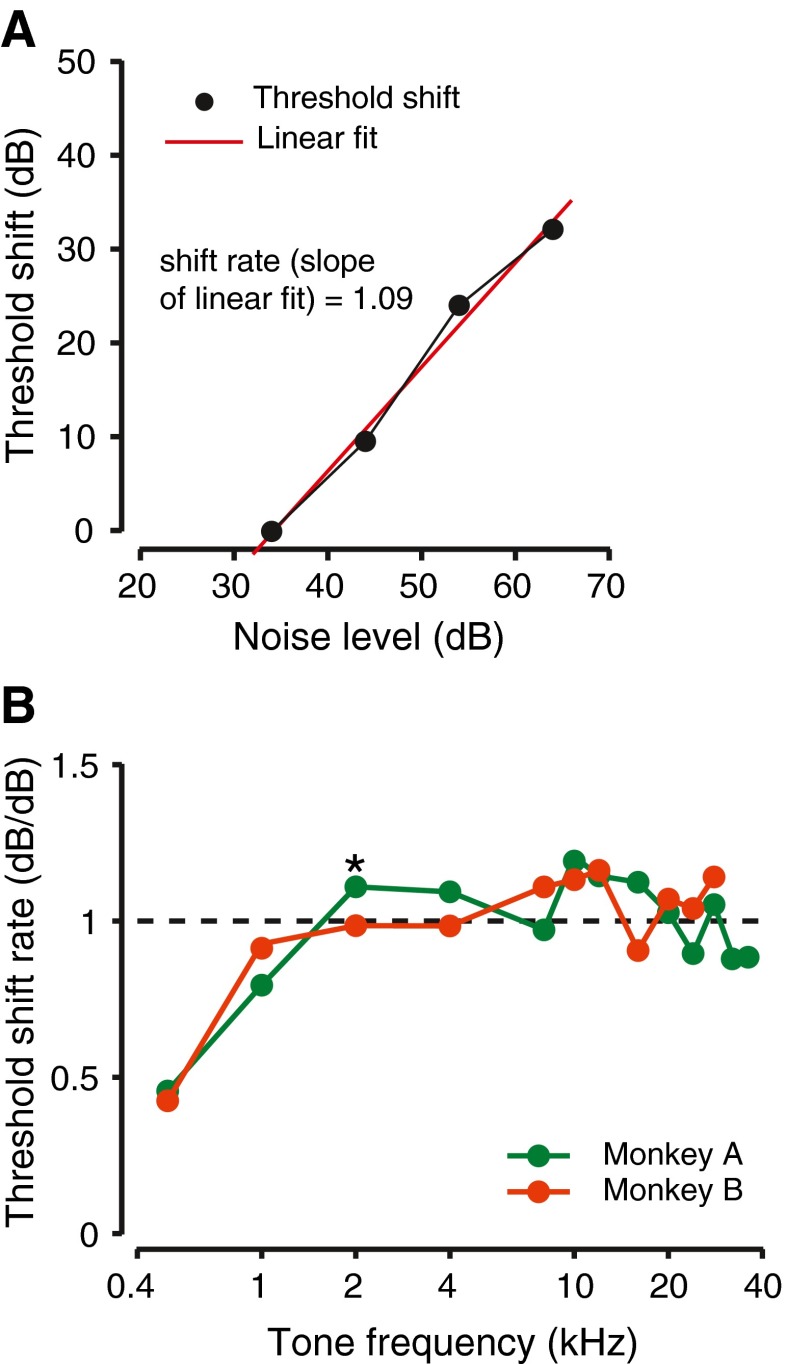
To quantify the main effect of noise, the threshold shift was plotted against the noise level evoking the threshold shift (Fig. 5A). A linear regression of the threshold shifts that were significantly different from zero (determined by resampling the data, see above) against the noise levels was computed. The slope of the linear fit was defined as the shift rate (or the threshold shift rate) and taken to be the quantitative incremental effect of noise on threshold. For the 2-kHz tone detection by monkey A (for which exemplar data have been shown), the shift rates were 1.09 dB/dB, not significantly different from the 1 dB/dB that has been postulated for ideal detection behavior (Gibson et al. 1985) and similar to human detection thresholds, which are reported to be signal-to-noise-ratio invariant (Hawkins and Stevens 1950). However, these measures are for single frequencies. To examine whether shift rates were similar across the hearing range, effects of noise were investigated for detection of tones that spanned the entire audible frequency range of the monkeys (250 Hz to 36 kHz). The resultant shift rates are plotted as a function of frequency in Figure 5B. For both monkeys tested, the shift rates were close to unity at frequencies higher than 1,000 Hz (compare data with dashed line). The shift rates at these frequencies were not significantly different from unity or from each other, and these were determined using resampling methods (F(21, 999) = 1.47, p = 0.0790, ANOVA). The shift rates were lower than one at frequencies less than 1,000 Hz and close to 0.5 at 250 H for both monkeys (Fig. 5B). These shift rates were significantly different from the shift rates obtained at frequencies higher than 1,000 Hz (F(25,999) = 17.6, p < 0.001, ANOVA; post hoc test t₉₉₉ = 2.59, p = 0.0049), determined by resampling methods. These results were similar to those described for humans by Hawkins and Stevens (1950) for frequencies lower than 500 Hz.

FIG. 5.

Rate of threshold shift with noise sound pressure level during the detection of tones background noise. A Calculation of shift rate. Threshold shift (obtained from analyses such as Figure 4B) is plotted as a function of noise level. Red line shows a linear fit through the data points and the slope of the line. Threshold shifts are from Figure 4B. B Shift rate over the audible range of frequency for the monkeys. Different colors show the data from different monkeys.

The effects of time varying signals or noise

The previous results dealt with steady-state tones and steady-state noise. However, auditory signals in daily life are time varying, and some have theorized that the auditory system is specialized for processing dynamic signals that would allow the system to better extract signals from a mixture of signal and noise (e.g., Gans 1992). One would predict that the detection of time-varying signals in static noise or static signals in time-varying noise would be enhanced, as predicted by auditory scene analysis (Bregman 1994).

Many studies have reported significant effects of modulation of the distractor as well (e.g., Hall et al. 1984; Verhey et al. 1999). In order to evaluate the effects of broadband noise modulated by a time varying envelope, broadband noise was amplitude-modulated as described in the “Methods” section and was used as background during detection of steady-state tones. Figure 6 shows the results of experiments investigating the effects of amplitude-modulated noise relative to steady-state noise of the same mean (or overall) amplitude. Even though we report here only the results of 10 Hz amplitude-modulated noise, we evaluated behavior under other modulation frequencies (5 Hz and 20 Hz). There were no significant differences in the performance metrics under the different modulation conditions that were tested, consistent with previous studies in humans (Verhey et al. 2003). The detection of tone in amplitude-modulated noise at 44 dB mean amplitude (green curve and symbols) is shown in comparison with detection of the same frequency in quiet (black curve and data points) and detection of the tone in 44 dB steady-state noise (red symbols and curve) in Figure 6A. Amplitude modulation of the noise caused a reduction in threshold relative to the threshold with the steady-state noise (see green vs. red vertical dashed line). The amplitude modulation of the noise caused a change in the threshold but not a change in the slope of the psychometric function. This reduction in threshold occurred at all modulation frequencies tested. The reduction in threshold shift is similar in magnitude to the effects observed in studies of modulated maskers in humans (e.g., Hall et al. 1984; Verhey et al. 1999).

FIG. 6.

Effect of amplitude modulation of noise on the detection of steady-state tones. A Psychometric function showing probability correct for detection of unmodulated tone alone (black symbols and line), detection of the unmodulated tone of the same frequency in steady-state noise at 44 dB (red) and detection in amplitude modulated noise (green) of the same mean sound pressure level. Figure convention is the same as in Figure 2B. B Shift in threshold as a result of modulating the noise amplitude as a function of tone frequency. Convention is similar to Figures 3A and 5B. The circled asterisk represents the condition shown in A.

The effects of amplitude-modulated noise were studied over a wide range of carrier frequencies to investigate the generalization of the effect. Figure 6B shows the difference in the threshold shift between the modulated noise and the steady-state noise conditions (referred to here as threshold change) as a function of frequency. Negative values of threshold change indicate that the amplitude-modulation of noise resulted in a lower detection threshold for the tone relative to the steady-state noise condition. At all frequencies tested, and for each monkey, the difference in the threshold shift was negative (Fig. 6B), indicating that masking by modulated noise was less effective than masking by steady-state noise at all frequencies. The exemplar is indicated with an asterisk. The threshold change at each frequency was significantly different from those obtained by chance, and these were evaluated by resampling the data under both conditions (steady-state noise and amplitude-modulated noise) and estimating the probability that the thresholds under amplitude-modulated noise conditions could have been drawn from the distribution of thresholds under steady-state noise conditions. In all cases, the probability was well under 0.001, suggesting that the thresholds were significantly different under the two conditions. The reaction times in both steady-state and amplitude-modulated noise showed the same range, and had slopes as a function of tone level that were not significantly different (F(1, 999) = 3.11, p = 0.0781, ANOVA, data not shown). Across all frequencies, the mean threshold change values were −11.7 dB (standard deviation (SD), 3.53 dB) for monkey A and −11.9 dB (SD, 5.02 dB) for monkey B.

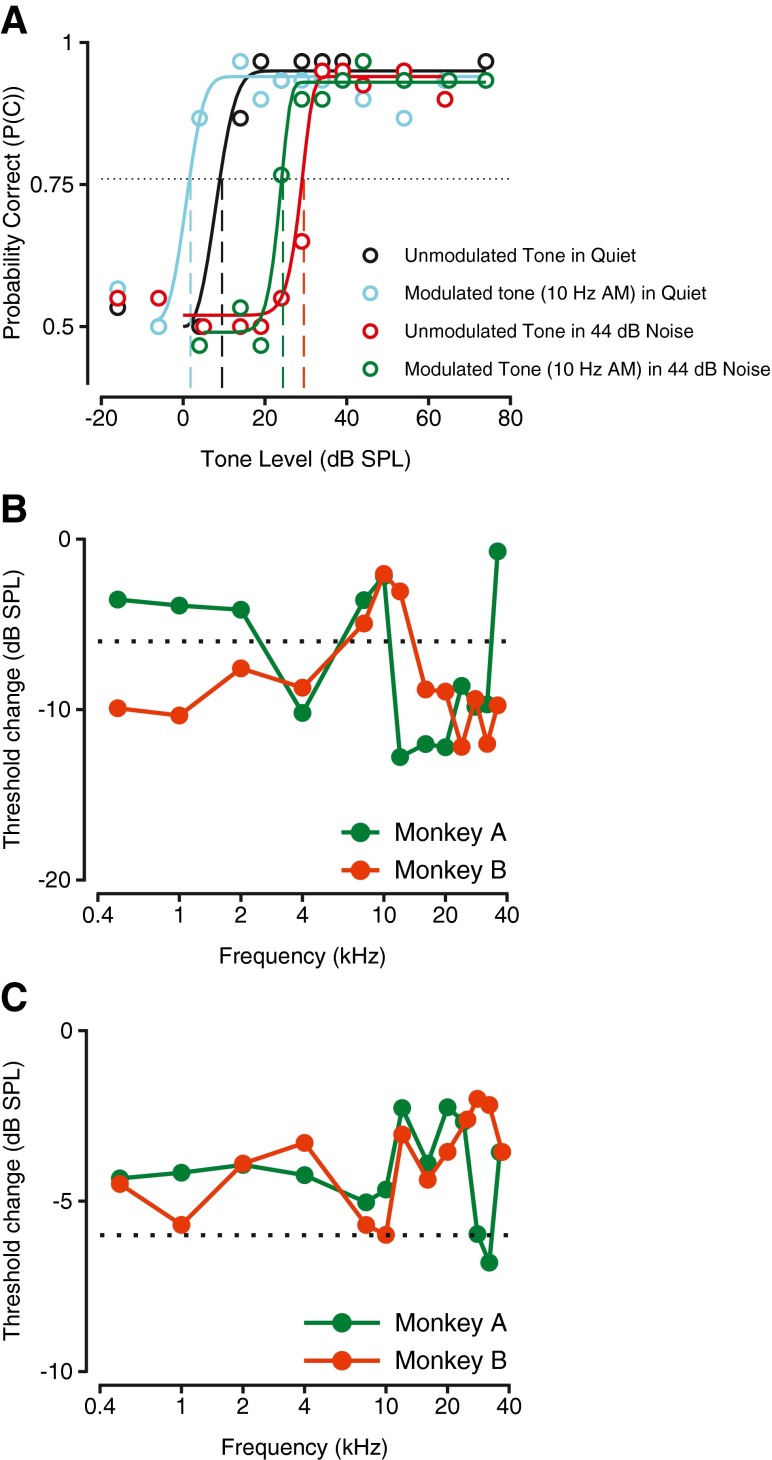
In daily life, not only can noise be time varying, the signal to be detected can also be dynamic. To investigate the effects of the signal being dynamic, tones were amplitude-modulated (see “Methods” for details) and used as the signal in the behavioral task. We report here the data using a modulation frequency of 10 Hz, but the data were also obtained and analyzed for 5-Hz and 20-Hz modulation frequencies. Changing the modulation frequency in that range did not affect any of the response parameters that are reported here. Physiological studies of the cochlear nucleus report that the neuronal thresholds to amplitude-modulated tones can be as much as 20 dB lower than thresholds to steady-state tones (Joris et al. 1994). To investigate the behavioral correlates of that report, detection of amplitude-modulated tones presented in isolation was first studied. Because the peak amplitude of amplitude-modulated tones is 6 dB higher than the mean amplitude, one way of examining the conferred advantage beyond energetic mechanisms, if any, would be to examine if the threshold reductions were greater than 6 dB. The behavioral effects of time varying signals during detection are shown relative to detection of steady-state tones in Figure 7. Figure 7A shows the psychometric functions derived from detecting steady-state tones presented alone (black) and from detecting the same frequency tone when it was amplitude-modulated at 10 Hz (cyan). The psychometric function for detection of amplitude-modulated tones was shifted to lower sound pressure levels, indicating that the monkeys were able to detect amplitude-modulated tones at lower mean tone levels than steady-state tones. In the case of the example shown, the threshold for detection of amplitude-modulated tone was about 8.9 dB lower than that for detection of steady-state tone. The difference in threshold was determined to be significantly different from a 6-dB threshold difference using bootstrap methods (t₉₉₉ = 2.73, p = 0.0032, t test). The slope of the psychometric function, range of reaction times, and the reaction time slopes were not significantly different under the two conditions (p = 0.19, permutation test, data not shown).

FIG. 7.

Effect of amplitude modulation of tone on detection of signals presented alone and presented in steady-state noise. A Psychometric function showing probability correct for detection of stimuli in various conditions as a function of stimulus sound pressure level. Black symbols represent tone alone, cyan represents amplitude-modulated tone presented alone. Red symbols represent steady-state tone of the same frequency in steady-state noise at 44 dB and green symbols represent detection performance of amplitude-modulated tone in 44 dB noise. Figure convention is the same as Figure 2B. B Threshold differences observed as a function of tone frequency when amplitude-modulated tones were presented in quiet conditions. Figure conventions are the same as Figure 3A and 5B. Dotted lines show −6 dB, the difference between the peak sound pressure levels of the two signals. C Threshold difference between amplitude-modulated tone and steady-state tone when presented in noisy background. Convention is similar to Figure 3A. Dotted lines show −6 dB, the difference in the peak sound pressure levels of the two signals.

Figure 7B shows how amplitude modulation of the tone influenced detection thresholds across the range of frequencies tested (0.5–40 kHz). At most frequencies, the detection thresholds were lower when the tone was amplitude-modulated than for the steady-state tone (note that almost all data points are on the negative half of the ordinate). These data are qualitatively consistent with the physiological studies mentioned earlier. However, if temporal processing conveyed advantages beyond purely energetic mechanisms then the resulting threshold changes would be more negative than −6 dB (dashed line, Fig. 7B). Both monkeys exhibited enhanced detection performance at higher frequencies (>12 kHz), where the threshold change was more negative than the −6 dB criterion. The other consistent feature across the two monkeys was that at frequencies close to 10 kHz, both monkeys showed threshold change values that were more positive than −6 dB. The data at the lower frequencies (<5 kHz) were inconsistent across the two monkeys. Monkey B showed threshold changes that were more negative than −6 dB in this frequency range, but monkey A showed threshold changes that were more positive than −6 dB. These results suggest that at least at high frequencies, something beyond just purely energetic methods may be at play. These may involve a very strong sensitivity to amplitude-modulated tones of that range but not necessarily in the lower frequency range. The neuronal mechanisms underlying these enhancements are currently being investigated.

Under a streaming concept, modulation of either the signal or the masker should improve their segregation and enhance scene analysis (Bregman 1994). However, there is no a priori reason that one should have a greater effect than the other. Based on the abovementioned and Figure 6B, one would predict that detection of amplitude-modulated tones in noise would occur at much lower thresholds than detection of steady-state tones in noise. To verify the prediction, behavioral performance was measured for detection of amplitude-modulated tones in continuous, steady-state broadband noise. Figure 7A shows representative data from monkey A. Detection of steady-state tone is shown with red symbols and curve while detection of amplitude-modulated tone in steady-state noise is shown in green. The psychometric function in the amplitude-modulated tone case (green) was shifted to lower tone levels relative to the steady-state tone detection in broadband noise. Figure 7C shows the differences in detection thresholds between amplitude-modulated tones in steady-state broadband noise and steady-state tones in steady-state broadband noise as a function of the tone frequency. The data from the two monkeys are shown as differently colored symbols and lines. Note that at all frequencies tested, the threshold change was negative, indicating that thresholds were lower when the tone to be detected in noise was amplitude-modulated. However, in most cases, the threshold change did not fall below the −6 dB level (dashed line, Fig. 7C), which accounts for peak sound pressure level difference in the tone to be detected between the two cases. At one frequency and for one monkey, 32 kHz for monkey A, the threshold change did exceed −6 dB; however, even for this case, the threshold change was not statistically different from −6 dB (t₉₉₉₉ = 1.07; p = 0.1423, t test after bootstrapping to get distribution of threshold change). These results suggest that any enhancements in detection beyond those predicted by energetic mechanisms due to time varying signal are reduced in noisy backgrounds.

Discussion

Comparison with published literature

The results in this paper correspond well with results for humans and macaques in previously published papers. Our first finding is about auditory thresholds of rhesus macaques (Fig. 3). The U-shaped audiogram has been shown to be constant feature of audiograms across all species examined so far (e.g., humans: Sivian and White 1933; Hawkins and Stevens 1950; cats: Costalupes 1983; Heffner and Heffner 1985; macaques: Stebbins et al. 1966; Pfingst et al. 1975, 1978; marmosets: Osmanski and Wang 2011; starlings: Kuhn et al. 1982; Okanoya and Dooling 1987; chinchillas: Miller 1970; Salvi et al. 1983). The range of audible frequencies of the macaque also corresponds well with previous literature on the audiograms of macaques (e.g., Stebbins et al. 1966; Pfingst et al. 1975, 1978; Bennett et al. 1983; Lonsbury-Martin et al. 1987; Jackson et al. 1999). Methodologically, the current study differed from earlier studies in two ways: (1) the current study used 200 ms of stimulus duration compared to 1 s or more used by earlier studies and (2) most earlier studies used closed field studies rather than the free field stimulation used in this study (e.g., Pfingst et al. 1975, 1978; Stebbins et al. 1966). Neither methodological difference impacted the results on the hearing range and the thresholds, as these were similar across studies and similar to the results reported in this paper.

There are very few studies describing reaction time metrics in auditory studies of macaques (e.g., Stebbins 1966; Pfingst et al. 1975). The result of the current study finds that reaction time decreased with increasing sound pressure level, consistent with earlier studies. The range of reaction times in this study (see Fig. 2) were consistent with the range of reaction times reported in those studies, even though the stimulus durations were very different (Stebbins 1966; Pfingst et al. 1975). Only one of those studies describes directly the rate of change of reaction time with sound pressure level (reaction time slope; Pfingst et al. 1975). That study describes that the rate of change of reaction time with stimulus intensity was largest at the lowest frequencies (<0.5 kHz) and at the highest frequency (45 kHz). The current study did not test the highest frequencies of Pfingst et al. but did investigate the lower frequencies and found them to be similar. The lower frequency results are also similar with the data of Stebbins (1966), though reaction time slope was not directly addressed in that study. The one difference between the current study and Stebbins (1966) is that the reaction times of the earlier study show a more exponential function rather than the linear function in this paper. It is possible that the sound level separation of 5 dB around threshold levels resulted in an undersampling of the sound level region that had stronger effects on reaction time and that the reaction time in this study was dominated by the higher sound pressure levels.

The primary investigation was of the effect of noise on thresholds and reaction times that constitute detection behaviors. Adding continuous noise caused two effects on detection: (1) thresholds were shifted to higher sound pressure levels and (2) false alarm rates were slightly elevated (Fig. 4). The shift of threshold to higher levels has been described extensively elsewhere (e.g., Hawkins and Stevens 1950, in humans) but mostly for other species. While the incremental effect of noise on thresholds has been described in detail for many other species, the same has not been described for nonhuman primates, especially macaques. The results of this paper show that noise shifts the tonal thresholds to higher sound pressure levels at the rate of 1 dB/dB over most of the audible range (Fig. 5), similar to human threshold shift rates for tones above 1 kHz (Hawkins and Stevens 1950). However, this was found to not hold for frequencies below 1,000 Hz, where thresholds for hearing were higher (Fig. 3). Reduced shift rates have been reported for humans for frequencies below 1 kHz (Hawkins and Stevens 1950). That same study also reported reduced shift rates at frequencies higher than 4 kHz (Hawkins and Stevens 1950); however, the current study found that shift rate did not dip far below 1 dB/dB up to 36 kHz (Fig. 5).

Noise did not affect reaction time slopes (Fig. 5). However, it did affect the range of reaction times elicited. Because the effect of noise on reaction time to detection was dependent only on the absolute sound pressure level of the signal, and noise shifted tone thresholds and the method used to calculate reaction times included only those tone sound pressure levels that were above threshold, the range of reaction times decreased as the noise level increased (Fig. 3). These results are reminiscent of results observed in studies of human detection, where the reaction time to detection of a tone in noise was found to depend strongly on the tone sound pressure level and not just signal-to-noise ratio (Kemp and Irwin 1979; Kemp 1984).

The enhancements provided by dynamic stimuli over static stimuli have been well studied in humans. The results with time varying noise suggest that detecting tones in amplitude-modulated noise provides detection enhancements of about 11 dB over steady-state noise of the same mean amplitude (Fig. 6). The threshold enhancements seen in this study are similar to the threshold enhancements observed in humans with modulated band-pass noise, with a passband that was one third octave or more wide (Hall et al. 1984, 1996; Verhey et al. 1999) in studies of comodulation masking release (CMR) mechanisms. Since the noise used in this study was wider than the critical band at all the frequencies tested (Gourevitch 1970), the effect of the noise modulation was maximal (Verhey et al. 1999). In humans, continuous band-pass noise caused smaller threshold reduction relative to band-pass noise that was simultaneously gated with the tone (Hall et al. 1996). Taken together, these results suggest that the threshold changes that were observed with amplitude-modulated noise could be a result of mechanisms similar to CMR. The reaction times in the presence of steady-state noise show similar magnitudes and variance as the reaction times in amplitude-modulated noise (data not shown). The threshold enhancements appeared to be independent of frequency (Fig. 6), though one monkey did not show any threshold enhancement at 36 kHz (Fig. 6B). This could just represent an effect of high tone threshold, but the tone threshold at that frequency for monkey B was no different from the tone threshold at 0.5 kHz. The current study does not allow for any interpretation of the mechanisms that could be in play to mediate the effects reported.

The threshold enhancements were not just present when there was temporal structure in the noise; they were obtained when there was temporal structure in the signal as well (Fig. 7). The peak sound pressure level of the amplitude-modulated tone were 6 dB louder than the peak sound pressure level of the corresponding steady-state tone at the same frequency. Thus, if linear energetic mechanisms were to apply, the thresholds of the amplitude-modulated tone would be 6 dB lower than the thresholds of corresponding steady-state tones. Those conditions did apply for some frequencies. For both monkeys, the threshold difference observed was not significantly different from those expected as a result of simple energetic considerations around 10 kHz. At higher frequencies, both monkeys showed threshold enhancements closer to 9 dB, but only one monkey showed threshold enhancements at frequencies 2 kHz and under (Fig. 7B). However, when the temporally modulated tones were detected in noisy backgrounds, threshold changes were not more negative than −6 dB at any frequency (Fig. 7C). This specific result suggests that the mechanisms that mediate detection enhancements in the absence of noise may be degraded in the presence of even the moderate levels of noise used in this particular study (44 dB). Since one possible mechanism involved is phase locking, it is possible that the changes observed in the temporal responses of central auditory neurons such as the changes in encoding and strength of encoding of temporal parameters (e.g., Rees and Moller 1987; Rees and Palmer 1989; Krishna and Semple 2000) could account for the results. It is not clear that these changes that occur in anesthetized preparations also occur in the awake preparation, but the behavioral results suggest the possibility. Another possibility is that the effects reported may be manifest in the responses of VIII nerve fibers. If one were to assume that the peaks of modulated tones are responsible for detection of modulated tones in noise, and the troughs of the noise for the detection of unmodulated tones in modulated noise, then the nonlinearities of the VIII nerve responses would play into one of the two situations, but not the other. The low noise condition of the modulated noise condition would involve less nonlinearities, whereas saturation and compression would come into play during detection of modulated tone in steady-state noise. Thus, the sensitivity in the modulated tone condition could be lower than in the modulated noise condition. Ongoing physiological measurements of neuronal activity in the cochlear nucleus would reveal if the second alternative is true.

All the results of this study, put together, highlight the similarity in detection behavioral metrics between humans and macaques. The results support the use of macaques as a model for human hearing. That result combined with anatomical studies that highlight the similarity of cortical (Rauschecker and Tian 2000; Arnott et al. 2004) and subcortical (Adams 1986; Moore and Osen 1979; Moore 1980) auditory pathways of humans and macaques suggest the similarity of neuronal underpinnings of the behavior between the two species.

Possible neurophysiological mechanisms

While the results of just these experiments do not shed any light on neurophysiological mechanisms by themselves, it is interesting to speculate on physiological mechanisms because macaques are a good species for neurophysiological studies. Previous studies have shown that detection in noise by humans is at least partly mediated by the olivocochlear bundle (e.g., Micheyl and Collet 1996). Studies of neuronal representation of tones in noise in decerebrate cats suggest that a specific neuronal population in the dorsal cochlear nucleus (Gibson et al. 1985) and another population in the inferior colliculus (Ramachandran et al. 2000) were the only subcortical neuronal populations that showed shift rates that matched the 1 dB/dB threshold shift rate that this study reports (Fig. 3). However, those studies were conducted in decerebrate preparations. One study reported that neurons in the ventral cochlear nucleus in awake cats showed larger shifts compared to similar neurons in decerebrate cats (May and Sachs 1992). However, that study did not measure detection behavior. Studies show that while macaques and humans have similar subcortical anatomy, they are different from cats and rats (Moore and Osen 1979; Moore 1980). How the difference in anatomy manifests in the neurophysiology, how the differences in the state of the animal will manifest itself in the neuronal encoding of tones in noise and in the relationship between neuronal and behavioral metrics of detection in noise remain interesting questions to be explored.