Skip to main content
PMC home page
Journal of Cerebral Blood Flow & Metabolism logoLink to Journal of Cerebral Blood Flow & Metabolism
. 2013 Apr 10;33(7):1058–1065. doi: 10.1038/jcbfm.2013.47

Arterial input function derived from pairwise correlations between PET-image voxels

Martin Schain 1,2,5,*, Simon Benjaminsson 2,3,5, Katarina Varnäs 1, Anton Forsberg 1,2, Christer Halldin 1,2, Anders Lansner 2,3,4, Lars Farde 1,2, Andrea Varrone 1,2
PMCID: PMC3705432  PMID: 23571279

Abstract

A metabolite corrected arterial input function is a prerequisite for quantification of positron emission tomography (PET) data by compartmental analysis. This quantitative approach is also necessary for radioligands without suitable reference regions in brain. The measurement is laborious and requires cannulation of a peripheral artery, a procedure that can be associated with patient discomfort and potential adverse events. A non invasive procedure for obtaining the arterial input function is thus preferable. In this study, we present a novel method to obtain image-derived input functions (IDIFs). The method is based on calculation of the Pearson correlation coefficient between the time-activity curves of voxel pairs in the PET image to localize voxels displaying blood-like behavior. The method was evaluated using data obtained in human studies with the radioligands [11C]flumazenil and [11C]AZ10419369, and its performance was compared with three previously published methods. The distribution volumes (VT) obtained using IDIFs were compared with those obtained using traditional arterial measurements. Overall, the agreement in VT was good (∼3% difference) for input functions obtained using the pairwise correlation approach. This approach performed similarly or even better than the other methods, and could be considered in applied clinical studies. Applications to other radioligands are needed for further verification.

Keywords: HRRT, image-derived input function, PET, pharmacokinetic modeling, voxel correlation

Introduction

Positron emission tomography (PET) is a molecular imaging modality, providing detailed examination of biochemical and metabolic brain biomarkers in vivo. Throughout recent years, the applications of PET have for instance lead to new insights into neurodegenerative and psychiatric disorders as well as to cognitive neuroscience.1, 2, 3

Positron emission tomography is associated with limited spatial resolution due to the challenging physical properties of emission tomography.4 Earlier PET systems normally had an estimated resolution of ∼6 mm full width at half maximum (FWHM), preventing accurate measurement of radioligand binding in small anatomic structures.5 However, methodological advancements in acquisition hardware and image reconstruction software have significantly improved the sensitivity and the resolution of more recently developed PET systems.6, 7, 8 The High Resolution Research Tomograph (HRRT, Siemens Molecular Imaging, Knoxville, TN, USA) is the state-of-the-art system for human brain PET imaging, with an estimated resolution of 1.5 mm FWHM in the center of the field of view, when modeled in the image reconstruction algorithm.9 The high resolution of the HRRT is a basis for improved quantification in small brain structures.10 In addition, the HRRT system has an extended axial field of view of 250 mm,6 allowing for a large proportion of the head and neck region to be covered in the PET images.

Pharmacokinetic modeling is a method frequently used to quantify receptor or transporter density from images obtained with PET. The radioactivity concentration in arterial plasma represents the model's input function, and is conventionally acquired from measurement of the radioactivity level in arterial blood. Arterial cannulation is however laborious, sensitive to errors, invasive, and can be associated with patient discomfort as well as potential adverse events. A non invasive procedure to estimate the radioactivity level in arterial blood would overcome these limitations, and is thus preferable.

Several methods to derive the radioactivity level of arterial blood directly from PET images have been suggested during recent years.11, 12, 13, 14 A majority of the methods are based on either manual or automatic segmentation of the carotid artery, in combination with means to compensate for signal artifacts induced by limited spatial resolution (i.e., partial volume effects). Due to the moderate resolution and high noise levels associated with PET, several methods have shown low reproducibility when implemented by other research groups, leading to a growing skepticism toward the feasibility of the concept.15 In a recent review article, it was stated that the difficulties connected with deriving the arterial input function from PET images are too many and too difficult to overcome considering the potential benefit of obviating on-line arterial sampling.16 However, most attempts to derive blood curves have been performed on PET data acquired on systems with significantly lower resolution compared with the HRRT. Since the carotid artery is a small elongated structure with a diameter of ∼5 mm,17 with complex hemodynamic patterns,18 system resolution is likely a fundamental factor for accurate measurement of the image-derived input function (IDIF).

For the analysis of functional magnetic resonance imaging (MRI) data, a new algorithm has recently been developed, which clusters voxels displaying similar statistical fluctuations over time.19 In the present study, we have adapted parts of this statistical tool to PET data, so that it clusters individual PET voxels with similar temporal radioactivity patterns. To assess the utility of the method in human PET imaging, it was evaluated using two different radioligands targeting different neurotransmitter systems, and displaying different kinetic properties.

The performance of the method was compared with that of three other methods, previously described by Chen et al.20 Mourik et al.,21 and Naganawa et al.22 These methods were selected from the literature since they, among others, have shown the best performance in the estimates of cerebral metabolic rate of glucose.15

Materials and methods

Rationale for Selection of Radioligands

Data obtained by PET examination in human subjects with two different radioligands were used in the present study. The radioligands were chosen for different purposes. [11C]flumazenil (GABAA-receptor radioligand) was chosen because its quantification often requires an input function, since the suitability of the pons as a reference region has been questioned.23 [11C]AZ10419369 (5HT1B-receptor radioligand)24 was included to evaluate the approximation of venous sampling as a substitute to arterial sampling, since its negligible metabolism in human subjects permits to use the total radioactivity in plasma as an estimate of the input function without need of metabolite correction.25

Subjects and Positron Emission Tomography Measurements

A total of 12 subjects were examined with the HRRT. Six subjects were examined using [11C]flumazenil, and their PET data consisted of baseline measurements in an occupancy study, which will be published elsewhere. Remaining six subjects were examined with [11C]AZ10419369. Subjects were healthy according to psychiatric and medical history, physical examination, laboratory testing, ECG, and magnetic resonance imaging (MRI). The procedures were approved by the Research Ethics Committee in Stockholm, Sweden, and the Radiation Safety Committee at Karolinska University Hospital, Stockholm, and were performed in accordance with the current amendment of the Declaration of Helsinki and International Conference on Harmonization/Good Clinical Practice guidelines. All subjects gave their written informed consent before participation. Injected masses, specific radioactivities, and subjects' ages and genders are given in Table 1. For each subject, a plaster helmet was made to minimize head motion during the acquisition.26 The radioactivity was administered as a bolus injection, immediately after which the intravenous line was flushed with saline. For all subjects, the radioactivity level in arterial blood was measured via an automatic blood sampling system (ABSS; Allogg Technology, Mariefred, Sweden) for the first 5 minutes, followed by manual arterial sampling at midpoint of each frame.27 In addition, for the [11C]AZ10419369 data, radioactivity levels were also measured in venous samples obtained at 3, 15, 30, 45, 60, and 90 minutes after injection.

Table 1. Experimental set-up. Median (min−max) values are reported.

Radioligand Age (years) Gender (M/F) Injected mass (μg) Specific radioactivity (GBq/μmol) Frame definition (s)
[11C]flumazenil 32 (23–34) 6/0 0.1 (0.06–0.23) 1,013 (467–1,616) 9 × 10, 2 × 15, 3 × 20, 4 × 30, 4 × 60, 4 × 180, 7 × 360
[11C]AZ10419369 65 (54–69) 4/2 0.82 (0.41–1.18) 239 (119–461) 8 × 10, 5 × 20, 4 × 30, 3 × 60, 4 × 180, 12 × 360
Open in a new tab

Positron emission tomography measurements were acquired in list mode for 63 minutes in case of [11C]flumazenil, and 93 minutes in case of [11C]AZ10419369. The PET images were reconstructed using Ordinary Poisson Ordered Subset Expectation Maximization, with 16 subsets and 10 iterations, including modeling of the system's point spread function.9 The frame definition for each of the radioligands is reported in Table 1. To compensate for potential residual motion, a post reconstruction frame-to-frame realignment algorithm was applied to all PET images.8

Magnetic Resonance Image Acquisition and Processing

For all the subjects, T1-weighted MR images were acquired using a 1.5-T MRI system (11 subjects were studied using the GE signa system scanner (GE Medical Systems, Milwaukee, WI, USA), and the remaining subject was imaged using the Gyroscan Intera system (Philips Medical Systems, Best, The Netherlands)). All MR images were segmented into gray and white matter, and coregistered to PET using SPM5 (Wellcome Department of Cognitive Neurology, University College London).

Methods for Image-Derived Input Function

To reduce the computational load, a subset of each PET image covering the neck was extracted (illustration of the image subset is shown in Supplementary Figure 1). This subset was used when estimating the blood signals using the four methods described below.

Pairwise correlation method

The novel approach is based on the Pearson product-moment correlation coefficient (PCC), r, which was calculated between all voxel pairs in a slightly smoothed (2 mm FWHM Gaussian filter) version of the image subset. That is, for voxels i and j, the PCC between their respective time-activity curve (TAC), xi and xj, with T time steps was calculated as

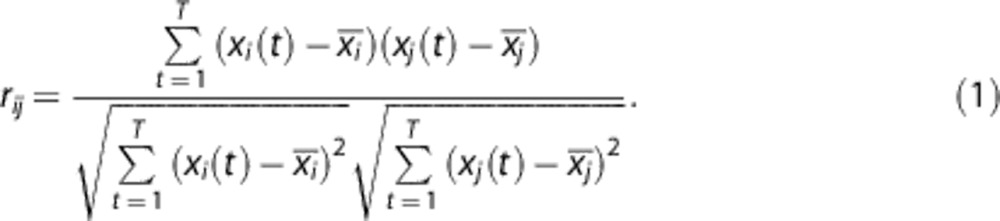graphic file with name jcbfm201347e1.jpg

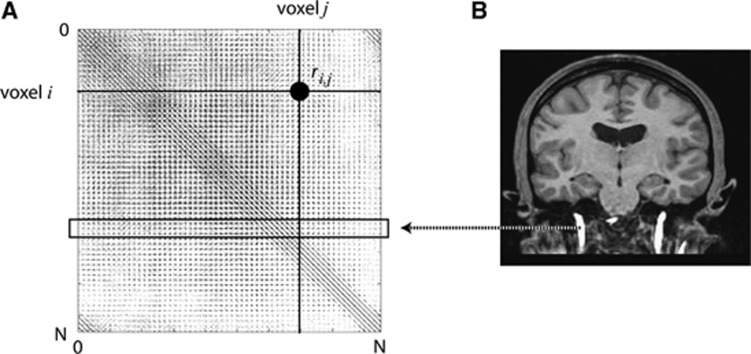
Pearson product-moment correlation coefficients of voxel pairs displaying a strong measure of correlation (| rij|>θ with 0<θ≤1) were stored in a sparse correlation matrix M, so that Mi,j=ri,j, for all i≠j. To avoid extracting noisy voxels located in the vessel, all autocorrelations were zeroed (Mi,i=0). A visual representation of M is shown in Figure 1A. The total number of voxels, N, was around 106 for each subject. Values for θ were set such that the correlation matrices were of manageable sizes, and estimated for each radioligand separately after preliminary evaluation of the data sets. They were set to 0.95 and 0.97 for [11C]flumazenil and [11C]AZ10419369, respectively. The size of M obtained with these thresholds was always <2 GB. Values for T (i.e., total number of time frames) are reported in Table 1. To extract blood voxels, coregistered MR images were segmented by applying an intensity threshold (Figure 1B) such that the resulting binary mask only included voxels from the carotid artery. Each extracted voxel was used as an index to the rows in M. The voxels in the columns of all selected rows were classified as blood voxels, and constituted a ‘carotid artery mask', which were applied to all time frames. The calculation of M for each subject was performed on 96 nodes of a CRAY XE6 (Lindgren at PDC-KTH: AMD Opteron 12-core 2.1 GHz processors, with 2 processors and 32 GB memory per node), and took 1 to 2 hours.

Figure 1.

Figure 1

Open in a new tab

(A) Pearson product-moment correlation coefficient (PCC) between all voxel pairs in an image subset (number of voxels N=∼106) stored in a sparse matrix M. The PCC between the time-activity curves of voxels i and j is highlighted. (B) Carotid artery voxels were segmented from coregistered magnetic resonance (MR) images and used as indices to rows in M to extract correlated (columnar) voxels.

The amount of spill-out of radioactivity from the carotid region of interest (ROI) varies throughout a PET measurement. In the initial phase when the radioactivity is still in the vessels, the spill-out is a major issue. At later time points, the radioactivity gradient between the vessels and their vicinity is smaller and could potentially be neglected. Therefore, only the first 3 minutes of the acquisition were corrected for partial volume effects using the geometric transfer matrix approach28 reduced to one compartment, and a 2 × 2 × 2 mm FWHM Gaussian filter. The width of the filter was set slightly higher than the measured system resolution, since the carotid artery is not in the center of the field of view.

To increase the agreement between the IDIF and the measured input function (MIF), late blood samples were used to scale the tail of the curves. For [11C]flumazenil, the average of the five latest blood samples were used, and for the [11C]AZ10419369 data, only the latest venous sample was used as a scaling factor.

Chen's method

The method has been described in detail in the literature.20 In short, manual ROIs were drawn on 16 consecutive planes below the circle of willis. For each of the carotids (left and right), ROIs for both the vessel and its vicinity were drawn. The measured blood curve obtained from the carotid artery ROI, CAmea, was then assumed to be described as

graphic file with name jcbfm201347e2.jpg

where CAtrue denotes the true (but unknown) radioactivity concentration in the arterial blood, and Cvic denotes the measured radioactivity in the vicinity ROIs. The two constants RC and SP denote recovery coefficient and the spill-in coefficient, respectively. In Chen's method, late blood samples are used to estimate the values of RC and SP, which are in turn used to calculate CAtrue for the whole measurement. For comparative purposes, the same number of blood samples was used as for the PWC method. The fitting was performed for each blood vessel separately. In those cases, RC and SP were <0 or >1, the parameters were reestimated with non negativity constraints applied, as described in the original paper.20

Mourik's method

Mourik's method relies on optimal reconstruction settings for HRRT data.29 To assess the clinical applicability, the standard reconstruction setting normally applied to HRRT data at Karolinska Institutet was used (see section Subjects and Positron Emission Tomography Measurements). To delineate ROIs for the carotids, a summation image of the early frames was smoothed, after which the 4 hottest pixels in 16 planes below the circle of willis were identified, as described as optimal ROI volume for the HRRT data.29 Those 64 voxels were applied to all image frames to obtain the IDIF. Also, the image-derived blood curves were scaled using late blood samples, as it has been reported to have beneficial effect on the performance of the method.

Naganawa's approach

Naganawa's method uses a modified FastICA implementation for performing independent component analysis (ICA).22 In this study, the ICA calculations were performed using the author's own matlab toolbox EPICA, freely available at http://home.att.ne.jp/lemon/mikan/EPICA.html. The method assumes that the signal obtained from the PET image is a linear combination of underlying independent components, of which the blood signal is one. More specifically, if two components in the data are more similar as compared with the other components, ICA tends to estimate them into a single component. The EPICA extracts two independent components by default. Since the blood TAC is more different than tissue TACs from all brain regions regardless of their kinetic properties, one of the components will correspond to the estimated blood TAC and the other to the tissue TAC.

The ICA only provides the shape of the independent components, and not their magnitude. Late blood samples were therefore used to scale the blood TAC. No correction for partial volume effects was applied since potential spill-out of radioactivity is in theory taken care of in the unmixing process. Those subjects for which the EPICA generated blood curves with negative values were discarded from the analysis.

Correction for Metabolites and Plasma Fractions

In PET kinetic modeling analyses, it is commonly assumed that only unchanged radioligand in plasma can pass the blood brain barrier and enter the brain. Therefore, to obtain the input functions, image-derived and measured blood curves were corrected for metabolite concentrations and plasma fractions. The parent fraction of [11C]flumazenil was measured using high-performance liquid chromatography of plasma samples obtained at 5, 10, 20, 30, and 40 minutes after injection, and the curve was fitted using the Hill function. [11C]AZ10419369 has negligible metabolism and was therefore not corrected for metabolites.25 The plasma-to-blood ratio was measured after centrifugation of the blood samples (arterial samples for [11C]flumazenil, and venous and arterial samples for [11C]AZ10419369). For estimation of the plasma-to-blood ratio at intermediate time points, several fitting functions were evaluated (logarithmic, exponential, linear, average, and the Michaelis–Menten equation (y(x)=αx/(β+x)). For [11C]flumazenil, the Michaelis–Menten equation was used since it provided smallest residuals, whereas for [11C]AZ10419369, the average plasma fraction was used since none of the more advanced models provided better fit.

Regions of Interest

The ROIs included in the study were specific for each radioligand, based on the knowledge of the receptor distribution in the brain. For [11C]flumazenil, the ROIs included were occipital cortex, frontal cortex, putamen, cerebellum, and pons, and for [11C]AZ10419369, occipital cortex, frontal cortex, putamen, ventral striatum, and cerebellum were used. All ROIs were manually delineated on each subject's MRI, and coregistered to the corresponding PET image. For both radioligands, the gray matter obtained from segmentation of the MRI was also included.

Quantification

The primary outcome measure was the distribution volume (VT), defined as the area under the curve (AUC) of the target TAC divided by the AUC of the input function, when extrapolated to infinity. VT was calculated with the Logan graphical analysis approach, using both IDIF and MIF.30 The time of equilibrium, t*, was set after preliminary evaluation of both data sets to verify that the slope of the Logan plot displayed linearity. The same t* was used for both MIF and IDIF, and was set to 21 minutes for [11C]flumazenil, and 33 minutes for [11C]AZ10419369. All calculations of VT were performed with PMOD v.3.2 (PMOD Group, Switzerland).

VT obtained with MIF was used as gold standard, and the methods were evaluated by investigating the percent difference between regional VT obtained with IDIF and MIF (calculated as 100 × {(VTIDIF−VTMIF)/VTMIF}, and by linear regression analysis. In addition, the agreement between the AUC and maximal peak height between IDIF and MIF were assessed.

Statistical Analysis

The agreement between IDIF and MIF was assessed using one-way repeated measures ANOVA, followed by pairwise comparisons using Bonferroni correction to adjust for multiple comparisons. Image-derived and MIFs were compared in terms of peak height and AUC. Also, VT values obtained in one representative ROI (occipital cortex) using both IDIF and MIF were compared in a similar manner. The significance level was set to 0.05. Aforementioned statistical analysis was performed using SPSS v. 20 (IBM Corporation, Somers, NY, USA).

Results

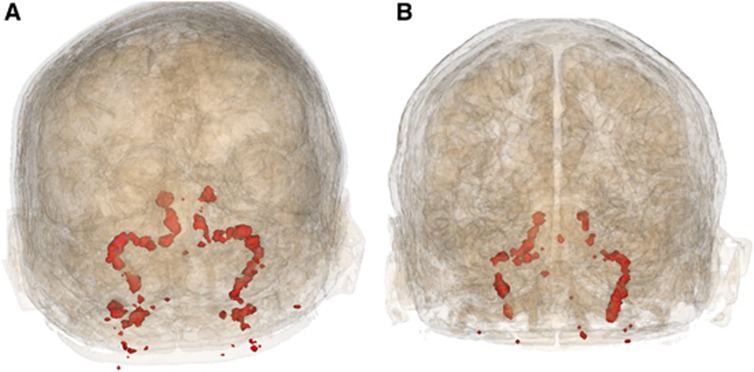
Pairwise Correlation Method

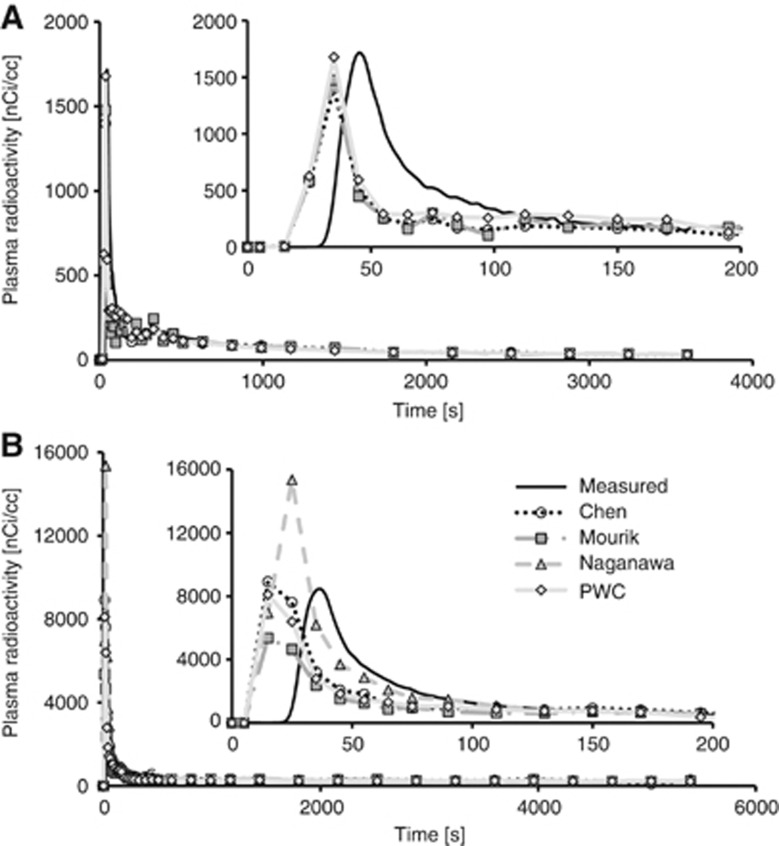
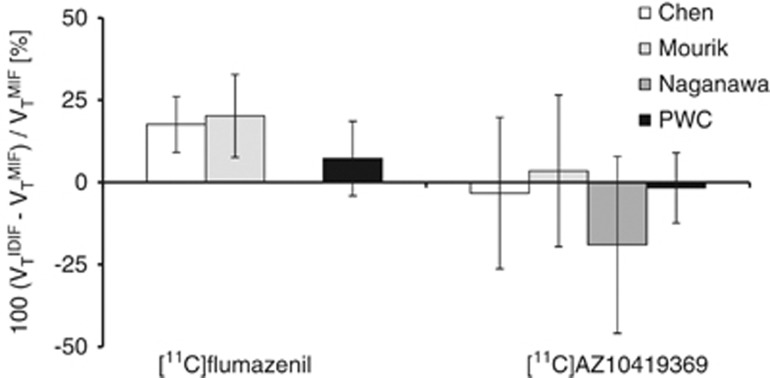
In all subjects, the PWC method enabled to identify clusters corresponding to the carotid artery (Figure 2). The radioactivity concentration in the carotids was corrected for spill-out on early frames (t<3 minutes), whereas the tail of the TAC (t>3 minutes) was scaled with manual samples. This approach provided image-derived blood curves in good agreement with those obtained from manual sampling (see Figure 3 for PWC and other methods). No statistical difference of AUC, peak height, or VT was found between MIFs and IDIFs obtained with the PWC method for [11C]flumazenil and [11C]AZ10419369. For [11C]flumazenil, the AUC of the input functions was on average slightly underestimated (6.9±14.2%) as compared with MIF (Table 2). The AUC of the IDIFs for the [11C]AZ10419369 data was in good agreement with the MIF (−2.3±14.8%, Table 2). The peak height generally showed larger across subject variability than the AUC for both radioligands; but the impact of peak height on the agreement of the outcome measures was limited. The difference between VT estimated with IDIF and MIF was on average 2.8±11.8% (Figures 4 and 5), ranging from 7.3±11.3% for [11C]flumazenil to −1.7±10.7% for [11C]AZ10419369. Linear regression analysis showed good agreement in the estimates of VT for both radioligands, with intercepts close to 0 and slopes and R2 values close to 1 (Table 2). Scatter plots of the regression analysis are shown in Supplementary Figure 2.

Figure 2.

Figure 2

Open in a new tab

Voxel clusters obtained from the PWC method using (A) [11C]flumazenil and (B) [11C]AZ10419369.

Figure 3.

Figure 3

Open in a new tab

Examples of all input functions for one subject per radioligand. (A) [11C]flumazenil (B) [11C]AZ10419369. Inserts highlights the early peak, corrected for spill-out of radioactivity.

Table 2. AUC and peak difference between IDIF and MIF (calculated as 100 × (IDIF−MIF)/IDIF), and linear regression analysis data for all radioligands and methods (scatter plots shown in Supplementary Figure 2).

  Input curves properties
 Linear regression analysis
  AUC difference (%) Peak difference (%) VT slope VT intercept VT R2
[11C]flumazenil
Chen −17.85±7.675 −26.89±20.86 1.21 −0.17 0.98
Mourik −19.27±10.62 −44.00±15.95 1.29 −0.45 0.95
PWC −6.91±14.22 2.03±41.17 1.1 −0.13 0.96
[11C]AZ10419369
Chen 8.63±36.27 −17.02±47.59 1.3 −0.25 0.89
Mourik −0.77±35.17 −36.68±37.33 1.35 −0.23 0.9
Naganawa 71.50±103.53 183.77±206.95 1.29 −0.21 0.9
PWC 2.29±14.82 7.02±18.35 1.01 −0.02 0.96
Open in a new tab

AUC, area under the curve; IDIF, image-derived input function; MIF, measured input function; PWC, pairwise correlation.

Bold values highlight the method providing slope and R2 closest to one, and intercept closest to zero.

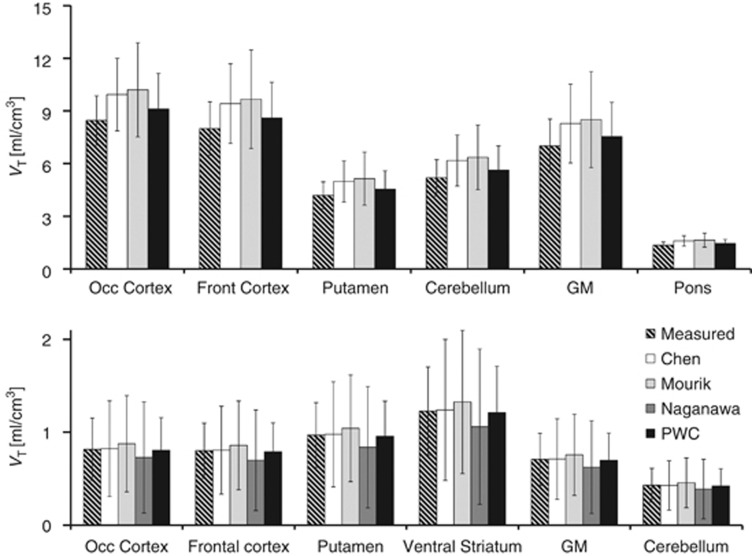
Figure 4.

Figure 4

Open in a new tab

VT obtained for each method. (A) [11C]flumazenil and (B) [11C]AZ10419369. Error bars reflect SD. GM, gray matter, PWC, pairwise correlation.

Figure 5.

Figure 5

Open in a new tab

Percent difference between VT estimated with image-derived input function (IDIF) and measured input function (MIF). Note that Naganawa's method could not be applied to the [11C]flumazenil data set.

Chen's Method

Neither the [11C]flumazenil nor the [11C]AZ10419369 data required non negativity constraints when estimating RC and SP. One of the [11C]AZ10419369 subjects, however, resulted in SP and RC>1 regardless of whether the constraints were applied or not. The difference in AUC between IDIF and MIF (Table 2) was comparable to that obtained using the PWC method for [11C]AZ10419369 (P=0.56), whereas for [11C]flumazenil, Chen's approach significantly underestimated the AUC of the IDIF (P=0.02). The agreement in peak height was also comparable to that obtained using the PWC method (P=0.168 and P=1.0 for [11C]flumazenil and [11C]AZ10419369, respectively, Table 2). The difference between VT obtained with IDIF and MIF was on average across both radioligands 7.2±20.2%. For each radioligand, the percent difference in VT was −3.3±23.0% (P=1.0) for [11C]AZ10419369, whereas a larger and significant discrepancy was observed for the [11C]flumazenil data (17.6±8.5%, P=0.01), as a result of the underestimated input functions (Figures 4 and 5).

For one of the [11C]flumazenil subjects, and three of the [11C]AZ10419369 subjects, the blood curve derived from one of the vessels could not be fitted according to equation (2), due to slightly anomalous shape of the blood curve at late time points. For each of these subjects, only the TAC from the remaining vessel was used.

Mourik's Method

For all subjects, Mourik's method provided ROIs located in the center of the carotid. Similarly to Chen's method, the agreement in AUC and peak height between IDIF and MIF (Table 2) was good for [11C]AZ10419369 (P=0.96 and P=0.45), whereas both AUC and peak height were significantly underestimated for [11C]flumazenil (P=0.04 and P=0.02). The difference between VT obtained from IDIF and MIF (Figures 4 and 5) was on average 11.9±20.3%, and ranged from 20.2±12.6% for [11C]flumazenil (P=0.03), to 3.5±23.1% for [11C]AZ10419369 (P=1.0).

Naganawa's Method

EPICA generated negative blood curves for all subjects measured with [11C]flumazenil. The whole data set was thus discarded from the analysis. In addition, one subject measured with [11C]AZ10419369 was also removed from the analysis due to negative blood component.

For the remaining data, EPICA successfully generated one curve displaying blood-like shape for each subject, normally with severely overestimated AUC and peak height (Table 2). VT estimated with input functions obtained with EPICA showed a large variability, and was on average substantially lower than that obtained using MIF (Figure 4). The percent difference was on average −19.0±26.9% (Figure 5). Due to the inconsistencies in the number of remaining subjects, and the overall poor performance, the results from Naganawa's method were not included in the ANOVA.

Discussion

In this study, we propose a new method for estimation of the IDIF. The method is based on the calculation of pairwise correlations between voxel pairs in the PET image. The performance of the method was evaluated by comparing VT obtained with the IDIF to that obtained with MIF, and compared with three other methods previously described. The method was evaluated using two different radioligands targeting different neurotransmitter systems and displaying different kinetic properties.

The Pairwise Correlation Method

In general, VT estimated with IDIF obtained with PWC was in good agreement to that obtained using MIF for both radioligands. A larger variability was observed for [11C]flumazenil data, where one subject displayed roughly 25% difference between VT obtained from IDIF and MIF. On average across the subjects measured with [11C]flumazenil, the agreement was substantially better (∼7% difference). The [11C]AZ10419369 data also displayed some variability in the agreement of regional VT, but the average difference between VT obtained from IDIF and MIF was <2%. The lowest agreement was generally found in cerebellum, which has a negligible density of 5HT1B receptors. The discrepancy between IDIF and MIF was likely related to the low value of VT in cerebellum, considering that the absolute maximal difference in VT was quite small (∼0.1 mL/cm3).

The agreement in VT obtained with the PWC method was better than that obtained with the other methods for both radioligands. For [11C]flumazenil, the PWC method was the only approach that did not result in significantly different VT values as compared with MIF, and for [11C]AZ10419369, the across subject variability was smaller. This improved agreement is likely related to the fact that the methods of Chen and Mourik classify voxels displaying a peak in early time frames as blood voxels, whereas the PWC method is based on correlations between voxels over all time frames. Therefore, the PWC approach has the advantage of excluding voxels with noise in early frames, and voxels displaying a non blood-like pattern in late frames.

Since the sparse correlation matrix M contains PCCs between all voxel pairs in the image, the PWC method uses an a priori assumption regarding which voxels are likely to display blood like behavior (i.e., which rows to extract). In this study, carotid artery voxels as segmented from MRI were used. This procedure could however be replaced with other means to obtain an initial guess of the spatial localization of the artery, for example, using the N hottest voxels on a summation image of early PET frames (similar to Mourik's method). Preliminary evaluation shows that the carotid artery ROI obtained from M is similar regardless of which of these methods were used for the initial guess (data for one subject are shown in Supplementary Figure 2). Also, the need of any initial guess may become obsolete if the PWC method is combined with a suitable graph clustering method.19, 31

Comparison Methods

The four methods for generation of IDIF compared in this study are conceptually different. The method described by Chen et al. is a straightforward technique, which mimics the methodology conventionally used to derive tissue TACs from PET images. The only prerequisites required for successful implementation is that the carotid artery to some extent is visible on a summation image of the early frames for the manual TACs to be delineated. However, with small ROIs, the image-derived blood curve may be noisy in late time frames, which may cause the fitting of RC and SP to fail. This becomes particularly challenging with radioligands with fast metabolism such as [carbonyl-11C]WAY-100635, which typically displays small area under the tail of the blood curve.32 Previous studies have shown that Chen's approach can be successfully applied to the radioligands [18F]FDG, [11C](R)-rolipram and [11C]PBR28.15, 33 This study provides further support for the applicability of Chen's method for [11C]AZ10419369, and to a lower extent, for [11C]flumazenil.

Mourik's method also provided VT values in good agreement to those obtained with MIF for [11C]AZ10419369, whereas the difference was larger for [11C]flumazenil. This reduced performance for [11C]flumazenil was surprising since the method has already been validated for this radioligand. One explanation could be that, in the present study, a different number of iterations were used for the PET image reconstruction. When Mourik et al.29 applied their method to [11C]flumazenil data acquired with the HRRT, they found good correspondence between MIF and IDIF using 16 iterations (compared with 10 in the present study). We have previously shown, using the NEMA phantom, that for a volume of 10 mm diameter, increasing the number of iterations from 10 to 16 has negligible effect on the recovery,9 whereas the noise level and reconstruction time are increased. However, when considering that Mourik's approach is based on very small ROIs, it is likely that the number of iterations could affect the signal recovery, depending on the radioligand. In the present study, Mourik's approach showed good performance for [11C]AZ10419369. Previous studies using [18F]FDG, [11C](R)-rolipram, [11C]PBR28, [11C]PIB, (R)-[11C]verapamil, and (R)-[11C]PK1119515, 33, 34 have shown better agreement between MIF and IDIF than the one we found for [11C]flumazenil. Thus, the performance of Mourik's approach may be radioligand dependent and, for some radioligands, the approach may require specific settings for the image reconstruction.

The method proposed by Naganawa et al. is a purely data-driven approach, only assuming that the signal obtained is a linear combination of underlying independent components. In the original publication, Naganawa et al.22 showed that the method provided very high precision when estimating the influx rate constant (Ki) for [18F]FDG data. Other studies have not been able to replicate this finding using neither [18F]FDG15 nor [11C](R)-rolipram or [11C]PBR28.33 In addition, when EPICA was applied to the data sets included in the present study, the calculated VT showed very large variability and substantial difference from the gold standard. Also, the lack of a non negativity constraint enables generation of blood curves that are biologically meaningless.35 Among the methods evaluated in this study, EPICA showed to be the least reliable for both radioligands. However, considering the complex nature of ICA, the result would likely improve if the algorithm was tuned for each radioligand used, for example, by modifying the cost function, the number of principal components included or altering the brain mask.36

Quantification Considerations

Generally, the agreement between VT obtained with IDIF and that obtained with MIF was more dependent on the agreement in the AUC between the input functions than on the agreement between their peak height ratio. Graphical methods for estimation of VT such as the Logan Plot or the Patlak Plot rely predominantly on the AUC of the input function. Thus, successful estimation of peak height becomes less valuable when estimating the IDIF if the outcome measures are calculated using graphical approaches. However, if compartmental modeling such as the two-tissue compartment model was used instead, the difference in peak height would probably be reflected by an increased variability in the radioligand influx rate constant K1, normally associated with blood flow, and consequently, a low accuracy in all rate constants. All methods evaluated in this study displayed a large variability in the peak heights, and should thus be used with caution in studies where changes in blood flow are expected.

Arterial and Venous Sampling

During the initial phase of the PET acquisition, arterial sampling is conventionally performed with high frequency, typically drawing ∼0.1 mL of arterial blood every second. Therefore, a method to generate IDIFs could be useful to derive the blood curve, substituting the need of frequent arterial sampling and the use of automated blood sampling systems. Still, all IDIF methods (including PWC) require at least one arterial sample to provide good accuracy in the estimates of VT. The need of arterial blood has been one of the major concerns regarding the wide applicability of IDIFs.16 Several methods without the need of blood samples have been proposed,14, 37, 38, 39 but their accuracy in the estimates of VT and cerebral metabolic rate of glucose has been shown to be significantly lower when compared with methods including arterial blood sampling.15, 33 Furthermore, even if a non invasive method was able to provide high accuracy in the blood curve estimate, multiple blood samples would still be needed to correct for plasma-to-blood ratio and radioactive metabolites, and to provide accurate estimates of binding parameters.

An interesting alternative is to investigate the possibility to replace arterial with venous samples when scaling the IDIF. For radioligands with similar metabolism in both venous and arterial blood, the metabolite analysis could be performed on venous samples. Also, if the radioactivity level is similar in venous and arterial plasma at late times of the acquisition, late venous samples could be used to scale the IDIF. In a recent study, Hahn and colleagues showed that IDIF together with venous samples could be used to quantify 5HT1A receptor binding using the radioligand [carbonyl-11C]WAY. The present study shows that also for [11C]AZ10419369 data, arterial samples can be replaced with venous samples. This interchangeability is possible since the radioactivity level is similar in venous and arterial plasma at late time points (data not shown), which is not the case for all radioligands. For other radioligands that show differences of radioactivity concentrations or parent fractions between arterial and venous plasma, a potential solution is to use the venous measurements to model the arterial plasma concentration,40 similarly to the work performed previously for nicotine concentrations.41

Future Aims

With regard to the PWC method, calculating the PCC for all voxels in a PET image is associated with a high computational load. For this study, a super computer was used to generate results within reasonable time. For the method to be applied in a more standard setting, the algorithm could be optimized by reducing the number of PCCs calculated (by including only artery voxels when generating the sparse correlation matrix, i.e., only including rows of interest in Figure 1A), and by executing the calculation on a graphical processing unit. This approach is currently under evaluation in our group.

Moreover, successful clustering of PET voxels using the PWC method has other potential applications. For instance, by applying the algorithm to parametric data, it may be possible to identify voxels correlating across subjects. This approach can be used for detecting and identifying pathologic patterns of radioligand binding on a group level, and possibly to derive classifiers which might serve as an aid in differentiating between control and patient groups. Hence, the PWC method provides new exploratory possibilities besides IDIF.

Conclusion

The PWC method was able to generate IDIFs which were similar to the MIFs for both radioligands evaluated in this study. For the [11C]AZ10419369 data, no arterial samples were needed for accurate estimation of IDIFs. Kinetic modeling using IDIFs provided VT values in good agreement to those obtained with MIF. Of the methods evaluated in this study, the PWC method showed best accuracy in the estimates of VT, whereas Chen's and Mourik's approaches were more radioligand dependent. The method described by Naganawa et al showed large variability of VT, and sometimes provided negative blood curves. Further validation to other radioligands is needed to assess the wide applicability of the algorithm in clinical studies. However, the PWC method provides a novel way of representing dynamic PET data, and may provide other exploratory applications.

Acknowledgments

The authors thank all the members of the PET group at the Karolinska Institutet for their excellent support during this study. The authors also thank Pawel Herman for helpful discussions regarding the PWC method. The calculations for the PWC method were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at PDC Center for High Performance Computing (PDC-HPC).

Lars Farde (co-author) is partly employed by Astra Zeneca.

Footnotes

Supplementary Information accompanies the paper on the Journal of Cerebral Blood Flow & Metabolism website (http://www.nature.com/jcbfm)

This study was supported by Stockholm Brain Institute.

Supplementary Material

Supplementary Information
Click here for additional data file. (2.9MB, ppt)

References

  1. Savitz JB, Drevets WC. Neuroreceptor imaging in depression. Neurobiol Dis. 2013;52:49–65. doi: 10.1016/j.nbd.2012.06.001. [DOI] [PubMed] [Google Scholar]
  2. Rajah MN, D'Esposito M. Region-specific changes in prefrontal function with age: a review of PET and fMRI studies on working and episodic memory. Brain. 2005;128:1964–1983. doi: 10.1093/brain/awh608. [DOI] [PubMed] [Google Scholar]
  3. Mosconi L, De Santi S, Rusinek H, Convit A, de Leon MJ. Magnetic resonance and PET studies in the early diagnosis of Alzheimer's disease. Expert Rev Neurother. 2004;4:831–849. doi: 10.1586/14737175.4.5.831. [DOI] [PubMed] [Google Scholar]
  4. Moses WW. Fundamental limits of spatial resolution in PET. Nucl Instrum Methods Phys Res A. 2011;648 (Supplement 1:S236–S240. doi: 10.1016/j.nima.2010.11.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brix G, Zaers J, Adam LE, Bellemann ME, Ostertag H, Trojan H, et al. Performance evaluation of a whole-body PET scanner using the NEMA protocol. National Electrical Manufacturers Association. J Nucl Med. 1997;38:1614–1623. [PubMed] [Google Scholar]
  6. de Jong HW, van Velden FH, Kloet RW, Buijs FL, Boellaard R, Lammertsma AA. Performance evaluation of the ECAT HRRT: an LSO-LYSO double layer high resolution, high sensitivity scanner. Phys Med Biol. 2007;52:1505–1526. doi: 10.1088/0031-9155/52/5/019. [DOI] [PubMed] [Google Scholar]
  7. Leroy C, Comtat C, Trebossen R, Syrota A, Martinot JL, Ribeiro MJ. Assessment of 11C-PE2I binding to the neuronal dopamine transporter in humans with the high-spatial-resolution PET scanner HRRT. J Nucl Med. 2007;48:538–546. doi: 10.2967/jnumed.106.037283. [DOI] [PubMed] [Google Scholar]
  8. Schain M, Toth M, Cselenyi Z, Stenkrona P, Halldin C, Farde L, et al. Quantification of serotonin transporter availability with [11C]MADAM—a comparison between the ECAT HRRT and HR systems. Neuroimage. 2012;60:800–807. doi: 10.1016/j.neuroimage.2011.12.047. [DOI] [PubMed] [Google Scholar]
  9. Varrone A, Sjoholm N, Eriksson L, Gulyas B, Halldin C, Farde L. Advancement in PET quantification using 3D-OP-OSEM point spread function reconstruction with the HRRT. Eur J Nucl Med Mol Imaging. 2009;36:1639–1650. doi: 10.1007/s00259-009-1156-3. [DOI] [PubMed] [Google Scholar]
  10. Schain M, Toth M, Cselenyi Z, Arakawa R, Halldin C, Farde L, et al. Improved mapping and quantification of serotonin transporter availability in the human brainstem with the HRRT. Eur J Nucl Med Mol Imaging. 2013;40:228–237. doi: 10.1007/s00259-012-2260-3. [DOI] [PubMed] [Google Scholar]
  11. Fung EK, Planeta-Wilson B, Mulnix T, Carson REA. Multimodal approach to image-derived input functions for brain PET. IEEE Nucl Sci Symp Conf Rec (1997) 2009;2009:2710–2714. doi: 10.1109/NSSMIC.2009.5401977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Liptrot M, Adams KH, Martiny L, Pinborg LH, Lonsdale MN, Olsen NV, et al. Cluster analysis in kinetic modelling of the brain: a noninvasive alternative to arterial sampling. Neuroimage. 2004;21:483–493. doi: 10.1016/j.neuroimage.2003.09.058. [DOI] [PubMed] [Google Scholar]
  13. Litton JE. Input function in PET brain studies using MR-defined arteries. J Comput Assist Tomogr. 1997;21:907–909. doi: 10.1097/00004728-199711000-00012. [DOI] [PubMed] [Google Scholar]
  14. Su KH, Wu LC, Liu RS, Wang SJ, Chen JC. Quantification method in [18F]fluorodeoxyglucose brain positron emission tomography using independent component analysis. Nucl Med Commun. 2005;26:995–1004. doi: 10.1097/01.mnm.0000184999.81203.5c. [DOI] [PubMed] [Google Scholar]
  15. Zanotti-Fregonara P, Fadaili el M, Maroy R, Comtat C, Souloumiac A, Jan S, et al. Comparison of eight methods for the estimation of the image-derived input function in dynamic [(18)F]-FDG PET human brain studies. J Cereb Blood Flow Metab. 2009;29:1825–1835. doi: 10.1038/jcbfm.2009.93. [DOI] [PubMed] [Google Scholar]
  16. Zanotti-Fregonara P, Chen K, Liow JS, Fujita M, Innis RB. Image-derived input function for brain PET studies: many challenges and few opportunities. J Cereb Blood Flow Metab. 2011;31:1986–1998. doi: 10.1038/jcbfm.2011.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Krejza J, Arkuszewski M, Kasner SE, Weigele J, Ustymowicz A, Hurst RW, et al. Carotid artery diameter in men and women and the relation to body and neck size. Stroke. 2006;37:1103–1105. doi: 10.1161/01.STR.0000206440.48756.f7. [DOI] [PubMed] [Google Scholar]
  18. Kerber CW, Heilman CB. Flow dynamics in the human carotid artery: I. Preliminary observations using a transparent elastic model. AJNR Am J Neuroradiol. 1992;13:173–180. [PMC free article] [PubMed] [Google Scholar]
  19. Benjaminsson S, Fransson P, Lansner A. A novel model-free data analysis technique based on clustering in a mutual information space: application to resting-state FMRI. Front Syst Neurosci. 2010;4:1–8. doi: 10.3389/fnsys.2010.00034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Chen BC, Germano G, Huang SC, Hawkins RA, Hansen HW, Robert MJ, et al. A new noninvasive quantification of renal blood flow with N-13 ammonia, dynamic positron emission tomography, and a two-compartment model. J Am Soc Nephrol. 1992;3:1295–1306. doi: 10.1681/ASN.V361295. [DOI] [PubMed] [Google Scholar]
  21. Mourik JE, Lubberink M, Klumpers UM, Comans EF, Lammertsma AA, Boellaard R. Partial volume corrected image derived input functions for dynamic PET brain studies: methodology and validation for [11C]flumazenil. Neuroimage. 2008;39:1041–1050. doi: 10.1016/j.neuroimage.2007.10.022. [DOI] [PubMed] [Google Scholar]
  22. Naganawa M, Kimura Y, Ishii K, Oda K, Ishiwata K, Matani A. Extraction of a plasma time-activity curve from dynamic brain PET images based on independent component analysis. IEEE Trans Biomed Eng. 2005;52:201–210. doi: 10.1109/TBME.2004.840193. [DOI] [PubMed] [Google Scholar]
  23. Delforge J, Pappata S, Millet P, Samson Y, Bendriem B, Jobert A, et al. Quantification of benzodiazepine receptors in human brain using PET, [C-11] Flumazenil, and a single-experiment protocol. J Cereb Blood Flow Metab. 1995;15:284–300. doi: 10.1038/jcbfm.1995.34. [DOI] [PubMed] [Google Scholar]
  24. Pierson ME, Andersson J, Nyberg S, McCarthy DJ, Finnema SJ, Varnas K, et al. [11C]AZ10419369: a selective 5-HT1B receptor radioligand suitable for positron emission tomography (PET). Characterization in the primate brain. Neuroimage. 2008;41:1075–1085. doi: 10.1016/j.neuroimage.2008.02.063. [DOI] [PubMed] [Google Scholar]
  25. Varnas K, Nyberg S, Halldin C, Varrone A, Takano A, Karlsson P, et al. Quantitative analysis of [11C]AZ10419369 binding to 5-HT1B receptors in human brain. J Cereb Blood Flow Metab. 2011;31:113–123. doi: 10.1038/jcbfm.2010.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Bergstrom M, Boethius J, Eriksson L, Greitz T, Ribbe T, Widen L. Head fixation device for reproducible position alignment in transmission CT and positron emission tomography. J Comput Assist Tomogr. 1981;5:136–141. doi: 10.1097/00004728-198102000-00027. [DOI] [PubMed] [Google Scholar]
  27. Farde L, Eriksson L, Blomquist G, Halldin C. Kinetic analysis of central [11C]raclopride binding to D2-dopamine receptors studied by PET—a comparison to the equilibrium analysis. J Cereb Blood Flow Metab. 1989;9:696–708. doi: 10.1038/jcbfm.1989.98. [DOI] [PubMed] [Google Scholar]
  28. Rousset OG, Ma Y, Evans AC. Correction for partial volume effects in PET: principle and validation. J Nucl Med. 1998;39:904–911. [PubMed] [Google Scholar]
  29. Mourik JE, van Velden FH, Lubberink M, Kloet RW, van Berckel BN, Lammertsma AA, et al. Image derived input functions for dynamic High Resolution Research Tomograph PET brain studies. Neuroimage. 2008;43:676–686. doi: 10.1016/j.neuroimage.2008.07.035. [DOI] [PubMed] [Google Scholar]
  30. Logan J. Graphical analysis of PET data applied to reversible and irreversible tracers. Nucl Med Biol. 2000;27:661–670. doi: 10.1016/s0969-8051(00)00137-2. [DOI] [PubMed] [Google Scholar]
  31. Schaeffer SE. Graph clustering. Comput Sci Rev. 2007;1:27–64. [Google Scholar]
  32. Hahn A, Nics L, Baldinger P, Ungersbock J, Dolliner P, Frey R, et al. Combining image-derived and venous input functions enables quantification of serotonin-1A receptors with [carbonyl-11C]WAY-100635 independent of arterial sampling. Neuroimage. 2012;62:199–206. doi: 10.1016/j.neuroimage.2012.04.047. [DOI] [PubMed] [Google Scholar]
  33. Zanotti-Fregonara P, Liow JS, Fujita M, Dusch E, Zoghbi SS, Luong E, et al. Image-derived input function for human brain using high resolution PET imaging with [C](R)-rolipram and [C]PBR28. PLoS ONE. 2011;6:e17056. doi: 10.1371/journal.pone.0017056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mourik JE, Lubberink M, Schuitemaker A, Tolboom N, van Berckel BN, Lammertsma AA, et al. Image-derived input functions for PET brain studies. Eur J Nucl Med Mol Imaging. 2009;36:463–471. doi: 10.1007/s00259-008-0986-8. [DOI] [PubMed] [Google Scholar]
  35. Naganawa M, Kimura Y, Ayumu M.(eds).. Modification of ICA for extracting blood vessel-related component in nuclear medicine: contrast function and nonnegative constraints 4th International Symposium on Independent Component Analysis and Blind Signal Separation (ICA2003); April 1-4 Nara: Japan; 2003 [Google Scholar]
  36. Mikhno A, Zanderigo F, Naganawa M, Laine AF, Parsey RV. Brain tissue selection procedures for image derived input functions derived using independent components analysis. Conf Proc IEEE Eng Med Biol Soc. 2012. pp. 5987–5990. [DOI] [PMC free article] [PubMed]
  37. Backes H, Ullrich R, Neumaier B, Kracht L, Wienhard K, Jacobs AH. Noninvasive quantification of 18F-FLT human brain PET for the assessment of tumour proliferation in patients with high-grade glioma. Eur J Nucl Med Mol Imaging. 2009;36:1960–1967. doi: 10.1007/s00259-009-1244-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Croteau E, Lavallee E, Labbe SM, Hubert L, Pifferi F, Rousseau JA, et al. Image-derived input function in dynamic human PET/CT: methodology and validation with C-11-acetate and F-18-fluorothioheptadecanoic acid in muscle and F-18-fluorodeoxyglucose in brain. Eur J Nucl MedMol Imaging. 2010;37:1539–1550. doi: 10.1007/s00259-010-1443-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Parker BJ, Feng DG. Graph-based Mumford-Shah segmentation of dynamic PET with application to input function estimation. IEEE Trans Nucl Sci. 2005;52:79–89. [Google Scholar]
  40. Syvanen S, Blomquist G, Appel L, Hammarlund-Udenaes M, Langstrom B, Bergstrom M. Predicting brain concentrations of drug using positron emission tomography and venous input: modeling of arterial-venous concentration differences. Eur J Clin Pharmacol. 2006;62:839–848. doi: 10.1007/s00228-006-0179-y. [DOI] [PubMed] [Google Scholar]
  41. Pitsiu M, Gries JM, Benowitz N, Gourlay SG, Verotta D. Modeling nicotine arterial-venous differences to predict arterial concentrations and input based on venous measurements: application to smokeless tobacco and nicotine gum. J Pharmacokinet Pharmacodyn. 2002;29:383–402. doi: 10.1023/a:1020957208071. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (2.9MB, ppt)

Articles from Journal of Cerebral Blood Flow & Metabolism are provided here courtesy of SAGE Publications

RESOURCES