Reliability of observers' subjective impressions of families: A generalizability theory approach

Abstract

Parenting was observed in videotaped interactions in 30 families referred for child conduct problems. Generalizability coefficients and the impact of varying numbers of raters were estimated. Two measurement designs were compared: All raters observed all families (“crossed” design) and a different rater observed each family (“nested” design). The crossed design provided higher generalizability coefficients than a nested design, implying inflated generalizability estimates if a crossed estimation model is used for a nested data collection. Three and four raters were needed to obtain generalizability coefficients in the .70–.80 range for monitoring and discipline, respectively. One rater was sufficient for a corresponding estimate for positive involvement and for an estimate in .80–.90 range for problem-solving. Estimates for skill encouragement were non-acceptable.

Systematic observations of family interactions have been important for the development of the Parent Management Training Oregon program (PMTO; Forgatch & DeGarmo, 2002; Forgatch & Martinez, 1999; Patterson, 1982, 2005; Patterson, Reid, & Dishion, 1992), which is an evidence-based parenting program for child and adolescent conduct problems that focuses on teaching essential parenting practices to parents. Observational research in the PMTO program involves specially trained observers viewing videos of structured family interactions. PMTO studies have reported that changes in observed parenting practices are associated with fewer conduct problems, both immediately after treatment termination and at follow-up several years later (Forgatch & DeGarmo, 2002; Martinez & Forgatch, 2001; Ogden & Hagen, 2008). However, little attention has been given to the psychometric properties of the macroanalytic procedures used to measure parenting abilities.

Lakes and Hoyt (2009) recommend generalizability theory (G-theory; Brennan, 2001a; Cronbach, Gleser, Nanda, & Rajaratnam, 1972; Wasserman, Levy, & Loken, 2009) as a framework to enhance the precision of assessments of reliability. In classical test theory (Cronbach & Shavelson, 2004), only one source of measurement error is considered, whereas G-theory allows several sources of measurement error to be taken into account. By including different sources of error, the underestimation of error variance or overestimation of generalizability will be prevented. G-theory assumes two types of studies: In G-studies, variance components are estimated, and in D-studies, error variance is defined and generalizability coefficients are estimated. In G-studies, variance due to raters, items and other facets of observation is partitioned into variance components that, in turn, are used in D-studies to assess generalizability coefficients that are tailored to the sources of error in the measurement design. In D-studies, changes in the generalizability coefficients may be assessed if the researcher decides to change the number of conditions within facets of observations, such as the number of raters and the number of items. Raters and items constituted two facets of observation for assessing the quality of mothers' parenting practices toward children who had been referred for conduct problems in the present study. Due to the common practice of applying a multifaceted design in PMTO research, G-theory was used as an analytic approach for this study. Generalizability coefficients were estimated for a measurement model in which all of the raters were assumed to have rated all of the families (raters were crossed with families) and for a model in which the raters were assumed to be unique to each family (raters were nested within families). Generalizability estimations were made for both models to indicate the number of raters that would be necessary to obtain acceptable reliability.

The PMTO Treatment Program for Child Conduct Problems

The manner in which parents raise their children is of vital importance for child development (Martinez & Forgatch, 2002). Negative (coercive) relational patterns in the family are thought to represent the etiological nexus of the development of antisocial behavior in children (Patterson et al., 1992). Specifically, how parents act toward their children, called parenting practices, is central to de-escalating problematic behavior and preventing children from becoming violent or criminal adults (Forgatch, DeGarmo, & Beldavs, 2005; Patterson, 1995). The aim of the PMTO treatment program is to help parents develop basic but crucial parenting skills that can minimize negative interactions and maximize positive interactions. The five central parenting practices included in the PMTO treatment program are discipline (predictable consequences, time-out), monitoring (knowing where and with whom the child is), positive involvement (effective communication, encouragement), skill encouragement (prompting and reinforcing desired behavior), and problem-solving (brainstorming, scaffolding) (Forgatch & DeGarmo, 2002).

Observations of Family Interactions

Haynes (2001) concluded that structured behavioral observations may be especially useful for detecting relational patterns that also occur in typical family interactions. Observations of structured family interactions have been crucial for studying the types of family interactions that might lead troubled children to pathological versus healthy developmental pathways (Patterson, 2005; Patterson et al., 1992; Roberts & Hope, 2001) because parents cannot recall many details of social interactions. Parents' reports of their discipline practices, for instance, are notably different from their actual discipline practices (Patterson et al., 1992; Reid, Baldwin, Patterson, & Dishion, 1988). Observational research can capture aspects of behavior that are difficult to study by other methods (Lindahl, 2001). The choice of which behaviors to observe is guided by the research question, which is informed by the theory and paradigms that direct the flow of observational data into categories relevant to the research question (Lindahl, 2001).

In PMTO observations, family interactions that take place in the laboratory or treatment facility are videotaped and coded by teams of trained raters. The central assumption is that the behavior of the families interacting in the laboratory setting can be generalized to family interactions in their everyday lives (Gardner, 1997, 2000; Haynes, 2001; Mori & Armendariz, 2001; Patterson, 1982, 2005; Patterson et al., 1992). The assumption of a high correlation between behavior occurring at home and in the clinic has been questioned by Mori and Armendariz (2001), but the assumption is considered to be justified in well-defined studies in the field of conduct problems (Gardner, 2000), such as the PMTO program in the present study. Coding of interactions is a procedure that can be performed at various levels of analysis (Lindahl, 2001). The microanalytic level of analysis involves coding second-to-second interactions of small units of behavior. By contrast, macroanalytic methods use large coding units that require the coders to apply global judgment. These methods are suited for coding meta-level processes, such as the ways in which parents raise their child.

Global observations using the Coders' Impression (CI) observational measure (CI; DeGarmo, Patterson, & Forgatch, 2004; Forgatch, Knutson, & Mayne, 1992) have been used in PMTO research since the 1980s to allow coders trained in microanalytic interaction coding to rate subjective and global (macroanalytic) impressions of family interactions (DeGarmo et al., 2004; Forgatch & DeGarmo, 2002; Patterson et al., 1992). Furthermore, the measure has been found to be sensitive to changes and has contributed to good convergent and predictive validity (DeGarmo et al., 2004). Using mainly the CI measure, Patterson and Forgatch (1995) found that trained coders' subjective judgments about parenting practices were better predictors of out-of-home placements and arrests 3 years later compared with changes in child behavior from baseline to treatment termination. Parental discipline and monitoring practices, as measured by the CI, are particularly important for predicting subsequent adjustment in children with conduct problems (Patterson, 2005).

Two Designs for Estimating the Reliability of Observations

Inter-observer reliability is an important aspect in evaluating observations of family interactions (Aspland & Gardner, 2003; Snyder et al., 2006). Estimations of the reliability of clinical assessments must consider essential features of the applied observation design. Such designs appear to differ with regard to the correspondence between the observed and the raters. In traditional psychometric test designs, the objects of measurements, typically persons, are crossed with raters; that is, the same team of raters rates all of the subjects. This design feature is also used in clinical observation studies. However, in clinical observations, each patient is frequently rated by his/her own specific rater; that is, the rater is nested within the patient. This nested design appears to be the typical PMTO research design for observing mothers' parenting behavior. In our study, we use both approaches: both a nested design and a crossed design in which different subgroups of two raters rated all of the mothers in their own specific sub-sample of mothers. Thus, the two different observation designs are used both outside and within the PMTO research context. In addition to raters, items are applied to rate mothers' parenting in PMTO observation designs. Therefore, both designs can be characterized by at least two dimensions or facets: Raters and items. The well-known and frequently used one-facet intraclass correlation of Cronbach's alpha may fail to account for all of the relevant sources of variation between coders in psychotherapy research (Wasserman et al., 2009). Estimates of inter-rater reliability using G-theory are likely to become more accurate by incorporating multiple sources of error into reliability coefficients (Crits-Christoph et al., 2011; Lakes & Hoyt, 2009). The multifaceted nature of the present designs justifies the application of G-theory, which has the capacity to simultaneously estimate multiple error terms associated with raters and items in the two observation designs (Cronbach & Shavelson, 2004). Because both observation designs are frequently used in clinical research and practice, we will compare their reliability estimates. Both designs will be further described within the framework of G-theory below. The number of applied raters differs in observation designs. Frequently, two raters are used. However, when applying the nested design, as described above, one rater is typically used in PMTO research. It is therefore of interest to examine the two types of design with regard to how many raters are needed to obtain acceptable reliability estimates.

Aims

The present multifaceted data collection design facilitates comparison between two observational procedures or measurement designs with regard to reliability estimation. The first aim was to assess the reliability based on G-theory for each of the five parenting practices, namely, discipline, positive involvement, problem-solving, skill encouragement, and monitoring, by means of the two measurement designs: (a) in which raters were crossed with mothers, and (b) in which raters were nested within mothers. The second aim was to estimate the number of raters needed to obtain reliable scores for each parenting practice by means of both measurement designs.

Method

Participants and Procedures

The observational data in the present study were sampled from a data pool of two large studies investigating PMTO in Norway: a randomized control trial (Ogden & Hagen, 2008) and a study investigating the implementation process (Ogden, Forgatch, Askeland, Patterson, & Bullock, 2005). Both studies were conducted as collaborations between the Norwegian Center for Child Behavioral Development at the University of Oslo and the Oregon Social Learning Centre (OSLC). The data were collected from 2001 to 2005 from families living in Norway who sought help for child conduct problems. Informed consent was obtained from the subjects. Ogden and Hagen (2008) reported that the mean age of the primary caregiver was 39 years (SD = SZ) = 6.49). Forty percent were single parents, and 25% had a college or higher university degree, 53% had finished high school, and 21% had completed junior high or elementary school. Moreover, 40% of the families received welfare. The families had contacted the child welfare or child mental health agencies because of child conduct problems, which could be any behavior consistent with the symptoms of Oppositional Defiant Disorder or Conduct Disorder, such as aggression, delinquency, or disruptive classroom behavior (Ogden & Hagen, 2008).

The data in the present study consisted of observations of video recordings of family interaction tasks. The families included in the study had children ranging in age from 8 to 12 years who were selected to receive the PMTO intervention. Of the observed families in the two PMTO studies, 20% were randomly selected to be rated by an additional observer, allowing for inter-rater reliability estimations. Sub-samples of families that had been observed by the same pair of coders were identified. Coder pair A observed 17 families, whereas coder pairs B and C observed five and eight families, respectively. Coder pairs A and B observed families pre-treatment, whereas coder pair C observed families post-treatment. It should be noted that although the present study used data from pre- and post-treatment assessments, our objective was to study reliability, not treatment effects.

For coder pair A, 12 of the 17 referred children were boys, and the father was present in 12 of the videotapes of the families engaged in structured interaction. For coder pair B, four of the five children were boys, and the father was present for three of the families. For coder pair C, the target child was a boy in seven of eight families, and the father was present for four of the families. In total, 23 boys and seven girls were included in this study.

The PMTO studies were approved by the Regional Ethical Committee for Medical Research Ethics, Southern Norway, and the Norwegian Data Inspectorate.

Observation. The interactions took place in a laboratory or clinic, and the families engaged in a set of tasks as directed by the test administrator. The tasks were intended to highlight central aspects of the families' interactional style. In the first task, the family was instructed to spend 5 minutes planning something enjoyable to do together during the next week. The second and third tasks were 10-minute problem-solving tasks. In the second task, the parents chose the issue, and in the third task, the child chose the issue. The subjects were instructed to choose from the Issues Checklist, which contains issues that often create conflicts in families (e.g., chores, school problems, bedtime, TV and computer time) (Prinz, Foster, Kent, & O'Leary, 1979). In the fourth task, the family was instructed to discuss the quality of their interaction for 10 minutes and to identify differences in how they talked together during the observation compared with how they typically talk together. The coders stopped the film and rated the items after each task. After observing all of the tasks, the coders completed the general items. The father was present for 19 of the 30 families, whereas the mothers were present in all of the family interactions.

The coders rated the families using two different observational formats: The macroanalytic CI measure that is analyzed in the present study, in which the coders rated their subjective impressions of the families they observed, and the microanalytic Family and Peer Process Code (FPPC), in which second-to-second interactions are registered. The inter-rater reliability training for the CI measure consisted of the coding team rating segments of sample films of families in structured interactions until they rated the families with a difference of no more than +1 on a Likert scale. No checks of inter-rater reliability were conducted after the initial training for the CI measure. The coders completed the CI measure (DeGarmo et al., 2004; Forgatch et al., 1992,) after the microanalytic coding.

Measures

The Coders Impressions measure. (CI; DeGarmo et al., 2004). The items in the CI measure were used as indicators of the five principal parenting constructs of the PMTO parenting practices: discipline, skill encouragement, problem-solving, positive involvement and monitoring. A 92-item version was used in the present study (Table I) (Ogden & Hagen, 2008).

Table I.

Means and standard deviations (SD) for parenting subscales in three sub-samples

	Discipline13 items, 1–5 scale Mean (SD)	Skill Encouragement 4 items, 1–7 scale Mean (SD)	Positive Involvement 32 items, 1–7 scale Mean (SD)	Problem Solving 32 items, 1–7 scale Mean (SD)	Monitoring 11 items, 1–7 scale Mean (SD))
Rater pair A. N = 17
A1	3.96 (.45)	4.93 (51)	4.80 (53)	4.16 (93)	5.32 (23)
A2	3.61 (.57)	5.01 (58)	4.82 (.57)	4.56 (.94)	5.04 (.39)
Mean	3.79	4.97	4.81	4.36	5.18
Rater pair B. N = 5					(N = 4)
B1	4.34 (35)	4.48 (1.16)	5.31 (43)	4.86 (71)	5.48 (21)
B2	3.58 (53)	4.58 (1.33)	5.38 (.49)	4.98 (.72)	4.90 (.29)
Mean	3.96	4.53	5.35	4.92	5.19
Rater pair C N = 8
C1	4.48 (36)	4.89 (93)	5.45 (31)	5.04 (95)	5.27 (25)
C2	4.23 (32)	5.20 (.52)	5.36 (.35)	5.07 (.72)	5.48 (:J7;
Mean	4.36	5.05	5.41	5.06	5.38
Weighted mean	3.97	4.92	5.06	4.64	5.24

Note. Higher scores indicate better parenting practices. Rater pair A observed 17 families pre-treatment; rater pair B observed five families pre-treatment; and rater pair C observed eight families post-treatment. Likert-type items were rescaled to a 1–7 scale, except for the discipline items, which were rescaled to a 1–5 scale. One family was excluded from the analyses for rater pair B on the monitoring scale because of missing data.

The CI measure was translated for a randomized controlled effectiveness study of the PMTO program in Norway (Ogden & Hagen, 2008) by bilingual members of the research group, who were supervised by reference persons or reference groups familiar with the instruments from previous research. The authors of that study reported alphas in the range of .79 to .86 for discipline, .95 to .98 for positive involvement, .90 to .96 for problem-solving and .63 to .72 for monitoring; they excluded skill encouragement due to low alphas. They also reported acceptable predictive validity for the translated version of the CI measure. Forgatch and DeGarmo (2002) and Forgatch et al. (2005) reported Cronbach's alphas ranging from .67 to .94 (mainly in the range .80–.90) for the five parenting subscales administered in American samples.

Examples of items representing the five parenting practices central to PMTO follow. Discipline (13 items): “Discipline style is overly strict,” with anchors 1 (“very untrue”) to 5 (“very true”). Skill encouragement (four items): “Skillfully prompted the youngster during the task as necessary,” with anchors 1 (“very untrue”) to 7 (“very true”). Problem-solving (32 items): “Showed willingness to discuss ideas suggested by others,” with anchors 1 (“very untrue”) to 7 (“very true”). Positive involvement (32 items): “The quality of the relationship between the parents and child was excellent,” with anchors 1 (“very poor”) to 7 (“very good”). Monitoring (11 items): “The mother gathered information from the youngster about activities/friends in an appropriate manner (e.g., direct, straightforward, interested, pleasant, etc.) with anchors 1 (“very true”) to 7 (“very untrue”).

Most of the items included in the parenting domains were worded positively, but certain items were worded negatively. These items were reverse-scored, such that a high score signifies positive parenting practices, whereas a low score signifies negative parenting practices. The ratings were scored using scanning software.

Data Analysis Procedures

Item transformation and scoring. The items of the CI parenting practice subscales contained different numbers of response categories: some items ranged from 1 to 4, others from 1 to 5 and still others from 1 to 7. These items were collected from publications in the field of child conduct problems over several decades by researchers at OSLC. The OSLC researchers did not change the original items or the scoring points; instead, the researchers transformed the items into the same range at a later stage. However, their procedure did not take the variance of the items into account. In the present study, the items were transformed to the same numeric scale within each subscale to provide comparable items for the analysis. For this purpose, linear equating was applied (Kolen & Brennan, 2004; McDonald, 1999). This procedure is presented in Appendix A, which can be accessed at www.sshf.no/stora2. The items were assigned to parenting practice scales on a conceptual basis.

Missing data. Missing data occurred when the observer of the videotaped family interaction did not record a score for an item. There were no missing values for the discipline or skill encouragement scales. On the 32-item problem-solving scale, one item contained missing values for six families. On the 32-item positive involvement scale, one item exhibited missing values for two families, and two items showed missing values for another family. On the monitoring scale (11 items), there were missing values on one item for 11 families, on two items for five families and on three items for three families. For each family, any missing values were replaced by the mean value obtained for the items with non-missing values in the corresponding scale. There were missing values for six items (54%) for one family on the monitoring scale, and this family was excluded from the analyses.

Table I provides descriptive statistics for the five parenting practice subscales after the application of linear equating for each rater pair. A high mean score indicates that the observer rated positive parenting.

G-theory applied to the present observational measurement design. As shown in Table II, the present study applies a measurement design consisting of three facets of observation: Raters (r), items (i) and fathers (f). The source of variation represented by mothers (m) would serve as being objects of measurement in the terminology of G-theory. Because mothers are nested (:) within the facet of fathers, the objects of measurement would formally be termed m:f. This measurement design is applied in each sub-sample of mothers and for each parenting subscale. Table II provides a specific illustration for the subscale discipline with its 13 items.

Table II.

Measurement design mri:f for each rater pair illustrated by the parenting practice discipline

	Sub-sample A
Item – i	Rater 1 1 2 3 4 5 6 7 8 9 10 11 12 13 Mother – m	Rater 2 1 2 3 4 5 6 7 8 9 10 11 12 13 Mother – m
F1 F2	1 – 13 14 – 17	1 – 13 14 – 17
	Sub-sample B
	Rater 3	Rater 4
F1 F2	18 – 20 21 – 22	18 – 20 21 – 22
	Sub-sample C
	Rater 5	Rater 6
F1 F2	23 – 26 27 – 30	23 – 26 27 – 30

Note. Father facet: Fl = father present, F2 = father absent.

This data collection design is designated as an (m:f)ri design, which reads that mothers are nested within, or specific to, the two levels of the father facet. Both fathers and mothers are crossed with both items and raters, which are crossed with each other. To apply generalizability theory to the (m:f)ri design, the present raters and items are considered to be random samples from their respective universes of admissible observations. Additionally, mothers are assumed to serve as a random sample from the population of mothers of the same type as included in the present study. Because there exist only two conditions of the father facet, absent vs. present, this facet is considered to be fixed. As will be shown below, 11 variance components can be estimated based on the (m:f)ri design to describe how the corresponding universe of admissible observations is composed. These components are called G-study variance components, and they represent the first step in a generalizability analysis (Brennan, 2001a). The method of variance component estimation is an ANOVA procedure that does not require assumptions about the distributional form (Brennan, 1994, 2001a). Unbiased variance components are obtained by solving a set of simultaneous linear EMS equations. The present unbalanced design (Table II), however, requires a specific procedure for estimating the G-study variance components. This procedure is explicated below.

In G-theory, a distinction is made between generalizability (G) studies and decision (D) studies. The purpose of a G-study is to anticipate multiple applications of a measurement procedure and to provide information about possible sources of variation for the present measurement purpose. In other words, the G-study should define the universe of admissible observations. A D-study, in contrast, applies the information provided by the G-study to design a best possible and/or relevant application for the actual measurement purpose. In planning a G-study, the researcher defines a universe of generalization, which implies determining the facets that he/she is intending to generalize across. The decision about the universe of generalization implies which sources of variation or facets would serve as measurement error or error of generalization. In a D-study, error variance and true score variance will be defined to estimate generalizability coefficients. In the present application of G-theory, two different D-studies are conducted based on the information provided by the G-study. These D-studies will allow us to estimate the generalizability associated with the two functions of raters being crossed with versus nested within mothers.

Table III lists the 11 sources of variability in the (m:f)ri design, the contributions of which to the observed scores can be estimated in terms of their variance components. The variance components of the four main effects (fathers, mothers within fathers, raters, and items) represent variation in their respective mean values. Mothers within fathers are representing individual differences among mothers and are considered to be the objects of measurement or alternatively universe-score (equivalent to true-score in classical test theory) variability. The three remaining main effects represent facets of observation. The 10 sources of variation associated with the facets of observation may create inaccuracies in generalizing from the particular sample of behavior to the universe of admissible observations. The variance component of fathers represents inconsistencies in scores from fathers being present versus absent during the interaction sessions. The variance components of raters and items represent inconsistencies among raters and items, respectively. In addition, each facet interacts with the objects of measurement as well as with other facets, constituting a total of 11 components (see the Venn diagram in Figure 1 at www.sshf.no/stora2). Table III also describes the interpretation of each variance component. It should be noted that the G-study components indicate the relative importance of a single or typical mother-father-rater-item combination in the respective universe of admissible observations.

Table III.

Sources of variability in the three-facet observational measurement design (m:f)ri

Source	Type of variation	Variance component
Fathers (f)	Constant effect due to absence versus presence of fathers	σf2
Mothers w. fathers (m:f)	Individual differences of mothers in parenting practice within fathers (Objects of measurement)	σmf2
Raters (r)	Constant effect for all mothers due to stringency of raters	σr2
Items (i)	Constant effect for all mothers due to inconsistencies of the level of parenting from one item to another	σi2
fr	Inconsistencies in raters' stringency from one father condition to another	σfr2
fi	Inconsistencies in item level of parenting from one father condition to another	σfi2
(m:f)r	Inconsistencies of raters' stringency of particular mothers' parenting behavior	σ(m:f)r2
(m:f)i	Inconsistencies from one item to another in particular mothers' parenting behavior	σ(m:f)i2
ri	Constant effect for all mothers due to differences in raters' stringency from one item to another	σri2
fri	Triple interaction indicating the extent to which the fi-interaction varies from one rater to another	σfri2
(m:f)rie	Residual variation consisting of the unique combination of (m:f), r and i; unmeasured facets; and/or random events	σ(m:f)ri2

Pooling of the variance components. Estimating variance components is a central feature of generalizability analysis. The present person sample consisted of three small sub-samples, as described above. The variance components were pooled across the three sub-samples to increase the stability of the estimates. For this purpose, the G-study variance components were first estimated separately for each of the three sub-samples by means of the software urGENOVA (Brennan, 2001b) due to the unbalanced design (Table II). It may be noted that the applied estimation method in urGENOVA (Henderson's method 1) provides random effects variance components and is a practical procedure, no matter how large the data set may be (Brennan, 2001a). Secondly, the corresponding sample-specific variance components were pooled by a weighting procedure in which the estimate of each of the corresponding variance components was weighted by the inverse of its sampling variance. Standard errors for the variance components in each sub-sample and for the pooled variance components were estimated by the software GENOVA (Crick & Brennan, 1983).

Two different D-study designs to estimate reliability. The present procedure for estimating D-study statistics in terms of universe-score variance components, error variance components and generalizability coefficients followed the procedure suggested by Brennan (2001b). The pooled G-study random effects variance components derived from urGENOVA assuming unbalanced design were inserted in GENOVA to estimate D-study statistics for different designs depending on the purpose of measurement. For the present D-study estimations the facets of items and raters were considered random, while the father facet was assumed fixed.

In D-studies, generalizability coefficients are estimated based on the variance components estimated in the G-study coupled with proper sample sizes. A general expression for the generalizability coefficient is given by

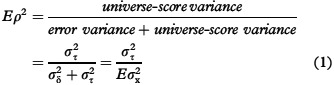As can be inferred from the expression above, σ_τ² is the universe-score variance (equivalent to the true-score variance in classical test theory), and σ_δ² is the error variance Eσ_x² is the expected observed variance, which is the total variance in a set of scores consisting of n′_r raters and n′_r items. The D-study design that will estimate the generalizability coefficient given that raters are crossed with mothers is designated as (m:f)RI. The uppercase letters R and I indicate that average scores are considered in the D-study design, which is used to estimate the generalizability coefficients for a given number of raters (n′_r) and items (n′_i) in the present case. This D-study design and the corresponding linear model will be labeled in terms of ‘crossed’ in subsequent sections for convenience. Given that raters are crossed (c) with mothers, the generalizability coefficient, Eρ_c² is then estimated by

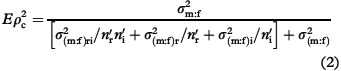The components in brackets constitute the error variance, σ_δ². The generalizability estimation for the crossed D-study design assumes that raters and items are randomly sampled from the universes of admissible raters and items, respectively. Both raters and items are crossed with mothers, implying that the same set of raters and items, respectively, are administered to all of the mothers. The error variance terms reflect this assumption. In contrast, G-theory also has the characteristic that the present G-study (m:f)ri design can estimate D-study statistics for a design in which raters are assumed to be nested within mothers, whereas items are still crossed with mothers, as in the typical PMTO design. This D-study is formally designated as an (R:m:f)I design, and this D-study design will be labeled as “nested” in subsequent sections. The rationale for allowing the G-study (m:f)ri design to accommodate both the crossed and the nested D-study designs is that both designs assume that raters and items are sampled from the same universe of admissible observations in which both items and raters are crossed with mothers. However, whereas both the respective samples of items and raters are administered to all mothers in the crossed D-study design, each mother in the nested D-study design is administered a different sample of the same number of raters. With respect to items, both designs assume the same sample of items being administered to all of the mothers (Brennan, 2001a; Shavelson & Webb, 1991).

The nested design has seven variance components, σ_f², σ_m:f², σ_r:m:f², σ_i², σ_fi², σ_(m:f)i², and σ_(r:m:f)i², (See the Venn diagram in Figure 2, accessed at www.sshf.no/stora2) of which five are identical to the variance components for the crossed design. Each of the two components σ_(r:m:f)i² and σ_(r:m:f)i²₎, however, contains confounded effects in the nested design, which means that each component consists of a mixture of three variance components identified in the crossed design, as shown below:

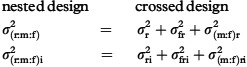Although the universe-score variance, σ_m:f², remains the same for both designs, the error variance would differ, as shown in the estimation formula for the generalizability coefficients, Eρ_n², for the nested (n) design.

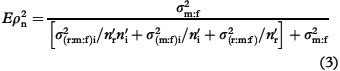The components in brackets constitute the error variance, σ_δ², for this design. One of the error terms, σ_(m:f)i², is the same in both designs. It should be noted that rater variance terms are included in the error variance in the nested design.

Results

G-study variance components. The estimated G-study variance components for the five parenting practices pooled across the three sub-samples and their standard errors are reported in Table IV. The variance components (σ_α²) in Table IV are also presented as percentages of the total variance for each subscale to allow for an estimation of their relative sizes.

Table IV.

Estimated G-study variance components for the (m:f)ri design and different D-study estimations

Subscale: G-study design:	Discipline (ni = 13)		(m:f)ri		Skill encouragement (ni = 4)
Source	df	σα2	(%)	σ(σα2)	Source	df	σα2	(%)	σ(σα2)
f	1	.0381	(5.6)	.0361	f	1	.000		.014
m:f	28	.049	(7.2)	.018	m:f	28	.138	(20.8)	.062
r	1	.030	(4.4)	.030	r	1	.001	(0.1)	.004
i	12	.172	(25.1)	.085	i	3	.014	(2.1)	.019
fr	1	.000		.003	fr	1	.000		.006
fi	12	.017	(2.5)	.013	fi	3	.000		.017
(m:f)r	28	.014	(2.0)	.009	(m:f)r	28	.005	(0.7)	.024
(m:f)i	336	.024	(3.6)	.016	(m:f)i	84	.202	(30.5)	.059
ri	2	.064	(9.4)	.030	ri	3	.000		.009
fri	12	.008	(1.2)	.010	fri	3	.000		.013
(m:f)rie	336	.267	(39.1)	.021	(m:f)rie	84	.304	(45.8)	.046
Total	779	.685				239	.664

D-study design:	Crossed2				Nested2				Crossed				Nested
nt	1	2	3	4	1	2	3	4	1	2	3	4	1	2	3	4
Mj	13	13	13	13	13	13	13	13	4	4	4	4	4	4	4	4
σ12	.049	.049	.049	.049	.049	.049	.049	.049	.138	.138	.138	.138	.138	.138	.138	.138
σδ2	.036	.019	.013	.011	.072	.037	.025	.019	.132	.091	.076	.071	.133	.092	.078	.071
Eρ2	.57	.72	.79	.82	.41	.57	.67	.72	.51	.60	.64	.66	.51	.56	.61	.64

Subscale: G-study design:	Positive involvement (ni = 32)		(m:f)ri		Problem-solving (ni = 32)
Source	df	σα2	(%)	σ(σα2)	Source	df	σα2	(%)	σ(σα2)
f	1	.002	(0.5)	.005	f	1	.001	(0.1)	.025
m:f	28	.052	(12.0)	.016	m:f	28	.389	(34.6)	.108
r	1	0		.001	r	1	.006	(0.5)	.007
i	31	.014	(3.2)	.007	i	31	.098	(8.7)	.032
fr	1	0		.001	fr	1	.000		.003
fi	31	.003	(0.8)	.005	fi	31	.001	(0.1)	.007
(m:f)r	28	.008	(1.8)	.004	(m:f)r	28	.036	(3.2)	.013
(m:f)i	868	.058	(13.4)	.012	(m:f)i	868	.135	(12.0)	.012
ri	31	.005	(1.0)	.005	ri	31	.034	(3.0)	.013
fri	31	.004	(0.8)	.006	fri	31	.001	(0.1)	.007
(m:f)rie	868	.286	(66.3)	.014	(m:f)rie	868	.424	(37.7)	.020
Total	1919				.432	1919	1.125

D-study design:	Crossed				Nested				Crossed				Nested
nt	1	2	3	4	1	2	3	4	1	2	3	4	1	2	3	4
ni	32	32	32	32	32	32	32	32	32	32	32	32	32	32	32	32
σr2	.052	.052	.052	.052	.052	.052	.052	.052	.389	.389	.389	.389	.389	.389	.389	.389
σδ2	.018	.010	.008	.006	.019	.010	.008	.006	.054	.029	.019	.017	.061	.045	.024	.015
Eρ2	.74	.84	.88	.90	.73	.83	.87	.89	.88	.94	.95	.96	.87	.93	.95	.96

Subscale:	Monitoring (ni = 11)
G-study design:	(m:f)ri
Source	df	σα2	(%)	σ(σα2)
f	1	.000		.131
m:f	28	1.618	(15.0)	.500
r	1	.853	(7.9)	.766
i	10	1.216	(11.2)	.774
fr	1	.000		.033
fi	10	.270	(2.5)	.215
(m:f)r	28	.004	(0)	.142
(m:f)i	280	.383	(3.6)	.364
ri	10	.726	(6.7)	.382
fri	10	.000		.159
(m:f)rie	280	5.722	(53.0)	.482
Total	1919	.432

D-study design:	Crossed				Nested
nr	1	2	3	4	1	2	3	4
ni	11	11	11	11	11	11	11	11
στ2	1.618	1.618	1.618	1.618	1.618	1.618	1.618	1.618
σδ2	.558	.298	.209	.166	1.478	.756	.516	.396
Eρ2	.74	.85	.89	.91	.52	.68	.76	.80

Note. f = fathers, m = mothers, r = raters, i = items. e = unmeasured facets that affect the measurement and/or random events. σ(σ²_α) = standard error of the variance component σ_α. The generalizability coefficients, E_ρ², were estimated based on pooled variance components across three sub-samples.¹ The variance component of the fixed father facet is likely biased. See endnote 1 for further elaboration. ² The crossed D-study design is formally designated as (m:f)RI, whereas the nested design is designated as (R:m:f)I.

For the subscale discipline, the variance component for the father facet was .038, which is 5.6% of the total variance. This finding indicates that the father facet affected the scores of the mothers' behavior to an extent, independently of raters and items. The presence or absence of the father exerted no noticeable influence on the ratings of the skill encouragement (0%), positive involvement (0.5%), problem-solving (0.1%), and monitoring (0%) parenting practices.¹

The variance component for mothers, σ_m:f², was .049, or 7.2% of the total variance in discipline, 20.8% in skill encouragement, 12.0% in positive involvement, 34.6% in problem-solving and 15% in monitoring. The rater variance, of, was .030, or 4.4% of the total variance on the discipline scale, which indicated that the raters disagreed to a certain extent in their ratings of discipline, independent of the other facets. Rater variance did not represent a noticeable effect in the other parenting practices (0% for skill encouragement and positive involvement and 0.5% for problem-solving), except for monitoring, for which it accounted for 7.9% of the total variance.

The variance component for items, σ_i², was .172 for discipline, which constituted 25.1% of the total variation. This finding suggests that the items differed in their mean values across the other facets to a substantial degree. There was little variability for items in the skill encouragement scale (2.1%) or for positive involvement (3.2%); more variability was due to items on the problem-solving (8.7%) and monitoring (11.2%) scales.

No variance was due to the interaction between the father facet and raters, σ_fr², on any parenting practice. This result indicated that the rank orders of the raters did not vary as a function of the father being present or absent in the videotapes of the family interaction.

Only 2.5% of the variance was due to interaction between the father facet and items, σ_fr², on the discipline scale, and little or no variance was accounted for by the variance component σ_fr² for the other parenting practices. This result indicated that the fathers' presence or absence had little influence on the rank ordering of items.

Across the parenting practices, 0–3.2% of the variance represented inconsistencies in the way raters rank-order mothers' behavior within fathers, expressed by the component σ²_(m:f). These small variance components suggest that the raters are mostly in agreement in how they rank-order mothers.

Variability was observed across the parenting practices as to the amount of variance accounted for by the component σ_(m._f)i. This component indicates inconsistency in how mothers within fathers are rank-ordered across items. The variance accounted for by this component varied from 3.6% to 30.5% across the subscales.

The interaction between raters and items, σ_ri², expresses the relative extent to which raters apply items inconsistently and accounts for 9.4% of the variance in discipline, 0% in skill encouragement, 1.0% in positive involvement, 3% in problem-solving, and 6.7% in monitoring.

The triple interaction of father by rater by items, σ_fri², accounted for a trivial amount of variance, as it represents 0–1.2% of the variance across the parenting practices. This component indicates that the rater by item interaction, just described, is not noticeably dependent on the father being present or absent in the family interaction.

The residual variance component, σ²_(m:f)ri, accounts for between 39.1% and 66.3% of the total variance across the parenting practices and is the strongest contribution to the total variance in all five scales. This component is a blending of the pure mother within father by rater by item interaction, unmeasured facets that affect the measurement and/or random events. It should be noted that the estimate of the variance component representing the triple interaction is a G-study component in G-theory terminology, which means that this component expresses the relative size of the variance components of scores for a single mother on a single item on a single rater, or, in other terms, the relative size of a single mother-father-rater-item combination in the universe of admissible observations. The term “error variance” is not a G-study term, strictly speaking. In a D-study, it is decided which variance components should serve the purpose of representing error variance and universe/true variance for estimating the generalizability coefficient. In the D-study, the variance components representing error variance will be reduced by increasing the sample size of the different random facets of observation, a principle that is used in classical test theory, as well as in G-theory. All of the error components are explicitly taken into account when estimating generalizability coefficients. High generalizability coefficients indicate that the impact of the error variance components is weak.

The described structure for the 11 variance components of the G-study design constitutes a system of variation that is helpful in assessing the generalizability of the observational measures for both the crossed and the nested D-study designs.

Generalizability coefficients. The G-study variance components presented in Table IV were inserted into the formulas for the generalizability coefficients presented above for both designs. Because the focus of attention in the present study is on observer reliability, the generalizability coefficients are estimated for different numbers of raters while holding constant the number of items in each subscale (Table IV).

The generalizability coefficients for the subscale discipline indicated that two raters were needed to obtain a generalizability of .72 when raters were assumed to be crossed with mothers. Four raters, however, would be needed to achieve a level of generalizability > .72 when raters were assumed to be nested within mothers. Rater variance was included in the error term for the generalizability coefficient in this model. This difference is a major reason why the results were not as promising for the nested model as they were for the crossed model. The error variance of the nested design consisted of the rater-oriented components σ²_r:m:f and σ²_(r:m:f)i, which caused the error variance in the nested model to be larger than the error variance in the crossed model. Thus, the generalizability coefficient associated with the crossed design will be larger than the generalizability coefficient for the nested design.

The generalizability coefficients for the skill encouragement parenting scale in both D-study designs were too low to be acceptable. A major reason for the low generalizability was the relatively strong influence of the error component (m:f)i (30.5%) in the error variance for both measurement models. It may also be noted that the generalizability coefficients for the two D-study designs were identical within two decimal points. This similarity was caused by zero or close to zero variance components entering the error variance for the nested design (see Equation 3 and Table IV).

The generalizability coefficients were high for both the positive involvement and the problem-solving scales. The ratings by one rater would result in an estimated coefficient of .74 for positive involvement and .88 for problem-solving. The small difference between the G- coefficients derived from the two designs is noteworthy, due to the error components being small and of approximately the same size in both models.

For the monitoring scale, a generalizability coefficient of .85 was obtained with two raters, whereas one rater would produce a coefficient of .74 when raters are assumed to be crossed with mothers. Four raters would be needed to achieve generalizability of .80 when raters are assumed to be nested within mothers.

Discussion

The present study is the first to assess the reliability of global observations of family interactions using the CI measure within a G-theory framework that included raters and items as facets of observation over which generalizations were made. Thus, the present approach to estimating reliability allowed for more sources of error than is possible with one-facet designs, such as when estimating Cronbach's alpha. This finding may suggest that prior estimations of reliability, such as application of the alpha coefficient, may have overestimated the level of reliability or underestimated the impact of error variance. The present study was made possible because several families in two PMTO studies were independently rated by two raters. Our study sample consisted of three small sub-samples. A different pair of raters rated each sub-sample. For analytical purposes, the sample-specific variance components were pooled to stabilize the estimates. The estimations were based on videotapes of a sample of 30 families.

This study focused on reliability estimation related to two measurement designs that are applied to the CI measure. The typical design for CI would treat raters nested within mothers. This design contrasts the mainstream procedures for estimating internal consistency reliability in which raters are crossed with mothers. The present study compared estimates of reliability obtained under the two assumptions where mothers were crossed with versus nested within raters, respectively. The different sets of estimations were made possible by G-theory.

This comparison is not only of interest to PMTO research but also of relevance to clinical observations in general. The present findings highlight the importance of applying an estimation procedure that should be in accordance with the actual test design. That condition would not hold if the crossed model is applied to estimate reliability in a design in which the nested model is assumed to have generated the data. In other words, if raters are nested within mothers or patients, as in typical PMTO research, but reliability is estimated under the assumption that raters and mothers are crossed, then the crossed model would likely produce inflated reliability coefficients or underestimate the error variance. The present results support this expectation.

This trend can be easily observed in Table IV for discipline and monitoring. The inflation is hardly recognizable, however, for skill encouragement, positive involvement and problem-solving. The reason can be discerned by comparing the variance components that enter the error variance for the generalizability coefficients estimated in the crossed and nested designs, respectively, in Equations 2 and 3. The error variance for the nested design contains more error terms than the error variance for the crossed design. As can be derived from inspecting Equations 2 and 3, the rater-oriented components of, σ²_r, σ²_fr, σ²_ri, of, and σ²_fri are additional error terms in the nested model, and their estimates are either zero or close to zero for the nested design for skill encouragement, positive involvement and problem-solving.

The second research question relates to the number of raters needed for obtaining reliable scores by applying the crossed and nested measurement designs. Table IV provides information concerning these numbers in the lower part of the table when assuming the number of items is the same as in the actual CI subscales.

When assuming one rater nested within mothers, as in the typical PMTO design, the reliability estimates are .41, .51, and .52 for discipline, skill encouragement, and monitoring, respectively. In contrast, the corresponding estimates for positive involvement and problem-solving are .73 and .87, respectively.

As would be expected, the generalizability coefficients increase with the number of raters. For the discipline scale applying the crossed model two raters are required to obtain a generalizability coefficient of .72, whereas four raters would be needed to surpass the .80 level. However, four raters would be needed to achieve a generalizability coefficient of .72 in the nested model. Similar inspections can be made for the other subscales. Coefficients for skill encouragement are not promising. Even assuming four raters, generalizability coefficient are not higher than .66 for both models. The obtained coefficients for positive involvement and problem-solving may be considered promising for both models. Assuming a crossed design, the estimated reliability for the monitoring scale is considered to be satisfactory. However, three raters must be used to achieve a coefficient of .76 for the monitoring scale in the nested model.

Inspection of variance component estimates provides information relevant to training and coder drift in psychotherapy research. A large patient x coder interaction warrants training to minimize this effect. When a substantial coder x item interaction is present standardization of the coding procedures and detailed item descriptions may be necessary (Wasserman et al., 2009). A promising aspect of the present results is that the rater-oriented components that represent typical error variance in the nested model, σ²_r, σ²_m, σ²_ri and σ²_fri, are of trivial size. However, the σ²_(m:f) component, which represents item inconsistency and is included in the error variance in both models, exerts a relatively strong influence on the scores in the skill encouragement scale, which represents a potential problem. In other words, the items indicated relatively strong heterogeneity that may represent a threat to validity. Although both positive involvement and problem-solving had high reliability estimates, the same type of heterogeneity is recognized, although not to the same extent. With the large number of items in these scales, one would expect strong reliability estimates.

In sum, the model in which raters are nested within mothers provided reliability estimates that were lower than the estimates for the model in which raters and mothers are crossed. This trend was particularly recognizable for the discipline and monitoring subscales, while exceptions were apparent in the positive involvement and problem-solving subscales. No matter which estimation model was applied, the skill encouragement subscale provided unacceptable estimates.

Implications for Future Observation Designs

The findings referred to above suggest that when applying the crossed model of analyses to the typical (clinical) CI measurement design in which raters are nested within mothers, reliability will generally be overestimated or the error of measurement will be underestimated. This result is particularly the case when using one or two raters. Thus, by using the typical nested clinical measurement design, more raters are needed than when applying the crossed design.

The presence or absence of the father had little or no impact on the mothers' parenting abilities. One important implication for future research in parenting may be, nevertheless, to include the father as a facet in the data collection design. Otherwise, the father facet may be a hidden facet and may affect the results in unknown ways.

When multiple sources of error are present and can be identified, G-theory can be viewed as a more conceptually relevant analytic strategy for reliability estimation than classical test theory (Cronbach & Shavelson, 2004). The results of the present study indicate that care should be exercised to establish a correspondence among the assessment design, the estimation model and the type of intended reliability inference.

Limitations

A concern in the present study is related to the small sample size of mothers. To reduce the inconsistency of estimates arising from the small sample size, sample-specific variance components were pooled across the three available sub-samples. Although the pooling procedure included 30 families which were rated by six raters the person sample remains a relatively small sample. This limitation could account for some of the observed inconsistencies. Therefore, replication of our findings in larger samples of persons is necessary.

Three random sub-samples provided data for two pre-treatment conditions and one post-treatment condition. Thus, treatment period might have been an additional source of variance that may have affected the present findings. Three approaches (not reported) were applied to shed light on possible differences in variance between pre and post-test conditions; (a) visual inspection of variances (standard deviations) in Table I, (b) applying one-sided and two sided F-tests of equality of variance terms, and finally (c) comparing the estimated structure of variance components in the three random samples. None of these approaches provided evidence of patterns of different variances for pre- and post-test conditions. Reservations for the low sample size with a corresponding lack of power may be taken into account for interpreting the non- significant F-tests referred to above. This state of affair suggests larger and non-confounded samples in future research.

We do not know the degree of overlap between the five parenting practices. These practices could have been studied by including the five parenting subscales with 92 items in a multivariate generalizability analysis, which would estimate correlations between the subscales. Strong correlations might indicate that the parenting practices reflect a general parenting capacity, rather than distinct parenting practices. Multivariate generalizability analysis was attempted by means of an equivalent procedure of pooling the variance and covariance components across the three sub-samples. However, estimated correlations above unity were obtained in each of the sub-samples, which may indicate that the implicit model may not be appropriate for the present data, likely because of the small sample sizes.

A microanalytic assessment of second-to-second interaction preceded the present macroanalytic CI measure. However, the extent to which training in the microanalytic assessment may have affected the raters' subjective impressions of the family interaction, as expressed in the present macroanalytic CI measure, is unknown.

The tasks in the structured interactions are another potential facet that was not considered in the analysis. Unfortunately, the items were not sampled to parenting scales in a way that made it possible to include tasks as a facet of observation. Future applications of the CI may consider taking tasks as a facet into account.

Conclusions

The present study focused on two models for estimating reliability related to (a) the commonly used model in which raters are crossed with persons (mothers) and (b) a model in which raters are nested within mothers. Both models provided promising reliability estimates for positive involvement and problem-solving. However, the two models yielded different results for discipline and monitoring. In addition, for skill encouragement both models failed to provide acceptable results. A larger error variance was associated with the typical PMTO procedure in which raters are nested within mothers. The common practice of assessing raters as if they were crossed with mothers will probably produce inflated generalizability estimates when applied to a data collection procedure where raters are nested within families as in the typical PMTO procedure. The present study demonstrates that the actual assessment design and the estimation model must be congruent to provide relevant reliability inferences.