Short abstract
Both in academic research and in clinical settings, virtual simulation of the cardiovascular system can be used to rapidly assess complex multivariable interactions between blood vessels, blood flow, and the heart. Moreover, metrics that can only be predicted with computational simulations (e.g., mechanical wall stress, oscillatory shear index, etc.) can be used to assess disease progression, for presurgical planning, and for interventional outcomes. Because the pulmonary vasculature is susceptible to a wide range of pathologies that directly impact and are affected by the hemodynamics (e.g., pulmonary hypertension), the ability to develop numerical models of pulmonary blood flow can be invaluable to the clinical scientist. Pulmonary hypertension is a devastating disease that can directly benefit from computational hemodynamics when used for diagnosis and basic research. In the present work, we provide a clinical overview of pulmonary hypertension with a focus on the hemodynamics, current treatments, and their limitations. Even with a rich history in computational modeling of the human circulation, hemodynamics in the pulmonary vasculature remains largely unexplored. Thus, we review the tasks involved in developing a computational model of pulmonary blood flow, namely vasculature reconstruction, meshing, and boundary conditions. We also address how inconsistencies between models can result in drastically different flow solutions and suggest avenues for future research opportunities. In its current state, the interpretation of this modeling technology can be subjective in a research environment and impractical for clinical practice. Therefore, considerations must be taken into account to make modeling reliable and reproducible in a laboratory setting and amenable to the vascular clinic. Finally, we discuss relevant existing models and how they have been used to gain insight into cardiopulmonary physiology and pathology.
1. Introduction
Computational hemodynamics is evolving to become a powerful tool for gaining insight into cardiovascular disease progression with applications to treatment [1] and surgical planning [2,3]. In many cases, computational modeling can provide essential metrics of blood flow that are otherwise immeasurable [4]. Recent advancements allow researchers to simulate multiple physiological systems, which are coupled and would be nearly impossible to recreate experimentally. This review focuses on computational hemodynamics of the pulmonary vasculature as it relates to the need for and clinical application of patient-specific pulmonary hemodynamics, the considerations required for successfully carrying out simulations, and an examination of the relevant literature.
1.1. Hemodynamics of Pulmonary Arterial Hypertension.
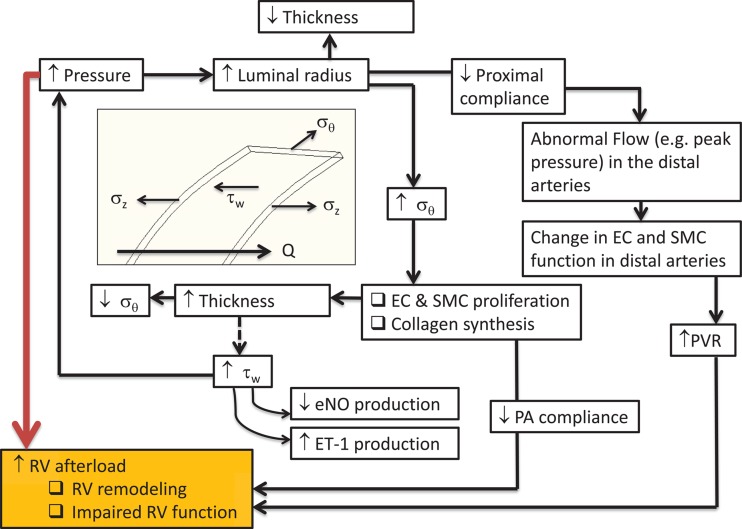
In pulmonary hypertension (PH), elevated resistance in the distal vasculature contributes to higher than normal pressure in the main pulmonary artery [5]. This initiates a vicious cycle in which the pulmonary vascular system perpetuates the progression of disease in an effort to restore homeostasis, ultimately causing an elevated ventricular load that leads to right ventricular hypotrophy and dysfunction (Fig. 1). Computational fluid dynamics (CFD) and fluid structure interaction (FSI) can be used to identify continuum flow and solid metrics that overwhelmingly contribute to right ventricular afterload and are a potential target for corrective intervention.
Fig. 1.
Outline of disease progression in chronic pulmonary hypertension. The white boxes refer to effects on the pulmonary arterial vasculature (vessel wall thickness, vessel wall stiffness, arterial pressure). The orange box refers to effects on the right ventricle. Note: EC = endothelial cells; SMC = smooth muscle cells; RV = right ventricle; Q = flow; σz = longitudinal stress; σθ = circumferential stress; τw = wall shear stress; eNO = endothelial nitric oxide; ET-1 = endothelin-1.
The arterial wall primarily consists of endothelial cells (ECs), smooth muscle cells (SMCs), and fibroblasts. These cells are surrounded, and structurally supported, by an extracellular matrix of collagen and elastin, which are engaged at different distensibility levels [6]. ECs respond to shear stress by releasing chemical messengers (nitric oxide and endothelin-1) to neighboring SMCs, thereby activating vasodilation and/or vasoconstriction in an effort to maintain physiological arterial pressure [7,8]. The walls of veins do not contain SMCs and, therefore, do not contribute directly to the pulmonary response to elevated blood pressure. For this reason, research and clinical efforts are focused primarily on the effects of the arterial circulation. Shear stress and the ensuing shear stress gradients arising from the local flow dynamics [9] and cyclic strain have both shown to impact EC morphology and alter gene expression [8,10,11], revealing the clinical relevance of these continuum metrics. Areas of nonphysiological shear stress and cyclic strain could develop intimal hyperplasia through disrupted apoptosis [12]. PH patients have been documented as having an impaired endothelium [13]. Identifying regional stress variations could explain and possibly predict endothelial response and remodeling.
The progression of PH is self-sustained in the normal physiological response of vascular tissue to increased pulmonary arterial pressure. A prolonged increase in luminal pressure and radius causes a decrease in vessel wall thickness, thereby increasing circumferential and axial wall stress. Normal long-term vascular response is to reduce this wall stress through adjustments to wall compliance and thickness via remodeling [14,15], which engages a destructive cycle that results in an increased load on the right ventricle (RV) (see Fig. 1). Vascular compliance, decreasing in response to arterial remodeling, directly leads to increased RV afterload [16] and ventricle–vascular decoupling [17]. Moreover, a decrease in upstream compliance results in higher pulse pressures and altered flow dynamics in the distal vessels [18].
1.2. Clinical Management of Pulmonary Arterial Hypertension.
The pulmonary vascular anatomy consists of the main pulmonary artery, which originates in the right ventricle, and bifurcates into the left and right pulmonary arteries. The arterial tree continues for approximately 15 generations until reaching the capillaries [19,20]. The pulmonary arterial system is complex compared with the systemic vasculature consisting of trifurcations and irregular branching sequences [19]. The peak systolic and mean physiological pressures in the pulmonary artery are 18–25 mmHg and 12–16 mmHg, respectively [21].
1.2.1. Classification and Therapies.
The classification of pulmonary hypertension has undergone a number of changes since the first classification was proposed in 1973. Only two categories, primary pulmonary hypertension (PPH) and secondary PH were originally recognized [22]. The Evian classification, which attempted to create categories of PH that shared common clinical and pathological characteristics, was proposed 25 years later [23]. This classification had a broader scope and included five different categories. Investigators were subsequently able to conduct clinical trials using well-defined groups of patients leading to the development and approval of eight different medications to treat PAH [24]. At the Third World Symposium on PAH held in Venice, five years after the Evian conference, the term PPH was abandoned in favor of idiopathic pulmonary hypertension (IPAH); familial PAH if a family history of PAH was present; or associated PAH if another cause such as human immunodeficiency virus (HIV) or connective tissue disease was implicated. Pulmonary veno-occlusive disease (PVOD) and pulmonary capillary hemangiomatosis (PCH) were also consolidated into a single subcategory of PAH [24].
The current PH classification and the one most commonly used, was provided in 2008 at the Fourth World Symposium on PH in Dana Point, California. The World Health Organization (WHO) classifies pulmonary arterial hypertension into five key WHO groups.
WHO Group I PH (pulmonary arterial hypertension—PAH) is diagnosed by the demonstration of pulmonary hypertension in the absence of chronic thromboembolic disease, pulmonary venous hypertension due to elevated left atrial pressure, hypoxemia, parenchymal lung disease, and systemic diseases such as progressive systemic sclerosis that have been associated with PAH [25]. Specifically, clinically available hemodynamic values obtained from right heart catheterization (RHC) suggest the onset of PAH at a resting mean pulmonary artery pressure (mPAP) ≥ 25 mmHg, with a pulmonary capillary wedge pressure ≤ 15 mmHg, and pulmonary vascular resistance (PVR) >3 Wood units [26]. PAH is a diagnosis of exclusion and is made only when the etiology of PH is deemed not to be secondary to any of the other four WHO Groups. PH-specific therapies are designed for, and are useful only in, this specific WHO group.
PH-specific therapies have traditionally focused on agents intended to promote pulmonary arterial/arteriolar vasodilation despite the fact that acute vasoreactivity is only present in <10% of these patients [27]. Vasodilator testing with short-acting agents such as adenosine, intravenous (IV) epoprostenol, or inhaled nitric oxide (NO) is recommended for all patients with newly diagnosed PAH. The aim is to identify patients with pulmonary vasoreactivity, defined as a reduction in mPAP of at least 10 mmHg to an absolute mPAP less than approximately 40 mmHg, with either no change or an increase in cardiac output [26]. Compared to nonresponders, patients with pulmonary vasoreactivity showed significant reduction in PVR and mPAP, as well as markedly improved survival (90% at five years) when treated with calcium channel blockers (CCB), albeit at much higher doses than are traditionally used to treat systemic hypertension [28].
Apart from CCBs, 3 three classes of PH-specific agents are currently being used: prostanoids, phosphodiesterase 5 (PDE-5) inhibitors, and endothelin-1 receptor antagonists (ERAs). Prostanoids have been the cornerstone of therapy for PAH for at least two decades. It aids in replenishing prostacyclin I2 that is depleted in PAH due to a deficiency of prostacyclin synthase. Epoprostenol (continuous intravenous), treprostinil (continuous subcutaneous, continuous intravenous, intermittent inhaled), and iloprost (intermittent inhaled) are the three approved medications in this category. Although they all improve symptoms, hemodynamics, and quality of life, only epoprostenol has been shown to improve survival [29]. PDE-5 inhibitors (sildenafil and tadalafil) are used to inhibit the hydrolysis of cyclic guanylyl monophoshate (GMP), mitigating the derangements of this pathway that lead to a reduction in nitric oxide synthase in PAH. It is proven to be an effective treatment for PAH leading to improved hemodynamics and increased six-minute walk distance but does not decrease the time to clinical worsening [30]. Endothelin-1 is a potent vasoconstrictor and smooth muscle mitogen that contributes to the pathogenesis of PAH. Two endothelin receptor antagonists, bosentan and ambrisentan, are commercially available for the treatment of PAH [31]. Although these agents were developed based on demonstrated abnormalities in the relevant pathophysiologic pathways and are prescribed with the rationale of promoting vasodilation, an emerging body of evidence supports the hypothesis that they also have significant antiproliferative properties that contribute to their efficacy [32]. The choice of initial therapy is based on clinical assessment with additional therapies being used according to clinical and hemodynamic response, as well as side effect profiles. Many patients are placed on combination therapy to maximize the additive effects of different classes.
1.2.2. Assessment of Pulmonary Hemodynamics.
The response to therapy is currently gauged by reassessment of pulmonary hemodynamics (mPAP, PVR, cardiac output (CO)), symptoms, exercise performance (most commonly measured with a six-minute walk), right ventricular function as assessed by echocardiography, and mortality [33]. Recently risk prediction models like the REVEAL risk score [34] (Registry to Evaluate Early and Long-Term Pulmonary Arterial Hypertension Disease Management) in the U.S. and the Scottish Composite Score (SCS) [35] in the U.K. have also been employed in clinical decision making, as tools to assess disease severity and aid in prognostication.
Despite advances in understanding the disease pathophysiology and great strides in developing PH-specific therapies, the general impact on survival has been limited [36–38]. From a clinical perspective, current screening and diagnostic paradigms inherently dictate that a patient is suspected to be at high risk, symptomatic, or that gross anomaly be identified on physical exam or imaging before the diagnosis of PAH is entertained. This is universal regardless of the field of medicine in which one may practice. Accentuation of the pulmonic component of the second heart sound, left parasternal lift, a fourth heart sound, and/or an increased jugular “a” wave [39] would prompt an astute clinician to consider the diagnosis of PAH. Prominent central pulmonary vascular markings or right ventricular enlargement as well as peripherally attenuated vascular markings on chest X-ray or a dilated main pulmonary artery on computed tomography (CT) would be equally concerning to the radiologist [33,39]. Elevated pulmonary artery systolic pressure on a transthoracic echocardiogram or an RHC or right ventricular systolic dysfunction by any imaging modality would also indicate to a physician the need to investigate further for PAH. No validated screening tool currently exists to detect the disease in its pre symptomatic or subclinical phase. This might partially explain the poor prognosis of the disease since many patients would have already had significant remodeling of the pulmonary arteries and some measure of RV dysfunction at diagnosis using conventional metrics [39].
Computational fluid dynamics and the ability to estimate hemodynamic continuum metrics (e.g., spatially averaged wall shear stress) of blood flow in the pulmonary arteries might prove to be a better screening tool for PAH [40]. Metrics available from computational analysis could also prove useful to study disease progression, for posttreatment assessment, and for surgical planning. As increased pulmonary vascular resistance is a major contributor to PAH, wall shear stress should increase with increased remodeling of the pulmonary vasculature and might be detected prior to significant measureable increases in PA pressures. The use of CFD to noninvasively assess the severity of PH and gauge response to PH-specific treatments would significantly revolutionize clinical practice in this field.
The current metrics being used to assess disease progression are invasive, expensive, or riddled with uncertainties. Right heart catheterization, transthoracic echocardiogram, and the six-minute walk test (6MWT) are the tools most widely used to gauge disease progression and response to treatment. RHC remains the gold standard for diagnosis of PAH. Improvements in hemodynamic parameters have been linked to response to treatment and increased survival. However, measurements of pulmonary hemodynamics must also be interpreted with a fair degree of caution since even during short-term continuous monitoring, catheter measured PAP can vary significantly in the absence of interventions [41]. Brief follow up measurements at intervals of months to years risk superimposing spurious and spontaneous variation (as well as temporary effects such as hydration status, sedation, and anxiety) on changes in the patient caused by disease progression or response to therapy [42]. Measurement inaccuracies can be compounded by errors in technique, such as failing to confirm the wedge position with wedged blood saturation (leading to imprecise pulmonary capillary wedge pressure (PCWP), relying on thermodilution cardiac output in the setting of tricuspid regurgitation (TR) or intracardiac shunts, studying the patient during volume expansion or dehydration [42], or not accounting for high tidal volumes or peak end expiratory pressures (PEEP) if the patient is on a mechanical ventilator. Furthermore, RHC is an invasive method with the ingrained risks of causing infection, bleeding complications, iatrogenic arrhythmias, transient complete heart block (in the setting of a preexisting left bundle branch block), jugular vein thrombosis, carotid artery injury, and pulmonary hemorrhage. Evidence exists that it might increase morbidity and mortality [43]. Noninvasive methods are, therefore, better suited for close observation of disease progression and treatment response.
Transthoracic echocardiography is a useful noninvasive tool for hemodynamic measurements. Its utility in PH includes assessing the peak systolic PA pressures and assessing RV function/dysfunction, which results from chronically elevated RV afterload. Doppler echocardiography is used to measure pressure gradients between chambers of the heart and quantify blood flow. Yock and Popp described the method to estimate RV systolic pressure and, thus, systolic PA pressure by measuring the velocity of tricuspid regurgitation (TRv) [44]. The peak velocity of TR (TRv) is dependent on the pressure difference between the RV and the right atrium (RA) during systole. This velocity is then used to calculate the pressure difference with a simplified form of the Bernoulli equation: . RA pressure is determined using a standardized approach and then added to the pressure gradient, providing an estimate of RV systolic pressure [45]. While this modality has obvious strengths like ease of performance and reproducibility, there is potential for underestimating systolic PA pressure because of variation in the angle of Doppler interrogation and/or because of the presence of severe TR [46]. In general, use of TRv to estimate SPAP (systolic pulmonary arterial pressure) often leads to underestimation compared with systolic PA pressure as determined by RHC [47]. In fact, in very advanced PH with severe RV systolic dysfunction the RA pressure is severely elevated and TRv may be negligible. Using the method described above would result in a falsely decreased SPAP and gross underestimation of disease severity.
Since right ventricle ejection fraction (RVEF) cannot be accurately obtained from echocardiographic measurements of RV volume, due to the complex RV geometry, several surrogate markers of RVEF have been developed and are used to gauge PH and RV disease progression. RV fractional area change (RV-FAC), the relative difference between end diastolic and end systolic RV area as seen in an apical four-chamber view does not require geometric assumptions and correlates well with RVEF. However, inadequate image quality frequently results in high intra- and interobserver variability [48]. In many instances the entire dilated RV cannot be fully focused in the echocardiographic field of view, making this technique impossible to perform.
Tricuspid annular plane systolic excursion (TAPSE) is a method based on the characteristic displacement of the tricuspid valve during systole. It is measured noninvasively by M-mode or 2D echocardiography and has excellent correlation with RVEF in various types of PH. However, TAPSE can also be reduced in patients with left ventricle (LV) dysfunction, thus decreasing the specificity of this method. Some authors contend that TAPSE is not reliable in detecting early RV systolic dysfunction [49,50]. RV strain and strain rate, measured either by tissue Doppler or speckle tracking echocardiography, show strong correlation with RV failure and may be preferable to TAPSE in some conditions. RV strain, strain rate, and RV regional transverse motion can also be assessed using cardiac magnetic resonance imaging (MRI) tissue tagging techniques. However, strain-imaging techniques by both methods are not yet widely employed.
The role of computed tomography (CT) imaging in PH has thus far been limited to measuring the diameter of the proximal PA, investigating the characteristics of the lung parenchyma to assess for interstitial fibrosis or emphysema, and evaluating the presence and burden of pulmonary emboli in chronic thromboembolic pulmonary hypertension (CTEPH). It is a routine test performed on every patient being investigated for PH. The possibility of using these images to evaluate PA geometry, noninvasively assess pulmonary hemodynamics by CFD, and validate the ensuing novel metrics to diagnose PH and clinically follow its progression would greatly enhance the physician's armamentarium in combating this disease.
2. Patient-Specific Computational Hemodynamics
Depending on the flow information required, hemodynamics in the pulmonary vascular system can be simulated in one or three dimensions. One-dimensional analysis can incorporate patient-specific anatomical metrics (e.g., conduit cross-sectional areas) and can accurately reveal general physiological flow conditions at any generation [51–55]. These simulations are computationally inexpensive and are easily coupled to the distal vasculature [51,56]. Three-dimensional flow simulations will reveal more details about regional flow dynamics but are more computationally expensive and require substantially more pre- and-postprocessing. The majority of this review will focus on 3D modeling unless otherwise specified.
The framework for conducting 3D patient-specific computational hemodynamic simulations begins with reconstructing the computational domain from thoracic computed tomography (CT) or magnetic resonance (MR) images [57]. A complex network of blood vessels must be segmented to a specific generation along the arterial tree (termed in this work as the generation of segmentation), usually limited by the image resolution. The virtual computational domain must undergo a series of preprocessing steps, which includes eliminating nonanatomical surface anomalies and adding inlet and outlet extensions. Finally, the geometry is divided into subdomains (meshing) to numerically solve the continuity (Eq. (1)) and momentum (Eq. (2)) equations, where is the velocity vector, p is the pressure, [τ] is the deviatoric stress tensor, and ρ is the blood density.
| (1) |
| (2) |
The intrinsic properties of blood are generally assumed to be Newtonian in large vessels, e.g., in Eq. (3), where μ is the dynamic viscosity and is the rate-of-deformation tensor. This assumption is valid for flow in large arteries [58] and without stagnation points [59].
| (3) |
In small vessels, it is advantageous to incorporate a non-Newtonian constitutive equation for blood [60]. Any constitutive model that attempts to capture the behavior of whole blood must consider its basic rheological characteristics. At low values of shear rate (less than 100 s−1), blood has a yield stress (τy) and is slightly shear thinning [61]. At higher values of shear rate (greater than 100 s−1), blood is essentially Newtonian. Neglecting shear thinning behavior, yield stress effects can be characterized using the Bingham plastic model (Eq. (4)), where is the second invariant of the rate-of-deformation tensor.
| (4) |
If the impacts of shear thinning effects are considered important, the Herschel–Bulkley (H-B) model (Eq. (5)) can be used in regions of low shear rate. However, this model should not be applied to account for flow scenarios where the range shear rate is both below and above 100 s− 1. In Eq. (5), m is the consistency index (P sn−1) and n is the shear thinning index. In cases where n = 1, the H-B model simplifies to Eq. (4), and m = μ.
| (5) |
The Carreau–Yasuda model (Eq. (6)) does not include a yield stress, but it is advantageous in that it is capable of capturing the Newtonian plateau in high shear ranges [62]. In Eq. (6), η0, η∞, λ, and α (= 2 for the Carreau model) are the zero-shear viscosity, Newtonian viscosity plateau, time constant, and a dimensionless parameter for the transition regions, respectively.
| (6) |
All of the aforementioned models convey a general sense of blood's rheological characteristics, but none of them establish a clear structure–function relationship. The Casson model [63] (Eq. (7)) fits well with empirical data and can be written as a function of blood hematocrit (Ht)
| (7) |
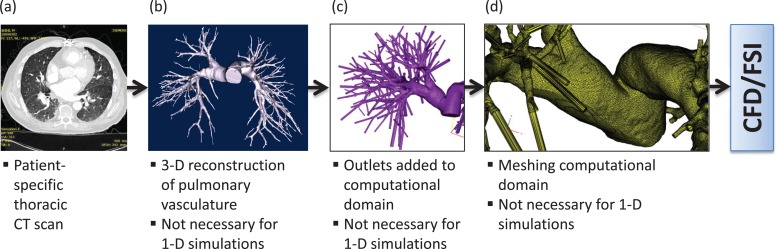
To simulate 3D patient-specific flow conditions for clinical applications, the procedure illustrated in Fig. 2 would have to be implemented for every available image dataset. Moreover; in addition to pre- and postprocessing, computational time can be a limiting factor for routine clinical use.
Fig. 2.
Procedure for conducting patient-specific computational modeling of pulmonary vasculature. (a) Starting with a thoracic CT scan of the patient, (b) a 3D solid model of the pulmonary vasculature is reconstructed. (c) The model outlets are truncated normal to the centerline and fixed to outlet extensions measuring 10 times the outlet diameter in length. (d) A volume mesh is applied to the entire solid model, which is imported into a numerical CFD/FSI simulation. Note: CFD = computational fluid dynamics; FSI = fluid-structure interaction.
2.1. Image Segmentation.
Patient-specific clinical images that reveal the structure of the vasculature can be obtained using volumetric CT or MRI without a contrast agent, although contrast-enhanced images are often preferred whenever available for better reconstruction accuracy [57]. Vessel tree segmentation is the process by which pixels in the image are labeled as part of the connected vascular network, distinct from the lung parenchyma or surrounding anatomical features (heart, chest wall, diaphragm, pulmonary tumors, etc.). Vessel tree labeling is then the process of traversing the segmented tree to identify and characterize the tree hierarchy and morphological features such as individual branch length, vessel radius, vessel tortuosity, and total vascular volume. Both the segmentation and labeling are limited by the quality and resolution of the initial volumetric scan. Often scans are obtained with a relatively large slice thickness. A typical diagnostic scan produces image voxel dimensions of 1 × 1 × 3 mm. Large voxel sizes relative to the size of the vessels of interest, especially in the direction of image acquisition, can lead to the artificial appearance of vessel discontinuities, and vessels smaller than the largest voxel dimension are typically undetectable due to partial volume effects. Historically, manual segmentation of the vascular tree is considered the gold standard, but this is time consuming and labor intensive, making clinical implementation impractical.
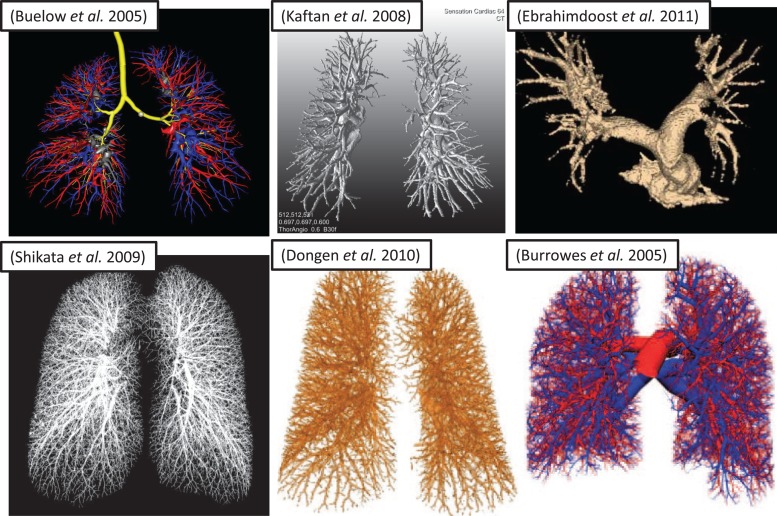
A successful segmentation method must reconstruct key anatomical structures and for most applications separate the arterial system from the venous system. Automatic segmentation of the pulmonary vascular tree requires first the segmentation of the lung cavity from the chest wall, mediastinum, and diaphragm. Simple thresholding and morphological operations work well in this task for most normal lungs, however, many patients present with large tumors, edema, and fibrosis create apparent connections between pulmonary vascular structures and the surrounding anatomical structures. This can be overcome with additional processing steps to separate the right and left hemilungs, followed by either automatic or semiautomatic snake-based separation of pulmonary lesions attached to the chest wall, as demonstrated with tumor-laden lungs by O'Dell [64]. Many existing partially or fully automated methods can rapidly reconstruct the vascular tree to a large number of generations [65–69], but most are susceptible to discontinuity artifacts present in the volumetric scans and are unable to reveal both distal and proximal vasculature (see Fig. 3). For successful CFD analysis, additional means are required to estimate or interpolate the segmentation results into a more realistic, continuous, and smooth vascular tree structure. Burrowes et al. [70] employed a novel technique for reconstructing a continuous 3D model of the pulmonary vasculature to the terminal bronchioles (Fig. 3). All reconstructed arteries assume circular cross sections based on the Strahler diameter ratios [71] and are represented as 1D finite elements in 3D space. The reconstruction even implemented an algorithm to introduce supernumerary vessels, which are typically ignored in CFD analysis because they are not perfused under normal physiological conditions [60]. Finally, due to the complexity of the resulting vascular networks and the requirement for manual preprocessing (discussed in Sec. 2.3), the available techniques are not yet suitable for directly implementing 3D CFD analysis in a clinical setting. The Burrowes et al. technique can be solved as a reconstructed patient-specific 3D domain. Nevertheless, it should be noted that this technique is not fully automatic, but if incorporated with other segmentation strategies such as those referenced above [65–69], it holds promise for rapid patient-specific pulmonary vasculature regeneration.
Fig. 3.
Resulting arterial trees, reconstructed using different automated and manual techniques from in vivo human volumetric CT scans. Different degrees of fine structure reconstruction are due, in part, to differences in image resolution: [65]-Buelow (voxel dimensions not given); [66] Shikata (0.6 × 0.6 × 1.3 mm); [67] Kaftan (0.6 × 0.6 × 0.6 mm); [68] Dongen (submillimeter, isotropic, but not specified); [69] Ebrahimdoost (0.66 × 0.66 × 1.0 mm); [70] Burrowes (0.68 × 0.68 × 1.4 mm).
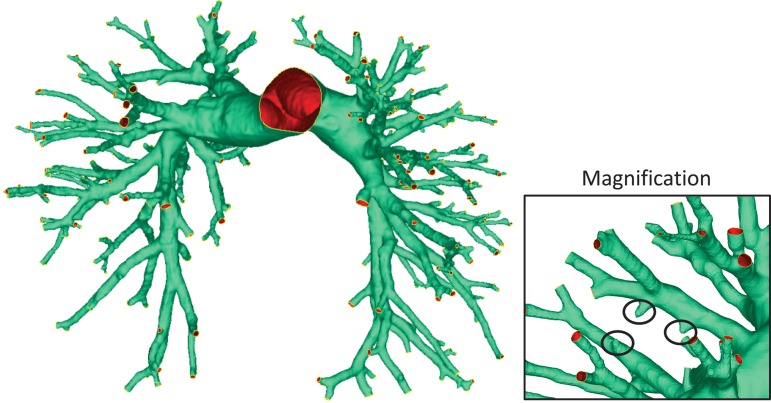
None of the previously mentioned automated segmentation techniques were validated against direct monitoring of the pulmonary arterial inlet and outflow cross-sectional areas. This is essential to assess the feasibility of implementing these procedures as computational domains for CFD/FSI simulations. The inlet-to-outlet-area ratio, IO = (, is a general metric that is associated with whether the flow will accelerate or decelerate within the computational domain. Segmenting the pulmonary vasculature as a preprocessing step to computational simulations presents some key questions that must be addressed. Figure 4 depicts the results of manual segmentation with focus on a branch scenario in which the image resolution prevents the full reconstruction of a bifurcating vessel. This poses a practical problem because neglecting these types of anomalies could significantly reduce the outflow cross-sectional area and does not replicate the actual patient-specific vasculature. On the other hand, truncating the vessels at locations where image contrast allows for utmost certainty would reduce the computational domain to only a few generations. More research must be done to determine the impact of truncating or neglecting parts of the vascular tree on the hemodynamics. Two simulations analyzing the same patient, but truncated at different levels, should arrive at the same fluid flow dynamics within a common region.
Fig. 4.
Vasculature generated by manual segmentation using Mimics. Magnification: example segmentation fault requiring manual intervention. Circled parts show branches that could not be fully segmented due to inadequate image resolution.
For 3D flow analysis, current semiautomatic segmentation methods appear to be the most practical option. Semiautomatic segmentation of the pulmonary vasculature can be done with commercial software (Mimics, Materialise, Belgium). Initially, thresholding is used to identify all vasculature within the Digital Imaging and Communications in Medicine (DICOM) image sequence. After thresholding, artery isolation can be accomplished using region growing algorithms and recognizing that arterial vessels are always accompanied by airways [70]. An iterative process of region growing and multiple slice editing can be used to impose a “mask” over the arterial vasculature.
Figure 5 shows the outcome of CFD simulations of the same vasculature manually segmented using Mimics by two individuals (models A and B), with matching inflow and outflow boundary conditions. While both geometries clearly share anatomical attributes in parts of the domain, it is evident that the level and meticulous nature of segmentation drastically influences the flow dynamics, especially considering that these simulations were carried out using a zero traction outflow boundary condition. Note that the stresses were bounded between 0 and 50 dyn/cm2 for comparison. Without consistency in the segmentation protocol, two techniques could arrive at essentially different morphologies with drastically different IO, which would inevitably result in a different flow dynamic. Overcoming this limitation is essential and should likely encompass a two-part approach: (1) consistency in image acquisition, processing (e.g., contrast enhancement), and thresholding and (2) boundary conditions adjusted to account for the IO. The simulations suggest that boundary conditions may have to be scaled according to IO to establish consistent flow patterns within the same vasculature. Other options are to develop improved automated methods to segment parts of the proximal vasculature while continuously verifying that IO is within the physiological norm with each generation. Therefore, patient-specific simulations of the pulmonary vasculature must be independent of the segmentation protocol; otherwise the simulations remain subjective and unreliable for clinical applications.
Fig. 5.
Wall shear stress distribution of patient-specific pulmonary vasculature, at two levels of segmentation (A and B). The hemodynamics are dependent on the number of tree generations that are segmented and the inlet-to-outlet cross-sectional area ratio. Both simulations are carried out with a zero traction outflow boundary condition. The segmentation with a greater total outlet cross-sectional area (B) develops lower pressure at the inlet and lower velocities in the terminal vessels (not indicated in figure).
2.2. Meshing.
The computational domain must be divided into a finite number of elements to discretize and solve the equations of motion [72,73]. The mesh must resolve the complex geometry of the pulmonary vasculature and be dense enough to expose the physiological flow dynamics. Anatomical computational domains can be discretized using tetrahedral [74] or sometimes hybrid [75] meshes. Hexahedral meshes might not be practical for the pulmonary vasculature as they can lead to large or small aspect ratios in geometries with abundant bifurcations [76]. These elements are normally small at the surface to capture the fluid boundary layer but grow in size as they get closer to the fluid core. Multiple layers of prism elements can be extruded from the polygonal mesh for capturing the boundary layer, but we have found that a transition to the neighboring tetrahedral elements will often negatively impact element quality.
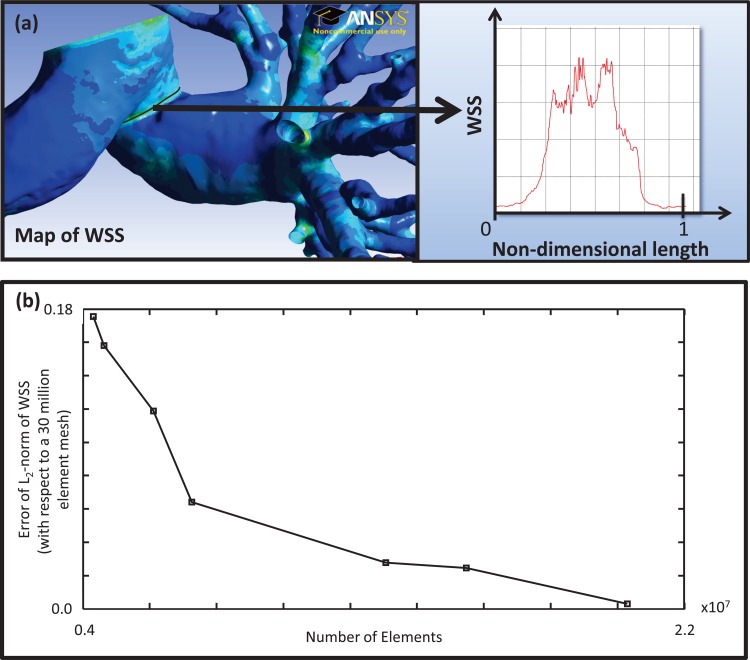
Grid independence is necessary for any numerical solution as it implies that the system of governing equations has been satisfied. Grid independence studies must be tailored to the flow characteristics of interest. Convergence of velocity and pressure at selected locations within the model, with decreasing grid spacing, has been commonly employed [18,77]. Nevertheless, flow characteristics such as velocity and pressure will reach grid independence before wall shear stress (WSS) and wall shear stress gradients (WSSG) [74]. The WSS continuum metric can be tested for grid independence by conducting constant flow rate simulations with sequentially increasing mesh density. After visually identifying a region of high spatial WSSG, a hypothetical line is drawn around the circumference of the vessel. The L2-norm of the WSS magnitude along the hypothetical line is considered to be a quantitative representation of the mesh density. Simulations of varying mesh densities can be compared against a conservative, exceptionally dense mesh that is assumed to yield the true solution. Figure 6(a) shows a hypothetical line superimposed onto the pulmonary WSS map and a plot of the WSS along its normalized axis. Figure 6(b) shows a mesh convergence study for a typical pulmonary vasculature solved using a finite volume method. The error of the L2-norm of the WSS falls below 10% at a tetrahedral mesh density of approximately 7.5 × 106 elements, which corresponds to a maximum edge length of 0.84 mm.
Fig. 6.
(a) Region of analysis for the mesh independence convergence study. (b) Mesh independence convergence data for pulmonary vasculature obtained with a commercial solver, Fluent (ANSYS), using steady state inlet plug flow with zero traction outflow boundary conditions. The graph depicts the residual error in the estimated wall shear stress (WSS) as a function of the number of elements in the mesh used for calculation.
2.3. Preprocessing.
The final computational domain developed from segmented thoracic images must be equipped with outlet and inlet extensions to ensure a fully developed flow condition and to avoid transferring numerical error into the pulmonary vessels, respectively [78]. At the inlet, a fully developed flow condition can be imposed (as described in Sec. 2.4), but it is still recommended that it be implemented sufficiently far from the inlet [72,79]. This may seem redundant, but no analytical profile shape will truly represent the physiological flow condition. Any outflow boundary condition, regardless of the physical principle used to develop it, is an approximation inherently flawed when compared to the true physiological flow at that level of vessel truncation. Each mesh element is strongly coupled to its neighbors during the governing equation discretization; therefore, outflow boundary conditions should be imposed downstream from the computational domain to minimize the introduction of nonphysiological flows into the domain [72,80,81]. In computational models that contain many outlets, the process of imposing outlet extensions should be done automatically to ensure feasibility of the modeling technique in a clinical setting. Algorithms are required to identify an outlet automatically and apply an extended mesh at the boundary. Because of the anatomical complexity of the pulmonary vasculature in a pathological condition, these algorithms will also need to identify and account for intersecting vessel geometries. The success of such an automated algorithm will undoubtedly depend on centerline extraction of the segmented geometry [76,82]. Even manually truncating the outlets of the polygonal surface requires centerline extraction to ensure that the extension is parallel to the flow, which can be done using open source (e.g., VMTK) or commercial software (e.g., Mimics). Techniques have been introduced for automatically identifying, truncating, and extending outlets [76], but attempts by our group to implement them to a complex pulmonary vascular tree have proven unsuccessful.
2.4. Inflow Boundary Conditions.
Imposing a fully developed inflow velocity profile can reduce inconsistencies between physiological and computational flows. Patient-specific inlet waveforms can be obtained through invasive right heart catheterization with a fluid-filled Swan–Ganz balloon tip catheter and a pressure-flow wire. If pressure is not required, transthoracic echocardiography (TTE) or magnetic resonance imaging with phase-contrast (PC-MRI) for velocity encoding [83] can be used to obtain velocity measurements noninvasively. The measured inlet waveform, being a periodic function, can be represented by using a complex Fourier series (Eq. (8)), which can typically represent the flow with approximately 10 harmonics [55]. In Eq. (8), Q(ωk) is the flow rate scalar in the frequency domain and ωk is the angular frequency () with period, T.
| (8) |
In steady, fully developed flow through cylindrical conduits, the velocity develops into a Poiseuille profile unless otherwise perturbed by surface roughness or other geometrical singularities. In pulsatile flow, the fluid inertia does not allow the flow to develop under a constantly changing pressure gradient. The Womersley solution (Eq. (9)) is an analytical representation of velocity as a function of time and radial coordinate location within the cross section [84,85]. Note that the velocity magnitude corresponds to the real part of Eq. (9), while the imaginary part contains information on the relative time point within the cardiac cycle.
| (9) |
PC-MRI measurements suggested that a plug profile is appropriate for the main pulmonary artery inlet [86]. Nevertheless, previous studies in dogs show significantly decreased flow near the vessel walls, with maximal flow at the center [87]. Additional work is needed to determine how the inlet velocity profile develops further downstream in the domain and how that impacts the flow dynamics.
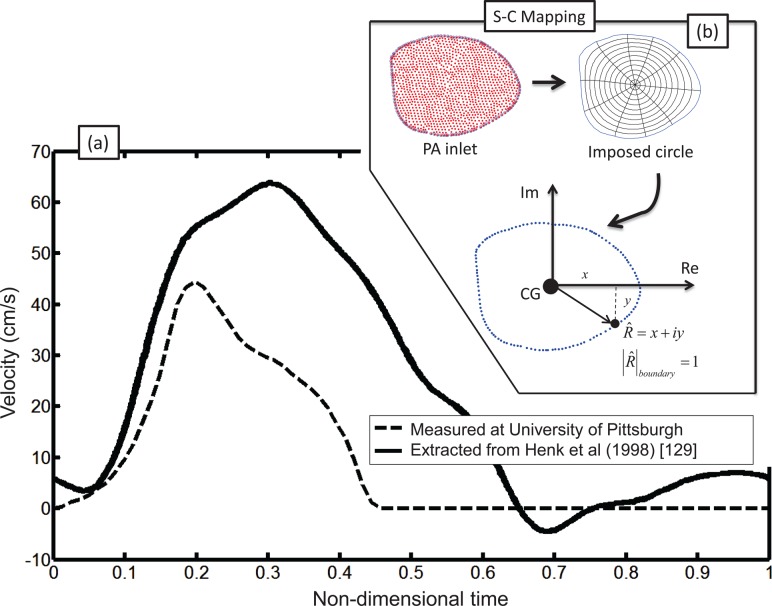
The velocity profiles defined by Eq. (9) as a function of the nondimensional radius (r/R), are intended to be applied to a circular cross section, which does not represent the anatomical shape of the vessels reconstructed from the patient-specific scans (see Fig. 7). Schwarz–Christoffel (SC) [79] mapping can be used to construct a map between the anatomically relevant patient-specific inlet cross section and a perfect circle. In addition, this technique can be used to impose experimentally obtained physiological inlet flow conditions on nonmatching reconstructed geometry.
Fig. 7.
(a) Inlet waveforms measured for pulmonary vasculature: solid—Henk et al. [129]; dashed—Swan–Ganz balloon tip catheter measurements of normal subject, taken at University of Pittsburgh Medical Center; (b) inlet of typical segmented pulmonary artery and Schwarz–Christoffel (SC) mapping procedure: A unit circle is superimposed onto the inlet. Any point within the domain can be represented as a complex number: , in which the modulus corresponds to the distance from the center of gravity (CG).
2.5. Outflow Boundary Conditions.
In all current computational modeling methods, a classical system of governing equations is constructed for finite points within the computational domain to generate a discretized system of equations of motion. To solve this system, flow or pressure must be specified at the inlets and outlets [72,88]. Because of limited image resolution, a reconstruction computational flow model of the entire pulmonary vasculature is not possible, and thus, outflow resistance/impedance at the truncated vessels must be representative of the distal vessels not readily obtained from the segmentation process [89]. Resistance embodies the frictional losses that must be replaced by an external driving force (pump). Conversely, impedance is a combination of the resistance and reactance, where the reactance is dependent upon the vessel wall compliance: the exchange of the fluid's kinetic energy and the elastic vessel's storage energy, which is constantly transferring and always remains conserved [84].
Much like the flow waveform, the pressure and impedance can be expressed as a Fourier series (Eqs. (10) and (11))
| (10) |
| (11) |
| (12) |
If patient-specific pressure and flow measurements are available, impedance magnitude can be obtained by conducting spectral analysis of the pressure and flow harmonics. Equation (12) is used to calculate each harmonic of the impedance in the frequency domain. For an intuitive grasp of the impedance concept in the frequency domain, at zero frequency the pressure and flow correspond to the mean resistance while the reactance disappears (Z(ω0) = Resistance).
Zero Traction.
One option for an outflow boundary condition is to set each outlet pressure to a constant value [89–91], which can result in nonphysiological flow within the computational domain because the flow split is entirely governed by the proximal (segmented) vascular geometry [91]. Although in idealized geometries, the zero traction outflow boundary condition has shown good agreement with experimental velocity profiles [92], the validity of these simulations is compromised for multioutlet domains. To represent the flow dynamics in the distal vasculature in an accurate manner, which in turn will influence flow behavior and the flow split in the proximal vessels, the pressure and flow must be coupled at each outlet.
Resistance.
A pure resistance outflow boundary condition does not account for the compliance of the distal arteries and keeps the pressure and flow in phase (see Fig. 8). An electrical circuit analogy of this condition represents a pure resistor, where the pressure corresponds to the voltage and the flow to the electrical current. Therefore, Ohm's law can be used to find the relationship between pressure (voltage) and flow (current) as in Eq. (13)
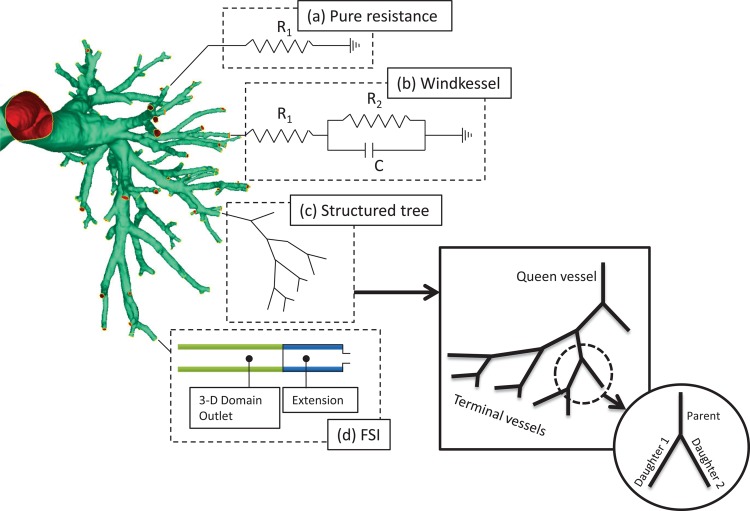
Fig. 8.
Outflow boundary conditions applied to pulmonary vascular models. (a) The pure resistance model consists of a single resistor causing a linear relationship between the outlet pressure and flow. (b) The Windkessel models extend the pure resistance model with a compliance term but do not capture fully the complex flow patterns through compliant vascular networks. (c) The structured tree model is a hypothetical reconstruction of the compliant vascular tree distal to each truncated outlet. The pressure-flow relationship at each outlet is calculated by computing the tree impedance. (d) The fluid-structure interaction (FSI) boundary condition is a useful add-on to any FSI simulation, which encompasses all the sophistication of the compliant structured tree.
| (13) |
Greinberg and Karniadakis [89] introduced a resistance outflow boundary condition for computational models with multiple outlets for cases in which the patient-specific outflow is measured. This could be applicable for computational pulmonary models that are truncated at the low-generation vessels. Measuring patient-specific flow rates using ultrasound or MRI is feasible in a clinical setting, making this outflow condition advantageous because directly imposing an outlet flow rate results in numerical convergence problems [93] that are avoided through resistance based outflow boundary conditions. Even without patient-specific flow split data, flow at each outlet can be estimated as proportional to the outlet radius to a specific power (Q outlet ∝ ra) [84]. Analysis of the minimization principle reveals that a is equal to 3, yet experiments on a resin cast of a human lung revealed a is equal to 2.3 [94]. Assigning the flow split ensures mass conservation, which might be particularly effective when combined with the Greinberg and Karniadakis technique, but implementation will not be trivial. When using commercial fluid flow solvers, the need for external subroutines of code for implementing outflow boundary conditions can be avoided by introducing porous medium extensions [95,96]. In a porous medium, much like in a pure resistance circuit, the pressure is linearly proportional to the flow (Eq. (13)). The medium's resistance is dictated by its porosity and permeability.
Windkessel.
A three-element Windkessel outflow boundary condition is a lumped model that accounts for the resistance and compliance of the distal vasculature [97,98]. Representing the distal arteries as an RCR electrical circuit reveals the pressure-flow relationship as an ordinary differential equation (Eq. (14)), where R 1 and R 2 are the resistances corresponding to the circuit in Fig. 8, and C is the capacitance (m5/N). The circuit is assumed to terminate at an arterial generation of zero pressure [99]. Equation (14) can be used to derive the impedance of the Windkessel model in the frequency domain (Eq. (15)) [100,101] but will not replicate the physiological oscillations measured for the high frequency harmonics [98].
| (14) |
| (15) |
Unlike the pure resistance model, flow and pressure are out of phase in the Windkessel but not to the extent of physiological values [56]. The Windkessel model has several limitations: (1) All flow fluctuations are transferred to the pressure, regardless of the frequency, making it very sensitive to noise [89] (2) The model cannot account for pressure peaks that occur as a result of wave reflections in naturally bifurcating arterial trees, which might not be as important for the pulmonary circulation as it is for the systemic circulation. More reflections lead to a discrepancy between the pressure and flow waves, which is generally not seen in the pulmonary arteries [102] (3) The Windkessel circuit parameters are not intuitively tied to morphometric data [103], making it difficult to establish patient specificity of the model in a clinical setting.
Structured Tree.
The structured tree outflow boundary condition involves generating a hypothetical arterial tree that represents all the vasculature distal to the truncation points of the image reconstructed geometry. Using the method outlined in Refs. [54,56], the pressure at each outlet of the computational domain can be found with Eq. (16) (convolution equation). In order to evaluate the integral in Eq. (16), the flow rate is required for the entire cardiac cycle. Therefore, when calculating for a given time point within the period, T, are known. The values for are taken from the previous time step. After subsequent time steps, the solutions for q(t) and p(t) should converge.
| (16) |
To find the impedance in Eq. (16), the structured tree is reconstructed from metamorphic data, which describes arterial radii, length, and compliance at each generation of the pulmonary vascular system [19,20] (see Fig. 8). The ultimate goal is to find the input impedance of the queen vessel, which is equal to the output impedance of the outlet for which the boundary conditions are being assigned. The overall strategy is to work backwards from the terminal vessels, where the impedance is assumed to be zero. The entrance impedance, Z(x = 0), can be found for the terminal vessels using Eq. (17).
| (17) |
where
A0 = unpressurized vessel cross sectional area (πr 0 2), r0 = unpressurized vessel radius, E = vessel Young's modulus, and h = vessel thickness.
J0 and J1 are Bessel functions of zero and first order, respectively, w0 = i2w2, w = Womersley number = , ν = kinematic viscosity, and c (wave propagation velocity) , and L = length of a vessel.
The impedance at the outlet of the parent vessels () is a function of the input impedance of the two daughter vessels () connected to its outlet (Eq. (18))
| (18) |
Calculating up the arterial tree using Eqs. (17) and (18), the input impedance can be found for the queen vessel that is connected to the outlet of the computational domain (BC). To achieve physiological pressure and proper left/right lung flow distribution, vessel radii along the arterial tree must be adjusted from the original morphometric data [104]. This tuning analysis can be used to determine the influence of disease on distal vasculature remodeling when patient-specific hemodynamic data are available for the proximal arteries. The impedance modulus of the structured tree boundary condition oscillates for harmonics at high frequency, which is more consistent with physiological measurements than the Windkessel boundary condition. It allows for wave reflections, encompasses anatomical features of the arterial tree, and can be modified to incorporate inspiration [88].
A properly applied impedance boundary condition can model the phase difference between flow and pressure and can even reveal spikes in the pressure waveform resulting from wave reflections. Depending on the hemodynamics being investigated, the large arteries can be modeled in 3D or 1D [51,101,103,104]. 1D models for the large arteries, coupled with an impedance outflow boundary condition, are computationally efficient and can incorporate patient-specific anatomical vessel dimensions without the need to do full segmentation [104]. In addition, they account for wave propagation effects based on vessel stiffness [52,56], which is a key metric of ventricular afterload. Incorporating conduit radius and vessel mechanical properties into a computational model results in a powerful tool that can be used to model vascular remodeling (narrowing and stiffening). One limitation of the 1D hemodynamic model is the assumption that the flow is fully developed in all vessels. This is clearly not the case for the pulmonary circulation, as the pulmonary vessels do not offer a sufficient entry length for the flow to develop. Finally, 1D models cannot reveal the dynamics of secondary flows or regional mapping of certain continuum metrics (e.g., WSS), rendering them inadequate for some clinical applications. 3D CFD models for large arteries are computationally more expensive and labor intensive. The ones currently available for the pulmonary circulation neglect vessel distensibility, resulting in an overestimation of WSS and absence of wave affects. Given the computational platforms available today, 3D CFD models coupled to complex boundary conditions may be feasible to implement in a research laboratory but impractical in a clinical setting. Deciding on an appropriate model for clinical application should be based on the patient-specific data available and the accuracy of the estimates required for effective clinical decision making.
2.6. Fluid-Structure-Interaction Models.
The rigid wall assumption made in CFD analysis has been shown to overestimate the regional shear stress [105]. Moreover, as a result of neglecting vessel compliance, all the energy of the pulse pressure is transferred to the distal vessels [18,96] and the reactive component of impedance in the flow dynamics is neglected. CFD analysis does not allow one to investigate the influence of compliance on the local hemodynamics or RV load and will not reveal the true mechanical stress experienced by the vessel. One strategy for overcoming the rigid vessel wall assumption made in CFD is through FSI modeling. This analysis is capable of simulating regional secondary flows without neglecting the coupling between the fluid (blood) and solid (arterial wall) domains [96,106]. It requires knowledge of the vessel's mechanical properties and is more computationally expensive than CFD [5]. Fluid-structure coupling in 3D hemodynamic simulations has generally been achieved by separately solving for the fluid and solid domains through mutual stresses calculated at their interfaces [96] or by numerically implementing vessel deformation equations into the boundary condition of the fluid domain [106].
Canine aorta studies suggest that arteries behave mostly as anisotropic linearly elastic materials within the physiological range of aortic pressures [107]. Nevertheless, this has not been confirmed in porcine aorta testing [108] and might significantly change for vessels that have undergone remodeling, where collagen engagement could occur at peak systole [14]. Destructive planar biaxial tensile testing of pulmonary vascular tissue can be performed to develop anisotropic constitutive equations [109,110]. Material equations have been correlated with extracellular matrix load-bearing protein content, which could be used to investigate disease progression [111,112]. Recently, ex vivo, nondestructive extension-inflation testing strategies have emerged for monitoring deformation under physiological inflation pressures [108,113,114]. They encompass true physiological load conditions and can yield more sophisticated microstructurally driven constitutive models that are directly correlated with protein content [112,115]. Incorporating these models into FSI simulations would be invaluable for directly correlating vessel mechanical properties at the protein level to wave propagation phenomena and ultimately ventricular load. FSI models with advanced constitutive material equations can also provide insight into the true mechanical stress of the vessel, which is both the cause and effect of vascular remodeling [15]. Correlated with microstructural properties, in a hypothetical scenario of limitless computational resources, FSI models could offer a complete representation of PH disease progression from collagen synthesis and cell proliferation in response to increased vascular stress to ventricular load.
In FSI analysis, the metric of interest for the solid domain is usually displacement, as it is coupled to the pressure and velocity metrics of the fluid domain [116]. When setting up an FSI simulation, three boundary considerations are necessary: (1) the slip between the fluid and solid domain on the inner surface (also necessary for CFD), (2) the perivascular pressure acting on the outer surface, and (3) the degree of freedom of displacement for nodes within and on the ends of the truncated solid domain. Slip—most computational models assume no slip between the inner surface of the solid domain and the fluid boundary. This is generally considered a safe assumption, but will clearly have an impact on the resulting shear stress estimations [117]. Perivascular pressure—the pressure acting on the outer surface of the vessel is generally considered to be spatially uniform [1,96], and experimentally obtained physiologically accurate pressures are currently unavailable. Therefore, while image-based relative area change (RAC) measurements with concurrent catheter pressure data cannot reveal true vessel constitutive properties or perivascular pressure [16], the resulting compliance would be a product of both and can be used as a first order approximation for FSI models. This technique is somewhat limited considering that it merely reveals strains in the radial direction but can be applied on a patient-specific basis and even for pre/posttreatment assessment. Nodal displacement—current computational schemes are capable of capturing both longitudinal and radial displacements of nodes on the inner/outer surface of the solid domain, which are necessary according to experimental measurements [118]. Nodes on the proximal and distal ends are usually constrained to be fixed [96,105] or occasionally allowed to move in the radial direction [1]. Nevertheless, since some approximation is necessary at these boundaries, it is common practice to apply them as far from the computational domain of interest as possible.
As in CFD, FSI models also require boundary conditions at vessel truncations for the fluid domain. Nonphysiological wave reflections can arise at truncations due to numerical error, which can be minimized by properly coupling the 3D domain to the distal vessel dynamics [119]. In addition to the boundary conditions described in Secs. 2.4 and 2.5, an FSI computational domain allows one to incorporate the distal vasculature as geometric entities directly attached to the truncated outlets [100] (see Fig. 8). Each truncated outlet within the domain is extended by an elastic tube that is connected to a rigid contraction, meant to incorporate the compliance and resistance of the distal vasculature. This technique is as effective for simulating wave dynamics as the structured tree model; however, much like the Windkessel model, input parameters are not anatomically intuitive. Its main advantage is that it requires minimal preprocessing and can be used with any commercially available FSI solver. Because this model essentially requires extending the computational domain, no additional computational resources would be necessary for calculating impedance-based boundary conditions.
2.7. Flow Metrics of Interest and Their Significance.
Multiple metrics can be used to quantify the computational hemodynamics in the pulmonary circulation. For constant flow rate simulations, regional stress distributions can be critical parameters of interest but are highly dependent on model setup and segmentation. As described previously, vascular homoeostasis is highly dependent on WSS distribution on the endothelium. In fact, the arterial wall will gradually increase lumen diameter in response to increased flow in an effort to normalize physiological WSS [120]. Endothelial cells have been shown to align themselves with the flow, which corresponds to the local direction of time-averaged stress, and stress metrics are shown to be directly correlated with cell proliferation and apoptosis [121]. For clinical applications, as WSS is generally available through noninvasive means, it would be useful to correlate continuum metrics available from CFD/FSI analysis with current metrics used to assess PH disease progression, currently obtained through invasive and expensive catheterization. Consequently, posttreatment followup comparison with pretreatment hemodynamics metrics is currently impractical. Current metrics used to assess treatment efficacy are as rudimentary as the six-minute walk test, where a patient is asked to walk at maximum pace for six minutes to evaluate his/her exercise performance [122]. This frequently utilized noninvasive metric is easily influenced by unrelated external variables (e.g., arthritis, obesity, age, etc.). Therefore, not only can computationally obtained continuum metrics reveal findings about PH pathology, but they would allow a physician to manage a patient's treatment by offering an invaluable clinical tool for continuously monitoring a patient's response to therapy.
The shear stress tensor within the flow is directly proportional to the velocity gradient, as shown in Eq. (3). In a computational simulation, the stress vector acting on the endothelial surface (the surface mesh element on the domain boundary with surface normal ) is calculated as follows
| (19) |
where is the instantaneous WSS vector calculated for each facet to generate a WSS map at any instant in the cardiac cycle. The mean WSS in the healthy pulmonary arteries has been measured at 1.7 dyn/cm2 [123]. During a single cardiac cycle, the WSS vector on a facet can rotate and even reverse directions. A WSS gradient (WSSG) at any instant within the cardiac cycle is defined by
| (20) |
where m is the time-averaged direction of the WSS vector over the entire cardiac cycle, and n is normal to m and tangent to the facet surface. The oscillatory shear index (OSI) provides insight into the level of shear flow without a definite direction (disturbed flow). ECs respond to shear flow with a clear direction in active maintenance of homeostasis. Typical regulatory mechanisms are disturbed, proinflammatory signaling pathways, which are maintained increasing the likelihood of vascular disease [90,121,124]. Equation (21) can be used to compute a map of OSI for each facet of the vascular surface.
| (21) |
OSI varies between 0 and 1/2, ranging between clearly directional and disturbed flow, respectively. An OSI value of 1/2 corresponds to a zero mean WSS vector.
3. Computational Models of the Pulmonary Vasculature
Cardiopulmonary hemodynamics modeling has been used to gain insight into multiple pathologies such as pulmonary hypertension [5,125] and pneumothorax [126], and as a surgical planning guide for cavopulmonary connections [127]. In this review, we focus on pulmonary hemodynamics modeling in healthy subjects and subjects with PH.
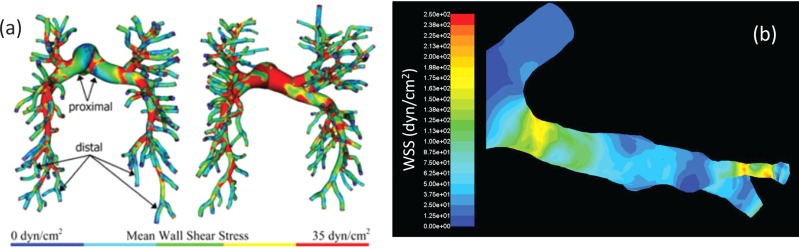
Spilker et al. [104] developed a patient-specific 1D finite element model of the pulmonary vasculature with a structured tree outflow boundary condition [54,56], which was reconstructed from morphometric data. This computational model was compared against a porcine model in which the dimensions of the outflow structured tree were iteratively tuned to an agreeable main PA pressure and flow split. The model was used to show that repairing a stenosis in a patient-specific arterial tree reconstruction did not significantly affect the flow dynamics. This study showed that a 1D numerical model is capable of predicting patient-specific hemodynamics but also yields limited information. The need to iteratively adjust outflow BC parameters for tuning to physiological pressures is a serious limitation because this information is rarely available in a clinical setting. To this end, Tang et al. [40] developed a 3D finite element CFD model of the pulmonary vasculature to examine the impact of exercise on arterial hemodynamics. The arteries were reconstructed based on lumen topology for large vessels and assumed to be circular for smaller vessels. They used a resistance outflow boundary condition to investigate shear stress distributions, OSI, and energy dissipation in six subjects. Resistance values were adjusted for each patient to agree with MRI-measured flow split and total vascular resistances. The study found that exercise increases mean WSS and decreases energy efficiency. OSI did not appear to be heavily influenced in either the small or large vessels. Typical WSS computed by Tang et al. were within the range found using 4D flow data [123]. Patient-specific CFD simulations conducted in our laboratory showed larger WSS in the distal vessels fully reconstructed from the segmented CT images (see Fig. 9). Tang et al. assumed circular cross sections for the small vessels, which prevented this overestimation in WSS.
Fig. 9.
(a) Wall shear stress (WSS) distribution calculated from Tang et al. [40]. (b) Magnification showing nonphysiological stress concentrations arising from uncompensated errors in segmentation using our model, which did not assume cylindrical vessels in the distal arteries but with similar inflow and outflow boundary conditions as used by Tang et al.
To circumvent the limitations of current image reconstruction algorithms, Hunter et al. presented a novel approach to pediatric patient-specific FSI simulations of the main, left, and right PAs [96]. Proximal arteries were segmented from biplane X-ray angiograms at middiastole, based on locating and reconstructing the lumen. The vessels were given a circumferentially uniform wall thickness of 10% of the lumen diameter [128]. The distal vascular resistance was modeled by adding a porous extension to the outlets of the computational domain, with porosity and permeability chosen for an approximately equal flow split. Here, they hypothesized that proximal compliance strongly influenced flow dynamics and that this information is useful for diagnosing and treating PH. The study investigated two cases: In case 1, they investigated pre/postoperative hemodynamics for a patient with a septal defect, which usually increases pulmonary flow and pressure. The outflow boundary conditions remained the same, but the postoperative flow rate and vascular stiffness were decreased. Postoperation dynamics showed a decrease in mean velocity, WSS, and inlet pressure. Simulations showed a complete postoperative pressure recovery and also showed a decrease in distal vascular resistance even though the porosity was unchanged. In case 2, the study investigated reactivity to distal vasodilatation by decreasing exit section permeability and proximal stiffness. The simulations revealed a substantially decreased postoperative inlet pressure and increased vessel distention. With this study, the authors concluded that modeling patient-specific pulmonary hemodynamics did not require labor-intensive reconstruction of the pulmonary arterial tree. Moreover, they suggest that FSI modeling of the proximal large vessels is sufficient for assessing disease progression and treatment options.
In a separate attempt to investigate the hemodynamic impact of vascular stiffness and distal vasodilatation, Su et al. [1] introduced a 2D model based on the following patient-specific information: cardiac output, Young's modulus (approximated from relative area changes), and pulmonary vascular resistance, along with other input parameters (such as PA diameter, wall thickness, and inlet profile) that can be adopted from the literature. The model was an axisymmetric lumen, bounded by an elastic vessel wall, with a pure resistance outflow boundary condition and a waveform at the inlet. For validation, the first harmonic of the impedance modulus and mean PA pressure were compared with patient-measured data. A reasonable fit was found between measured and simulated mean PA pressures, but impedance was less accurate. The model was used to show how flow dynamics are affected by disease progression and vascular stiffness. One interesting find was that disease progression to a point of vessel distention that activates collagen engagement further acts to increase mean and peak pressure and WSS. In this case, decreasing distal resistance through vasodilation does appear to decrease pressure but substantially increases WSS. Additional investigations are needed to further our understanding of how FSI model simplifications impact the reliability of the modeling outcomes.
4. Future Work and Recommendations
The main priority for future work in computational hemodynamics modeling of the pulmonary circulation should be to determine the impact of limited image spatial resolution and segmentation algorithms on our ability to model pulmonary flow dynamics accurately. The role of computational modeling in the clinic is envisioned as an alternate resource for assessing hemodynamic variables noninvasively. Therefore, outflow boundary conditions used in the model should not require tuning based on physiological measurements that must be obtained invasively. Furthermore, as proximal stiffness is a key player in pulmonary arterial hypertension progression, computational models should incorporate the role of stiffness/compliance in vascular–ventricular coupling to investigate how pulmonary arteries respond to hypertensive conditions. To this end, localized WSS distributions may predict endothelial phenotype, which in turn might correlate with response to specific classes of therapy and/or rates of disease progression. If clinical studies demonstrate such correlations, the logical next step would be to use patient-specific hemodynamic models for decision making of individualized therapies, frequency of subsequent hemodynamic assessments, and the potential need for lung transplant surgery. Such studies that evaluate the role of computational hemodynamics in the clinic are feasible as current clinical care protocols for patients with PAH frequently include contrast-enhanced chest CT for customary followups.
Acknowledgment
The authors would like to acknowledge research funding from National Institutes of Health (NIH) award 1P01HL103455-01, the University of Pittsburgh, the University of Texas at San Antonio's Department of Biomedical Engineering, and The University of Texas System Board of Regents' Science and Technology Acquisition and Retention (STARS) program. The use of Ansys Fluent software is gratefully facilitated through an academic agreement with Ansys, Inc. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Contributor Information
V. O. Kheyfets, Department of Biomedical Engineering, The University of Texas at San Antonio, AET 1.360, One UTSA Circle, San Antonio, TX 78249
W. O'Dell, Department of Radiation Oncology, University of Florida, Shands Cancer Center, P.O. Box 100385, 2033 Mowry Road, Gainesville, FL 32610
T. Smith, Western Allegheny Health System, Allegheny General Hospital, Gerald McGinnis Cardiovascular Institute, 320 East North Avenue, Pittsburgh, PA 15212
J. J. Reilly, Department of Medicine, The University of Pittsburgh, 1218 Scaife Hall, 3550 Terrace Street, Pittsburgh, PA 15261
E. A. Finol, Department of Biomedical Engineering, The University of Texas at San Antonio, AET 1.360, One UTSA Circle, San Antonio, TX 78249, e-mail: ender.finol@utsa.edu.
References
- [1]. Su, Z. , Hunter, K. S. , and Shandas, R. , 2012, “Impact of Pulmonary Vascular Stiffness and Vasodilator Treatment in Pediatric Pulmonary Hypertension: 21 Patient-Specific Fluid-Structure Interaction Studies,” Comput. Meth. Prog. Biomed., 108(2), pp. 617–628. 10.1016/j.cmpb.2011.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. De Leval, M. R. , Dubini, G. , Migliavacca, F. , Jalali, H. , Camporini, G. , Redington, A. , and Pietrabissa, R. , 1996, “Use of Computational Fluid Dynamics in the Design of Surgical Procedures: Application to the Study of Competitive Flows in Cavopulmonary Connections,” J. Thorac. Cardiovasc. Surg., 111(3), pp. 502–513. 10.1016/S0022-5223(96)70302-1 [DOI] [PubMed] [Google Scholar]
- [3]. Taylor, C. A. , and Steinman, D. A. , 2010, “Image-Based Modeling of Blood Flow and Vessel Wall Dynamics: Applications, Methods and Future Directions,” Sixth International Bio-Fluid Mechanics Symposium and Workshop, March 28–30, 2008 Pasadena, CA, (Ann. Biomed. Eng., 38(3), pp. 1188–1203). 10.1007/s10439-010-9901-0 [DOI] [PubMed] [Google Scholar]
- [4]. Taylor, C. A. , and Figueroa, C. A. , 2009, “Patient-Specific Modeling of Cardiovascular Mechanics,” Ann. Rev. Biomed. Eng., 11, pp. 109–134. 10.1146/annurev.bioeng.10.061807.160521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Hunter, K. S. , Feinstein, J. A. , Ivy, D. D. , and Shandas, R. , 2010, “Computational Simulation of the Pulmonary Arteries and Its Role in the Study of Pediatric Pulmonary Hypertension,” Prog. Pediatr. Cardiol., 30(1–2), pp. 63–69. 10.1016/j.ppedcard.2010.09.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Khamdaeng, T. , Luo, J. , Vappou, J. , Terdtoon, P. , and Konofagou, E. E. , 2012, “Arterial Stiffness Identification of the Human Carotid Artery Using the Stress-Strain Relationship In Vivo ,” Ultrasonics, 52(3), pp. 402–411. 10.1016/j.ultras.2011.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Resnick, N. , Yahav, H. , Shay-Salit, A. , Shushy, M. , Schubert, S. , Zilberman, L. C. , and Wofovitz, E. , 2003, “Fluid Shear Stress and the Vascular Endothelium: For Better and for Worse,” Prog. Biophys. Mol. Biol., 81(3), pp. 177–199. 10.1016/S0079-6107(02)00052-4 [DOI] [PubMed] [Google Scholar]
- [8]. Ando, J. , and Yamamoto, K. , 2011, “Effects of Shear Stress and Stretch on Endothelial Function,” Antioxid. Redox. Signal., 15(5), pp. 1389–1403. 10.1089/ars.2010.3361 [DOI] [PubMed] [Google Scholar]
- [9]. Depaola, N. , Gimbrone, M. A. Jr. , Davies, P. F. , and Dewey, C. F., Jr. , 1992, “Vascular Endothelium Responds to Fluid Shear Stress Gradients,” Arterioscler. Thromb., 12(11), pp. 1254–1257. 10.1161/01.ATV.12.11.1254 [DOI] [PubMed] [Google Scholar]
- [10]. Kakisis, J. D. , Liapis, C. D. , and Sumpio, B. E. , 2004, “Effects of Cyclic Strain on Vascular Cells,” Endothelium, 11(1), pp. 17–28. 10.1080/10623320490432452 [DOI] [PubMed] [Google Scholar]
- [11]. Toda, M. , Yamamoto, K. , Shimizu, N. , Obi, S. , Kumagaya, S. , Igarashi, T. , Kamiya, A. , and Ando, J. , 2008, “Differential Gene Responses in Endothelial Cells Exposed to a Combination of Shear Stress and Cyclic Stretch,” J. Biotechnol., 133(2), pp. 239–244. 10.1016/j.jbiotec.2007.08.009 [DOI] [PubMed] [Google Scholar]
- [12]. Haga, M. , Chen, A. , Gortler, D. , Dardik, A. , and Sumpio, B. E. , 2003, “Shear Stress and Cyclic Strain May Suppress Apoptosis in Endothelial Cells by Different Pathways,” Endothelium, 10(3), pp. 149–157. 10.1080/713715223 [DOI] [PubMed] [Google Scholar]
- [13]. Rabinovitch, M. , 2008, “Molecular Pathogenesis of Pulmonary Arterial Hypertension,” J. Clin. Invest., 118(7), pp. 2372–2379. 10.1172/JCI33452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Tian, L. , Lammers, S. R. , Kao, P. H. , Albietz, J. A. , Stenmark, K. R. , Qi, H. J. , Shandas, R. , and Hunter, K. S. , 2012, “Impact of Residual Stretch and Remodeling on Collagen Engagement in Healthy and Pulmonary Hypertensive Calf Pulmonary Arteries at Physiological Pressures,” Ann. Biomed. Eng., 40(7), pp. 1419–1433. 10.1007/s10439-012-0509-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Humphrey, J. D. , 2008, “Mechanisms of Arterial Remodeling in Hypertension: Coupled Roles of Wall Shear and Intramural Stress,” Hypertension, 52(2), pp. 195–200. 10.1161/HYPERTENSIONAHA.107.103440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Wang, Z. , and Chesler, N. C. , 2011, “Pulmonary Vascular Wall Stiffness: An Important Contributor to the Increased Right Ventricular Afterload With Pulmonary Hypertension,” Pulm. Circ., 1(2), pp. 212–223. 10.4103/2045-8932.83453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Fourie, P. R. , Coetzee, A. R. , and Bolliger, C. T. , 1992, “Pulmonary Artery Compliance: Its Role in Right Ventricular-Arterial Coupling,” Cardiovasc. Res., 26(9), pp. 839–844. 10.1093/cvr/26.9.839 [DOI] [PubMed] [Google Scholar]
- [18]. Scott-Drechsel, D. , Su, Z. , Hunter, K. , Li, M. , Shandas, R. , and Tan, W. , 2012, “A New Flow Co-Culture System for Studying Mechanobiology Effects of Pulse Flow Waves,” Cytotechnology, 64(6), pp. 649–666. 10.1007/s10616-012-9445-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Huang, W. , Yen, R. T. , Mclaurine, M. , and Bledsoe, G. , 1996, “Morphometry of the Human Pulmonary Vasculature,” J. Appl. Physiol., 81(5), pp. 2123–2133. [DOI] [PubMed] [Google Scholar]
- [20]. Huang, W. , Zhou, Q. , Gao, J. , and Yen, R. T. , 2011, “A Continuum Model for Pressure-Flow Relationship in Human Pulmonary Circulation,” Mol. Cell Biomech., 8(2), pp. 105–122. 10.3970/mcb.2011.008.105 [DOI] [PubMed] [Google Scholar]
- [21]. Nauser, T. D. , and Stites, S. W. , 2001, “Diagnosis and Treatment of Pulmonary Hypertension,” Am. Fam. Physician, 63(9), pp. 1789–1798. [PubMed] [Google Scholar]
- [22]. Hatano, S. , and Strasser, T. , 1975, Primary Pulmonary Hypertension: Report on a WHO Meeting, Geneva, 15–17 October 1973, World Health Organization, Geneva. [Google Scholar]
- [23]. Ap, F. , 2001, “Clinical Classification of Pulmonary Hypertension,” Clin. Chest Med., 22(3), pp. 385–391. 10.1016/S0272-5231(05)70278-1 [DOI] [PubMed] [Google Scholar]
- [24]. Simonneau, G. , Robbins, I. M. , Beghetti, M. , Channick, R. N. , Delcroix, M. , Denton, C. P. , Elliott, C. G. , Gaine, S. P. , Gladwin, M. T. , Jing, Z. C. , Krowka, M. J. , Langleben, D. , Nakanishi, N. , and Souza, R. , 2009, “Updated Clinical Classification of Pulmonary Hypertension,” J. Am. Coll. Cardiol., 54(1 Suppl), pp. S43–S54. 10.1016/j.jacc.2009.04.012 [DOI] [PubMed] [Google Scholar]
- [25]. Badesch, D. B. , Champion, H. C. , Sanchez, M. A. , Hoeper, M. M. , Loyd, J. E. , Manes, A. , Mcgoon, M. , Naeije, R. , Olschewski, H. , Oudiz, R. J. , and Torbicki, A. , 2009, “Diagnosis and Assessment of Pulmonary Arterial Hypertension,” J. Am. Coll. Cardiol., 54(1 Suppl), pp. S55–S66. 10.1016/j.jacc.2009.04.011 [DOI] [PubMed] [Google Scholar]
- [26]. Mclaughlin, V. V. , Archer, S. L. , Badesch, D. B. , Barst, R. J. , Farber, H. W. , Lindner, J. R. , Mathier, M. A. , Mcgoon, M. D. , Park, M. H. , Rosenson, R. S. , Rubin, L. J. , Tapson, V. F. , Varga, J. , 2009, “ACCF/AHA 2009 Expert Consensus Document on Pulmonary Hypertension: A Report of the American College of Cardiology Foundation Task Force on Expert Consensus Documents and the American Heart Association Developed in Collaboration with the American College of Chest Physicians; American Thoracic Society, Inc.; and the Pulmonary Hypertension Association,” J. Am. Coll. Cardiol., 53(17), pp. 1573–1619. 10.1016/j.jacc.2009.01.004 [DOI] [PubMed] [Google Scholar]
- [27]. Rubin, L. J. , 2002, “Therapy of Pulmonary Hypertension: The Evolution From Vasodilators to Antiproliferative Agents,” Am. J. Respir. Crit. Care Med., 166(10), pp. 1308–1309. 10.1164/rccm.2208008 [DOI] [PubMed] [Google Scholar]
- [28]. Sitbon, O. , Humbert, M. , Jais, X. , Ioos, V. , Hamid, A. M. , Provencher, S. , Garcia, G. , Parent, F. , Herve, P. , and Simonneau, G. , 2005, “Long-Term Response to Calcium Channel Blockers in Idiopathic Pulmonary Arterial Hypertension,” Circulation, 111(23), pp. 3105–3111. 10.1161/CIRCULATIONAHA.104.488486 [DOI] [PubMed] [Google Scholar]
- [29]. Mclaughlin, V. V. , 2002, “Survival in Primary Pulmonary Hypertension: The Impact of Epoprostenol Therapy,” Circulation, 106(12), pp. 1477–1482. 10.1161/01.CIR.0000029100.82385.58 [DOI] [PubMed] [Google Scholar]
- [30]. Galie, N. , Ghofrani, H. A. , Torbicki, A. , Barst, R. J. , Rubin, L. J. , Badesch, D. , Fleming, T. , Parpia, T. , Burgess, G. , Branzi, A. , Grimminger, F. , Kurzyna, M. , and Simonneau, G. , 2005, “Sildenafil Use in Pulmonary Arterial Hypertension Study Sildenafil Citrate Therapy for Pulmonary Arterial Hypertension,” N. Engl. J. Med., 353(20), pp. 2148–2157. 10.1056/NEJMoa050010 [DOI] [PubMed] [Google Scholar]
- [31]. Agarwal, R. , and Gomberg-Maitland, M. , 2011, “Current Therapeutics and Practical Management Strategies for Pulmonary Arterial Hypertension,” Am. Heart J., 162(2), pp. 201–213. 10.1016/j.ahj.2011.05.012 [DOI] [PubMed] [Google Scholar]
- [32]. Clapp, L. H. , Finney, P. , Turcato, S. , Tran, S. , Rubin, L. J. , and Tinker, A. , 2002, “Differential Effects of Stable Prostacyclin Analogs on Smooth Muscle Proliferation and Cyclic Amp Generation in Human Pulmonary Artery,” Am. J. Respir. Cell Mol. Biol., 26(2), pp. 194–201. 10.1165/ajrcmb.26.2.4695 [DOI] [PubMed] [Google Scholar]
- [33]. Hoendermis, E. S. , 2011, “Pulmonary Arterial Hypertension: An Update,” Neth. Heart J., 19(12), pp. 514–522. 10.1007/s12471-011-0222-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Benza, R. L. , Miller, D. P. , Gomberg-Maitland, M. , Frantz, R. P. , Foreman, A. J. , Coffey, C. S. , Frost, A. , Barst, R. J. , Badesch, D. B. , Elliott, C. G. , Liou, T. G. , and Mcgoon, M. D. , 2010, “Predicting Survival in Pulmonary Arterial Hypertension: Insights From the Registry to Evaluate Early and Long-Term Pulmonary Arterial Hypertension Disease Management (Reveal),” Circulation, 122(2), pp. 164–172. 10.1161/CIRCULATIONAHA.109.898122 [DOI] [PubMed] [Google Scholar]
- [35]. Lee, W. T. , Ling, Y. , Pepke-Zeba, J. , Peacock, A. J. , and Johnson, M. K. , 2012, “Predicting Survival in Pulmonary Arterial Hypertension in the UK,” Eur Respir J., 40(3), pp. 604–611. 10.1183/09031936.00196611 [DOI] [PubMed] [Google Scholar]
- [36]. Agarwal, R. , and Gomberg-Maitland, M. , 2012, “Prognostication in Pulmonary Arterial Hypertension,” Heart Fail. Clin., 8(3), pp. 373–383. 10.1016/j.hfc.2012.04.011 [DOI] [PubMed] [Google Scholar]
- [37]. Galie, N. , Palazzini, M. , and Manes, A. , 2010, “Pulmonary Arterial Hypertension: From the Kingdom of the Near-Dead to Multiple Clinical Trial Meta-Analyses,” Eur. Heart J., 31(17), pp. 2080–2086. 10.1093/eurheartj/ehq152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. O'Callaghan, D. S. , and Humbert, M. , 2012, “A Critical Analysis of Survival in Pulmonary Arterial Hypertension,” Eur. Respir. Rev., 21(125), pp. 218–222. 10.1183/09059180.00003512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Mcgoon, M. , Gutterman, D. , Steen, V. , Barst, R. , Mccrory, D. C. , Fortin, T. A. , and Loyd, J. E. , 2004, “Screening, Early Detection, and Diagnosis of Pulmonary Arterial Hypertension ACCP Evidence-Based Clinical Practice Guidelines,” Chest, 126, pp. 14S–34S. 10.1378/chest.126.1_suppl.14S [DOI] [PubMed] [Google Scholar]
- [40]. Tang, B. T. , Fonte, T. A. , Chan, F. P. , Tsao, P. S. , Feinstein, J. A. , and Taylor, C. A. , 2011, “Three-Dimensional Hemodynamics in the Human Pulmonary Arteries Under Resting and Exercise Conditions,” Ann. Biomed. Eng., 39(1), pp. 347–358. 10.1007/s10439-010-0124-1 [DOI] [PubMed] [Google Scholar]
- [41]. Rich, S. , D'alonzo, G. E. , Dantzker, D. R. , and Levy, P. S. , 1985, “Magnitude and Implications of Spontaneous Hemodynamic Variability in Primary Pulmonary Hypertension,” Am. J. Cardiol., 55(1), pp. 159–163. 10.1016/0002-9149(85)90319-4 [DOI] [PubMed] [Google Scholar]
- [42]. Mcgoon, M. D. , and Kane, G. C. , 2009, “Pulmonary Hypertension—Diagnosis and Management,” Mayo Clin. Proc., 84(2), pp. 191–207. 10.4065/84.2.191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43]. Dalen, J. E. , and Bone, R. C. , 1996, “Is It Time to Pull the Pulmonary Artery Catheter?,” JAMA, 276(11), pp. 916–918. 10.1001/jama.1996.03540110070035 [DOI] [PubMed] [Google Scholar]
- [44]. Yock, P. G. , and Popp, R. L. , 1984, “Noninvasive Estimation of Right Ventricular Systolic Pressure by Doppler Ultrasound in Patients With Tricuspid Regurgitation,” Circulation, 70(4), pp. 657–662. 10.1161/01.CIR.70.4.657 [DOI] [PubMed] [Google Scholar]
- [45]. Fakhri, A. A. , Hughes-Doichev, R. A. , Biederman, R. W. , and Murali, S. , 2012, “Imaging in the Evaluation of Pulmonary Artery Hemodynamics and Right Ventricular Structure and Function,” Heart Fail. Clin., 8(3), pp. 353–372. 10.1016/j.hfc.2012.04.004 [DOI] [PubMed] [Google Scholar]
- [46]. Rudski, L. G. , Lai, W. W. , Afilalo, J. , Hua, L. , Handschumacher, M. D. , Chandrasekaran, K. , Solomon, S. D. , Louie, E. K. , and Schiller, N. B. , 2010, “Guidelines for the Echocardiographic Assessment of the Right Heart in Adults: A Report from the American Society of Echocardiography Endorsed by the European Association of Echocardiography, a Registered Branch of the European Society of Cardiology, and the Canadian Society of Echocardiography,” J. Am. Soc. Echocardiogr., 23(7), pp. 685–713. 10.1016/j.echo.2010.05.010 [DOI] [PubMed] [Google Scholar]
- [47]. Fisher, M. R. , Forfia, P. R. , Chamera, E. , Housten-Harris, T. , Champion, H. C. , Girgis, R. E. , Corretti, M. C. , and Hassoun, P. M. , 2009, “Accuracy of Doppler Echocardiography in the Hemodynamic Assessment of Pulmonary Hypertension,” Am. J. Respir. Crit. Care Med., 179(7), pp. 615–621. 10.1164/rccm.200811-1691OC [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Roberts, J. D. , and Forfia, P. R. , 2011, “Diagnosis and Assessment of Pulmonary Vascular Disease by Doppler Echocardiography,” Pulm. Circ., 1(2), pp. 160–181. 10.4103/2045-8932.83446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. López-Candales, A. , Rajagopalan, N. , Saxena, N. , Gulyasy, B. , Edelman, K. , and Bazaz, R. , 2006, “Right Ventricular Systolic Function Is Not the Sole Determinant of Tricuspid Annular Motion.,” Am. J. Cardiol., 98(7), pp. 973–977. 10.1016/j.amjcard.2006.04.041 [DOI] [PubMed] [Google Scholar]
- [50]. Kjaergaard, J. , Iversen, K. K. , Akkan, D. , Møller, J. E. , Køber, L. V. , Torp-Pedersen, C. , and Hassager, C. , 2009, “Predictors of Right Ventricular Function as Measured by Tricuspid Annular Plane Systolic Excursion in Heart Failure,” Cardiovasc. Ultra., 7(51), pp. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Formaggia, L. , Lamponi, D. , and Quarteroni, A. , 2003, “One-Dimensional Models for Blood Flow in Arteries,” J. Eng. Math., 47(3), pp. 251–276. 10.1023/B:ENGI.0000007980.01347.29 [DOI] [Google Scholar]
- [52]. Olufsen, M. S. , Peskin, C. S. , Kim, W. Y. , Pedersen, E. M. , Nadim, A. , and Larsen, J. , 2000, “Numerical Simulation and Experimental Validation of Blood Flow in Arteries With Structured-Tree Outflow Conditions,” Ann. Biomed. Eng., 28(11), pp. 1281–1299. 10.1114/1.1326031 [DOI] [PubMed] [Google Scholar]
- [53]. Olufsen, M. S. , and Nadim, A. , 2004, “On Deriving Lumped Models for Blood Flow and Pressure in the Systemic Arteries,” Math. Biosci. Eng., 1(1), pp. 61–80. 10.3934/mbe.2004.1.61 [DOI] [PubMed] [Google Scholar]
- [54]. Olufsen, M. S. , 2000, “A One-Dimensional Fluid Dynamic Model of the Systemic Arteries,” Stud. Health Technol. Info., 71, pp. 79–98. 10.3233/978-1-60750-915-8-79 [DOI] [PubMed] [Google Scholar]
- [55]. Johnson, D. A. , Rose, W. C. , Edwards, J. W. , Naik, U. P. , and Beris, A. N. , 2011, “Application of 1D Blood Flow Models of the Human Arterial Network to Differential Pressure Predictions,” J. Biomech., 44(5), pp. 869–876. 10.1016/j.jbiomech.2010.12.003 [DOI] [PubMed] [Google Scholar]
- [56]. Olufsen, M. S. , 1999, “Structured Tree Outflow Condition for Blood Flow in Larger Systemic Arteries,” Am. J. Physiol., 276(1), pp. H257–H268. [DOI] [PubMed] [Google Scholar]
- [57]. Vignon-Clementel, I. E. , Marsden, A. L. , and Feinstein, J. A. , 2010, “A Primer on Computational Simulation in Congenital Heart Disease for the Clinician,” Prog. Ped. Cardiol., 30(1–2), pp. 3–13. 10.1016/j.ppedcard.2010.09.002 [DOI] [PubMed] [Google Scholar]
- [58]. Box, F. M. , Van Der Geest, R. J. , Rutten, M. C. , and Reiber, J. H. , 2005, “The Influence of Flow, Vessel Diameter, and Non-Newtonian Blood Viscosity on the Wall Shear Stress in a Carotid Bifurcation Model for Unsteady Flow,” Invest. Radiol., 40(5), pp. 277–294. 10.1097/01.rli.0000160550.95547.22 [DOI] [PubMed] [Google Scholar]
- [59]. Xiang, J. , Tremmel, M. , Kolega, J. , Levy, E. I. , Natarajan, S. K. , and Meng, H. , 2011, “Newtonian Viscosity Model Could Overestimate Wall Shear Stress in Intracranial Aneurysm Domes and Underestimate Rupture Risk,” J. Neurointerv. Surg., 4(5), pp. 351–357. 10.1136/neurintsurg-2011-010089 [DOI] [PubMed] [Google Scholar]
- [60]. Tawhai, M. , Clark, A. , Donovan, G. , and Burrowes, K. , 2011, “Computational Modeling of Airway and Pulmonary Vascular Structure and Function: Development of a Lung Physiome,” Crit. Rev. Biomed. Eng., 39(4), pp. 319–336. 10.1615/CritRevBiomedEng.v39.i4.50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61]. Boyd, J. , Buick, J. M. , and Green, S. , 2007, “Analysis of the Casson and Carreau–Yasuda Non-Newtonian Blood Models in Steady and Oscillatory Flows Using the Lattice Boltzmann Method,” Phys. Fluid., 19(9), pp. 093103. 10.1063/1.2772250 [DOI] [Google Scholar]
- [62]. Abraham, F. , Behr, M. , and Heinkenschloss, M. , 2005, “Shape Optimization in Steady Blood Flow: A Numerical Study of Non-Newtonian Effects,” Comput. Meth. Biomech. Biomed. Eng., 8(2), pp. 127–137. 10.1080/10255840500180799 [DOI] [PubMed] [Google Scholar]
- [63]. Merrill, E. W. , 1969, “Rheology of Blood,” Physiol. Rev., 49(4), pp. 863–888. Available at: http://web.mit.edu/andrew3/Public/Papers/1969/Merrill/1969_PhYSIOLOCIICAL%20REVIEWEs_Rheology%20of%20Blood_Merrill.pdf [DOI] [PubMed] [Google Scholar]
- [64]. O'Dell, W. G. , 2012, “Automatic Segmentation of Tumor-Laden Lung Volumes From the LIDC Database,” SPIE, 8315(1), p. 831531. 10.1117/12.911379 [DOI] [Google Scholar]
- [65]. Buelow, T. , Wiemker, R. , Blaffert, T. , Lorenz, C. , and Renisch, S. , 2005, “Automatic Extraction of the Pulmonary Artery Tree From Multi-Slice CT Data,” Medical Imaging 2005: Physiology, Function, and Structure from Medical Images, Proceedings of the SPIE, pp. 730–740. [Google Scholar]
- [66]. Shikata, H. , Mclennan, G. , Hoffman, E. A. , and Sonka, M. , 2009, “Segmentation of Pulmonary Vascular Trees From Thoracic 3D CT Images,” J. Biomed. Imag., 2009, pp. 1–11. 10.1155/2009/636240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67]. Kaftan, J. N. , Kiraly, A. P. , Bakai, A. , Das, M. , Novak, C. L. , and Aach, T. , 2008, “Fuzzy Pulmonary Vessel Segmentation in Contrast Enhanced CT Data,” Medical Imaging 2008: Image Processing; Proceedings of the SPIE, 6914, p. 69141Q. [Google Scholar]
- [68]. Van Dongen, E. , and Van Ginneken, B. , 2010, “Automatic Segmentation of Pulmonary Vasculature in Thoracic CT Scans With Local Thresholding and Airway Wall Removal,” 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, pp. 668–671. [Google Scholar]
- [69]. Ebrahimdoost, Y. , Qanadli, S. D. , Nikravanshalmani, A. , Ellis, T. J. , Shojaee, Z. F. , and Dehmeshki, J. , 2011, “Automatic Segmentation of Pulmonary Artery (PA) in 3D Pulmonary CTA Images,” 17th International Conference on Digital Signal Processing (DSP), pp. 1–5. [Google Scholar]
- [70]. Burrowes, K. S. , Hunter, P. J. , and Tawhai, M. H. , 2005, “Anatomically Based Finite Element Models of the Human Pulmonary Arterial and Venous Trees Including Supernumerary Vessels,” J. Appl. Physiol., 99(2), pp. 731–738. 10.1152/japplphysiol.01033.2004 [DOI] [PubMed] [Google Scholar]
- [71]. Horsfield, K. , 1978, “Morphometry of the Small Pulmonary Arteries in Man,” Circ. Res., 42(5), pp. 593–597. 10.1161/01.RES.42.5.593 [DOI] [PubMed] [Google Scholar]
- [72]. Tu, J. , Yeoh, G. H. , and Liu, C. , 2008, Computational Fluid Dynamics—a Practical Approach, Elsevier Inc., Burlington, MA. [Google Scholar]
- [73]. Spiegel, M. , 2011, “Patient-Specific Cerebral Vessel Segmentation With Application in Hemodynamic Simulation,” Ph.D. Thesis, Universität Erlangen Nürnberg, Erlangen, Germany.
- [74]. Prakash, S. , and Ethier, C. R. , 2001, “Requirements for Mesh Resolution in 3D Computational Hemodynamics,” ASME J. Biomech. Eng., 123(2), pp. 134–144. 10.1115/1.1351807 [DOI] [PubMed] [Google Scholar]
- [75]. Bove, E. L. , De Leval, M. R. , Migliavacca, F. , Guadagni, G. , and Dubini, G. , 2003, “Computational Fluid Dynamics in the Evaluation of Hemodynamic Performance of Cavopulmonary Connections After the Norwood Procedure for Hypoplastic Left Heart Syndrome,” J. Thorac. Cardiovasc. Surg., 126(4), pp. 1040–1047. 10.1016/S0022-5223(03)00698-6 [DOI] [PubMed] [Google Scholar]
- [76]. Antiga, L. , Ene-Iordache, B. , and Remuzzi, A. , 2003, “Computational Geometry for Patient-Specific Reconstruction and Meshing of Blood Vessels From MR and CT Angiography,” IEEE Trans. Med. Imag., 22(5), pp. 674–684. 10.1109/TMI.2003.812261 [DOI] [PubMed] [Google Scholar]
- [77]. Steinman, D. A. , Hoi, Y. , Fahy, P. , Morris, L. , Walsh, M. T. , Aristokleous, N. , Anayiotos, A. , Papaharilaou, Y. , Arzani, A. , Shadden, S. , Berg, P. , Janiga, G. , Bols, J. , Segers, P. , Bressloff, N. W. , Cibis, M. , Gijsen, F. H. , Cito, S. , Pallarés, J. , Browne, L. D. , Costelloe, J. A. , Lynch, A. G. , Degroote, J. , Vierendeels, J. , Fu, W. , Qiao, A. , Hodis, S. , Kallmes, D. F. , Kalsi, H. , Long, Q. , Kheyfets, V. O. , Finol, E. A. , Kono, K. , Malek, A. M. , Lauric, A. , Menon, P. G. , Pekkan, K. , Moghadam, M. E. , Marsden, A. L. , Oshima, M. , Katagiri, K. , Peiffer, V. , Mohamied, Y. , Sherwin, S. J. , Schaller, J. , Goubergrits, L. , Usera, G. , Mendina, M. , Valen-Sendstad, K. , Habets, D. F. , Xiang, J. , Meng, H. , Yu, Y. , Karniadakis, G. E. , Shaffer, N. , and Loth, F. , 2013, “Variability of CFD Solutions for Pressure and Flow in a Giant Aneurysm: The SBC2012 CFD Challenge,” ASME J. Biomech. Eng., 135(2), p. 021016. 10.1115/1.4023382 [DOI] [PubMed] [Google Scholar]
- [78]. Nielsen, P. M. F. , and Wittek, A. , 2012, Computational Biomechanics for Medicine: Deformation and Flow, Springer, New York. [Google Scholar]
- [79]. Boutsianis, E. , Gupta, S. , Boomsma, K. , and Poulikakos, D. , 2008, “Boundary Conditions by Schwarz-Christoffel Mapping in Anatomically Accurate Hemodynamics,” Ann. Biomed. Eng., 36(12), pp. 2068–2084. 10.1007/s10439-008-9571-3 [DOI] [PubMed] [Google Scholar]
- [80]. Ponzini, R. , Lemma, M. , Morbiducci, U. , Montevecchi, F. M. , and Redaelli, A. , 2008, “Doppler Derived Quantitative Flow Estimate in Coronary Artery Bypass Graft: A Computational Multiscale Model for the Evaluation of the Current Clinical Procedure,” Med. Eng. Phys., 30(7), pp. 809–816. 10.1016/j.medengphy.2007.09.004 [DOI] [PubMed] [Google Scholar]
- [81]. Pekkan, K. , Dasi, L. P. , De Zelicourt, D. , Sundareswaran, K. S. , Fogel, M. A. , Kanter, K. R. , and Yoganathan, A. P. , 2009, “Hemodynamic Performance of Stage-2 Univentricular Reconstruction: Glenn Vs. Hemi-Fontan Templates,” Ann. Biomed. Eng., 37(1), pp. 50–63. 10.1007/s10439-008-9591-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82]. Antiga, L. , Piccinelli, M. , Botti, L. , Ene-Iordache, B. , Remuzzi, A. , and Steinman, D. A. , 2008, “An Image-Based Modeling Framework for Patient-Specific Computational Hemodynamics,” Med. Biol. Eng. Comput., 46(11), pp. 1097–1112. 10.1007/s11517-008-0420-1 [DOI] [PubMed] [Google Scholar]
- [83]. Kauczor, H. U. , Ley-Zaporozhan, J. , and Ley, S. , 2009, “Imaging of Pulmonary Pathologies: Focus on Magnetic Resonance Imaging,” Proc. Am. Thorac. Soc., 6(5), pp. 458–463. 10.1513/pats.200901-002AW [DOI] [PubMed] [Google Scholar]
- [84]. Zamir, M. , 2000, The Physics of Pulsatile Flow, Springer-Verlag, New York. [Google Scholar]
- [85]. Womersley, J. R. , 1955, “Method for the Calculation of Velocity, Rate of Flow and Viscous Drag in Arteries When the Pressure Gradient Is Known,” J. Physiol., 127(3), pp. 553–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86]. Morgan, V. L. , Roselli, R. J. , and Lorenz, C. H. , 1998, “Normal Three-Dimensional Pulmonary Artery Flow Determined by Phase Contrast Magnetic Resonance Imaging,” Ann. Biomed. Eng., 26(4), pp. 557–566. 10.1114/1.125 [DOI] [PubMed] [Google Scholar]
- [87]. Miyasaka, K. , and Takata, M. , 1993, “Flow Velocity Profile of the Pulmonary Artery Measured by the Continuous Cardiac Output Monitoring Catheter,” Can. J. Anaesth., 40(2), pp. 183–187. 10.1007/BF03011318 [DOI] [PubMed] [Google Scholar]
- [88]. Clipp, R. B. , and Steele, B. N. , 2009, “Impedance Boundary Conditions for the Pulmonary Vasculature Including the Effects of Geometry, Compliance, and Respiration,” IEEE Trans. Biomed. Eng., 56(3), pp. 862–870. 10.1109/TBME.2008.2010133 [DOI] [PubMed] [Google Scholar]
- [89]. Grinberg, L. , and Karniadakis, G. E. , 2008, “Outflow Boundary Conditions for Arterial Networks With Multiple Outlets,” Ann. Biomed. Eng., 36(9), pp. 1496–1514. 10.1007/s10439-008-9527-7 [DOI] [PubMed] [Google Scholar]
- [90]. Morbiducci, U. , Gallo, D. , Massai, D. , Consolo, F. , Ponzini, R. , Antiga, L. , Bignardi, C. , Deriu, M. A. , and Redaelli, A. , 2010, “Outflow Conditions for Image-Based Hemodynamic Models of the Carotid Bifurcation: Implications for Indicators of Abnormal Flow,” ASME J. Biomech. Eng., 132(9), p. 091005. 10.1115/1.4001886 [DOI] [PubMed] [Google Scholar]
- [91]. Vignon-Clementel, I. E. , Figueroa, C. A. , Jansen, K. E. , and Taylor, C. A. , 2006, “Outflow Boundary Conditions for Three-Dimensional Finite Element Modeling of Blood Flow and Pressure in Arteries,” Comput. Meth. Appl. Mech. Eng., 195, pp. 3776–3796. 10.1016/j.cma.2005.04.014 [DOI] [Google Scholar]
- [92]. Botnar, R. , Rappitsch, G. , Scheidegger, M. B. , Liepsch, D. , Perktold, K. , and Boesiger, P. , 2000, “Hemodynamics in the Carotid Artery Bifurcation: A Comparison Between Numerical Simulations and In Vitro MRI Measurements,” J. Biomech., 33(2), pp. 137–144. 10.1016/S0021-9290(99)00164-5 [DOI] [PubMed] [Google Scholar]
- [93]. Ansys, 2011, ANSYS® Academic Research, Release 14.0, Help System, Coupled Field Analysis Guide, ANSYS, Inc, Canonsburg, PA. [Google Scholar]
- [94]. Horsfield, K. , and Woldenberg, M. J. , 1989, “Diameters and Cross-Sectional Areas of Branches in the Human Pulmonary Arterial Tree,” Anat Rec, 223(3), pp. 245–251. 10.1002/ar.1092230302 [DOI] [PubMed] [Google Scholar]
- [95]. Orlando, W. , Shandas, R. , and Degroff, C. , 2006, “Efficiency Differences in Computational Simulations of the Total Cavo-Pulmonary Circulation With and Without Compliant Vessel Walls,” Comput Methods Programs Biomed, 81(3), pp. 220–227. 10.1016/j.cmpb.2005.11.010 [DOI] [PubMed] [Google Scholar]
- [96]. Hunter, K. S. , Lanning, C. J. , Chen, S. Y. , Zhang, Y. , Garg, R. , Ivy, D. D. , and Shandas, R. , 2006, “Simulations of Congenital Septal Defect Closure and Reactivity Testing in Patient-Specific Models of the Pediatric Pulmonary Vasculature: A 3D Numerical Study With Fluid-Structure Interaction,” ASME, J. Biomech. Eng., 128(4), pp. 564–572. 10.1115/1.2206202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97]. Kung, E. , and Taylor, C. , 2011, “Development of a Physical Windkessel Module to Re-Create In Vivo Vascular Flow Impedance for In Vitro Experiments,” Cardiovasc. Eng. Tech., 2(1), pp. 2–14. 10.1007/s13239-010-0030-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98]. Westerhof, N. , Lankhaar, J.-W. , and Westerhof, B. , 2009, “The Arterial Windkessel,” Med. Bio. Eng. Comput., 47(2), pp. 131–141. 10.1007/s11517-008-0359-2 [DOI] [PubMed] [Google Scholar]
- [99]. Vignon-Clementel, I. E. , Figueroa, C. A. , Jansen, K. E. , and Taylor, C. A. , 2010, “Outflow Boundary Conditions for 3D Simulations of Non-Periodic Blood Flow and Pressure Fields in Deformable Arteries,” Comput. Meth. Biomech. Biomed. Eng., 13(5), pp. 625–640. 10.1080/10255840903413565 [DOI] [PubMed] [Google Scholar]
- [100]. Pahlevan, N. M. , Amlani, F. , Hossein Gorji, M. , Hussain, F. , and Gharib, M. , 2011, “A Physiologically Relevant, Simple Outflow Boundary Model for Truncated Vasculature,” Ann. Biomed. Eng., 39(5), pp. 1470–1481. 10.1007/s10439-011-0246-0 [DOI] [PubMed] [Google Scholar]
- [101]. Formaggia, L. , Lamponi, D. , Tuveri, M. , and Veneziani, A. , 2006, “Numerical Modeling of 1D Arterial Networks Coupled With a Lumped Parameters Description of the Heart,” Comput. Meth. Biomech. Biomed. Eng., 9(5), pp. 273–288. 10.1080/10255840600857767 [DOI] [PubMed] [Google Scholar]
- [102]. Van Den Bos, G. C. , Westerhof, N. , and Randall, O. S. , 1982, “Pulse Wave Reflection: Can It Explain the Differences Between Systemic and Pulmonary Pressure and Flow Waves? A Study in Dogs,” Circ. Res., 51(4), pp. 479–485. 10.1161/01.RES.51.4.479 [DOI] [PubMed] [Google Scholar]
- [103]. Steele, B. N. , Olufsen, M. S. , and Taylor, C. A. , 2007, “Fractal Network Model for Simulating Abdominal and Lower Extremity Blood Flow During Resting and Exercise Conditions,” Comput. Meth. Biomech. Biomed. Eng., 10(1), pp. 39–51. 10.1080/10255840601068638 [DOI] [PubMed] [Google Scholar]
- [104]. Spilker, R. L. , Feinstein, J. A. , Parker, D. W. , Reddy, V. M. , and Taylor, C. A. , 2007, “Morphometry-Based Impedance Boundary Conditions for Patient-Specific Modeling of Blood Flow in Pulmonary Arteries,” Ann. Biomed. Eng., 35(4), pp. 546–559. 10.1007/s10439-006-9240-3 [DOI] [PubMed] [Google Scholar]
- [105]. Bazilevs, Y. , Hsu, M. C. , Benson, D. J. , Sankaran, S. , and Marsden, A. L. , 2009, “Computational Fluid–Structure Interaction: Methods and Application to a Total Cavopulmonary Connection,” Comput. Mech., 45(1), pp. 77–89. 10.1007/s00466-009-0419-y [DOI] [Google Scholar]
- [106]. Figueroa, C. A. , Vignon-Clementel, I. E. , Jansen, K. E. , Hughes, T. J. R. , and Taylor, C. A. , 2006, “A Coupled Momentum Method for Modeling Blood Flow in Three-Dimensional Deformable Arteries,” Comput. Meth. Appl. Mech. Eng., 195(41–43), pp. 5685–5706. 10.1016/j.cma.2005.11.011 [DOI] [Google Scholar]
- [107]. Zhou, J. , and Fung, Y. C. , 1997, “The Degree of Nonlinearity and Anisotropy of Blood Vessel Elasticity,” Proc. Natl. Acad. Sci. USA, 94(26), pp. 14255–14260. 10.1073/pnas.94.26.14255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108]. Kim, J. , and Baek, S. , 2011, “Circumferential Variations of Mechanical Behavior of the Porcine Thoracic Aorta During the Inflation Test,” J. Biomech., 44(10), pp. 1941–1947. 10.1016/j.jbiomech.2011.04.022 [DOI] [PubMed] [Google Scholar]
- [109]. Sacks, M. S. , 2000, “Biaxial Mechanical Evaluation of Planar Biological Materials,” J. Elast., 61(1–3), pp. 199–246. 10.1023/A:1010917028671 [DOI] [Google Scholar]
- [110]. Sacks, M. S. , and Sun, W. , 2003, “Multiaxial Mechanical Behavior of Biological Materials,” Ann. Rev. Biomed. Eng., 5, pp. 251–284. 10.1146/annurev.bioeng.5.011303.120714 [DOI] [PubMed] [Google Scholar]
- [111]. Lammers, S. R. , Kao, P. H. , Qi, H. J. , Hunter, K. , Lanning, C. , Albietz, J. , Hofmeister, S. , Mecham, R. , Stenmark, K. R. , and Shandas, R. , 2008, “Changes in the Structure-Function Relationship of Elastin and Its Impact on the Proximal Pulmonary Arterial Mechanics of Hypertensive Calves,” Am. J. Physiol. Heart. Circ. Physiol., 295(4), pp. H1451–H1459. 10.1152/ajpheart.00127.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112]. Sacks, M. S. , 2003, “Incorporation of Experimentally-Derived Fiber Orientation Into a Structural Constitutive Model for Planar Collagenous Tissues,” ASME J. Biomech. Eng., 125(2), pp. 280–287. 10.1115/1.1544508 [DOI] [PubMed] [Google Scholar]
- [113]. Genovese, K. , Lee, Y. U. , and Humphrey, J. D. , 2011, “Novel Optical System for In Vitro Quantification of Full Surface Strain Fields in Small Arteries: II. Correction for Refraction and Illustrative Results,” Comput. Meth. Biomech. Biomed. Eng., 14(3), pp. 227–237. 10.1080/10255842.2010.545824 [DOI] [PubMed] [Google Scholar]
- [114]. Genovese, K. , Lee, Y. U. , and Humphrey, J. D. , 2011, “Novel Optical System for In Vitro Quantification of Full Surface Strain Fields in Small Arteries: I. Theory and Design,” Comput. Meth. Biomech. Biomed. Eng., 14(3), pp. 213–225. 10.1080/10255842.2010.545823 [DOI] [PubMed] [Google Scholar]
- [115]. Kao, P. H. , Lammers, S. R. , Tian, L. , Hunter, K. , Stenmark, K. R. , Shandas, R. , and Qi, H. J. , 2011, “A Microstructurally Driven Model for Pulmonary Artery Tissue,” ASME J. Biomech. Eng., 133(5), p. 051002. 10.1115/1.4002698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116]. Quaini, A. , Canic, S. , Glowinski, R. , Igo, S. , Hartley, C. J. , Zoghbi, W. , and Little, S. , 2012, “Validation of a 3D Computational Fluid–Structure Interaction Model Simulating Flow Through an Elastic Aperture,” J. Biomech., 45(2), pp. 310–318. 10.1016/j.jbiomech.2011.10.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [117]. Zhu, Y. , and Granick, S. , 2002, “Limits of the Hydrodynamic No-Slip Boundary Condition,” Phys. Rev. Lett., 88(10), p. 106102. 10.1103/PhysRevLett.88.106102 [DOI] [PubMed] [Google Scholar]
- [118]. Bukač, M. , Čanić, S. , Glowinski, R. , Tambača, J. , and Quaini, A. , 2013, “Fluid–Structure Interaction in Blood Flow Capturing Non-Zero Longitudinal Structure Displacement,” J. Comput. Phys., 235, pp. 515–541. 10.1016/j.jcp.2012.08.033 [DOI] [Google Scholar]
- [119]. Formaggia, L. , Gerbeau, J. F. , Nobile, F. , and Quarteroni, A. , 2001, “On the Coupling of 3D and 1D Navier–Stokes Equations for Flow Problems in Compliant Vessels,” Comput. Meth. Appl. Mech. Eng., 191(6–7), pp. 561–582. 10.1016/S0045-7825(01)00302-4 [DOI] [Google Scholar]
- [120]. Zarins, C. K. , Zatina, M. A. , Giddens, D. P. , Ku, D. N. , and Glagov, S. , 1987, “Shear Stress Regulation of Artery Lumen Diameter in Experimental Atherogenesis,” J. Vasc. Surg., 5(3), pp. 413–420. 10.1067/mva.1987.avs0050413 [DOI] [PubMed] [Google Scholar]
- [121]. Kleinstreuer, C. , 2006, Biofluid Dynamics—Principles and Selected Applications, CRC Press; Taylor and Francis Group, LLC, Boca Raton, FL. [Google Scholar]
- [122]. Miyamoto, S. , Nagaya, N. , Satoh, T. , Kyotani, S. , Sakamaki, F. , Fujita, M. , Nakanishi, N. , and Miyatake, K. , 2000, “Clinical Correlates and Prognostic Significance of Six-Minute Walk Test in Patients With Primary Pulmonary Hypertension. Comparison With Cardiopulmonary Exercise Testing,” Am. J. Respir. Crit. Care Med., 161(2), pp. 487–492. 10.1164/ajrccm.161.2.9906015 [DOI] [PubMed] [Google Scholar]
- [123]. Sotelo, J. A. , Bachler, P. , Chabert, S. , Hurtado, D. , Irarrazaval, P. , Tejos, C. , and Uribe, S. , 2012, “Normal Values of Wall Shear Stress in the Pulmonary Artery From 4D Flow Data,” J. Cardiovasc. Magn. Reson., 14(1 Suppl), p. W66. 10.1186/1532-429X-14-S1-W66 [DOI] [Google Scholar]
- [124]. Chien, S. , 2008, “Effects of Disturbed Flow on Endothelial Cells,” Ann. Biomed. Eng., 36(4), pp. 554–562. 10.1007/s10439-007-9426-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125]. Hunter, K. S. , Lee, P. F. , Lanning, C. J. , Ivy, D. D. , Kirby, K. S. , Claussen, L. R. , Chan, K. C. , and Shandas, R. , 2008, “Pulmonary Vascular Input Impedance Is a Combined Measure of Pulmonary Vascular Resistance and Stiffness and Predicts Clinical Outcomes Better Than Pulmonary Vascular Resistance Alone in Pediatric Patients With Pulmonary Hypertension,” Am. Heart J., 155(1), pp. 166–174. 10.1016/j.ahj.2007.08.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126]. Christophe, J. J. , Ishikawa, T. , Imai, Y. , Takase, K. , Thiriet, M. , and Yamaguchi, T. , 2012, “Hemodynamics in the Pulmonary Artery of a Patient With Pneumothorax,” Med. Eng. Phys., 34(6), pp. 725–732. 10.1016/j.medengphy.2011.09.016 [DOI] [PubMed] [Google Scholar]
- [127]. De Leval, M. R. , Dubini, G. , Migliavacca, F. , Jalali, H. , Camporini, G. , Redington, A. , and Pietrabissa, R. , 1996, “Use of Computational Fluid Dynamics in the Design of Surgical Procedures: Application to the Study of Competitive Flows in Cavo-Pulmonary Connections,” J. Thorac. Cardiovasc. Surg., 111(3), pp. 502–513. 10.1016/S0022-5223(96)70302-1 [DOI] [PubMed] [Google Scholar]
- [128]. Rodes-Cabau, J. , Domingo, E. , Roman, A. , Majo, J. , Lara, B. , Padilla, F. , Anivarro, I. , Angel, J. , Tardif, J. C. , and Soler-Soler, J. , 2003, “Intravascular Ultrasound of the Elastic Pulmonary Arteries: A New Approach for the Evaluation of Primary Pulmonary Hypertension,” Heart, 89(3), pp. 311–315. 10.1136/heart.89.3.311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129]. Henk, C. B. , Schlechta, B. , Grampp, S. , Gomischek, G. , Klepetko, W. , and Mostbeck, G. H. , 1998, “Pulmonary and Aortic Blood Flow Measurements in Normal Subjects and Patients After Single Lung Transplantation at 0.5 T Using Velocity Encoded Cine MRI,” Chest, 114(3), pp. 771–779. 10.1378/chest.114.3.771 [DOI] [PubMed] [Google Scholar]