The Association of Wall Mechanics and Morphology: A Case Study of Abdominal Aortic Aneurysm Growth

Short abstract

The purpose of this study is to evaluate the potential correlation between peak wall stress (PWS) and abdominal aortic aneurysm (AAA) morphology and how it relates to aneurysm rupture potential. Using in-house segmentation and meshing software, six 3-dimensional (3D) AAA models from a single patient followed for 28 months were generated for finite element analysis. For the AAA wall, both isotropic and anisotropic materials were used, while an isotropic material was used for the intraluminal thrombus (ILT). These models were also used to calculate 36 geometric indices characteristic of the aneurysm morphology. Using least squares regression, seven significant geometric features (p < 0.05) were found to characterize the AAA morphology during the surveillance period. By means of nonlinear regression, PWS estimated with the anisotropic material was found to be highly correlated with three of these features: maximum diameter (r = 0.992, p = 0.002), sac volume (r = 0.989, p = 0.003) and diameter to diameter ratio (r = 0.947, p = 0.033). The correlation of wall mechanics with geometry is nonlinear and reveals that PWS does not increase concomitantly with aneurysm diameter. This suggests that a quantitative characterization of AAA morphology may be advantageous in assessing rupture risk.

Introduction

A localized dilatation of the abdominal aorta is termed an abdominal aortic aneurysm (AAA). The rupture of AAAs continues to be a leading cause of morbidity and mortality in the United States, especially in patients older than 65 years of age. If an AAA ruptures, 50% of the patients will die prior to reaching the hospital. Of those patients that reach the operating room, only 50% will successfully have the aneurysm repaired [1]. In an effort to prevent rupture, patients with known AAA undergo periodic abdominal ultrasound or CT scan surveillance. When the aneurysm grows to a diameter of 5.0–5.5 cm or is shown to expand at a rate greater than 1 cm/yr, elective operative repair is undertaken. While this strategy certainly prevents a number of potentially catastrophic ruptures, AAA rupture can occur at sizes less than 5 cm.

From a biomechanical standpoint, aneurysm rupture occurs when wall stress exceeds wall strength. By using noninvasive techniques, such as finite element analysis (FEA), wall stress can be estimated for patient specific AAA models, which can perhaps more carefully predict the rupture potential of a given aneurysm, regardless of size. FEA is a computational method that can be used to evaluate complicated structures such as aneurysms. To this end, it was reported earlier that AAA peak wall stress provides a better assessment of rupture risk than the commonly used maximum diameter criterion [2]. What has yet to be examined; however, is the relationship between wall stress and AAA geometry during aneurysm growth. Such a finding has the potential for providing individualized predictions of AAA rupture potential during patient surveillance. The purpose of this investigation is to estimate peak wall stress for a case study of one AAA under surveillance and evaluate its potential correlation with geometric features characteristic of the aneurysm's morphology.

Methods

Patient Population.

Our study was conducted on a single patient at Allegheny General Hospital (AGH) in Pittsburgh, PA. The patient is a 60 year-old African-American female with an extensive cardiac history, which included two prior coronary artery bypass grafting procedures. CT scans after 12/03/2004 were performed as a part of routine surveillance for patients with AAA. A total of six CT scans were performed during the three-year surveillance period with the final CT scan showing a contained rupture that promoted emergency endovascular repair of the aneurysm. Table 1 shows the size of the patient's AAA at each follow-up as measured by the staff radiologist or vascular surgeon. This study was subject to Internal Review Board approvals at AGH and Carnegie Mellon University (CMU). No patient consent was necessary since the data was collected during a retrospective review.

Table 1.

Past medical history, follow-up date and maximum aneurysm diameter of the AAA patient under surveillance (CAD = coronary artery disease; CABG X 2 = coronary artery bypass grafting; COPD = chronic obstructive pulmonary disease; A. Fib = atrial fibrillation; Pulm Htn = pulmonary hypertension; CHF = congestive heart failure)

Past medical history	CT scan date	Dmax (cm)a	Dmax (cm)b
CAD	12/03/04	4.5	4.4
CABG X 2	5/12/05	4.8	4.6
COPD	3/20/06	5.0	4.9
A. Fib	9/18/06	5.0	5.0
Pulm Htn	1/29/07	5.1	5.1
CHF	4/12/07	5.1	5.3

^aMaximum diameter estimated by the patient's vascular surgeon using the largest minor axis at an oblique cross-section perpendicular to the vessel centerline.

^bMaximum diameter estimated by our in-house software using the equation outlined in the Appendix at an oblique cross-section perpendicular to the vessel centerline.

Finite Element Analysis.

Using in-house segmentation and meshing software (AAAVASC v.1.0, Carnegie Mellon University [3,9]), six 3D AAA models were generated consisting of the AAA wall and intraluminal thrombus (ILT), and used for FEA simulations. The 3D models featured individual, regional variations of wall thickness based on estimations made from the contrast-enhanced CT images using a previously validated image processing algorithm [3] used by our laboratory for geometry quantification of electively repaired AAAs [4,8]. The AAA wall and ILT were assumed hyperelastic and incompressible materials. Both isotropic [5,12–14] and anisotropic [6] constitutive material models were used to characterize the AAA wall, while the ILT was modeled as an isotropic material [7]. FEA was performed with ADINA 8.6 (Adina R&D Inc., Watertown, MA) for each AAA model with a loading pressure of 120 mmHg applied to the inner surfaces of the ILT and wall. The proximal and distal ends of the AAA were considered fixed to replicate anatomical tethering of the aorta.

Geometry Quantification.

Image segmentation yields three contours to delineate the lumen, outer wall, and inner wall, which includes both the thrombus and lumen regions [3]. Patient specific three-dimensional models of the AAA at each follow-up were constructed from the segmented data and characterized quantitatively by calculating thirty-six indices [4,8,9]. These indices include 1D size, 2D shape, 3D size and shape features, and indices to describe the local variations in aortic wall thickness and curvature along the AAA outer wall surface. All indices are calculated from the segmented CT images with the following exceptions: surface meshes are used to compute three second-order curvature based indices (GAA, MAA, and MLN), two 3D shape indices (IPR and NFI) and two 3D size indices (V and S). The reader is referred to the Appendix for a complete list of indices and the mathematical description used in this feature based approach.

Statistical Analysis.

Least squares regression was applied to fit a trend line to the geometric indices. The t-statistic was computed to determine statistically significant features based on the slope of the trend line. The significant indices from the trend analysis were used to assess the potential correlations between peak wall stress (PWS) for both the isotropic and anisotropic wall material models via quadratic regression.

Results

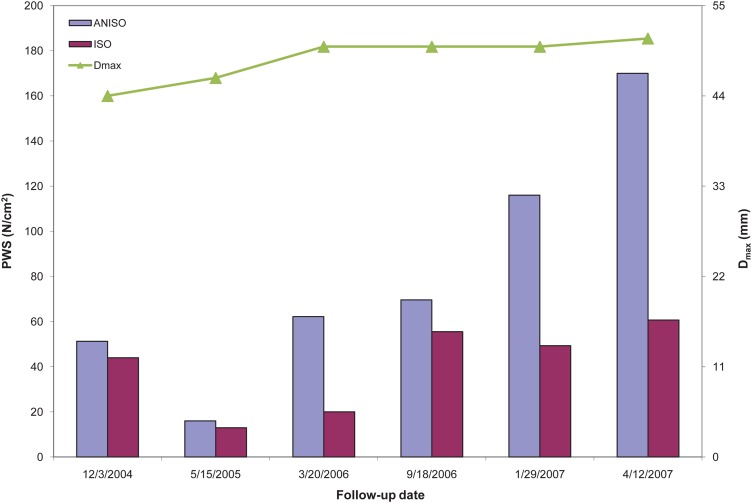
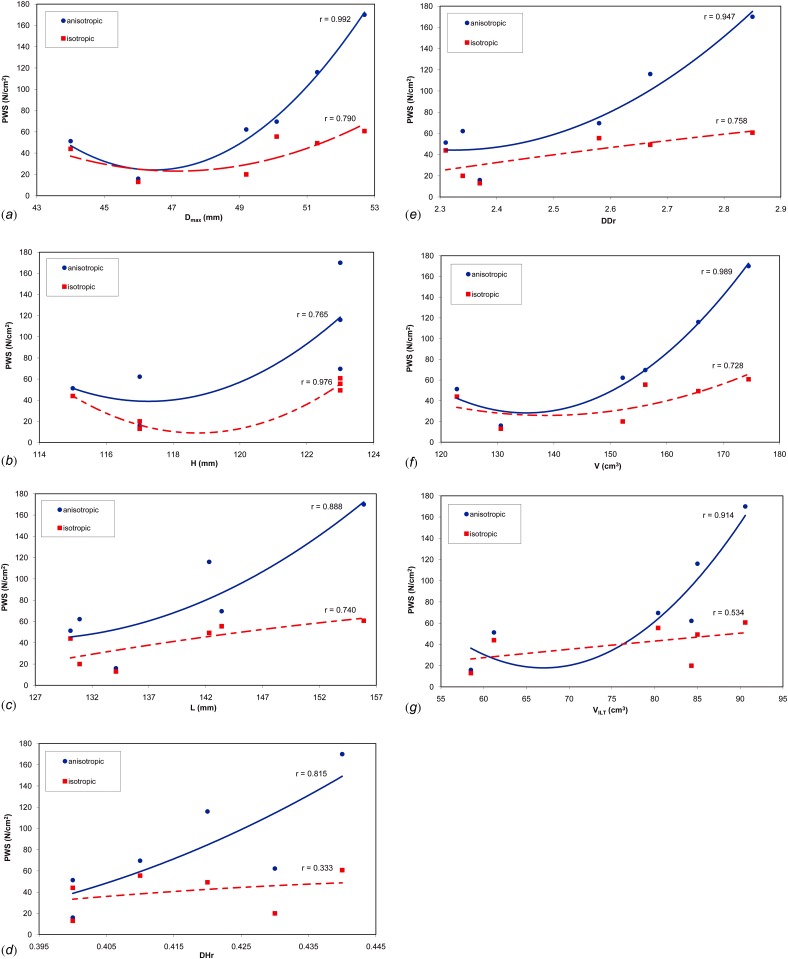
FEA simulations show a trend toward increasing PWS with each subsequent follow-up scan (Fig. 1). The highest peak wall stress is obtained for the last geometry of the surveillance period for both material models. PWS was commonly found either immediately proximal or distal to the ILT on the inner wall surface. Following the application of our laboratory's feature-based approach for geometry quantification [8,9], there were seven significant geometric features characterizing the AAA shape and size during the surveillance period (Table 2). These features only take into account the geometry of the aneurysm over the surveillance period. An assessment of potential correlations of the PWS estimated with the anisotropic material model and these features resulted in the following statistical parameters: maximum diameter (r = 0.992, p = 0.002), sac volume (r = 0.989, p = 0.003), diameter to diameter ratio (r = 0.947, p = 0.033), ILT volume (r = 0.914, p = 0.067), length of AAA (r = 0.888, p = 0.097), diameter to height ratio (r = 0.815, p = 0.194), and height of AAA (r = 0.765, p = 0.267). Similarly for the PWS estimated with the isotropic material model: height (r = 0.976, p = 0.010), maximum diameter (r = 0.790, p = 0.231), diameter to diameter ratio (r = 0.758, p = 0.278), length of AAA (r = 0.740, p = 0.305), volume (r = 0.728, p = 0.322), ILT volume (r = 0.534, p = 0.605), and diameter to height ratio (r = 0.333, p = 0.838). The relationship between PWS and the seven significant geometric features is illustrated in Fig. 2.

Fig. 1.

Time dependency of maximum aneurysm diameter (D_max) and peak wall stress (PWS) for the isotropic and anisotropic wall material models during the surveillance period

Table 2.

Statistically significant geometric indices resulting from the feature based approach for geometry quantification and least squares regression for the six follow-up dates, with their corresponding r and p-values

Geometric index	12/3/2004	5/12/2005	3/20/2006	9/18/2006	1/29/2007	4/12/2007	r	p
Dmax (mm)	44.1	46.0	49.2	50.1	51.3	52.7	0.979	0.001
H (mm)	115.0	117.0	117.0	123.0	123.0	123.0	0.844	0.010
L (mm)	130.1	134.1	130.9	143.4	142.3	155.9	0.815	0.014
DHr	0.40	0.40	0.43	0.41	0.42	0.44	0.723	0.032
DDr	2.3	2.4	2.3	2.6	2.7	2.9	0.899	0.004
V (cm3)	122.8	130.6	152.2	156.2	165.6	174.5	0.964	0.001
VILT (cm3)	61.2	58.5	84.3	80.4	85.0	90.6	0.782	0.019

Fig. 2.

Peak wall stress (PWS) relative to the seven significant geometric indices: (a) maximum aneurysm diameter (D_max); (b) height (H); (c) length (L); (d) maximum diameter to height ratio (DHr); (e) maximum diameter to proximal neck diameter ratio (DDr); (f) aneurysm sac volume (V); (g) intraluminal thrombus volume (V_ILT)

Discussion

The initial AAA diagnosis typically means continued surveillance by abdominal ultrasound or CT imaging until the aneurysm reaches a predetermined size at which time elective repair is recommended, either by open or endovascular surgery. Unfortunately, this process for assessing the aneurysm rupture potential does not take into account other patient specific characteristics of the aneurysm. In contrast, using patient specific geometric features allows for the inclusion of highly individualized indices in this assessment, which may be more relevant to rupture risk than the conventional maximum diameter criterion. In addition, using estimations of peak wall stress for rupture risk assessment yields a representation of the wall mechanics of the aneurysm at a given follow-up date during the surveillance period. The combination of biomechanics and geometry tools may enable us to determine which features of an aneurysm can make it more prone to rupture.

Previous studies have also reported on the role of geometric parameters with regard to PWS. By examining 15 patients with a wide range of AAA size, Georgakarakos et al. [15] recently showed a positive linear correlation between PWS and internal tortuosity. They then applied a linear regression model to obtain an optimal predictive equation for rupture risk. This equation includes both maximum diameter and internal tortuosity for the calculation of PWS. Others have taken a different approach to the use of geometric factors in wall stress analysis by examining a specific region of the aneurysm. Li [16], for example, found that the stress in the shoulder region of an aneurysm could be an indicator of expansion. In this study, he analyzed 44 patients that had 2 CT scans each and found that as the aneurysm diameter increased the stress at the shoulder region decreased. In a study of 39 patients, Giannoglou et al. [17] found that the mean centerline curvature was a significant predictor of PWS and subsequent rupture. AAA rupture below the 5.0 cm threshold is not an uncommon occurrence. As such, Pappu et al. [19] studied 15 patients with small aneurysms (<5.5 cm) and used centerline projection to calculate a tortuosity index. This index was then used to differentiate between aneurysm classes. Due to the association between PWS and tortuosity, they postulate that their tortuosity index could be used as a surrogate for rupture potential.

The present work shows how PWS increases over time within a given aneurysm during a surveillance period in which six abdominal CT exams were performed. This is despite the fact that the maximum AAA diameter changed scarcely over the course of the follow-up. We found that PWS correlates significantly with several geometric indices, namely, maximum diameter (D_max), sac volume (V), and maximum diameter to proximal neck diameter ratio (DDr) for the wall anisotropic material model, and aneurysm height (H) for the isotropic material model. Modeling AAA biomechanics using the isotropic material model reported by Raghavan and Vorp [5] has the added clinical advantage of being previously used to discriminate between ruptured and unruptured AAAs [1,2,11]. However, biaxial tensile testing of AAA tissue specimens corroborated the anisotropic characteristics of the aneurysm wall [20], which we previously accounted for in the postulation of a hyperelastic, anisotropic constitutive equation [6]. Therefore, from a biomechanical viewpoint, the estimation of an anisotropic AAA wall stress distribution is a more accurate depiction of the true state of stress of the aneurysm. The decrease in PWS observed for the second follow-up date indicates that maximum diameter alone does not predict the relative state of stress of an aneurysm. Moreover, other geometric features such as ILT volume, which decreased at the second follow-up (see Table 2), may play a key role in the ensuing PWS.

Prior work also suggests that maximum diameter alone does not provide sufficient information to assess the risk of rupture, as it does not offer an assessment of the amount of aortic dilation [21]. The native aorta of each individual varies in size, with women typically having smaller AAAs than men, but with rates of rupture up to five times greater. This suggests that the aortic dilation may be greater in females who have the same maximum diameter as their male counterparts, but smaller native aortas. The diameter to diameter ratio (DDr), which is the ratio of maximum diameter to proximal neck diameter, may provide an assessment of the amount of aortic dilation. Cappeller et al. [10] confirmed that a reasonable threshold for elective repair and rupture risk prediction is 2.2 < DDr ≤ 3.3, and more recently DDr > 2.5 [21]. Given this threshold, our patient would have been deemed at a high risk of rupture at the fourth follow-up.

The work presented herein is limited to a single AAA patient that underwent watchful waiting before exhibiting a contained rupture. Given the asymptomatic nature of AAA disease, it is unlikely that many subjects with a history of six CT exams prior to repair can be studied in a retrospective analysis of existing records. Nevertheless, validation of our findings related to the correlation of PWS with geometric features can be accomplished with a prospective study based on patient recruitment at an early stage of the disease when the aneurysm is perceived to be “small”.

Conclusion

Estimated by means of finite element analysis using an anisotropic constitutive material model for the AAA wall, peak wall stress is significantly correlated with maximum aneurysm diameter, sac volume, and maximum diameter to proximal neck diameter ratio, for a single aneurysm closely followed during a surveillance period spanning 28 months. The final CT scan during the surveillance period yielded a FEA model with the highest peak wall stress of the six models analyzed. The correlation of wall mechanics with geometry is nonlinear and reveals that peak wall stress does not necessarily increase directly proportional to aneurysm diameter.

APPENDIX

1-D Size Indices

Nomenclature	Name	Equation
D max	Maximum diameter
D neck, d	Distal neck diameter	$D_i=\frac{4A_i}{P_i}$
D neck, p	Proximal neck diameter
H	Height of AAA
L	Length of AAA centerline
H neck	Height of neck
L neck	Length of neck centerline
H b	Bulge Height
d c	Centroid distance of D max
C max	Maximum Compactness
C max	Minimum Compactness	$C_i=\frac{P_i^2}{4\pi A_i}$
C ave	Average Compactness

The maximum diameter (D_max) was measured using both a plane in the axial direction and a plane perpendicular to the vessel's centerline. A _i is the cross-sectional area and P _i is the perimeter of the same cross section, for every i ^th cross section along the centerline. The centerline is derived based on the method described in Choi et al. [18] All diameter measurements refer to the diameter assessed with the outer wall boundary.

2-D Size Indices

Nomenclature	Name	Equation
DHr	Diameter-Height ratio	$\mathit{DHr}=\frac{D_{\mathit{max}}}{H}$
DDr	Diameter-Diameter ratio	$\mathit{DDr}=\frac{D\hspace{1em}\mathit{max}}{\mathit{Dneck},\hspace{1em}p}$
Hr	Height ratio	$\mathit{Hr}=\frac{H}{H_{\mathit{neck}}}$
BL	Bulge location	$\mathit{BL}=\frac{H_b}{H}$
B	Asymmetry	$\beta =1\frac{d_c}{-D_{\mathit{max}}}$
T	Tortuosity	$T=\frac{L}{d}$ *

^* d is the Euclidean distance from the centroid of the cross section where D _neck, p is located to the centroid of the cross section at the AAA distal end.

3-D Size Indices

Nomenclature	Name	Equation
V	AAA Volume
S	AAA Surface Area	N/A *
V ILT	Intraluminal thrombus volume
γ	AAA sac to ILT volume ratio	$\gamma =\frac{V_{\mathit{ILT}}}{V}$

^*These features are computed by fitting a triangular mesh to the outer wall surface topology and generating a tetrahedral volume mesh for the ILT. The same surface meshes are used to compute second-order curvature based indices, as described below.

3-D Shape Indices

Nomenclature	Name	Equation
IPR	Isoperimetric Ratio	$\mathit{IPR}=\frac{S}{V^{2/3}}$
NFI	Non-fusiform Index	$\mathit{NFI}=\frac{\frac{S}{V^{2/3}}}{\frac{S_{\mathit{fusiform}}}{V_{\mathit{fusiform}}^{2/3}}}=\frac{\mathit{IPR}}{{\mathit{IPR}}_{\mathit{fusiform}}}$

An idealized fusiform aneurysm, based on the patient-specific neck diameter, maximum AAA diameter and height of the aneurysm sac, was modeled using Eq. (1) by Finol and Amon [22] to compute V _fusiform and S _fusiform.

$$\begin{array}{c}\multicolumn{1}{c}{f_{\mathit{FUSIFORM}}(z)=\left(\frac{D_{\mathit{max}}-D_{\mathit{neck}2}}{4}\right)[1+\mathit{sin}(\frac{2\pi z}{H}-\frac{\pi }{2})]+\frac{D_{\mathit{neck}2}}{2},\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}0\le z\le H}\end{array}$$ (1)

Second Order Curvature Based Indices

Nomenclature	Name	Equation
GAA	Area averaged Gaussian curvature	$\mathit{GAA}=\frac{\sum _{\mathit{all}\hspace{1em}\mathit{elements}}{K}_j{S}_j}{\sum _{\mathit{all}\hspace{1em}\mathit{elements}}{S}_j}$
MAA	Area averaged Mean curvature	$\mathit{MAA}=\frac{\sum _{\mathit{all}\hspace{1em}\mathit{elements}}{M}_j{S}_j}{\sum _{\mathit{all}\hspace{1em}\mathit{elements}}{S}_j}$
MLN	L2 norm of the Mean curvature	$\mathit{MLN}=\frac{1}{4\pi }\sqrt{\sum _{\mathit{all}\hspace{1em}\mathit{elements}}(M_j^2{S}_j)}$

The curvature indices are computed from the triangular surface meshes. Two principal curvatures, k ₁ and k ₂, are computed to determine the Mean (M) and Gaussian curvatures (K) for each node, as defined in Eqs (2) and (3):

$$M=\frac{k_1+k_2}{2}$$ (2)

$$K=k_1{k}_2$$ (3)

K _j and M _j are the Gaussian and Mean curvatures associated with the jth triangular shell of the surface mesh, defined as the average curvatures computed on the three shell nodes, and S _j is the surface area of the jth triangular shell.

Wall Thickness Indices

Nomenclature	Name	Equation
t w, max	Maximum wall thickness
t w, min	Minimum wall thickness
t w, ave	Average wall thickness	N/A *
t w, Dmax_ave	Average wall thickness at D max

^*Thickness was computed with respect to the axial plane as well as a plane perpendicular to the centerline. The average thickness was found by taking the mean of the average thickness computed at each cross-section in the CT image stack, which in turn is estimated based on the spatial location of select points on the spline-fitted user generated contour during image segmentation.

Note: An extensive description of these geometric features and the mathematical derivation of the equations included in this supplementary material can be found in [4,8,9] where some of the indices were used to characterize the geometry of electively repaired and ruptured AAAs.