A Multiscale Approach to Modeling the Passive Mechanical Contribution of Cells in Tissues

Short abstract

In addition to their obvious biological roles in tissue function, cells often play a significant mechanical role through a combination of passive and active behaviors. This study focused on the passive mechanical contribution of cells in tissues by improving our multiscale model via the addition of cells, which were treated as dilute spherical inclusions. The first set of simulations considered a rigid cell, with the surrounding ECM modeled as (1) linear elastic, (2) Neo-Hookean, and (3) a fiber network. Comparison with the classical composite theory for rigid inclusions showed close agreement at low cell volume fraction. The fiber network case exhibited nonlinear stress–strain behavior and Poisson's ratios larger than the elastic limit of 0.5, characteristics similar to those of biological tissues. The second set of simulations used a fiber network for both the cell (simulating cytoskeletal filaments) and matrix, and investigated the effect of varying relative stiffness between the cell and matrix, as well as the effect of a cytoplasmic pressure to enforce incompressibility of the cell. Results showed that the ECM network exerted negligible compression on the cell, even when the stiffness of fibers in the network was increased relative to the cell. Introduction of a cytoplasmic pressure significantly increased the stresses in the cell filament network, and altered how the cell changed its shape under tension. Findings from this study have implications on understanding how cells interact with their surrounding ECM, as well as in the context of mechanosensation.

1. Introduction

Understanding the mechanics of biological and bioengineered tissues is difficult; unlike synthetic composite materials (e.g. laminates), tissues are comprised of different components (cells, fibrous protein networks, proteoglycans) that are distributed inhomogeneously, exhibit nonlinear mechanical behavior [1,2], and can be highly anisotropic. In particular, cells play a complex role in the mechanics of native and bioengineered tissues. In addition to a passive component of cells as inclusions within an extracellular matrix (ECM), active mechanical contributions also exist from the interactions between cells with the surrounding ECM (e.g., compaction, remodeling).

Early phenomenological and continuum modeling approaches to understand tissue biomechanics (e.g., Refs. [1,3]) considered both the cell and the matrix as continuous materials. Evolution of such models has generally involved incorporation of microstructural detail and/or cellular phenomenon to develop improved constitutive laws, e.g., models that incorporate fiber orientation distributions to capture anisotropic behavior of the ECM surrounding the cells [4–6], incorporation of “anisotropy tensors” to account for cell orientation within a tissue [7–10], or a mathematical model motivated by localized variations in the pericellular region [11,12]. In addition, multilevel finite element approaches have been used to account for tissue inhomogeneity by discretizing cells from the surrounding ECM to consider cells as separate entities [13]. While such models have had some success in predicting tissue mechanics, the lack of microstructural detail in their formulation limits their ability to explore the respective contributions and interactions between different components within a tissue. In contrast, structural approaches attempt to understand tissue biomechanics by incorporating microstructural details directly into the model to elucidate composition-structure-function relationships in biological tissues. One such model is the tensegrity approach by Ingber and coworkers [14–17], who proposed that cytoskeletal filaments and the ECM form a tensegrity structure in combination with one another. The cellular solid model considered the cytoskeletal filaments as struts forming the edges of a cubic cell that can bend and stretch under deformation [18–20]. Biopolymer models [21,22] utilize flexible polymer theories by treating the single segments of the network as wormlike chains; Boyce and co-workers extended the concept to create an eight-chain volume-averaged network model [23]. The above mentioned models, while beginning to incorporate network microstructure detail into the model formulation, contain simplified network representations that assume ordered periodicity within the network.

Research in our group focuses on developing a comprehensive model to predict the mechanical behavior of biological and bioengineered tissues via a multiscale approach, with the fibrillar components of the ECM represented as large random interconnected networks. Multiscale modeling allows integration of the microstructural details of different components into the modeling framework; hence capturing better the structural and mechanical complexities that exist in a tissue, and relating structure and mechanics on the microstructural level to overall tissue mechanics at the macroscopic level. Recent efforts in extending this model have focused on the ECM, with the fibrous material (e.g. collagen) represented by a fiber network and other nonfibrous components (e.g. proteoglycans) represented as a solid Neo-Hookean material. This framework has been successfully used to model tissues and tissue equivalents, e.g., arteries [24], collagen–agarose cogels [25,26], as well as model tissue damage [27]. A significant gap in this model, however, is the absence of cells, which are integral components in most tissues. The current work represents an improvement of the multiscale model via the addition of cells, and investigates the passive mechanical contribution of cells to overall tissue mechanics. As such, it constitutes an extension of our early study on passive cellular contribution based on Hashin's solution [28] for a composite of rigid inclusions in a homogeneous, linear, and isotropic elastic matrix.

2. Materials and Methods

2.1. Multiscale Model Formulation.

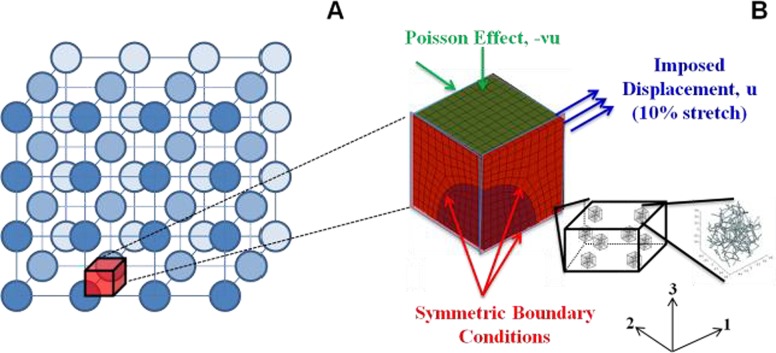
Cells were modeled as dilute, noninteracting spherical inclusions embedded within a fibrous ECM network. Cells were assumed to be dilute and noninteracting, such that they could be considered as organized in a periodic lattice (Fig. 1(a)). As such, a simplified mesh geometry containing a sphere in a box was sufficient to describe the cell-matrix system. Finite element mesh generation was performed in abaqus (Dassault Systèmes Americas Corp., Waltham, MA); the cell was represented by an eighth of a sphere contained within a cube, with three symmetry planes as shown in Fig. 1(b). Three mesh geometries, corresponding to 5, 10, and 15% cell by volume, were created. For each case, tensile tests of up to 10% stretch in the 1 direction were simulated by imposing displacement of 0.5% stretch per step on the positive 1 face over 20 steps; stress free boundary conditions were prescribed on the positive 2 and 3 faces by allowing compaction on these faces (Fig. 1(b)).

Fig. 1.

(a) Schematic representation of cells within a tissue organized in a periodic lattice, based on the assumption that cells are dilute, noninteracting, and spherical in shape. (b) Finite-element mesh showing boundary conditions and three symmetry planes. In the multiscale formulation, each Gauss point in every element is associated with a unique representative volume element (RVE) comprised of a random, interconnected network.

Our multiscale model couples the macroscopic scale (i.e. finite element mesh representing the tissue level) with the microscopic scale (representing the fibrous ECM network) via volume averaging; a summary of the methodology is described here, with more detailed description found in Refs. [29,30]. Briefly, each of the eight Gauss points in every element is associated with a unique representative volume element (RVE) comprised of a network of randomly oriented fibrils (Fig. 1(b)), with the fibrils interconnected at crosslinks represented by freely rotating pin joints. Initial guesses for the displacements of each RVE boundary are determined by linear interpolation of the nodal displacements to every Gauss point within the element; in turn, these nodal displacements are determined by the imposed macroscopic boundary conditions as described in Fig. 1(b). Force balances within each RVE are solved instead of a constitutive equation at each Gauss point. At static equilibrium, the vector sum of forces exerted by fibrils connected at each crosslink is zero, and the macroscopic (averaged) RVE Cauchy stress tensor, ${\sigma }_{\mathit{ij}}^{\mathrm{macro}}$, can be computed by the forces exerted by the fibrils on the RVE boundaries

$${\sigma }_{\mathit{ij}}^{\mathrm{macro}}=\frac{1}{V}{\int }_V{\sigma }_{\mathit{ij}}^{\mathrm{micro}}\mathit{dV}=\frac{1}{V}\sum _{\genfrac{}{}{0ex}{}{\mathrm{boundary}}{\mathrm{crosslinks}}}{x}_i{F}_j$$ (1)

where V is the RVE volume, x_i is the ith component of the coordinate where the fibril intersects the boundary, and F_j is the jth component of the force acting on the boundary by the fibril. ${\sigma }_{\mathit{ij}}^{\mathrm{micro}}$ is the microscopic stress tensor of individual fibrils in the network; for a single fiber intersecting with a boundary,

$${\oint }_{\mathit{dV}}{\sigma }_{\mathit{ij}}^{\mathrm{micro}}{n}_i\mathit{dS}=F_j$$ (2)

where F_j is as defined above, and n_i is the unit normal of the boundary intersected by the fibril in question. The force exerted by each fibril, F, is governed by the exponential constitutive equation [31,32]

$$F=\frac{A}{B}(\exp \left({\mathit{BE}}_f\right)-1)$$ (3)

In the above equation, A and B are material constants for each individual fibril. The constant A is a measure of fibril stiffness, and B captures the degree of nonlinearity in mechanical behavior of individual fibrils. E_f is the fibril Green strain computed from the fibril stretch ratio, λ_f:

$$E_f=\frac{1}{2}({\lambda }_f^2-1)$$ (4)

At small strains (i.e., as λ_f  → 1), a Taylor series expansion around E_f = 0 reduces Eq. (3) to a linear elastic fibril. The components of this force in each direction (F_j in Eq. (1)) are computed by multiplying the force F (in Eq. (3)) with the respective directional cosines for each fibril. Solving the macroscopic force balance yields the following expression for the divergence of the macroscopic Cauchy Stress tensor

$${\sigma }_{\mathit{ij},i}^{\mathrm{macro}}=\frac{1}{V}{\oint }_{\mathit{dV}}({\sigma }_{\mathit{ij}}^{\mathrm{micro}}-{\sigma }_{\mathit{ij}}^{\mathrm{macro}})u_{k,i}{n}_k\mathit{dS}$$ (5)

where u_k is the RVE boundary displacement and n_k is the unit normal vector, and ${\sigma }_{\mathit{ij}}^{\mathrm{macro}}$ defined in Eq. (1); Eq. (2) allows calculation of the integral of ${\sigma }_{\mathit{ij}}^{\mathrm{micro}}$ in terms of the boundary forces. The final deformation of each RVE at each Gauss point is dependent on the solution of Eq. (5) upon convergence.

2.2. Model Specification

2.2.1. Rigid Cell.

Cells were first modeled as rigid inclusions by fixing all the nodes in the spherical region of the mesh. These simulations were motivated by our previous work on fibroblast-populated collagen gels, which compared experimental data to an analytical solution of an inclusion-based model [28]. While we acknowledge that cells are generally deformable, this set of simulations allowed for direct comparison between our multiscale model predictions and this analytical solution. Developed by Hashin, this theory of linear elastic spherical inclusions embedded in an elastic, homoegeneous, isotropic matrix gave analytical expressions for approximating the composite bulk modulus (K*) and shear modulus (G*) from material constants of the inclusion (K_p, G_p), matrix (K_m, G_m, Poisson's ratio ν_m), and volume fraction of inclusions (c). In the limit of rigid inclusions (i.e., K_p, G_p → ∞), these expressions reduce to [33]

$$\frac{K^{*}}{K_m}=1+\frac{3(1-{\nu }_m)c}{(1+{\nu }_m)(1-c)}$$ (6)

$$\frac{G^{*}}{G_m}=1+\frac{15(1-{\nu }_m)c}{2(4-5{\nu }_m)(1-c)}$$ (7)

Three different cases were considered for the surrounding ECM: (1) linear elastic material (Hookean), (2) hyperelastic material (Neo-Hookean), and (3) a network of fibers, using our multiscale model as described above. Simulations for these three ECM cases were performed with rigid cell volume fractions of 0%, 5%, 10%, and 15%. In the no cell case (i.e., 0% cell volume fraction), results for the linear elastic and Neo-Hookean matrix cases were obtained directly from their respective constitutive equations (Eqs. (8) and (9) below); for the case of the ECM containing a network of fibers, the mesh for 5% cell volume fraction was used, with all elements (including the cell elements) assigned as ECM elements. The linear elastic matrix was governed by Hooke's law

$${\sigma }_{\mathit{ij}}^{\mathrm{matrix}}=2G_m{\varepsilon }_{\mathit{ij}}+\frac{2G_m{\nu }_m}{(1-2{\nu }_m)}{\varepsilon }_{\mathit{kk}}{\delta }_{\mathit{ij}}$$ (8)

where ε_ij is the small strain tensor. These simulations were run in matlab (The Mathworks, Inc., Natick, MA) using a custom code. The form of the Neo-Hookean equation used is [24,34]

$${\sigma }_{\mathit{ij}}^{\mathrm{matrix}}=\frac{G_m}{J}(B_{\mathit{ij}}-{\delta }_{\mathit{ij}})+\frac{2G_m{\nu }_m}{J(1-2{\nu }_m)}\left(\ln J\right){\delta }_{\mathit{ij}}$$ (9)

where J is the determinant of the deformation tensor F_ij ≡ ∂x_i/∂X_j, and B_ij is the left Cauchy–Green deformation tensor given by B_ij = F_ikF_jk. For these elastic models, the matrix shear modulus was set at G_m = 4.2 kPa, similar in magnitude to the value used to model the nonfibrillar matrix of the arterial wall [24,35]. While soft tissues typically exhibit high Poisson's ratios in tension, often values greater than 1 [36–38], Eqs. (6)–(9) are governed by elasticity theory and are only valid for Poisson's ratios ranging between −1 and 0.5; as such, the matrix Poisson's ratio was set at ν_m = 0.3 for these models.

For an ECM comprising of a fibrous network, a Voronoi network of fibrils was used, generated from Voronoi tessellation about random seed points. Voronoi networks have a connectivity of four at each crosslink, similar to experimental observations of average connectivity in acellular collagen gels from confocal microscopy [39]. In addition, Voronoi networks have been used successfully to predict network mechanics in collagen gels [40]. All Voronoi networks generated contained approximately 350 fibrils; each element was assigned a unique Voronoi network (with this same network for all 8 Gauss points within that element) randomly chosen from a set of 100 different networks. Hence, all 8 RVEs in each element have the same microstructure. Three simulations were made for the case of a network of fibers, which a different pool of 100 Voronoi networks used for each run. Values for materials constants A and B were 340 nN and 2.5 respectively, obtained from previous experimental result for pure collagen gels [41]. For the Neo-Hookean and network cases, simulations were run using a 128 processor cluster at the Minnesota Computing Institute, with wall times on the order of 12 h.

2.2.2. Cell Containing Network of Filaments.

To include cell deformability, the filamentous structures on the cell were modeled using the same Voronoi networks as described above, with the same governing Eq. (3) for individual filaments. In addition, cells were assumed to be incompressible in the short term (e.g., during the duration of a tensile test). To impose incompressibility, a hydrostatic pressure term, p, was added to Eq. (1) to compute the Cauchy stress in the cell elements

$$〈{\sigma }_{\mathit{ij}}^{\mathrm{cell}}〉=\frac{1}{V}\sum _{\genfrac{}{}{0ex}{}{\mathrm{boundary}}{\mathrm{crosslinks}}}{x}_i{F}_j-p{\delta }_{\mathit{ij}}$$ (10)

where p is the (uniform) pressure in the cell. This pressure, acting similarly to a Lagrange multiplier, represents the effect of the cytosol (i.e., intracellular fluid) on the cell, and was varied to allow the cell to maintain constant total volume. Individual elements within the cell were not required to maintain volume, representing the ability of water to move within the cell but not across the cell membrane at the time scale of interest. The relative stiffness between the cell and matrix regions was changed by altering the value of the material constant A in Eq. (3):

• (a) A _cell = 340 nN, A _matrix = 3400 nN – matrix ten times stiffer than the cell
• (b) A _cell = 3400 nN, A _matrix = 340 nN – cell ten times stiffer than the matrix
• (c) A _cell = 340 nN, A _matrix = 340 nN – same stiffness for cell and matrix

Case (c) did not reduce to a simple box with fibrils of similar properties throughout because of the incompressibility of the cell region. Because of the computational cost of running these multiscale simulations, a coarser 10 vol. % finite element mesh containing 608 elements was used; mesh refinement was checked against a finer mesh containing 1812 elements, which resulted in a mean difference of less than 3% in the stress–strain response for case (c). Similar to the rigid cell case with the ECM represented by a network of fibers, each element contained a unique Voronoi network randomly selected from a pool of 100 different networks; for each case, three simulations were run using a different pool for each run. To quantify the orientation of the networks, the network orientation tensor was calculated as

$$\mathrm{\Omega }=\frac{1}{l_{\mathrm{total}}}\sum l_i\left[\begin{array}{ccc}\multicolumn{1}{c}{{\cos }^2{\mathrm{\alpha }}_{\mathrm{i}}}& \hfill \cos {\mathrm{\alpha }}_{\mathrm{i}}\cos {\mathrm{\beta }}_{\mathrm{i}}\hfill & \hfill \cos {\mathrm{\alpha }}_{\mathrm{i}}\cos {\mathrm{\gamma }}_{\mathrm{i}}\hfill \\ \multicolumn{1}{c}{\cos {\mathrm{\alpha }}_{\mathrm{i}}\cos {\mathrm{\beta }}_{\mathrm{i}}}& \hfill {\cos }^2{\mathrm{\beta }}_{\mathrm{i}}\hfill & \hfill \cos {\mathrm{\beta }}_{\mathrm{i}}\cos {\mathrm{\gamma }}_{\mathrm{i}}\hfill \\ \multicolumn{1}{c}{\cos {\mathrm{\alpha }}_{\mathrm{i}}\cos {\mathrm{\gamma }}_{\mathrm{i}}}& \hfill \cos {\mathrm{\beta }}_{\mathrm{i}}\cos {\mathrm{\gamma }}_{\mathrm{i}}\hfill & \hfill {\cos }^2{\mathrm{\gamma }}_{\mathrm{i}}\hfill \end{array}\right]$$ (11)

where l _total is the total length of all fibers in the network, l_i is the length of fiber i, and cos α_i, cos β_i, and cos γ_i are the directional cosines of fiber i with respect to the 1, 2, and 3 axis directions, respectively. For an isotropic network, Ω₁₁ = Ω₂₂ = Ω₃₃ = 1/3, and all off diagonal components are 0.

2.3. Statistical Analysis.

Statistical analyses were done using the commercial statistical package in origin (OriginLab Corporation, Northampton, MA). Comparisons of material properties between two groups were performed using a two tailed unpaired t-test. For multiple groups, a 1-way anova F-test, coupled with multiple comparisons using the Bonferroni procedure, was used.

3. Results

3.1. Rigid Cell.

Plots of the undeformed meshes, as well as Cauchy σ₁₁ stress distributions after 10% stretch, are shown in Fig. 2, with the rigid cell removed for clarity. As expected, higher stresses were observed with increasing cell volume in all matrix cases, as the proportion of the infinitely stiff cell component increased. Stress concentrated in the matrix at the leading edge of tension in front of the cell, where the effect of the rigid cell was most felt. The largest stresses around this leading edge were observed for the network material cases; in contrast, in the matrix-only regions above the cell, the network material exhibited lower stresses than the linear elastic and Neo-Hookean matrix cases. These results demonstrate the highly nonlinear mechanical behavior of the Voronoi networks compared to the Hookean and Neo-Hookean models: larger stresses in the matrix elements near the cell were contrasted with smaller stresses in the matrix-only region above the cell. It should be emphasized that this effect of large stress gradients within the composite arises from the degree of nonlinearity in the network model, and not from the relative stiffness of the fiber network compared to the constitutive models. Since the Hookean and Neo-Hookean models have a linear dependence on G_m, changing G_m will alter the magnitude of the stresses developed in the composite; the stress distributions, however, within the composite will be unchanged. In comparison, the high degree of nonlinearity in the network model will still produce larger differences in stresses within the composite (compared to the Hookean and Neo-Hookean models), with much higher stresses in the leading front of the cell contrasted with smaller stresses in the cell-free region above the cell. Similar stress gradients to our network model may be observed if constitutive models with higher degrees of nonlinearity are used, e.g., the Ogden model. Similarly, it is expected that increasing the fiber stiffness parameter A (in Eq. (3)) will increase the magnitude of the stresses developed, while increasing the degree of nonlinearity (parameter B) will alter the stress gradients developed within the composite.

Fig. 2.

Undeformed meshes, as well as Cauchy stress (σ₁₁) distributions after 10% strain (averaged over three runs for each), for the cases of a linear elastic matrix, Neo-Hookean matrix, and a fiber network at rigid cell volume fractions of 5%, 10%, and 15%. The rigid cells were removed for clarity. In general, larger stresses were observed with increasing cell volume fraction. Variations in cell stresses in the fiber network cases were due to the uniqueness of Voronoi networks used for each element.

This nonlinear stress–strain behavior of the network material, similar to the mechanical behavior of soft tissues [1,2], is also shown in Fig. 3. In contrast, the linear elastic and Neo-Hookean matrix cases showed relatively linear stress–strain characteristics that largely coincided with each other at all cell proportions. While lower stresses were observed in the network material composites for 0, 5, and 10% cell volume cases, rapidly increasing stress in the network material for the 15 vol. % cell case resulted in the overall composite stress overtaking the linear elastic and Neo-Hookean matrix cases at 10% strain. Unlike the smooth stress distributions in the linear elastic and Neo-Hookean matrix cases, greater variations were observed in the network matrix cases, attributed to the different Voronoi networks used for each element: slight differences in network mechanical behavior exist within the set of unique networks even though all networks had approximately the same number of fibers.

Fig. 3.

Cauchy stress σ₁₁ versus engineering strain for the linear elastic matrix, Neo-Hookean matrix, and fiber network cases at rigid cell volume fractions of 0%, 5%, 10%, and 15%. Stress–strain curves for the linear elastic and Neo-Hookean matrix cases appeared linear and largely coincided with each other. The fiber network case exhibited nonlinear stress–strain behavior, similar to that of soft tissues. Error bands in the fiber network cases are 95% confidence intervals, n = 3 for each case.

Quantitative comparisons of composite elastic modulus (E*) and Poisson's ratio between the different models are shown in Fig. 4. Comparison of these material properties for the linear elastic matrix case with the Hashin model showed close agreement at low cell proportions, with larger deviations from the Hashin solution with increasing cell volume. Consistent with the qualitative observations of the stress–strain behavior in Fig. 3, the network material exhibited a nonlinear increase in composite stiffness with cell volume (Fig. 4(a)), compared to more gradual increases for the linear elastic and Neo-Hookean matrix cases. These results were consistent with experimental data from our previous study which showed increasing stiffness in our cell-seeded collagen gel tissue equivalents with cell volume fraction [33]. Results for the composite Poisson's ratio, ν*, showed values for the network models that were larger than the elastic theory limit of 0.5 for incompressible materials (Fig. 4(b)). This observation is consistent with our previous studies using these networks [25], and is a consequence of the looseness of the Voronoi network structure which allows the ECM to collapse significantly. That the composite Poisson's ratio, ν*, decreased with increasing cell proportion for the linear elastic and Neo-Hookean matrix cases (Fig. 4(c)) was expected since the rigid cell resisted compaction. The network material case, however, did not exhibit the same decreasing trend in ν*; in fact, Fig. 4(c) indicated higher Poisson's ratios for all cell proportions compared to the matrix only (i.e. 0 vol. %) case, although the difference was only statistically significant for the 15 vol. % cell (p = 0.047).

Fig. 4.

Plots at 10% stretch of (a) composite elastic modulus E*, (b) composite Poisson's ratio ν*, and (c) composite Poisson's ratio normalized with Poisson's ratio of the matrix, ν*/ν_m, compared with the Hashin model. The * represents statistical significance at the 95% level. Model results showed close agreement with the Hashin solution at lower volume fractions. Unlike the linear elastic and Neo-Hookean matrix cases, the Poisson's ratio for the fiber network case did not decrease with increasing cell volume fraction. Error bars for the fiber network cases are 95% confidence intervals, n = 3 for each case.

3.2. Cell Containing Network of Filaments.

Figure 5 shows plots of the Cauchy stress distributions after 10% stretch for the compressible and incompressible cell cases, averaged over the three simulations for each case, with varying relative stiffness for the cell and matrix components as described in Sec. 2.2.2. Here, a compressible cell is defined as the case without an intracellular pressure. The mottled appearance of stresses in these models can be attributed to variation among the 100 networks randomly sampled for each element. This phenomenon is especially noticeable in the compressible cell case with equal stiffness values for both the cell and matrix: even though the composite is effectively comprised of Voronoi networks prescribed with the same material properties, the mottled appearance is a consequence of slight differences in mechanical behavior between the networks used in each element. Altering the relative stiffness of the cell and matrix resulted in different stress distributions in the matrix around the cell. In the case of a stiffer cell (top row), higher resistance to the macroscopic stretch from the cellular filament network caused the matrix ahead of the cell in the stretch direction to bear a larger proportion of the overall deformation; hence producing higher matrix stresses around this region compared to the cell free region above it. Conversely, in the stiffer matrix case (bottom row), the compliant cell bore a disproportionately larger amount of deformation compared to the matrix ahead of the cell, thereby relieving stress in the matrix compared to the cell-free region above.

Fig. 5.

Cauchy stress (σ₁₁) distributions at 10% stretch of the 10× stiffer cell (first row), equal cell and matrix stiffness (second row), and the 10× stiffer matrix (third row) cases, for both the compressible and incompressible cells (averaged over three runs for each case). Stress distributions around the cell differed depending on the relative stiffness of cell and matrix. In all cases, introduction of a cytoplasmic pressure to enforce incompressibility increased the stresses borne by the cell filament networks.

In all cases, incorporation of hydrostatic pressure to enforce incompressibility increased the stresses borne by the filament networks in the cell, countered by similar qualitative increases in matrix stresses directly ahead of the cell in the stretch direction, as the matrix bore a larger proportion of the overall stretch. These higher stresses in the cell networks were the result of restricted rotation of the filaments about their cross-links into the direction of stretch due to the outward pressure exerted against the cell membrane, shown qualitatively by the selected RVE plots of fiber stretches in Fig. 6(a), and quantified by the lower < Ω₁₁> values for the incompressible cell case in Fig. 6(b). The added resistance to cell deformation by the pressure consequently decreased the overall Poisson's ratio of the composite in all cases (Fig. 7), but this difference was not significant at the 95% level for the equal stiffness case. Similar to the rigid cell cases, no significant differences in ν* were observed across all cases of the compressible cell; for the incompressible cell, the Poisson's ratio for the 10× stiffer cell was significantly higher than that of the 10× stiffer matrix (p = 0.0036), and equal cell and matrix stiffness cases (p = 0.0285).

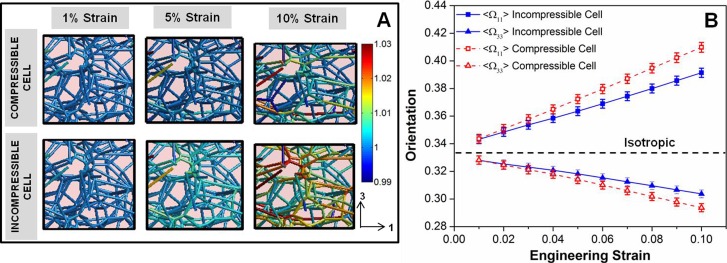
Fig. 6.

(a) Representative cell filament network at 1%, 5%, and 10% strain for the compressible and incompressible cell cases, showing the distribution of filament stretches in the networks. Larger filament stretches were observed for the incompressible cell case. (b) Average filament orientation in the 1- (Ω₁₁) and 3- (Ω₃₃) directions versus strain for the compressible and incompressible cell cases. Introduction of a cytoplasmic pressure inhibited filament rotation into the direction of stretch, such that the filaments were less oriented in the incompressible cell. Error bars are 95% confidence intervals, n = 112 (total number of cell elements).

Fig. 7.

Composite Poisson's ratio, ν*, at 10% stretch for the compressible and incompressible cell cases, with different relative stiffness of cell and matrix. The * and # represent statistical significance at the 95% level. No significant differences were observed between the different relative stiffness cases for the compressible cell. The 10× stiffer cell case had significantly higher ν* than the 10× stiffer matrix (p = 0.0036) and equal stiffness (p = 0.0285) cases for the incompressible cell. Error bars represent 95% confidence intervals, with n = 3 for each case.

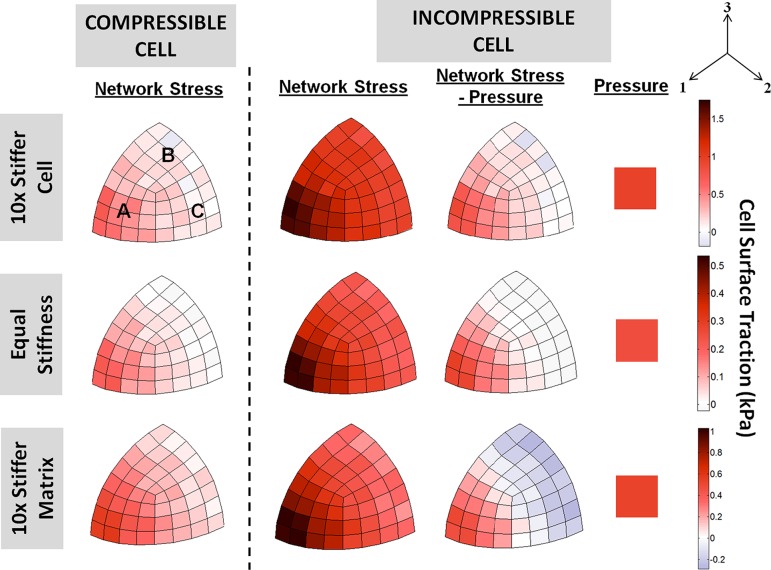
The traction on the cell surface (averaged over three runs) was plotted for both the compressible and incompressible cell in Fig. 8. The magnitude of the traction stress from the cell filament network was computed by n_in_jσ_ij, where n_i and n_j both are the unit normal to each cell surface element, and σ_ij is the averaged Cauchy stress tensor of the cell element. Similar traction stress distributions were observed for all compressible cell cases: the cell networks developed large tensile stresses in region facing the 1-direction (i.e., direction of macroscopic stretch—exemplified by region A in the 10× stiffer compressible cell), contrasted with smaller stresses in the regions facing the transverse directions (i.e. regions under the Poisson effect—regions B and C). Since the transverse surfaces were stress free, the cell regions B and C were expected to be stress free regardless of the relative stiffness between the cell and the matrix, as confirmed by model simulations using a Neo-Hookean formulation for both cell and matrix (data not shown). In the 10× stiffer cell and 10× stiffer matrix cases, however, these regions exhibited nonzero tensile stresses. This result is likely a consequence of the asymmetric mechanical behavior of these networks, which are strong in tension but very weak in compression; hence producing a net positive traction even in these transverse regions. Introduction of the cytoplasmic pressure to render the cell incompressible had the effect of increasing the tensile stresses in the networks throughout the cell. While the overall stress state of the cell (“Network Stress–Pressure” plots in Fig. 8) showed similar stress distributions to those in the compressible cell cases, addition of pressure had the effect of increasing the magnitudes of both the tensile and compressive stresses on the cell, with regions B and C now more evidently under compression, especially in the 10× stiffer matrix case.

Fig. 8.

Cell surface traction at 10% stretch of the 10× stiffer cell (first row), equal cell and matrix stiffness (second row), and the 10× stiffer matrix (third row) cases, for both the compressible and incompressible cells (averaged over three runs for each case). In the compressible cell cases, large tensile stresses were observed in the direction of tension (region A). The cell surface region under the Poisson effect (regions B and C) did not exhibit large compressive stresses. Addition of pressure increased the surface traction from the cell filament network, and slightly increased the overall compressive stress in regions B and C.

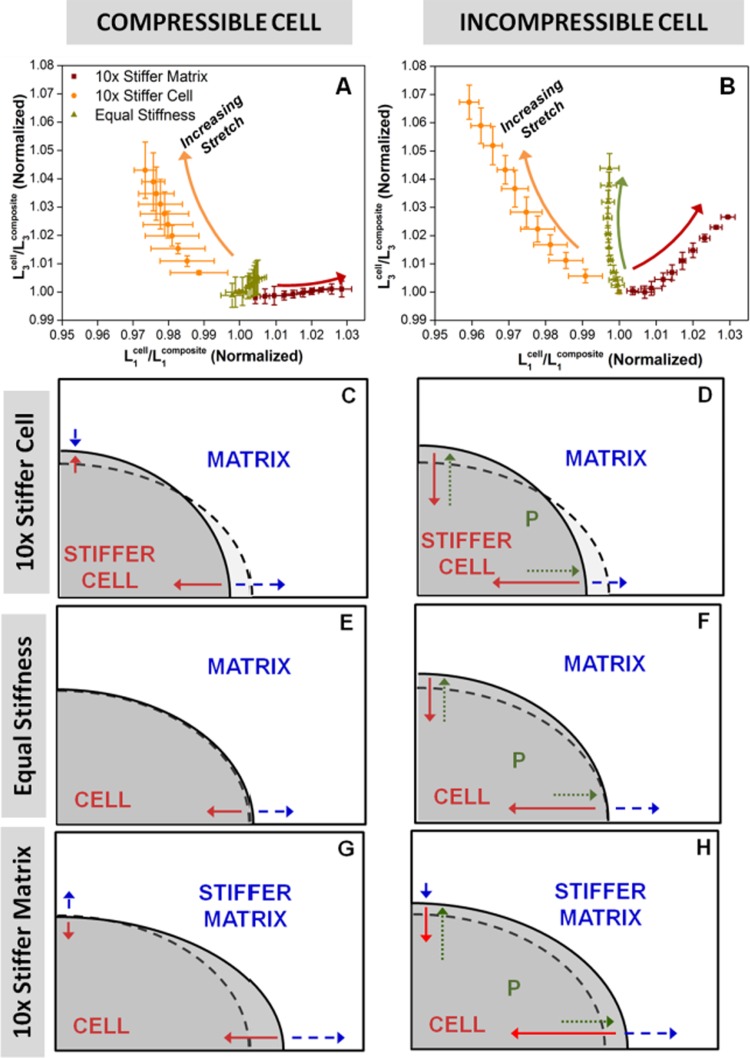
Figures 9(a) and 9(b) show dimensional changes for the cell in the 1 and 3 directions for the compressible and incompressible cell cases, respectively, with schematic drawings underneath (Figs. 9(c)–9(h)) illustrating the differences in cell shape after deformation, as well as the stresses exerted on the cell surface at static equilibrium. The normalized ratio of cell dimension to overall composite (cell + fiber matrix) dimension on either axis is a measure of the relative deformation of the cell compared to that of the overall composite. On the abscissa, a value greater than 1 means the cell stretch is greater than that of the composite in the 1-direction. Conversely, on the ordinate axis, a value greater than 1 indicates that the cell contracts less in the 3-direction than the matrix. For the compressible cell cases, the equal stiffness case exhibited little change in cell proportion in both directions under stretch, a result that was as expected. The 10× stiffer matrix case showed an increase in cell proportion in the 1-direction, but it did not predict a similar increase in cell deformation in the compressive 3-direction, a result that reinforced the idea that these networks, while strong in tension, had little compressive strength. While the 10× stiffer cell showed expected higher resistance to deformation in both directions, the above result strongly suggested that the increased resistance to compression was not due to a direct increase in cell compressive stiffness, but a consequence of lesser rotation into the direction of stretch due to increased tensile stiffness, which prevented compaction of the cell by inhibiting the collapse of the cell's filament network. In the compressible cell cases (Figs. 9(c), 9(e), and 9(g)), matrix tension in the 1-direction was always balanced by cell tension. For the stiff cell (Fig. 9(c)), the matrix pushed in on the cell, whereas for the stiff matrix, σ₂₂ was positive for the cell, indicating that the cell was being pulled out by the matrix. Enforcing cell incompressibility (Figs. 9(d), 9(f), and 9(h)) had the effect of increasing the stresses of the filamentous networks in all cases; this increase in filamentous stress was countered by the cytoplasmic pressure pushing outward against the cell surface, such that the net effect was an increase in cell dimension in the 3-direction in all cases. In the 1-direction, this pressure exerted stress on the cell surface in the same direction as the matrix in tension, but did not cause the cell to elongate in this direction in all cases; in fact, cell dimension decreased for both the 10× stiffer cell and 10× stiffer matrix cases (albeit only a slight decrease in the latter). This observation could be explained by the fact that the intracellular pressure preserves volume by resisting changes to the overall cell shape. Hence, the net effect of this pressure is that the cell bears a smaller proportion of the overall deformation in both the tensile and compressive directions (compared to the case without pressure), as shown from comparison of Figs. 9(a) and 9(b). As a result, the filamentous network develops larger tensile stresses (due to restricted rotation into the direction of stretch, shown in Fig. 6) that counters the effect of intracellular pressure working in tandem with the ECM tension.

Fig. 9.

(a)–(b): Normalized ratio of cell dimension to composite dimension in the 3-direction versus the 1-direction. Addition of pressure increased the cell proportion in the 3-direction for all cases. (c)–(h): Schematic drawings showing differences in cell shape, and the stresses exerted on the cell surface at equilibrium; dotted lines represent the equal cell and matrix stiffness case without pressure. In the compressible cell cases (c), (e), (g), matrix tension in the 1-direction was always balanced by cell tension. In the incompressible cell cases, (d), (f), (h), the outward-exerting pressure pushed out against the cell to increase cell proportion in the 3-direction.

4. Discussion

This study represented a major improvement to our multiscale model to understand soft tissue biomechanics by incorporating a major component of such tissues: cells. We acknowledge, however, that several critical assumptions were used in the model development. First, the cell matrix interface was modeled as continuous even though cells are known to attach to the matrix via discrete focal adhesions [42,43]; Guilak and Mow [12] asserted that such an assumption was not unreasonable based on experimental evidence of numerous focal adhesion points for chondrocyte attachment to its pericellular matrix from confocal and electron microscopy [44,45]. In addition, the microstructural representations of both the ECM and cell were simplified to contain only a network. In reality, the ECM is generally comprised of other biomacromolecules (e.g. proteoglycans) which exist within the network interstitium, and which alter the overall mechanics of the tissue. For the cell, this reduced representation comprised entirely of a network of cytoskeletal filaments was chosen based on studies showing that the cytoskeleton was predominantly responsible for structural integrity and stiffness in a cell [46], and hence is a reasonable first approximation for modeling the passive mechanical contribution of cells. The current model also accounts for equilibrium mechanical properties only, ignoring the viscoelastic behavior of both the cell and ECM. Nevertheless, development of this model helped gain significant insight into the cellular mechanical microenvironment, and laid the groundwork for future work incorporating further microstructural and mechanical details for the cell and ECM.

Comparison of the inclusion based model of Hashin with our finite element model results showed close agreement at low cell volume fractions; deviation at higher cell concentrations were expected since the Hashin model is only relevant at low inclusion densities. While our previous work on cell-seeded collagen gels showed close agreement of Young's modulus predicted by the Hashin model with experimental data at low cell volume fractions [33], such models are unable to generate the highly nonlinear stress–strain behavior of soft tissues. In addition, elastic theories preclude Poisson's ratios larger than 0.5, while many tissues have been shown to exhibit Poisson's ratios with values much higher than this elastic limit in tension. The ability of our multiscale network simulations to generate nonlinear stress–strain behavior (as shown in Fig. 3) and Poisson's ratios beyond the elastic limit demonstrates a more viable and accurate model for application towards soft tissue biomechanics.

The multiscale model predicted similar composite Poisson's ratios regardless of the volume fraction of rigid cell. This unexpected result suggests that the composite Poisson's ratio is dependent only on the collapse of the network in the matrix above the cell, caused by fiber rotation about their crosslinks. Across all volume fractions of rigid cell, the matrix-only region (above the cell) experiences the same amount stretch—hence the same degree of network collapse—to produce similar Poisson's ratios.

The model assumption that cells are incompressible is reasonable, validated by experimental data on single chondrocytes where an apparent Poisson's ratio of 0.49 was reported, although this value was shown to decrease with increasing axial strain [47]. Modeling the cell as compressible and incompressible, however, generally represents two extreme cases of the effect of the intracellular fluid; in reality, a cell is likely to be “moderately” compressible and dependent on the time scale of observation. In such cases, we hypothesize that our results would lie between our extreme cases of the compressible and incompressible cells. The resistance to filament rotation into the direction of stretch due to the pressure (Fig. 6) would cause the network to stretch to an intermediate extent, thereby producing stresses bounded by the current results. Similarly, the intracellular pressure would resist cell compression, though to a smaller extent than the incompressible cell case shown in Fig. 9(b).

In a tissue under tension, the tensile stress on the cell by the fibrillar matrix has the effect of elongating the cell into the direction of stretch; such changes in cell shape and alignment are similar to experimental observations of contact guidance of cells, where cells preferentially elongate with the underlying matrix fibrils aligned under stretch [48,49].

Model results from this study show complex effects of relative cell and matrix stiffness, as well as cytoplasmic pressure, on the overall cellular mechanical microenvironment, which has implications on understanding cellular mechanosensation. That cells respond differently to varying substrate stiffness has been extensively studied, in terms of various cell properties and processes such as cell attachment [50] and morphology [51], proliferation [52], stem cell differentiation [53], and migration [54]. The justification for modeling the three different scenarios for the relative stiffness between the cell and the matrix was based on experimental results on different cell types showing a wide range of cell stiffness, e.g., from ∼0.2 kPa in fibroblasts, to 42 kPa in cardiac myocytes [46]. From our previous studies, the elastic (tangent) modulus of 2 mg/mL acellular collagen gels was found to be on the order of 10 kPa [41]; compacted gels would exhibit significantly higher modulus. Hence, our three scenarios were designed to qualitatively cover a wide combination of cell types entrapped in different ECM. The current work shows that the stiffness of the matrix relative to that of the cell can also affect the qualitative and quantitative nature of strain transfer from the tissue to the cell. Even in the compressible cell case, the net transverse stress acting on a cell can be tensile or compressive depending on the relative stiffness of the cell and matrix. When the cell is incompressible, the existence of the cytoplasmic pressure can cause significant filamentous tension even in the transverse directions, which might be expected to be in compression or nearly stress free. To the best of our knowledge, there are no published experimental data on detailed stress and/or strain fields of cells entrapped in a matrix under tension, for comparison with our model predictions. Recently developed techniques, however, have the potential of quantifying cell/matrix stresses and strains in tissues under tension, e.g., measurement of three-dimensional traction forces exerted by cells entrapped in a hydrogel [55], and generation of three-dimensional strain maps of cells with their surrounding matrix [56]. The combination of these experimental techniques with computational modeling can provide a clearer picture of the cellular mechanical microenvironment in tissues. Such findings can have implications on improving tissue engineering design, in terms of providing the optimal level of mechanical signaling to promote desired growth and remodeling by the cells.