The Importance of Patient-Specific Regionally Varying Wall Thickness in Abdominal Aortic Aneurysm Biomechanics

Short abstract

Abdominal aortic aneurysm (AAA) is a vascular condition where the use of a biomechanics-based assessment for patient-specific risk assessment is a promising approach for clinical management of the disease. Among various factors that affect such assessment, AAA wall thickness is expected to be an important factor. However, regionally varying patient-specific wall thickness has not been incorporated as a modeling feature in AAA biomechanics. To the best our knowledge, the present work is the first to incorporate patient-specific variable wall thickness without an underlying empirical assumption on its distribution for AAA wall mechanics estimation. In this work, we present a novel method for incorporating regionally varying wall thickness (the “PSNUT” modeling strategy) in AAA finite element modeling and the application of this method to a diameter-matched cohort of 28 AAA geometries to assess differences in wall mechanics originating from the conventional assumption of a uniform wall thickness. For the latter, we used both a literature-derived population average wall thickness (1.5 mm; the “UT” strategy) as well as the spatial average of our patient-specific variable wall thickness (the “PSUT” strategy). For the three different wall thickness modeling strategies, wall mechanics were assessed by four biomechanical parameters: the spatial maxima of the first principal stress, strain, strain-energy density, and displacement. A statistical analysis was performed to address the hypothesis that the use of any uniform wall thickness model resulted in significantly different biomechanical parameters compared to a patient-specific regionally varying wall thickness model. Statistically significant differences were obtained with the UT modeling strategy compared to the PSNUT strategy for the spatial maxima of the first principal stress (p = 0.002), strain (p = 0.0005), and strain-energy density (p = 7.83 e–5) but not for displacement (p = 0.773). Likewise, significant differences were obtained comparing the PSUT modeling strategy with the PSNUT strategy for the spatial maxima of the first principal stress (p = 9.68 e–7), strain (p = 1.03 e–8), strain-energy density (p = 9.94 e–8), and displacement (p = 0.0059). No significant differences were obtained comparing the UT and PSUT strategies for the spatial maxima of the first principal stress (p = 0.285), strain (p = 0.152), strain-energy density (p = 0.222), and displacement (p = 0.0981). This work strongly recommends the use of patient-specific regionally varying wall thickness derived from the segmentation of abdominal computed tomography (CT) scans if the AAA finite element analysis is focused on estimating peak biomechanical parameters, such as stress, strain, and strain-energy density.

1. Introduction

Abdominal aortic aneurysm (AAA) is an irreversible, localized growth, typically in the infrarenal region of the aorta. Nearly 8% of the population above 65 years old is diagnosed with this disease [1], which has been shown to be associated with smoking history, heredity, and male gender. As it is asymptomatic, vascular surgeons may opt for surgical intervention or follow a wait-and-watch strategy if their assessment of the risk of rupture is low. Different criteria, such as maximum diameter, growth rate, wall stiffness, thickness of intraluminal thrombus (ILT), wall tension, etc., have been proposed for predicting rupture risk [2], which should be weighed against the risk of surgery, given that most AAA patients are elderly. The maximum diameter criterion is widely used in clinical practice [3], with the threshold diameter for decision making (typically 5.5 cm) following an evidence-based approach. However, an autopsy study of 473 AAA cases found that 13% of aneurysms 5 cm in diameter or smaller ruptured, whereas 60% of aneurysms of diameter greater than 5 cm did not [4]. Diameter-based rules for rupture prediction fail for 10%–25% patients in small and large AAA [5]. Hence, there is a clear need to accurately assess rupture risk on a patient-specific basis by using more rigorous, scientific means. A biomechanics-based approach can be helpful toward achieving this goal by accurately modeling the individual AAA geometry.

Wall thickness is an important geometry variable that can potentially increase the accuracy of AAA biomechanical analysis. Rupture is a local phenomenon that should be assessed by modeling spatially varying local geometry, thereby eliminating the role of globally defined criteria, such as diameter and sac volume for patient-specific rupture risk analysis. Vascular wall thickness is believed to be an influential geometric feature for biomechanical stress evaluation. From a mechanics perspective, the shape of an aneurysm and the thickness of the artery should govern dominantly the stress distribution compared to the overall size of the aneurysm [6]. Acknowledging that there are limitations inherent to image acquisition sequences and resolution, deriving accurate segmentation and geometric modeling algorithms are highlighted as open problems in computational vascular biomechanics [7]. Thickness, nonlinear material behavior, strength of the AAA wall, and the spatial distribution of these variables are said to be essential for achieving accurate finite element (FE) simulations and, therefore, also for a realistic prediction of AAA rupture risk [8,9].

Few studies report experimental measurements of aneurysmatic wall thickness [10–12,33] and with large differences in their findings, as described in Table 1. The autopsy-based observation that AAA rupture location occurs mostly on the posterior wall [4] is in agreement with the finding by Raghavan et al. [11] that wall thickness is slightly less in the posterior region compared to the anterior region. It should be noted that the severity of a posterior wall rupture is relatively less than that of an anterior wall rupture. Hence, it is more likely that posterior wall rupture cases are documented in the medical literature, since a patient with anterior wall rupture may not reach a hospital alive, thereby compounding the aforementioned observations. In a healthy aorta, the anterior wall is thicker than the posterior [10] and with a mean wall thickness of 1.39 mm [13]. The challenge of estimating regional variations of wall thickness and the subsequent incorporation in FE analysis is a complex one. Hence, the assumption of a uniform wall thickness in numerical models reported in the literature is questionable, and there is need for addressing whether the regional variations are needed on a patient-specific basis. To that end, Martufi et al. [14] reported the validation of a set of matlab routines for estimating regional vessel wall thickness from CT images by comparing it with postmortem AAA tissue measurements [11], resulting in an average relative difference of 7.8%. A framework for semiautomatic vessel wall detection and quantification of thickness using contrast-enhanced CT images was described by Shum et al. [15], resulting in low repeatability and reproducibility errors when compared to the manual segmentations performed by trained vascular surgeons. Quantitative assessment of AAA geometry [16] has shown promising results, with wall thickness being one of the morphological indicators significant for rupture risk stratification. These developments are paving the way for noninvasive, automatic geometric assessment of AAAs yielding population stratification in clinical practice.

Table 1.

Brief summary of previously reported experimental measurements on wall thickness (eAAA—electively repaired AAA; rAAA—ruptured AAA)

Authors	Year	Reported thickness (mm)	Method	Authors' comments
Di Martino et al. [12]	2006	eAAA 2.5 ± 0.1	Optical method (laser)	Thickness is inversely correlated with local strength; only anterior wall tested; use of laser measurement eliminates compression due to caliper
		rAAA 3.6 ± 0.3
mean 2.9
Raghavan et al. [11]	2006	minimum 0.23	Caliper measurement	No discernible difference in thickness for small and large aneurysm; thickness slightly lower in posterior and right walls; thickness low in ruptured aneurysm near site of rupture
		maximum 4.26
median 1.48
Thubrikar et al. [10]	2001	posterior 2.73 ± 0.46	Customized micrometer with resistivity meter	Thickness decreases from posterior to lateral to anterior walls; accuracy 0.05 mm
		lateral 2.52 ± 0.67
anterior 2.09 ± 0.51
Kazi et al. [33]	2003	w/ILT ∼(0.6 to 1.8)	Masson trichrome staining with electron microscopy	Wall region covered with ILT thinner than that without ILT
w/o ILT ∼(0.9 to 2.3)

The objectives of the present work are to establish a framework for utilizing regionally varying patient-specific wall thickness (estimated from medical images) in finite element meshes and to investigate the importance of vessel thickness in the ensuing AAA wall mechanics. We address the hypothesis that the geometrical modeling of patient-specific wall thickness results in significantly different biomechanics compared to that obtained using the assumption of uniform wall thickness. This study focuses exclusively on AAA wall-only models to avoid the complex and compounded effects of ILT shape, intraluminal pressure, and initial stresses, which also introduce patient-specific variability in the predicted mechanics. Four biomechanical parameters, namely the maxima of the first principal stress, first principal strain, strain-energy density, and displacement magnitude, are analyzed to accomplish the aforementioned objectives. To the best of our knowledge, this is the first study that incorporates regionally varying patient-specific wall thickness obtained noninvasively in an in vivo assessment of computational AAA biomechanics.

2. Methods

2.1. The AAA Subject Population.

Our study population consists of 100 human subjects with electively repaired AAAs. Existing CT images were collected as part of a retrospective study following Institutional Review Board approval at Alleghany General Hospital, Carnegie Mellon University, and The University of Texas at San Antonio. The image datasets were collected in a DICOM format with a scan size of 512 × 512 pixels, segmented, and reduced to a cohort of 28 datasets represented by an AAA maximum diameter in the range of 50–55 mm in the horizontal plane. The important imaging variables for the shortlisted cohort are summarized in Table 2. Note that these variables were constant for each individual image dataset.

Table 2.

Summary of DICOM image data for the shortlisted patient cohort (units: millimeter)

Quantity	Minimum	Maximum	Mean	Mode
Pixel spacing	0.6699	0.9511	0.7781	0.7422
Slice spacing	1.5	5.0	3.2	3.0
Max. diameter	50.00	54.75	52.36	53.78

There were three motivating factors for focusing the study on this cohort of 28 datasets with a 50–55-mm maximum diameter range. (1) Maximum diameter in this range is the commonly used norm for risk of rupture assessment in clinical practice, and aneurysm size has been positively correlated with rupture incidence [17]. Considering CT pixel sizes and the variability in image segmentation due to interobserver differences, a span of approximately 5 mm in AAA diameter was deemed appropriate for this study. Thus, the select cohort represents a group of patients for which elective repair would be recommended, due to their perceived high risk of rupture [3]. (2) From a clinical point of view, there is consensus that AAAs below 40 mm in maximum diameter are less likely to rupture and surgical intervention is not recommended unless there is an alternate reason to do so. Conversely, aneurysms larger than 60 mm are commonly recommended for immediate intervention [3]. It is the range of sizes between 40 mm and 60 mm that has been the focus of debate for clinical management, and hence, more focused research is necessary in this size range. (3) The availability of contrast-enhanced CT scans for patients with AAA diameters in the range of 50–55 mm is high, since it is at these sizes that the risk of radiation exposure is offset by the need for improved image resolution for presurgical planning purposes. Availability of CT images of larger aneurysms is scarce, since surgical intervention is recommended prior to reaching an advanced stage of growth or performed on an emergency basis if the patient becomes symptomatic.

2.2. Image Segmentation.

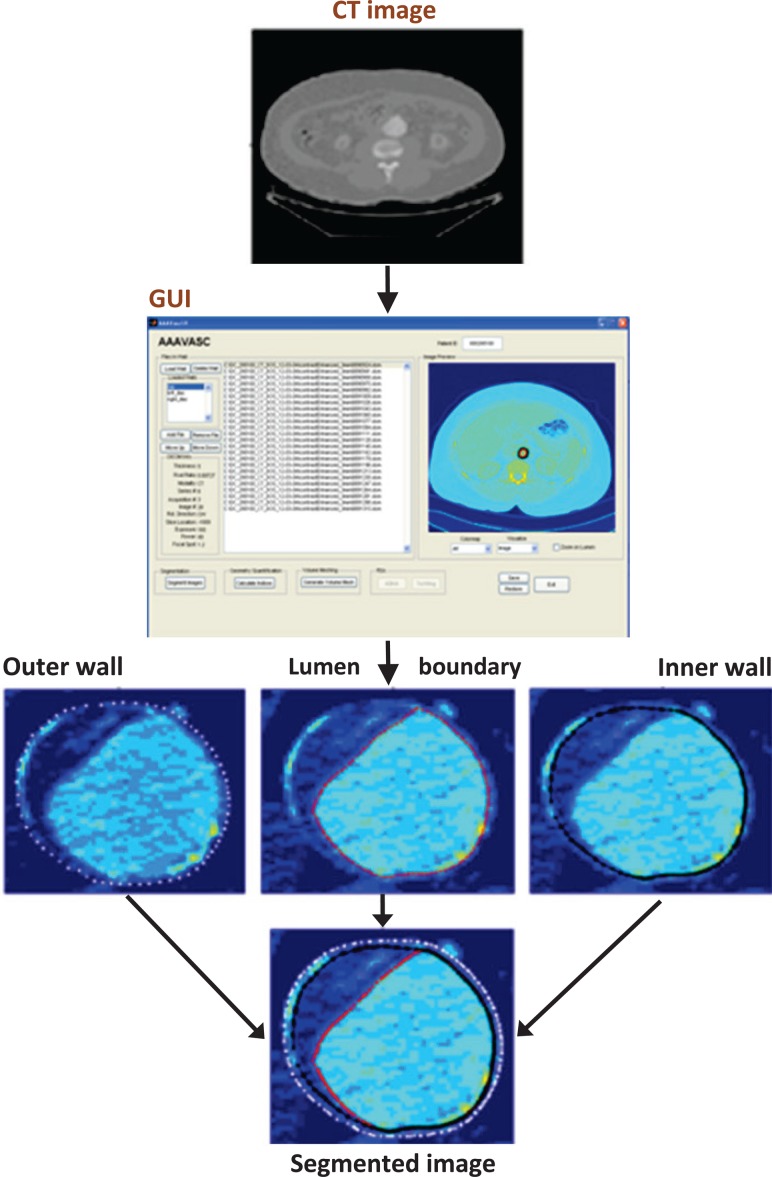
The image datasets were processed as follows. The mean diameter was 52.36 mm with a standard deviation 1.49 mm, average pixel size of 0.7781 mm, and the mode value of slice spacing 3.0 mm. CT images between the renal arteries and approximately 3 inches distal to the iliac bifurcation were segmented using our in-house matlab code VESSEG [15], shown schematically in Fig. 1. Semiautomatic algorithms in VESSEG define splines for the outer wall boundary, inner wall boundary, and lumen boundary for each image. AAA wall thickness was estimated at 72 equispaced points along the splines on every slice in the sac by calculating the minimum distance between the inner and outer splines, resulting in a point cloud of wall thickness distribution, as illustrated in Fig. 2. Reproducibility and interobserver variability assessments, reported earlier in Ref. [15], highlight the ability of the segmentation code to measure in-plane, regionally varying wall thickness. The output of the image segmentation is a 4-region binary mask composite, which is imported into an in-house finite element meshing code for spatial discretization of the geometry. The Appendix provides details on the estimated statistics of in vivo wall thickness of the AAA sac provided by VESSEG and AAAMesh.

Fig. 1.

Framework for image segmentation with capability for variable wall thickness estimation [15]

Fig. 2.

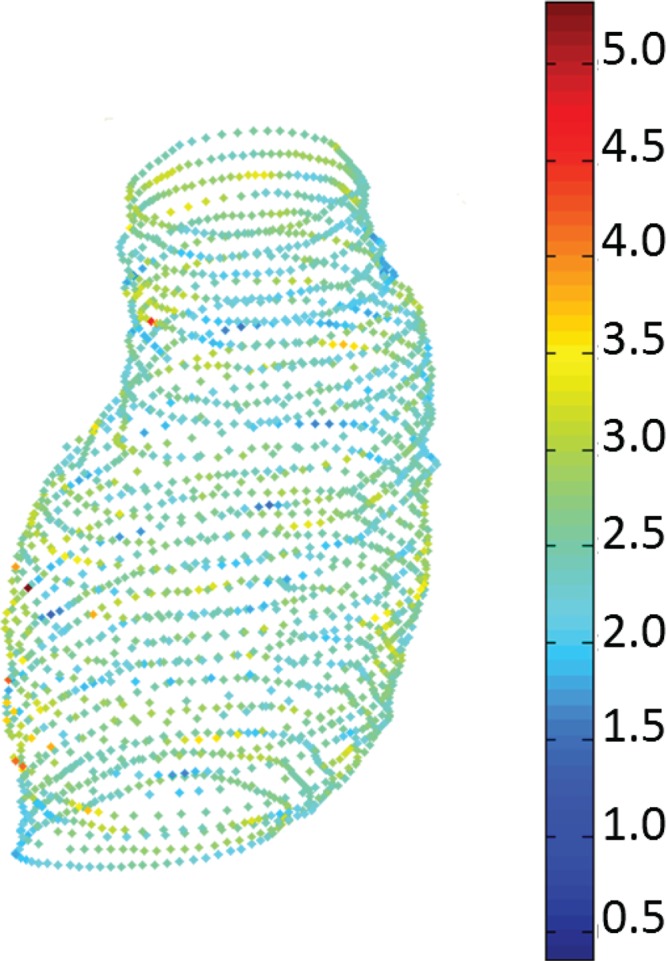
Estimated wall thickness distribution (in mm) in a point cloud resulting from a segmented CT dataset [17]

2.3. Finite Element Discretization.

The matlab-based mesh generation code AAAMesh (v1.0, The University of Texas at San Antonio, San Antonio, TX) [18,19] was employed for generating both surface and volume meshes of each image dataset. A triangular surface tessellation of the AAA outer wall boundary was created from the distance field, which in turn was derived from the binary masks output by VESSEG. The tessellation was then converted to a quadrangle tessellation, where local node normals were evaluated for all surface nodes. The surface tessellation was extruded inward along the local node normal directions to form two layers of hexahedral elements with an aspect ratio of approximately 1.0. For each of the 28 datasets, three FE meshes were generated: (i) uniform thickness model (UT)—with a uniform wall thickness of 1.5 mm; (ii) patient-specific uniform thickness model (PSUT)—with a uniform thickness equal to the patient-specific mean wall thickness obtained by averaging the spatially varying wall thickness values; and (iii) patient-specific nonuniform thickness model (PSNUT)—with patient-specific, regionally varying wall thickness. This approach yielded 84 different AAA models (three for each AAA image dataset, corresponding to each wall thickness modeling strategy in the select cohort), which were subject to FE analysis.

2.3.1. Patient-Specific Nonuniform Wall Thickness (PSNUT).

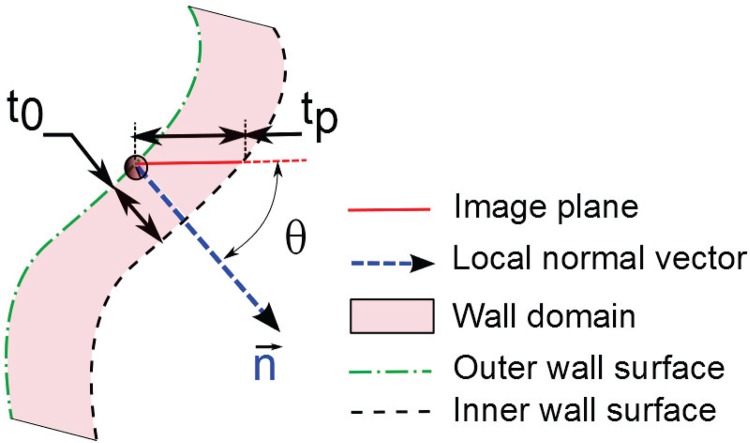
Patient-specific, regionally varying wall thickness was modeled at each node of the finite element mesh utilizing the in-plane thickness (t_p) previously estimated at 72 discrete points per CT image [15]. A correction factor was applied by multiplying t_p by the cosine of the angle θ formed by the average local surface normal at each wall thickness data point (calculated from the four nearest-neighbor surface tessellation nodes and their respective surface normal directions) and the horizontal plane to obtain the true normal thickness t ₀ (see Fig. 3), provided $\theta \le {\theta }_{\mathrm{threshold}}$ to avoid excessive thinning as $\theta \to 90\mathrm{\hspace{1em}}\mathrm{deg}$. In this work, we used ${\theta }_{\mathrm{threshold}}=53\mathrm{\hspace{1em}}\mathrm{deg}$; if $\theta >{\theta }_{\mathrm{threshold}}$, the cosine of ${\theta }_{\mathrm{threshold}}$ was used for the correction factor. A distance-weighted interpolation with four nearest-neighbor wall thickness data points was used for every surface tessellation node to calculate the individual length of surface extrusion from t ₀ defined at the data points. If any of the nearest-neighbor data points is at a distance greater than the threshold distance (i.e., d _threshold, typically set at three times the CT image spacing), it is replaced by an imaginary data point with a wall thickness value corresponding to the healthy common iliac artery wall thickness (t _iliac = 1.05 mm [13]; i.e., $\mathrm{if}\hspace{1em}\hspace{1em}\hspace{1em}{d}_i>d_{\mathrm{threshold}}\Rightarrow d_i=t_{\mathrm{iliac}}$). This strategy ensures that the wall thickness at the aortoiliac bifurcation will be consistent with common estimates available in the literature if the CT image estimated thickness was unavailable due to insufficient image resolution or excessive image noise. Hence, among p neighboring thickness data points considered, if d_k and $t_k^0$ denote the distances of the kth nearest neighbor and the corresponding cosine-corrected thicknesses, the weights are given by

Fig. 3.

Schematic of cosine correction for mesh extrusion

$$w_k=\frac{1}{d_{k}S}$$ (1)

where $S=\sum _{i=1}^p\frac{1}{d_i}$. The distance interpolated thickness (t ₁) is given by

$$t_1=\sum _{k=1}^p{w}_k{t}_k^0$$ (2)

with p = 4. To ensure a smooth transition of thickness from the aneurysm sac to the common iliac arteries, a weighted interpolation thickness strategy was applied for the surface nodes located within a height z_w of the aortoiliac bifurcation. This strategy was based on the distance δ_z of the surface tessellation node under consideration with respect to the last CT image with known wall thickness data points, as given by Eq. (3). The nodal wall thickness in this transition region approximates the mean thickness of the last CT image, t_m, as the node is closer to it,

$$t_2=\frac{{\delta }_z}{z_w}{t}_1+(1-\frac{{\delta }_z}{z_w})t_m$$ (3)

where t ₂ = t ₁ for all other surface tessellation nodes that are not in the transition region.

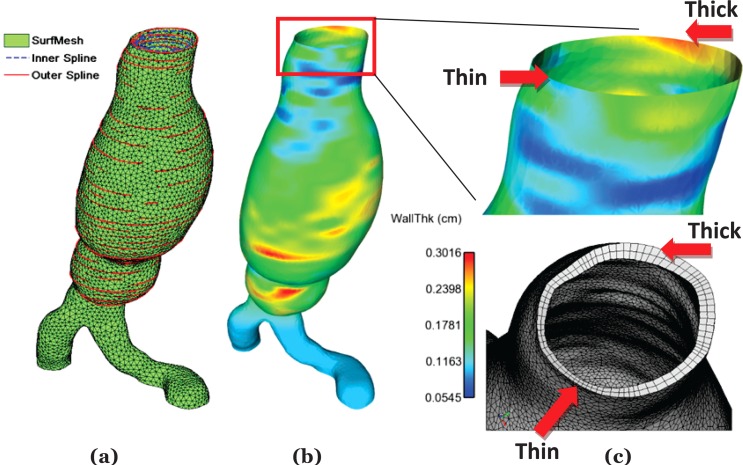
Twenty-seven-noded hexahedral elements were generated by assembling the extruded and original surface nodes. Using an exemplary AAA case, Fig. 4 illustrates the intermediate steps followed to generate regionally varying wall thickness, a qualitative comparison of thickness distribution, and the final mesh after surface extrusion.

Fig. 4.

Intermediate steps in wall thickness implementation and qualitative assessment with final mesh; (a) superposition of splines and surface mesh; (b) interpolated wall thickness; (c) qualitative assessment of thickness modeling by comparing interpolated thickness distribution and final FE volume mesh

2.3.2. Material Model.

Raghavan and Vorp [20] characterized the material properties of the aneurysmatic abdominal aorta based on 69 tissue specimens. It was observed that the strain energy function was dependent only on the first invariant of the left Cauchy–Green deformation tensor. Hence, as a special case of the generalized power law neo-Hookean hyperelastic material model, the following constitutive equation was proposed:

$$W=c_1(I_1-3)+c_2{(I_1-3)}^2$$ (4)

where W is the strain energy function (SEF), I ₁ is first invariant of the left Cauchy–Green tensor, and c ₁ and c ₂ are material coefficients determined, experimentally yielding the following population averages: c ₁ = 17.4 N/cm² and c ₂ = 188.1 N/cm². This SEF was implemented in the present work with nearly incompressible material properties.

Biological tissues have a large water content, which justifies the use of an incompressibility constraint. With a far lower shear modulus, the bulk modulus-to-shear modulus ratio in soft tissues is large, posing a challenge for numerical stability of the Finite Element Analysis (FEA) model. Hence, the AAA wall is modeled as slightly compressible (Poisson ratio, ν = 0.499) and the following three modifications are introduced in the SEF by the solver ADINA [21,22]: (1) substituting for the invariants I ₁, I ₂, and I ₃, the reduced invariants J ₁, J ₂, and J ₃ are given by $J_1=I_1{I}_3^{-(1/3)}$, $J_2=I_2{I}_3^{-(2/3)}$, and $J_3=I_3^{(1/2)}$; (2) removing the condition I ₃ = 1; and (3) adding the volumetric strain energy density $W_v=(1/2)\kappa {(J_3-1)}^2$, where κ is the bulk modulus. Pressure is separately interpolated by implementing the mixed u-p formulation.

2.4. Finite Element Analysis.

The wall domains reconstructed from the 28 AAA medical image datasets and meshed with 27-noded hexahedral elements were simulated using the commercial FEA solver ADINA (ADINA R&D, Watertown, MA, v8.8.3), which solves the force equilibrium, constitutive, and strain compatibility equations of elasticity iteratively. This analysis consists of a large displacement and large strain problem, for which the total Lagrangian formulation is used with an implicit scheme for the nonlinear quasistatic simulation [23]. A mixed interpolation (u-p) strategy is used to avoid volumetric “locking”, since the material behavior is modeled as hyperelastic and nearly incompressible. Twenty-seven-noded elements have a node at the center and are recommended for mixed interpolation formulations used with hyperelastic materials. A uniform pressure load was applied on the inner wall surface and was gradually increased from 0 mmHg to 120 mmHg in 24 equal steps. All degrees of freedom at the proximal and distal ends of the AAA model were constrained. The basic equations of static equilibrium were solved using an energy criterion with a threshold ratio of out-of-balance energy set to 0.001 for iteration convergence. Stress tensor ($\tilde{\mathbf{\sigma }}$), strain tensor ($\tilde{\mathbf{\sigma }}$), and displacement ($\overrightarrow{\mathbf{\delta }}$) data were saved at time instants corresponding to an equilibrium at 40 mmHg, 80 mmHg (state of stress at the diastolic phase neglecting the initial deformation at diastole), and 120 mmHg (stress at the peak systolic pressure neglecting the initial deformation at diastole).

A total of 28 × 3 = 84 simulations were executed, one per AAA geometry corresponding to each wall thickness modeling strategy. These were carried out on a 12-core, 96-GB RAM Dell^™ Precision T7500 workstation and a 6-core, 46-GB RAM, Dell^™ Precision workstation with Intel Xeon processors running a Linux operating system (CentOS 6.2). The computational cost of each simulation was 90 min of central processing unit time, on average, after adopting an optimized simulation execution strategy. A generalized bash command script was written to launch the simulations in sequence without user intervention and maintain output files ready for postprocessing.

Postprocessing of the ADINA output files was performed with ensight (Computational Engineering International Inc., Apex, NC, v10.0.2 d). Principal stresses (σ ₁, σ ₂, σ ₃) and principal strains (ε ₁, ε ₂, ε ₃) were derived from the locally averaged stress tensor ($\tilde{\mathbf{\sigma }}$) and strain tensor ($\tilde{\mathbf{\sigma }}$), respectively, by evaluating three eigenvalues of the corresponding tensor for every node. Strain energy density (ψ) was calculated from the stresses and strains. For the ith node, the nodal strain energy density (ψⁱ) was calculated from the principal stresses and strains, as given by Eq. (5),

$${\psi }^i=\frac{1}{2}({\sigma }_1^{\mathrm{i}}\times {\mathrm{\varepsilon }}_1^{\mathrm{i}}+{\sigma }_2^{\mathrm{i}}\times {\mathrm{\varepsilon }}_2^{\mathrm{i}}+{\sigma }_3^{\mathrm{i}}\times {\mathrm{\varepsilon }}_3^{\mathrm{i}})$$ (5)

Spatial maxima were identified for the first principal stress (σ_max = max(σ ₁)), first principal strain (ε_max = max(ε ₁)), strain energy density (ψ_max = max(ψ)), and displacement magnitude (${\mathbf{\delta }}_{\mathbf{max}}=\max (\Vert \overrightarrow{\mathbf{\delta }}\Vert )$). Both global maxima and aneurysm sac maxima were logged, since the global maxima can occur in highly curved regions near the aortoiliac bifurcation.

2.5. Mesh Sensitivity Studies.

Based on a previous uniform wall thickness analysis [24], a representative AAA model was used for mesh sensitivity studies with the aforementioned wall material model. A first study was performed with a consistent a priori guessed surface tessellation size while varying the number of layers of elements across the thickness from 1 to 7. This resulted in mesh sizes in the range of 31,884 to 223,188 quadratic hexahedral elements. The spatial maxima of the biomechanical parameters were evaluated to determine the optimal number of layers required for the wall mesh. In a second study, six different mesh densities, all with two layers of wall elements each, were created for convergence assessment. These meshes were generated by varying the average edge length of the surface tessellation (i.e., a larger edge length yields a coarser wall volume mesh), resulting in a range of 14,580 to 106,566 quadratic hexahedral elements. Thus, six FEA simulations were executed for this analysis and the incremental percentage changes of the same biomechanical parameters were calculated using the parameters of the immediate coarser mesh as a reference.

2.6. Statistical Analysis.

Statistical analysis was performed to assess the significance of the three wall thickness modeling strategies in the ensuing four biomechanical parameters. Mean ± standard deviations were calculated for each of the following: σ_max, ε_max, ψ_max, and δ_max for the UT, PSUT, and PSNUT strategies. Based on biomechanics principles, we also postulated three broad conjectures about how the expected behavior of the biomechanical parameters might depend on assumptions about the wall thickness distribution and then used the data collected from the simulations to assess the adequacy of these conjectures, which are:

• (CA) The expected behavior of all biomechanical parameters for the wall thickness strategy PSNUT is different than that for the wall thickness strategy UT

• (CB) The expected behavior of all biomechanical parameters for the wall thickness strategy PSNUT is different than that for the wall thickness strategy PSUT

• (CC) The expected behavior of all biomechanical parameters for the wall thickness strategies PSUT and UT are about the same

Assessing the adequacy of each of the aforementioned conjectures involves performing four tests of hypotheses, one for each biomechanical parameter. For example, assessing the adequacy of conjecture CA in regard to first principal stress involves testing the hypothesis $\mathrm{H}0:\mathrm{\hspace{1em}}{\mu }^{{\sigma }_{1_{\mathrm{PSNUT}}}}={\mu }^{{\sigma }_{1_{\mathrm{UT}}}}$ against the hypothesis $\mathrm{H}1:\mathrm{\hspace{1em}}{\mu }^{{\sigma }_{1_{\mathrm{PSNUT}}}}\ne {\mu }^{{\sigma }_{1_{\mathrm{UT}}}}$, where ${\mu }^{{\sigma }_{1_{\mathrm{PSNUT}}}}$ denotes the average first principal stress obtained for the wall thickness strategy PSNUT. Each of the hypotheses was tested using a paired t-test, since the biomechanical parameters were measured under different wall thickness distributions for the same group of patients. A total of 4 × 3 = 12 paired t-tests were performed, each with significance level 0.05.

3. Results

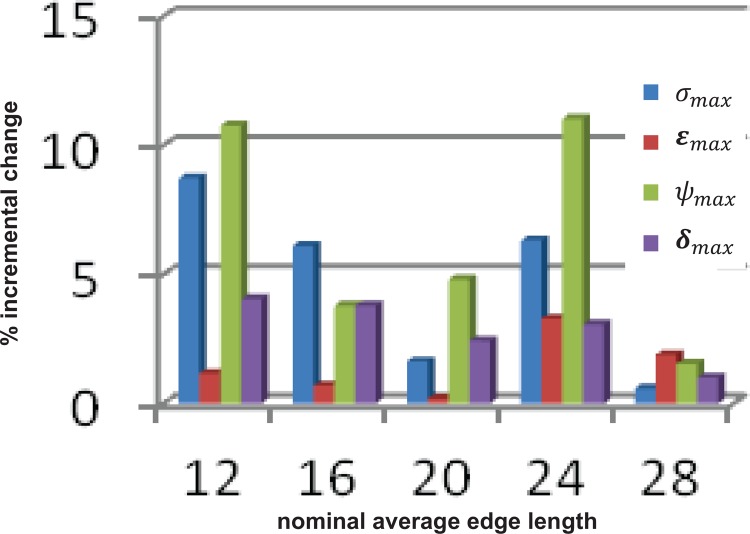
The first mesh sensitivity study, involving refinement along the thickness (extrusion) direction, resulted in reasonably minor percentage differences for all biomechanical parameters at the first level of refinement (i.e., using a two-layer volume mesh resulted in ±5% variations in these parameters compared to the one-layer mesh). Smaller relative differences were obtained, with the subsequent levels of refinement corresponding to three- to seven-layer volume meshes. Hence, the two-layer wall mesh configuration was adopted for the second mesh sensitivity study, which explored the effects of surface tessellation size on the wall mechanics. Figure 5 illustrates the percentage difference in the biomechanical parameters for each decrease in mesh size (mesh size is represented by a nominal factor indicative of the average surface tessellation edge length and decreases from right to left along the x-axis). These results indicate that a surface tessellation edge length of 16, which results in quadratic hexahedral elements of average aspect ratio of 1.0, is the optimal combination of relatively low average percentage differences in the biomechanical parameters and high mesh quality. For the reasons detailed in Sec. 4.3, a combination of an element edge length = 16 and two layers of wall extrusion was adopted for all subsequent FEA simulations, which resulted in mesh sizes in the range 43,482–89,808 quadratic hexahedral elements for the 28 AAA geometries.

Fig. 5.

Outcome of the mesh sensitivity study showing incremental percentage differences (y-axis) in the biomechanical parameters as a function of the average edge length of the surface tessellation (x-axis; a larger edge length indicates a coarser mesh). An increase in the edge length depicted along the x-axis results in a quadratic increase in the number of elements in the mesh.

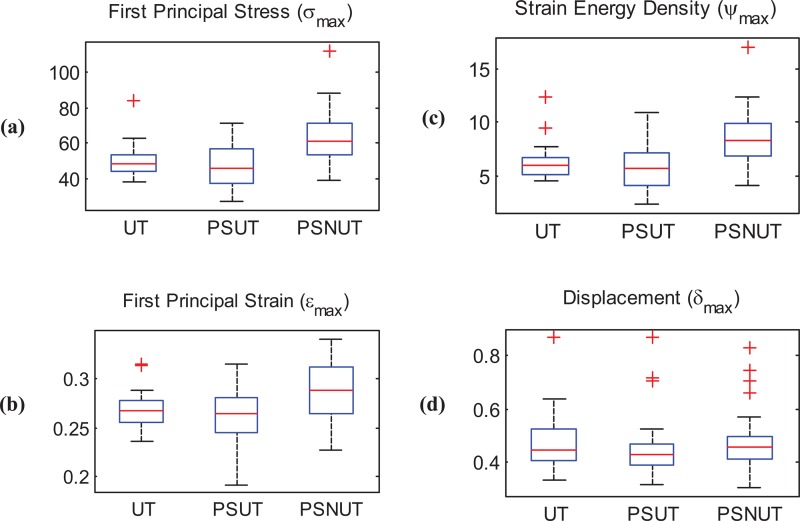
First principal stress, first principal strain, strain energy density, and displacements were analyzed to explore variability in the outcome of the 84 simulations using the UT, PSUT, and PSNUT strategies for modeling the AAA wall. Table 3 provides details on the mean and standard deviations of the maximum biomechanical parameters. Larger variability was found in the maximum first principal stress compared to variability in the maximum first principal strain, strain energy density, and displacement. These findings are represented graphically in the box-and-whisker plots of Fig. 6, the simple observation of which indicates greater differences in the maximum first principal stress compared to the other three biomechanical parameters.

Table 3.

Mean and standard deviation of the maximum biomechanical parameters for the three wall thickness modeling strategies

	σmax (N/cm2)	εmax	ψmax (erg/cm3)	δmax (cm)
UT	50.18 ± 9.45	0.2674 ± 0.0191	627,305 ± 162,427	0.4697 ± 0.1067
PSUT	47.36 ± 12.50	0.2594 ± 0.0299	674,615 ± 209,152	0.4489 ± 0.1246
PSNUT	63.56 ± 15.51	0.2870 ± 0.0290	864,754 ± 281,825	0.4738 ± 0.1256

Fig. 6.

Box-and-whisker plots highlighting differences for the three wall thickness modeling strategies; (a) maximum first principal stress (N/cm²); (b) maximum first principal strain; (c) maximum strain energy density (10⁵erg/cm³); (d) maximum displacement (cm)

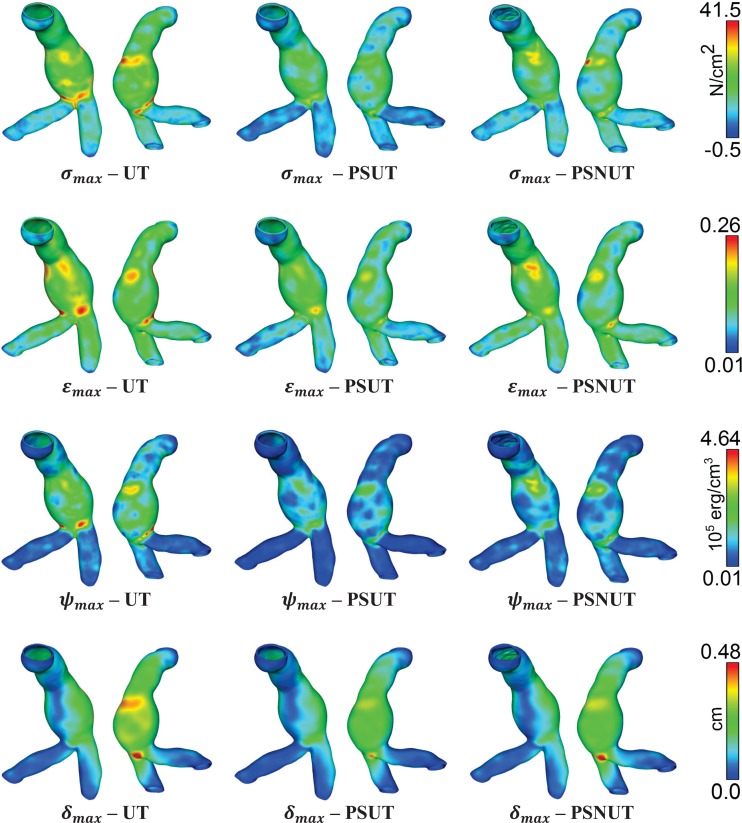
The paired t-tests indicate that the data support conjecture (CA) for the biomechanical parameters σ_max, ε_max, and ψ_max but not for δ_max, as the respective p values are 0.0002, 0.0005, 7.83e–5, and 0.773. Likewise, the tests indicate that the data support conjecture (CB), this time for all biomechanical parameters, with respective p values of 9.68e–7, 1.03e–8, 9.94e–8, and 0.0059. Finally, the tests also indicate that the data support conjecture (CC) for all biomechanical parameters, with respective p values of 0.285, 0.152, 0.222, and 0.0981. A comparative regional distribution of the four biomechanical parameters obtained by the UT, PSUT, and PSNUT strategies is shown in Fig. 7 using an exemplary AAA model.

Fig. 7.

Comparison of the regional distribution of biomechanical parameters for a representative AAA model obtained with UT—uniform thickness (0.15 cm), PSUT—patient-specific uniform thickness (0.2044 cm), PSNUT—patient-specific nonuniform thickness (0.2044 ± 0.0487 cm). σ_max—maximum principal stress, ε_max—maximum principal strain, ψ_max—strain energy density, δ_max—maximum displacement magnitude.

4. Discussion

This work represents an investigation of in vivo computational analysis of AAA biomechanics with implementation of patient-specific regionally varying wall thickness and the estimation of relative differences in biomechanical parameters when using the traditional assumption of a uniform wall thickness. It advances the field of vascular biomechanics by presenting a realistic modeling strategy for patient-specific analysis, as wall thickness is an important aspect of the vessel geometry that affects its mechanics [6]. As seen in our analysis of 28 AAA models resulting from the processing of clinical image datasets, modeling regional distributions of individual wall thickness of the AAA sac resulted in statistically significant changes in the outcome of FE analysis assessed by the maxima of at least three biomechanical parameters of interest: first principal stress, first principal strain, and strain energy density.

4.1. The Need for Modeling Nonuniform Wall Thickness.

Recently, Doyle et al. [25] inflated silicon AAA phantoms until rupture and used high-speed photography to identify the location of material failure. They note that the average thickness at the site of rupture was significantly lower than the global mean thickness, which agrees with the observation made by Raghavan et al. [11] for human ruptured AAAs. However, they further comment that the rupture location is not necessarily found at the thinnest region of the wall and that wall thickness does not correlate with the pressure required for rupture. Doyle and colleagues also note that the location of rupture was generally not at the maximum diameter. Their observations support the notion that rupture is a local phenomenon, and thus, it becomes necessary to model regional geometric variations accurately, especially wall thickness.

The outcome of the present work strongly advocates for the need to implement patient-specific nonuniform thickness modeling. Since the population sample was selected using a diameter-matched approach, this yields a size-based geometric index as the study control variable. In addition, the range of diameters is justified by the fact that all 28 patients would have been eligible for elective repair in the majority of hospitals in the U.S. Based on the analysis of the 84 simulations, the PSNUT modeling strategy results in significantly higher maximum principal stresses, principal strains, and strain energy densities compared to the UT and PSUT strategies. An average relative difference of about 20% was observed in PSUT and UT with respect to PSNUT for the three aforementioned biomechanical parameters. The difference in displacements, however, was not statistically significant. A qualitative observation of Fig. 7 indicates that, while the regional distribution of these parameters is similar for a representative AAA model, irrespective of the wall thickness approach used, their magnitudes are different.

The importance of modeling regionally varying wall thickness is in agreement with the recent report by Shum et al. [16], where wall thickness was one of the four important morphological indices that adequately discriminated between ruptured and unruptured AAAs. In that study, the statistical analysis of the morphological metrics showed that maximum diameter alone would have classified ruptured and electively repaired aneurysms with 38.2% accuracy, whereas wall thickness was one the four features used in a decision tree model that had 86.6% accuracy. The thickness estimates for the present work was previously derived by Shum and colleagues using the method described in Ref. [15], which is the only resource, to our knowledge, with the capability to assess thickness at 72 points on each CT image with low relative errors with respect to reference standards. With the segmentation capabilities of VESSEG, noninvasive quantification of AAA geometry was made possible [14,16,26], as well as the wall mechanics assessment with regional distributions of wall thickness, as described herein.

4.2. Wall Extrusion Versus Mask Dilation Approach.

We have established in our framework that volume mesh generation by means of surface tessellation extrusion is a technique inherently suitable for this purpose. A similar approach has been previously reported for AAA modeling but for a uniform wall thickness assumption [8,27]. However, outward extrusion from the inner wall surface [8,28] has the disadvantage that bifurcations exhibit high concavity, which limits the thickness of the extrusion to a value unrealistically small. This bifurcation challenge can be solved if we perform extrusion inwards (from the outer wall surface), representing the bifurcation region as a convex surface. Our thickness calculations were found to be robust against the variation of θ_threshold and d _threshold [19].

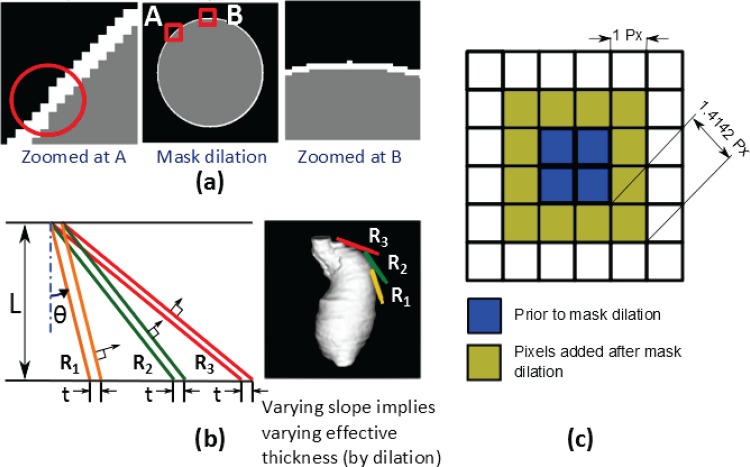
An alternative approach for image-based modeling of uniform vascular wall thickness, widely used in multipurpose image segmentation and 3D reconstruction software (e.g., SIMPLEWARE, MIMICS, AMIRA, etc.), is to use mask dilation. However, as seen in Fig. 8, there are many shortcomings of this approach. In-plane errors originate from discrepancies introduced due to the rectangular grid of the image and discrete mask dilating operations (Fig. 8(a)). Additionally, when images are stacked in 3D after dilation, the actual thickness along the local surface normal is dependent on the direction of the normal itself for given constant dilation value “t” (Fig. 8(b)). Finally, the effective in-plane dilation is varying from 1 dilation length along the grid axes to 1.4142 dilation lengths along a direction 45 deg to the axes, as seen in Fig. 8(c). These differences in wall thickness are subtle but important, as a 1-pixel error may yield a significantly different wall geometry, given that the typical wall thickness of the abdominal aorta is about 1.5–2.0 mm, while the size of 1 pixel on a CT image is about 0.75 mm. Therefore, a discrete error of 1 pixel yields a local difference of ∼40% in wall thickness. These errors may also have implications for the accurate and robust execution of the subsequent mesh generation operations, as it may result in an unrealistic intersection of the inner and outer wall surfaces. Additionally, intermediate surface-smoothing actions may distort the actual wall thickness of the final volume mesh. Hence, mask operations are recommended for bulky domains, such as ILT and lumen, but not for thin walls, for which a surface extrusion operation is intrinsically appropriate.

Fig. 8.

Limitations of a mask dilation approach for wall thickness modeling; (a) errors due to inherent differences in rectangular image grid and circular shape of the anatomy; (b) effective thickness along the local normal direction is a function of the slope in the plane normal to the image for the same dilation t in the image plane (L denotes the direction of image stacking); (c) schematic with 1 px dilation showing nonuniform dilation around the periphery (Px—pixel resolution)

4.3 . A Note on Mesh Convergence.

Our mesh convergence study also explains the interesting finding that a consistent improvement in simulation results is not necessarily achieved for anatomically complex geometries with ever-increasing surface mesh refinements. In Fig. 5, a low relative error for wall stress obtained with the coarsest mesh is likely due to the fact that maximum stresses typically occur at highly curved regions, especially ones with a saddle point [29]. Piecewise linear facets cannot accurately model these surface details with coarse mesh sizes. Thus, even though the relative error is small, the absolute wall stress upon which the error was calculated is not accurate. As the facet size becomes smaller in the finer meshes, these smaller features of the anatomical surface are captured from the image volume data. This is why there is a sudden increase in the relative error with further refinements. On the other hand, the normal vectors used for extrusion may come close to each other as facet size is reduced (denser surface tessellation) and are likely to yield either intruded or high aspect ratio volume elements, since the thickness of the extrusion remains the same. The aspect ratio was optimal for size 16 for an average wall thickness of 1.5 mm. Mesh refinement will also lead to deterioration of the element aspect ratio unless the number of layers across the thickness is not increased, which can occur only in discrete steps. This may explain in part why there is an increase in the relative error in Fig. 5 as the mesh is further refined.

4.4. Limitations.

The present work is focused on the development of a method to apply reliably patient-specific nonuniform wall thickness from medical images in AAA FEA simulations. It is subject to limitations that should be taken into account when extending the applicability of its findings for clinical management of AAA disease. The patient-specific data considers only 28 AAA datasets, which is a relatively small population size. The FEA simulations do not account for the presence of ILT (identified in the segmentation of the image datasets) or anisotropy of the aortic wall [30,31], nor was a growth and remodeling constitutive model considered (e.g., with elastin, collagen, and smooth muscle cell activation). Therefore, one issue that remains unaddressed is whether patient-specific regional variations in wall thickness for AAA wall adjacent to ILT would have as significant of an effect on peak wall stress or any other biomechanical end point as compared to the same FEA models with uniform wall thickness. Moreover, this work did not take into account patient-specific intraluminal blood pressure as a boundary condition, and initial stresses were ignored. Nevertheless, as noted earlier [25], AAA wall stress distributions do not change significantly with increasing internal pressure. Hence, it is inferred that the outcome of this work may still be relevant for AAA rupture risk assessment, as it is based on the comparison of wall thickness modeling strategies for the same constitutive material model and intraluminal pressure. Even though additional considerations, like anisotropy and ILT, would add more precision in patient-specific modeling targeted at individualized course of treatment, we believe that the results obtained under this controlled study are relevant on a population scale. Similarly, Fillinger et al. [32] were able to classify ruptured and unruptured cases using peak wall stress (sensitivity 94%, specificity 81%) without including ILT and wall anisotropy considerations. A limitation of the wall extrusion approach is that, for thick walls that also have large local surface curvature, volume elements are likely to intersect with each other. However, we expect the approach to be suitable for modeling most large human blood vessels. Finally, when the local surface is more or less tangential to the image acquisition planes, the segmentation becomes complex and even a small error in segmentation yields inaccuracies in the wall thickness estimation. Hence, additional work is necessary to improve image segmentation algorithms suitable for such regions.

5. Conclusions

Our in-house framework for modeling nonuniform wall thickness has been successfully implemented for AAA biomechanical analysis in a cohort of 28 patient-specific image datasets. Based on the level of significance achieved when testing the statistical hypotheses, we conclude that individual regionally varying wall thickness and its accurate implementation in numerical models should be a required feature for rupture risk analysis of AAA. A uniform wall thickness assumption, typically used in the literature, will yield statistically different stresses, strains, and strain energy densities compared to a regionally varying wall thickness model. Moreover, statistically similar wall mechanics should be expected irrespective of the uniform thickness used in the model. Maximum wall displacement, however, appears to be influenced more by global features, such as shape and size, than the local thickness variations. The proposed approach is robust and can be readily applied to any patient image data to extend the present work to cohorts belonging to other size ranges. To confirm the validity of the findings of the present work, future studies should incorporate a multilayer wall structure and the use of anisotropic material properties based on growth and remodeling theory.

Appendix

See Table 4.

Table 4.

Estimated statistics of in vivo wall thickness of the AAA sac. In-plane measured wall thickness corrected for local normal direction from 28 patient-specific AAA models (unit: cm).

Model	Min.	Mean	Std. Dev.	Max.
U001	0.028	0.189	0.060	0.481
U009	0.037	0.140	0.044	0.349
U013	0.051	0.118	0.027	0.251
U019	0.058	0.173	0.026	0.309
U020	0.078	0.191	0.048	0.405
U024	0.061	0.129	0.023	0.229
U030	0.056	0.167	0.050	0.366
U031	0.053	0.200	0.048	0.368
U032	0.055	0.122	0.026	0.265
U033	0.041	0.125	0.020	0.215
U037	0.076	0.204	0.048	0.399
U038	0.064	0.246	0.047	0.361
U043	0.065	0.227	0.057	0.350
U044	0.073	0.174	0.040	0.415
U046	0.075	0.122	0.016	0.182
U049	0.065	0.149	0.036	0.347
U051	0.064	0.166	0.026	0.348
U056	0.041	0.180	0.070	0.480
U058	0.053	0.167	0.044	0.310
U060	0.058	0.129	0.035	0.336
U061	0.059	0.188	0.063	0.390
U075	0.057	0.127	0.023	0.240
U076	0.065	0.152	0.022	0.268
U089	0.063	0.135	0.028	0.252
U101	0.050	0.211	0.059	0.609
U106	0.046	0.111	0.024	0.345
U107	0.084	0.149	0.001	0.284
U132	0.037	0.197	0.069	0.537